A Heteroclinic Bifurcation in a Motion of Pendulum: Numerical-Topological Approach

Abstract

Dynamical systems are frequently modeled by differential equations, the change in the solution structure of such systems as parameters vary is fundamental for understanding the phenomena. In this paper, we consider a system of differential equations with a parameter $\gamma$, which is understood from mechanics of a pendulum moving in the potential energy $V_\gamma (x) = \frac{x^2}{2} - \gamma \frac{x^3}{3} -\frac{x^4}{4}, \gamma > 0$. The global dynamics and the steady state of the system are analyzed. We verify and prove the existence of the heteroclinic bifurcation between two saddles of the system using numerical and topological methods.

Introduction

Dynamical systems usually represent classical mechanics using differential equations. The control theory deals with influencing the behavior of these dynamics. Recently, many studies have been conducted to explain exciting models, see [1, 2, 8, 12, 16, 17, 19, 20]. A pendulum is a motivating example, which has been studied for many centuries. The first study of the pendulum was started by Italian scientist Galileo Galilei after he watched a suspended lamp swing back and forth in 1588, he began serious investigations in 1602. Later on, French physicist Jean Foucault developed the Foucault pendulum. He used it in 1851 to show the earth’s rotation, see [4]. In 1953, Hughes studied the properties of the simple pendulum, see [15].

The pendulum system has many interesting bifurcations, see [3, 13, 22, 26, 28, 30]. In particular, we can find the heteroclinic bifurcation in many studies that have been conducted to understand the pendulum system. Dabbs and Smith in [6] used planar Melnikov techniques to determine a parameter set that preserves the coexistence of both heteroclinic and homoclinic orbits in a rotating pendulum. In [7], the nonlinear oscillations of the forced and damped rotating pendulum was explored, and the Melnikov functions due to the heteroclinic orbit was computed to reveal the transverse heteroclinic orbit. The splitting of heteroclinic orbits was accomplished in [18] by discretizing spatial or temporal derivatives in nonlinear equations that supported such solutions. According to Rabinowitz [24], there are heteroclinic orbits of autonomous Hamiltonian systems connecting two equilibria. In [29], a specific case of autonomous Hamiltonian systems was considered, and analytic methods were utilized to establish the existence of the heteroclinic orbits of discrete pendulum equation linking every two adjacent points.

Fig. 1

A pendulum in motion

In this research, we explain the construction of a motion of pendulum system in potential energy that is found in [14]. We use the combination of the numerical method and topological theorems that has been successfully applied to the existence of bifurcation in dynamical systems. In particular, we study the stability of the desired system, and we use the Maple software to show the phase portrait of before, after and at heteroclinic bifurcation where the value of the parameter $\gamma$ is approximated. Then, the Conley index theorems and Morse sets are applied to prove the existence of the heteroclinic bifurcation in the system. To make a conceptual idea of a motion of pendulum with potential energy V(x), we should understand the similarity between the bead-on-wire and the pendulum. Take a pendulum whose motion is restricted to a plane (moves in one direction), with a bob (mass m) on a string of length l, as illustrated in Fig. 1. The arc length of the pendulum is $l\theta$ (theta in radians), the velocity of the bob is $l\theta '$, and the tangential component of its acceleration is $l\theta ''$. The forces acting on the bob of a pendulum are its weight $w = mg$ (g is gravity) and the tension T of the string. Newton’s second law is one of the most important in all of physics, the vector sum of the forces F acting on an object is equal to the object’s mass m multiplied by its acceleration a as in the Eq. (1).

$$\begin{aligned} F = ma. \end{aligned}$$

(1)

Using Fig. 1 and the fact $a =l\theta ''$, the Eq. (1) can be written in terms of $\theta$ to depict the action of the pendulum as moving opposite to

$$\begin{aligned} -mg \sin ({\theta }) = ml\theta ''. \end{aligned}$$

(2)

which is equivalent to

$$\begin{aligned} \theta ''=-K \sin ({\theta }), \, \Bigl (\frac{g}{l}\Bigr ) = K. \end{aligned}$$

(3)

The Eq. (3) is second order differential equation that shows the motion of the pendulum with one variable $\theta$. In order to solve the Eq. (3), we rewrite it in first order by putting $y = \theta '$ then $y' = \theta ''$, so we get the following system of first order of differential equations

$$\begin{aligned} \begin{aligned} {\theta '}&= y, \\ {y'}&= - K \sin ({\theta }). \end{aligned} \end{aligned}$$

(4)

On the other hand, a physical particle moving without friction in a style involving only one variable x, the potential energy V(x) is introduced by a general theory in physics, which is defined by the force equation

$$\begin{aligned} mx'' = -\frac{dV(x)}{dx}. \end{aligned}$$

(5)

The one parameter mechanical system (5) is second order differential equation that can be converted to system of first order differential equations by putting $y = mx'$ then $y' = mx''$ to get the following system

$$\begin{aligned} \begin{aligned} {x'}&=m^{-1} y, \\ {y'}&= -\frac{dV(x)}{dx}. \end{aligned} \end{aligned}$$

(6)

where y represents the velocity of the particle up to a constant multiple. The solution of Eq. (5) acts almost like the x-coordinate of a bead of mass m sliding without friction on a wire whose graph is V(x) in a constant gravitational field with $g=1$. The equation $F = m a$ describes the motion of the bead with acceleration in terms of the arc length. To go over the details, let s be the arc length along the wire of a semi circular shape as shown in Fig. 2 (If s(t) describes the motion of the bead, $s''(t)$ is the acceleration), then $V(x) = -\sqrt{l^2 -x^2}$. As $x=l \sin (\theta )$, we have

$$\begin{aligned} \frac{dV}{dx} = \frac{x}{\sqrt{l^2 -x^2}} = \frac{l \sin {\theta }}{l \cos {\theta }} = \tan {\theta } \end{aligned}$$

(7)

Fig. 2

Bead on a wire of semi circular shape

Because the arc length along the wire is measured by s(x).

$$\begin{aligned} s(x) = \int _0^x \sqrt{1 + (dV/dx)^2} \end{aligned}$$

(8)

Then

$$\begin{aligned} \frac{dV}{ds} = \frac{dV/dx}{ds/dx} = \frac{dV/dx}{\sqrt{1 + (dV/dx)^2}} \end{aligned}$$

(9)

Using the fact $s''(t)= - \frac{dV}{ds}$, the force can be written as in the following

$$\begin{aligned} F = m s''(t)= -m \frac{dV}{ds} = -m\frac{dV/dx}{\sqrt{1 + (dV/dx)^2}} = -m \frac{\tan {\theta }}{\sqrt{1 + \tan ^2{\theta }}} =- m \sin {\theta } \end{aligned}$$

(10)

This implies the Eq. (11) that describes the motion of a bead on a circular wire.

$$\begin{aligned} s'' = - \sin {\theta } \end{aligned}$$

(11)

As $s = l \theta$, the Eq. (11) can be written as

$$\begin{aligned} \theta '' = - (1/l) \sin {\theta } \end{aligned}$$

(12)

which describes the motion of pendulum in Eq. (3). Thus, the analogy between the pendulum and the bead-on-wire is completed.

Back to the pendulum system, Eqs. (3) and (4) are of the proper mathematical form (5) and (6) for a mechanical system with one degree of freedom, so there exists a potential function $V(\theta )$. Combining Eqs. (3) and (5) implies that

$$\begin{aligned} \frac{dV(\theta )}{d\theta } = K \sin ({\theta }) \end{aligned}$$

(13)

Adding a perturbation term to the system of the pendulum (4) to represent friction, a physically more realistic situation. The motion of the pendulum bob obey the following equation

$$\begin{aligned} \begin{aligned} {\theta '}&= y,\\ {y'}&= - K \sin ({\theta }) -\epsilon y. \end{aligned} \end{aligned}$$

(14)

where $\epsilon$ is a friction coefficient and we have assumed that the friction is proportional to the velocity. Substitute the Eq. (13) in the Eq. (14) to get the system

$$\begin{aligned} \begin{aligned} {\theta '}&= y,\\ {y'}&= - \frac{dV(\theta )}{d\theta } -\epsilon y. \end{aligned} \end{aligned}$$

(15)

In particular, using the potential energy $V_\gamma (x) = \frac{x^2}{2} - \gamma \frac{x^3}{3} -\frac{x^4}{4}, \, \gamma > 0$ for the motion of the pendulum, $\epsilon = 0.1$, and replacing $\theta$ by x, we get the desired system

$$\begin{aligned} \begin{aligned} {x'}&= y,\\ {y'}&= -x + \gamma x^2 +x^3 -0.1 y. \end{aligned} \end{aligned}$$

(16)

Figure 3 represents the potential $V_{\alpha }(x)$. It is clear that, the parameter $\alpha$ controls the difference in height of the two peaks and the x-coordinate of the two corresponding saddles. The blue curve is for $\alpha = 0.2$, black for $\alpha = 0.14$. and red for $\alpha = 0.1$. A heteroclinic bifurcation between the two saddles of the system (16) is detected in Sects. 3 and 4 at a value of $\alpha$ closed to 0.14.

Fig. 3

Potential $V_{\alpha }(x)$ for the system (16)

This paper is organized as follows$:$ In the next section, we study the stability of the equilibria of system (16). In Sect. 3, we study the bifurcations like heteroclinic saddle connections using numerical method through Maple software. The topological method is used in Sect. 4 to detect the heteroclinic bifurcation through the Conley index technique. In conclusion section, the results of the motion of pendulum are summarized, and future work is suggested.

Steady States and Their Stability

To study the stability of the equilibria of system (16), note that its Jacobian matrix takes the form

$$\begin{aligned} J = \begin{bmatrix} 0 &{} 1 \\ 3x^2+2\gamma x -1 &{} - 0.1 \end{bmatrix}. \end{aligned}$$

(17)

The equilibria of system (16) are solutions of the equations

$$\begin{aligned} \begin{aligned} 0&= y,\\ 0&= -x + \gamma x^2 +x^3 -0.1 y. \end{aligned} \end{aligned}$$

(18)

and are given by $E_0 =(0,0)$, $E_1 = (A,0)$ and $E_2 = (B,0)$ where the values of A and B are determined in the Eqs. (19) and (20).

$$\begin{aligned} A = \frac{-\gamma + \sqrt{{\gamma }^2 +4}}{2}, \, \gamma >0 \end{aligned}$$

(19)

and

$$\begin{aligned} B = \frac{-\gamma - \sqrt{{\gamma }^2 +4}}{2}, \, \gamma >0 \end{aligned}$$

(20)

Since $\gamma > 0$, it follows that $A>0$. We notice that when $\gamma$ increases, the equilibrium point (A, 0) moves from the point (1, 0) toward the origin. In the same way, as we consider $\gamma > 0$, it follows that $B<0$, and the equilibrium point (B, 0) is moving away from the point $(-1,0)$ to the left on the x-axis, see the graph of A and the graph of B in Fig. 4.

Fig. 4

Graph of A and graph of B

The Jacobian matrix evaluated at the equilibrium point $E_0 = (0,0)$ is

$$\begin{aligned} J(E_0) = \begin{bmatrix} 0 &{} 1\\ -1 &{} -0.1 \end{bmatrix} . \end{aligned}$$

(21)

We summarize the stability of $E_0$ in the following theorem.

Theorem 2.1

The equilibrium point $E_0 = (0,0)$ is stable.

Proof

From the Jacobian matrix (21), the eigenvalues of $J(E_0)$ are

$$\begin{aligned} \left. \lambda _{1,2}\right| _{(0,0)} = \frac{-0.1 \pm i\sqrt{3.99}}{2}. \end{aligned}$$

(22)

We notice that $Re(\lambda _{1,2}) < 0$ so $E_0$ is stable. $\square$

We summarize the stability of $E_{1}=(A,0)$ and $E_{1}=(B,0)$ in the following theorem.

Theorem 2.2

The equilibrium points $E_1 = (A,0)$ and $E_{1}=(B,0)$ are saddles.

Proof

The Jacobian matrix evaluated at $E_1 = (A,0)$ is

$$\begin{aligned} J(E_1) = \begin{bmatrix} 0 &{} 1\\ 3A^2 + 2\gamma A -1 &{} - 0.1 \end{bmatrix}, \end{aligned}$$

(23)

and so the eigenvalues of $J(E_1)$ are

$$\begin{aligned} \left. \lambda _{1,2}\right| _{(A,0)} = \frac{-0.1 \pm \sqrt{-3.99+12A^2 +8\gamma A}}{2}. \end{aligned}$$

(24)

We notice from the Fig. 5 that $\left. \lambda _{1}\right| _{(A,0)} = \frac{-0.1 + \sqrt{-3.99+12A^2 +8\gamma A}}{2} > 0$ and $\left. \lambda _{2}\right| _{(A,0)} = \frac{-0.1 - \sqrt{-3.99+12A^2 +8\gamma A}}{2} < 0$, which means that $E_1$ is saddle. In the same way, we find that the eigenvalues of $J(E_2)$ are

$$\begin{aligned} \left. \lambda _{1}\right| _{(B,0)} = \frac{-0.1 \pm \sqrt{-3.99+12B^2 +8\gamma B}}{2}. \end{aligned}$$

(25)

and hence, one eigenvalue is positive and the another one is negative, see Fig. 6 which means that $E_2$ is saddle. $\square$

Fig. 5

Graph of eigenvalues at (A,0)

Fig. 6

Graph of eigenvalues at (B,0)

Numerical Approach

The heteroclinic bifurcation is a connection from $\alpha$-limit set to $\omega$-limit set, see [23]. Let $\Gamma$ be a Hausdorff topological space with flow $\varphi$, then $\omega$-limit set of a subset $Y \subset \Gamma$ is given by

$$\begin{aligned} \omega (Y):= \mathrm{Inv}\big (\overline{\varphi (Y,[0,\infty ))} \big ) = \bigcap _{t > 0 } {\overline{ \varphi (Y,[t,\infty ))}}. \end{aligned}$$

(26)

and the $\alpha$-limit set ($\omega ^*$-limit set) of a subset $Y \subset \Gamma$ is given by

$$\begin{aligned} \alpha (Y):= \mathrm{Inv}\big (\overline{\varphi (Y,(-\infty ,0])} \big ) = \bigcap _{t< 0 } {\overline{ \varphi (Y,(-\infty ,t])}}. \end{aligned}$$

(27)

In this section, we study the numerical solution of the system (16), in particular we focus on three stages

• 1. Before the heteroclinic bifurcation, this case is explained in Table 1 and Fig. 7a in which we choose $\gamma<< \gamma ^{*}$.

• 2. After the heteroclinic bifurcation, this case is explained in Table 2 and Fig. 7b in which we choose $\gamma>> \gamma ^{*}$.

• 3. We approximate $\gamma ^*$, which is the value of the parameter $\gamma$, where the heteroclinic bifurcation is happened. This case is explained in Table 3 and Fig. 7c.

Table 1 Before heteroclinic bifurcation

Table 2 After heteroclinic bifurcation

Table 3 At heteroclinic bifurcation

Fig. 7

a Before, b after and c at heteroclinic bifurcation

The parameter $\gamma$ controls the change of the solution structure in the dynamical system (16), and consequently the direction of the flow in its phase portrait is changing as the parameter $\gamma$ is varying. We use the Maple software for screening the flow in the phase portrait as $\gamma$ is growing. When $\gamma = 0.1$, the red trajectory that comes from the saddle (B, 0) is underneath the blue trajectory that comes in the saddle (A, 0) which is shown in Fig. 7a. In this situation, it is clear that the saddle (B, 0) is $\alpha$-limit set which plays as a repeller and the saddle (A, 0) is $\omega$-limit set which plays as a attractor. We can find the initial points of the colored trajectories of the solution in the Table 1. This case is known as “before heteroclinic bifurcation” which is mentioned in stage 1. In the second stage, we notice that when $\gamma = 0.2$ the red trajectory changes its position to become above the blue trajectory. This case is shown in Fig. 7b, and its initial points of the colored trajectories of the solution are illustrated in the Table 2, and it is known as “after heteroclinic bifurcation” which is pointed to in stage 2. The heteroclinic bifurcation is detected at $\gamma =\gamma ^{*} \approx 0.1414$ where the red and blue trajectories are merged. This case is happened when $\gamma$ increases, the red trajectory moves upward and the blue trajectory moves downward and they are consolidated at the value $\gamma ^*$. This bifurcation is shown in Fig. 7c, and the initial points of the colored trajectories of the solution for this stage are explained in the Table 3. This kind of bifurcation is called “heteroclinic bifurcation” which is mentioned in stage 3.

Topological Method

To investigate the existence and behavior of a system’s families of solutions, topological techniques can be combined with rigorous numerical computation. At any parameter value, the dynamical system can be represented by a Conley–Morse graph which is a directed graph with certain algebraic information (Homology groups). Changes of dynamics (at different parameter values) can be registered by changes in the Conley–Morse graphs.

In this section we state necessary definitions and theorems to detect the heteroclinic saddle connection, for more information see [5, 9,10,11, 21, 25, 27]. We use homology with coefficients in the finite field ${\mathbb Z}_2$, S will always denote an isolated invariant set and the homological Conley index of S, $CH_q(S)$, is the relative homology $H_q(N,L)$, where q is a homology index.

Definition 4.1

A pair of compact sets (N, L) is called an index pair of S where $L \subset N \subset \mathbb R^n$ if

• 1. $S = \mathrm{Inv}(\overline{N\setminus L})$, and $\overline{N\setminus L}$ is an isolating neighborhood of S in X,

• 2. L is positively invariant in N that is given $x \in L$ and $\varphi ( x,[0, t]) \subset N$, then $\varphi ( x,[0, t]) \subset L$,

• 3. L is an exit set for N that is given $x \in N$ and $t_{1} > 0$ such that $\varphi (x,t_{1}) \not \in N$, then there exists $t_{0} \in [0, t_{1}]$ such that $\varphi (x,[0, t_0] ) \subset N$ and $\varphi (x,t_{0}) \in L$.

The homotopical Conley index of S, h(S), is defined as the pointed homotopy type of the quotient space N/L. We summarize the Conley index of some basic isolated invariant sets in Table 4.

Table 4 Conley index of some basic isolated invariant sets

A partial order on a set $\mathcal {P}$ is a relation < on $\mathcal {P}$ that satisfies: if (1) $\pi < \pi$ never holds for $\pi \in \mathcal {P}$, and (2) if $\pi < \pi ^{'}$ and $\pi ^{'} < \pi ^{''}$ then $\pi < \pi ^{''}$.

Definition 4.2

Let $(\mathcal {P}, <)$ be a partially ordered set. A subset $I \subset \mathcal {P}$ is called an interval if $p< r < q$ with p, $q \in I$ implies $r \in I$. The set of intervals in < is denoted $I(<)$. Points p, $q \in \mathcal {P}$ are called adjacent if $\{p,q \} \in$ $I(<)$, i.e., $\{p,q \}$ or $\{q, p \}$ is an interval in $\mathcal {P}$.

If p, $q \in \mathcal {P}$ and neither $p < q$ nor $q < p$, then we say that p and q are noncomparable.

Definition 4.3

Let S be a compact invariant set (not necessarily isolated). A (<-ordered) Morse decomposition of S is a collection $M(S) = \{ M(p) \mid p \in \mathcal {P} \}$ of mutually disjoint compact invariant subsets of S such that if $x \in S \setminus \underset{p \in \mathcal {P}}{\bigcup } M(p)$, then there exist $q < p \quad (p, q \in \mathcal {P})$ with $\omega (x) \subset M(q)$ and $\alpha (x) \subset M(p)$, i.e., $x \in C\bigl (M(p),M(q)\bigr )$ (connection from M(p) to M(q) ).

In general, any ordering on $\mathcal {P}$ satisfying the above property is called admissible (for the flow). The invariant set M(p) is called Morse set. Moreover, if S is isolated, then each M(p) is also isolated. The flow on S defines an ordering on Morse sets and, hence a partial order $<_F$ on $\mathcal {P}$. $<_F$ is defined by setting $\pi ^{'} <_F \pi$ if and only if there exists a sequence of distinct elements of $\mathcal {P}, \pi ^{'}= \pi _{0},\ldots ,\pi _{n}= \pi$, such that $C(\pi _{j},\pi _{j-1} ) \ne \emptyset$ for each $j=1,\ldots ,n$. A subset $A \subset S$ is an attractor in S if there exists an open neighborhood U of A in S such that $A = \omega (U)$. If A is an attractor in S, the dual repeller of A in S is defined by $A^{*}:=\{x \in S \mid \omega (x) \cap A =\emptyset \}$. In the flow ordering on invariant subsets of S, we write $A <_F A^*$ to indicate that a flow comes from the repeller $A^*$ and lands at the attractor A.

Definition 4.4

Let S be an isolated invariant set (in a local flow X), and let the collection of invariant sets $\{M (p)\mid p \in (\mathcal {P}, <)\}$ be a Morse decomposition of S with admissible ordering <, then an associated connection matrix is a linear map

$$\begin{aligned} \Delta : \underset{p\in \mathcal {P} }{\bigoplus } CH_*(M(p)) \rightarrow \underset{p\in \mathcal {P} }{\bigoplus } CH_*(M(p)), \end{aligned}$$

where $\Delta (p,q): CH_*(M(q)) \rightarrow CH_*(M(p))$ is the corresponding (p, q)-component of $\Delta$ such that the following conditions are satisfied:

• 1. $\Delta$ is strictly upper triangular, so that if $\Delta (p,q) \ne 0$ implies $p < q$.

• 2. $\Delta$ is a boundary map if each $\Delta (p,q)$ is of degree $-1$ and $\Delta ^2 = 0$.

• 3. For every interval I, $CH_*(M(I)) \cong \frac{Ker \Delta (I)}{Im \Delta (I)}$.

The collection of all connection matrices of a system with a parameter $\gamma$ is denoted by $\mathscr {C}\mathscr {M}(M_{\gamma })$, where $\gamma$ is defined on some open interval.

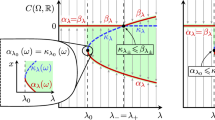
Let (X, d) be a compact metric space, and $\Lambda$ be an interval in ${\mathbb R}$. Then a parametrized family of local flows is

$$\begin{aligned} \phi :(X \times \Lambda ) \times {\mathbb R}\rightarrow X \end{aligned}$$

such that $\phi ^\lambda \mid X^\lambda = \phi \mid X \times \{\lambda \}$ is a local flow for each $\lambda \in \Lambda$.

There is a space of isolated invariant sets for the product parameterization with underlying set

$$\begin{aligned} \mathscr {S} = \mathscr {S}(\phi )= \{(S^{\lambda }, X^{\lambda })| S^{\lambda } \text {is an isolated invariant set in}\,X^{\lambda }\}. \end{aligned}$$

Theorem 4.5

[5] If $S^{\lambda }$ and $S^{\mu }$ are related by continuation and c is a path in $\mathscr {S}$ from $S^{\lambda }$ to $S^{\mu }$ then (associated to the path-homotopy class of c) there is a homotopy equivalence $\uptheta _{[c]}$: $h(S^{\lambda }) \rightarrow h(S^{\mu })$.

The homotopy equivalence $\theta _{[c]}$ induces a homology isomorphism $CH_*(S^{\lambda }) \rightarrow CH_*(S^{\mu })$.

Corollary 4.6

[10, Corollary 5.2] If c is as in Theorem 4.5, then there is an isomorphism $(\uptheta _{[c]})_*$: $CH_*(S^{\lambda }) \rightarrow CH_*(S^{\mu })$ associated to the path homotopy class of  c.

The most important property of the connection matrices is stated in the following theorem

Theorem 4.7

[11] If $\Delta \in \mathscr {C}\mathscr {M}(M), p$ and q are adjacent in the flow ordering, and $\Delta (p, q) \ne 0$, then $C\bigl (M(q), M(p)\bigr ) \ne \emptyset$.

Back to the system (16), the flow of the Fig. 7 can be depicted as in Fig. 8 where the Conley–Morse graph is used to study the changes of dynamics when the parameter $\gamma<< \gamma ^*$ and $\gamma>> \gamma ^*$.

Fig. 8

Conley–Morse graph of the flow before and after the bifurcation

The Morse sets: M(1) represents the stable equilibrium (0, 0), M(2) represents the saddle equilibrium point (A, 0) and M(3) represents the saddle equilibrium point (B, 0).

We use the connection matrix continuation theory to prove that there exists a parameter value $\gamma ^*$ such that $C\big (M_{\gamma ^*}(3),M_{\gamma ^*}(2)\big ) \ne \emptyset$. We start studying the system (16) when the parameter varies in the interval $\gamma \in (0,\gamma ^*)$, and we observe over this interval that there are two orbits from the saddles to the sink. Therefore, if $0< \gamma<< \gamma ^*$, then $\mathscr {C}\mathscr {M}(M_{\gamma })$ contains a single matrix, and it is in the form $\Delta _1$ with admissible ordering $<_1$. To find the connection matrix $\Delta _1$, let $S_1$ be the compact invariant set of the graph “Before heteroclinic bifurcation” in Fig. 8, then $S_1$ consists of the Morse sets {M(1), M(2), M(3)} and the connections {$C\big (M(2),M(1)\big )$, $C\big (M(3),M(1)\big )$}. Then a ($<_1$-ordered) Morse decomposition of $S_1$ is a collection $M(S_1) = \{ M(p) \mid p \in \mathcal {P}_1 = \{ 1,2,3\} \}$ with flow ordering $M(1) <_1 M(2)$ and $M(1) <_1 M(3)$. Then

(28)

In the matrix $\Delta _1$, we use the letter H to represent the homological Conley index such that $H_0(1)$ represents the Morse set M(1) with its Conley index $q=0$, $H_1(2)$ represents the Morse set M(2) with its Conley index $q=1$, and $H_1(3)$ represents the Morse set M(3) with its Conley index $q=1$. For example the entry $\Delta _1(1,3)$ represents $(H_0(1),H_1(3))$. We put $\Delta _1(1,2) = \, \cong$ to indicate that there is a connection orbit from $H_1(2)$ to $H_0(1)$, the same way for $\Delta _1(1,3) = \, \cong$. Also from the definition 4.4, the matrix $\Delta _1$ is strictly upper triangular, and each entry in $\Delta _1$ has degree $-1$, we must have $\Delta _1(2,3) = 0$ ( $H_1(2)$ and $H_1(3)$ are saddles so their indices are equal, see Table 4, so the degree from $H_1(3)$ to $H_1(2)$ is not $-1$, and hence $\Delta _1(2,3) = 0$, see condition two in Definition 4.4).

If $\gamma>> \gamma ^*$, we notice that $H_1(3)$ and $H_0(1)$ are noncomparable under the flow ordering, then $\mathscr {C}\mathscr {M}(M_{\gamma })$ contains a single matrix, and it is in the form $\Delta _2$ in which $\Delta _2(1,3) = 0$. In the same technique, let $S_2$ be the compact invariant set of the graph “After heteroclinic bifurcation” in Fig. 8, then a ($<_2$-ordered) Morse decomposition of $S_2$ is a collection $M(S_2) = \{ M(p) \mid p \in \mathcal {P}_2 = \{ 1,2,3\} \}$ with flow ordering $M(1) <_2 M(2)$. Then

From the Conley–Morse graphs and admissible partial orderings of the Morse sets of the “Before heteroclinic bifurcation” and “After heteroclinic bifurcation” Morse decomposition, one can compute in each case a unique connection matrix. Let $\mathscr {C}\mathscr {M}_1$ and $\mathscr {C}\mathscr {M}_2$ be the first and the second collections of connection matrices respectively represented above. Define $\gamma _i \in \{\gamma \in (0, \infty )| \mathscr {C}\mathscr {M}(M_{\gamma }) = \mathscr {C}\mathscr {M}_i\}$ for $i = 1,2$. We notice that $\gamma _1$ and $\gamma _2$ are disjoint and both nonempty. The local connection matrix continuation theorem in [10] and the connection matrix existence theorem in [11] imply that each $\gamma _i$ is open. The connection matrix continuation theory says that there exists a parameter $\gamma ^* \in (0,\infty )\setminus \{\gamma _1 \cup \gamma _2\}$ where the set of connection matrices $\mathscr {C}\mathscr {M}(M_{\gamma ^*})$ contains both matrices

$$\begin{aligned} \biggl ( \begin{matrix} 0 &{}\;\; \cong &{}\;\; \cong \\ 0 &{}\;\; 0 &{}\;\; 0\\ 0 &{}\;\; 0 &{}\;\; 0 \end{matrix} \biggr ) \quad \text {and} \quad \biggl ( \begin{matrix} 0 &{}\;\; \cong &{}\;\; 0\\ 0 &{}\;\; 0 &{}\;\; 0 \\ 0 &{}\;\; 0 &{}\;\; 0\end{matrix} \biggr ). \end{aligned}$$

(29)

$\Delta (1,3)$ is nontrivial in the first matrix, therefore $1 <_F 3$ in the flow ordering of $M_{\gamma ^*}$. We claim that $M_{\gamma ^{*}}(1)$ and $M_{\gamma ^{*}}(3)$ are not adjacent under the flow ordering. Suppose they are adjacent, then according to the computations of $\gamma _1$ and $\gamma _2$, the $\Delta (1,3)$ connection matrix entry is uniquely determined and is either an isomorphism or trivial (I.e., 0 or $\cong$). However, $\Delta (1,3)$ is not uniquely determined, and this proves the claim. This implies that $1<_F 2 <_F 3$, then $C(M_{\gamma ^*}(3),M_{\gamma ^*}(2)) \ne \emptyset$. Therefore, there is a connecting orbit at $\gamma ^*$ between the saddles $M_{\gamma ^*}(2)$ and $M_{\gamma ^*}(3)$ which is the heteroclinic bifurcation in the motion of pendulum that is described in the system (16).

The heteroclinic bifurcation was investigated in many methods for many formulas of pendulum equations, we can summarize some of these methods in the Table 5.

Table 5 Comparison of some investigation methods for the heteroclinic bifurcation in the pendulum

Conclusion

A motion of the pendulum is represented by a system of first ODE, and it has an interesting heteroclinic bifurcation, this bifurcation is detected by numerical-topological method. Combining the rigorous numerical computation to the topological method confirm the existence of the heteroclinic bifurcation in the system (16). In future work, we suggest improving the system (16) of the pendulum by modifying the friction term to detect a homoclinic bifurcation using numerical-topological method.