A Quantitative Approach to $n{\text {th}}$-Order Nonlinear Fuzzy Integro-Differential Equation

Abstract

In recent decades, both the fuzzy differential and fuzzy integral equations have attracted the researcher because the fuzzy operators produce appropriate predictions of problems in an uncertain environment. In this paper, we use fuzzy concepts to study $n^{th}$-order nonlinear integro-differential equations. For the proposed problem, through the modified fuzzy Laplace transform method, we derive the general procedure of the solution. To demonstrate the accuracy and appropriateness of the method, we present some numerical problems. We also provide graphical representation by the use of Matlab 2017 to compare the exact and approximate solution. We solve different problems having second-order, fifth-order, and a system of nonlinear fuzzy integro-differential equations through the developed scheme. We simulate the numerical results via 2D and 3D graphs for the different values of uncertainty. In the end, we provide the discussion and concluding remarks of the article.

Introduction

An integro-differential equation (IDE) is an equation that involves both the integral and differential operators of the unknown function, initially was introduced by Volterra in early 1900. Integro-differential equations (IDEs) attracted researchers due to their vast applications in social sciences, physical sciences, biological sciences, and engineering. Initially, Volterra and many other authors [1,2,3,4,5] discussed the integro-differential equations in various directions like heat flow, income distribution problem, Risk Management Analysis. However, dealing with the exact parameters is almost impossible in many real-life situations. Therefore, the researchers have worked on such cases to investigate the solution of fuzzy IDEs. Zadeh provided the basic idea of the fuzzy set in 1965 [6]. The arithmetic operations for fuzzy calculus were introduced by Prade and Dubois in 1978 [7]. Fuzzy integral equations (FIEs), fuzzy differential equations (FDEs) and fuzzy integro-differential equations (FIDEs) offer an appropriate framework for the mathematical simulation of uncertain real-world problems [42,43,44]. However, it is good to adopt various numerical techniques that formulate the numerical integration for the fuzzy integral equations that can’t be solved explicitly. Various computational techniques have been used for solving FDEs and FIEs [8,9,10,11,12,13]. In ref [14, 15], FIDEs have been used to model physical systems in a variety of ways. FIDEs are a natural technique to simulate the ambiguity of dynamic systems in a fuzzy framework. As a result, various scientific domains like physics, geography, medicine, and biology place a high value on the solution of various FIDEs. The modified Adomian decomposition method was used by Hamoud and Ghadle [16] to solve the fuzzy Volterra integro-differential equation (IDE). Hooshangian [17] suggested a solution for the fuzzy Volterra IDE of the nth-degree using a nonlinear fuzzy kernel and the extended Hakuhara derivative to turn it into a nonlinear integral equation. As a result, researchers have recently focused their efforts on developing an efficient and accurate algorithm for studying fuzzy integral equations. Many researchers have demonstrated the existence, uniqueness, and other aspects of the solution of nonlinear fuzzy Volterra and Fredholm IDEs of $n^{th}$-order under strongly-generalized differentiability [17,18,19,20]. Since physical phenomena are almost nonlinear, we’re interested in nonlinear integro-differential equations. It’s challenging to discover an approximate solution for the nonlinear integro-differential equation. The Adomian decomposition method divides the proposed problem into linear and nonlinear components in the form of a sequence, the terms of which are specified by a recursive relationship using Adomian polynomials, yielding the solution. Some basic work on different parts of the Adomian decomposition approach is included by Andrianov [24], Venkatarangan [25, 26], and Wazwaz [27]. Khuri [28, 29] proposed a modified variation of the Laplace decomposition approach. We get analytical solutions for the integro-differential equations using the Laplace Adomian decomposition method. In this work, we extend the idea of Khanlari et al. [30] in fuzzy concepts and solve nonlinear fuzzy IDEs of nth-order through modified fuzzy Laplace transform method, so we have an equation

$$\begin{aligned} \mathcal {\tilde{G}}^{(n)}(\mathcal {X},\varpi _{0})=g(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt, \end{aligned}$$

(1)

with IC: $\mathcal {\tilde{G}}^{(j)}(0,\varpi _{0})=\beta _{j};\;j=0,1,\cdots ,n-1,$ where $\mathcal {\tilde{G}}^{(n)}(\mathcal {X},\varpi _{0})$ is the $n^{th}$-order derivative of the fuzzy function and is already given, $g(\mathcal {X},\varpi _{0})$ and $\mathcal {K}(\mathcal {X},t)$ are the fuzzy functions, and $\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right)$ is a nonlinear term that appear under the integral, i.e., $\ln \left( \mathcal {\tilde{G}}(t,\varpi _{0})\right)$, $\exp \left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) ,$ and $\mathcal {\tilde{G}}^{(2)}(\mathcal {X},\varpi _{0})$ etc., $\varpi _{0}\in [0,1]$ is a fuzzy parameter, and $\gamma$ is a constant parameter. The two-variable function $\mathcal {K}(\mathcal {X},t)$ is called kernel of nonlinear fuzzy IDE and depends on variable $\mathcal {X}$ and t. $a(\mathcal {X})$ and $b(\mathcal {X})$ are known to be the limits of this fuzzy IDE. If these limits are constant, then Eq.(1) is called nonlinear fuzzy Fredholm IDE, and if one of these limits is variable, say $b(\mathcal {X})$ is variable, then this equation is said to be nonlinear fuzzy Volterra IDE. The parametric case of Eq.(1) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}^{(n)}(\mathcal {X},\varpi _{0}) &{} =\underline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\underline{\mathcal {K}(\mathcal {X},t)\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) }dt,\\ \overline{\mathcal {\tilde{G}}}^{(n)}(\mathcal {X},\varpi _{0}) &{} =\overline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\overline{\mathcal {K}(\mathcal {X},t)\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) }dt, \end{array}\right. } \end{aligned}$$

where $\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) =\left( \underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) ,\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) \right)$ and $g(\mathcal {X},\varpi _{0})=(\underline{g}(\mathcal {X},\varpi _{0}),\overline{g}(\mathcal {X},\varpi _{0})),$ with kernel

$$\begin{aligned} \underline{\mathcal {K}(\mathcal {X},t)\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) }=&{\left\{ \begin{array}{ll} \mathcal {K}(\mathcal {X},t)\underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) , &{} \mathcal {K}(\mathcal {X},t)\ge 0,\\ \mathcal {K}(\mathcal {X},t)\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) , &{} \mathcal {K}(\mathcal {X},t)<0, \end{array}\right. } \\ \overline{\mathcal {K}(\mathcal {X},t)\mathcal {F}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) }=&{\left\{ \begin{array}{ll} \mathcal {K}(\mathcal {X},t)\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) , &{} \mathcal {K}(\mathcal {X},t)\ge 0,\\ \mathcal {K}(\mathcal {X},t)\underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) , &{} \mathcal {K}(\mathcal {X},t)<0. \end{array}\right. } \end{aligned}$$

The following is how the paper was organised: The introduction and motivation for the manuscript are offered in Sect. 1. The paper’s preliminary knowledge is presented in Sect. 2. The main work of the paper is found in Sect. 3, which gives a full explanation of fuzzy nonlinear IDE of $n{\text {th}}$-order. In this section, we also present numerical simulations of the results in the form of 2D and 3D plots for various levels of uncertainty. The problem’s convergence analysis and error estimate are presented in Sect. 4. The conclusion of the paper and future work are presented in Sect. 4.

Preliminaries

This section is devoted to the basic concepts of fuzzy set theory. For more detail about fuzzy sets and fuzzy differential equations, the reader may access to [31,32,33,34,35, 42].

Definition 2.1

Let $\tilde{g}:\mathbb {R}\rightarrow [0,1]$ be a membership function, then $\tilde{g}$ is called a fuzzy number if it fulfills the following conditions

• (i) $\tilde{g}$ is fuzzy convex $\left( \tilde{g}(ky+(1-k)v)\ge \min (\tilde{g}(y),\tilde{g}(v))\,\,\forall \,k\in [0,1],\,\,y,v\in \mathbb {R}\right)$.

• (ii) $\tilde{g}$ is upper semicontinous on $\mathbb {R}$.

• (iii) $\tilde{g}$ is normal (for any $y_{0}\in \mathbb {R};\,\tilde{g}(y_{0})=1$).

• (iv) The closure of $\{d\in \mathbb {R},\,\tilde{g}(d)>0\}$ is a compact.

Definition 2.2

Let $\mathscr {R}_{\mathbb {F}}$ be the set of all fuzzy numbers with bounded $\varpi _{0}$-level intervals. If $a\in \mathscr {R}_{\mathbb {F}}$, then the $\varpi _{0}$-level set

$$\begin{aligned} {}[a]^{\varpi _{0}}=\{\mathcal {X}\in \mathbb {R}:a(\mathcal {X})\ge \varpi _{0},0<\varpi _{0}\le 1\}, \end{aligned}$$

is a closed bounded interval. The above equation can be written as

$$\begin{aligned} {}[a]^{\varpi _{0}}=[a_{1}{}^{\varpi _{0}},a_{2}{}^{\varpi _{0}}]=[\underline{a}(\varpi _{0}),\overline{a}(\varpi _{0})], \end{aligned}$$

and $\exists$ $t_{0}\in \mathbb {R}$ such that $a(t_{0})=1$.

Definition 2.3

Let $\mathcal {U}$ be a fuzzy number represented in parametric form as $[\underline{\mathcal {U}}(\vartheta ),\,\overline{\mathcal {U}}(\vartheta )]$ such that $0\le \vartheta \le 1$, and fulfills properties given below

• (i) $\underline{\mathcal {U}}(\vartheta )$ is increasing function, left continuous, bounded over (0, 1] and right continuous at 0.

• (ii) $\overline{\mathcal {U}}(\vartheta )$ is decreasing, left continuous, bounded over (0, 1] and right continuous at 0.

• (iii) $\underline{\mathcal {U}}(\vartheta )\le \overline{\mathcal {U}}(\vartheta )$.

Also, if $\underline{\mathcal {U}}(\vartheta )=\overline{\mathcal {U}}(\vartheta )=\vartheta$. Then $\vartheta$ is called crisp number.

Definition 2.4

Consider that $\mathcal {U}=\left( \underline{\mathcal {U}},\,\overline{\mathcal {U}}\right) ,\,\mathcal {V}=\left( \underline{\mathcal {V}},\,\overline{\mathcal {V}}\right)$ be two fuzzy numbers and for $\vartheta \in \left[ 0,1\right]$ , also $\mathcal {K}$ is a scalar, then the addition, subtraction and scalar multiplication, respectively, are stated as:

• (i) $\mathcal {U}+\mathcal {V}=\left( \underline{\mathcal {U}}(\vartheta )+\underline{\mathcal {V}}(\vartheta ),\,\overline{\mathcal {U}}(\vartheta )+\overline{\mathcal {V}}(\vartheta )\right) ;$

• (ii) $\mathcal {U}-\mathcal {V}=\left( \underline{\mathcal {U}}(\vartheta )-\underline{\mathcal {V}}(\vartheta ),\,\overline{\mathcal {U}}(\vartheta )-\overline{\mathcal {V}}(\vartheta )\right) ;$

• (iii) $\mathcal {K}\cdot \mathcal {U}={\left\{ \begin{array}{ll} \left( \mathcal {K}\underline{\mathcal {U}}(\vartheta ),\,\mathcal {K}\overline{\mathcal {U}}(\vartheta )\right) &{} if\,\mathcal {K}\ge 0\\ \left( \mathcal {K}\overline{\mathcal {U}}(\vartheta ),\,\mathcal {K}\underline{\mathcal {U}}(\vartheta )\right) &{} if\,\mathcal {K}<0 \end{array}\right. }$.

Consider the mapping $\mathcal {D}:\,\mathscr {R}_{\mathbb {F}}\times \mathscr {R}_{\mathbb {F}}\longrightarrow \mathbb {R}$ is defined as:

$$\begin{aligned} \mathcal {D}\left( \tilde{g},\tilde{h}\right) =\underset{0\le \varpi _{0}\le 1}{\sup }\left\{ \left| \underline{\tilde{g}}\left( \varpi _{0}\right) -\underline{\tilde{h}}\left( \varpi _{0}\right) \right| ,\left| \overline{\tilde{g}}\left( \varpi _{0}\right) -\overline{\tilde{h}}\left( \varpi _{0}\right) \right| \right\} , \end{aligned}$$

where $\tilde{g}=\left[ \underline{\tilde{g}}\left( \varpi _{0}\right) ,\overline{\tilde{g}}\left( \varpi _{0}\right) \right]$ and $\tilde{h}=\left[ \underline{\tilde{h}}\left( \varpi _{0}\right) ,\overline{\tilde{h}}\left( \varpi _{0}\right) \right] .$ Then, $\mathcal {D}$ is a metric on $\mathscr {R}_{\mathbb {F}}$ satisfying the properties:

• (i) $\mathcal {D}\left( \tilde{g}+\tilde{m},\tilde{h} +\tilde{m}\right) =\mathcal {D}\left( \tilde{g},\tilde{h}\right) \,\text {for all}\,{{\tilde{g},\tilde{h},\tilde{m}\in \mathscr {R}_{\mathbb {F}}};}$

• (ii) $\mathcal {D}\left( \mathcal {K}\tilde{g}, \mathcal {K}\tilde{h}\right) =\left| \mathcal {K}\right| \mathcal {D} \left( \tilde{g},\tilde{h}\right) \,\text {for all}\,\tilde{g},\tilde{h}\in \mathscr {R}_{\mathbb {F}};$

• (iii) ${\mathcal {D}}\left( \tilde{g}+\tilde{m}, \tilde{h}+ \tilde{n} \right) \le \mathcal {D} \left( \tilde{g},\tilde{m}\right) +\mathcal {D}\left( \tilde{h}, \tilde{n} \right) \,\text {for all}\,\tilde{g}, \tilde{h},\tilde{m},{\tilde{n}}\in \mathscr {R}_{\mathbb {F}};$

  $\left( \mathcal {D},\mathscr {R}_{\mathbb {F}}\right)$ is a complete metric space.

Definition 2.5

Let $\mathcal {U}:\mathbb {R}\longrightarrow \mathscr {R}_{\mathbb {F}}$ be a fuzzy-valued function, then $\mathcal {U}$ is continuous if for $\chi _{0}\in \mathbb {F}$ and for each $\varepsilon >0$, there exists $\delta >0$ such that:

$$\begin{aligned} \mathcal {D}\left( \mathcal {U}(\chi ),\mathcal {U}(\chi _{0})\right)<\varepsilon \,\text {whenever}\,\left| \chi -\chi _{0}\right| <\delta . \end{aligned}$$

-

Definition 2.6

Let $\mathcal {U}:\mathbb {R}\longrightarrow \mathscr {R}_{\mathbb {F}}$ be a fuzzy-valued function and $\chi _{0}\in \mathbb {R}$ then $\mathcal {U}$ is differential at $\chi _{0}$. If $\exists$ $\mathcal {U}^{\prime }\left( \chi _{0}\right) \in \mathscr {R}_{\mathbb {F}}$ such that:

• (i) $\underset{h\longrightarrow 0+}{\lim }\frac{\mathcal {U}\left( \chi _{0}+h\right) -\mathcal {U}\left( \chi _{0}\right) }{h}=\underset{h\longrightarrow 0 +}{\lim }\frac{\mathcal {U}\left( \chi _{0}\right) -\mathcal {U}\left( \chi _{0}-h\right) }{h}=\mathcal {U}^{\prime }\left( \chi _{0}\right) ,$

• (ii) $\underset{h\longrightarrow 0-}{\lim }\frac{\mathcal {U}\left( \chi _{0}+h\right) -\mathcal {U}\left( \chi _{0}\right) }{h}=\underset{h\longrightarrow 0-}{\lim }\frac{\mathcal {U}\left( \chi _{0}\right) -\mathcal {U}\left( \chi _{0}-h\right) }{h}=\mathcal {U}^{\prime }\left( \chi _{0}\right) .$

Theorem 2.7

Consider $\mathcal {U}:\mathbb {R}\longrightarrow \mathscr {R}_{\mathbb {F}}$ as a fuzzy-valued function defined as $\mathcal {U}(\chi )=\left[ \underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) , \overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) \right]$ for each $\varpi _{0}\in [0,1]$ and $\mathcal {U}$ is differentiable, then $\underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right)$ and $\overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right)$ are differential and $\mathcal {U}^{\prime }(\chi )=\left[ \underline{\mathcal {U}}^{\prime }\left( \chi ,\varpi _{0}\right) ,\overline{\mathcal {U}}^{\prime }\left( \chi ,\varpi _{0}\right) \right]$.

Theorem 2.8

Consider $\mathcal {U}:\mathbb {R}\longrightarrow \mathscr {R}_{\mathbb {F}}$ as a fuzzy-valued function defined as $\mathcal {U}(\chi )=\left[ \underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) ,\overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) \right]$ for each $\varpi _{0}\in [0,1]$. If $\mathcal {U}$ and $\mathcal {U}^{\prime }$ are differential, then $\underline{\mathcal {U}}^{\prime }\left( \chi ,\varpi _{0}\right)$ and $\overline{\mathcal {U}}^{\prime }\left( \chi ,\varpi _{0}\right)$ are differential and $\mathcal {U}^{\prime \prime }(\chi )=\left[ \underline{\mathcal {U}}^{\prime \prime }\left( \chi ,\varpi _{0}\right) ,\overline{\mathcal {U}}^{\prime \prime }\left( \chi ,\varpi _{0}\right) \right]$.

Theorem 2.9

Consider a fuzzy-valued function $\mathcal {U}(\chi )$ defined on $\left[ 0,1\right]$ such that $\underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right)$ and $\overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right)$ are Riemann-integrable on $\left[ 0,1\right]$, for each $b\ge a$ and $\exists$ positive constant $\underline{\mathcal {M}}\left( \varpi _{0}\right)$ and $\overline{\mathcal {M}}\left( \varpi _{0}\right)$ such that

$$\begin{aligned} \int _{a}^{b}\left| \underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) \right| d\chi \le \underline{\mathcal {M}}\left( \varpi _{0}\right) \;\text {and}\;\int _{a}^{b}\left| \overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) \right| d\chi \le \overline{\mathcal {M}}\left( \varpi _{0}\right) , \end{aligned}$$

for every $b\ge a$. Then $\mathcal {U}(\chi )$ is an improper fuzzy Riemann integrable on $\left[ 0,\infty \right]$, and $\mathcal {U}(\chi )$ is a fuzzy number. Also, we have:

$$\begin{aligned} \int _{a}^{\infty }\mathcal {U}(\chi )d\chi =\left( \int _{a}^{\infty }\underline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) d\chi ,\int _{a}^{\infty }\overline{\mathcal {U}}\left( \chi ,\varpi _{0}\right) d\chi \right) . \end{aligned}$$

Theorem 2.10

The sum of two fuzzy Riemann integrable functions is also a fuzzy Riemann integrable. Moreover, we have

$$\begin{aligned} \int _{a}^{\infty }\left( \mathcal {U}(\chi )+\mathcal {V}(\chi )\right) d\chi =\int _{a}^{\infty }\mathcal {U}(\chi )d\chi +\int _{a}^{\infty }\mathcal {V}(\chi )d\chi . \end{aligned}$$

Definition 2.11

Let $\mathcal {U}$ be a continuous fuzzy valued-function. Assume that $\mathcal {U}(\chi )\cdot e^{-s\chi }$ is improper fuzzy Reimann-integrable on $[0,\infty )$. Then its fuzzy Laplace transform is represented by

$$\begin{aligned} \mathcal {L}[\mathcal {U}(\chi )]=\int _{0}^{\infty }\mathcal {U}(\chi )\cdot e^{-s\chi }d\chi . \end{aligned}$$

For $0\le \vartheta \le 1$ the parametric form of $\mathcal {U}(\chi )$ is represented by

$$\begin{aligned} \int _{0}^{\infty }\mathcal {U}(\chi ,\vartheta )\cdot e^{-s\chi }d\chi =\left[ \int _{0}^{\infty }\underline{\mathcal {U}}(\chi ,\vartheta )\cdot e^{-s\chi }d\chi ,\int _{0}^{\infty }\overline{\mathcal {U}}(\chi ,\vartheta )\cdot e^{-s\chi }d\chi \right] . \end{aligned}$$

Hence,

$$\begin{aligned} \mathcal {L}\left[ \mathcal {U}(\chi ,\vartheta )\right] =\left[ \mathcal {L}\left[ \underline{\mathcal {U}}(\chi ,\vartheta )\right] ,\mathcal {L}\left[ \overline{\mathcal {U}}(\chi ,\vartheta )\right] \right] . \end{aligned}$$

Definition 2.12

A fuzzy Laplace transform in term of fuzzy convolution is defined by

$$\begin{aligned} \mathcal {L}\left[ (\mathcal {U}*\mathcal {V})(\chi )\right] =\mathcal {L}\left[ \mathcal {U}(\chi )\right] \cdot \mathcal {L}\left[ \mathcal {V}(\chi )\right] , \end{aligned}$$

where $\mathcal {U}*\mathcal {V}$, define the fuzzy convolution between the two fuzzy-valued functions $\mathcal {U}(\chi )$ and $\mathcal {V}(\chi )$ i.e.

$$\begin{aligned} \left( \mathcal {U}*\mathcal {V}\right) (\chi )=\int _{0}^{\chi }\mathcal {U}(\vartheta )*\mathcal {V}(\chi -\vartheta )d\vartheta \end{aligned}$$

Definition 2.13

Let $\mathcal {U}(\chi )$ and $\mathcal {V}(\chi )$ be continuous fuzzy-valued functions and $\mathcal {C}_{1}$, $\mathcal {C}_{2}$ two real constants, then

$$\begin{aligned} \mathcal {L}\left[ \mathcal {C}_{1}\mathcal {U}(\chi )+\mathcal {C}_{2}\mathcal {V}(\chi )\right] =\mathcal {C}_{1}\mathcal {L}\left[ \mathcal {U}(\chi )\right] +\mathcal {C}_{2}\mathcal {L}\left[ \mathcal {V}(\chi )\right] . \end{aligned}$$

Main Work

Modified Laplace Adomian Decomposition Method

To solve the nonlinear fuzzy IDE of n$^{th}$ order in a fuzzy sense, the parametric form of Eq. (1) can be written as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}^{(n)}(\mathcal {X},\varpi _{0}) &{} =\underline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt,\\ \underline{\mathcal {\tilde{G}}}^{(j)}(0,\varpi _{0}) &{} =\underline{\beta }_{j};\quad j=0,1,\cdots ,n-1, \end{array}\right. }\\ {\left\{ \begin{array}{ll} \overline{\mathcal {\tilde{G}}}^{(n)}(\mathcal {X},\varpi _{0}) &{} =\overline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt,\\ \overline{\mathcal {\tilde{G}}}^{(j)}(0,\varpi _{0}) &{} =\overline{\beta }_{j};\quad j=0,1,\cdots ,n-1, \end{array}\right. } \end{array}\right. } \end{aligned}$$

(2)

applying Laplace transform on Eq. (2)

$$\begin{aligned} {\left\{ \begin{array}{ll} s^{n}{\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})\right] -\sum _{i=1}^{n}s^{n-i}\underline{\mathcal {\tilde{G}}}^{(i-1)}(0,\varpi _{0})\\ ={\mathcal {L}}\left[ \underline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt\right] ,\\ s^{n}{\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})\right] -\sum _{i=1}^{n}s^{n-i}\overline{\mathcal {\tilde{G}}}^{(i-1)}(0,\varpi _{0})\\ ={\mathcal {L}}\left[ \overline{g}(\mathcal {X},\varpi _{0})+\gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt\right] , \end{array}\right. } \end{aligned}$$

applying the initial conditions, the above equations can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=1}^{n}s^{n-i}\underline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}[\underline{g}(\mathcal {X},\varpi _{0})]}{s^{n}}\\ &{} \quad +\frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt\right] ,\\ {\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=1}^{n}s^{n-i}\overline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}\left[ \overline{g}(\mathcal {X},\varpi _{0})\right] }{s^{n}}\\ &{} \quad +\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) dt\right] . \end{array}\right. } \end{aligned}$$

(3)

Consider that the lower and upper fuzzy limit solutions of Eq. (3) can be extended by the Laplace decomposition algorithm into an infinite series as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0}) &{} ={\displaystyle \sum _{n=0}^{\infty }\underline{\mathcal {\tilde{G}}}_{n}(\mathcal {X},\varpi _{0})},\\ \overline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0}) &{} ={\displaystyle \sum _{n=0}^{\infty }\overline{\mathcal {\tilde{G}}}_{n}(\mathcal {X},\varpi _{0})}, \end{array}\right. } \end{aligned}$$

(4)

and nonlinear lower and upper limit terms $\left( \underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) ,\overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) \right)$ can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) &{} =\sum _{n=0}^{\infty }\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0}),\\ \overline{\mathcal {F}}\left( \mathcal {\tilde{G}}(t,\varpi _{0})\right) &{} =\sum _{n=0}^{\infty }\overline{\mathbb {A}}_{n}(t,\varpi _{0}), \end{array}\right. } \end{aligned}$$

(5)

where $\left( \underline{\mathcal {\mathbb {A}}_{n}}(t,\varpi _{0}),\overline{\mathbb {A}}_{n}(t,\varpi _{0})\right)$ are the Adomian polynomials [36]. Using Eq. (4) and Eq. (5) in Eq. (3), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \sum _{n=0}^{\infty }\underline{\mathcal {\tilde{G}}}_{n}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=1}^{n}s^{n-i}\underline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}[\underline{g}(\mathcal {X},\varpi _{0})]}{s^{n}}\\ &{} \quad + \frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\sum _{n=0}^{\infty }\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0})dt\right] ,\\ {\mathcal {L}}\left[ \sum _{n=0}^{\infty }\overline{\mathcal {\tilde{G}}}_{n}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=1}^{n}s^{n-i}\overline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}\left[ \overline{g}(\mathcal {X},\varpi _{0})\right] }{s^{n}}\\ &{} \quad +\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\sum _{n=0}^{\infty }\overline{\mathbb {A}}_{n}(t,\varpi _{0})dt\right] , \end{array}\right. } \end{aligned}$$

(6)

we get the following results by comparing both sides of Eq. (6)

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}_{0}(\mathcal {X},\varpi _{0})\right] &{} =\frac{s^{n-1}\underline{\beta }_{0}}{s^{n}},\\ {\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}_{0}(\mathcal {X},\varpi _{0})\right] &{} =\frac{s^{n-1}\overline{\beta }_{0}}{s^{n}}, \end{array}\right. } \end{aligned}$$

(7)

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}_{1}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=2}^{n}s^{n-i}\underline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}[\underline{g}(\mathcal {X},\varpi _{0})]}{s^{n}}\\ &{} \quad +\frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{0}(t,\varpi _{0})dt\right] ,\\ {\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}_{1}(\mathcal {X},\varpi _{0})\right] &{} =\frac{\sum _{i=2}^{n}s^{n-i}\overline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}\left[ \overline{g}(\mathcal {X},\varpi _{0})\right] }{s^{n}}\\ &{} \quad +\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{0}(t,\varpi _{0})dt\right] , \end{array}\right. } \end{aligned}$$

(8)

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}_{2}(\mathcal {X},\varpi _{0})\right] &{} =\frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{1}(t,\varpi _{0})dt\right] ,\\ {\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}_{2}(\mathcal {X},\varpi _{0})\right] &{} =\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{1}(t,\varpi _{0})dt\right] , \end{array}\right. } \end{aligned}$$

(9)

going on this way, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}\left[ \underline{\mathcal {\tilde{G}}}_{n+1}(\mathcal {X},\varpi _{0})\right] &{} =\frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0})dt\right] ;\,\,n\ge 1,\\ {\mathcal {L}}\left[ \overline{\mathcal {\tilde{G}}}_{n+1}(\mathcal {X},\varpi _{0})\right] &{} =\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{n}(t,\varpi _{0})dt\right] ;\,\,n\ge 1. \end{array}\right. } \end{aligned}$$

(10)

Applying inverse Laplace transform to Eqs. (7)–(10), we get

$$\begin{aligned}&{\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}_{0}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{s^{n-1}\underline{\beta }_{0}}{s^{n}}\right] ,\\ \overline{\mathcal {\tilde{G}}}_{0}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{s^{n-1}\overline{\beta }_{0}}{s^{n}}\right] , \end{array}\right. } \\&{\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}_{1}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{\sum _{i=2}^{n}s^{n-i}\underline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}[\underline{g}(\mathcal {X},\varpi _{0})]}{s^{n}}+\frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{0}(t,\varpi _{0})dt\right] \right] ,\\ \overline{\mathcal {\tilde{G}}}_{1}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{\sum _{i=2}^{n}s^{n-i}\overline{\beta }_{i-1}}{s^{n}}+\frac{{\mathcal {L}}\left[ \overline{g}(\mathcal {X},\varpi _{0})\right] }{s^{n}}+\frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{0}(t,\varpi _{0})dt\right] \right] , \end{array}\right. } \\&{\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}_{2}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{1}(t,\varpi _{0})dt\right] \right] ,\\ \overline{\mathcal {\tilde{G}}}_{2}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{1}(t,\varpi _{0})dt\right] \right] , \end{array}\right. } \end{aligned}$$

In general,

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\mathcal {\tilde{G}}}_{n+1}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{1}{s^{n}}{\mathcal {L}}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0})dt\right] \right] ;\,\,n\ge 1,\\ \overline{\mathcal {\tilde{G}}}_{n+1}(\mathcal {X},\varpi _{0}) &{} =\mathcal {L}^{-1}\left[ \frac{1}{s^{n}}\mathcal {L}\left[ \gamma \int _{a(\mathcal {X})}^{b(\mathcal {X})}\mathcal {K}(\mathcal {X},t)\overline{\mathbb {A}}_{n}(t,\varpi _{0})dt\right] \right] ;\,\,n\ge 1. \end{array}\right. } \end{aligned}$$

(11)

The parametric solution of Eq. (2) is

$$\begin{aligned} \mathcal {\tilde{G}}(\mathcal {X},\varpi _{0})=\left[ \underline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0}),\overline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})\right] , \end{aligned}$$

where $\underline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})$ and $\overline{\mathcal {\tilde{G}}}(\mathcal {X},\varpi _{0})$ contains all solutions for lower and upper case, respectively. The results of the convergence and error estimate of the proposed method are given in [38].

Test Problems

In this section, we will solve the nonlinear fuzzy integro-differential equations for different higher orders through the developed procedure. Also, we will solve system of nonlinear fuzzy integro-differential equation of second order and solve population growth model in fuzzy sense through the proposed scheme.

Example 3.1

Consider the following non-linear fuzzy Fredholm integro-differential equation as

$$\begin{aligned} \tilde{w}^{\prime \prime }(x,\varpi _{0})=\sinh (x)+x-\int _{0}^{1}x(\cosh ^{2}(t)-\tilde{w}^{2}(t,\varpi _{0}))dt, \end{aligned}$$

(12)

under the initial conditions $\tilde{w}(0)=[\varpi _{0}-1,1-\varpi _{0}],\tilde{w}^{\prime }(0)=[\varpi _{0}-2,1-2\varpi _{0}],\,\varpi _{0}\in [0,1]$.

Solution. The equivalent form of Eq. (12) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =\sinh (x)+x-\int _{0}^{1}x(\cosh ^{2}(t)-\underline{\tilde{w}}^{2}(t,\varpi _{0}))dt,\\ \overline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =\sinh (x)+x-\int _{0}^{1}x(\cosh ^{2}(t)-\overline{\tilde{w}}^{2}(t,\varpi _{0}))dt, \end{array}\right. } \end{aligned}$$

under the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(0,\varpi _{0})=[\varpi _{0}-1], &{} \underline{\tilde{w}}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2],\\ \overline{\tilde{w}}(0,\varpi _{0})=[1-\varpi _{0}], &{} \overline{\tilde{w}}^{\prime }(0,\varpi _{0})=[1-2\varpi _{0}]. \end{array}\right. } \end{aligned}$$

Implementing fuzzy Laplace transform to the lower case of the above equation and using the initial conditions, we have

$$\begin{aligned} \mathcal {L}[\underline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{(\varpi _{0}-1)}{s}+\frac{(\varpi _{0}-2)}{s^{2}}+\frac{1}{s^{2}(s^{2}-1)}+\frac{1}{s^{4}}\\&-\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\underline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]. \end{aligned}$$

Now applying Laplace inverse, we have

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})=&(\varpi _{0}-1)+(\varpi _{0}-3)x+\sinh (x)\nonumber \\&+\frac{x^{3}}{6}-\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\underline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]\Biggr ], \end{aligned}$$

(13)

the series solution of the considered problem is given by

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})=\sum _{n=0}^{\infty }\tilde{\underline{w_{n}}}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\underline{\tilde{w}}^{2}(t,\varpi _{0})$ into Adomian polynomial as $\underline{\tilde{w}}^{2}(t,\varpi _{0})=\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0}),$ Eq. (13) gets the form

$$\begin{aligned}&{\sum _{n=0}^{\infty }}\underline{\tilde{w}}_{n}(x,\varpi _{0})=(\varpi _{0}-1)+(\varpi _{0}-3)x+\sinh (x)\\&\qquad +\frac{x^{3}}{6}-\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0}))dt\biggr ]\Biggr ], \end{aligned}$$

where $\tilde{\underline{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\underline{\tilde{w}}_{n}(t,\varpi _{0})\underline{\tilde{w}}_{n-j}(t,\varpi _{0}),}$ comparing above equation term wise, we get

$$\begin{aligned} \underline{\tilde{w}}_{0}(x,\varpi _{0})= & {} \sinh (x),\\ \underline{\tilde{w}}_{1}(x,\varpi _{0})= & {} (\varpi _{0}-1)+(\varpi _{0}-3)x, \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})=&\underline{\tilde{w}}_{0}(x,\varpi _{0})+\underline{\tilde{w}}_{1}(x,\varpi _{0})+\underline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \underline{\tilde{w}}(x,\varpi _{0})=&\sinh (x)+(\varpi _{0}-1)+(\varpi _{0}-3)x+... \end{aligned}$$

Implementing the fuzzy Laplace transform to the upper case of the considered problem, we get

$$\begin{aligned} \mathcal {L}[\overline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{(1-\varpi _{0})}{s}+\frac{(1-2\varpi _{0})}{s^{2}}+\frac{1}{s^{2}(s^{2}-1)}+\frac{1}{s^{4}}\\&-\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\overline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]. \end{aligned}$$

Applying Laplace inverse, we have

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0}) =&(1-\varpi _{0})+(1-2\varpi _{0})x+\sinh (x)+\frac{x^{3}}{6}\nonumber \\&-\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\overline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]\Biggr ], \end{aligned}$$

(14)

so, the series solution of the considered problem is given by

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})=&\sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\overline{\tilde{w}}^{2}(t,\varpi _{0})$ into Adomian polynomial as $\overline{\tilde{w}}^{2}(t,\varpi _{0})=\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0})$, Eq. (14) gets the form

$$\begin{aligned} \sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0})=&(1-\varpi _{0})+(1-2\varpi _{0})x+\sinh (x)+\frac{x^{3}}{6}\\&\quad -\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}x(\cosh ^{2}(t)-\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0}))dt\biggr ]\Biggr ], \end{aligned}$$

where $\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})={\displaystyle \sum \nolimits _{j=0}^{n}\overline{\tilde{w}}_{n}(t,\varpi _{0})\overline{\tilde{w}}_{n-j}(t,\varpi _{0}),}$ comparing the above equation term wise, we get

$$\begin{aligned} \overline{\tilde{w}}_{0}(x,\varpi _{0})= & {} \sinh (x),\\ \overline{\tilde{w}}_{1}(x,\varpi _{0})= & {} (1-\varpi _{0})+(1-2\varpi _{0})x, \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})=&\overline{\tilde{w}}_{0}(x,\varpi _{0})+\overline{\tilde{w}}_{1}(x,\varpi _{0})+\overline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \overline{\tilde{w}}(x,\varpi _{0})=&\sinh (x)+(1-\varpi _{0})+(1-2\varpi _{0})x+... \end{aligned}$$

So the solution is given

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =\sinh (x)+(\varpi _{0}-1)+(\varpi _{0}-3)x+...\\ \overline{\tilde{w}}(x,\varpi _{0}) &{} =\sinh (x)+(1-\varpi _{0})+(1-2\varpi _{0})x+... \end{array}\right. } \end{aligned}$$

Fig. 1

Simulation of Example 1 in 2D

Fig. 2

Simulation of Example 1 in 3D

Fig. 3

Simulation of Example 1 at various uncertainty values

Example 3.2

Consider the following nonlinear fuzzy Fredholm integro-differential equation

$$\begin{aligned} \tilde{w}^{\prime \prime }(x,\varpi _{0})=-e^{-x}+\int _{0}^{1}\tilde{w}^{2}(x,\varpi _{0})dx, \end{aligned}$$

(15)

under the initial conditions $\tilde{w}(0,\varpi _{0})=[\varpi _{0}-1,1-\varpi _{0}],\tilde{w}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2,1-2\varpi _{0}]$, where $0\le x\le 1$, and $\varpi _{0}\in [0,1]$.

Solution. The equivalent form of Eq. (15) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =-e^{-x}+\int _{0}^{1}\underline{\tilde{w}}^{2}(x,\varpi _{0})dx,\\ \overline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =-e^{-x}+\int _{0}^{1}\overline{\tilde{w}}^{2}(x,\varpi _{0})dx, \end{array}\right. } \end{aligned}$$

(16)

under the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(0,\varpi _{0})=[\varpi _{0}-1], &{} \underline{\tilde{w}}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2],\\ \overline{\tilde{w}}(0,\varpi _{0})=[1-\varpi _{0}], &{} \overline{\tilde{w}}^{\prime }(0,\varpi _{0})=[1-2\varpi _{0}]. \end{array}\right. } \end{aligned}$$

Let solve for lower cut, applying Laplace transform and using the initial conditions

$$\begin{aligned} \mathcal {L}[\underline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{\varpi _{0}-1}{s}+\frac{\varpi _{0}-2}{s^{2}}-\frac{1}{s^{2}(s+1)}+\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\underline{\tilde{w}}^{2}(x,\varpi _{0}))dx\biggr ]. \end{aligned}$$

Now applying Laplace inverse, we have

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})= & {} \varpi _{0}+(\varpi _{0}-3)x-e^{-x}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\underline{\tilde{w}}^{2}(x,\varpi _{0}))dx\biggr ]\Biggr ], \end{aligned}$$

(17)

the series solution of the considered problem is given by

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})&=\sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\underline{\tilde{w}}^{2}(x,\varpi _{0})$ into Adomian polynomial as $\underline{\tilde{w}}^{2}(x,\varpi _{0})=\tilde{\underline{\mathbb {A}}}_{n}(x,\varpi _{0}),$ Eq. (17) gets the form

$$\begin{aligned} {\displaystyle \sum _{n=0}^{\infty }}\underline{\tilde{w}}_{n}(x,\varpi _{0})=\varpi _{0}+(\varpi _{0}-3)x-e^{-x}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\sum _{n=0}^{\infty }\tilde{\underline{\mathbb {A}}}_{n}(x,\varpi _{0})dx\biggr ]\Biggr ], \end{aligned}$$

where $\tilde{\underline{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\underline{\tilde{w}}_{j}(x,\varpi _{0})\underline{\tilde{w}}_{n-j}(x,\varpi _{0}),}$ comparing term wise above equation, we have

$$\begin{aligned} \underline{\tilde{w}}_{0}(x,\varpi _{0})= & {} \varpi _{0}+(\varpi _{0}-3)x,\\ \underline{\tilde{w}}_{1}(x,\varpi _{0})= & {} -e^{-x}+\left( \frac{7\varpi _{0}^{2}}{6}-\frac{5\varpi _{0}}{2}+\frac{3}{2}\right) x^{2}, \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})= & {} \underline{\tilde{w}}_{0}(x,\varpi _{0})+\underline{\tilde{w}}_{1}(x,\varpi _{0})+\underline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \underline{\tilde{w}}(x,\varpi _{0})= & {} \varpi _{0}+(\varpi _{0}-3)x-e^{-x}+\left( \frac{7\varpi _{0}^{2}}{6}-\frac{5\varpi _{0}}{2}+\frac{3}{2}\right) x^{2}+... \end{aligned}$$

Implementing the fuzzy Laplace transform to the upper case of the considered problem, we get

$$\begin{aligned} \mathcal {L}[\overline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{1-\varpi _{0}}{s}+\frac{1-2\varpi _{0}}{s^{2}}-\frac{1}{s^{2}(s+1)}+\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\overline{\tilde{w}}^{2}(x,\varpi _{0})dx\biggr ], \end{aligned}$$

now applying Laplace inverse, we have

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} -\varpi _{0}+2(1-\varpi _{0}x)-e^{-x}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\overline{\tilde{w}}^{2}(x,\varpi _{0})dx\biggr ]\Biggr ], \end{aligned}$$

(18)

the series solution of the considered problem is given by

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} \sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\overline{\tilde{w}}^{2}(x,\varpi _{0})$ into Adomian polynomial as $\overline{\tilde{w}}^{2}(x,\varpi _{0})=\overline{\tilde{\mathbb {A}}}_{n}(x,\varpi _{0}),$ Eq. (18) gets the form

$$\begin{aligned} {\displaystyle \sum _{n=0}^{\infty }}\overline{\tilde{w}}_{n}(x,\varpi _{0})=-\varpi _{0}+2(1-\varpi _{0}x)-e^{-x}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{1}\sum _{n=0}^{\infty }\overline{\tilde{\mathbb {A}}}_{n}(x,\varpi _{0})dx\biggr ]\Biggr ], \end{aligned}$$

where $\overline{\tilde{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\overline{\tilde{w}}_{j}(x,\varpi _{0})\overline{\tilde{w}}_{n-j}(x,\varpi _{0})},$ comparing term wise the above equation, we have

$$\begin{aligned} \overline{\tilde{w}}_{0}(x,\varpi _{0})= & {} -\varpi _{0}+2(1-\varpi _{0}x),\\ \overline{\tilde{w}}_{1}(x,\varpi _{0})= & {} -e^{-x}+\left( \frac{13\varpi _{0}^{2}}{6}-4\varpi _{0}+2\right) x^{2}, \end{aligned}$$

and so on. So the desired solution for the upper case is

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} \overline{\tilde{w}}_{0}(x,\varpi _{0})+\overline{\tilde{w}}_{1}(x,\varpi _{0})+\overline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \overline{\tilde{w}}(x,\varpi _{0})= & {} -\varpi _{0}+2(1-\varpi _{0}x)-e^{-x}+\left( \frac{13\varpi _{0}^{2}}{6}-4\varpi _{0}+2\right) x^{2}+... \end{aligned}$$

So the solution is given

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =\varpi _{0}+(\varpi _{0}-3)x-e^{-x}+\left( \frac{7\varpi _{0}^{2}}{6}-\frac{5\varpi _{0}}{2}+\frac{3}{2}\right) x^{2}+...\\ \overline{\tilde{w}}(x,\varpi _{0}) &{} =-\varpi _{0}+2(1-\varpi _{0}x)-e^{-x}+\left( \frac{13\varpi _{0}^{2}}{6}-4\varpi _{0}+2\right) x^{2}+... \end{array}\right. } \end{aligned}$$

(19)

Fig. 4

Simulation of Example 2 in 2D

Fig. 5

Simulation of Example 2 in 3D

Fig. 6

Simulation of Example 2 at uncertainty values

Example 3.3

Consider the 5$^{th}$ order nonlinear fuzzy Volterra integro-differential equation as

$$\begin{aligned} \tilde{w}^{(5)}(x,\varpi _{0})=1+\int _{0}^{x}(x-t)\tilde{w}^{2}(t,\varpi _{0})dt, \end{aligned}$$

(20)

under the initial conditions $\tilde{w}(0,\varpi _{0})=[\varpi _{0}-1,1-\varpi _{0}],\,\tilde{w}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2,1-2\varpi _{0}], \tilde{w}^{(2)}(0,\varpi _{0})=\tilde{w}^{(3)}(0,\varpi _{0})=\tilde{w}^{(4)}(0,\varpi _{0})=0$, where $\varpi _{0}\in [0,1]$.

Solution. The equivalent form of Eq. (20) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}^{(5)}(x,\varpi _{0}) &{} =1+\int _{0}^{x}(x-t)\underline{\tilde{w}}^{2}(t,\varpi _{0})dt,\\ \overline{\tilde{w}}^{(5)}(x,\varpi _{0}) &{} =1+\int _{0}^{x}(x-t)\overline{\tilde{w}}^{2}(t,\varpi _{0})dt, \end{array}\right. } \end{aligned}$$

(21)

under the initial condition

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(0,\varpi _{0})=[\varpi _{0}-1], &{} \underline{\tilde{w}}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2],\\ \overline{\tilde{w}}(0,\varpi _{0})=[1-\varpi _{0}], &{} \overline{\tilde{w}}^{\prime }(0,\varpi _{0})=[1-2\varpi _{0}]. \end{array}\right. } \end{aligned}$$

Solve Eq. (21) for lower cut, applying Laplace transform and using the initial conditions

$$\begin{aligned} \mathcal {L}[\underline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{\varpi _{0}-1}{s}+\frac{\varpi _{0}-2}{s^{2}}+\frac{1}{s^{6}}+\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\underline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]. \end{aligned}$$

Now applying Laplace inverse, we have

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})= & {} (\varpi _{0}-1)+x(\varpi _{0}-2)+\frac{x^{5}}{120}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\underline{\tilde{w}}^{2}(t,\varpi _{0}))dt\biggr ]\Biggr ],\nonumber \\ \end{aligned}$$

(22)

now the series solution of the considered problem is given by

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})&=\sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\underline{\tilde{w}}^{2}(t,\varpi _{0})$ into Adomian polynomial as $\underline{\tilde{w}}^{2}(t,\varpi _{0})=\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0}),$ Eq. (22) gets the form

$$\begin{aligned} {\displaystyle \sum _{n=0}^{\infty }}\underline{\tilde{w}}_{n}(x,\varpi _{0})=(\varpi _{0}-1)+x(\varpi _{0}-2)+\frac{x^{5}}{120}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\sum _{n=0}^{\infty }\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0})dt\biggr ]\Biggr ], \end{aligned}$$

where $\tilde{\underline{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\underline{\tilde{w}}_{j}(x,\varpi _{0})\underline{\tilde{w}}_{n-j}(x,\varpi _{0})}$ comparing term wise the above equation, we get

$$\begin{aligned} \underline{\tilde{w}}_{0}(x,\varpi _{0})= & {} (\varpi _{0}-1)+x(\varpi _{0}-2),\\ \underline{\tilde{w}}_{1}(x,\varpi _{0})= & {} \frac{x^{5}}{120}+\frac{(\varpi _{0}-1)^{2}x^{7}}{5040}+\frac{(2-3\varpi _{0}+\varpi _{0}^{2})x^{8}}{20160}+\frac{(\varpi _{0}-2)^{2}x^{9}}{181440}, \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned} \underline{\tilde{w}}(x,\varpi _{0})= & {} \underline{\tilde{w}}_{0}(x,\varpi _{0})+\underline{\tilde{w}}_{1}(x,\varpi _{0})+\underline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \underline{\tilde{w}}(x,\varpi _{0})= & {} (\varpi _{0}-1)+x(\varpi _{0}-2)+\frac{x^{5}}{120}+\frac{(\varpi _{0}-1)^{2}x^{7}}{5040}\\&+\frac{(2-3\varpi _{0}+\varpi _{0}^{2})x^{8}}{20160}+\frac{(\varpi _{0}-2)^{2}x^{9}}{181440}+... \end{aligned}$$

Now implementing the fuzzy Laplace transform to the upper case of the considered problem, we get

$$\begin{aligned} \mathcal {L}[\overline{\tilde{w}}(x,\varpi _{0})]= & {} \frac{(1-\varpi _{0})}{s}+\frac{(1-2\varpi _{0})}{s^{2}}+\frac{1}{s^{6}}+\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\overline{\tilde{w}}^{2}(t,\varpi _{0})dt\biggr ], \end{aligned}$$

now applying Laplace inverse, we have

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} (1-\varpi _{0})+x(1-2\varpi _{0})+\frac{x^{5}}{120}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\overline{\tilde{w}}^{2}(t,\varpi _{0})dt\biggr ]\Biggr ],\nonumber \\ \end{aligned}$$

(23)

now the series solution of the considered problem is given by

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} \sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0}). \end{aligned}$$

Also, decomposing the nonlinear term $\overline{\tilde{w}}^{2}(t,\varpi _{0})$ into Adomian polynomial as $\overline{\tilde{w}}^{2}(t,\varpi _{0})=\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0}),$ Eq. (23) gets the form

$$\begin{aligned} {\displaystyle \sum _{n=0}^{\infty }}\overline{\tilde{w}}_{n}(x,\varpi _{0})=(1-\varpi _{0})+x(1-2\varpi _{0})+\frac{x^{5}}{120}+\mathcal {L}^{-1}\Biggl [\frac{1}{s^{5}}\mathcal {L}\biggl [\int _{0}^{x}(x-t)\sum _{n=0}^{\infty }\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})dt\biggr ]\Biggr ], \end{aligned}$$

where $\overline{\tilde{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\overline{\tilde{w}}_{j}(x,\varpi _{0})\overline{\tilde{w}}_{n-j}(x,\varpi _{0})}$, comparing term wise the above equation, we get

$$\begin{aligned} \overline{\tilde{w}}_{0}(x,\varpi _{0})= & {} (1-\varpi _{0})+x(1-2\varpi _{0}),\\ \overline{\tilde{w}}_{1}(x,\varpi _{0})= & {} \frac{x^{5}}{120}+\frac{(1-\varpi _{0})^{2}x^{7}}{5040}+\frac{(1-3\varpi _{0}+2\varpi _{0}^{2})x^{8}}{20160}+\frac{(1-2\varpi _{0})^{2}x^{9}}{181440}, \end{aligned}$$

and so on. So the desired solution for the upper case is

$$\begin{aligned} \overline{\tilde{w}}(x,\varpi _{0})= & {} \overline{\tilde{w}}_{0}(x,\varpi _{0})+\overline{\tilde{w}}_{1}(x,\varpi _{0})+\overline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \overline{\tilde{w}}(x,\varpi _{0})= & {} (1-\varpi _{0})+x(1-2\varpi _{0})+\frac{x^{5}}{120}+\frac{(1-\varpi _{0})^{2}x^{7}}{5040}\\&+\frac{(1-3\varpi _{0}+2\varpi _{0}^{2})x^{8}}{20160}+\frac{(1-2\varpi _{0})^{2}x^{9}}{181440}+... \end{aligned}$$

So the solution is given

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)+x(\varpi _{0}-2)+\frac{x^{5}}{120}+\frac{(\varpi _{0}-1)^{2}x^{7}}{5040}\\ &{} \quad +\frac{(2-3\varpi _{0}+\varpi _{0}^{2})x^{8}}{20160}+\frac{(\varpi _{0}-2)^{2}x^{9}}{181440}+...\\ \overline{\tilde{w}}(x,\varpi _{0}) &{} =(1-\varpi _{0})+x(1-2\varpi _{0})+\frac{x^{5}}{120}+\frac{(1-\varpi _{0})^{2}x^{7}}{5040}\\ &{} \quad +\frac{(1-3\varpi _{0}+2\varpi _{0}^{2})x^{8}}{20160}+\frac{(1-2\varpi _{0})^{2}x^{9}}{181440}+... \end{array}\right. } \end{aligned}$$

(24)

Fig. 7

Simulation of Example 3 in 2D

Fig. 8

Simulation of Example 3 in 3D

Fig. 9

Simulation of Example 3 at various uncertainty values

Example 3.4

Consider the system of nonlinear fuzzy Volterra integro-differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{w}^{\prime \prime }(x,\varpi _{0}) &{} =-\sin (x)+\int _{0}^{x}[\tilde{w}^{2}(t,\varpi _{0})+\tilde{v}^{2}(t,\varpi _{0})]dt,\\ \tilde{v}^{\prime \prime }(x,\varpi _{0}) &{} =-\cos (x)+\int _{0}^{x}[\tilde{w}^{2}(t,\varpi _{0})-\tilde{v}^{2}(t,\varpi _{0})]dt, \end{array}\right. } \end{aligned}$$

(25)

under the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{w}(0,\varpi _{0})=[\varpi _{0}-1,1-\varpi _{0}], &{} \tilde{w}(0,\varpi _{0})=[\varpi _{0}-2,1-2\varpi _{0}],\\ \tilde{v}(0,\varpi _{0})=[\varpi _{0}-1,1-\varpi _{0}], &{} \tilde{v}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2,1-2\varpi _{0}], \end{array}\right. } \end{aligned}$$

where $\varpi _{0}\in [0,1]$.

Solution. The equivalent form of Eq. (25) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =-\sin (x)+\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})+\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt,\\ \underline{\tilde{v}}^{\prime \prime }(x,\varpi _{0}) &{} =-\cos (x)+\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})-\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt,\\ \overline{\tilde{w}}^{\prime \prime }(x,\varpi _{0}) &{} =-\sin (x)+\int _{0}^{x}[\overline{\tilde{w}}^{2}(t,\varpi _{0})+\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt,\\ \overline{\tilde{v}}^{\prime \prime }(x,\varpi _{0}) &{} =-\cos (x)+\int _{0}^{x}[\overline{\tilde{w}}^{2}(t,\varpi _{0})-\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt, \end{array}\right. } \end{aligned}$$

(26)

under the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(0,\varpi _{0}) &{} =[\varpi _{0}-1],\underline{\tilde{w}}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2],\\ \underline{\tilde{v}}(0,\varpi _{0}) &{} =[\varpi _{0}-1],\,\,\underline{\tilde{v}}^{\prime }(0,\varpi _{0})=[\varpi _{0}-2],\\ \overline{\tilde{w}}(0,\varpi _{0}) &{} =[1-\varpi _{0}],\,\,\,\,\overline{\tilde{w}}^{\prime }(0,\varpi _{0})=[1-2\varpi _{0}],\\ \overline{\tilde{v}}(0,\varpi _{0}) &{} =[1-\varpi _{0}],\,\,\,\,\overline{\tilde{v}}^{\prime }(0,\varpi _{0})=[1-2\varpi _{0}]. \end{array}\right. } \end{aligned}$$

Now implementing the fuzzy Laplace transform to the lower case of the considered problem, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {L}[\underline{\tilde{w}}(x,\varpi _{0})] &{} =\frac{(\varpi _{0}-1)}{s}+\frac{(\varpi _{0}-2)}{s^{2}}-\frac{1}{s^{2}(s^{2}+1)}+\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})+\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ],\\ \mathcal {L}[\underline{\tilde{v}}(x,\varpi _{0})] &{} =\frac{(\varpi _{0}-1)}{s}+\frac{(\varpi _{0}-2)}{s^{2}}-\frac{1}{s(s^{2}+1)}+\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})-\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]. \end{array}\right. } \end{aligned}$$

Now applying Laplace inverse, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)+x(\varpi _{0}-2)-x+\sin (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})+\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]\Biggr ],\\ \underline{\tilde{v}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)+x(\varpi _{0}-2)-1+\cos (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\underline{\tilde{w}}^{2}(t,\varpi _{0})-\underline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]\Biggr ], \end{array}\right. } \end{aligned}$$

(27)

now the series solution of the considered problem is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =\sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(x,\varpi _{0}),\\ \underline{\tilde{v}}(x,\varpi _{0}) &{} =\sum _{n=0}^{\infty }\underline{\tilde{v}}_{n}(x,\varpi _{0}). \end{array}\right. } \end{aligned}$$

Also, decomposing the nonlinear terms $\underline{\tilde{w}}^{2}(t,\varpi _{0})$ and $\underline{\tilde{v}}^{2}(t,\varpi _{0})$ into Adomian polynomials as $\underline{\tilde{w}}^{2}(t,\varpi _{0})=\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0})$ and $\underline{\tilde{v}}^{2}(t,\varpi _{0})=\tilde{\underline{\mathbb {B}}}_{n}(t,\varpi _{0}),$ Equation (27) gets the form

$$\begin{aligned} {\left\{ \begin{array}{ll} {\displaystyle \sum _{n=0}^{\infty }}\underline{\tilde{w}}_{n}(x,\varpi _{0}) &{} =(\varpi _{0}-1)+x(\varpi _{0}-2)-x+\sin (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}\sum _{n=0}^{\infty }\biggl [\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0})+\tilde{\underline{\mathbb {B}}}_{n}(t,\varpi _{0})\biggr ]dt\biggr ]\Biggr ],\\ \sum _{n=0}^{\infty }\underline{\tilde{v}}_{n}(x,\varpi _{0}) &{} =(\varpi _{0}-1)+x(\varpi _{0}-2)-1+\cos (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}\sum _{n=0}^{\infty }\biggl [\tilde{\underline{\mathbb {A}}}_{n}(t,\varpi _{0})-\tilde{\underline{\mathbb {B}}}_{n}(t,\varpi _{0})\biggr ]dt\biggr ]\Biggr ], \end{array}\right. } \end{aligned}$$

where $\tilde{\underline{\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\underline{\tilde{w}}_{n}(t,\varpi _{0})\underline{\tilde{w}}_{n-j}(t,\varpi _{0})}$ and $\tilde{\underline{\mathbb {B}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{n}\tilde{\underline{v}}_{n}(t,\varpi _{0})\tilde{\underline{v}}_{n-j}(t,\varpi _{0})}$, comparing above equation term wise, we get

$$\begin{aligned}&{\left\{ \begin{array}{ll} \underline{\tilde{w}}_{0}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-x,\\ \underline{\tilde{v}}_{0}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-1, \end{array}\right. } \\&{\left\{ \begin{array}{ll} \underline{\tilde{w}}_{1}(x,\varpi _{0}) &{} =x(\varpi _{0}-2)+\sin (x)+\frac{x^{3}}{60}\biggl (50+5x+x^{2}-5\varpi _{0}(x+12)+20\varpi _{0}^{2}\biggr ),\\ \underline{\tilde{v}}_{1}(x,\varpi _{0}) &{} =x(\varpi _{0}-2)+\cos (x)+\frac{x^{3}}{60}\biggl (-30+5x+x^{2}-5\varpi _{0}(x-4)\biggr ), \end{array}\right. } \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned}&{\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =\underline{\tilde{w}}_{0}(x,\varpi _{0})+\underline{\tilde{w}}_{1}(x,\varpi _{0})+\underline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \underline{\tilde{v}}(x,\varpi _{0}) &{} =\underline{\tilde{v}}_{0}(x,\varpi _{0})+\underline{\tilde{v}}_{1}(x,\varpi _{0})+\underline{\tilde{v}}_{2}(x,\varpi _{0})+... \end{array}\right. }\\&{\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-x+x(\varpi _{0}-2)+\sin (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (50+5x+x^{2}-5\varpi _{0}(x+12)+20\varpi _{0}^{2}\biggr )+...\\ \underline{\tilde{v}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-1+x(\varpi _{0}-2)+\cos (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (-30+5x+x^{2}-5\varpi _{0}(x-4)\biggr )+... \end{array}\right. } \end{aligned}$$

Now implementing the fuzzy Laplace transform to the upper case of the considered problem, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {L}[\overline{\tilde{w}}(x,\varpi _{0})] &{} =\frac{(1-\varpi _{0})}{s}+\frac{(1-2\varpi _{0})}{s^{2}}-\frac{1}{s^{2}(s^{2}+1)}+\frac{1}{s^{2}}\mathcal {L}\Biggl [\int _{0}^{x}\biggl [[\overline{\tilde{w}}^{2}(t,\varpi _{0})+\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]\Biggr ],\\ \mathcal {L}[\overline{\tilde{v}}(t,\varpi _{0})] &{} =\frac{(1-\varpi _{0})}{s}+\frac{(1-2\varpi _{0})}{s^{2}}-\frac{1}{s(s^{2}+1)}+\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\overline{\tilde{w}}^{2}(t,\varpi _{0})-\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ], \end{array}\right. } \end{aligned}$$

Now applying Laplace inverse, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{\tilde{w}}(x,\varpi _{0}) &{} =(1-\varpi _{0})+x(1-2\varpi _{0})-x+\sin (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\overline{\tilde{w}}^{2}(t,\varpi _{0})+\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]\Biggr ],\\ \overline{\tilde{v}}(t,\varpi _{0}) &{} =(1-\varpi _{0})+x(1-2\varpi _{0})-1+\cos (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\overline{\tilde{w}}^{2}(t,\varpi _{0})-\overline{\tilde{v}}^{2}(t,\varpi _{0})]dt\biggr ]\Biggr ], \end{array}\right. } \end{aligned}$$

(28)

the series solution of the considered problem is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \overline{\tilde{w}}(x,\varpi _{0}) &{} =\sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0}),\\ \overline{\tilde{v}}(t,\varpi _{0}) &{} =\sum _{n=0}^{\infty }\overline{\tilde{v}}_{n}(x,\varpi _{0}). \end{array}\right. } \end{aligned}$$

Also, decomposing the nonlinear terms $\overline{\tilde{w}}^{2}(t,\varpi _{0})$ and $\overline{\tilde{v}}^{2}(t,\varpi _{0})$ into Adomian polynomials as $\overline{\tilde{w}}^{2}(t,\varpi _{0})=\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})$ and $\overline{\tilde{v}}^{2}(t,\varpi _{0})=\overline{\tilde{\mathbb {B}}}_{n}(t,\varpi _{0}),$ Eq. (28) gets the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _{n=0}^{\infty }\overline{\tilde{w}}_{n}(x,\varpi _{0}) &{} =(1-\varpi _{0})+x(1-2\varpi _{0})-x+\sin (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})+\overline{\tilde{\mathbb {B}}}_{n}(t,\varpi _{0})]dt\biggr ]\Biggr ],\\ \sum _{n=0}^{\infty }\overline{\tilde{v}}_{n}(x,\varpi _{0}) &{} =(1-\varpi _{0})+x(1-2\varpi _{0})-1+\cos (x)\\ &{} \quad +\mathcal {L}^{-1}\Biggl [\frac{1}{s^{2}}\mathcal {L}\biggl [\int _{0}^{x}[\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})-\overline{\tilde{\mathbb {B}}}_{n}(t,\varpi _{0})]dt\biggr ]\Biggr ], \end{array}\right. } \end{aligned}$$

where $\overline{\tilde{\mathbb {A}}}_{n}(t,\varpi _{0})={\displaystyle \sum \nolimits _{j=0}^{n}\overline{\tilde{w}}_{n}(t,\varpi _{0})\overline{\tilde{w}}_{n-j}(t,\varpi _{0})}$and $\overline{\tilde{\mathbb {B}}}_{n}(t,\varpi _{0})={\displaystyle \sum \nolimits _{j=0}^{n}\overline{\tilde{v}}_{n}(t,\varpi _{0})\overline{\tilde{v}}_{n-j}}{(t,\varpi _{0})}$, comparing term wise above equation, we get

$$\begin{aligned}&{\left\{ \begin{array}{ll} \overline{\tilde{w}}_{0}(x,\varpi _{0}) &{} =(1-\varpi _{0})-x,\\ \overline{\tilde{v}}_{0}(x,\varpi _{0}) &{} =(1-\varpi _{0})-1, \end{array}\right. }\\&{\left\{ \begin{array}{ll} \overline{\tilde{w}}_{1}(x,\varpi _{0}) &{} =x(1-2\varpi _{0})+\sin (x)+\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)+20\varpi _{0}^{2}\biggr ),\\ \overline{\tilde{v}}_{1}(x,\varpi _{0}) &{} =x(1-2\varpi _{0})+\cos (x)+\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)\biggr ), \end{array}\right. } \end{aligned}$$

and so on. So the desired solution for the upper case is

$$\begin{aligned}&{\left\{ \begin{array}{ll} \overline{\tilde{w}}(x,\varpi _{0}) &{} =\overline{\tilde{w}}_{0}(x,\varpi _{0})+\overline{\tilde{w}}_{1}(x,\varpi _{0})+\overline{\tilde{w}}_{2}(x,\varpi _{0})+...\\ \overline{\tilde{v}}(x,\varpi _{0}) &{} =\overline{\tilde{v}}_{0}(x,\varpi _{0})+\overline{\tilde{v}}_{1}(x,\varpi _{0})+\overline{\tilde{v}}_{2}(x,\varpi _{0})+... \end{array}\right. } \\&{\left\{ \begin{array}{ll} \overline{\tilde{w}}(x,\varpi _{0}) &{} =(1-\varpi _{0})-x+x(1-2\varpi _{0})+\sin (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)+20\varpi _{0}^{2}\biggr )+...\\ \overline{\tilde{v}}(x,\varpi _{0}) &{} =(1-\varpi _{0})-1+x(1-2\varpi _{0})+\cos (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)\biggr )+... \end{array}\right. } \end{aligned}$$

So the solution is given

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-x+x(\varpi _{0}-2)+\sin (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (50+5x+x^{2}-5\varpi _{0}(x+12)+20\varpi _{0}^{2}\biggr )+...\\ \underline{\tilde{v}}(x,\varpi _{0}) &{} =(\varpi _{0}-1)-1+x(\varpi _{0}-2)+\cos (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (-30+5x+x^{2}-5\varpi _{0}(x-4)\biggr )+... \end{array}\right. }\\ {\left\{ \begin{array}{ll} \overline{\tilde{w}}(x,\varpi _{0}) &{} =(1-\varpi _{0})-x+x(1-2\varpi _{0})+\sin (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)+20\varpi _{0}^{2}\biggr )+...\\ \overline{\tilde{v}}(x,\varpi _{0}) &{} =(1-\varpi _{0})-1+x(1-2\varpi _{0})+\cos (x)\\ &{} \quad +\frac{x^{3}}{60}\biggl (10-5x+x^{2}+5\varpi _{0}(x-4)\biggr )+... \end{array}\right. } \end{array}\right. } \end{aligned}$$

(29)

Fig. 10

Simulation of Example 4 in 2D

Fig. 11

Simulation of Example 4 in 3D

Fig. 12

Simulation of Example 4 at various uncertainty values

Example 3.5

The fuzzy sense of the population growth model [37] is given by

$$\begin{aligned} \tilde{w}^{\prime }(t,\varpi _{0})=10\tilde{w}(t,\varpi _{0})-10\tilde{w}^{2}(t,\varpi _{0})-10\tilde{w}(t,\varpi _{0})\int _{0}^{t}\tilde{w}(x,\varpi _{0})dx, \end{aligned}$$

(30)

under the initial condition $\tilde{w}(0,\varpi _{0})=[\varpi _{0}-1,1-\varpi _{0}],$ where $\varpi _{0}\in [0,1]$.

Solution. The equivalent form of Eq. (30) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}^{\prime }(t,\varpi _{0}) &{} =10\underline{\tilde{w}}(t,\varpi _{0})-10\underline{\tilde{w}}^{2}(t,\varpi _{0})-10\underline{\tilde{w}}(t,\varpi _{0})\int _{0}^{t}\underline{\tilde{w}}(x,\varpi _{0})dx,\\ \overline{\tilde{w}}^{\prime }(t,\varpi _{0}) &{} =10\overline{\tilde{w}}(t,\varpi _{0})-10\overline{\tilde{w}}^{2}(t,\varpi _{0})-10\overline{\tilde{w}}(t,\varpi _{0})\int _{0}^{t}\overline{\tilde{w}}(x,\varpi _{0})dx, \end{array}\right. } \end{aligned}$$

under the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(0,\varpi _{0}) &{} =\left[ \varpi _{0}-1\right] ,\\ \overline{\tilde{w}}(0,\varpi _{0}) &{} =\left[ 1-\varpi _{0}\right] . \end{array}\right. } \end{aligned}$$

Implementing fuzzy Laplace transform to the lower case of the above equation and using the initial condition, we have

$$\begin{aligned} \mathcal {L}\left[ \underline{\tilde{w}}(t,\varpi _{0})\right] =\frac{\left( \varpi _{0}-1\right) }{s-10}-\frac{10}{s-10}\mathcal {L}\left[ \underline{\tilde{w}}^{2}(t,\varpi _{0})\right] -\frac{10}{s-10}\mathcal {L}\left[ \underline{\tilde{w}}(t,\varpi _{0})\int _{0}^{t}\underline{\tilde{w}}(x,\varpi _{0})dx\right] , \end{aligned}$$

applying Laplace inverse, we have

$$\begin{aligned} \underline{\tilde{w}}(t,\varpi _{0})&=\left( \varpi _{0}-1\right) e^{10t}-\mathcal {L}^{-1}\left[ \frac{10}{s-10}\mathcal {L}\left[ \underline{\tilde{w}}^{2}(t,\varpi _{0})\right] \right] \nonumber \\&\quad -\mathcal {L}^{-1}\left[ \frac{10}{s-10}\mathcal {L}\left[ \underline{\tilde{w}}(t,\varpi _{0})\int _{0}^{t}\underline{\tilde{w}}(x,\varpi _{0})dx\right] \right] , \end{aligned}$$

(31)

the series solution of the considered problem is given by

$$\begin{aligned} \underline{\tilde{w}}(t,\varpi _{0})={\displaystyle \sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(t,\varpi _{0})}. \end{aligned}$$

Also, decomposing the nonlinear term $\underline{\tilde{w}}^{2}(t,\varpi _{0})$ into Adomian polynomial as $\underline{\tilde{w}}^{2}(t,\varpi _{0})=\sum _{n=0}^{\infty }\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0}),$ Eq. (31) gets the form

$$\begin{aligned} {\displaystyle \sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(t,\varpi _{0})}&=\left( \varpi _{0}-1\right) e^{10t}-\mathcal {L}^{-1}\left[ \frac{10}{s-10}\mathcal {L}\left[ \sum _{n=0}^{\infty }\underline{\mathcal {\mathbb {A}}}_{n}(t,\varpi _{0})\right] \right] \\&\quad -\mathcal {L}^{-1}\left[ \frac{10}{s-10}\mathcal {L}\left[ \sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(t,\varpi _{0})\int _{0}^{t}\sum _{n=0}^{\infty }\underline{\tilde{w}}_{n}(x,\varpi _{0})dx\right] \right] , \end{aligned}$$

where $\underline{\mathcal {\mathbb {A}}}_{n}={\displaystyle \sum \nolimits _{j=0}^{\infty }\underline{\tilde{w}}_{j}(t,\varpi _{0})}\underline{\tilde{w}}_{n-j}(t,\varpi _{0}),$ comparing the term wise above equation, we have

$$\begin{aligned} {\displaystyle \underline{\tilde{w}}_{0}(t,\varpi _{0})}=\left( \varpi _{0}-1\right) e^{10t}, \\ {\displaystyle \underline{\tilde{w}}_{1}(t,\varpi _{0})}=\frac{11}{10}\left( \varpi _{0}-1\right) ^{2}\left( e^{10t}-e^{20t}\right) +\left( \varpi _{0}-1\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) , \end{aligned}$$

and so on. So the desired solution for the lower case is

$$\begin{aligned} \underline{\tilde{w}}(t,\varpi _{0})=\underline{\tilde{w}}_{0}(t,\varpi _{0})+\underline{\tilde{w}}_{1}(t,\varpi _{0})+\ldots \end{aligned}$$

$$\begin{aligned} \underline{\tilde{w}}(t,\varpi _{0})&=\left( \left( \varpi _{0}-1\right) e^{10t}\right) +\left( \frac{11}{10}\left( \varpi _{0}-1\right) ^{2}\left( e^{10t}-e^{20t}\right) \right. \\&\quad \left. +\left( \varpi _{0}-1\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) \right) +\ldots \end{aligned}$$

Similarly, for upper case we will get

$$\begin{aligned} \overline{\tilde{w}}_{0}(t,\varpi _{0})= & {} \left( 1-\varpi _{0}\right) e^{10t}, \\ \overline{\tilde{w}}_{1}(t,\varpi _{0})= & {} \frac{11}{10}\left( 1-\varpi _{0}\right) ^{2}\left( e^{10t}-e^{20t}\right) +\left( 1-\varpi _{0}\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) , \end{aligned}$$

and so on. So the desired solution for the upper case is

$$\begin{aligned} \overline{\tilde{w}}(t,\varpi _{0})&=\overline{\tilde{w}}_{0}(t,\varpi _{0})+\overline{\tilde{w}}_{1}(t,\varpi _{0})+\ldots \\ \overline{\tilde{w}}(t,\varpi _{0})&=\left( \left( 1-\varpi _{0}\right) e^{10t}\right) +\left( \frac{11}{10}\left( 1-\varpi _{0}\right) ^{2}\left( e^{10t}-e^{20t}\right) \right. \\&\quad \left. +\left( 1-\varpi _{0}\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) \right) +\ldots \end{aligned}$$

So, the solution is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \underline{\tilde{w}}(t,\varpi _{0}) &{} =\left( \left( \varpi _{0}-1\right) e^{10t}\right) +\left( \frac{11}{10}\left( \varpi _{0}-1\right) ^{2}\left( e^{10t}-e^{20t}\right) \right. \\ &{}\quad \left. +\left( \varpi _{0}-1\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) \right) +\ldots \\ \overline{\tilde{w}}(t,\varpi _{0}) &{} =\left( \left( 1-\varpi _{0}\right) e^{10t}\right) +\left( \frac{11}{10}\left( 1-\varpi _{0}\right) ^{2}\left( e^{10t}-e^{20t}\right) \right. \\ &{}\quad \left. +\left( 1-\varpi _{0}\right) ^{2}\left( t\sinh \left( 10t\right) +t\cosh \left( 10t\right) \right) \right) +\ldots \end{array}\right. } \end{aligned}$$

Conclusion and Future Work

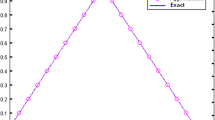
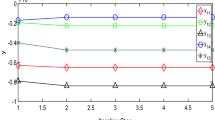
In this paper, we have studied a nonlinear integro-differential equation of the nth order in a fuzzy context. To obtain an approximate solution to the proposed model via a fuzzy modified Laplace transformation, we have developed a proper procedure. Some examples of various orders are given to ensure the accuracy of the proposed method. We have computed a solution to a nonlinear system of fuzzy integro-differential equations of second order. We have simulated the numerical results of the problems in terms of 2D and 3D graphs in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. The graphs indicate that the solution represents a fuzzy number because the lower bound is an increasing function while the upper bound is a decreasing function. For various values of uncertainty, we also presented the dynamics of the derived solutions of the examples in Figs. 3, 6, 9, and 12. We have studied an application of the nonlinear fuzzy IDE in the population model. The analysis was carried out through the proposed method. Nowadays, fractional order operators have got tremendous attention of the researchers due to its heredity and memory features [39,40,41]. Also, fuzzy fractional operators have been used for the modeling of different phenomena [42,43,44]. In the future, one may solve the proposed equation using various analytical methods in a fuzzy concept under the different fractional operators.