Introduction

Higher-order boundary value problems are considered as one of the most important models to be dealing with while modelling both linear and nonlinear phenomena in real life. These models have been used for simulating several natural phenomena in science and engineering including thermodynamics, fluid mechanics, astronomy and astrophysics, and many other similar models. They have been used to simulate the action of heated fluid with the action of rotation [1, 2].

Also, the torsional vibration of some uniform beams is modelled by higher-order boundary value problems (BVP) in [3]. In addition, it has been used in modeling the viscoelastic or inelastic flows and studying the effect on the deformation on beams which can be simulated using a fourth-order BVP [4]. Many other models are simulated using these higher-order versions of the BVP and the reader can refer to [5,6,7,8] and their references.

The study of the higher-order boundary value problem (HBVP) has gotten the immense attention of researchers’s community for the last few decades. This was the reason that many researchers tried to investigate the solution to these problems using different techniques. These techniques are based on many different approaches and each has its advantages and disadvantages. For example, the reproducing kernel space method [9], sinc-Galerkin method [10], differential transform [11], homotopy perturbation method [12,13,14], quintic spline [15], Adomian decomposition method [16, 17], B-spline method [18], non-polynomial spline functions [19], Chebychev polynomial solutions [20], Euler matrix method [21], Galerkin residual technique with Bernstein and Legendre polynomials [22], variational iteration method [23], homotopy perturbation [24], Legendre-homotopy method [25], Haar wavelets [26], Legendre-Galerkin method [27], wavelet based hybrid method [28], Laplace series decomposition method [29], Quintic B-spline collocation method [30] and Spectral monic chebyshev approximation [31]. In addition, the fractional-order models of this class of equations gain sand increasing interest with the rise of the fractional calculus due to their applications and ability to simulate complex phenomenons. Ganji et. al use a fractional-order model to simulate the brain tumor and their behaviors [32]. Also, Ganji et. al in [33] investigated a fractional population model including the prey-predator and logistic models. A novel numerical approach in [34] was presented to find the solution of a fractional optimal control problem with the Mittag–Lefler kernel. A collocation method based on shifted Chebyshev polynomials of the third kind was introduced in [35] by Polat et. al to solve the multi-term fractional model of fractional order. Further models and methods were proposed for solving real-life phenomenon like the wave equation [36], Bagely–Torvik equation [37, 38], ODE with Gomez–Atangana–Caputo derivative [39], fractional KdV and KdV-Burgers [40], time-fractional Fisher’s model [41], time-fractional Klein-Gordon equations [42], fractional order diffusion equation [43] and mathematical model of atmospheric dynamics of CO2 gas [44].

In this paper, we are concerned with the study of the HBVP in the form

$$\begin{aligned} u^{(2r)}(x)+\sum _{m=0}^{2r-1}\sigma _{m}u^{(m)}(x)=\xi (x,u(x)), \quad 0\le x \le 1,\quad r=2,3,4,\ldots \end{aligned}$$
(1.1)

with boundary conditions

$$\begin{aligned} u^{(i)}|_{x=0}=\alpha _{i}, \quad u^{(i)}|_{x=1}=\beta _{i},\quad i=0,1,2,\ldots ,r-1, \end{aligned}$$
(1.2)

where \(\xi (x,u(x))\) and u(x) are both continuous functions defined on the interval \(0\le x\le 1\) and \(\sigma _{m}\) is a constant.

We are concerned in this work with the application of a novel collocation method based on Genocchi polynomials for solving Eq. (1.1). Genocchi collocation (GC) techniques have been playing an increasing role in solving different types of application problems. Researchers have been trying to expand the use of this technique for solving application problems in different areas of science and engineering. For example, Genocchi polynomials have been used for solving fractional partial differential equations using the definitions of Atangana-Baleanu derivative [45]. Also, a fractional model of the SEIR epidemic has been investigated in [46] with the aid of the same polynomials. Other models including nonlinear fractional differential equations [47], integral and integrodifferential equations [48], and delay differential equations [49]. As far as we knew, this is the first attempt to solve HBVP using the Genocchi collocation technique.

The novelty of the proposed technique can be summarized in the following few points:

  • A novel numerical technique based on the Genocchi polynomials is presented.

  • This technique is applied for the linear and nonlinear case and the nonlinear system especially is solved using a new iterative technique.

  • The method is tested on five different examples to ensure that the method is effective and accurate.

The organization of the paper is as follows: Sect. 2 provides some preliminaries regarding the proposed technique. Section 3, presents the function approximation, fundamental relations, Genocchi operational matrix, GC scheme, and a few related theorems. The upper bound for the proposed method is illustrated in Sect. 4 in details. Section 5 describes the results and discussions. Conclusions and future research guidance are listed in the last section.

Basic Definitions

In this section, some basics regarding the Genocchi numbers and polynomials shall be presented. Genocchi polynomials have been widely used in multiple areas of mathematics including the complex analytic number and other relative branches. We can define the Genocchi polynomials and Genocchi numbers by the generating functions [49,50,51]:

$$\begin{aligned}&Q(x,t)=\frac{2te^{xt}}{e^{t}+1}=\sum _{n=0}^{\infty }G_n (x) \frac{t^n}{n!}, \quad \quad \quad (|t|<\pi ) \end{aligned}$$
(2.1)
$$\begin{aligned}&Q(t)=\frac{2t}{e^{t}+1}=\sum _{n=0}^{\infty }G_n\frac{t^n}{n!}, \quad \quad \quad (|t|<\pi ) \end{aligned}$$
(2.2)

where \(G_n(x)\) are the Genocchi polynomials of degree n and are defined on interval [0, 1] as

$$\begin{aligned} G_n (x)=\sum _{k=0}^{n} \left( {\begin{array}{c}n\\ k\end{array}}\right) G_k x^{n-k}, \end{aligned}$$
(2.3)

where \(G_k\) is the Genocchi numbers.

These polynomials have many interesting properties and the most important among them is the differential property which can be generated by differentiating both sides of Eq. (2.3) concerning x, then we have

$$\begin{aligned} \frac{dG_n(x)}{dx}=nG_{n-1}(x). \qquad n\ge 1 \end{aligned}$$
(2.4)

If we differentiate (2.3) k times then we have

$$\begin{aligned}&\frac{d^kG_n(x)}{dx^k}={\left\{ \begin{array}{ll} 0,\qquad \qquad \qquad \qquad n \le k \\ k! \left( {\begin{array}{c}n\\ k\end{array}}\right) G_{n-k}(x). \qquad n > k, \end{array}\right. } k ,n \in N \cup \{0\} \end{aligned}$$
(2.5)
$$\begin{aligned}&G_n(1)+G_n(0)=0. \qquad n>1 \end{aligned}$$
(2.6)

Next, we will use the differential property to generate the Genocchi operational matrix of differentiation which will be used later for solving Eq. (1.1).

Genocchi Differentiation Matrices

First, we express the approximate solution in Eq. (1.1) in the following form

$$\begin{aligned} u_N(x)=\sum _{n=1}^{N}c_n G_n(x)=\mathbf {G}(x)\mathbf {C}, \quad \quad \quad (N\ge 2r) \end{aligned}$$
(2.7)

where \(\mathbf {C}\) are the unknown Genocchi coefficients and \(\mathbf{G}(x) \) are the Genocchi polynomials of the first kind, then they are given by

$$\begin{aligned} \mathbf {C}^T= \begin{bmatrix} c_1&c_2&\ldots&c_N \end{bmatrix}, \qquad \mathbf {G}(x)=\begin{bmatrix} G_1(x)&G_2(x)&\ldots&G_N(x) \end{bmatrix}. \end{aligned}$$

The \(k^{th}\) derivative of \(u_N(x)\) can be expressed by

$$\begin{aligned} u_N^{(k)} (x)=\sum _{n=1}^{N}c_n G_n^{(k)} (x)=\mathbf {G}^{k}(x) \mathbf {C} = \mathbf {G}(x) \mathbf {M}^k \mathbf {C},\qquad \qquad k=1,2,\ldots ,2r \end{aligned}$$
(2.8)

where \(\mathbf{M} \) is \(N \times N\) operational matrix of derivative, and can be defined as

$$\begin{aligned} \mathbf {M}=\begin{bmatrix} 0 &{} 2 &{}0 &{}\cdots &{}0\\ 0 &{} 0&{}3&{}\cdots &{}0\\ \vdots &{} \vdots &{}\vdots &{}\cdots &{}\vdots \\ 0 &{} 0&{}0&{}\cdots &{}N\\ 0 &{} 0&{}0&{}\cdots &{}0\\ \end{bmatrix}. \end{aligned}$$
(2.9)

Using collocation points defined by

$$\begin{aligned} x_i=\frac{i-1}{N-1},\qquad i=1,2,\ldots ,N \end{aligned}$$

to approximate the Genocchi polynomials, we reach the following

$$\begin{aligned} \mathbf {G}=\begin{bmatrix} G_1(x_1)&{}G_2(x_1)&{}\ldots &{}G_N(x_1)\\ G_1(x_2)&{}G_2(x_2)&{}\ldots &{}G_N(x_2)\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ G_1(x_N)&{}G_2(x_N)&{}\ldots &{}G_N(x_N)\\ \end{bmatrix}. \end{aligned}$$

In the next section, we shall demonstrate the main steps for applying the collocation technique based on Genocchi polynomials.

Genocchi Collocation Technique

In this section, we shall investigate the adaptation of our proposed technique for solving a linear and nonlinear form of the HBVP. First, we begin with the linear form in the next subsection.

Case I: Linear Case

We first begin by letting \(\xi (x,u)=f(x)\) into the main equation which may lead us to

$$\begin{aligned} \frac{d^{2r}u(x)}{dx^{2r}}+ \sum _{m=0}^{2r-1}{\sigma _m}{\frac{d^{m}u(x)}{dx^{m}}}=f(x). \qquad 0\le x \le 1 ,\quad r=2,3,\ldots \end{aligned}$$
(3.1)

The approximate solution for u(x) can be represented by

$$\begin{aligned} u(x)\approx u_N(x)=\sum _{n=1}^{N}c_n G_n(x)=\mathbf {G}(x)\mathbf {C}, \end{aligned}$$
(3.2)

where the Genocchi coefficients vector \(\mathbf {C}\) and the Genocchi polynomials vector \( \mathbf {G}(x)\) are given by

$$\begin{aligned} \mathbf {C}^T= \begin{bmatrix} c_1&c_2&\ldots&c_N \end{bmatrix}, \qquad \mathbf {G}(x)=\begin{bmatrix} G_1(x)&G_2(x)&\ldots&G_N(x) \end{bmatrix}, \end{aligned}$$

and the \(k^{th}\) derivative of \(u_N(x)\) can be expressed in the form

$$\begin{aligned} u_N^{(k)} (x)=\sum _{n=1}^{N}c_n G_n^{(k)} (x)=\mathbf {G}(x) \mathbf {M}^k \mathbf {C}. \qquad \qquad k=1,2,\ldots ,2r \end{aligned}$$
(3.3)

After substituting the approximate solution represented in Eq. (3.2) and its derivatives from Eq. (3.3), we reach the following theorem.

Theorem 3.1

If the assumed approximate solution for the problem (3.1) in Eq. (3.2), then the discrete Genocchi system for determining the unknown coefficients can be represented in the form

$$\begin{aligned} \sum _{n=1}^N\,c_n\,G_n^{(2r)}(x_i)+\sum _{m=0}^{2r-1}\sum _{n=1}^N\,c_n\,\sigma _{m}\,\,G_n^{(m)}(x_i) =\sum _{i=1}^N\,f(x_i) . \end{aligned}$$
(3.4)

Proof

If we replace the approximate solution defined in Eqs. (3.2), (3.3) into the main equation in (3.1) and then by applying the collocation points \(x = x_i\) defined as

$$\begin{aligned} x_i=\frac{i-1}{N-1}, \qquad i=1,2,\ldots ,N \end{aligned}$$

we reach the following matrix form for the Genocchi system as

$$\begin{aligned} \varvec{\Theta } C=\varvec{\Xi } \end{aligned}$$
(3.5)

where

$$\begin{aligned} \varvec{\Theta }=\left[ \mathbf {M}^{2r}+\sum _{m=0}^{2r-1}\sigma _m \mathbf {M}^m\right] \mathbf {G} \end{aligned}$$

and

$$\begin{aligned} \varvec{\sigma }_m=\begin{bmatrix} \sigma _m&{}0&{}\ldots &{}0\\ 0&{}\sigma _m&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}\sigma _m\\ \end{bmatrix},\qquad \varvec{\Xi }=\begin{bmatrix} f(x_1)\\ f(x_2)\\ \vdots \\ f(x_{N})\\ \end{bmatrix}. \end{aligned}$$

Also, the boundary conditions can be described in the form

$$\begin{aligned} \mathbf {G}(0)\mathbf {M}^i\mathbf {C}=[\alpha _i],\qquad \mathbf {G}(1)\mathbf {M}^i\mathbf {C}=[\beta _i]. \qquad i=0,1,\ldots ,r-1 \end{aligned}$$

Finally, replacing the first and last r rows of the augmented matrix \([\varvec{\Theta }, \varvec{\Xi }]\) with boundary conditions, then the new augmented matrix becomes

$$\begin{aligned} {\bar{\varvec{\Theta }} C=\bar{\Xi }}, \end{aligned}$$

which gives a \(N \times N\) system of linear algebraic equations. By solving this system the unknown coefficients \(\mathbf {C}\) can be evaluated. \(\square \)

Next, we will investigate the application of Genocchi collocation method for solving the nonlinear form of Eq. (1.1).

Case II: Nonlinear Case

In this subsection, we assign the value of \(\xi (x,u)=f(x)-q(x)(u(x))^v\) in Eq. (1.1). Thus, we reach the following equation

$$\begin{aligned} \frac{d^{2r}u(x)}{dx^{2r}}+ \sum _{m=0}^{2r-1}{\sigma _m}{\frac{d^{m}u(x)}{dx^{m}}}+q(x)\left( u(x)\right) ^v=f(x). \qquad 0\le x \le 1 ,\quad r=2,3,\ldots \end{aligned}$$
(3.6)

The nonlinear term in Eq. (3.6) after substituting collocation points \( x=x_i\) is needed to be evaluated and to do this we need the following theorem.

Theorem 3.2

[52] The nonlinear term of the function \(u^v(x_i),i=1,2,\ldots ,N\) can be expressed as in the following form

$$\begin{aligned} \begin{aligned} \begin{bmatrix} u^v(x_1)\\ u^v(x_2)\\ \vdots \\ u^v(x_{N})\\ \end{bmatrix}&=\begin{bmatrix} u(x_1)&{}0&{}\ldots &{}0\\ 0&{}u(x_2)&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}u(x_{N})\\ \end{bmatrix}^{v-1} \begin{bmatrix} u(x_1)\\ u(x_2)\\ \vdots \\ y(x_{N})\\ \end{bmatrix}\\&=\bar{(\varvec{U})}^{v-1}\mathbf {U}\\&=(\bar{\varvec{G}\bar{C}})^{v-1}\mathbf {GC} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \bar{\varvec{G}}=\begin{bmatrix} G(x_1)&{}0&{}\ldots &{}0\\ 0&{}G(x_2)&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}G(x_{N})\\ \end{bmatrix},\qquad \bar{\varvec{C}}=\begin{bmatrix} \mathbf {C}&{}0&{}\ldots &{}0\\ 0&{}\mathbf {C}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}\mathbf {C}\\ \end{bmatrix}. \end{aligned}$$

Substituting this into Eq. (3.6), we conclude to the next theorem.

Theorem 3.3

If the approximate solution of the discrete Genocchi system of Eq. (3.6) after expanding the nonlinear term using Theorem 3.2, then the system can be expressed in the form

$$\begin{aligned} \frac{d^{2r}u(x_i)}{dx^{2r}}+ \sum _{m=0}^{2r-1}{\sigma _m}{\frac{d^{m}u(x_i)}{dx^{m}}}+q(x_i)\left( u(x_i)\right) ^v=f(x_i). \qquad 0\le x \le 1 ,\quad r=2,3,\ldots \end{aligned}$$
(3.7)

By the same way presented in Sect. 3.1 and with the aid of the previous theorem, the Genocchi matrix system can be written in matrix form

$$\begin{aligned} {\tilde{\varvec{\Theta }} C=\varvec{\Xi }} \end{aligned}$$

where

$$\begin{aligned} \tilde{\varvec{\Theta }}=\left( \left[ \mathbf {M}^{2r}+\sum _{m=0}^{2r-1}\sigma _m \mathbf {M}^m \right] +\mathbf {Q}({\bar{\varvec{G}}\bar{C}})^{v-1}\right) \mathbf {G}, \end{aligned}$$

and

$$\begin{aligned}&\displaystyle e_m=\begin{bmatrix} \sigma _m&{}0&{}\ldots &{}0\\ 0&{}\sigma _m(x_2)&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}\sigma _m(x_{N})\\ \end{bmatrix},\qquad \mathbf {Q}=\begin{bmatrix} q(x_1)&{}0&{}\ldots &{}0\\ 0&{}q(x_2)&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}q(x_{N})\\ \end{bmatrix},\\&\displaystyle \varvec{\Xi }=\begin{bmatrix} f(x_{1})\\ f(x_{2})\\ \vdots \\ f(x_{N})\\ \end{bmatrix}. \end{aligned}$$

It is worth mentioning that the nonlinear part in Eq. (3.6) may take the form \(\xi (x,u)=f(x)-q(x)u^v(x) u^{(r)}(x)\) or \(\xi (x,u)=f(x)-q(x)u^{(v)}(x) u^{(r)}(x)\), then the approximation for this part shall take the form

$$\begin{aligned} \begin{aligned} u^v(x) u^{(r)}(x)&=(\bar{\varvec{U}})^v \mathbf {U}^{(r)}\\&=({\bar{\varvec{G}} \bar{C}})^v \mathbf {G M}^r\mathbf {C}\\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \begin{bmatrix} u^{(v)}(x_1) u^{(r)}(x_1)\\ u^{(v)}(x_2) u^{(r)}(x_2)\\ \vdots \\ u^{(v)}(x_N) u^{(r)}(x_N)\\ \end{bmatrix}&=\begin{bmatrix} u^{(v)}(x_1)&{}0&{}\ldots &{}0\\ 0&{}u^{(v)}(x_2)&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}u^{(v)}(x_N)\\ \end{bmatrix}\begin{bmatrix} u^{(r)}(x_1)\\ u^{(r)}(x_2)\\ \vdots \\ u^{(r)}(x_N)\\ \end{bmatrix}\\&=({\bar{\varvec{U}}})^{(v)} \mathbf {U}^{(r)}\\&=({\bar{\varvec{G}} (\bar{M})}^v \bar{\varvec{C}})\mathbf {G M}^r \mathbf {C}\\ \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\bar{\varvec{M}}}=\begin{bmatrix} \mathbf {M}&{}0&{}\ldots &{}0\\ 0&{}\mathbf {M}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}\mathbf {M}\\ \end{bmatrix}. \end{aligned}$$

Replacing the first r and last r rows of the augmented matrix with boundary conditions matrices then the augmented matrix becomes as

$$\begin{aligned} {\breve{\varvec{\Theta }} C=\bar{\Xi }}. \end{aligned}$$

Solving this \( (N \times N)\) linear system to obtain N unknown coefficients using the algorithm in [52]. In the next section, we acquire the upper bound of error for the proposed method.

Error Analysis

In this section, we shall provide the error bound for the approximated function f(x). First, suppose that the function f(x) be an arbitrary element of \(H=L^2 [0,1]\) and \(U=span\{{G_1 (x),G_2 (x), \ldots ,G_N (x)}\} \subset H \) where \(\{{G_n (x)}\}_{n=1}^N \) is the set of Genocchi polynomials. Let f(x) has a unique best approximation in the space U, that we can say that \( f^* (x)\) such that \(\forall u(x) \in U \) and \(\left\| f(x)-f^* (x)\right\| _2 \le \left\| f(x)-u(x)\right\| _2 \). Since, \( f^* (x)\in U \), there exist a unique coefficient in the form \({\{c_n \}}_{n=1}^N \) such that

$$\begin{aligned} f(x) \cong f^*(x)=\sum _{n=1}^{N}c_n G_n(x)=\mathbf {C G(x)}, \end{aligned}$$

where \(\mathbf {C}=\left[ c_1,c_2,c_3,\ldots ,c_N \right] \), \(\mathbf {G(x)}=\left[ G_1 (x),G_2 (x),\ldots ,G_N (x)\right] ^{T}\). In order to obtain the values of the coefficients, we need the following lemmas.

Lemma 4.1

Assume that \(f\in H=L^2 [0,1]\) , is an arbitrary function that can be approximated by the Genocchi series \(\sum _{n=1}^{N}c_n G_n(x)\), then the unknown coefficients \({\{c_n \}}_{n=1}^N \) can be evaluated from the following form

$$\begin{aligned} c_n=\frac{1}{2 n!} \left( f^{(n-1)} (1)+f^{(n-1)} (0)\right) . \end{aligned}$$

Proof

For proof, please refer to [49]. \(\square \)

Lemma 4.2

Suppose that \(f(x) \in C^{(n+1)} [0,1]\) and \( U=span\{{G_1 (x),G_2 (x),\ldots ,G_N (x)}\}\) where \(C^T G\) is the best approximation of the function f(x) out of U, then

$$\begin{aligned} \left\| \xi _N (f)\right\| \le \frac{h^{\frac{2n+3}{2}}W}{(n+1)! \sqrt{2n+3}}\qquad , x\in [x_i,x_{i+1} ] \subseteq [0,1] \end{aligned}$$

where \(\left\| \xi _N (f)\right\| =\left\| f(x)-C^T G\right\| \) and \(W=\max \limits _{ x\in [0,1]} |f^{(n+1)} (x)| \) and \(h=x_{i+1}-x_i\) .

Proof

For proof, please refer to [47]. \(\square \)

With the aid of the previous two lemmas, we reach the following theorem.

Theorem 4.1

Suppose that the function u(x) be an enough smooth function and that \(u_N (x)\) be the truncated Genocchi series solution of u(x). Then the error bound can be in the form

$$\begin{aligned} \left\| u(x)-u_N (x)\right\| _ \infty \le \varvec{\aleph } \frac{\mathbf {W}}{(n+1)! \sqrt{2n+3}}, \end{aligned}$$

where \(\varvec{\aleph }=\frac{\frac{2n+3}{2}}{1-\ell _\mathcal {M}}\) and \(\mathbf {W}=\max \limits _{ x\in [0,1]} |f^{(n+1)} (x)|\).

Proof

The operator form of Eq. (1.1) can be in the following form

$$\begin{aligned} {\mathcal {L}} u=u^{(2r)}=f(x)+{\mathcal {M}}{(x,u(x))}, \end{aligned}$$
(4.1)

where the differential operator \({\mathcal {L}}\) can be defined by

$$\begin{aligned} {\mathcal {L}}=\frac{d^{2r}}{dx^{2r}}, \end{aligned}$$
(4.2)

and the inverse of the operator \({\mathcal {L}}^{-1}\) is considered as the 2r fold integral operator of the differential operator \({\mathcal {L}}\) and can take the form

$$\begin{aligned} {\mathcal {L}}^{-1}=\underbrace{\int _{0}^{x} \ldots \int _{0}^{x}(.)}_{(2r)times} \underbrace{dx}_{(2r)times}. \end{aligned}$$
(4.3)

Then, by applying the inverse operator \({\mathcal {L}}^{-1}\) defined before on Eq. (1.1) we get

$$\begin{aligned} \begin{aligned} u(x)&={\mathcal {L}}^{-1} f(x)+{\mathcal {L}}^{-1} {\mathcal {M}}{(x,u(x))} \\&=\underbrace{\int _{0}^{x} \ldots \int _{0}^{x} f(x)}_{(2r)times} \underbrace{dx}_{(2r)times} +\underbrace{\int _{0}^{x} \ldots \int _{0}^{x}{\mathcal {M}}{(x,u(x))}}_{(2r)times} \underbrace{dx}_{(2r)times}\\&= {\mathcal {F}}(x)+{\mathcal {H}}(x,u(x)). \end{aligned} \end{aligned}$$
(4.4)

Next, if we approximate both the functions f(x) and u(x) using the truncation of the Genocchi polynomials as \(\chi (x)\) and \({\mathcal {H}}(x,u_N(x))\), respectively, then the approximation for \(u_{N}(x)\) can be defined in the form

$$\begin{aligned} u_N (x)=\chi (x)+{\mathcal {H}}(x,u_N(x)). \end{aligned}$$
(4.5)

Therefore, by subtracting the last two equations we conclude that

$$\begin{aligned} \begin{aligned} \left\| u(x)-u_N (x)\right\| _ \infty&=\left\| {\mathcal {F}}(x)-\chi (x)+{\mathcal {H}}(x,u(x))-{\mathcal {H}}(x,u_N(x))\right\| _\infty \\&=\left\| {\mathcal {F}}(x)-\chi (x))\right\| +\left\| {\mathcal {H}}(x,u(x))-{\mathcal {H}}(x,u_N(x))\right\| _\infty \\&\le \left\| {\mathcal {F}}(x)-\chi (x)\right\| +\ell _{\mathcal {M}}\left\| u(x)-u_N (x)\right\| _ \infty , \end{aligned} \end{aligned}$$
(4.6)

where \(\ell _{\mathcal {M}}\) defined as the Lipschitz constant for the function \({\mathcal {M}}(x,u_N(x))\), then

$$\begin{aligned} \begin{aligned} \left\| u(x)-u_N (x)\right\| _ \infty&\le \frac{1}{1-\ell _{\mathcal {M}}}\left\| {\mathcal {F}}(x)-\chi (x)\right\| _ \infty \\&\le \frac{1}{1-\ell _{\mathcal {M}}}\left\| {\mathcal {F}}(x)- \xi _N (f(x))\right\| _ \infty \end{aligned}. \end{aligned}$$
(4.7)

Finally, with the aid of Lemma (4.2) we reach the following

$$\begin{aligned} \begin{aligned} \left\| u(x)-u_N (x)\right\| _ \infty&\le \frac{1}{1-\ell _{\mathcal {M}}} \frac{h^{\frac{2n+3}{2}}W}{(n+1)! \sqrt{2n+3}} \\&\le \varvec{\aleph } \frac{h^\frac{2n+3}{2} \mathbf {W}}{(n+1)! \sqrt{2n+3}}, \end{aligned} \end{aligned}$$
(4.8)

where \(\varvec{\aleph }=\frac{1}{1-\ell _m}\) .

From Eq. (4.8) we can conclude that the theorem gives the error for \(u_N (x)\) which shall give the solution when using sufficient values of n. \(\square \)

Residual Error Function

In this subsection, we can easily check the accuracy of the suggested method in terms of the residual error function. Since the truncated Genocchi series in Eq. (2.7) is considered as an approximate solution of Eq. (1.1), then by substituting the approximate solution \(u_N (x)\) and its derivatives into Eq. (1.1), the resulting equation must be satisfied and when substituting the collocation points defined as

$$\begin{aligned} x=x_i \in [0,1],\qquad i=1,2,\ldots ,N. \end{aligned}$$

The residual error function for the approximate solution can be calculated in the from

$$\begin{aligned} \mid \Re _N (x_i)\mid =\mid u^{(2r)}(x)+\sum _{m=0}^{2r-1}\sigma _{m}u^{(m)}(x)-\xi (x,u)\mid \cong 0, \end{aligned}$$
(4.9)

or

$$\begin{aligned} \Re _N (x_i)\le 10^{-\tau _{i}}, \end{aligned}$$

where \(\Re _N (x_i)\) are the residual error function defined at the collocation points \(x_i\) and \(\tau _{i}\) is any positive integer that can be pre-described and can be defined as the tolerance for reaching the desired error. Then, the value of the number of iterations N is increased until the residual error \(\Re _N (x_i)\) at each of the points become smaller than the prescribed tolerance \(10^{\tau _{i}}\) which shall prove that the method converge to the desired solution as the residual error approaches zero. Also, we can calculate the error function at each of the collocation points to prove the efficiency of the proposed technique that can be described as

$$\begin{aligned} \Re _N (x_i)= u_{N}^{(2r)}(x)+\sum _{m=0}^{2r-1}\sigma _{m}u_{N}^{(m)}(x)-\xi (x,u_N(x)). \end{aligned}$$

Then, if \(u_N (x) \rightarrow 0\) , as N has sufficiently enough value, then the residual error decreases and this proves that the proposed method converge correctly.

Numerical Simulation

In this section, we are interested to show the efficiency of our proposed method for solving the class of HOBVP through different forms of linear and nonlinear examples. The method is tested and compared to other relevant methods form the literature including [23, 26, 27, 31, 52,53,54,55,56,57,58,59,60,61,62]. The results presented are being acquired with the aid of Matlab 2015. Also, the performance will be checked through calculating the maximum absolute error from the following equation

$$\begin{aligned} \left\| \mathbf {e}_N(x)\right\| =max(u(x)-u_N(x)) \end{aligned}$$

Example 5.1

[52,53,54,55] In our first example, we consider a linear form of the BVP with variable c in the form

$$\begin{aligned} \frac{d^4 u}{dx^4}=(1+c)\frac{d^2 u}{dx^2}-c u+\frac{1}{2}c x^2-1,\qquad 0\le x\le 1 , \end{aligned}$$

with boundary conditions

$$\begin{aligned} u(0)=u^{\prime }(0)=1 , \qquad u(1)=\sinh (1)+\frac{3}{2} , \qquad u^{\prime }(1)=\cosh (1)+1 , \end{aligned}$$

and exact solution

$$\begin{aligned} u(x)=1+\frac{1}{2}x^2+\sinh (x) . \end{aligned}$$

We need first to find the approximate solution \(u_N(x)\) in terms of Genocchi series for \(N=6\) in the form

$$\begin{aligned} u(x)=c_1G_1(x)+c_2G_2(x)+\cdots +c_6G_6(x). \end{aligned}$$

Then

$$\begin{aligned} \mathbf {M}^2=\begin{bmatrix} 0 &{}\quad 0 &{}\quad 6 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 12 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 20 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 30 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{bmatrix}, \mathbf {M}^4=\begin{bmatrix} 0 &{}\quad 0 &{} \quad 0 &{}\quad 0 &{}\quad 120 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 360\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}. \end{aligned}$$

Using collocation points \(x_i=\frac{i-1}{5},\quad i=1,2,\ldots ,6\), then the augmented matrix can be acquired in the form

$$\begin{aligned}{}[\varvec{\Theta ,\Xi }]=\begin{bmatrix} 10 &{}\quad -10&{}\quad -66 &{}\quad 142 &{}\quad 120&{}\quad -720&{},&{}- 1\\ 10 &{}\quad -6 &{}\quad -70.8&{}\quad 87.12&{}\quad 234.88&{}\quad -501.5808&{},&{}-0.8\\ 10 &{}\quad -2 &{}\quad -73.2&{}\quad 29.36&{}\quad 293.28&{}\quad -178.9056&{},&{}-0.2\\ 10 &{}\quad 2 &{}\quad -73.2&{}\quad -29.36&{}\quad 293.28&{}\quad 178.9056&{},&{}0.8\\ 10 &{}\quad 6 &{}\quad -70.8&{}\quad -87.12&{}\quad 234.88&{}\quad 501.5808&{},&{}2.2\\ 10 &{}\quad 10 &{}\quad -66&{}\quad -142&{}\quad 120&{}\quad 720&{},&{}4\\ \end{bmatrix}. \end{aligned}$$

Also, the augmented matrix for the boundary conditions can take the forms

$$\begin{aligned} {[}\theta _1;\alpha _0]= & {} \begin{bmatrix} 1&{}\quad -1 &{}\quad 0 &{} \quad 1 &{}\quad 0 &{}\quad -3 &{},&{} 1\\ \end{bmatrix},\\ {[}\theta _1;\alpha _1]= & {} \begin{bmatrix} 0&{}\quad 2 &{}\quad -3 &{}\quad 0 &{}\quad 5 &{}\quad 0 &{}, &{} 1\\ \end{bmatrix},\\ {[}\Theta _3,\beta _0]= & {} \begin{bmatrix} 1&{}\quad 1 &{}\quad 0 &{}\quad -1 &{}\quad 0 &{}\quad 3 &{},&{} 2.6752\\ \end{bmatrix},\\ {[}\Theta _4,\beta _1]= & {} \begin{bmatrix} 0&{}\quad 2&{}\quad 3 &{}\quad 0 &{}\quad -5&{}\quad 0&{}, &{} 2.5341\\ \end{bmatrix}. \end{aligned}$$

Replacing the first two and last two rows with the previous representation of the boundary conditions, the new augmented matrix takes the form

$$\begin{aligned}{}[{\bar{\varvec{\Theta }}},{\bar{\varvec{\Xi }}}]=\begin{bmatrix} 1&{}\quad -1 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad -3 &{},&{} 1\\ 0&{}\quad 2 &{}\quad -3 &{} \quad 0 &{}\quad 5 &{}\quad 0 &{}, &{} 1\\ 10 &{}\quad -2 &{}\quad -73.2&{}\quad 29.36&{}\quad 293.28&{} -178.9056&{},&{}-0.2\\ 10 &{}\quad 2 &{}\quad -73.2&{} \quad -29.36&{}\quad 293.28&{} 178.9056&{},&{}0.8\\ 1&{}\quad 1 &{}\quad 0 &{}\quad -1 &{}\quad 0 &{}\quad 3 &{},&{} 2.6752\\ 0&{}\quad 2&{}\quad 3 &{}\quad 0 &{}\quad -5&{}\quad 0&{}, &{} 2.5341\\ \end{bmatrix}. \end{aligned}$$

Then, by solving the above system the Genocchi coefficients can be found as

$$\begin{aligned} \mathbf {C}=\begin{bmatrix} 1.8376\\ 0.8858\\ 0.2645\\ 0.0529\\ 0.0044\\ 0.0016\\ \end{bmatrix}, \end{aligned}$$

and the approximate solution is

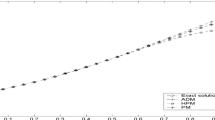
$$\begin{aligned} u_6(x)=1+x+0.4997x^2+0.1678x^3-0.0017x^4+0.0094x^5. \end{aligned}$$

Our method is tested in this example and the results are shown in Table 1 for the maximum absolute error for \(c=10\) and different values of N and compared with Bernoulli method in [52] besides the maximum residual error. Also, Table 2 compare the maximum absolute error for the differential transform method [53], reproductive Kernel method [54], Haar wavelet method [55] and Genocchi method for different values of c at \(N=18\) . It can be noticed from these tables that our method perform better than the other mentioned methods and this can be also witness from Fig. 1 in which the exact and approximate solution are drawn at \(N=18\) and \(c=10\).

Table 1 Absolute and residual error comparison for Example 5.1
Full size table
Table 2 Maximum error comparison for Example 5.1
Full size table
Fig. 1
figure 1

Solution profiles for Example 5.1

Full size image

Example 5.2

[26, 27, 56] Next, we consider our next example of the sixth-order BVP in the special form with a variable coefficient c in the form

$$\begin{aligned} \frac{d^6 u}{dx^6}=(1+c)\frac{d^4 u}{dx^4}-c \frac{d^2 u}{dx^2}+c x,\qquad 0\le x\le 1 \end{aligned}$$

with conditions in the form

$$\begin{aligned}&u(0)= u^{\prime }(0)=1,\quad u^{\prime \prime }(0)=0,\\&u(1)=\sinh (1)+\frac{7}{6} ,\quad u^{\prime }(1)=\cosh (1)+\frac{1}{2} ,\quad u^{\prime \prime }(1)=\sinh (1)+1 , \end{aligned}$$

with exact solution

$$\begin{aligned} u(x)=1+\frac{1}{6}x^3+\sinh (x) . \end{aligned}$$

Table 3 shows the maximum absolute error comparison at \(N=18\) for different values of \((c=10,100,1000)\) with maximum residual error (\(6.4429E-11,6.4429E-11,6.4429E-11\)) between Genocchi method, Variational decomposition method [56], Legendre Galerkin method [27] and wavelet method [26]. In addition, Fig. 2 illustrates the behavior of exact and approximate solution at \(N=18\).

Table 3 Comparison of maximum absolute error for Example 5.2
Full size table
Fig. 2
figure 2

Comparison between exact and approximate Genocchi solution for Example 5.2

Full size image

Example 5.3

[31] Next, we consider another form of the linear sixth-order BVP defined on an extended interval of \([-1,1] \) in the form

$$\begin{aligned} \frac{d^{6}u}{dx^{6}}+u=6[2 x \cos (x)+5 \sin (x)],\qquad -1<x<1 \end{aligned}$$

with boundary conditions

$$\begin{aligned}&u(-1)=u(1)=0,\\&u'(-1)=u'(1)=2 \sin (1),\\&u''(-1)=-u''(1)=4 \cos (1)+2\sin (1), \end{aligned}$$

the exact solution of this problem is

$$\begin{aligned} u(x)=\left( x^2-1\right) \sin (x) . \end{aligned}$$

In this example, we have done the same steps for solving the linear system only with changing the interval of the Genocchi polynomials to \([-1,1]\). Maximum absolute errors for (\(N=20, 24\)) obtained by our method are compared with results obtained by spectral monic Chebyshev approximation [31] and represented in Table 4.

Table 4 Maximum absolute error for Example 5.3
Full size table

Example 5.4

[59] Consider the nonlinear tenth-order BVP of the form

$$\begin{aligned} \frac{d^{10}u}{dx^{10}}=e^{-x}u^{2},\qquad 0<x<1 \end{aligned}$$

with boundary conditions

$$\begin{aligned} u^{(2i)}(0)=1,\qquad u^{(2i)}(1)=e,\qquad \qquad i=0,1,2,3,4 \end{aligned}$$

the exact solution of this problem is

$$\begin{aligned} u(x)=e^x . \end{aligned}$$

The values of the maximum absolute error for different values of N with \( tol=10^{-7}\) are tabulated in Table 5. Also, a comparison is presented for absolute error obtained by Genocchi method with thr new iterative method (NIM) [59] for \(N=14\) in Table 6 .The exact and approximate solution in Fig. 3.

Table 5 Maximum absolute error for Example 5.4
Full size table
Table 6 Error comparison for Example 5.4
Full size table
Fig. 3
figure 3

Comparison between exact and Genocchi solution for Example 5.4

Full size image
Table 7 Comparison of absolute error for Example 5.5
Full size table
Fig. 4
figure 4

Comparison between exact and Genocchi solution for Example 5.5

Full size image

Example 5.5

[23, 61] Consider the following nonlinear twelfth order BVP

$$\begin{aligned} \frac{d^{12}u}{dx^{12}}-\frac{d^3u}{dx^3} - 2e^x u^2=0,\qquad 0\le x \le 1 \end{aligned}$$

with boundary conditions

$$\begin{aligned}&u(0)=u^{\prime \prime }(0)=u^{(4)}(0)=u^{(6)}(0)=u^{(8)}(0)=u^{(10)}(0)=1,\\&u(1)=u^{\prime \prime }(1)=u^{(4)}(1)=u^{(6)}(1)=u^{(8)}(1)=u^{(10)}(1)=\frac{1}{e}, \end{aligned}$$

the exact solution of the problem is

$$\begin{aligned} u(x)= e^{-x} . \end{aligned}$$

Table 7 represents approximate solution compared with the exact solution, and the absolute error obtained by our method with \(N=16\) and \(tol=10^{-10}\) compared with absolute error obtained by Optimal Homotopy Asymptotic Method (OHAM) [61] and Variational iteration method [23]. Figure 4 expresses the relation between exact and approximate Genocchi solution.

Conclusion

In this paper, we have developed a collocation technique based on the Genocchi polynomials for solving a wide class of linear and nonlinear higher-order BVP. The method is analyzed and the basic definitions for the Genocchi polynomials are introduced and then has been used to solve a general form of the problem. The nonlinear form of the presented equation is investigated using this technique and the resulting nonlinear system of algebraic equations is then solved using a novel iterative algorithm that produces the unknown coefficients with less computational effort. To verify the technique, several linear and nonlinear examples of different order are presented and the acquired results are provided throughout some tables and figures. The results show the superiority of the proposed technique to other techniques from the literate especially for the nonlinear examples with the new iterative algorithm. The behavior of the solution can be witnessed from the figures and this supports the claim that the method is fast and effective for providing accurate results. It will be interesting to see in the future how this method will work in solving the nonlinear higher-order delay differential equations.