Introduction

The lattice Boltzmann method (LBM) has attracted much attention in the last decade, and has been considered an alternative approach for modeling and solving several physics and engineering problems. Initially developed from lattice gas automata (LGA) method [34], LBM can also be seen as a discrete version of the Boltzmann equation, which is a mesoscopic approach to study the behavior of a group of particles. Important governing phenomena in fluid mechanics such as mass and momentum conservation equations are well simulated by LBM. Therefore, LBM has shown to be an efficient tool for simulating transport phenomena problems [6, 20, 25]. Furthermore, researchers have been working on different techniques to use LBM to simulate a wide range of problems, such as multiphase flows [14, 22], compressible flows [3, 18], and porous media [11, 23], among others. Also, LBM has shown to be well-suited for parallel computing due to its high locality, and several implementations under homogeneous and heterogeneous system with central processing units (CPUs) and/or graphics processing units (GPUs) [8, 13, 16, 30, 32].

One of the difficulties that arise when using LBM to solve engineering problems is a well-suited model for addressing energy conservation. Many efforts have been made to solve thermal fluid problems, and researchers have used different approaches. One may separate these in three groups: multispeed approach, double population approach and hybrid approach [7, 12, 21].

The multispeed approach is an extension of athermal LBM, in which a single velocity distribution function (VDF) is used. However, in order to correctly capture thermal effects, one should consider a higher number of particle speeds than athermal LBM [12, 21]. Some drawbacks that this approach presents are higher computational resources requirements and severe instabilities. For these reasons, some authors argue that it is not an advantageous approach.

The double population approach, as the name itself suggests, utilizes two distribution functions, one for the velocity field and another one for the temperature or an energy related variable. This approach exhibits good numerical stability and an easily adjustable Prandtl (\(\text {Pr}\)) number [12]. However, most studies consider temperature as a passive scalar, under assumption that viscous dissipation and compression work are negligible. To overcome this, different strategies have been developed to include these effects under double population framework.

In fact, strategy proposed by [12] is used in the present work. In their model, second distribution function is related to total energy instead of temperatures and both compression work and viscous dissipation are easily incorporated through source terms, related to velocity distribution function, in the collision step. This strategy simplifies inclusion of complicated spatial gradient terms, which are usually computed through finite differences or similar schemes in earlier approaches. Although some authors argue that double distribution function approach is not very effective [7, 21], several works have shown good results regarding natural and mixed convection in a square cavity, mostly using passive scalar or internal energy extension approaches [1, 2, 5, 9, 17, 29, 33].

The hybrid approach presents some similarity to double population approach, once velocity fields are still solved by LBM, but now, energy equation is numerically solved by different methods, such as finite differences or finite-volume methods. Lallemand and Luo [21] argues that this approach allows one to avoid inherent LBM instabilities and since these cannot be eliminated even by increasing the number of speeds, they claim this to be the best alternative to simulate thermal fluid flows.

To take advantage of parallel characteristics of LBM, we chose to use double distribution function approach in this paper, by implementing traditional collision and streaming steps in a GPU. First, a validation is conducted for classical natural convection in a square cavity, and results show a good agreement with benchmark solutions from literature. Afterwards, numerical experiments regarding different mixed convection flow conditions are conducted in a 2D lid-driven square cavity. Main contribution of this paper is employment of a double population thermal LBM, developed by [12], for modeling a two-dimensional mixed convection cavity flow problem.

This paper is organized as follows. Section 2 presents the macroscopic flow governing equations for the problems studied, and the assumptions made to derive them. In Sect. 3, the numerical thermal LBM is presented for the two dimensional case, using the D2Q9 lattice model, as well as the boundary conditions implemented to assure macroscopic conditions in the boundary regions. In Sect. 4, numerical procedures employed, namely algorithm, grid dependency tests, shear stresses calculation, stopping criterion and code development and running times, are described. In Sect. 5, results obtained and respective discussions are presented. Finally, conclusions from results are presented.

Problem Formulation

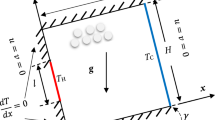
Physical problems under consideration are schematically shown in Fig. 1. First, natural convection in a two-dimensional square cavity of side L is addressed, in which two sidewalls are kept at distinct temperatures \(T_h\) and \(T_c\) (such that \(T_h > T_c\)), while bottom and top walls are considered to be adiabatic. Also, for this case, all velocity components are considered to be zero on the boundaries (\(U_0 = 0\)).

In second problem, a constant upward velocity \(U_0\) is taken into account at the left wall of square cavity. Furthermore, flow is investigated either when the moving wall is maintained at \(T_c\) or at \(T_h\). Accordingly, it is expected to observe flow regimes where buoyancy effects either aid or oppose to rotating flow driven by the moving wall.

In both problems, flow is considered to be two-dimensional, steady, laminar with constant fluid properties, except for the density. This property depends on temperature so that buoyancy term of momentum equation in vertical direction (i.e. gravitational force field direction) is modeled by invoking Boussinesq approximation. This procedure is valid when the temperature difference \({\varDelta } T = T_h - T_c\) is small compared to the average temperature \(T_0\). Viscous dissipation and compression work are considered negligible in the energy conservation equation. Under these assumptions, the governing equations for mass (i.e. continuity), momentum and energy conservation can be written as:

$$\begin{aligned}&\varvec{\nabla } \cdot {\varvec{u}} = 0, \end{aligned}$$
(1a)
$$\begin{aligned}&\varvec{\nabla } \cdot (\rho {\varvec{u}} {\varvec{u}}) = -\varvec{\nabla } p + \varvec{\nabla } \cdot \left[ \mu \left( (\varvec{\nabla }{\varvec{u}}) + (\varvec{\nabla }{\varvec{u}}^T) - (\varvec{\nabla } \cdot {\varvec{u}}){\varvec{I}}\right) \right] + \rho {{\varvec{g}}} [1 - \beta (T - T_{\text {ref}})],\nonumber \\ \end{aligned}$$
(1b)
$$\begin{aligned}&\varvec{\nabla } \cdot \left( {\varvec{u}} T\right) =\varvec{\nabla } \cdot (\alpha \varvec{\nabla } T), \end{aligned}$$
(1c)

where \({\varvec{u}} = (u,v)\) is the 2D velocity vector comprised by, respectively, horizontal u and vertical v components, \(\rho \) stands for density, \(\alpha \) is the thermal diffusivity, p stands for pressure, \(\beta \) is the thermal expansion coefficient, \({{\varvec{g}}}\) is the acceleration due to gravity force field, T is the temperature, \(\mu \) is the dynamic viscosity and subscript \(\text {ref}\) stands for reference temperature.

Fig. 1
figure 1

Schematic representation and boundary conditions for natural (\(U_0 = 0\)) and mixed convection problems (\(U_{0} > 0\))

Full size image

The lid-driven square cavity problem is a well known benchmark problem since it can be employed for distinct practical applications. This kind of flow occurs in coating industries, e.g. producing photographic paper. For this case, field inside cavity has influence on final coating quality [31]. Another application is in electronic systems cooling, since the cavity configuration presents some interesting properties against leakage [27]. Other industrial applications are seen in in chemical processes [19], lubrication grooves in roller bearings, and other cooling systems such as nuclear reactors [4].

Methodology

Lattice Boltzmann Method

In order to solve problems described in previous sections, thermal lattice Boltzmann method (LBM) proposed by [12] is employed. Briefly, this method is described by the evolution in time of two distribution functions: the velocity distribution function f (VDF), related to mass and momentum conservation quantities, and the total energy distribution function h (EDF), related to flow total energy conservation.

Time evolution of discretized distribution functions \(f_i\) and \(h_i\) are described as follows:

$$\begin{aligned}&{f}_i({\mathbf {x}}+{\mathbf {c}}_i {\varDelta } t,t + {\varDelta } t) - {f}_i({\mathbf {x}},t)= - \omega _f \left[ {f}_i({\mathbf {x}},t) - f_i^{\text {eq}}({\mathbf {x}},t)\right] + {\varDelta } t \left( 1-\frac{\omega _f}{2} \right) F_i, \qquad \end{aligned}$$
(2a)
$$\begin{aligned}&{h}_i({\mathbf {x}}+{\mathbf {c}}_i {\varDelta } t,t + {\varDelta } t) - {h}_i ({\mathbf {x}}, t) = -\omega _h \left[ {h}_i ({\mathbf {x}}, t) - h_i^{\text {eq}}({\mathbf {x}},t)\right] \nonumber \\&\quad + Z_i (\omega _h - \omega _f) \left( {f}_i({\mathbf {x}}, t) - f_i^{\text {eq}}({\mathbf {x}}, t) + F_i \frac{{\varDelta } t}{2} \right) {\varDelta } t + q_i, \end{aligned}$$
(2b)

where the index i relates to discrete velocity set \({\varvec{c}}_i\), \(Z = \varvec{c_i} \cdot {\varvec{u}} - {\varvec{u}}^2 / 2\), \({\mathbf {x}} = (x,y)\) is the position vector, and \(\omega _f\) and \(\omega _h\) are the collision frequencies related to velocity and energy distribution functions. For D2Q9 scheme, weight coefficients \(w_i\) and \({\mathbf {c}}_i\) are:

$$\begin{aligned} w_{i}=\left\{ \begin{array}{l}{4 / 9 \text{ for } i=9} \\ {1 / 9 \text{ for } i=\{1\dots 4\}} \\ {1 / 36 \text{ for } i=\{5\dots 8\}} \end{array}\right. , \end{aligned}$$
(3)

and:

$$\begin{aligned} {\mathbf {c}}_{i}=\left\{ \begin{array}{l}{(0,0) \text{ for } i=9} \\ {( \pm 1,0)c,(0, \pm 1)c \text{ for } i=\{1 \ldots 4\}} \\ {( \pm 1, \pm 1)c \text{ for } i=\{5\ldots 8\}} \end{array}\right. , \end{aligned}$$
(4)

where \(c = {\varDelta } x{}/ {\varDelta } t\), so that distribution functions are advected to neighbor nodes in one time step.

Equilibrium VDF and EDF are given by:

$$\begin{aligned}&f_i^{\text {eq}}=w_{i} \rho \left[ 1+\frac{{\varvec{c}}_{i} \cdot {\varvec{u}}}{c^2_s}+\frac{1}{2}\left( \frac{{\varvec{c}}_{i} \cdot {\varvec{u}}}{c^2_s}\right) ^{2}-\frac{{\varvec{u}}^{2}}{2 c^2_s}\right] , \end{aligned}$$
(5a)
$$\begin{aligned}&h_i^{\text {eq}}= w_{i} \rho c_s^{2} \left[ \frac{{\varvec{c}}_{i} \cdot {\varvec{u}}}{c^2_s}+\left( \frac{{\varvec{c}}_{i} \cdot {\varvec{u}}}{c^2_s}\right) ^{2}-\frac{{\varvec{u}}^{2}}{c^2_s}+\frac{1}{2}\left( \frac{{\varvec{c}}_{i} \cdot {\varvec{c}}_{i}}{c^2_s}-D\right) \right] +E f_i^{\text {eq}}, \end{aligned}$$
(5b)

where \(c^2_s = 1/{}3c^2\) is the lattice sound speed, and D is the number of spatial dimensions considered. Terms \(F_i\) and \(q_i\) are related to acceleration \({\varvec{a}}\) due to external force field \({\mathbf {F}} = \rho {\varvec{a}}\) through:

$$\begin{aligned} F_i= & {} w_i \rho \left( \frac{{\varvec{c}}_i \cdot {\varvec{a}} }{c_s^2} + \frac{ ({\varvec{c}}_i \cdot {\varvec{a}}) ({\varvec{c}}_i \cdot {\varvec{u}}) }{c_s^4} - \frac{{\varvec{a}} \cdot {\varvec{u}} }{c_s^2} \right) , \end{aligned}$$
(6a)
$$\begin{aligned} q_{i}= & {} {\varDelta } t \left( 1 - \frac{\omega _h}{2} \right) {\varvec{c}}_i \cdot {\varvec{a}} \left[ w_i \frac{\rho E }{c_s^2} + \left( 1 - \frac{\omega _f}{2} \right) {f}_i({\varvec{x}}, t) \right. \nonumber \\&+ \left. \frac{\omega _f}{2} f_i^{\text {eq}}({\varvec{x}}, t) + \left( 1 - \frac{\omega _f}{2} \right) F_i {\varDelta } t/2 \right] . \end{aligned}$$
(6b)

Macroscopic fields can be evaluated through VDF and EDF as follows:

$$\begin{aligned} \rho= & {} \sum _i {f}_i, \end{aligned}$$
(7a)
$$\begin{aligned} \rho {\varvec{u}}= & {} \sum _i {\varvec{c}}_i {f}_i + \frac{{\varDelta } t}{2} \rho {\varvec{a}}, \end{aligned}$$
(7b)
$$\begin{aligned} \rho E= & {} \sum _{i} {h}_i + \frac{{\varDelta } t}{2} \rho {\varvec{u}} \cdot {\varvec{a}}, \end{aligned}$$
(7c)

where total energy E takes into account internal and kinetic energies, i.e. \(E = c_v T + ({\varvec{u}} \cdot {\varvec{u}})/{}2\), and \(c_v\) is the specific heat coefficient at constant volume.

Through Chapman–Enskog analysis [12], it can be shown that these equations accurately recovers the Navier-Stokes equations up to second order terms:

$$\begin{aligned}&\partial _{t} \rho +\nabla \cdot (\rho {\varvec{u}})=0 \end{aligned}$$
(8a)
$$\begin{aligned}&\partial _{t}(\rho {\varvec{u}})+\varvec{\nabla } \cdot (\rho \varvec{u} {\varvec{u}})=-\varvec{\nabla } p_{0}+\varvec{\nabla } \cdot \varvec{\tau }+\rho {\varvec{a}}, \end{aligned}$$
(8b)
$$\begin{aligned}&\partial _{t}(\rho E)+\varvec{\nabla } \cdot \left[ \left( p_{0}+\rho E\right) {\varvec{u}}\right] =\varvec{\nabla } \cdot (\lambda \varvec{\nabla } T)+\varvec{\nabla } \cdot (\varvec{\tau } \cdot {\varvec{u}} )+\rho {\varvec{u}} \cdot {\varvec{a}}, \end{aligned}$$
(8c)

where \(p_0 = \rho c_s^2\) is the pressure, \(\varvec{\tau } = \mu \left[ (\varvec{\nabla }{\varvec{u}}) + (\varvec{\nabla }{\varvec{u}}^T) - (\varvec{\nabla } \cdot {\varvec{u}}){\varvec{I}}\right] \) is the viscous stress tensor. Viscosity, \(\mu \), and thermal conductivity, \(\lambda \), are related to collision frequencies \(\omega _h\) and \(\omega _f\) through:

$$\begin{aligned} \begin{aligned} \lambda&= \rho c_s^2 \left( \frac{1}{\omega _h} - \frac{{\varDelta } t}{2} \right) \gamma c_p, \\ \mu&= \rho c_s^2 \left( \frac{1}{\omega _f} - \frac{{\varDelta } t}{2} \right) , \end{aligned} \end{aligned}$$
(9)

where \(\gamma \) is the heat capacity ratio.

Boussinesq Approximation

Buoyancy force can be calculated by using Boussinesq approximation:

$$\begin{aligned} \rho {{\varvec{g}}} = \rho _{\text {ref}} {{\varvec{g}}} - \rho _{\text {ref}} {{\varvec{g}}} \beta (T - T_{\text {ref}}), \end{aligned}$$
(10)

where \({{\varvec{g}}}\) is the acceleration due to gravity force field, \(\rho _{\text {ref}}\) is the fluid density at \(T_{\text {ref}}\), and \(\beta \) is the thermal expansion coefficient. In fact, constant part \(\rho _{\text {ref}} \varvec{\textit{g}}\) can be embedded into the pressure, such that effective external force field used in LBM is given by:

$$\begin{aligned} \rho {\varvec{a}} = - \rho _{\text {ref}} {{\varvec{g}}} \beta (T - T_{\text {ref}}). \end{aligned}$$
(11)

In this situation, pressure field predicted by LBM is actually only the dynamic part \(p^{'} = p_{\text {ref}} - \rho _{\text {ref}} \textit{g} y\), where y corresponds to vertical coordinate. As compressible work is negligible, this modification does not play an important role, and it has shown to produce reasonable results [1, 5, 7, 12].

Applying Boussinesq approximations, stationary dimensionless version of Eqs. (8a), (8b) and (8c) can be rewritten by using the following dimensionless variables:

$$\begin{aligned}&\begin{aligned} X&= \frac{x}{H}, \\ Y&= \frac{y}{H}, \end{aligned}&\begin{aligned} U&=\frac{u}{U_{c}}, \\ V&=\frac{v}{U_{c}}, \end{aligned}&\begin{aligned} t^{*}&= \frac{t U_{c}}{H}, \\ \theta&= \frac{T-T_C}{T_H-T_C}. \end{aligned} \end{aligned}$$
(12)

where x and y are, respectively, the horizontal and vertical position (Fig. 1), and t is time. Thus:

$$\begin{aligned}&\nabla ^{*} \cdot {\varvec{U}} = 0, \end{aligned}$$
(13a)
$$\begin{aligned}&\varvec{\nabla ^{*}} \cdot (\rho \varvec{U} {\varvec{U}})=-\varvec{\nabla ^{*}} p_{0}^{*}+ \frac{1}{\text {Re}}\varvec{\nabla ^{*}} \cdot \varvec{\tau ^{*}} - \text {Ri} \, \theta \varvec{{\hat{e}}}, \end{aligned}$$
(13b)
$$\begin{aligned}&\varvec{\nabla ^{*}} \cdot (\rho {\varvec{U}} \theta ) = \varvec{\nabla ^{*}} \cdot \left( \frac{\gamma }{{\text {Pr}} {\text {Re}}} \varvec{\nabla ^{*}} \theta \right) -\gamma {\text {Ec}} p_{0}^{*} \varvec{\nabla ^{*}} \cdot {\varvec{U}} +\frac{\gamma \mathrm {Ec}}{{\text {Re}}} \varvec{\tau ^{*}}: \varvec{\nabla ^{*}} {\varvec{U}}, \end{aligned}$$
(13c)

where versor \(\varvec{{\hat{e}}}\) indicates gravitational field direction \(\varvec{{\hat{e}}} = {{\varvec{g}}}{}/||{{\varvec{g}}}||\). Prandtl, Reynolds, Grashof and Richardson numbers are given by:

$$\begin{aligned} \text {Pr}=\frac{\nu }{\alpha }, \quad \text {Re}=\frac{U_{c} H}{\nu }, \quad \text {Gr}=\frac{g \beta H^{3} {\varDelta } T}{\nu ^{2}}, \quad \text {Ri}=\frac{\text {Gr}}{\text {Re}^2}, \end{aligned}$$
(14)

where \(\nu \) is the kinematic viscosity. Characteristic velocity \(U_c\) for Reynolds number is equal to cavity left wall velocity \(U_c = U_0\) for mixed convection cases. For pure natural convection, i.e., when \(U_0 = 0\), characteristic velocity is related to thermal diffusivity and boundary dimension through \(U_c = \alpha /{H}\).

Boundary Conditions

Macroscopic boundaries conditions for all cases considered in this work are summarized in Table 1.

Table 1 Velocity and thermal boundary conditions considered for all case studies
Full size table

Implementation of boundary conditions for proposed problems was accomplished by extrapolating the nonequilibrium distribution functions of nearest neighbor sites to boundary nodes. Mathematically, this is expressed for, respectively, VDF and EDF as:

$$\begin{aligned}&f_{i}\left( {\varvec{x}}_{b}\right) =f_i^{\text {eq}}\left( {\varvec{x}}_{b}, \rho _{b}, {\varvec{u}}_{b}\right) +\left[ f_{i}\left( {\varvec{x}}_{f}\right) -f_{i}^{(e q)}\left( {\varvec{x}}_{f}\right) \right] , \end{aligned}$$
(15a)
$$\begin{aligned}&h_{i}\left( {\varvec{x}}_{b}\right) =h_i^{\text {eq}}\left( {\varvec{x}}_{b}, \rho _{b}, E_{b}\right) +\left[ h_{i}\left( {\varvec{x}}_{f}\right) -h_{i}^{(e q)}\left( {\varvec{x}}_{f}\right) \right] , \end{aligned}$$
(15b)

where \({\varvec{x}}_b\) is the boundary position, \({\varvec{x}}_n\) is the nearest neighbor node, \({\varvec{u}}_b\) is velocity to be imposed at boundary sites, \(E_b\) is the boundary imposed total energy, which can be computed from boundaries temperatures and velocities values. The value of \(\rho _b\) does not necessarily represent the fluid density at the boundary, and it can be seen as a free model parameter to be fine-tuned. For this work, the value \(\rho _b = \rho ({\varvec{x}}_f)\) has been used, as it has shown to be a suitable approximation [12].

Numerical Procedure

Numerical Algorithm

Commonly in LBM literature, Eq. 2 are decomposed in two steps for numerical solution: collision (also referred to as relaxation) and streaming (also known as propagation). These steps can be mathematically described as:

$$\begin{aligned}&\text {Collision step:}&f_{i}^{*}({\mathbf {x}}, t)=\left( 1 -\omega _f \right) {f}_i({\mathbf {x}},t) + \omega _f f_i^{\text {eq}}({\mathbf {x}},t) + {\varDelta } t \left( 1-\frac{\omega _f}{2} \right) F_i \nonumber \\&&h_{i}^{*}({\mathbf {x}}, t) = \left( 1 -\omega _h \right) h_{i}({\mathbf {x}}, t) + \omega _h h_i^{\text {eq}}({\mathbf {x}},t) \end{aligned}$$
(16a)
$$\begin{aligned}&&+\quad {} Z_i (\omega _h - \omega _f) \left( {f}_i({\mathbf {x}}, t) - f_i^{\text {eq}}({\mathbf {x}}, t) + F_i \frac{{\varDelta } t}{2} \right) {\varDelta } t + q_i, \end{aligned}$$
(16b)
$$\begin{aligned}&\text {Streaming step:}&f_{i}\left( {\mathbf {x}}+{\mathbf {c}}_{i} {\varDelta } t, t\right) =f_{i}^{*}({\mathbf {x}}, t), \end{aligned}$$
(16c)
$$\begin{aligned}&&h_{i}\left( {\mathbf {x}}+{\mathbf {c}}_{i} {\varDelta } t, t\right) =h_{i}^{*}({\mathbf {x}}, t), \end{aligned}$$
(16d)

where superscript \(*\) denotes a relaxed distribution population. Boundary conditions are applied after streaming step. Basically, the algorithm consists in an iterative sequence of these steps until a stopping criterion is achieved. Detailed studies regarding data structures, CPU, memory efficiency and addressing modes can be seen in [16, 24] and [28]. Our codes implement two-lattice algorithm, which allows to easily fuse collision and streaming steps.

Grid Independence Tests

Grid independence tests were performed for both problems proposed in the following manners. For natural convection in square cavity problem, an average Nusselt number, \(\overline{\text {Nu}}\), was assessed as proposed by [15]:

$$\begin{aligned} \overline{\text {Nu}} = \frac{q^{\prime }}{q_c^{\prime }}, \end{aligned}$$
(17)

where \(q^{\prime }\) is the linear heat flux across the cavity, and \(q_c^{\prime }\) is the linear heat flux considering a pure conduction in cavity with stationary fluid:

$$\begin{aligned} q_c^{\prime } = \frac{\mu c_p}{\text {Pr}} \frac{T_h - T_c}{L} H. \end{aligned}$$
(18)

Heat flux across the cavity takes into account diffusion and convection heat transfer mechanisms. However, in steady state, heat flux is constant across cavity and it can be easily evaluated considering the heat flux across one of the stationary walls. This value can be computed by finding the average heat flux resulting from numerically simulated temperature gradients obtained from simulation.

Average Nusselt number has been computed from LBM simulations using lattices ranging from \(8 \times 8\) up to \(2048 \times 2048\) sites, for increasing Rayleigh numbers, namely \(\text {Ra} = 10^3, 10^4, 10^5\) and \(10^6\), while Prandtl and Eckert numbers were fixed respectively at \(\text {Pr} = 0.71\), and \(\text {Ec} = ({\alpha /{}H})^2/{}c_p {\varDelta } T = 10^{-30}\). VDF collision frequency was fixed at \(\omega _f = 1.6\) [12]. All other parameters can be determined from the number of grid nodes and dimensionless parameters.

Figure 2 shows results from aforesaid grid independence analyses. Variations observed were under 0.3% for meshes greater than 512 points under all flow conditions studied. For high accuracy sake, subsequent LBM simulations in this work used \(1024 \times 1024\) lattices for mixed convection and \(2048 \times 2048\) lattices for natural convection problems.

Fig. 2
figure 2

Grid independence analyses in terms of average Nusselt number across square cavity for increasing Rayleigh number

Full size image
Fig. 3
figure 3

Grid independence study with respect to the x velocity profile across mid vertical plane, for the mixed convection problem

Full size image

For mixed convection, grid independence was assessed by studying the velocity profile across the mid vertical plane in the cavity. For these simulations, Reynolds and Richardson numbers were respectively set to \(\text {Re} = U_0 H/{} \nu = 100\) and \(\text {Ri} = \text {Ra}/{}\text {Pr}\text {Re}^2 = 1\), which guarantees same order of magnitude for shear and buoyancy effects. Also, tests were carried out considering the opposing buoyancy case in relation to the shear stress effects. Variation of the velocity profile was determined by:

$$\begin{aligned} \text {Profile variation} = \frac{\int _{0}^{H} \left( u_{x,m+1} - u_{x,m} \right) ^2 dy }{\int _{0}^{H} (u_{x,m+1})^2 dy }, \end{aligned}$$
(19)

where \(m+1\) and m are indices indicating results from, respectively, a finer and a coarser mesh. Grid independence results are shown in Fig. 3 and Table 2. From visual results, differences to finest grid simulated are very difficult to be observed, specially to meshes finer than \(160 \times 160\). As a compromise between accuracy and CPU time, LBM simulations in the next section for mixed convection adopted \(1024 \times 1024\) lattice.

Shear Stresses Calculation

Dimensionless shear stresses are calculated by using results of velocity fields and applying the following relation:

$$\begin{aligned} \tau _{xy} = \frac{\mu \left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right) }{\tau _0}, \end{aligned}$$
(20)

where \(\tau _0 = \mu U_0{}/H\) is a stress value based on characteristic properties of the problem. These equations are applied to show shear stresses in mixed convection simulation results.

Stopping Criterion

Simulations and tests were performed until a stationary regime was achieved. In order to assure this condition, it was established the following stopping criterion:

$$\begin{aligned} \sqrt{ \frac{ \sum \sum _{x,y} \left( {\varPhi }_k({\varvec{x}},t ) - {\varPhi }_{k-n}({\varvec{x}},t ) \right) ^2 }{ \sum \sum _{x,y} {\varPhi }^{2}_{k-n}({\varvec{x}},t ) } } \le 10^{-6} \end{aligned}$$
(21)

where \({\varPhi }\) represents the monitored variable, k is the field variable evaluated at k-th time step and n stands for how many time steps apart from each other. In this work, both total energy E and velocity fields \({\varvec{u}}\) were assured to obey the stopping criterion with \(n = 100\). In the latter case, quadratic operations are calculated as dot products.

Table 2 x-component velocity profile divergence across the mid vertical plane between \((m+1)\)-th and m-th meshes
Full size table

Code Development and Running Times

Due to high locality of LBM, several authors have been applying general-purpose computing on graphics processing units (GPGPU) [8, 32]. In this paper, for the natural convection case, a serial and parallelized version were developed by using C and Compute Unified Device Architecture (CUDA) extension language. Hardware for LBM simulations comprised AMD Ryzen 7 1700 (3.0GHz) and NVIDIA GeForce 1080 Ti. Processing times for a \(1024 \times 1024\) grid regarding both versions are summarized in Table 3, in which stopping criterion previously in Eq. 21 was employed. It should be noted that simulations were simply coded and no special optimizations or fine tuning were carried out in this study.

Table 3 Serial and parallelized processing times for the natural convection time regarding a \(1024 \times 1024\) grid
Full size table
Fig. 4
figure 4

Natural convection streamlines for a \(\text {Ra} = 10^3\), b \(\text {Ra} = 10^4\), c \(\text {Ra} = 10^5\), d \(\text {Ra} = 10^6\)

Full size image

It is worth mentioning that, in order to reduce running time, results from coarser meshes were interpolated and used as an initial solution for the finer ones in all cases.

Results and Discussions

Pure Natural Convection

Figures 4 and 5 show natural convection results obtained for, respectively, streamlines and isotherms. One can observe that, for \(\text {Ra} = 10^3\), a vortex is formed in the center of the square cavity. This structure is typical of natural convection cavity flows. As Ra number increases, natural convection currents are intensified, and central vortex assumes an elliptic shape. When \(\text {Ra} = 10^5\), central vortex breaks in two structures and convection effects are more notable near wall regions due to higher temperature gradient in these areas. For greater convective effects, such as when \(\text {Ra} = 10^6\), a new central vortex is formed besides those two near wall regions. This behavior is well documented and is in agreement with literature [10, 12, 15, 26].

Fig. 5
figure 5

Natural convection isotherms for a \(\text {Ra} = 10^3\), b \(\text {Ra} = 10^4\), c \(\text {Ra} = 10^5\), d \(\text {Ra} = 10^6\)

Full size image

Through isotherm lines, one can analyze the role of heat transfer mechanisms according to the Rayleigh number. For \(\text {Ra} = 10^3\), velocities due to buoyancy effects are very low and predominant mechanism observed is conduction with small convective effects. As Rayleigh number increases, convective effects become more predominant. This is the reason why isotherms approach horizontal lines in the central region. On the other hand, conduction effects become more confined near to wall regions, fact that becomes evident as isotherms are fairly vertical in these areas [12, 15].

Maximum values of horizontal, \(U_{max}\), and vertical, \(V_{max}\), velocities along, respectively, vertical and horizontal planes located at \(x = H{}/2\) and \(y = H{}/2\) were compared to other results from literature. Dimensionless positions \(Y = y{}/H\) and \(X = x{}/H\) of, respectively, maximum horizontal and vertical velocities are also compared, as well as average Nusselt number in the cavity. Comparison of these values for \(\text {Ra} = 10^3, 10^4, 10^5\) and \(10^6\) are summarized in Table 4. It is worth mentioning that velocities values are normalized by characteristic (i.e reference) velocity flow \(U_c = \alpha /{}H\). One may see that results obtained are in well agreement with those observed in literature.

Table 4 Comparisons to the literature about average Nusselt number, maximum velocities in the mid planes and their locations for distinct natural flow conditions
Full size table

Mixed Convection

Numerically simulated streamlines and isotherms are shown in Fig. 6, whereas dimensionless shear stresses are exhibited in Fig. 7. Streamlines were exhibited again along with dimensionless shear stresses for visualization purposes. Also, it is worth mentioning that for all cases, Reynolds number was fixed at \(\text {Re} = 100\), and only Richardson number, \(\text {Ri}\) was varied. Three different regimes can be identified: pure natural convection (\(\text {Ri} \gg 1\)), pure forced convection (\(\text {Ri} \ll 1\)) and mixed convection (\(\text {Ri} \thickapprox 1\)).

In forced convection regime, velocity field inside cavity is influenced by left wall movement, mainly because of shear stress effects. This forms a shear driven clockwise vortex inside the square cavity. Also, two smaller counter-clockwise vortices can be observed near the top and bottom right corner. One can observe this behavior in the flow for \(\text {Ri} = 0.01\), for both cases when buoyancy effects either aid or oppose shear stress effects. This fact shows buoyancy effects are negligible in these conditions, and flow is shear driven predominant.

Fig. 6
figure 6

Streamlines and isotherm lines for different Ri number conditions for buoyancy effects a aiding and b opposing to left wall movement

Full size image
Fig. 7
figure 7

Streamlines and shear stress tensor for different Ri number conditions for buoyancy effects a aiding and b opposing to left wall movement

Full size image

Analyzing the case in which left wall is held at \(T_H\) (Fig. 6a), one may see significant differences in streamlines and isotherms with Richardson number. This fact allows one to conclude that both buoyancy and shear stress effects play significant roles. As Richardson number increases, streamlines and isotherms gradually assume behavior seen in pure natural convection, shown in Figs. 4 and 5. In fact, cases with \(\text {Ri} = 10\) and \(\text {Ri} = 100\) present great resemblance with previous natural convection results. As for the shear stresses (Fig. 7a), one may observe that highest values in magnitude for low Richardson numbers are restricted to left wall boundary. This fact corroborates shear effect predominancy on these flows. As Richardson number increases, buoyancy effects become predominant and high values of shear stresses are restricted only near wall regions. The case with \(\text {Ri} = 100\) represents pure natural convection phenomenon.

When left wall is held at \(T_C\) (Fig. 6b), natural convection effects are more prominent, once it is possible to observe a counter-clockwise vortex formation near the hot wall region, in opposition to the clockwise vortex driven by left wall movement. At \(\text {Ri} = 0.5\), both vortices possess similar characteristic length magnitude, which indicates similar buoyancy and shear effects. As Richardson number increases, i.e., as buoyancy effects relevancy increases in comparison to shear stress effects, one may observe that area occupied by counter-clockwise vortex grows and clockwise vortex diminishes. For \(\text {Ri} = 10.0\), the clockwise vortex due to left wall movement is confined to a small region in the computational domain. For \(\text {Ri} = 100.0\), this same vortex is even smaller, and it is visible only in a very small portion near to bottom left corner. Regarding shear stresses effects (Fig. 7b), a similar behavior to previous case is observed. For low \(\text {Ri}\) numbers, high values of \(\tau _{xy}\) are observed near left wall region, due to movement of this region. Very high values are seen specially near top and bottom left corners due to the high velocity gradients in these regions. For high values of \(\text {Ri}\) numbers, velocity fields inside cavity are induced by buoyancy effects, and their magnitudes become much higher than left wall upwards velocities. In this case, shear stresses are much higher in regions near the wall, in which velocities vary from a finite value to zero. Such behavior allows to conclude that shear stress plays negligible role in this case (\(\text {Ri} = 100\)) and flow is dominated by buoyancy effects.

Fig. 8
figure 8

Dimensionless velocity profiles across the mid vertical plane in the square cavity for buoyancy effects a aiding b opposing the left wall movement

Full size image

From observations regarding both buoyancy aiding and opposing situations, one may classify the following flow regimes: forced convection when \(\text {Ri} < 0.1\), mixed convection when \(0.1 \le \text {Ri} \le 10\), and natural convection when \(\text {Ri} > 10.0\). These very same tests were performed by [4] using a control volume-based finite difference technique and both results are in well agreement.

Dimensionless velocity profiles across mid vertical plane are shown in Fig. 8. Results presented by these profiles corroborate what was observed by streamlines and isotherm lines regarding buoyancy and shear stress effects. For \(\text {Ri} = 0.01\) and \(\text {Ri} = 0.1\), differences in velocity profiles are very subtle. For Richardson numbers equal or greater to 0.5, natural convection play significant role in the flow. This fact can be observed by the great rise in velocity magnitudes for aiding buoyancy effects and reduction in values for opposing buoyancy to the left wall movement. In fact, the formation of the counter-clockwise vortex when buoyancy effects opposes the left wall movement is very clear in the velocity profiles, specially for \(\text {Ri}\) greater than 1.0.

Conclusion

Conclusions of this paper are:

  • Despite criticism to double population approach, total energy based approach developed by [12] has shown a very robust and good stability results for different flow conditions;

  • Results from the present work (namely: average Nusselt number and maximum horizontal/vertical velocities and their locations) were compared to counterparts in the literature and the good agreement between them suggests that total energy based LBM is equally valid as classic approaches (e.g additional population as passive scalar and finite-differences method).

  • By using double population approach, parallel computing for time evolution of velocity is very similar to that for total energy distribution functions so both can be coded in a single function. In this work, GPU speedups were observed to be about 25 times when compared to serial versions of natural convection codes;

  • Regarding mixed convection flow, three different flow regimes were observed and categorized: natural convection (\(\text {Ri} < 0.1\)), mixed convection (\(0.1 \le \text {Ri} \le 10.0\)) and forced convection (\(\text {Ri} > 100.0\)).