Introduction

One of the most important methods that evaluate the numerical solutions of the differential equations is the spectral method. We express the solution as the expansion of polynomials. Numerical schemes are used to solve and investigate different kinds of fractional differential equations such as [1,2,3] using Jacobi operational matrix for solving linear multi-term fractional differential equations, the space-fractional order diffusion equation and fractional reaction-subdiffusion equation with variable order. [4] solutions of third and fifth-order differential equations by using Petrov-Galerkin methods, [5] solutions of fractional differential equations by using shifted Jacobi spectral approximations. The numerical solution of the nonlinear time-fractional telegraph equation using the neutron transport process [6]. Numerical evaluation of the time-fractional Klein–Kramers model is obtained by incorporating the subdiffusive mechanisms [7]. Solving the modified time-fractional diffusion equation using a meshless method [8]. The most used spectral methods are the Galerkin, Collocation, and Tau methods: Numerical solution of fractional reaction–subdiffusion problem using an improved localized radial basis-pseudospectral collocation method [9]. [10, 11] numerical solutions of fractional Telegraph equation by using Legendre-Galerkin algorithm and Legendre Wavelets spectral tau algorithm. [12] solution of fractional rheological models and Newell–Whitehead–Segel equations using shifted Legendre collocation method. [13] numerical solution of differential eigenvalue problems by using tau method. Solving fractional advection-dispersion problems using Chebyshev method and tau-Jacobi algorithm [14, 15]. [16] numerical solutions of time-fractional Klein–Gordon equations by clique polynomials. [17,18,19] using generalized Lucas (tau and collocation) method for solving multi-term fractional differential equations and fractional pantograph differential equation. [20] numerical solutions for coupled system of fractional differential equations using generalized Fibonacci tau method.

Recently, the approximate solutions of the integral equations are evaluated by different methods. These methods help to solve different kinds of integral equations with small error and a small number of unknowns: numerical solution of nonlinear fractional integro-differential equations with variable order derivative using the Bernstein polynomials and shifted Legendre polynomials [21,22,23]. Specially, solutions of Volterra–Fredholm integral equations: Solving nonlinear mixed Volterra–Fredholm integral equations using variational iteration method [24]. [25, 26] solutions using Taylor collocation and Taylor polynomial methods, [27] solutions using Legendre collocation method. Solutions using Chebyshev method and second kind Chebyshev [28,29,30] solutions using Lagrange collocation method. [31] solutions by continuous-time and discrete-time spline collocation methods. [32] solving using Hybrid function method, [33] using the Adomian decomposition method. In this article, we numerically study the Volterra–Fredholm integral equations and apply the operational matrices based on the generalized Lucas polynomials. We compared the obtained results with the Taylor collocation (TC) method [25], the Taylor polynomial (TP) method [26], and the Lagrange collocation (LC) method [30]. The best of our work is the first to use the generalized Lucas collocation method for solving Volterra–Fredholm integral equation. This method is certainly will verify high accurate results and fortunately takes shorter times.

Consider the Volterra–Fredholm integral equation [27]

$$\begin{aligned} N(y)~V(y)+L(y)~V(\gamma (y))=h(y)+\alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~V(t)~dt+\alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)~ V(\gamma (t))~dt \end{aligned}$$
(1)

where V(y) is an unknown function. L(y), N(y), \(\gamma (y),\) and h(y) are known and defined on the interval \(\left[ 0,\ell \right] , 0\le \gamma (y)<\infty \). \(\beta _{1}(y,t)\) and \(\beta _{2}(y,t)\) are known functions on \(\left[ 0,\ell \right] \times \left[ 0,\ell \right] .\) \(\alpha _{1}\) and \( \alpha _{2}\) are real constants.

The organization of this paper is as follows: Sect. 1 contains a brief history of the subject of our work. In Sect. 2, some properties of the generalized Lucas polynomials, which will be used in the following sections, are introduced. In Sect. 3, we describe the algorithm of this method using the generalized Lucas polynomials for solving Volterra–Fredholm integral equation. In Sect. 4, the convergence and error analysis are examined. We give some examples and compared them with other techniques in Sect. 5. In the last, Sect. 6 we introduce some conclusions.

Properties and Used Formulas

The main aim of this section is to recall some important properties and formulas of the generalized Lucas polynomials which will be used further [17, 34,35,36].

The generalized Lucas polynomials \(\left\{ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) \right\} _{m\ge 0}\)( \(\nu _{1}\) and \(\nu _{2}\) are non zero real numbers). Which has the recurrence relation:

$$\begin{aligned} \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) =\ \nu _{1}~y~ \varphi _{m-1}^{\nu _{1},\nu _{2}}\left( y\right) +\nu _{2}~\ \varphi _{m-1}^{\nu _{1},\nu _{2}}\left( y\right) ,\ \ m\ge 2. \end{aligned}$$
(2)

With initial values: \(\varphi _{0}^{\nu _{1},\nu _{2}}\left( y\right) =2, ~\varphi _{1}^{\nu _{1},\nu _{2}}\left( y\right) =\nu _{1}y.\)

\(\varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) \) has the Binet’s form:

$$\begin{aligned} \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) =\frac{\left( \nu _{1}~y+\sqrt{\nu _{1}^{2}y^{2}+4\nu _{2}}\right) ^{m}+\left( \nu _{1}~y- \sqrt{\nu _{1}^{2}y^{2}+4\nu _{2}}\right) ^{m}}{2^{m}} m\ge 0. \end{aligned}$$
(3)

Assume that we can expand the function V(y) in terms of generalized Lucas polynomials:

$$\begin{aligned} V(y)\ =\sum \limits _{m=0}^{\infty }e_{m}\ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) . \end{aligned}$$
(4)

Let the approximation of V(y) be

$$\begin{aligned} V(y)\approx V_{K}(y)\ =\sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) =E^{T}\ \Phi (y), \end{aligned}$$
(5)

where

$$\begin{aligned} \Phi (y)=\left[ \varphi _{0}^{\nu _{1},\nu _{2}}\left( y\right) ,\varphi _{1}^{\nu _{1},\nu _{2}}\left( y\right) ,...,\varphi _{K}^{\nu _{1},\nu _{2}}\left( y\right) \right] ^{T}, \end{aligned}$$
(6)

and the coefficients

$$\begin{aligned} E^{T}=\left[ e_{0},e_{1},...,e_{K}\right] , \end{aligned}$$
(7)

must be determined.

The Algorithm of the Method

In this section, we use the generalized Lucas polynomials to approximate the solution of Eq. (1). Suppose that \(0\le \gamma (y)<\ell .\) From the approximation (5), we have

$$\begin{aligned} V(\gamma (y))\approx \sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( \gamma (y)\right) . \end{aligned}$$
(8)

From Eqs. (5) and (8) then Eq. (1) is rewritten as:

$$\begin{aligned}&N(y)~\sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) +L(y)~\sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( \gamma (y)\right) \nonumber \\&\quad = h(y)+\alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~ \sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( t\right) ~dt \nonumber \\&\qquad +\alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)~\sum \limits _{m=0}^{K}e_{m}\ \ \varphi _{m}^{\nu _{1},\nu _{2}}\left( \gamma (t)\right) ~dt. \end{aligned}$$
(9)

Let

$$\begin{aligned} g_{m}(y)= & {} N(y)\ \varphi _{m}^{a,b}\left( y\right) +L(y)~\varphi _{m}^{\nu _{1},\nu _{2}}\left( \gamma (y)\right) \nonumber \\&-\alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~\varphi _{m}^{\nu _{1},\nu _{2}}\left( t\right) ~dt-\alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)\ \varphi _{m}^{\nu _{1},\nu _{2}}\left( \gamma (t)\right) ~dt. \end{aligned}$$
(10)

Therefore we can write Eq. (9) in the form:

$$\begin{aligned} \sum \limits _{m=0}^{K}e_{m}~g_{m}(y)=h(y). \end{aligned}$$
(11)

Where Eq. (11) has \(K+1\) roots. So we have a system of equations

$$\begin{aligned} \sum \limits _{m=0}^{K}e_{m}~g_{m}(y_{i})=h(y_{i}), \end{aligned}$$
(12)

where

$$\begin{aligned} y_{i}=\frac{i}{K},~i=0,1,...,K. \end{aligned}$$

The matrix form of equation (12) is given by

$$\begin{aligned} G^{T}~E=H, \end{aligned}$$

where

$$\begin{aligned} G=(g_{mi})\text {, }i,m=0,1,....K, \end{aligned}$$

and

$$\begin{aligned} H=[h(y_{0}),h(y_{0}),...,h(y_{K})]^{T}. \end{aligned}$$

The unknown constants can be determined by the following equation:

$$\begin{aligned} E=(G^{T})^{-1}H. \end{aligned}$$

Convergence and Error Analysis

In this section, we investigate the convergence and error analysis of generalized Lucas expansion of V–FIE. The following theorems are satisfied:

Theorem 1

If V(y) is defined on [0, 1] and \(\left| V^{(i)}(0)\right| \le \ell ^{i},\) \(i\ge 0\) where \(\ell \) is a positive constant and if V(y) has the expansion:

$$\begin{aligned} V(y)\ =\sum \limits _{m=0}^{\infty }e_{m}\ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) . \end{aligned}$$

Then:

  1. 1)

    \(~\left| e_{m}\right| \le \frac{ \left| \nu _{1}\right| ^{-m}\ell ^{m}\cosh \left( 2\left| \nu _{1}\right| ^{-1}\nu _{2}^{\frac{1}{2}}\ell \right) }{m~!},\)

  2. 2)

    The series converges absolutely.

Proof

See [17] \(\square \)

If \(\varepsilon _{K}(y)=\left| V(y)-V_{K}(y)\right| \) then we have the following truncation error:

Theorem 2

Let V(y) satisfy the assumptions stated in theorem (1). Moreover \( \varepsilon _{K}(y)=\sum \limits _{m=K+1}^{\infty }e_{m}\ \varphi _{m}^{\nu _{1},\nu _{2}}\left( y\right) \) be the truncation error so:

$$\begin{aligned} \left| \varepsilon _{K}(y)\right| <\frac{2e^{\ell \left( 1+\sqrt{ 1+\nu _{1}^{-2}\nu _{2}}\right) ~}}{\left( K+1\right) !}\cosh \left( 2\ell \left( 1+\sqrt{1+\nu _{1}^{-2}\nu _{2}}\right) \right) \left( 1+\sqrt{ 1+\nu _{1}^{-2}\nu _{2}}\right) ^{K+1}. \end{aligned}$$

Proof

See [17] \(\square \)

Now, we give an estimated value for the error of the numerical solution of Eq. (1) obtained by the proposed method.

Theorem 3

Let \(\ \varepsilon _{K}^{\gamma }(y)=\varepsilon _{K}(\gamma (y)),\) \( \epsilon _{K}=\underset{0\le y\le \ell }{~\max }\varepsilon _{K}(y)\) and \(\ \epsilon _{K}^{\gamma }=\underset{0\le y\le \ell }{~\max } \varepsilon _{K}^{\gamma }(y)\), and

$$\begin{aligned} R_{K}(y)= & {} \mid N(y)~V_{K}(y)+L(y)~V_{K}(\gamma (y))-\alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~V_{K}(t)~dt \\&-\alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)~V_{K}(\gamma (t))~dt~-h(y)\mid , \end{aligned}$$

let

$$\begin{aligned} \mathfrak {R}_{K}=\underset{0\le y\le \ell }{~\max }R_{K}(y), \end{aligned}$$

and if \(\left| N(y)\right| \le N_{1},\left| L(y)\right| \le L_{1},\left| \beta _{1}(y,t)\right| \le \Psi _{1},\left| \beta _{2}(y,t)\right| \le \Psi _{2}\) and \(\left| \gamma (y)\right| \le \lambda .\) Where \(N_{1},L_{1},\Psi _{1},\Psi _{2}\) and \( \lambda \) are positive constants. Then we have the following global error estimate:

$$\begin{aligned} \mathfrak {R}_{K}\le 2~\sigma ~\frac{e^{\ell \left( 1+\sqrt{1+\nu _{1}^{-2}\nu _{2}}\right) ~}}{\left( K+1\right) !}\cosh \left( 2\ell \left( 1+\sqrt{1+\nu _{1}^{-2}\nu _{2}}\right) \right) \left( 1+\sqrt{1+\nu _{1}^{-2}\nu _{2}}\right) ^{K+1}, \end{aligned}$$

where

$$\begin{aligned} \sigma =\max \left\{ N_{1},L_{1},\left| \alpha _{1}\right| \Psi _{1}\lambda ,\left| \alpha _{2}\right| \Psi _{2}\ell \right\} . \end{aligned}$$

Proof

From Eq. (1), we have

$$\begin{aligned} h(y)=N(y)~V(y)+L(y)~V(\gamma (y))-\alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~V(t)~dt -\alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)~V(\gamma (t)) ~dt. \end{aligned}$$

So

$$\begin{aligned} R_{K}(y)\le & {} \left| N(y)~\varepsilon _{K}(y)\right| +\left| L(y)~\varepsilon _{K}^{\gamma }(y)\right| +\left| \alpha _{1}\int \limits _{0}^{\gamma (y)}\beta _{1}(y,t)~\varepsilon _{K}(t)~dt\right| \\&+\left| \alpha _{2}\int \limits _{0}^{\ell }\beta _{2}(y,t)~\varepsilon _{K}^{\gamma }(t)~dt~\right| . \end{aligned}$$

From the assumptions of the theorem, we have

$$\begin{aligned} R_{K}(y) \le N_{1}\left| ~\varepsilon _{K}(y)\right| +L_{1}\left| ~\varepsilon _{K}^{\gamma }(y)\right| +\left| \alpha _{1}\right| \Psi _{1}\lambda \left| ~ \varepsilon _{K}(y)\right| +\left| \alpha _{2}\right| \Psi _{2}\ell \left| ~\varepsilon _{K}^{\gamma }(y)\right| . \end{aligned}$$

Then we obtain

$$\begin{aligned} \mathfrak {R}_{K}\le \left\{ N_{1}+L_{1}+\left| \alpha _{1}\right| \Psi _{1}\lambda +\left| \alpha _{2}\right| \Psi _{2}\ell \right\} ~\max \left( \varepsilon _{K}(y),\varepsilon _{K}^{\gamma }(y)\right) . \end{aligned}$$

From Theorem (2) , so the proof is completed. \(\square \)

Numerical Examples

In this section, we introduce a numerical approach to solve Eq. (1) using the generalized Lucas collocation (GLC) method and compare our results within [25, 26, 30]. Numerical examples are presented to show the validity, effectiveness, and accuracy of the method.

Example 1

Suppose that the following V–FIE [27]

$$\begin{aligned} \left( \sin y\right) ~V(y)+\left( \cos y\right) ~ V(e^{y})=h(y)+\int \limits _{0}^{e^{y}}e^{y+t}~V(t)~ dt-\int \limits _{0}^{1}e^{y+t}~V(e^{t})~dt. \end{aligned}$$
(13)

The exact solution of this equation is \(V(y)=y^{2}\), where

$$\begin{aligned} h(y)= & {} \frac{1}{3}e^{y}\left( -1+e^{3}\right) +e^{y}\left\{ 2-e^{e^{y}}\left[ 2+e^{y}\left( -2+e^{y}\right) \right] \right\} \nonumber \\&+e^{2y}\cos y+y^{2}\sin y. \end{aligned}$$

Table 1 shows that the absolute error which obtained by the GLC method is better than that obtained by the Taylor collocation (TC) method [25], the Taylor polynomial (TP) method [26], and the Lagrange collocation (LC) method [30]. The last two columns clarify the time used for the running program (CPU time) and the difference between two consecutive errors (\(C_{K}\)).

Table 1 Comparison between absolute errors with different values of K
Full size table

CPU time

\(C_{K}\)

6.546

\(2\times 10^{-16}\)

17.22

\(1\times 1^{-16}\)

52.642

\(9.2\times 10^{-15}\)

Example 2

Suppose that the following V–FIE [27]

$$\begin{aligned} y^{2}V(y)+e^{y}V(2y)=h(y)+\int \limits _{0}^{2y}e^{y+t}V(t)dt-\int \limits _{0}^{1}e^{y-2t}V(2t)dt. \end{aligned}$$
(14)

The exact solution of this equation is \(V(y)=\sin y\), where

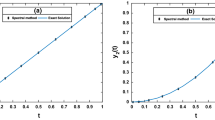
$$\begin{aligned} h(y)= & {} -\frac{1}{4}e^{y}-\frac{1}{4}e^{-2+y}\cos 2+\frac{1}{2}e^{3y}\cos 2y-\frac{1}{4}e^{-2+y}\sin 2+y^{2}\sin y \\&+e^{y}\sin 2y-\frac{1}{2}e^{3y}\sin 2y. \end{aligned}$$

In Table 2, there is a comparison between the absolute errors of the present method with the Taylor collocation (TC) method [25], the Taylor polynomial (TP) method [26], and the Lagrange collocation (LC) method [30]. In Figure 1 we illustrate the results of the present method at \(K=2,5,8\) and 9. The Figure shows that the convergence is exponential and the errors are better when the values of K are large.

Table 2 Maximum absolute errors with various values of K
Full size table

CPU time

\(C_{K}\)

3.985

\(7.4\times 10^{-2}\)

32.797

\(1.6\times 1^{-4}\)

69.436

\(2.1\times 10^{-8}\)

82.406

\(4.24\times 10^{-8}\)

Fig. 1
figure 1

Graph of the error at K=2, 5, 8 and 9

Full size image

Example 3

Suppose that the following V–FIE

$$\begin{aligned} V(y)=h(y)+\int \limits _{0}^{y}y~tV(t)dt+\int \limits _{0}^{1}\left( y-t\right) V(t)dt. \end{aligned}$$
(15)

The exact solution of this equation is \(V(y)=y^{\frac{1}{2}}\), where

$$\begin{aligned} h(y)=\frac{-2}{5}y^{\frac{7}{2}}-\frac{2}{3}y+y^{\frac{1}{2}}+\frac{2}{5}. \end{aligned}$$

Table 3 lists The numerical results obtained by the proposed method for \(K= \) 8, 12 and 9 and different values of \(\nu _{1}\) and \(\nu _{2}\). The absolute errors of this method are plotted in Figure 2. We observe from the Figure that the convergence is exponential.

Table 3 Results of absolute errors for various values of K, \(\nu _{1}\) and \(\nu _{2}\)
Full size table

CPU time

\(C_{K}\)

11.438

\(3.4\times 10^{-2}\)

45.14

\(2\times 10^{-2}\)

77.937

\(2.1\times 10^{-3}\)

Fig. 2
figure 2

Graph of the absolute error at K=8, 12, 16 and different values of \(\nu _{1}\) and \(\nu _{2}\)

Full size image

Example 4

Suppose that the following V–FIE [27]

$$\begin{aligned} V(y)=h(y)+\int \limits _{0}^{\ln \left( y+1\right) }e^{y+t}V(t)dt-\int \limits _{0}^{1}e^{y+\ln \left( t+1\right) }V(\ln \left( t+1\right) )dt. \end{aligned}$$
(16)

The exact solution of this equation is \(V(y)=e^{-y}\), where

$$\begin{aligned} h(y)=e^{-y}+e^{y}\left( 1-\ln \left( y+1\right) \right) . \end{aligned}$$

In Table 4, we compare our results with the others and notice that the absolute error in the proposed method is better than the others for large values K. The errors of this method are displayed at \(K=2,5,8\) and 9 in Figure 3. It is clear from the Figure that the absolute errors decrease drastically with increasing the number of steps.

Table 4 Comparison between the absolute errors with various values of K
Full size table

CPU time

\(C_{K}\)

4.015

\(5\times 10^{-3}\)

54.64

\(9.7\times 1^{-7}\)

112.937

\(6.19\times 10^{-11}\)

128.611

\(2.09\times 10^{-12}\)

Fig. 3
figure 3

Graph of the error at N=2, 5, 8 and 9

Full size image

Conclusions

This work aims to solve V–FIEs using the collocation based on the operational matrix of the generalized Lucas polynomials. By this method, the main problem is reduced the V–FIEs for four examples to a system of linear algebraic equations which significantly simplifies the problem, these equations are solved by Mathematica software. Then evaluate the errors. Numerical results are compared with those obtained by other techniques [25, 26, 30] to verify the accuracy of this method. The spectral results, that are obtained, point that this algorithm is high adequacy, viable and easy in applications. We discuss the convergence and error analysis. This method can solve applications in different fields in science such as mathematics, chemistry, physics, biology, fluid, engineering, mechanics, by using fractional differential equations and integral equations.