Introduction

Researchers have been attracted towards the study of fluid and heat flow in porous media due to its various applications in crystal growth, solidification process, contaminant transport, groundwater flow, electrochemical process, electronic cooling, oil extraction and many other engineering applications. Books [1,2,3] illustrate the importance and applications of porous media flows.

Roy and Basak [4] analyzed the flows inside a square cavity due to natural convection along with the non-uniform boundaries for different values of Prandtl number and Rayleigh number. Kefayati et al. [5] discussed the flow reactions by varying the Prandtl number on the MHD natural convective open square cavity. Basak and Chamkha [6] studied the natural convective heat flows obtained in a cavity containing nanofluid by using the heatlines or heatfunction. Raji et al. [7] assayed the heatlines due to periodically cooled cavity on natural convection. A hike in heat transfer of about \(46.1\%\) is found for a periodically cooled wall as compared to a constantly cooled boundary. Saeid et al. [8] discussed the fluid flow and heat transfer behavior due to the partially heated wall/fin at the bottom on the natural convective cavity of square-shaped. The study also discusses variation in heat transfer as a result of different shapes in fins mounded to the bottom. Venkatadri et al. [9] investigated quadratic or non-linear convection in a square cavity with an applied magnetic field. The investigation reveals that increasing the non-linear convection parameter increases the heat transfer rate.

Beckermann et al. [10] performed non Darcian natural convection in the rectangular-shaped porous cavity using a SIMPLER algorithm. Lauriat and Prasad [11] used the Darcy-Brinkman-extended model for analyzing the heat transfer and fluid flow that occurred by natural convection. Misra and Sarkar [12]considered various equations for modeling the fluid flow via porous media in a cavity. Among the considered models, predicted heat transfer is more for the Darcy flow model. Hossain et al. [13] studied the fluid flow and heat transfer that occurs inside a cavity filled with incompressible fluid in porous media due to the heated bottom boundary. Saeid [14] assayed the flow behaviors by the effect of ununiformly (sinusoidal) partially heated bottom boundary in a porous cavity. Advancement in Nusselt number is found for an increase in length of the heated source and thermal amplitude ratio. Basak et al. [15] highlighted the natural convective flow behavior in a porous cavity with a differentially or sinusoidally heated bottom boundary. Oztop et al. [16] investigated the inclination angle, sinusoidally distributed bottom boundary effects on natural convective inclined, porous, open cavity. The investigation reveals that the inclination angle is totally responsible for a change in the flow behavior and a higher thermal amplitude ratio hikes the heat transfer rate. Altawallbeh et al. [17] focused on analyzing natural convective flow on the porous cavity under the magnetic field effects. The cavity used in the analysis is heated from the bottom and salted from the right. The results from the analysis show that the heat transfer and mass transfer processes get affected by applying the magnetic field effect. Ramakrishna et al. [18] conducted heatline analysis on natural convective porous cavity. Study describes the heat flow in a cavity by applying various thermal boundary conditions and aspect ratios. Janagi et al. [19] analysed the fluid flow and heat transfer by natural convection in cold water placed inside a porous square cavity. A rise in heat transfer (\(Nu\)) is found by increasing the Darcy number. Nandalur et al. [20] studied the natural convective flow behaviour in solid block occupied porous square cavity. Reduction in flow intensity and heat transfer rate are detected by increasing the size of solid block.

Ghasemi et al. [21] discussed the action of a magnetic field (acts along the horizontal direction) in a free convective square cavity filled with the nanofluid. Sun and Pop [22] investigated fluid flow behavior and heat transfer by the heated wall of Cu-water nanofluid filled inclined right-angled triangle porous enclosure. Pop et al. [23,24,25] studied the influence of Rayleigh number, Brownian parameter, Lewis number, thermophoresis parameter behavior in a cavity by using Buongiorno’s nanofluid model. They studied the flow behaviors in various shaped porous cavities with different types of boundary conditions. Balla et al. [26] focused on the analysis of the MHD boundary layer natural convective flow of various nanofluids by heating the left wall of the inclined porous cavity. It is noted that the Cu-water nanofluid provides a higher heat transfer rate and TiO2-water nanofluid provides a lesser heat transfer rate. Also, Balla et al. [27] analyzed the fluid flow, temperature distribution, nanoparticle distribution, Nusselt number and skin friction due to the effects such as radiation, heat generation/absorption on a free convective cavity. Kasaeian et al. [28] reviewed the heat transfer and nanofluid flow in a porous enclosure of different shapes using available nanofluid models. They assayed with various boundary conditions such as partially heated, sinusoidally heated, differentially heated, heat flux boundaries, suction and injection. Rashad et al. [29] discussed the heat transfer in a porous cavity for a localized heater at the bottom wall. Various types of nanofluid and different configurations of cooling are considered in the study. It is found that Cu nanoparticles provide a higher heat transfer rate and Ag nanoparticles provide a lower heat transfer rate. Sheikholeslami et al. [30,31,32] investigated MHD natural convective flow of a nanofluid in various shaped cavities. The results show that the enhancement in the heat transfer occurs for increasing the Darcy number, solid volume fraction, Rayleigh number and also, detraction in the heat transfer occurs for increasing the Hartmann number. Sheremet et al. [33] made an analysis on MHD natural convection by considering geothermal viscosity effects in a nanofluid-filled porous cavity. Balla et al. [34, 35] explored the heat transfer and fluid flow process within a square porous cavity due to the natural convection in charge of viscous dissipation and magnetic field effects. Tao et al. [36] reviewed the heatline concept of heat flow in a cavity of different shapes and orientations. The study highlights the importance of heatlines and complications involved in solving it. Jino et al. [37, 38] studied MHD free convection in nanofluid (Cu-water) filled porous cavity by using carman kozeny equation porous model. Alluguvelli et al. [39] addressed the free convective heat transfer and fluid flow of Fe3O4-ethylene glycol nanofluid inside a porous cavity. The findings show that the fluid velocity and heat transfer increases by increasing the radiation and Rayleigh number. Jino and Vanav [40] investigated the heat trajectories that flow within a porous cavity filled with the nanofluid. The cavity is heated linearly towards bottom of the cavity and the heat flow inside the cavity is illustrated clearly using the heatline visualization.

The study considers the non-linear convection effects with the residence of magnetic field. Study of nanofluid flow in a porous media useful in many technologies and engineering applications such as predicting ground water flows, contaminant transport, bio-convection, etc. By incorporating the non-linear or quadratic term in the density variation process with the temperature or natural convective process is essential to design a better simulation era. A finer variation in the fluid flow and the heat transfer in the engineering problems/applications can be spotted, and also to increase the modeling efficiency. With increasing accuracy, escalating costs and scarcity of resources, finer methods/techniques are in demand. Here quadratic natural convection (non-linear convection) is considered to demonstrate the flow behavior that occurs by changing the non-linear convection parameter, \(\lambda \).

Problem Definition

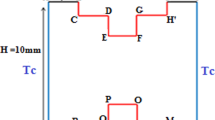
A square shaped two-dimensional porous cavity with all interior angles of the cavity of 90° as shown in Fig. 1. Both the vertically walls are maintained at a lower temperature \({(T}_{c})\), the bottom horizontal wall is continued with constant higher temperature \(\left({T}_{h}\right)\) and the top horizontal wall is preserved adiabatically. The porous cavity is accommodated with water-Cu based nanofluid. The two-dimensional flow velocities \(u,v\) along the directions \(x,y\) are considered zero overall horizontal and vertical walls. The applied magnetic field vector is directed as a horizontal position from the left.

Fig. 1
figure 1

Physical problem model

Full size image

To predict the flow behavior, a set of governing equations is derived with presuming the nanoparticle and base fluids are in thermal equilibrium, Boussinesq approximation with other constant thermophysical properties and neglecting the radiation effects. With the consideration of the linear density variation, non-linear density variation with the temperature is also appended. The derived version of the two-dimensional governing equations for the nanofluid flow within a porous cavity in the form of continuity, momentum, and energy equations as [9, 15, 21],

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$
(1)
$$ \rho_{n} \left[ {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right] = \mu_{n} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{u}{K}} \right) - \frac{\partial p}{{\partial x}} $$
(2)
$$ \rho_{n} \left[ {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}}} \right] = \mu_{n} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{v}{K}} \right) - \frac{\partial p}{{\partial y}} - \sigma_{n} B^{2} v + \left( {\rho \beta } \right)_{n} g\left( {T - T_{c} } \right) + \left( {\rho \beta^{*} } \right)_{n} g\left( {T - T_{c} } \right)^{2} $$
(3)
$$ \left( {\rho c_{p} } \right)_{n} \left[ {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right] = k_{n} \left( {\nabla^{2} \cdot {\varvec{T}}} \right) $$
(4)

The dimensional Eqs. (1–4) can be updated non-dimensionally as,

$$ \frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0 $$
(5)
$$ U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}} = \frac{{\mu_{n} }}{{\rho_{n} \alpha_{fl} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }} - \frac{U}{Da}} \right) - \frac{\partial P}{{\partial X}} $$
(6)
$$ \begin{aligned} U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}} &= \frac{{\mu_{n} }}{{\rho_{n} \alpha_{fl} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }} - \frac{V}{Da}} \right) - \frac{\partial P}{{\partial Y}}\\ &\quad + \frac{{\left( {\rho \beta } \right)_{n} }}{{\rho_{n} \beta_{fl} }}RaPr\left( {\theta + { }\lambda \theta^{2} } \right) - Ha^{2} {{Pr}}\left( V \right) \end{aligned} $$
(7)
$$ U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}} = \frac{{\alpha_{n} }}{{\alpha_{fl} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) $$
(8)

In the above equation, dimensionless variables are \(X = \frac{x}{H}, Y = \frac{y}{H}, U = \frac{uH}{{\alpha_{fl} }}, V = \frac{vH}{{\alpha_{fl} }}, P = \frac{{pH^{2} }}{{\rho_{n} \alpha_{fl}^{2} }}, \theta = \frac{{T - T_{C} }}{{T_{h} - T_{c} }}\).

Non-dimensional parameters in Eqs. (5–8) are \(Ra = \left( {\left( {T - T_{c} } \right)\beta_{fl} gH^{3} } \right)/\left( {\nu_{fl} \alpha_{fl} } \right)\), the Rayleigh number, \(Da = K/H^{2}\), the Darcy number, \(Pr = \nu_{fl} /\alpha_{fl}\), the Prandtl number, \(\lambda = \left( {T_{h} - T_{c} } \right)\beta^{*} /\beta_{fl}\), the non-linear temperature parameter and \(Ha = \sqrt {\sigma_{n} /\rho_{n} \nu_{n} } \left( {BH} \right)\), the Hartmann number, respectively. Here \(X, Y, U, V, P \) and \(\theta\) are the dimensionless space variables, velocity components, pressure and temperature, respectively. Also, \(\sigma , \beta , \beta^{*}\) and \(g\) represents the electrical conductivity, thermal expansion coefficient in first order, thermal expansion coefficient in second-order and gravity. \(B\) in the momentum equation illustrates the applied magnetic field acts perpendicular to the gravity.

The properties of nanofluid [21] are \(\rho_{n} = \left( {1 - \phi } \right)\rho_{fl} + \phi \rho_{p}\) is the effective density, \(k_{n} = k_{fl} \left[ {\left[ {k_{p} + 2k_{fl} - 2\phi \left( {k_{fl} - k_{p} } \right)} \right]/\left[ {k_{p} + 2k_{fl} - 2\phi \left( {k_{fl} - k_{p} } \right)} \right]} \right]\) is the thermal conductivity, \(\left( {\rho c_{p} } \right)_{n} = \left( {1 - \phi } \right)\left( {\rho c_{p} } \right)_{fl} + \phi \left( {\rho c_{p} } \right)_{p}\) is the heat capacitance, \(\left( {\rho \beta } \right)_{n} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{fl} + \phi \left( {\rho \beta } \right)_{p}\) is the thermal expansion coefficient, \(\mu_{n} = \mu_{fl} /\left( {1 - \phi } \right)^{2.5}\) is the effective dynamic viscosity and \(\alpha_{n} = k_{n} /\left( {\rho c_{p} } \right)_{n}\) is the nanofluid’s thermal diffusivity.

The no-slip conditions \(\left( {U = 0, V = 0} \right)\) are imposed on every sides of the cavity and proposed thermal boundaries as shown in Fig. 1, \(\theta = 0\) for vertical walls, \(\partial \theta /\partial Y = 0\) for top wall and \(\theta = 1\) at the bottom wall respectively.

The dimensionless governing Eqs. (5–7) can be rewritten as vorticity-streamfunction \(\left( {\omega - \psi } \right)\) method as [41],

$$ \nabla^{2} \psi = \frac{\partial U}{{\partial Y}} - \frac{\partial V}{{\partial X}} $$
(9)
$$ U\frac{\partial \omega }{{\partial X}} + V\frac{\partial \omega }{{\partial Y}} = \frac{{\mu_{n} }}{{\rho_{n} \alpha_{fl} }}\left( {\frac{{\partial^{2} \omega }}{{\partial X^{2} }} + \frac{{\partial^{2} \omega }}{{\partial Y^{2} }} - \frac{\omega }{Da}} \right) + \frac{{\left( {\rho \beta } \right)_{n} }}{{\rho_{n} \beta_{fl} }}RaPr\left( {\frac{\partial \theta }{{\partial X}} + \lambda \frac{{\partial \theta^{2} }}{\partial X}} \right) - Ha^{2} Pr\frac{\partial V}{{\partial X}} $$
(10)

The respective Neumann boundary conditions for the vorticity and the streamfunction can also be found in the article by Wilkes and Churchill [41].

The flow patterns are pictured as streamlines (9) to describe the fluid motion, Heatlines \(\left( {\nabla^{2} \Pi = \partial U\theta /\partial Y - \partial V\theta /\partial X} \right)\) to describe the heat flow and isotherms \(\left( \theta \right)\). Local Nusselt number is given as \(Nu_{l} = - \left( {\partial \theta /\partial Y} \right)(k_{n} /k_{fl} )\) and integrating the local Nusselt along the heated boundary provides with the average Nusselt number, \(Nu\).

Numerical Solutions

A machine code was developed to solve the energy (8) and vorticity (10) equation using the implicit finite difference method and the streamfunction/heatfunction equations are solved using the Successive Over Relaxation (SOR) method by incorporating the Neumann boundaries [41]. Fortran compiler is used in order to execute the code until the achievement of necessary convergence condition (relative differences between recent iterations of \(\xi\) is less than or equal to \(10^{ - 6}\)).

$$ \mathop \sum \limits_{i,j} \left| {\xi_{i,j}^{n + 1} - \xi_{i,j}^{n} } \right| \le 10^{ - 6} $$
(11)

Here \(\xi\) is suitable for \(\psi , \omega , \theta\) and \(\Pi\). Grid independent study of \(42 \times 42\), \(62 \times 62\), \(82 \times 82\), \(102 \times 102\), \(122 \times 122\), \(142 \times 142\) and \(162 \times 162\) is carried out as shown in Fig. 2 to detect the suitable grid and the whole computation is carried out with an immobile, constant spacing grid resolution of \(122 \times 122\). In order to establish the validation of work, the streamlines and isotherms obtained by Venkatadri et al. [9], Basak et al. [15], Ghasemi et al. [21] and by current machine code were compared. Figure 3, Fig. 4 and Table 1 illustrate the comparative results, which are good in agreement.

Fig. 2
figure 2

Grid independent study

Full size image
Fig. 3
figure 3

Work by a-Venkatadri et al.,(2017) and b-current study

Full size image
Fig. 4
figure 4

Work by a-Basak et al. (2006) and b-current study

Full size image
Table 1 Average Nusselt number comparison at \({{Ra}} = 10^{3}\) and \({{Ha}} = 30\)
Full size table

Results and Discussion

Results obtained for the quadratic natural convection on Cu-water filled porous square cavity under the magnetic field effects are described using the visualization techniques such as \(\psi - \) streamlines, \(\Pi - \) heatlines and \(\theta - \) isotherms. In addition, the heat transfer process is illustrated using the \(Nu_{l} -\) local Nusselt number and \(Nu -\) average Nusselt number. The results are discussed for several parameters such as \(Da -\) Darcy number \((10^{ - 5} \) to \( 10^{ - 1} )\), \(\lambda - \) non-linear temperature parameter \(( - 1 \) to \(1)\), \(Ha - \) Hartmann number \((0 \) to \(50)\), Rayleigh number \((10^{3}\) to \(10^{6} )\), \(\phi - \) nanoparticle solid volume fraction \((0.01 \) to \(0.03)\) and \(Pr - \) Prandtl number (6.2) with properties listed in Table 2.

Table 2 Properties
Full size table

Figure 5 shows flow attained in the absence of non-linear convection \(\left( {\lambda = 0} \right)\) for various values of \(Da\). Other parameters responsible for flow structures are \(Ra = 10^{6} , \phi = 0.02\) and \(Ha = 5\) respectively. Streamlines pictured at lower \(Da = 10^{ - 5}\), it is found that a weaker circulation and its magnitude increases with the increase in \(Da. \) This growth in the magnitude of circulation is due to the improved permeability. A smooth variation in temperature contour with \(\theta = 0.1\) shifted towards the side wall is noted at \(Da = 10^{ - 5}\) and this shifting towards the side walls rises with \(Da = 10^{ - 4}\) to \(\theta = 0.5\). More distributed temperature is noted at higher \(Da = 10^{ - 2}\) and \(10^{ - 1} .\) An orthogonally directed heatlines with respect to the isotherms at lower \(Da = 10^{ - 5}\) signifies the conduction dominated mode of heat transfer. Small curvature in heatlines at \(Da = 10^{ - 4}\) denotes a beginning of convection effects and complete circulations obtained for heatlines at \(Da = 10^{ - 2}\) denotes the domination effect of convective heat transfer. More dense lines in the middle of the heatlines and stronger circulations at \(Da = 10^{ - 1} \) signifies increased convective heat transfer effects.

Fig. 5
figure 5

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Da}} = 10^{ - 5} ,{{b}} - {{Da}} = 10^{ - 4} ,{{ c}} - {{Da}} = 10^{ - 2} ,{{ d}} - {{Da}} = 10^{ - 1}\) at \({\uplambda } = 0,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Ha}} = 5\)

Full size image

Flow patterns attained in the presence of non-linear convection parameter, \(\lambda = 1\) are shown in Fig. 6. By considering the non-linear convection, the same flow behavior patterns are observed with an increased magnitude of streamline as compared to \(\lambda = 0\). The vertically symmetric circulations are due to the cooled side walls and no-slip conditions at each wall. For higher \(Da\), the streamline intensities are more as compared to only linear convection. The temperature distribution inside the cavity increases as the thermal boundary layer increases. At \(Da = 10^{ - 1}\), temperature contour \(\theta = 0.4\) covers the majority of the cavity. Circulation is generated at \(Da = 10^{ - 4}\) for \(\lambda = 1\) due to advancement of buoyancy force, indicating the action of convective heat transfer. But no circulations are seen in the case when \(\lambda = 0\). On higher \(Da\), arbitrarily shaped circulation generated in streamlines and heatlines shows an increased buoyancy effect. Heatlines for both the \(\lambda = 0 \) and \(1\) indicate heat transfer occurs from the bottom wall to both the side walls. An increase in the circulation intensity of heatlines signs the domination effects of convection over the conductive mode of heat transfer.

Fig. 6
figure 6

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Da}} = 10^{ - 5} ,{{b}} - {{Da}} = 10^{ - 4} ,{{ c}} - {{Da}} = 10^{ - 2} ,{{ d}} - {{Da}} = 10^{ - 1}\) at \({\uplambda } = 1,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Ha}} = 5\)

Full size image

Figure 7 illustrates the flow visualization attained due to the reduction of non-linear convection \(\left( {{\uplambda } = - 1} \right)\). Streamlines for \(Da = 10^{ - 5}\), the circulations are shifted towards the top of the cavity by giving space to generate the secondary circulations. The growth in primary circulations is found for an increase in the \(Da\) and secondary circulation increases till \(Da = 10^{ - 2}\) and a further increase in \(Da\) to \(10^{ - 1} \) reduces the secondary circulation. The temperature distribution is symmetry along the vertical midline with \(\theta = 0.1\) is distorted for \(Da = 10^{ - 5}\) and \(\theta = 0.1, 0.2\) is distorted for \(Da = 10^{ - 4}\). The curvy nature of the temperature contour \(\theta \le 0.4\) is found in the higher \(Da = 10^{ - 2}\) and \(Da = 10^{ - 1}\). The curvy nature observed in the temperature contour and circulations in heatlines describes the domination of convective heat transfer. Less dense in the middle region of heatlines implies the lesser heat transfer occurs as compared to the cases \(\lambda = 0\) and \(1\).

Fig. 7
figure 7

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Da}} = 10^{ - 5} ,{{b}} - {{Da}} = 10^{ - 4} ,{{ c}} - {{Da}} = 10^{ - 2} ,{{ d}} - {{Da}} = 10^{ - 1}\) at \({\uplambda } = - 1,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Ha}} = 5\)

Full size image

Flow description on the variation of \(Ha\) at \(\lambda = 0, Da = 10^{ - 3} , Ra = 10^{6}\) and \(\phi = 0.02\) is shown in Fig. 8. In the absence of magnetic field effect \((Ha = 0\)), the maximum streamline magnitude \(\left| {\psi_{max } } \right| = 14\) and reduction in the maximum value of streamline has occurred for the increment in the value of \(Ha\). The observed maximum value of streamline \(\left| {\psi_{max } } \right| = 12\) for \(Ha = 25\) and \(\left| {\psi_{max } } \right| = 8\) for \(Ha = 50\) respectively. The action of the opposition of buoyancy force by the magnetic field is clearly seen in the heatlines. Heatline circulation and denser lines in the middle of the circulation are reduced for \(Ha = 25 {{and}} 50\).

Fig. 8
figure 8

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Ha}} = 0,{{b}} - {{Ha}} = 25,{{ c}} - {{Ha}} = 50\) at \({\uplambda } = 0,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Da}} = 10^{ - 3}\)

Full size image

Figure 9 represents the flow patterns for \(Ha = 0, 25 \) and \(50\) in the presence of non-linearity convection parameter, \(\lambda = 1\). A hike in streamline magnitude is observed as compared to \(\lambda = 0\). This is due to the action of buoyancy force is supported by the addition of non-linear convection. Reduction in flow intensity is also found for an increase in the \(Ha\). Suppression in the temperature contour at the middle of the cavity and reduction in the denser lines in the heatline signifies the reduction in the heat transfer rate from the heated boundary. Still, the denser lines in the middle of the heatline and heatline circulation are more in the case \(\lambda = 1\) as compared to \(\lambda = 0\).

Fig. 9
figure 9

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Ha}} = 0,{{b}} - {{Ha}} = 25,{{ c}} - {{Ha}} = 50\) at \({\uplambda } = 1,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Da}} = 10^{ - 3}\)

Full size image

The flow behavior for various values of \(Ha\) at \(\lambda = - 1\) is shown in Fig. 10. Reduced flow velocity with a pair of secondary circulations is generated as compared to previous cases. Shrink in streamline primary circulation pair and growth in secondary circulation pairs are observed for the increase in \(Ha\). In isotherms, temperature contour \(\theta = 0.4\) realigned to smooth vertical symmetry at \(Ha = 50\). Heatline circulations are reduced for an increase in the \(Ha\) with decreased denser middle line is found along with the birth of secondary circulations in heatlines at the bottom of the cavity. Developed secondary circulations are responsible for the generation of secondary circulations pairs in the heatlines at \(Ha = 50\).

Fig. 10
figure 10

\({psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Ha}} = 0,{{b}} - {{Ha}} = 25,{{ c}} - {{Ha}} = 50\) at \({\uplambda } = - 1,{{ Ra}} = 10^{6} ,{ }\phi = 0.02,{{ and Da}} = 10^{ - 3}\)

Full size image

Buoyancy driven effects at \(Da = 10^{ - 3}\) are illustrated in Fig. 11 at \(\phi = 0.02\) and \(Ha = 5\). Streamline flow experiences an increase in flow circulation by increasing \(Ra\). This increase in the magnitude of the circulation is due to the increased buoyancy effects, making the fluid rush and mix well. At \(Ra = 10^{3}\), the temperature distribution is smooth as a linearly varying contour, and its orthogonally oriented heatlines are direct lines without circulation. Also, the heatlines describe the heat transfer mode, which is purely based on conduction. Separation of temperature contour \(\theta = 0.1\) and slight curvy nature in heatlines are found at \(Ra = 10^{4}\). For increase in \(Ra = 10^{5}\), the isothermal contours experience separation among them for \(\theta \le 0.5\) and moves towards both the side walls of cold temperature. Increased temperature distribution over the cavity and circulations generated in the heatlines denotes the convective heat transfer occurring in the cavity. At higher Rayleigh number (say \(Ra = 10^{6}\)) more bends in the temperature contours are observed for θ ≤ 0.5 increased intensity of circulations and denser middle lines on heatlines describes the dominant effect of the convection, and thus, more heat transfer occurs.

Fig. 11
figure 11

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - {{Ra}} = 10^{3} ,{{b}} - {{Ra}} = 10^{4} ,{{ c}} - {{Ra}} = 10^{5} ,{{ d}} - {{Ra}} = 10^{6}\) at \({\uplambda } = 1,{ }\phi = 0.02,{{ Da}} = 10^{ - 3} {{ and Ha}} = 5\)

Full size image

Flow visualizations obtained due to the variation in nanoparticle concentration in the base fluid are shown in Fig. 12. A slight decrease in the flow intensity is tracked in the streamlines \(\left( {\left| \psi \right| = 18} \right)\) for solid volume fractions on \(\phi = 0.01, 0.02 \) and \(0.03\). This reduction in the flow field is due to increased viscosity, which is obtained by increasing the distribution of \(Cu\) nanoparticles. But circulations are improved in the heatline contours, which are clearly visible at \(\left| \Pi \right| = 8\). The circulation of \(\Pi = - 8\) and \(\Pi = 8\) gets fulfilled for the variation while in \(\phi = 0.01\) to \(\phi = 0.03\). This illustrates that the heat transfer gets enhanced for an increase in the solid volume fraction of the nanoparticle.

Fig. 12
figure 12

\({\psi}\) streamlines, \({\uptheta } - { }\) isotherms and \({\Pi } - { }\) heatlines for \({{a}} - \phi = 0.01,{{b}} - \phi = 0.02,{{ c}} - \phi = 0.03{ }\) at \({\uplambda } = - 1,{{ Ra}} = 10^{6} ,{{ Da}} = 10^{ - 3} {{ and Ha}} = 5\)

Full size image

Heat transfer occurs over the length of the bottom wall at \(\phi = 0.02, Ra = 10^{6} , Da = 10^{ - 3}\) and \(Ha = 5\) is illustrated in Fig. 13. The addition of the non-linearity convection parameter increases the heat transfer in the overall length of the cavity. It is noted that the \(Nu_{l}\) reduces towards the center portion because the fluid/heat flow separation appears at the middle of the cavity (vertically symmetric). Moreover, \(Nu_{l}\) increases towards either side of the wall due to the sudden discontinuity in the temperature at both the edges. Reduction in heat transfer over a majority of the wall is established as an increasing function of \(Ha\). This is because of the weakening in the heatline circulation by the imposition of a magnetic field.

Fig. 13
figure 13

\({{Nu}}_{{{l}}} - { }\) Local Nusselt number at \({{Ra}} = 10^{6} ,{ }\phi = 0.02\) and \({{Da}} = 10^{ - 3}\) of bottom wall \({{a}} - {{Ha}} = 5\) and \({{b}} - {\uplambda } = 1.\)

Full size image

Figure 14 represents the heat transfer rate observed from the cavity’s bottom wall for various parameters of \(\lambda , \phi , Da, Ha, Ra\) with the base of \(\phi = 0.02, Da = 10^{ - 3} , Ha = 5, Ra = 10^{6}\). At \(Da = 10^{ - 5}\), almost the same heat transfer is observed for all the values of \(\lambda\). But it is found that the \(Nu\) increases with respect to the increase in \(\lambda\) and \(Da\). As Darcy number controls the permeability level of the cavity, the convection effect due to buoyancy force becomes prominent on a higher value of \(Da\) and thus increasing the heat transfer rate. It is noticed that the lesser heat transfer takes place on \(Ra = 10^{3}\) and \(10^{4}\) due to the weaker buoyancy effect at this stage. But a small increase in the \(Nu\) occurs at \(Ra = 10^{3}\) because diffusion governs the flow and conduction dominates (no circulation in the heatlines is observed in Fig. 11—\(\Pi\)). On higher values of \(Ra\), the buoyancy effect becomes significant and heat flow by convection improves (\(\left| \Pi \right|_{max} = 3\) at \(Ra = 10^{5}\) and \(\left| \Pi \right|_{max} = 10.5\) at \(Ra = 10^{6}\)). Nu also increases with \(\lambda\) due to the exertion of non-linearity convection effects. At \(Ra \ge 10^{4}\), convection heat transfer comes into the picture to increase the average Nusselt number. Application of magnetic field (Lorentz force) suppresses the fluid motion, thus causing the convection-based heat transfer. \(Nu\) decreases as Hartmann number increases irrespective of the \(\lambda\). A minor increase in the Nusselt number is found for augmentation in the solid volume fraction of the nanoparticle as its thermal conductivity of the nanofluid increases.

Fig. 14
figure 14

\({{ Nu}} - { }\) Average Nusselt number for various values of \({\uplambda },{{ Da}},{{ Ra}},{{ Ha}},{ }\phi\)

Full size image

Conclusions

The present study includes the \(Cu\)-water nanofluid’s steady, quadratic natural convective flow on a square, porous cavity under the action of an applied magnetic field. Flow patterns observed due to uniformly heated bottom boundary by various parameters are discussed. It is noted that streamline flow behavior increases with an increase in \(Ra\) and \(Da\) for all the values of \(\lambda = 0, 1, - 1\). A secondary pair of circulations are generated in the case of \(\lambda = - 1\). The magnitude of streamlines is reduced for an increase \(Ha\) and \(\phi\). The heatlines are used to observe the visualization of heat flow from the bottom wall of the cavity to both the cooled vertical side walls. An improved intensity of circulations produced in the heatlines shows the convective heat transfer behavior. Heat transfer increases for an increase in the cavity’s permeability, buoyance force effect and solid volume fraction of nanoparticles. Convective heat transfer is significantly observed for higher values of \(Da, Ra\) and \(\lambda\). Reduction in heatline circulation occurs due to an increase in the \(Ha,\) and this indicates a reduction in convective heat transfer for an increase in the magnitude of the applied magnetic field effect. Non-linear natural convection effects or quadratic natural convection effects are thus considered to design/predict the better natural convective flow models and help in the identification of the minor variation in the fluid flow and heat flow processes.