Introduction

Fracture mechanics and the study of crack propagation can be considered as an exciting branch in elastic theory. It is an essential tool used to develop mechanical components' performance in the current area of materials science. Cracks or inclusions are present practically in all structural materials, either as natural defects or fabrication processes. In 1957, Irwin first provided the stress intensity factor concept, a quantity that denotes the state of stress at the tip of the crack. The stress singularity near the edge of the finite damage is vital because of the practical application. Fortunately, for most cases, the cracks are so small that their presence does not significantly impact the material's strength. But in those cases where the cracks are exceptionally large enough or in the future, they may become so due to fatigue, stress corrosion cracking, etc. It is essential to concentrate on them to determine the strength of the materials. The theory and problems related to crack geometry in isotropic materials have emerged as a vital research area in recent times, mostly due to the rapid growth in construction engineering.

Consequently, the study of diffraction of P-waves about finite cracks has become vital to ensure safe and robust structures. The crack problem in fracture mechanics has a wide range of civil engineering applications for designing load-bearing components for vehicles, power generation, and transmission. It has a highly request for industrial engineering in creating metal and polymer-forming processes, machining, etc.

Initially, the authors consider the single dynamic crack due to mathematical difficulties in calculating the solutions for multiple damages. For that reason, the research was confined to a limited area. At first, Jain and Kanwal [1] are recovered that complexity and solved their problems by taking multiple cracks in an elastic medium. After that, the problem containing single or two cracks in an isotropic elastic medium is suggested by Loeber and Sih [2], Mal [3], Srivastava et al. [4, 5], Bostrom [6], Das and Ghosh [7], Dhaliwal et al. [8, 9], Pramanik et al. [10] and many others. Infinite elastic medium's diffraction issues on two coplanar Griffith cracks were apparent up by Jain and Kanwal [11]. They considered the diffraction of normally incident p-waves by two parallel rigid strips fixed into an isotropic medium. It has derived the estimated formula for the displacement, stress tensor field. In a single strip, the limiting result has been provided for the first time in this area. Lowengrub [12] considered the problem of a pair of coplanar cracks at the interface of two bonded dissimilar isotropic elastic half-planes. They applied the Fourier transform technique to obtain a simultaneous set of triple integral equations containing a kernel. Many authors studied multiple crack's diffraction problems, but most of the issues were either implicate diffraction of shear waves or infinite media [13]. Srivastava et al. [14] discussed a more difficult and complex problem about boundaries in the media. They solved this problem using shear waves' interaction with Griffith crack interface situated of multi bonded dissimilar elastic half-spaces. Stress propagation through periodic cracks in between two bonded different antithetical orthotropic half-planes is discussed by Garg [15]. The work is shown that the determination of the stress and displacement fields in the tip of periodic collinear cracks at the interface region of two different half-planes through the transformation method. Munshi and Mandal [16] suggested diffraction of p-waves by edge crack in an infinitely long elastic strip. The Fourier transform technique had been employed to obtain the expression of the integral equation and finally solved. Das et al. [17] addressed the problem of symmetric edge cracks in an orthotropic strip under normal loading by seeking the solution of a pair of simultaneous integral equations with Cauchy type singularities. The problem by the diffraction of P-waves by an asymmetric position of a single crack is discussed by Basak [18]. The crack was located in an infinite orthotropic strip through two boundaries. A Fredholm integral equation of the second kind has been found, and finally, these equations are solved to get the analytical expression of the stress intensity factor. The dispersion of p waves by edge crack in an infinite orthotropic strip is solved by Nandi [19]. The unknown stress distribution outside the crack has been calculated by imposing Fourier transform, and finally, normal stress at a distant point is derived and plotted against various parameters. Nandi et al. [20] proposed the work of interaction of three coplanar interfacial cracks at the interface of two dissimilar elastic mediums for incident antiplane shear waves. The system of four integral equations is obtained by utilizing the transformation technique. This set of equations are solved by using the Hilbert transform and Cooke's result. The physical quantities are accepted and presented graphically for different materials. Palas et al. [21] investigated the interfacial crack problem of diffraction of P-waves by a Griffith crack. In the case of normal incidence, the boundary conditions are slightly changed to solve the displacement equation. The perturbation method is used and find the expressions of SIF and COD to plot the graphs to show the influence of various orthotropic materials constants. Naskar et al. [22] discussed the dynamic stress intensity factor for the problem of P waves interaction on a Griffith in an infinite isotropic media. For a time-dependent solution, numerical Laplace inversion has been applied using Zakian's Algorithm. Palas [23] is solved a problem of semi-infinite crack interaction by p-waves in a semi-infinite elastic half-space. The Wiener–Hopf technique method is employed to reduce the difficulties in boundary conditions. The SIF and COD were plotted by different crack layer distance values from the surface to crack depth. Impact of Cattaneo–Christov heat flux model in the flow of variable thermal conductivity fluid over a variable ticked surface is addressed by Hayat et al. [24]. A comparative study of Casson fluid with homogeneous-heterogeneous reactions has been solved by Khan et al. [25].

Though many research works have been done on the interaction or diffraction of various body waves due to finite and semi-infinite cracks between different mediums, maximum research problems considered either the interaction of shear waves or p-waves by the cracks in orthotropic medium. As per the best of our knowledge, the issue included the interaction of longitudinal waves by four collinear Griffith carks in isotropic medium has not been suggested before.

This work deals with P-waves' interaction between four collinear Griffith cracks symmetrically positioned in an infinite elastic medium. The Fourier integral transformation is employed to convert the problem for solving a group of five integral equations, which have been further reduced to the solution of integrodifferential equations. After applying the Hilbert transform technique, the integrodifferential equations are solved to calculate the SIF and COD for a small frequency. The graphs of SIF and COD show the nature of these two physical quantities against frequency. We tried to show the influence of material properties on the SIF and plotted the graphs against different crack lengths. This result is very much applicable to bridges, roads, and buildings fractures to reduce the damages.

Formation of the Problem

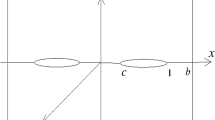
The elastic waves are diffracted by the cracks positioned in an infinite homogeneous isotropic elastic medium. The cracks are supposed to inhabit the location \({d}_{1}\le |{x}_{1}|\le {d}_{2}\), \({d}_{3}\le |{x}_{1}|\le d, -\infty <{z}_{1}<\infty , {y}_{1}=\pm 0.\) The normalization method is applied on all crack lengths by ‘\(d\)’ and substitution of \(\frac{{x}_{1}}{d}=x,\) \(\frac{{y}_{1}}{d}=y\), \(\frac{{z}_{1}}{d}=z,\) \(\frac{{d}_{1}}{d}=a,\) \(\frac{{d}_{2}}{d}=b,\) \(\frac{{d}_{3}}{d}=c,\) the crack position can be written as \(a\le |x|\le b\), \(c\le |x|\le 1, -\infty <z<\infty , y=\pm 0\) (Fig. 1), the cartesian coordinate system \((x,y,z)\) is referred. The problem geometry is displayed in the below figure, Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

In the direction of the y-axis, the incident time-harmonic body waves are moving. In longitudinal waves, the medium's displacement passes in the same direction or the opposite direction to the direction of wave propagation. The propagation of waves has been shown in the following figure Fig. 2

Fig. 2
figure 2

P-waves propagation

Full size image

The crack mode is shown in Fig. 3, where the tensile stress is normal to the crack plane.

Fig. 3
figure 3

Mode-I crack: Horizontal Movement

Full size image

In the homogeneous isotropic medium, the Navier equation of motion for the elastic wave is taken \(\rho \frac{{\partial ^{2} u}}{{\partial t^{2} }} = (\lambda + 2\mu )\Delta \Delta .u - \mu \Delta \times \Delta u\), where the symbols have their usual meanings. For isotropic medium longitudinal waves, the governing equation takes the following form

$$\frac{{\partial }^{2}{\phi }_{1}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\phi }_{1}}{\partial {y}^{2}}+{k}_{1}^{2}{\phi }_{1}=0,\frac{{\partial }^{2}{\psi }_{1}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\psi }_{1}}{\partial {y}^{2}}+{k}_{2}^{2}{\psi }_{1}=0$$
(1)

where \({k}_{i}=d\omega /{c}_{i}\), (i = 1,2), the dilatational and shear wave speeds are defined by the notations\({c}_{1}=\sqrt{\frac{\lambda +2\mu }{\rho }}\), \({c}_{2}=\sqrt{\frac{\mu }{\rho }}\) and the Lame’s constant are \(\lambda \) and \(\mu \) with \(\rho \) being the density of the material. The notation \(d\) is an arbitrary constant, and \(\omega \) is the wave frequency.

The dimensionless displacement components are defined as \(u\) and \(v\) correspondingly in the direction of \(x\), \(y\). The relation between displacement components and potential functions (\({\phi }_{1}\) and \({\psi }_{1}\) are called the scalar and vector potentials) are defined as

$$u=\frac{\partial {\phi }_{1}}{\partial x}-\frac{\partial {\psi }_{1}}{\partial y},v=\frac{\partial {\phi }_{1}}{\partial y}+\frac{\partial {\psi }_{1}}{\partial x}$$
(2)

In fracture mechanics, the diffracted wave generated due to incident longitudinal wave is essential at the crack's tip. It dramatically affects the stress intensity factor, so we have considered the diffracted wave analysis. The diffracted field satisfies the equation Eq. (1).

The discussion of problem is symmetric with respect to y-axis, it is enough to study the half space \(x\ge 0\). For a crack subjected to uniform normal stress \(-{p}_{0}\), the conditions to be specified for y = o are

$${\sigma }_{yy}(x,0)=-{p}_{0},x\epsilon {I}_{2},{I}_{4}$$
(3)
$$v(x,0)=0,x\epsilon {I}_{1},{I}_{3},{I}_{5}$$
(4)
$${\sigma }_{xy}(x,0)=0,x<\infty $$
(5)

where \({p}_{0}\) is a fixed constant which has been found by using the relation between stress and displacement is given by \(d{\sigma }_{yy}=(\lambda +2\mu )(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})-2\mu \frac{\partial u}{\partial x}\). The authors Mandal et al. [26] are calculated the value of \({p}_{0}\). The intervals are showing the boundaries \({I}_{1}=[0,a],{I}_{2}=(a,b),{I}_{3}=[b,c],{I}_{4}=(c,1),{I}_{5}=[1,\infty ).\)

Once the equation in (1) is solved to obtain \({\phi }_{1}\) and \({\psi }_{1}\), using Fourier transform technique and separation of variables. The solutions of Eq. (1) are

$${\phi }_{1}(x,y)=\frac{2}{\pi }{\int }_{0}^{\infty }{A}_{1}(\zeta ){e}^{-\alpha |y|}cos(\zeta x)d\zeta $$
(6)
$${\psi }_{1}(x,y)=\frac{2}{\pi }{\int }_{0}^{\infty }{A}_{2}(\zeta ){e}^{-\beta |y|}sin(\zeta x)d\zeta $$
(7)

\({A}_{1}(\zeta )\) and \({A}_{2}(\zeta )\) are the unknown variables with Fourier transformed variable \(\zeta \). The following relations express the notation α and β

$$\begin{aligned} \alpha & = \sqrt {\zeta ^{2} - k_{1}^{2} } ,\zeta > \,k_{1} \\ & = - i\sqrt {k_{1}^{2} - \zeta ^{2} } ,k_{1} >\,\zeta \\ \end{aligned} $$
$$\begin{aligned} \beta & = \sqrt {\zeta ^{2} - k_{2}^{2} } ,\zeta > \,k_{2} \\ & = - i\sqrt {k_{2}^{2} - \zeta ^{2} } ,k_{2} > \zeta \\ \end{aligned} $$

Using the functional values of \({\phi }_{1}\) and \({\psi }_{1}\) in Eq. (2), the expressions for displacement components are readily obtained as

$$u(x,y)=\frac{2}{\pi }{\int }_{0}^{\infty }\left[-{e}^{-\alpha |y|}+2\alpha \beta (2{\zeta }^{2}-{k}_{2}^{2}{)}^{-1}{e}^{-\beta |y|}\right]\zeta {A}_{1}(\zeta )sin(\zeta x)d\zeta $$
(8)
$$v(x,y)=\frac{2}{\pi }{\int }_{0}^{\infty }\left[-{e}^{-\alpha |y|}+2{\zeta }^{2}(2{\zeta }^{2}-{k}_{2}^{2}{)}^{-1}{e}^{-\beta |y|}\right]\alpha {A}_{1}(\zeta )cos(\zeta x)d\zeta $$
(9)

The time factor \({e}^{i\omega t}\) is repressed throughout the analysis but to be understood. The stresses associated with the displacement field of Eqs. (8), (9) are

$$d{\sigma }_{xy}=\frac{2\mu }{\pi }{\int }_{0}^{\infty }2\alpha \zeta \left[{e}^{-\alpha |y|}-{e}^{-\beta |y|}\right]{A}_{1}(\zeta )sin(\zeta x)d\zeta $$
(10)
$$d{\sigma }_{yy}=\frac{2\mu }{\pi }{\int }_{0}^{\infty }\left[(2{\zeta }^{2}-{k}_{2}^{2}){e}^{-\alpha |y|}-4\alpha \beta {\zeta }^{2}(2{\zeta }^{2}-{k}_{2}^{2}{)}^{-1}{e}^{-\beta |y|}\right]{A}_{1}(\zeta )cos(\zeta x)d\zeta $$
(11)
$$d{\sigma }_{xx}=-\frac{2\mu }{\pi }{\int }_{0}^{\infty }\left[(2{\alpha }^{2}+{k}_{2}^{2}){e}^{-\alpha |y|}-4\alpha \beta {\zeta }^{2}(2{\zeta }^{2}-{k}_{2}^{2}{)}^{-1}{e}^{-\beta |y|}\right]{A}_{1}(\zeta )cos(\zeta x)d\zeta $$
(12)

The solutions are given by equations Eqs. (8–12) may also be used for generalized plane stress by \((1+2\nu )E/(1+\nu {)}^{2}\) and \(\nu /(1+\nu )\) where \(E\) is Young’s modulus and \(\nu \) is a Poisson ratio. In Eqs. (8), (9), the unknown functions \({A}_{1}(\zeta )\) and \({A}_{2}(\zeta )\) can be evaluated from the boundary condition (5), which remain to be specified. The third boundary condition (5) leads to the relation between these two constants in the following way.

$${A}_{2}(\zeta )=\frac{2\alpha \zeta }{2{\zeta }^{2}-{k}_{2}^{2}}{A}_{1}(\zeta )$$
(13)

The Eqs. (3) and (4) can be used to arrive at the system of dual integral equations where \(\varphi (\zeta )\) is the unknown function.

$${\int }_{0}^{\infty }\zeta [1+H(\zeta )]\varphi (\zeta )cos(\zeta x)d\zeta =-\frac{\pi }{2}\frac{{p}_{0}}{\mu },x\epsilon {I}_{2},{I}_{4}$$
(14)
$${\int }_{0}^{\infty }\varphi (\zeta )cos(\zeta x)d\zeta =0,x\epsilon {I}_{1},{I}_{3},{I}_{5}$$
(15)

The functions \(\phi (\zeta )\) and \(H(\zeta )\) are expressed as

$$\varphi (\zeta )=\frac{2\alpha ({k}_{1}^{2}-{k}_{2}^{2})}{2{\zeta }^{2}-{k}_{2}^{2}}{A}_{1}(\zeta )$$
$$H\left(\zeta \right)=\frac{4\alpha \beta {\zeta }^{2}-(2{\zeta }^{2}-{k}_{2}^{2}{)}^{2}}{2\alpha \zeta \left({k}_{2}^{2}-{k}_{1}^{2}\right)}-1\to0\mathrm{ as} \zeta \to\infty $$

Solution

The trivial solution of the above Eqs. (14, 15) are defined by the following way

$$\varphi (\zeta )=\frac{1}{\zeta }{\int }_{a}^{b}f({t}^{2})sin(\zeta t)dt+\frac{1}{\zeta }{\int }_{c}^{1}g({s}^{2})sin(\zeta s)ds$$
(16)

The unknown functions are \(f({t}^{2})\) and \(g({s}^{2})\), which will be determined by utilizing the boundary conditions. The function \(\phi (t)\) is considered in such a way that the Eq. (15) is satisfied automatically, and the Eq. (14) is produced \(\frac{1}{\sqrt{x-1}}\) type of singularity at the crack's tip, which is physically consistent with the problem. To find the expressions of \(f({t}^{2})\) and \(g({s}^{2})\), we are using a result that is discussed in (Gradshteyn and Ryzhik [27]). The result is defined by

$${\int }_{0}^{\infty }\frac{sin(ty)cos(xy)}{y}dy=\left\{\begin{array}{ll}\frac{\pi }{2},t>x& \\ 0,x>t& \end{array}\right.$$

By putting the above expression in Eq. (15) under Eq. (16) leads to the conditions

$${\int }_{a}^{b}f({t}^{2})dt=0$$
(17)
$${\int }_{c}^{1}g({s}^{2})ds=0$$
(18)

Now, we are using the following result (Gradshteyn and Ryzhik [27])

$${\int }_{0}^{\infty }\frac{sin(ty)sin(xy)}{y}dy=\frac{1}{2}\mathrm{log}|\frac{t+x}{t-x}|$$

and

$$\frac{sin(\zeta t)sin(\zeta x)}{{\zeta }^{2}}={\int }_{0}^{x}{\int }_{0}^{t}\frac{vw{J}_{0}(\zeta v){J}_{0}(\zeta w)}{\sqrt{({t}^{2}-{v}^{2})({x}^{2}-{w}^{2})}}dvdw.$$

in Eq. (14) to get the simple expression. After a long algebraic calculations, it can be written in the following way

$${\int }_{a}^{b}\frac{tf({t}^{2})}{{t}^{2}-{x}^{2}}dt+{\int }_{c}^{1}\frac{sg({s}^{2})}{{s}^{2}-{x}^{2}}ds=q-\frac{d}{dx}{\int }_{a}^{b}f({t}^{2})dt{\int }_{0}^{x}{\int }_{0}^{t}\frac{vwL(v,w)dvdw}{\sqrt{({t}^{2}-{v}^{2})({x}^{2}-{w}^{2})}}-\frac{d}{dx}{\int }_{c}^{1}g({s}^{2})ds{\int }_{0}^{x}{\int }_{0}^{s}\frac{vwL(v,w)dvdw}{\sqrt{({s}^{2}-{v}^{2})({x}^{2}-{w}^{2})}},x\epsilon {I}_{2}, $$
(19)

where \(q=-\frac{\pi }{2}\frac{{p}_{0}}{\mu }\)

$$L(v,w)={\int }_{0}^{\infty }\zeta H(\zeta ){J}_{0}(\zeta v){J}_{0}(\zeta w)d\zeta $$
(20)

The function \({J}_{0}()\) is the zero-order Bessel function.

It is to be noted that \(L(v,w)\) is represented by the eq's semi-infinite integral. (14) has a slow rate of convergence. Applying a contour integration technique (Mandal and Ghosh [28]), the semi-infinite integral has therefore been converted to the following finite integrals by considering \(\gamma =\frac{{k}_{1}}{{k}_{2}}<1\) and \(\zeta ={k}_{2}\xi \)

$$L(v,w)=-i\frac{{k}_{2}^{2}}{2}{\int }_{0}^{\gamma }\frac{4{\xi }^{2}\sqrt{{\gamma }^{2}-{\xi }^{2}}\sqrt{1-{\xi }^{2}}+(2{\xi }^{2}-1{)}^{2}}{(1-{\gamma }^{2})\sqrt{{\gamma }^{2}-{\xi }^{2}}}{J}_{0}({k}_{2}\xi v){H}_{0}^{(1)}({k}_{2}\xi w)d\xi -i\frac{{k}_{2}^{2}}{2}{\int }_{\gamma }^{1}\frac{4{\xi }^{2}\sqrt{1-{\xi }^{2}}}{1-{\gamma }^{2}}{J}_{0}({k}_{2}\xi v){H}_{0}^{(1)}({k}_{2}\xi w)d\xi ,w>v$$
(21)

The Bessel function \({J}_{0}\) and the Hankel function \({H}_{0}^{(1)}\) are extended as series and applied for small frequency. The product of these two functions are explained as

$${J}_{0}({k}_{2}\xi v){H}_{0}^{(1)}({k}_{2}\xi w)=\frac{2i}{\pi }\mathrm{log}{k}_{2}+[1+\frac{2i}{\pi }(\nu +\mathrm{log}\frac{\xi w}{2})]$$

and applying in Eq. (21), we obtain

$$L(v,w)=\frac{2}{\pi }P{k}_{2}^{2}\mathrm{log}{k}_{2}+O({k}_{2}^{2})$$
(22)

where

$$P=\frac{1}{2}{\int }_{0}^{\gamma }\frac{4{\xi }^{2}\sqrt{{\gamma }^{2}-{\xi }^{2}}\sqrt{1-{\xi }^{2}}+(2{\xi }^{2}-1{)}^{2}}{(1-{\gamma }^{2})\sqrt{{\gamma }^{2}-{\xi }^{2}}}d\xi +\frac{1}{2}{\int }_{\gamma }^{1}\frac{4{\xi }^{2}\sqrt{1-{\xi }^{2}}}{1-{\gamma }^{2}}d\xi $$
(23)

The selecting of the expressions of \(f({t}^{2})\) and \(g({s}^{2})\) in Eq. (16) are depending on the kernel function see in Eq. (22). According to the kernel, the functions \(f({t}^{2})\) and \(g({s}^{2})\) are expanded in the following way.

$$f({t}^{2})={f}_{0}({t}^{2})+{k}_{2}^{2}\mathrm{log}{k}_{2}{f}_{1}({t}^{2})+O({k}_{2}^{2})$$
$$g({s}^{2})={g}_{0}({s}^{2})+{k}_{2}^{2}\mathrm{log}{k}_{2}{g}_{1}({s}^{2})+O({k}_{2}^{2})$$
(24)

Utilizing the above functions \(f({t}^{2})\), and \(g({s}^{2})\) and the expression of \(L(v,w)\) (Eq. 22) in Eq. (19) and compare the coefficients of powers of \({k}_{2}\) from both sides, and we get

$${\int }_{a}^{b}\frac{t{f}_{0}({t}^{2})dt}{{t}^{2}-{x}^{2}}+{\int }_{c}^{1}\frac{s{g}_{0}({s}^{2})ds}{{s}^{2}-{x}^{2}}=q,x\epsilon {I}_{2},{I}_{4}$$
(25)
$${\int }_{a}^{b}\frac{t{f}_{1}({t}^{2})dt}{{t}^{2}-{x}^{2}}+{\int }_{c}^{1}\frac{s{g}_{1}({s}^{2})ds}{{s}^{2}-{x}^{2}}=-\frac{2P}{\pi }[{\int }_{a}^{b}t{f}_{0}({t}^{2})dt+{\int }_{c}^{1}s{g}_{0}({s}^{2})ds],x\epsilon {I}_{2},{I}_{4}$$
(26)

and the conditions (17, 18) under the expansions (24) lead to

$${\int }_{a}^{b}{f}_{i}({t}^{2})dt=0i=\mathrm{0,1}$$
(27)
$${\int }_{c}^{1}{g}_{i}({s}^{2})ds=0i=\mathrm{0,1}$$
(28)

The Hilbert transform technique has been applied in Eq. (25). We obtained the following expression

$${\int }_{a}^{b}\frac{t{f}_{0}({t}^{2})dt}{{t}^{2}-{x}^{2}}=\frac{\pi }{2}{F}_{1}(x)x\epsilon {I}_{2}$$
(29)

where

$${F}_{1}(x)=-[\frac{{p}_{0}}{\mu }+\frac{2}{\pi }{\int }_{c}^{1}\frac{s{g}_{0}({s}^{2})ds}{{s}^{2}-{x}^{2}}]$$
(30)

Cooke’s result [29] is applied to obtain the solution of the integral Eq. (29) is found to be

$${f}_{0}\left({t}^{2}\right)=-\frac{{p}_{0}}{\mu }\frac{\sqrt{{t}^{2}-{a}^{2}}}{\sqrt{{b}^{2}-{t}^{2}}}-\frac{2}{\pi }\frac{\sqrt{{t}^{2}-{a}^{2}}}{\sqrt{{b}^{2}-{t}^{2}}}{\int }_{c}^{1}\frac{\sqrt{{s}^{2}-{b}^{2}}}{\sqrt{{s}^{2}-{a}^{2}}}\frac{s{g}_{0}\left({s}^{2}\right)ds}{{s}^{2}-{t}^{2}}+\frac{{D}_{1}}{\sqrt{({t}^{2}-{a}^{2})({b}^{2}-{t}^{2})}}$$
(31)

And \({D}_{1}\) is a fixed constant, which is calculated by using Eq. (27) for i = 0.

The singular integral equation is produced by substitution of the value of \({f}_{0}({t}^{2})\) from Eq. (31) in Eq. (25) for \(x\epsilon {I}_{4}\)

$${\int }_{c}^{1}\frac{\sqrt{{s}^{2}-{b}^{2}}}{\sqrt{{s}^{2}-{a}^{2}}}\frac{s{g}_{0}({s}^{2})ds}{{s}^{2}-{x}^{2}}=\frac{\pi }{2}{F}_{2}(x)x\epsilon {I}_{4}$$
(32)

where

$${F}_{2}\left(x\right)=-\frac{{p}_{0}}{\mu }+\frac{{D}_{1}}{{x}^{2}-{a}^{2}}$$

The finite Hilbert Transform technique is applied to find the solution of the integral Eq. (32) in the form

$${g}_{0}({s}^{2})=-\frac{{p}_{0}}{\mu }\sqrt{\frac{({s}^{2}-{a}^{2})({s}^{2}-{c}^{2})}{({s}^{2}-{b}^{2})(1-{s}^{2})}}+\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}\frac{{D}_{1}\sqrt{{s}^{2}-{c}^{2}}}{\sqrt{({s}^{2}-{a}^{2})({s}^{2}-{b}^{2})(1-{s}^{2})}}+\frac{{D}_{2}\sqrt{{s}^{2}-{a}^{2}}}{\sqrt{({s}^{2}-{b}^{2})({s}^{2}-{c}^{2})(1-{s}^{2})}}$$
(33)

where the unknown fixed constant is \({D}_{2}\) to be determined by using Eq. (28) for i = 0.

Now substituting the value of \({g}_{0}({s}^{2})\) from Eq. (33) into the Eq. (31) and integrating, \({f}_{0}({t}^{2})\) is obtained in the following form

$${f}_{0}({t}^{2})=-\frac{{p}_{0}}{\mu }\sqrt{\frac{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}{({b}^{2}-{t}^{2})(1-{t}^{2})}}+\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}\frac{{D}_{1}\sqrt{{c}^{2}-{t}^{2}}}{\sqrt{({t}^{2}-{a}^{2})({b}^{2}-{t}^{2})(1-{t}^{2})}}-\frac{{D}_{2}\sqrt{{t}^{2}-{a}^{2}}}{\sqrt{({b}^{2}-{t}^{2})({c}^{2}-{t}^{2})(1-{t}^{2})}}$$
(34)

To get the analytical expressions of \({g}_{1}({s}^{2})\) and \({f}_{1}({t}^{2})\), we applied the same procedure using the above result.

$${f}_{1}({t}^{2})=-\frac{4PR}{{\pi }^{2}}\sqrt{\frac{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}{({b}^{2}-{t}^{2})(1-{t}^{2})}}+\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}\frac{{E}_{1}\sqrt{{c}^{2}-{t}^{2}}}{\sqrt{({t}^{2}-{a}^{2})({b}^{2}-{t}^{2})(1-{t}^{2})}}-\frac{{E}_{2}\sqrt{{t}^{2}-{a}^{2}}}{\sqrt{({b}^{2}-{t}^{2})({c}^{2}-{t}^{2})(1-{t}^{2})}}$$
(35)
$${g}_{1}({s}^{2})=-\frac{4PR}{{\pi }^{2}}\sqrt{\frac{({s}^{2}-{a}^{2})({s}^{2}-{c}^{2})}{({s}^{2}-{b}^{2})(1-{s}^{2})}}+\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}\frac{{E}_{1}\sqrt{{s}^{2}-{c}^{2}}}{\sqrt{({s}^{2}-{a}^{2})({s}^{2}-{b}^{2})(1-{s}^{2})}}+\frac{{E}_{2}\sqrt{{s}^{2}-{a}^{2}}}{\sqrt{({s}^{2}-{b}^{2})({s}^{2}-{c}^{2})(1-{s}^{2})}}$$
(36)

where \({E}_{1}\) and \({E}_{2}\) are the unknown constants to be found from the Eq. (27) and Eq. (28) (for i = 1) respectively and

$$R=-\frac{{p}_{0}}{\mu }[{I}_{a}^{b}+{I}_{c}^{1}]+\left[\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}{D}_{1}+{D}_{2}\right]M$$
$${I}_{i}^{j}={\int }_{i}^{j}\frac{t\sqrt{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}dt}{\sqrt{({b}^{2}-{t}^{2})(1-{t}^{2})}}$$
$$M=\frac{{c}^{2}-{b}^{2}}{\sqrt{({c}^{2}-{a}^{2})(1-{b}^{2})}}\left[\Pi (\frac{\pi }{2},\frac{{b}^{2}-{a}^{2}}{{c}^{2}-{a}^{2}},p)+\Pi (\frac{\pi }{2},\frac{1-{c}^{2}}{1-{b}^{2}},p)-F(\frac{\pi }{2},p)\right]$$
$$p=\frac{\sqrt{(1-{c}^{2})({b}^{2}-{a}^{2})}}{\sqrt{(1-{b}^{2})({c}^{2}-{a}^{2})}}$$

where the functions \(F()\), \(\Pi ()\) are defined as elliptic integrals of the first and third kind, the unknown fixed constants \({D}_{i}\) and \({E}_{i}(i=\mathrm{1,2})\) will be found by Eq. (27) and Eq. (28)

\({D}_{i}=\frac{{p}_{0}}{\mu }{C}_{i},{E}_{i}=\frac{4PR}{{\pi }^{2}}{C}_{i},i=\mathrm{1,2}\) where

$${C}_{1}=\left[\frac{{J}_{a}^{b}{K}_{c}^{1}+{J}_{c}^{1}{K}_{a}^{b}}{{J}_{a}^{b}{L}_{c}^{1}+{J}_{c}^{1}{L}_{a}^{b}}]\sqrt{\frac{{c}^{2}-{a}^{2}}{1-{a}^{2}}},{C}_{2}=[\frac{{L}_{a}^{b}{K}_{c}^{1}-{L}_{c}^{1}{K}_{a}^{b}}{{J}_{a}^{b}{L}_{c}^{1}+{J}_{c}^{1}{L}_{a}^{b}}\right],$$
$${J}_{i}^{j}={\int }_{i}^{j}\frac{\sqrt{{t}^{2}-{a}^{2}}dt}{\sqrt{({c}^{2}-{t}^{2})({b}^{2}-{t}^{2})(1-{t}^{2})}}$$
$${K}_{i}^{j}={\int }_{i}^{j}\frac{\sqrt{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}dt}{\sqrt{({b}^{2}-{t}^{2})(1-{t}^{2})}},{L}_{i}^{j}={\int }_{i}^{j}\frac{\sqrt{{c}^{2}-{t}^{2}}dt}{\sqrt{({b}^{2}-{t}^{2})({t}^{2}-{a}^{2})(1-{t}^{2})}}$$

On substituting the values of \({D}_{i}\) and \({E}_{i}\) (i = 1,2), in the Eqs. (33)-(36), it yields

$${f}_{i-1}({t}^{2})=-{A}_{i}\left[1-\frac{{C}_{1}}{{t}^{2}-{a}^{2}}\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}+\frac{{C}_{2}}{{c}^{2}-{t}^{2}}\right]\sqrt{\frac{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}{({b}^{2}-{t}^{2})(1-{t}^{2})}},(i=\mathrm{1,2})$$
(37)
$${g}_{i-1}({s}^{2})=-{A}_{i}\left[1-\frac{{C}_{1}}{{s}^{2}-{a}^{2}}\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}-\frac{{C}_{2}}{{s}^{2}-{c}^{2}}\right]\sqrt{\frac{({s}^{2}-{a}^{2})({s}^{2}-{c}^{2})}{({s}^{2}-{b}^{2})(1-{s}^{2})}},(i=\mathrm{1,2})$$
(38)

where

$${A}_{1}=\frac{{p}_{0}}{\mu },{A}_{2}=\frac{4PR}{{\pi }^{2}}$$

Quantities of Physical Interest

The normal stress \({\sigma }_{yy}(x,0)\) on the plane \(y=0\) outside the crack \((|x|>1)\) is found. The stress field's singular character may find by solving for \({\sigma }_{yy}(x,0)\). Therefore, it is clear that the normal stress outside the crack has a square root singularity at the crack tip. The values of functions \(f({t}^{2})\) and \(g({s}^{2})\) are inserting in the expression of the stress component in Eq. (11). After some algebraic manipulation, the stress intensity factors are found at the crack tip points \(x=a,\) \(x=b,\) \(x=c\), and \(x=1\) denoted by \({N}_{a},\) \({N}_{b},\) \({N}_{c}\), and \({N}_{1}\). The state of stress at the crack tips is determined by a quantity called the stress intensity factor (SIF), which is defined by

$${N}_{a}=\underset{ x\to a-}{\mathrm{lim}}[\frac{\sqrt{a-x} {\sigma }_{yy}(x,0) }{{p}_{0}}{]}_{0<x<a}$$
(39)

In this problem, the SIF can find as

$$SIF=\frac{{C}_{1}}{\sqrt{2a({b}^{2}-{a}^{2})}}[1-\frac{4P}{{\pi }^{2}}N{k}_{2}^{2}\mathrm{log}{k}_{2}]+O({k}_{2}^{2})$$
(40)

Similarly, we can find the stress intensity factors of remaining crack tips (\(x=b,\) \(x=c\), and \(x=1\)) as

$$ \begin{aligned} N_{b} & = \mathop {{\text{lim}}}\limits_{{~x \to b + }} \left[ {\frac{{\sqrt {x - b} ~~~\sigma _{{yy}} \left( {x,0} \right)~~}}{{p_{0} }}} \right]_{{b < x < c}} = \left[ {\sqrt {\frac{{\left( {b^{2} - a^{2} } \right)\left( {c^{2} - b^{2} } \right)}}{{2b\left( {1 - b^{2} } \right)}}} - C_{1} \sqrt {\frac{{\left( {c^{2} - b^{2} } \right)\left( {1 - a^{2} } \right)}}{{2b\left( {b^{2} - a^{2} } \right)\left( {c^{2} - a^{2} } \right)\left( {1 - b^{2} } \right)}}} } \right. \\ & \quad \left. { + C_{2} \sqrt {\frac{{b^{2} - a^{2} }}{{2b\left( {c^{2} - b^{2} } \right)\left( {1 - b^{2} } \right)}}} } \right]\left[ {1 - \frac{{4P}}{{\pi ^{2} }}Nk_{2}^{2} {\text{log}}k_{2} } \right] + O\left( {k_{2}^{2} } \right) \\ \end{aligned} $$
(41)
$$N_{c} = \mathop {{\text{lim}}}\limits_{{~x \to c - }} \left[ {\frac{{\sqrt {c - x} ~~~\sigma _{{yy}} \left( {x,0} \right)~~}}{{p_{0} }}} \right]_{{b < x < c}} = C_{2} \sqrt {\frac{{c^{2} - a^{2} }}{{2c\left( {c^{2} - b^{2} } \right)\left( {1 - c^{2} } \right)}}} \left[ {1 - \frac{{4P}}{{\pi ^{2} }}Nk_{2}^{2} {\text{log}}k_{2} } \right] + O\left( {k_{2}^{2} } \right)$$
(42)
$$\begin{aligned} N_{1} & = \mathop {{\text{lim}}}\limits_{{~x \to 1 + }} \left[ {\frac{{\sqrt {x - 1} ~~~\sigma _{{yy}} \left( {x,0} \right)~~}}{{p_{0} }}]_{{x > 1}} = } \right[\sqrt {\frac{{\left( {1 - a^{2} } \right)\left( {1 - c^{2} } \right)}}{{2\left( {1 - b^{2} } \right)}}} \\ & \quad - C_{1} \sqrt {\frac{{1 - c^{2} }}{{2\left( {1 - b^{2} } \right)\left( {c^{2} - a^{2} } \right)}}} - C_{2} \sqrt {\frac{{1 - a^{2} }}{{2\left( {1 - b^{2} } \right)\left( {1 - c^{2} } \right)}}} ]\left[ {1 - \frac{{4P}}{{\pi ^{2} }}Nk_{2}^{2} {\text{log}}k_{2} } \right] + O\left( {k_{2}^{2} } \right) \\ \end{aligned}$$
(43)

where

$$N=\left[{I}_{a}^{b}+{I}_{c}^{1}\right]-\left[\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}{C}_{1}+{C}_{2}\right]M$$

Another quantity of physical interest is the crack opening displacement (COD) defined by

$$\Delta v(x,0)=v(x,0+)-v(x,0-)=\left\{\begin{array}{ll}2{\int }_{x}^{b}f({t}^{2})dt,a\le x\le b& \\ & \\ 2{\int }_{x}^{1}g({s}^{2})ds,c\le x\le 1& \end{array}\right.$$
(44)

The equations Eq. (37) and Eq. (38) are used to obtain the expression COD. Since the problem is symmetric with respect to the x-axis therefore we write the crack opening displacement (COD) for as

$$\Delta v(x,0)=-2\left[{A}_{1}+{A}_{2}{k}_{2}^{2}\mathrm{log}{k}_{2}\right]{\int }_{x}^{b}\sqrt{\frac{({t}^{2}-{a}^{2})({c}^{2}-{t}^{2})}{({b}^{2}-{t}^{2})(1-{t}^{2})}}\times \left[1-\frac{{C}_{1}}{{t}^{2}-{a}^{2}}\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}+\frac{{C}_{2}}{{c}^{2}-{t}^{2}}\right]dt,a\le x\le b$$
(45)

and

$$\Delta v(x,0)=-2\left[{A}_{1}+{A}_{2}{k}_{2}^{2}\mathrm{log}{k}_{2}\right]{\int }_{x}^{1}\sqrt{\frac{({s}^{2}-{a}^{2})({s}^{2}-{c}^{2})}{({s}^{2}-{b}^{2})(1-{s}^{2})}}\times \left[1-\frac{{C}_{1}}{{s}^{2}-{a}^{2}}\sqrt{\frac{1-{a}^{2}}{{c}^{2}-{a}^{2}}}-\frac{{C}_{2}}{{s}^{2}-{c}^{2}}\right]ds,c\le x\le 1$$
(46)

Results and Discussions

The effect of wave number on SIF has been shown on the graphs (Figs. 4, 5, 6 and 7) using different crack lengths. For the description of the inner and outer cracks, the internal crack's length is dissimilar \((a=\mathrm{0.2,0.3,0.4})\), and the external crack's length is constant as like \((b=0.6,c=0.8)\). The cracks' slope is projected against frequency \({k}_{2}(0.1\le k2\le 1)\) at stress intensity factors. It is shown in Figs. 4, 5, 6 and 7. In these figures, initially, the stress intensity factor increases with frequency and then slowly reducing. The values of SIF are showing more for low values of inner crack and after. The stress graphs tend to linear when it gradually increases in the distance between internal cracks.

Fig. 4
figure 4

SIF \(({N}_{a})\) versus frequency \({k}_{2}\) with constant outside crack length; (—)Material-1; (-—-)Material-2; a = 0.2, 0.3, 0.4; b = 0.6; c = 0.8

Full size image
Fig. 5
figure 5

SIF \(({N}_{b})\) versus frequency \({k}_{2}\) with constant outside crack length; (—)Material-1; (-—-)Material-2; a = 0.2, 0.3, 0.4; b = 0.6; c = 0.8

Full size image
Fig. 6
figure 6

SIF \(({N}_{c})\) versus frequency \({k}_{2}\) with constant outside crack length; (—)Material-1; (-—-)Material-2; a = 0.2, 0.3, 0.4; b = 0.6; c = 0.8

Full size image
Fig. 7
figure 7

SIF \(({N}_{1})\) versus frequency \({k}_{2}\) with constant outside crack length; (—)Material-1; (-—-)Material-2; a = 0.2, 0.3, 0.4; b = 0.6; c = 0.8

Full size image

Furthermore, when we fixed the length of the outer cracks as \((a=0.2,c=0.8)\) with the distance from internal damages, the graph we observed as like same if increases in \(b\) value such as \((\mathrm{0.4,0.5,0.6})\) the curvature of the stress intensity factor are also getting a boost. It means that inner cracks and outer cracks distance being reducing. When we keep non-variable values of internal cracks like \((a=0.2,b=0.4)\), we observed that the exterior cracks increase because the stress intensity factor's curvature increases. i.e., the length between the inner crack and outer crack decreases. The mechanical materials' properties play a vital role in SIF and COD. The effect of various parametric (density, shear modulus, Young's modulus) values of different SIF and COD materials. To evaluate the SIF, we choose two types of steel and aluminum (see Table 1). The peak values of the SIF of steel is higher than the aluminum peak values. We can conclude that the importance of SIF is more for higher density materials.

Table 1 Engineering elastic constant
Full size table

The peak point of stress intensity factors is increased, but it has reduced against frequencies and tending to zero after a particular time. This result is very consistent with the physical nature of the crack. The displayed configurations (Figs. 4, 5, 6 and 7) conclude that the values of SIF rely on the geometry of the crack and the applied load spreading. If the applied load is constant, then the SIF decreases with the growing values of dimensionless frequency, which means that crack will not propagate further if the applied load does not exceed the load's critical value. It has been observed that fracture happens when the stress intensity factor's values exceed a particular limit called the critical stress intensity factor.

The COD is displayed for different crack lengths in Fig. 8; it shows that COD's value decreases as the value of 'x' increases. Therefore the COD is highest at the center of the crack, and it decreases as we move along the damage towards the crack tip and tends to zero at the crack's end (x = a). Initially, COD values are increased after reaching the highest value, it is reduced and finally growing to zero.

Fig. 8
figure 8

COD vs distance for Material-1; a = 0.2, 0.3, 0.4; b = 0.6; c = 0.8

Full size image

The impact of crack lengths on SIF has been shown on the graphs (Figs. 9a, b and c). In this part, we have plotted the graphs of SIF against crack lengths. We varied the inner and outer crack lengths and plotted the graphs of SIF. Keeping the external crack length fixed (c = 0.8), stress intensity factors at the tip \((a,b)\) of the inner crack have been plotted against the other crack lengths. It is observed from Fig. 9(a, b) that the stress intensity factors slowly increase with increasing the values of crack size (\(c\)). Also, with the increase in the distance between the inner crack and outer crack, the peak of stress intensity factors is increased where the other crack lengths (\(a=0.2,b=0.8\)) are fixed. It is found that the nature of stress intensity factors remains the same in all cases.

Fig. 9
figure 9

SIF vs inner (a a = 0.2, c = 0.8, b b = 0.4, c = 0.8) and outer(c a = 0.2, b = 0.4) crack lengths (—) Material-1; (-—-) Material-2

Full size image

Comparison

This section has discussed some results of previously published papers and compared our results to show the correctness and validation. Most of the authors have been solved their problems by taking two or three coplanar cracks with antiplane shear waves in the orthotropic medium. We tried to show the expressions of solutions and graphs if we take same type of problem either in othotropic medium or shear waves consideration. The following discussions are:

The diffraction of Elastic-waves by three coplanar Griffith cracks in an Orthotropic Medium is addressed by Sarkar et al. [30]. We suggested the diffraction of elastic-waves by four coplanar Griffith Cracks in an Infinite Elastic Medium in the present problem. The kernels are (Eq. (20) and Eq. (39) of Sarkar et al. [30] same and all other terms look similar to the expression of SIF in both the works. For more correctness, we plotted the graphs by taking four cracks in Sarkar's work. This graph in Fig. 5 is similar to the graphs of Sarkar et al. [30].

Next, we have to compare our works with Sarkar et al. [28]. Interaction of elastic waves with two coplanar Griffith cracks in an orthotropic medium is solved by Sarkar et al. [28]. In both works, the waves' considerations are the same, but the number of cracks and mediums is dissimilar. They introduced the orthotropic medium but in this work is an isotropic medium-based. The relation between the constants of isotropic and orthotropic is C11 = C22 = \(\lambda +2\mu \), C12 = \(\lambda \). After conversion of isotropic materials constant to orthotropic materials constant, the expressions of SIF and COD are coming similar, and the graphs are looking like same. In both pieces, the figures for SIF increase, and after reaching a certain point, it is decreased.

The four coplanar moving Griffith cracks in an infinite elastic medium is Das and Ghosh [31]. We considered the diffraction of P-waves by four collinear Griffith cracks in an infinite elastic medium in the present problem. However, the same problem in the isotropic medium was solved by Das and Ghosh [31] by applying the integral equation method physically; it is different from our research work. They considered a static problem, but our problem is dynamic. Our result is related to Das and Ghosh [31], which agrees with this obtained result. In isotropic media results for a static case, we consider the displacement equation.

$$\left(\lambda +2\mu \right)\frac{{\partial }^{2}u}{\partial {x}^{2}}+\mu \frac{{\partial }^{2}u}{\partial {y}^{2}}+\left(\lambda +\mu \right)\frac{{\partial }^{2}v}{\partial x\partial y}=0$$
$$\mu \frac{{\partial }^{2}v}{\partial {x}^{2}}+\left(\lambda +2\mu \right)\frac{{\partial }^{2}v}{\partial {y}^{2}}+\left(\lambda +\mu \right)\frac{{\partial }^{2}u}{\partial x\partial y}=0$$

where λ, μ is Lame's constants. Therefore, using the above equations, the stress intensity factors become the same as Das and Ghosh [31] obtained for static cases. For more validation of this work, we draw the graph of COD for inner crack tip b. (Fig. 10)

Fig. 10
figure 10

Stress intensity factor versus frequency

Full size image

This graph (Fig. 11) is similar to the diagram (Fig. 4) of Das and Ghosh [31].

Fig. 11
figure 11

Variation of crack opening displacement with x/b on the crack of the inner pair

Full size image

Conclusions

The analytical determination of SIF, COD due to multiple crack propagation and infinite elastic medium to P-waves incidence ware was carried out in this present study. Hilbert transformation, Fourier transforms are imposed to reduce the complication of five singular integral equations, which have been obtained in this work. The Goodwin and Fox method is employed to get the final numerical solution. The numerical values of the stress intensity factor and crack opening displacement have been displayed graphically to show the influence of different parameters on the stress intensity factor and crack opening displacement. In all cases, the variation of SIF and COD are found to be prominent for other isotropic materials. The aim of the study of these physical quantities (SIF, COD) is the prediction of possible arrest of the cracks within a specific range of frequency by monitoring applied load so that we can avoid the fracture. If the composites model is considered practically for an experiment, the crack can obstruct accordingly. This study may continue on an earthquake to reduce the damages to the earth's surface buildings. Protection of structures and critical infrastructures from seismic hazards will be one of the main targets in civil engineering. The proposed work will provide sufficient outlay for designing and developing solid mechanics with crack and improving the seismology area to reduce the earthquake's damages.