Introduction

Many models of chemical, physical and biological processes are often expressed in terms of differential equations or systems of differential equations [1,2,3]. If the systems obtained in modeling these processes are non-linear, coupled or rigid, their solution becomes difficult and computationally expensive. For this reason, there is a need for efficient numerical methods to solve mathematical modeling problems.

For example, Djouad et al. [4] applied a second order Rosenbrock scheme for gas phase chemical kinetics, because the stiffness induced by different timescales magnitudes seriously restricts the integration time step of these models.

Jajarmi et al. [5] presented a new mathematical model for the dengue fever outbreak based on a system of fractional differential equations. To simulate this model they used a new and efficient numerical method, in which they transform the system of equations into an equivalent integral equation. Then the trapezoidal method was used to approach the fractional integral operator. Currently, control techniques also are being used to optimize the solution of problems of great interest [6,7,8].

Among these applications, the Anaerobic Digestion (AD) process has become an important source of research. Anaerobic Digestion is a biochemical process of producing biogas, which is the biological degradation of biomass [9,10,11], the most abundant raw material in the world. Biomass is composed of substances of organic origin (plants, animals and microorganisms). Unlike fossil fuels, such as oil and coal, biomass is renewable in a short period of time [12, 13]. Biogas can be used to generate electrical, thermal and mechanical energy [14, 15].

The anaerobic digestion is a complex process, consisting of several stages of metabolic interactions, in the absence of oxygen, and performed by a community of microbial populations. This process can be divided into four phases of biodegradation: hydrolysis, acidogenisis, acetogenesis, and methanogenesis [14, 16,17,18]. The mathematical model for the AD process is obtained according to the number of chemical reactions presented in each stage of the process. This modeling provides a set of coupled and nonlinear ordinary differential equations. The numerical integration of these equations allows accurately predict the concentrations of chemical species at any time given the initial conditions.

The Adomian Decomposition Method (ADM) is a powerful technique that can be used for solving the AD problem, since it is computationally convenient, accurate and physically realistic. Adomian [19] demonstrated that with the ADM it is possible to solve linear and nonlinear differential equations, obtaining continuous solutions. The ADM technique involves the decomposition of nonlinear terms into the differential equation(s) in a series of polynomials.

Currently, the ADM technique has been used by many researches in several areas to solve problems of linear and nonlinear equations, involving initial and/or boundary conditions [20,21,22,23]. In addition, ADM can be used to solve systems of nonlinear differential equations and also to the solution of higher-order differential equations [24, 25]. Some researchers have introduced modifications in the ADM technique [26, 27]. For example, Younker [28] modified the ADM to solve a system of coupled differential equations describing rates of chemical reaction.

In this paper, we develop a mathematical model for the AD process with five chemical reactions, where the pulp is the substrate. In this model, Gibbs free energy (\(\varDelta \)G) is used to calculate the rate of each reaction and, from the results, it can be concluded that this is a good alternative in the absence of the respective rates.

Motivated by the efficiency of ADM, the main objective of this article is to show that it is possible to obtain the solution of the proposed model using only three Adomian terms. For this, the Adomian polynomials are constructed analytically and the modified ADM is used to numerically solve the system of ordinary differential equations of the model.

The rest of this paper is structured as follow. Section 2 presents the phases of the AD process. Section 3 presents the mathematical formulation of the problem. In Sect. 4 the classic ADM and iterative ADM are described. In this section the Adomian polynomials of the AD system problem are also calculated. In Sect. 5 the results of the simulations are presented to illustrate the accuracy and efficiency of the proposed technique. The paper ends with conclusions and perspectives.

Chemical Modeling

The phases of the anaerobic digestion process are:

Hydrolysis is the first stage of degradation, in which complex organic molecules like carbohydrates, proteins and fats decompose to form soluble monomers. Reactions are catalyzed by enzymes excreted from the hydrolytics and fermentative bacterias, such as cellulase, protease and lipase. A hydrolysis reaction where the organic waste is divided into a sugar (glucose) can be represented by Eq. (1).

$$\begin{aligned} C_6 H_{10}O_{5} + H_2O = C_6 H_{12}O_6. \end{aligned}$$
(1)

Acidogenesis sugars are fermented to produce simple organic compounds, specially short-chain (volatile) acids (e.g. propionic, formic, lactic, butyric, or succinic acids), ketones (e.g. glycerol, acetone) and alcohols (e.g. ethanol, methanol). The following is an example of product obtained on acidogenesis phase and its respective value of \(\varDelta \)G:

$$\begin{aligned} C_6 H_{12}O_6 \rightarrow C_4H_8O_2 + 2CO_2 + 2H_2, \ \ \varDelta \text {G} = -264,19 \ \text {KJ/mol}. \end{aligned}$$
(2)

Acetogenesis is the third stage, where the fermentation of carbohydrates occurs and results in a combination of acetate, carbon dioxide (\(CO_2\)), and hydrogen (\(H_2\)). The long chain fatty acids, formed from lipid hydrolysis, are oxidized to acetate or propionate and gaseous hydrogen is formed. An acetogenesis reaction can be represented by Eq. (3).

$$\begin{aligned} 2C_4H_8O_2+2H_2O+CO_2 \rightarrow 4C_2H_4O_2 + CH_4, \ \ \ \varDelta \text {G} = -35 \ \text {KJ/mol}. \end{aligned}$$
(3)

Methanogenesis performed by methanogen microorganisms, is the last stage of anaerobic digestion, where methane and carbon dioxide are produced. At this stage, the methanogenic archaea mainly converts acetic acid, hydrogen and carbon dioxide into methane. Methanogenic archaea are divided into two main groups [29]:

  • Acetoclastic methanogenesis they produce methane from acetic acid or methanol. These are the predominant microorganisms in anaerobic digestion, responsible for about 60 to 70% of all methane production.

  • Hydrogenotrophic methanogenesis they produce methane from hydrogen and carbon dioxide, using carbon dioxide (\(CO_2\)) as a source of carbon, and hydrogen as a reducing agent.

Reactions related to the stage of methanogenesis are presented in Table 1, along with the \(\varDelta \hbox {G}^{\circ }\) value of each reaction.

Table 1 Reactions related to the methanogenesis phase
Full size table

If the substrate composition is known, and the total conversion of the substrate into biogas occurs, the theoretical yield of \(CH_4\) and \(CO_2\) can be estimated from the chemical reaction [30, 31] given by

$$\begin{aligned}&C_nH_pO_q + \left[ n-\frac{p}{4} - \frac{q}{2} \right] H_2O \rightarrow \left[ \frac{n}{2}+\frac{p}{8} - \frac{q}{4} \right] CH_4\nonumber \\&\quad + \left[ \frac{n}{2}-\frac{p}{8} + \frac{q}{4} \right] CO_2, \end{aligned}$$
(4)

where \(C_nH_pO_q\) is organic matter, and p, q, and n are dimensionless coefficients.

Mathematical Modeling of the AD Process

The mathematical formulation of the anaerobic digestion process is associated to the four phases described previously: hydrolysis, acidogenesis, acetogenesis and methanogenesis. The mathematical model provides a set of ordinary differential equations that must be solved numerically, due to the coupling of the set of equations.

The general stoichiometric equation of any chemical process can be defined by Eq. (5)

$$\begin{aligned} \sum _{j=1}^{N_s} \nu _j Y_j = 0, \end{aligned}$$
(5)

where \(\nu _j\) is the stoichiometric coefficient of j-th species \(Y_j\) and \(N_s\) is the number of species. The stoichiometric coefficients are negative numbers for reagents and positive for products, by convention.

The rates of elementary reactions can be calculated from the law of mass action [32], by the formula

$$\begin{aligned} r_i= k_i \prod _{j}^{N_s} Y_j^{\nu _{ij}}, \end{aligned}$$
(6)

where \(Y_j\) is the molar concentration of species j, and \(k_i\) the rate coefficients that can be calculated using the Gibbs free energy (\(\varDelta \)G) of each reaction [33]

$$\begin{aligned} k_i=\text {exp}\left( -\frac{\varDelta \text {G}}{\text {R}\text {T}_i}\right) , \end{aligned}$$
(7)

where R=8.3144 J/Kmol is the universal gas constant and T\(_i\) is the absolute temperature (in Kelvins).

The kinetic system of ordinary differential equations (ODEs) is written as:

$$\begin{aligned} \displaystyle \frac{d Y_j}{dt}= \sum _{i}^{N_R} \nu _{ij} r_i, \ \ j=1, \cdots , N_s. \end{aligned}$$
(8)

In general, the kinetic system of ODEs is of first order and nonlinear. Each species participates in several reactions, with its corresponding production rate.

The system of ODEs of the problem considers the reactions of the phases: (I) hydrolysis, (II) acidogenesis, (III) acetogenesis, (IV) hydrogenotrophic methanogenesis, and (V) acetoclastic methanogenesis. Table 2 shows the set of chemical reactions of the stages (I), (II), (III), (IV) and (V) used to write the kinetic system of ODEs.

Table 2 Set of chemical reactions of the anaerobic digestion process
Full size table

Table 3 shows the chemical compounds involved in the anaerobic digestion process, described previously. Each chemical compound is associated with its chemical formula and abbreviations.

Table 3 Chemical compounds, chemical formulas and abbreviations
Full size table

The concentration variations \( Y_j \) (\(j = 1, \cdots , 8\)) are based on Eq. (8). So, the kinetic system of ODEs is composed of eight ordinary differential equations, providing the initial value problem:

(9)

Adomian Decomposition Method

Consider the initial value problem for a system of first-order equations of the following form

$$\begin{aligned} \left\{ \begin{array}{c} y'_{1}(t)=f_1(t, y_1, \ldots , y_m), \ \ y_1(0)=y_{1,0}\\ y'_{2}(t)=f_2(t, y_1, \ldots , y_m), \ \ y_2(0)=y_{2,0}\\ \vdots \\ y'_{m}(t)=f_m(t, y_1, \ldots , y_m), \ \ y_m(0)=y_{m,0}\\ \end{array}\right. , \end{aligned}$$
(10)

where \(f_k(t, y_1, \ldots , y_m) \), \(k = 1, 2, \ldots , m\) are linear and nonlinear functions.

We write the system (10) for the k-th equation as:

$$\begin{aligned} Ly_k = f_k(t, y_1, \ldots , y_m), \ k=1, \ldots , m, \end{aligned}$$
(11)

where L is the linear operator, in this case the time derivative \(\text {d}/\text {d}t\).

The Adomian decomposition method consists of separating each function \(f_k\) in a linear part and a nonlinear part, writing equation (11) as follows

$$\begin{aligned} Ly_k = R_k(t, y_1, y_2, \ldots , y_m )+ N_k(t, y_1, y_2, \cdots , y_m), \end{aligned}$$
(12)

where \(R_k(t, y_1, y_2, \ldots , y_m)\) are linear operators and \(N_k(t, y_1, y_2, \ldots , y_m)\) are nonlinear operators.

Applying the inverse operator \(\displaystyle L^{-1}(\cdot )=\int _{0}^{t}\left( \cdot \right) \text {d}t\) on both sides of equation (12) results

$$\begin{aligned} y_k = y_k(0) + L^{-1}\left[ R_k(t, y_1, y_2, \ldots , y_m )+ N_k(t, y_1, y_2, \cdots , y_m)\right] , \end{aligned}$$
(13)

where \(y_k(0)\) is the initial condition of the problem.

Based on the ADM [34,35,36,37], we seek the solution \(\{y_1, \cdots , y_m \}\) as

$$\begin{aligned} y_k=\displaystyle \lim _{n\rightarrow \infty } \sum _{i=0}^{n}y_{k,i}. \end{aligned}$$
(14)

The nonlinear terms of \(N_k(t, y_{1}, y_{2}, \ldots , y_{m}), k=1, \ldots , m\) are assumed to be analytic functions that can be expressed by an infinite series given by

$$\begin{aligned} N_k(t, y_{1}, y_{2}, \ldots , y_{m})=\displaystyle \sum _{n=0}^{\infty } A_{k, n}, \ k=1, \ldots , m, \end{aligned}$$
(15)

where the \(A_{k,n}\) are the Adomian polynomials calculated by the formula

$$\begin{aligned} \displaystyle A_{k,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}N_k\left( t, \sum _{i=0}^{\infty } \lambda ^{i}y_{1,i}, \sum _{i=0}^{\infty } \lambda ^{i}y_{2,i}, \ldots , \sum _{i=0}^{\infty } \lambda ^{i}y_{m,i} \right) \right] _{\lambda =0}. \end{aligned}$$
(16)

Taking the first \(n+1\) terms of the n-th approximation of \(y_k\) as

$$\begin{aligned} y_{k}=\displaystyle \sum _{i=0}^{n}y_{k,i} \end{aligned}$$
(17)

and the substitution of Eqs. (15) and (17) in Eq. (13) gives

$$\begin{aligned} y_k= & {} \displaystyle \sum _{i=0}^{n} y_{k, i}= y_k(0) + \nonumber \\&+ L^{-1}\left[ R_k(t, y_1, y_2, \cdots , y_m ) + \sum _{i=0}^{n} A_{k, i} \right] , k=1, \ldots , m. \end{aligned}$$
(18)

The first term in this series is given by the initial condition

$$\begin{aligned} y_k(0)=y_{k, 0}, \ k=1, 2, \ldots , m. \end{aligned}$$

The other terms are given by the following recurrence formula:

$$\begin{aligned} y_{k, i+1} =L^{-1} (A_{k,i} + R_k), \ k=1, 2, \cdots , m, \ \ i=0, \ldots , n. \end{aligned}$$
(19)

Then, the solution of the system (10) by ADM is given by

$$\begin{aligned} y_k=y_{k,0}+y_{k,1}+\cdots +y_{k,n}, \ \ k=1, \ldots , m. \end{aligned}$$
(20)

Modified Adomian Method

In some situations, the polynomial functions may diverge as the independent variable (in this case, time t) increases. To solve this problem, we use a modification of the Adomian decomposition, proposed by Younker [28], where the time variable is discretized, so that the initial value of each interval is given by the final solution of the previous interval. For this, the mesh is defined as

$$\begin{aligned} t_j=t_0+jh, \ j=0, \ldots , n_f, \end{aligned}$$
(21)

where h is the size of each interval, given by \(h=\displaystyle \frac{t_{n_{f}}-t_0}{n_f}\).

Thus, the solution given by equation (18) is valid, within a time interval, as follows:

$$\begin{aligned} y_{k,i+1}^{j+1}=y_k(t_{j})+L^{-1}\left[ R_k + \sum _{i=0}^{n} A_{k, i} \right] , \ k=1, \ldots , m. \end{aligned}$$
(22)

For example, consider the following problem

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dy(t)}{dt}= -y(t)^3 \\ y(0)=1 \end{array}\right. . \end{aligned}$$
(23)

This equation is formed only by a nonlinear part \(N(y)=-y(t)^3\). Then, the Adomian polynomials that compose this part are given by equation

$$\begin{aligned} A_n = \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -\left( \sum _{i=0}^{n} \lambda ^{i}y_i \right) ^3 \right) \right] _{\lambda =0}, \ A_0=-y_0^3; \end{aligned}$$
(24)

So, the first term to approximate the solution of the problem is given by the initial condition \(y_0=y(0)\). The second term of the approximation, \(y_1\), is calculated by:

$$\begin{aligned} y_1=L^{-1}(A_0)= \displaystyle \int _0^t A_0 dt, \end{aligned}$$
(25)

or,

$$\begin{aligned} y_1=\displaystyle \int _0^t A_0 dt = -y_0^3 t, \end{aligned}$$
(26)

and with this new approximation, the next Adomian polynomial is calculated as follows

$$\begin{aligned} A_1= & {} \frac{1}{1!} \left[ \frac{d^1}{d\lambda ^{1}}\left( -\left( \sum _{i=0}^{1} \lambda ^{i}y_i \right) ^3 \right) \right] _{\lambda =0}\nonumber \\= & {} \frac{d^1}{d\lambda ^{1}}\left( -(\lambda ^0y_0+\lambda ^1y_1)^3 \right) =3y_0^5t. \end{aligned}$$
(27)

Thus, the approximation of \(y_2\) is given by

$$\begin{aligned} y_2=L^{-1}(A_1)= \displaystyle \int _0^t A_1 dt = \displaystyle \int _0^t 3y_0^5t dt= \frac{3}{2}y_0^5t^2. \end{aligned}$$
(28)

Using three terms, we obtain the following solution:

$$\begin{aligned} y=y_0+y_1+y_2 = y(0)- y(0)^3t+\frac{3}{2} y(0)^5t^2. \end{aligned}$$
(29)

After replacing the value of y(0) results:

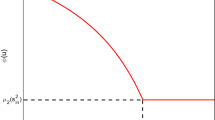
$$\begin{aligned} y=1-t+\frac{3}{2}t^2. \end{aligned}$$
(30)

Equation (30) was obtained by the classical method of decomposition of Adomian. Figure 1 shows the analytical solution of the PVI given in (23), for the approximations obtained through the classic ADM with two terms and three terms, and the approximation using the modified ADM with three terms. The integration interval was divided into 15 subintervals of \(h=0.1\).

Fig. 1
figure 1

Analytical solution of the initial value problem given in (23) and approximations obtained by the classic and modified Adomian methods

Full size image

The classic Adomian method has disadvantages, as shown in Fig. 1. Increasing the number of Adomian terms only causes a delay in the divergence of the solution. The modified technique, proposed by Younker [28], solved the problem with only three Adomian terms with \(h=0.1\).

Solution of the Problem by the Adomian Decomposition Method

The Adomian polynomials of the system (9) are calculated as follow:

  1. (1)

    \(\displaystyle A_{1,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -k_0\sum _{i=0}^{n} \lambda ^{i}y_{1,i} y_{8,i}\right) \right] _{\lambda =0}\)

  2. (2)

    \(\displaystyle A_{2,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( k_0\sum _{i=0}^{n} \lambda ^{i}y_{1,i} y_{8,i}\right) \right] _{\lambda =0}\)

  3. (3)

    \(\displaystyle A_{3,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -k_2\sum _{i=0}^{n} \lambda ^{i}y_{3,i} y_{8,i} \sqrt{y_{6,i}}\right) \right] _{\lambda =0}\)

  4. (4)

    \(\displaystyle A_{4,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( k_2\sum _{i=0}^{n} \lambda ^{i}y_{3,i} y_{8,i} \sqrt{y_{6,i}}-2k_4\sum _{i=0}^{n} \lambda ^{i}y_{4,i}^2\right) \right] _{\lambda =0}\)

  5. (5)

    \(\displaystyle A_{5,n}{=} \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( \frac{1}{2} k_2\sum _{i=0}^{n} \lambda ^{i}y_{3,i} y_{8,i} \sqrt{y_{6,i}}{+}\frac{1}{2} k_3\sum _{i=0}^{n} \lambda ^{i}y_{7,i}^2 \sqrt{y_{6,i}}{+} 2k_4\sum _{i=0}^{n} \lambda ^{i}y_{4,i}^2\right) \right] _{\lambda =0}\)

  6. (6)

    \(\displaystyle A_{6,n}{=} \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -\frac{1}{2} k_2\sum _{i=0}^{n} \lambda ^{i}y_{3,i} y_{8,i} \sqrt{y_{6,i}}{-}\frac{1}{2} k_3\sum _{i=0}^{n} \lambda ^{i}y_{7,i}^2 \sqrt{y_{6,i}}{+} 2k_4\sum _{i=0}^{n} \lambda ^{i}y_{4,i}^2\right) \right] _{\lambda =0}\)

  7. (7)

    \(\displaystyle A_{7,n}= \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -2 k_3\sum _{i=0}^{n} \lambda ^{i}y_{7,i}^2 \sqrt{y_{6,i}}\right) \right] _{\lambda =0}\)

  8. (8)

    \(\displaystyle A_{8,n}{=} \frac{1}{n!} \left[ \frac{d^n}{d\lambda ^{n}}\left( -k_0\sum _{i=0}^{n} \lambda ^{i}y_{1,i} y_{8,i}{-}k_2\sum _{i=0}^{n} \lambda ^{i}y_{3,i} y_{8,i} \sqrt{y_{6,i}}{+}k_3\sum _{i=0}^{n} \lambda ^{i}y_{7,i}^2 \sqrt{y_{6,i}}\right) \right] _{\lambda =0}\)

Then, the second and third terms of the series are obtained for each equation of the system

Second term

  • Equation 1.

    $$\begin{aligned} A_{1,0}= & {} -k_0y_{1,0}y_{8,0}\\ y_{1,1}= & {} \displaystyle \int _{0}^{t}A_{1,0}\text {d}t=A_{1,0}t \end{aligned}$$

  • Equation 2.

    $$\begin{aligned} A_{2,0}= & {} k_0y_{1,0}y_{8,0}\\ y_{2,1}= & {} \displaystyle \int _{0}^{t}A_{2,0}\text {d}t-\int _{0}^{t}k_1y_{2,0}\text {d}t=(A_{2,0}-k_1y_{2,0})t \end{aligned}$$

  • Equation 3.

    $$\begin{aligned} A_{3,0}= & {} -k_2y_{3,0}y_{8,0}\sqrt{y_{6,0}}\\ y_{3,1}= & {} \displaystyle \int _{0}^{t}A_{3,0}\text {d}t+\int _{0}^{t}k_1y_{2,0}\text {d}t=(A_{3,0}+k_1y_{2,0})t \end{aligned}$$

  • Equation 4.

    $$\begin{aligned} A_{4,0}= & {} 2k_2y_{3,0}y_{8,0}\sqrt{y_{6,0}}-2k_4y_{4,0}^2\\ y_{4,1}= & {} \displaystyle \int _{0}^{t}A_{4,0}\text {d}t=A_{4,0}t \end{aligned}$$

  • Equation 5.

    $$\begin{aligned} A_{5,0}= & {} \displaystyle \frac{1}{2}k_2y_{3,0}y_{8,0}\sqrt{y_{6,0}}+\frac{1}{2}k_3 \sqrt{y_{6,0}} y_{7,0}^2+2k_4y_{4,0}^2\\ y_{5,1}= & {} \displaystyle \int _{0}^{t}A_{5,0}\text {d}t=A_{5,0}t \end{aligned}$$

  • Equation 6.

    $$\begin{aligned} A_{6,0}= & {} \displaystyle -\frac{1}{2}k_2y_{3,0}y_{8,0}\sqrt{y_{6,0}}-\frac{1}{2}k_3 \sqrt{y_{6,0}} y_{7,0}^2+2k_4y_{4,0}^2\\ y_{6,1}= & {} \displaystyle \int _{0}^{t}A_{6,0}\text {d}t+ \int _{0}^{t}2k_1y_{2,0}\text {d}t=(A_{6,0}+2k_1y_{2,0})t \end{aligned}$$

  • Equation 7.

    $$\begin{aligned} A_{7,0}= & {} \displaystyle -2k_3 \sqrt{y_{6,0}} y_{7,0}^2\\ y_{7,1}= & {} \displaystyle \int _{0}^{t}A_{7,0}\text {d}t+ \int _{0}^{t}2k_1y_{2,0}\text {d}t=(A_{7,0}+2k_1y_{2,0})t \end{aligned}$$

  • Equation 8.

    $$\begin{aligned} A_{8,0}= & {} -k_0y_{1,0}y_{8,0}-k_2y_{3,0}y_{8,0}\sqrt{y_{6,0}}+k_3 \sqrt{y_{6,0}} y_{7,0}^2\\ y_{8,1}= & {} \displaystyle \int _{0}^{t}A_{8,0}\text {d}t=A_{8,0}t \end{aligned}$$

Third term

Equation 1.

$$\begin{aligned} A_{1,1}= & {} -k_0y_{1,1}y_{8,1}=-k_0(A_{1,0}t)(A_{8,0}t)\\ y_{1,2}= & {} \displaystyle \int _{0}^{t}-k_0A_{1,0}A_{8,0}t^2\text {d}t=-k_0A_{1,0}A_{8,0}\displaystyle \frac{t^3}{3} \end{aligned}$$

Equation 2.

$$\begin{aligned} A_{2,1}= & {} k_0y_{1,1}y_{8,1}=k_0(A_{1,0}t)(A_{8,0}t)\\ y_{2,2}= & {} \displaystyle k_0A_{1,0}A_{8,0}\frac{t^3}{3}-k_1(A_{2,0}-k_1y_{2,0})\frac{t^2}{2} \end{aligned}$$

Equation 3.

$$\begin{aligned} A_{3,1}= & {} -k_2y_{3,1}y_{8,1}\sqrt{y_{6,1}}=-k_2(A_{3,0}+k_1y_{2,0})A_{8,0}t^2 \sqrt{(A_{6,0}+2k_1y_{2,0})t}\\ y_{3,2}= & {} \displaystyle k_1(A_{2,0}-k_1y_{2,0})\frac{t^2}{2}-\frac{2}{7}k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}t^3 \end{aligned}$$

Equation 4.

$$\begin{aligned} A_{4,1}= & {} 2k_2(A_{3,0}+k_1y_{2,0})A_{8,0}t^2\sqrt{(A_{6,0}+2k_1y_{2,0})t}-2k_4A_{4,0}^2t^2\\ y_{4,2}= & {} \displaystyle \left[ \frac{4}{7}k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}-\frac{2}{3} k_4 A_{4,0}^2\right] t^3 \end{aligned}$$

Equation 5.

$$\begin{aligned} A_{5,1}= & {} \displaystyle \frac{1}{2}k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}t^2\\&+ \frac{1}{2}k_3 (A_{7,0}+2k_1y_{2,0})^2\sqrt{(A_{6,0}+2k_1y_{2,0})t} t^2+2k_4A_{4,0}^2 t^2\\ y_{5,2}= & {} \displaystyle \left[ \frac{1}{7}k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}\right. \\&+ \left. \frac{1}{7}k_3 (A_{7,0}+2k_1y_{2,0})^2\sqrt{(A_{6,0}+2k_1y_{2,0})t} +\frac{2}{3} k_4A_{4,0}^2 \right] t^3 \end{aligned}$$

Equation 6.

$$\begin{aligned} A_{6,1}= & {} \displaystyle -\frac{1}{2} k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}t^2\\- & {} \frac{1}{2} k_3 (A_{7,0}+2k_1y_{2,0})^2\sqrt{(A_{6,0}+2k_1y_{2,0})t} t^2 +2k_4A_{4,0}^2 t^2\\ y_{6,2}= & {} \displaystyle k_1(A_{2,0}-k_1y_{2,0})t^2 -\frac{1}{7}\sqrt{(A_{6,0}+2k_1y_{2,0})t}\left[ k_2(A_{3,0}+k_1y_{2,0})A_{8,0})\right. \\&+\left. k_3(A_{7,0}+2k_1y_{2,0})^2\right] t^3+\frac{2}{3}k_4A_{4,0}^2t^3 \end{aligned}$$

Equation 7.

$$\begin{aligned} A_{7,1}= & {} \displaystyle -2k_3 \sqrt{y_{6,1}} y_{7,1}^2=-2k_3 \sqrt{(A_{6,0}+2k_1y_{2,0})t}(A_{7,0}+2k_1y_{2,0})^2t^2\\ y_{7,2}= & {} \displaystyle k_1(A_{2,0}-k_1y_{2,0})t^2-\frac{4}{7} k_3 \sqrt{(A_{6,0}+2k_1y_{2,0})t}(A_{7,0}+2k_1y_{2,0})^2t^3 \end{aligned}$$

Equation 8.

$$\begin{aligned} A_{8,1}= & {} \displaystyle -k_0(A_{1,0}t)(A_{8,0}t)-k_2(A_{3,0}+k_1y_{2,0})A_{8,0}\sqrt{(A_{6,0}+2k_1y_{2,0})t}t^2\\&+k_3(A_{7,0}+2k_1y_{2,0})^2\sqrt{(A_{6,0}+2k_1y_{2,0})t}t^2\\ y_{8,2}= & {} \displaystyle -\frac{1}{3} k_0A_{1,0}A_{8,0}t^3-\frac{2}{7}\sqrt{(A_{6,0}+2k_1y_{2,0})t}\left[ k_2(A_{3,0}+k_1y_{2,0})\right. \\&- \left. k_3(A_{7,0}+2k_1y_{2,0})^2 \right] t^3 \end{aligned}$$

Then, the solution of the system (9) by the method of Adomian using two and three terms, respectively, is given by

Simulation and Discussion

To simulate the anaerobic digestion process, the set of chemical reactions are presented in Table 2, where the cellulose is the substrate.

Calculate the constants \(k_1, \ldots , k_4\), with Eq. (7), where \(k_0=1\) [38], T\(_i\)= 298.15K and \(\varDelta \)G values given in Equations (2), (3) and in Table 1. The results are shown in Table 4.

Table 4 Data for simulations of the process of biogas production
Full size table
Fig. 2
figure 2

Concentration of biogas and cellulose obtained by the modified Adomian Decomposition method

Full size image

According to Adomian decomposition convergence theory, it is suggested to use more than one term in the series to obtain the solution. Then, the system (9) is solved by the modified Adomian method, considering \(h=0.1\) and three Adomian terms.

Figure 2 shows the solution obtained for the biogas production and the consumption of the substrate. Biogas production increases rapidly in the first days of the process. Thereafter, the solution tends to the value six, and the methanogenic phase continues for the entire period. Figure 2 also shows the consumption of cellulose (substrate). The concentration of cellulose decreases over time, tending to zero, indicating the consumption of all substrate. In addition, anaerobic decomposition of glucose, as a 100% cellulose substrate product, is possibly given globally as \(C_6H_{12}O_6 \rightarrow 3CH_4 + 3CO_2\) (see Eq. (4)), i.e. with 1 kmol of glucose, 6 kmols of biogas can be produced, which is consistent with the result obtained.

Conclusions and Future Work

In this work, a model for the biogas production process was presented, considering cellulose as a substrate. With the Gibbs free energy value, the rate of production of each reaction was estimated. The problem was solved by the Modified Adomian Decomposition Method, providing values that agree with the global solution. The results show that, with the modified ADM, the coupled set of nonlinear ordinary differential equations, obtained from the anaerobic digestion problem, can be solved efficiently. This is the main contribution of this research. In addition, the use of just three Adomian terms makes the problem attractive for future research. Thus, based on the references of Jajarmi et al. [39, 40], who use the modal series method to solve nonlinear optimal control problems (OCPs), future work will be focused on the ADM applied to the OCPs.