Introduction

Normal or ordinary diffusion is an essentially well understood transport process. It is characterized by the linear evolution with time of the mean squared displacement of the transported agent. A more intriguing, complex phenomenon is that of anomalous diffusion. Such a process is classified as either sub-diffusive or super-diffusive, depending on whether the mean squared displacement evolution with time is slower or faster than ordinary diffusion, respectively [1,2,3]. Rather than being exceptional, observations of anomalous diffusion are frequently reported [4]. Examples include charge carriers transport in amorphous semiconductors [5]; bacterial motion [6]; transport in micelle systems [7], in fractal geometries [8, 9], in porous media [10, 11], and in random fractured networks [12]; bead dynamics in polymeric networks [13, 14], and single-file particle diffusion [15,16,17,18,19], among others.

In a recent work, Zhang and Padrino [20] (hereinafter ZP) applied the ensemble averaging method to model mass diffusion in random networks consisting of tortuous channels and junction pockets. In this configuration, pockets have volume but their typical size is considered to be small in comparison with the length of the channels. Quantities of interest, such as mass density, are thus assumed spatially uniform inside pockets. Starting with the statement of mass conservation, they derived an averaged transport equation for the pocket mass density. To attain closure, mass transport inside a channel was considered a one-dimensional diffusion process. The resulting macroscopic expression is an integro-differential equation accounting for statistical properties of the network, such as pocket distribution, connectivity, channel length, and cross-sectional area. Compared to the classical diffusion equation, the closed averaged equation contains two additional terms that include time integrals representing history effects of mass diffusion inside the channels. They noted that the so-called dual-porosity model [21] is equivalent to the leading order approximation of the integration kernel in their new model when the diffusion time scale inside the channels is small compared to the macroscopic time scale.

ZP then applied the averaged transport equation to the case of one-dimensional diffusion in an ensemble of random networks in the semi-infinite space. They solved the governing equation numerically finding that the pocket mass density at early times is a function of the similarity variable \(x t^{-1/4}\) instead of \(x t^{-1/2}\) corresponding to ordinary diffusion, regime to which the mass diffusion evolves after the initial sub-diffusive behavior. They explained that the initial sub-diffusion, which for certain cases can be even slower before its transition to classical diffusion, persists until the concentration profile inside a channel becomes linear. By using random walk theory, they recovered this trend. They also confirmed the sub-diffusive behavior of their numerical results by carrying out an asymptotic analysis for small time. Nevertheless, they did not pursue further the analytical work and did not present an exact solution of the chosen initial-boundary value problem in the limit of small time.

The aim of this article is to report on the exact solution in the limit of small time and to compare its predictions with the numerical results given in ZP. To write the exact solution, we present the model equation within the framework of fractional calculus. Recently, the author [22] used this tool to present a solution to the same problem for small-time by writing the governing equation as a fractional integral equation with known analytical solution from the literature given in terms of the Fox H-function. For ease of computation, it was re-written in terms of the Meijer G-function, available in computer calculus programs. Excellent agreement with the numerical results in ZP was attained. In contrast, in the present work, by casting the small-time governing equation as a fractional differential equation instead of a fractional integral equation, an alternative, more convenient form of the solution is written—also extracted from the literature —this time in terms of the Wright function. This function is defined as a relatively simple series, easy to program (see below). For the interval considered here for its argument, the series exhibits fast convergence.

Although the fractional calculus has been known for more than two centuries [23, 24], its application to modeling anomalous diffusion seems to be rather recent [25,26,27,28,29]. The differential equations of fractional order have proven to be well suited to the theoretical analysis of anomalous diffusion [29], in which case they give rise to the so-called fractional diffusion equation [28, 30]. This equation has been obtained from a rigorous application of the theory of continuous time random walks [29, 31,32,33]. For discussions on the fundamental and applications of fractional calculus, the reader is referred to some of the comprehensive monographs written on the subject (e.g., [24, 34,35,36,37,38,39,40,41]).

One-Dimensional Diffusion in a Random Network

After introducing in the ensemble-averaged mass balance the one-dimensional ordinary diffusion model for the mass flux in individual channels, ZP obtained a linear, integro-differential equation for the pocket mass density evolution in random networks at the macroscale, valid in the three-dimensional space. An important feature of the approach proposed by ZP in the application of the ensemble-averaging formalism is that processes other than diffusion can be adopted to model mass transport in a channel and attain closure. Depending on the chosen model, a non-linear averaged equation may result. Another essential element of the ensemble average method applied in ZP is the introduction of the probability density function \(P({{{\varvec{x}}}}, {{{\varvec{y}}}},\ell )\) of having a pocket at \({{{\varvec{x}}}}\) connected to another pocket at \({{{\varvec{y}}}}\) by a channel of length \(\ell \). In the model derivation, the networks are assumed to be statistically isotropic so that they write \(P({{{\varvec{x}}}}, {{{\varvec{y}}}},\ell ) = \hat{P}({{{\varvec{x}}}}, r,\ell )/(4 \pi r^2)\), with distance \(r = | {{{\varvec{y}}}} - {{{\varvec{x}}}}|\). For a particular application of the model, the functional form of \(\hat{P}\) must be specified.

Considering as a test problem the one-dimensional diffusion in a random network occupying the half-line, they wrote the governing averaged equation for the evolution of the pocket mass density \(\rho _p (x, t)\) in dimensionless form as

$$\begin{aligned} \frac{\partial \rho _p}{\partial t} + 4 \frac{\theta _c}{\theta _p} \int ^t_{0} \left[ K(t-\tau ) - K(4t-4\tau )\right] \frac{ \partial \rho _p}{\partial \tau } d \tau = \frac{\partial ^2 \rho _p}{\partial x^2} + \frac{\partial ^2 }{\partial x^2} \int _{0}^t K(4t- 4\tau ) \frac{\partial \rho _p }{\partial \tau } d \tau , \end{aligned}$$
(1)

for \(x > 0\) and \(t > 0\), and subjected to the initial and boundary conditions

$$\begin{aligned} \rho _p (x,0^+)&= 0, \quad x > 0, \end{aligned}$$
(2)
$$\begin{aligned} \rho _p (0^+ , t)&= 1, \quad \rho _p (+\,\infty , t) = 0, \quad t > 0. \end{aligned}$$
(3)

The problem was non-dimensionalized using \(\ell _0 \sqrt{\kappa _0 \theta _c/\theta _p}\), \(\ell _0^2/\widetilde{D}\), and \(\rho _{0}\) as the length, time, and mass density scales, respectively. Here, \(\ell _0\) denotes the typical channel length; \(\rho _0\), the pocket mass density on \(x=0^+\); \(\widetilde{D}\), the cross-sectional-area-weighted average diffusion coefficient inside the channel; \(\theta _c\) and \(\theta _p\), the channel and pocket volume fractions, respectively, and \(\kappa _0 = \pi /(8 \mathcal {T}_0^2)\), where \(\mathcal {T}_0\) is a reference tortuosity. Parameter \(\kappa _0\) results from the additional assumptions, introduced for this particular test problem, namely, that the density function \(\hat{P}\) is also homogeneous and modeled with the Maxwell-Boltzmann distribution with its mean given by \(\ell _0 /\mathcal {T}_0\), and that all connecting channels have the fixed length \(\ell _0\). The kernel K in the memory integrals of (1) is given by the series

$$\begin{aligned} K(u)=2\sum _{j=1}^\infty e^{-j^2\pi ^2 u} =\frac{1}{\sqrt{\pi u}} \left( 1+ 2\sum _{j =1}^\infty e^ {- {j^2 }/{u}} \right) -1, \end{aligned}$$
(4)

which arises from the Fourier Series solution of ordinary diffusion in a single channel. ZP proposed a numerical approach consisting in casting the general linear integro-differential mass balance equation from which (1) is obtained into a system of linear partial differential equations. To this system, they applied the finite volume method and explicit time integration. After employing this numerical approach to solve (1), they found that, for small time and for different values of the channel-to-pocket volume fraction ratio \(\theta _c/\theta _p\), the pocket mass density behaves as a function of the one variable \(x t^{-1/4}\), thereby showing self-similarity. They show that a point of constant pocket density changes its position according to \(x \propto t^{1/4}\), corresponding to an anomalous, sub-diffusive process [4]. After the early-time sub-diffusion, the transport process transitions to the ordinary diffusion similarity law. Their analytical investigation of the leading order balance in the diffusion equation in the limit of small time (see Appendix A.6 in their paper) confirmed this result. This leading order balance is given by the first and last terms in (1), i.e.

$$\begin{aligned} \frac{\partial \rho _p}{\partial t} = \frac{ 1}{2 \sqrt{\pi } } \int _{0}^t (t- \tau )^{-\frac{1}{2}} \frac{\partial }{\partial \tau } \left( \frac{\partial ^2 \rho _p}{\partial x^2} \right) d \tau , \end{aligned}$$
(5)

subjected to the initial and boundary conditions (2) and (3). In writing (5), the fact that, according to (4), K(u) becomes \((\pi u)^{-1/2}\) for small u was used. In the next section, we write the exact solution to this problem in two different but equivalent forms with the aid of elementary concepts from fractional calculus.

Analysis by Fractional Calculus

We begin the analysis by introducing some useful definitions and identities from fractional calculus. These are taken from the works of Gorenflo and Mainardi [23] and Mainardi, Pagnini, and Gorenflo [42] unless otherwise noted. The Riemann–Liouville fractional integral of order \(\beta > 0\) is defined as

$$\begin{aligned} {}_tJ^\alpha = \frac{1}{\Gamma (\alpha )} \int _0^t (t - \tau )^{\alpha -1} f(\tau ) d \tau , \quad \alpha > 0, \end{aligned}$$
(6)

where \(\Gamma ()\) denotes the Gamma function. Conventionally, \({}_tJ^0 = I\). This operator satisfies

$$\begin{aligned} {}_tJ^\alpha {}_tJ^\beta = {}_tJ^\beta {}_tJ^\alpha = {}_tJ^{\alpha +\beta }, \quad \alpha \geqslant 0, \,\, \beta \geqslant 0. \end{aligned}$$
(7)

In terms of this integral operator, we now introduce the fractional derivative of order \(\alpha \) in the Caputo sense, denoted as \({}_tD^\alpha _*\), and defined by

$$\begin{aligned} {}_tD^\alpha _*f(t) = {}_tJ^{m-\alpha } {}_tD^m f(t), \end{aligned}$$
(8)

respectively, with \(m-1 < \alpha \leqslant m\), where m is a positive integer. Here, the operator \({}_tD^m \equiv d^m / dt^m \). In the particular case of \(m = 1\), this definition may be written in explicit form as

$$\begin{aligned} {}_tD^\alpha _*f(t)= {\left\{ \begin{array}{ll} \displaystyle \frac{1}{\Gamma (1-\alpha )} \int _0^t (t-\tau )^{-\alpha } \frac{d f}{d \tau }(\tau ) d\tau , &{}\quad 0< \alpha < 1, \\ \displaystyle \frac{d f}{d \tau } , &{}\quad \alpha = 1, \end{array}\right. } \end{aligned}$$
(9)

Letting \( \mathscr {D}_\alpha = \Gamma (\alpha )/(2 \sqrt{\pi })\), we can now write (5) as

$$\begin{aligned} \frac{\partial \rho _p}{\partial t} = \mathscr {D}_\alpha \, {}_t D^{1-\alpha }_*\frac{\partial ^2 \rho _p }{\partial x^2} , \end{aligned}$$
(10)

with \(\alpha = 1/2\). For the sake of the discussion, in what follows we will consider the general case \(0< \alpha <1\), except where noted otherwise.

To find a solution of (10), let us apply the integral operator \({}_tJ^{1-\alpha }\) to both sides of this equation and use \({}_tD^\alpha _*= {}_tJ^{1-\alpha } {}_tD^1\). This yields

$$\begin{aligned} {}_tJ^{1-\alpha } \frac{\partial \rho _p}{\partial t}= & {} \mathscr {D}_\alpha \, {}_tJ^{1-\alpha } {}_tJ^\alpha {}_tD^1 \frac{\partial ^2 \rho _p }{\partial x^2} , \nonumber \\ {}_tD^{\alpha }_*\rho _p= & {} \mathscr {D}_\alpha \, {}_tJ^{1} {}_tD^1 \frac{\partial ^2 \rho _p }{\partial x^2} , \nonumber \\ {}_tD^{\alpha }_*\rho _p= & {} \mathscr {D}_\alpha \frac{\partial ^2 \rho _p }{\partial x^2} - \mathscr {D}_\alpha \frac{\partial ^2 \rho _{p o} }{\partial x^2}, \end{aligned}$$
(11)

where we have used the fact that \( {}_tJ^{1} {}_tD^1 f(t) = f(t) - f(0^+)\) and \(\rho _{p o} (x) = \rho _p (x, 0^+)\) is the initial condition. In the particular case treated here, \(\rho _{po} (x) = 0\), and (11) reduces to the fractional diffusion equation

$$\begin{aligned} {}_tD^{\alpha }_*\rho _p = \mathscr {D}_\alpha \frac{\partial ^2 \rho _p }{\partial x^2} . \end{aligned}$$
(12)

Green’s functions for this equation for the entire and half lines have been obtained by Mainardi [43] (see also [44]). By applying the Laplace transform, Gorenflo, Luchko, and Mainardi [45] obtained the solution of (12) with constant initial and boundary conditions, a particular case of the so-called “signalling” problem, in terms of the Wright function (see their Theorem 6). By specializing their result to conditions (2) and (3), with \(\alpha = 1/2\), we have the solution

$$\begin{aligned} \rho _p (x,t) = W_{-{\tiny 1/4},1} \left( - \eta \right) , \quad \eta = x \, t^{-1/4}/\sqrt{\mathscr {D}_\alpha } = \sqrt{2} \, x \, t^{-1/4}. \end{aligned}$$
(13)

The Wright function is defined by [46]

$$\begin{aligned} W_{\nu , \mu } (z) = \sum _{k=0}^\infty \frac{z^k}{k! \Gamma (\nu k + \mu )}, \end{aligned}$$
(14)

where \(\nu > -1\) and \(\mu \) are real numbers; z is a complex number. Expression (13) not only confirms that the pocket mass density is self-similar with similarity variable \(x t^{-1/4}\), as shown originally by ZP, but also gives a functional form of the dependency.

Expressions (5), (10), or (12) represent the small-time asymptotics arising from the general mass transport equation (1), valid at any time, which, in turn, resulted from ensemble-averaging the statement of mass conservation written for a collection of channels connected by junction pockets. On the other hand, fractional time derivatives acting on the pressure gradient have been introduced, on a somewhat heuristic basis, to describe transport in porous media with significant disorder or heterogeneities or with time-dependent permeability [47,48,49,50,51]. Other alike forms of memory effects in the flux, based on the theory of continuum time random walks, have been used to model flow to fracture wells or in reservoirs showing both obstacles and preferential passages [52, 53].

It is convenient to write the solution (13) in terms of generalized hypergeometric functions which can be directly computed using well-known computer algebra and calculus software. The analysis by Luchko [54] for the Wright function with \(\nu = -1/2\) is extended here to the somewhat more involved case with \(\nu = -1/4\). The generalized hypergeometric function is defined as

$$\begin{aligned} _pF_q \left( a_1, \ldots , a_p; b_1, \ldots , b_q; z \right) = \sum _{n=0}^\infty \frac{(a_1)_n \cdots (a_p)_n}{(b_1)_n \cdots (b_q)_n} \frac{z^n}{n!}, \end{aligned}$$
(15)

when this series converges. Here \((a)_n\) denotes the Pochhammer’s symbol defined as

$$\begin{aligned} (a)_n = a (a+1) (a+2) \cdots (a+n-1) = \Gamma \left( a + n \right) / \Gamma \left( a \right) \quad \text {with} \quad a \ne 0, -1, -2, \ldots . \end{aligned}$$
(16)

To write (13) in terms of generalized hypergeometric functions, the recurrence, reflection, and duplication relations for the Gamma function, namely,

$$\begin{aligned} \Gamma (z+1)= & {} z \Gamma (z), \end{aligned}$$
(17)
$$\begin{aligned} \Gamma (z) \Gamma (z-1)= & {} \pi / \sin (\pi z ), \end{aligned}$$
(18)

and

$$\begin{aligned} \Gamma (2 z) = \pi ^{-1/2} 2^{2z-1} \Gamma (z) \Gamma \left( z+\frac{1}{2}\right) \quad \text {for} \quad 2z \ne 0, -1, -2, \ldots , \end{aligned}$$
(19)

respectively, will prove to be useful. Here, z is a complex number. In addition, relation \(\Gamma (n+1) = n!\), for integer \(n \geqslant 0\), will also be needed.

We begin by splitting the defining series of (13) into a series summing only over even indexes plus a series summing only over odd indexes, i.e.

$$\begin{aligned} W_{-1/4,1} ( x ) = \sum _{k=0}^\infty \frac{x^k}{k! \Gamma \left( 1 -\frac{1}{4} k \right) } = \sum _{\ell =0}^\infty \frac{x^{2 \ell }}{(2 \ell )! \,\, \Gamma \left( 1 -\frac{1}{2} \ell \right) } + \sum _{\ell =0}^\infty \frac{x^{2 \ell +1}}{(2 \ell +1)! \,\, \Gamma \left( 1 -\frac{1}{2} \ell - \frac{1}{4} \right) }, \end{aligned}$$
(20)

and repeating the procedure for each of these series yields

$$\begin{aligned} W_{-1/4,1} ( x )= & {} \sum _{n=0}^\infty \frac{x^{4 n}}{(4 n)! \,\, \Gamma \left( 1 -n \right) } + \sum _{n=0}^\infty \frac{x^{4n +2}}{(4 n + 2)! \,\, \Gamma \left( 1 -n - \frac{1}{2} \right) } \nonumber \\&+ \sum _{n=0}^\infty \frac{x^{4 n+1}}{(4 n+1)! \,\, \Gamma \left( 1 -n -\frac{1}{4}\right) } + \sum _{n=0}^\infty \frac{x^{4n +3}}{(4 n + 3)! \,\, \Gamma \left( 1 -n - \frac{3}{4} \right) }.\qquad \end{aligned}$$
(21)

For the first series in the right-hand side of (21) we have

$$\begin{aligned} \sum _{n=0}^\infty \frac{x^{4 n}}{(4 n)! \,\, \Gamma \left( 1 -n \right) } = 1, \end{aligned}$$
(22)

because, by the reflection property (18), \(1/\Gamma (1-n) = 0\) for \(n \geqslant 1\). Calculations for each of the last three series in the right-hand side of (21) are very similar. It thus suffices to present in some detail the calculations for one of them. For instance, for the third series we can write

$$\begin{aligned} \sum _{n=0}^\infty \frac{x^{4 n+1}}{(4 n+1)! \,\, \Gamma \left( 1 -n -\frac{1}{4}\right) }= & {} \frac{x}{\pi } \sum _{n=0}^\infty \frac{ \Gamma \left( n +\frac{1}{4}\right) \sin \pi \left( n+\frac{1}{4} \right) }{(4 n+1)! } x^{4 n} \nonumber \\= & {} \frac{x\sqrt{\pi }}{2 \sqrt{2}} \sum _{n=0}^\infty \frac{ \Gamma \left( n +\frac{1}{4}\right) \sin \pi \left( n+\frac{1}{4} \right) }{\Gamma \left( n+\frac{1}{2} \right) \Gamma \left( n+\frac{3}{4} \right) \Gamma \left( n+\frac{5}{4} \right) n! } \left( \frac{x}{4}\right) ^{4 n} \nonumber \\= & {} \frac{x\sqrt{\pi }}{4} \frac{ \Gamma \left( \frac{1}{4}\right) }{\Gamma \left( \frac{1}{2} \right) \Gamma \left( \frac{3}{4} \right) \Gamma \left( \frac{5}{4} \right) } \sum _{n=0}^\infty \frac{ \left( \frac{1}{4}\right) _n }{\left( \frac{1}{2} \right) _n \left( \frac{3}{4} \right) _n \left( \frac{5}{4} \right) _n n! } \left( - \frac{x^4}{256}\right) ^{ n} \nonumber \\= & {} \frac{x \Gamma \left( \frac{1}{4} \right) }{\sqrt{2} \pi } {_1}F_3 \left( \frac{1}{4} ; \frac{1}{2}, \frac{3}{4}, \frac{5}{4} ; - \frac{x^4}{256} \right) , \end{aligned}$$
(23)

where the first equality results from using the reflection relation (18) for \(\Gamma (1-n-1/4)\); the second equality is found by computing \((4 n+1)! = \Gamma (4 n+2)\), applying the duplication formula (19), and the identity \(\Gamma (n+1) = n!\); the third equality comes from expanding the sine function in the numerator of the second equality and using Prochhammer’s symbol (16), and, finally, the last equality is obtained from the definition of the generalized hypergeometric function (15) and by applying duplication relation (19) to compute \(\Gamma (5/4)\).

Computing the remaining two series in (21) results in

$$\begin{aligned} \rho _p (x,t) = W_{-{\tiny 1/4},1} \left( - \eta \right)= & {} 1 - \frac{\eta \Gamma \left( \frac{1}{4} \right) }{\sqrt{2} \pi } {_1}F_3 \left( \frac{1}{4} ; \frac{1}{2}, \frac{3}{4}, \frac{5}{4} ; - \frac{\eta ^4}{256} \right) \nonumber \\&+\, \frac{{~~~~}\eta ^2 {~~} }{2 \sqrt{\pi }} {_1}F_3 \left( \frac{1}{2} ; \frac{3}{4}, \frac{5}{4}, \frac{3}{2} ; - \frac{\eta ^4}{256} \right) \nonumber \\&-\, \frac{\eta ^3 \Gamma \left( \frac{3}{4} \right) }{6 \sqrt{2} \pi } {_1}F_3 \left( \frac{3}{4} ; \frac{5}{4}, \frac{3}{2}, \frac{7}{4} ; - \frac{\eta ^4}{256} \right) . \end{aligned}$$
(24)

Next, the two forms of the solution for pocket mass density \(\rho _p\) written in this section are evaluated for a meaningful interval of the similarity variable and their predictions plotted against the numerical results of ZP.

Comparison with Numerical Results

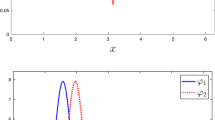
We now proceed to evaluate the exact solutions (13) and (24) to compare with the numerical solution obtained by ZP using the finite volume method. We computed these expressions for the interval \(0 \leqslant x \, t^{-1/4} \leqslant 4\), determined from the numerical data in ZP. Expression (24) is directly evaluated using the corresponding method available in well-known computer calculus software. The results are shown in Fig. 1. Note that \(\rho _p\) falls from one to practically zero within this interval.

Fig. 1
figure 1

Pocket mass density as a function of \(x t^{-1/4}\). The solid line represents the numerical results obtained in ZP using three values of the channel-to-pocket volume fraction ratio \(\theta _c/\theta _p\), whereas symbols and correspond to results from (13) and (24), respectively

Full size image

ZP considered model equation (1) subjected to conditions (2) and (3) and computed the pocket mass density \(\rho _p\) as a function of the position x for various times t and for three values of the channel-to-pocket volume fraction ratio, namely, \(\theta _c/\theta _p = 0.005\), 0.05, and 5. They plotted \(\rho _p\) versus variable \(x t^{-1/4}\) for each time and the last two values of \(\theta _c/\theta _p\) and found that, for times smaller than certain threshold, all the curves fall onto each other, indicating that \(\rho _p\) is self-similar with similarity variable \(x t^{-1/4}\) in agreement with their theoretical result in the limit of small time—for \(\theta _c/\theta _p = 0.005\), their figure 3 shows that the same early-time self-similarity holds. For our purpose, we picked three sets of data from their results, one for each \(\theta _c/\theta _p\), making sure that each set corresponds to a time where \(\rho _p\) is self-similar with respect to \(x t^{-1/4}\). In Fig. 1, we plotted the pocket density \(\rho _p\) versus \(x t^{-1/4}\) for the three data sets, showing that each set of numerical results falls onto the exact solution; hence, excellent agreement exists between the exact and numerical results. This serves as validation of the numerical approach presented by ZP.

It should be said that a path to convert the representations (13) and (24) to the forms of the solution given in [22] is not evident. We realized they are equivalent by plotting them against the numerical results.

The transition from the initial sub-diffusion similarity described by \(x t^{-1/4}\) to the ordinary diffusion similarity depending on \(x t^{-1/2}\) is affected by the channel-to-pocket volume fraction ratio. This is explained in detail in ZP. If the channel-to-pocket volume fraction ratio is greater than one, the channel storage capacity change is significant. The loss of the sub-diffusive similarity \(x t^{-1/4}\) is caused by the emergence of the second term on the left-hand side of (1) as a function of time. The transition between the early sub-diffusive similarity and the terminal ordinary diffusion then passes through an intermediate stage of even slower sub-diffusion because of the increase in channel capacity. On the other hand, if the channel-to-pocket volume fraction ratio is much smaller than one, the second term in the left-hand side of (1) is negligible, and the transition occurs very rapidly. In both cases, ordinary diffusion becomes dominant at about a single-channel diffusion time when the density profile inside the channels approaches linearity.

Summary and Conclusion

We studied early-time mass diffusion in random networks made of pockets and connecting channels. In the case of diffusion in the half-line, the leading order balance for mass diffusion in the limit of small time was given by ZP from their ensemble averaged diffusion equation, valid for any time. By using concepts from fractional calculus, we recast this small-time equation in the form of a fractional diffusion equation for which an exact solution has been obtained in the literature in terms of the Wright function. We re-wrote this solution as a sum of generalized hypergeometric functions. In both cases, the solution shows that the average pocket mass density is a function of the similarity variable \(x t^{-1/4}\), corresponding to sub-diffusive transport. Predictions from these two equivalent expressions match very well numerical results obtained by ZP using the finite volume method.