Interface Crack at Orthotropic Media

Abstract

This paper deals with the diffraction of SH-waves by a Griffith crack located at the interface of two bonded dissimilar orthotropic half spaces. The mixed boundary value problem has been reduced to the solution of Fredholm integral equation of second kind by applying Fourier and Abel transforms. Stress intensity factor at the tip of the crack has been calculated by solving integral equation using perturbation method for low frequency and plotted against dimensionless frequency.

Introduction

In the fabrication process the cracks or faults are essential. Analytic study of the arrest of crack propagation or faults are very important for civil, aerospace, nuclear and mechanical engineering. The growing use of composite materials in many engineering applications demands the fundamental understanding of the response of cracked orthotropic bodies under stress. Interfacial crack is one of the most common failure modes in fibre-reinforced composite laminates. The interfacial imperfection usually forms the nucleus of the fracture initiation and propagation in the medium. From the engineering point of view, composite materials are highly anisotropic materials formed by orthotropic layers. Thus the study of interfacial cracks between orthotropic media is of great importance in the analysis of fracture of composites. The diffraction of waves in presence of cracks has important application in seismology as the earth is considered as composite material. Srivastava et al. [1] studied the interaction of antiplane shear waves by a Griffith crack at the interface of two bonded dissimilar elastic half-spaces and Srivastava et al. [2] also studied the interaction of shear waves with a Griffith crack situated in an infinitely long elastic strip. The problem of the edge crack in orthotropic elastic half-plane was considered by De and Patra [3]. Interaction of elastic waves with a periodic array of coplanar Griffith cracks in an orthotropic elastic medium has been solved by Mandal and Ghosh [4]. The diffraction of elastic waves by three coplanar Griffith cracks in an orthotropic medium has been studied by Sarkar et al. [5]. Das et al. [6] solved the problem of determining the stress intensity factor for an interfacial crack between two orthotropic half planes bonded to a dissimilar orthotropic layer with a punch. Das et al. [7] studied diffraction of SH-Waves by a Griffith crack in an infinite transversely orthotropic medium. Das et al. [8] solved the problem of determining the stress intensity factor (SIF) due to symmetric edge cracks in an orthotropic strip under normal loading. The problem of two perfectly bonded dissimilar orthotropic strip with an interfacial crack is studied by Li [9]. Elastostatic problem of an infinite row of parallel cracks in an orthotropic medium is analyzed by Sinharoy [10]. Monfared and Ayatollahi [11] investigated the problem of determining the dynamic SIF of multiple cracks in an orthotropic strip with functionally graded materials coating. The problem of interaction of three interfacial Griffith cracks between two bonded dissimilar orthotropic half spaces has been studied by Mukherjee and Das [12]. Mukhopadhyay et al. [13] have studied to find the SIF of an edge crack in bonded orthotropic materials. Itou [14] solved the problem of finding the SIF for two parallel interface cracks between a nonhomogeneous bonding layer and two dissimilar orthotropic half-spaces under tension. The diffraction of an antiplane shear wave by two coplanar Griffith cracks in an infinite elastic medium has been considered by Itou [15]. The problem of P-wave interaction by an asymmetric crack in an orthotropic strip is studied by Basak and Mandal [16]. Li [17] analyzed the collinear crack problem for an orthotropic functionally graded coating-substrate structure. Garg [18] studied stress distribution near periodic cracks at the interface of two bonded dissimilar orthotropic half planes. Satapathy [19] deduced the stresses in an orthotropic strip containing a Griffith crack. Marin [20] investigated the problem of a temporally evolutionary equation in elasticity of micropolar bodies with voids. The problem of a evolutionary equation in thermoelasticity of dipolar bodies has been studied by Marin [21, 22]. But the problem of diffraction of SH-waves at composite interface has not been considered yet.

In this paper, we have considered the diffraction of elastic SH-waves by the interface crack at two orthotropic half spaces. The problem has been reduced to that of solving the Fredholm integral equation of the second kind by applying Fourier and Abel transform. The solution of this integral equation has been obtained for low frequency using perturbation technique. This solution is then used for calculating numerical values of dynamic SIF at the tip of the crack. The SIF has been plotted against frequency for different orthotropic materials.

Formulation of the Problem

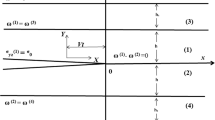
We consider a crack of finite width located at the interface of two bonded dissimilar orthotropic half spaces. The location of the crack is given by $|x_1|\le a$, $-\infty<z_1<\infty$, $y_1=0$ at the interface of two half spaces $y_1>0$ and $y_1<0$. By normalizing all the lengths by $'a'$ and putting $x_1/a=x$, $y_1/a=y$ and $z_1/a=z$, the location of the crack become $|x|<1$, $-\infty<z<\infty$, $y=0$ (Fig. 1).

Fig. 1

Geometry of the problem

The nonzero stress components are

$$\begin{aligned} \tau _{yz(j)}=\mu _{12(j)}\frac{\partial w_j}{\partial y} \end{aligned}$$

(1)

and displacement equation of motion for orthotropic materials are

$$\begin{aligned} c_{55(j)}\frac{\partial ^2 w_j}{\partial x^2}+c_{44(j)}\frac{\partial ^2 w_j}{\partial y^2}=\frac{a^2}{c_{s(j)}^2}\frac{\partial ^2 w_j}{\partial t^2},\quad j=1,2. \end{aligned}$$

(2)

where $c_{55(j)}$ and $c_{44(j)}$ are elastic constants and $c_{s(j)}^2=\frac{\mu _{12(j)}}{\rho _j}$ with $\rho _j$ being the density of the materials. Substitution of $w_j(x,y,t)=w_j(x,y)e^{-i\omega t}$ in Eq. (2) yields

$$\begin{aligned} c_{55(j)}\frac{\partial ^2 w_j}{\partial x^2}+c_{44(j)}\frac{\partial ^2 w_j}{\partial y^2}+\frac{a^2\omega ^2}{c_{s(j)}^2}w_j=0 \end{aligned}$$

(3)

which is to be solved subject to the boundary conditions

$$\begin{aligned} \tau _{yz(1)}(x,0^+)= & {} \tau _{yz(2)}(x,0^-)=-\tau _0,\quad |x|\le 1 \end{aligned}$$

(4)

$$\begin{aligned} \tau _{yz(1)}(x,0^+)= & {} \tau _{yz(2)}(x,0^-),\quad |x|>1\end{aligned}$$

(5)

$$\begin{aligned} w_{(1)}(x,0^+)= & {} w_{(2)}(x,0^-), \quad |x|>1 \end{aligned}$$

(6)

where $\tau _0$ is a constant. The term $e^{-i\omega t}$ which is common to all field variables is omitted in the sequel. The solution of the Eq. (3) are taken to be

$$\begin{aligned} w_1(x,y)= & {} \int _0^\infty A_1(\xi )e^{-\beta _1y}\cos (\xi x)d\xi ,\quad y>0 \end{aligned}$$

(7)

$$\begin{aligned} w_2(x,y)= & {} \int _0^\infty A_2(\xi )e^{\beta _2y}\cos (\xi x)d\xi ,\quad y<0 \end{aligned}$$

(8)

where $\beta _j=P_j^{\frac{1}{2}}(\xi ^2-k_{s(j)}^2)^{\frac{1}{2}}$, $P_j={(\frac{c_{55(j)}}{c_{44(j)}})}$ and $k_{s(j)}^2=\frac{a^2\omega ^2}{c_{s(j)}^2c_{55(j)}}.$ The non vanishing stress components are given by

$$\begin{aligned} \tau _{yz(j)}=-\mu _{12(j)}\int _0^\infty A_j(\xi )\beta _je^{-\beta _jy}\cos (\xi x)d\xi , \quad j=1,2. \end{aligned}$$

(9)

In Eqs. (7) and (8) $A_1(\xi )$ and $A_2(\xi )$ are unknown functions which will be determined with the help of boundary conditions.

Derivation of the Integral Equation

From the boundary condition (5), i.e., $\tau _{yz(1)}(x,0^+)=\tau _{yz(2)}(x,0^-)$ for all x yields

$$\begin{aligned} A_2(\xi )=-\frac{\mu _{12(1)}\beta _1}{\mu _{12(2)}\beta _2}A_1(\xi ) \end{aligned}$$

(10)

The boundary conditions (4) and (6) lead to the following dual integral equations

$$\begin{aligned}&\int _0^\infty \beta _1A_1(\xi )\cos (\xi x)d\xi =\frac{\tau _0}{\mu _{12(1)}},\quad |x|<1 \end{aligned}$$

(11)

$$\begin{aligned}&\int _0^\infty \left( \frac{\mu _{12(2)}\beta _2+\mu _{12(1)}\beta _1}{\beta _2}\right) A_1(\xi )\cos (\xi x)d\xi =0,\quad |x|<1 \end{aligned}$$

(12)

Substituting

$$\begin{aligned} \left( \frac{\mu _{12(2)}\beta _2+\mu _{12(1)}\beta _1}{\beta _2}\right) A_1(\xi )=B(\xi ) \end{aligned}$$

(13)

the above integral equations become

$$\begin{aligned}&\int _0^\infty B(\xi )\cos (\xi x)d\xi =0, \quad |x|>1 \end{aligned}$$

(14)

$$\begin{aligned}&\int _0^\infty \xi [1+H(\xi )]B(\xi )\cos (\xi x)d\xi =\frac{\tau _0(\mu _{12(1)}+\mu _{12(2)})}{\mu _{12(1)}},\quad |x|<1 \end{aligned}$$

(15)

where

$$\begin{aligned} H(\xi )=\frac{(\mu _{12(1)}+\mu _{12(2)})\beta _1\beta _2}{(\mu _{12(1)}\beta _1+\mu _{12(2)}\beta _2)\xi }-1 \end{aligned}$$

(16)

and $H(\xi )\rightarrow 0$ as $\xi \rightarrow \infty$. Let the trial solution of the above system of dual integral equation be

$$\begin{aligned} B(\xi )=\frac{\tau _0(\mu _{12(1)}+\mu _{12(2)})}{\mu _{12(1)}}\int _0^1tg(t)\tau _0(\xi t)dt \end{aligned}$$

(17)

In the Eq. (17), $B(\xi )$ is considered in this form so that the Eq. (14) is automatically satisfied and Eq. (15) yields $\frac{1}{\sqrt{x-1}}$ type of singularity at the tip of the crack which is physically consistent with the problem. From the Eq. (15) we get the following Fredholm integral equation of the second kind for determining the unknown function g(t) as

$$\begin{aligned} g(u)+\int _0^1tg(t)L(u,t)dt=1 \end{aligned}$$

(18)

where

$$\begin{aligned} L(u,t)=\int _0^\infty \xi H(\xi )J_0(\xi u)J_0(\xi t)d\xi \end{aligned}$$

(19)

In derivation of integral equation (18) the fixed point theorem method adopted by Zhang and Chen [23] can also be applied. The integrand in (19) has no poles, it has only branch points at $\xi =k_{s(1)}$, $\xi =k_{s(2)}$. The infinite integral (19) can be converted into integrals with finite limits by contour integration method (Mandal and Ghosh [4]) as follows: let

$$\begin{aligned} I=\int _{k_{s(1)}}^\infty \xi M(\xi ,\beta _2,\beta _1)J_0(\xi u)J_0(\xi t)d\xi \end{aligned}$$

(20)

where $M(\xi ,\beta _2,\beta _1)=H(\xi )$ and $2J_0(\xi t)=H_0^{(1)}(\xi t)+H_0^{(2)}(\xi t).$ We consider the integrals

$$\begin{aligned}&I_1=\oint _{c_1}\xi M(\xi ,\beta _2,\beta _1)J_0(\xi u)H_0^{(1)}(\xi t)d\xi ,\quad t>u \end{aligned}$$

(21)

$$\begin{aligned}&I_2=\oint _{c_2}\xi M(\xi ,\beta _2,\beta _1)J_0(\xi u)H_0^{(2)}(\xi t)d\xi \end{aligned}$$

(22)

The contour $C_1$ and $C_2$ are defined in Fig. 2.

Fig. 2

$\hbox {Complex}(\xi ,\eta )$ plane

After integrating along the contours we have the following integral:

$$\begin{aligned} L(u,t)= & {} -i(\mu _{12(1)}+\mu _{12(2)})k_{s(1)}^2\int _0^{\gamma }\frac{\sqrt{P_1} (\gamma ^2-\xi ^2)^{\frac{1}{2}}\sqrt{P_2}(1-\xi ^2)^{\frac{1}{2}}}{\sqrt{P_1}\mu _{12(1)}(1-\xi ^2)^{\frac{1}{2}}+ \sqrt{P_2}\mu _{12(2)}(\gamma ^2-\xi ^2)^{\frac{1}{2}}}\nonumber \\&\times J_0(\xi k_{s(1)}u)H_0^{(1)}(\xi k_{s(1)}t)d\xi \nonumber \\&-\mu _{12(2)}(\mu _{12(1)}+\mu _{12(2)})k_{s(1)}^2\int _{\gamma }^1\frac{ \sqrt{P_1} (\gamma ^2-\xi ^2)P_2(1-\xi ^2)^{\frac{1}{2}}}{P_1\mu _{12(1)}^2 (1-\xi ^2)+P_2\mu _{12(2)}^2(\gamma ^2-\xi ^2)}\nonumber \\&\times J_0(\xi k_{s(1)}u)H_0^{(1)}(\xi k_{s(1)}t)d\xi , t>u \end{aligned}$$

(23)

where $\gamma =\frac{k_{s(2)}}{k_{s(1)}}$. For $t<u$ we get the integral by interchanging t and u in (23).

Quantities of Physical Interest

The singular part of the stress component in the neighbourhood of the crack tip can be obtained for $|x|>1$ as

$$\begin{aligned} \tau _{yz(1)}(x,0^+)= & {} \tau _{yz(2)}(x,0^-)\nonumber \\= & {} -\tau _0(\mu _{12(1)}+\mu _{12(2)})\int _0^\infty \frac{\beta _1\beta _2\cos (\xi x)d\xi }{\mu _{12(1)}\beta _1+\mu _{12(2)}\beta _2}\int _0^1tg(t)J_0(\xi t)dt\qquad \end{aligned}$$

(24)

For large $\xi$, $\beta _1=\xi$, $\beta _2=\xi$ (for small $k_1,k_2$), $\tau _{yz}$ takes the form

$$\begin{aligned} \tau _{yz(1)}(x,0^+)=\tau _0x\frac{g(1)}{(x^2-1)^{\frac{1}{2}}}+O(1) \end{aligned}$$

(25)

Dynamic stress intensity $\hbox {factor}(SIF)$ denoted by K at the tip of the crack is defined by the relation

$$\begin{aligned} K=\lim _{x\rightarrow 1^{+}}\Bigg |\frac{\tau _{yz(1)}(x,0^+)(x-1)^{\frac{1}{2}}}{\tau _{0}}\Bigg | \end{aligned}$$

(26)

and is obtained as

$$\begin{aligned} K= & {} \lim _{x\rightarrow 1^{+}}(x-1)^{\frac{1}{2}}\Bigg |\frac{\tau _0xg(1)}{(x^2-1)^{\frac{1}{2}}}\Bigg |\nonumber \\= & {} \frac{\tau _0|g(1)|}{\sqrt{2}} \end{aligned}$$

(27)

Solution of the Integral Equation

Following Srivastava et al. [1], we obtained iterative solution of the integral equation using perturbation method. The iterative solution is valid for small values of $k_{s(1)}$ and $k_{s(2)}$. The numerical values of $SIF (K)$ has been obtained for different values of frequencies. For small values of the argument the Bessel functions $J_0(x)$ and $H_0^{(1)}(x)$ has been expanded in ascending powers of x as $J_0(x)=\sum _{n=0}^{\infty }a_{2n}x^{2n}$, $H_0^{(1)}(x)=[1+\frac{2i}{\pi }log(\frac{x}{2})]J_0(x)+i\sum _{n=0}^{\infty }b_{2n}x^{2n}$ where $a_0=1$ and the values of $a_{2n}$ and $b_{2n}$ are given by Abramowitz and Stegun [24, p. 36]. Using the above expression in (23), L(u, t) can be expressed as

$$\begin{aligned} L(u,t)= & {} \left( k_{s(1)}^2log(k_{s(1)})\right) L_1(u,t)+k_{s(1)}^2L_2(u,t)\\&+\,\left( k_{s(1)}^2log(k_{s(1)})\right) ^2L_3(u,t) +\left( k_{s(1)}^4log(k_{s(1)})\right) L_4(u,t)\\&+\,o\left( k_{s(1)}^4\right) \end{aligned}$$

where

$$\begin{aligned} L_1(u,t)= & {} \frac{2M_0}{\pi }\\ L_2(u,t)= & {} \frac{2N_0}{\pi }+\left( b_0-i+\frac{2}{\pi }log\left( \frac{t}{2}\right) \right) M_0 \\ L_3(u,t)= & {} 0\\ L_4(u,t)= & {} \frac{2a_2M_2}{\pi }(u^2+t^2),\quad u<t\\ M_{2n}= & {} \int _0^\gamma \alpha _{2n}(\xi )d\xi +\int _\gamma ^1 \beta _{2n}(\xi )d\xi \\ N_{2n}= & {} \int _0^\gamma \alpha _{2n}(\xi )log(\xi )d\xi +\int _\gamma ^1 \beta _{2n}(\xi )log(\xi )d\xi , \\ \alpha _{2n}(\xi )= & {} (\mu _{12(1)}+\mu _{12(2)})\frac{\xi ^{2n}\sqrt{P_1}(\gamma ^2-\xi ^2)^{\frac{1}{2}}\sqrt{P_2}(1-\xi ^2)^{\frac{1}{2}}}{\sqrt{P_1}\mu _{12(1)}(1-\xi ^2)^{\frac{1}{2}}+\sqrt{P_2}\mu _{12(2)}(\gamma ^2-\xi ^2)^{\frac{1}{2}}}\\ \beta _{2n}(\xi )= & {} \mu _{12(2)}(\mu _{12(1)}+\mu _{12(2)})\frac{\xi ^{2n}\sqrt{ P_1}(\gamma ^2-\xi ^2)P_2 (1-\xi ^2)^{\frac{1}{2}}}{P_1\mu _{12(1)}^2(1-\xi ^2)+P_2\mu _{12(2)}^2(\gamma ^2-\xi ^2)}\\ \end{aligned}$$

Also assuming that g(u) can be expanded in the form

$$\begin{aligned} g(u)= & {} g_0(u)+k_{s(1)}^2log(k_{s(1)})g_1(u)+k_{s(1)}^2g_2(u)\nonumber \\&+\,(k_{s(1)}^2log(k_{s(1)}))^2g_3(u)+k_{s(1)}^4log(k_{s(1)})g_4(u)+o(k_{s(1)}^4) \end{aligned}$$

(28)

the following expressions are obtained

$$\begin{aligned} g_0(u)= & {} 1\\ g_1(u)= & {} -\int _0^1tL_1(u,t)dt=-\frac{M_0}{\pi }\\ g_2(u)= & {} -\int _0^1tL_2(u,t)dt=-\frac{N_0}{\pi }- \frac{M_0}{\pi }\left( b_0-i+\frac{2}{\pi }log\left( \frac{1}{2}\right) \right) +(1-u^2)\frac{M_0}{2\pi }\\ g_3(u)= & {} -\int _0^1t[L_1(u,t)g_1(t)+L_3(u,t)]dt=\left( \frac{M_0}{\pi }\right) ^2\\ g_4(u)= & {} -\int _0^1t[L_1(u,t)g_2(t)+L_2(u,t)g_1(t)+L_4(u,t)]dt\\= & {} \frac{M_0}{\pi }\left\{ {\frac{2N_0}{\pi }+M_0\left( b_0-i+\frac{2}{\pi }log\frac{1}{2}\right) }\right\} + (1+2u^2)\frac{a_2M_2}{2\pi }-(3-2u^2)\left( \frac{M_0}{2\pi }\right) ^2.\\ \end{aligned}$$

With the help of above expression g(u) can be obtained from (28).

For isotropic media we substitute $C_{44} = C_{55} =\mu$, where $\mu$ is Lame’s constant and we deduce the following expressions

$$\begin{aligned}&P_1=1,\quad P_2=1\\&\alpha _{2n}(\xi )=(\mu _{12(1)}+\mu _{12(2)})\frac{\xi ^{2n}(\gamma ^2-\xi ^2)^{\frac{1}{2}}(1-\xi ^2)^{\frac{1}{2}}}{\mu _{12(1)}(1-\xi ^2)^{\frac{1}{2}}+\mu _{12(2)}(\gamma ^2-\xi ^2)^{\frac{1}{2}}}\\&\beta _{2n}(\xi )=\mu _{12(2)}(\mu _{12(1)}+\mu _{12(2)})\frac{\xi ^{2n}(\gamma ^2-\xi ^2) (1-\xi ^2)^{\frac{1}{2}}}{\mu _{12(1)}^2(1-\xi ^2)+\mu _{12(2)}^2(\gamma ^2-\xi ^2)} \end{aligned}$$

The remaining terms are same. These results coincide with the expressions obtained by Srivastava [1] for isotropic materials.

Numerical Results and Discussions

The Fredholm integral equation (18) is solved by perturbation method for low frequency and is given by (28). Numerical values of g(1) has been computed for $\gamma =\frac{k_{s(2)}}{k_{s(1)}}<1$ for fixed values of $k_{s(2)}(0.0022784)$. Different orthotropic materials are given in Tables 1 and 2. The values of engineering elastic constants have been taken from [25,26,27].

Table 1 Engineering elastic constants

Table 2 Engineering elastic constants

Fig. 3

SIF versus dimensionless frequency for Type-1 and Type-2 materials

Fig. 4

SIF versus dimensionless frequency for Type-3 and Type-4 materials

After calculating g(1), $\hbox {SIF}(K)$ is obtained numerically and is plotted (Figs. 3, 4) against the dimensionless frequency $(k_{s(1)})$ for different orthotropic materials. Figures 3 and 4 show the variation of $\hbox {SIF}(K)$ against the dimensionless frequency for different orthotropic materials which are similar in nature. For both the materials $\hbox {SIF}(K)$ first increases and then decreased rapidly with increase in frequency $k_{s(1)}$ and finally tending to zero.

Conclusion

The $\hbox {SIF}(K)$ has been obtained at the tip of the crack at the orthotropic bimaterial interface subject to shear wave incidence. The singularities and discontinuties associated with the incidence shear waves and crack have been predicted in the solution. The dynamic response of the crack has been analyzed for the variation of wave frequency. Also the effect of material orthotropy has been shown in graphs.