Mixed Convective Flow of a Casson Fluid over a Vertical Stretching Sheet

Abstract

A coupled nonlinear boundary value problem arising from a mixed convective flow of a non-Newtonian fluid at a vertical stretching sheet with variable thermal conductivity is investigated in this paper. Casson fluid model is used to describe the non-Newtonian fluid behavior. Using a similarity transformation, the governing equations are transformed into a system of coupled, nonlinear ordinary differential equations and the analytical solutions for the velocity and temperature fields are obtained via a semi-analytical algorithm based on the optimal homotopy analysis method. To validate the method, comparisons are made with the available results in the literature for some special cases and the results are found to be in excellent agreement. The characteristics of the velocity and the temperature fields in the boundary layer have been analyzed for several sets of values of the Casson parameter, the Prandtl number, the temperature dependent thermal conductivity parameter, the velocity exponent parameter and the mixed convection parameter. The presented results through graphs and tables reveal substantial effects of the pertinent parameters on the flow and heat transfer characteristics. Furthermore, an error analysis is offered using an exact residual error and average residual error methods.

Introduction

During the past few decades, several researchers proposed analytical and semi analytical methods based on the topological concepts of homotopy which have become very popular and efficient in solving nonlinear coupled differential equations [1, 2]: these methods depend on the $\hbar$ curves. Recently Marinca et al. [3–5] introduced an optimal homotopy asymptotic method which controls the convergence of the series solution. In general, the optimal homotopy asymptotic method is based on a generalized zeroth-order deformation equation and does not consider the mth-order deformation equation as in homotopy analysis method (HAM). Liao [6] was the first to introduce one of the easiest and highly reliable methods called the optimal homotopy analysis method (OHAM). This method contains only three convergence control parameters at any level of approximation which is computationally efficient. Liao [6] further introduced a new kind of averaged residual error, which can be used to find the optimal convergence-control parameters efficiently.

In recent years, researchers analyzed the coupled nonlinear boundary value problems arising in technological industries by numerical methods. The study of fluid flow over a stretching sheet is one such technologically interesting industrial problem which has attracted numerous researchers due to its applications to problems such as food processing, petroleum drilling, annealing and tinning of copper wires, manufacturing of plastic films, extraction of polymer sheets, crystal growing, paper production, and so on. Seminal analysis by Crane [7] reveals that, in a polymer industry, it is inevitable to consider plastic stretching sheet and hence obtained a similarity solution to the problem of stretching sheet with a linear surface velocity. The transfer of heat around these objects has applications in many fields, including the design of spacecraft, the nuclear reactors and many types of transformers/generators. In view of this, Carragher and Crane [8] analyzed the heat transfer at a stretching sheet under the condition that the temperature difference between the surface and the free stream, namely, $(T_w -T_\infty )$ is appreciably large (for details see Refs. [9–18]).

All the above researchers restricted their analyses to flow and heat transfer over a horizontal plate. Most of the problems arising in technological industry, based on mixed convection flow over a heated vertical sheet is of considerable interest and are challenge to physicists, engineers and Mathematicians. The findings of such a physical phenomenon will have a definite bearing on plastics, fabrics, and polymer industries. In view of this, Moutsoglou and Chen [19] analyzed numerically the effect of buoyancy parameter on a continuously moving inclined stretching surface. Further, Vajravelu [20] obtained exact solution for hydromagnetic convection at a continuous moving surface with uniform suction and established that when $(T_w >T_\infty )$ the fluid in the boundary-layer will be heated up and thus the free convection currents will set in. Chen [21] extended the model by Vajravelu [20] and analyzed the laminar mixed convection in boundary layers adjacent to a vertical stretching sheet by assuming the velocity and temperature of the sheet to vary as $u_{w}(x)={ Bx}^{m}$ and $T_{w}(x)-T_{\infty }={ Ax}^{n}$. Recently, Ali et al. [22] examined mixed convection heat transfer in an incompressible viscous fluid over a vertical stretching sheet by taking external magnetic field into account.

It is interesting to note that, for all practical purposes of the industry, the non-Newtonian fluids play a more vital and appropriate role than that of the Newtonian fluids. Some of the different types of non-Newtonian fluids are viscoelastic fluids, Rivlin–Erickson fluids, Maxwell fluids, couple stress fluids, micro-polar fluids, power law fluids. Fluids such as molten plastics, artificial fibers, flows related to the drilling of wells in petroleum industry, food stuffs or slurries are considered as non-Newtonian. The complexity of these models has made it difficult to report all its properties in a single constitutive equation. This nonlinear behavior between the stress and the rate of strain of the non-Newtonian fluids has attracted researchers to analyze its characteristic behavior. However, in the literature, the above mentioned non-Newtonian fluids were studied under several physical situations (see for details Refs. [23–35]). In particular, Prasad et al. [35] studied extensively the power law model for three different cases, namely the Newtonian model and non-Newtonian pseudo-plastic model etc. There is one more non-Newtonian fluid model available in the literature namely, Casson fluid model. The best examples for Casson fluid model are jelly, tomato sauce, honey, soup and concentrated fruit juices etc. We more often encounter these fluids in day to day life. The Casson fluid rheological model is preferred for human blood and chocolate. At low shear rates this fluid describes the flow characteristics of blood accurately. In the year 1959 Casson [36] presented the model for the flow of viscoelastic fluids with prominent and distinct features. Further, Charm and Kurland [37] used Casson’s equation to calculate the shear strength of blood and to describe its viscometry at shear rates below $5\,\hbox {s}^{-1}$. Recently, Mustafa et al. [38] obtained analytical solution for flow and heat transfer of a Casson fluid via homotopy analysis method (HAM). Further, Pramanik [39] used Casson fluid model to characterize the non-Newtonian fluid behavior and investigated flow and heat transfer past an exponentially stretching surface in presence of thermal radiation.

In view of the above studies, in the present paper, we analyze the effect of variable thermal conductivity on the heat transfer of a non-Newtonian Casson fluid at a non-isothermal vertical stretching sheet. This is in contrast to the work of Vajravelu [20] to Casson model where the thermal conductivity was treated as constant. The governing equations for flow and heat transfer have been nondimensionalized by using a suitable similarity transformation and solved the resulting nonlinear coupled differential equations for several set of values of the relevant parameters by an optimal homotopy analysis method (OHAM). The obtained analytical results are analyzed for the flow and heat transfer characteristics. The analysis reveals that the fluid flow is appreciably influenced by the physical parameters. It is expected that the results obtained will not only provide useful information for industrial application but also complement the existing literature.

Mathematical Formulation

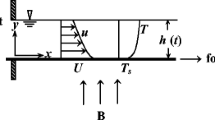
Consider a mixed convective boundary layer flow of a viscous incompressible Casson fluid past an impermeable stretching vertical heated sheet. Let the origin be at the slit, through which the sheet (see Fig. 1) is drawn in the fluid.

Fig. 1

Physical model and coordinate system (heated sheet)

Two equal and opposite forces are applied along the x-axis so that the sheet is stretched, keeping the origin fixed. The coordinate system has its origin located at the centre of the sheet with the x-axis extending along the sheet, while the y-axis is measured normal to the surface of the sheet and is positive in the direction from the sheet to the fluid. The continuous stretching surface is assumed to have a power law velocity variations $U_w=U_0 x^{n}$ and a temperature difference $T_w -T_\infty ={ Ax}^{r}$. Here, $U_0 (U_0 >0)$ is the parameter related to the surface stretching speed, the stretching sheet is assumed to be warmer than that of the ambient fluid such that $A>0$ and n, r are the exponents. The positive and negative values of n indicate that the surface is accelerated and decelerated from the slot respectively. The rheological equation of state for an isotropic and incompressible Casson fluid is given by (see for details Mustafa et al. [38])

$$\begin{aligned} \tau _{ij}=\left\{ {{\begin{array}{l} {2\left( {\mu _B +P_y /\sqrt{2\pi }} \right) e_{ij},\quad \pi >\pi _c}\\ {2\left( {\mu _B +{P}_y /\sqrt{2\pi _c}} \right) e_{ij}, \quad \pi <\pi _c}\\ \end{array}}} \right. , \end{aligned}$$

(1)

where $\pi =e_{ij} e_{ij}$ and $e_{ij}$ is the (i, j)th component of deformation rate, $\pi$ is the product of the component of deformation rate with itself, $\pi _c$ is a critical value of this product based on the non-Newtonian model, $\mu _B$ is the plastic dynamic viscosity of non-Newtonian fluid and $P_y$ is the yield stress of the fluid. Using the Boussinesq and boundary layer approximations (see for details Prasad et al. [26]), the governing equations for mass, momentum and energy for the Casson fluid model are given by

$$\begin{aligned} u_x +v_y= & {} 0, \end{aligned}$$

(2)

$$\begin{aligned} uu_x +vu_y= & {} \nu \left( {1+\frac{1}{\beta }} \right) \left( {u_y} \right) _y \pm g\, \beta _T (T-T_\infty ), \end{aligned}$$

(3)

$$\begin{aligned} uT_x +vT_y= & {} \left( {k(T)T_y} \right) _y . \end{aligned}$$

(4)

The suffix denotes partial differentiation with respect to the independent variables, where u and v are the velocity components in the x and y directions respectively, $\nu$ is the kinematic viscosity, $\beta =\mu _B \sqrt{2\pi _c}/P_y$ is the non-Newtonian Casson parameter, g is the gravitational acceleration, $\beta _T$ is the thermal expansion coefficient, T is the temperature, $T_\infty$ is the temperature of the fluid far away from the stretching surface and k(T) is the temperature dependent thermal conductivity given by

$$\begin{aligned} k(T)=k_\infty \left( {1+\varepsilon \frac{(T-T_\infty )}{\Delta T}} \right) , \end{aligned}$$

(5)

where $\Delta T=T_w -T_\infty$, $\varepsilon$ is a small parameter depending on the nature of the fluid, $k_\infty$ are the thermal conductivity of the fluid far away from the stretching surface (see for details Chiam [40]). The second term on the right hand side of Eq. (3) represents the buoyancy force, and its ‘$+$’ and ‘−’ signs indicate buoyancy assisting and opposing the flow respectively. In case of buoyancy assisting flow, the x-axis points upwards along the direction of stretching sheet, whereas in case of buoyancy opposing flow, the x-axis points vertically downwards. Substituting Eq. (5) in Eq. (4), we obtain

$$\begin{aligned} u \frac{\partial T}{\partial x} +\left( {v -\frac{k_\infty \varepsilon }{\Delta T}\frac{\partial T}{{}\partial y}} \right) \frac{\partial T}{\partial y}=\left[ {k_\infty \left( {1+\frac{\varepsilon }{\Delta T}\left( {T-T_\infty } \right) } \right) } \right] \frac{\partial ^{2} T}{\partial y^{2}}. \end{aligned}$$

(6)

The appropriate boundary conditions for the problem are

$$\begin{aligned} u\left( {x, y} \right)= & {} U_w=U_0\, x^{n},\quad v\left( {x, y} \right) =0,\quad T\left( {x, y} \right) =T_w \left( x \right) =T_\infty +Ax^{r} \hbox { at } y=0, \nonumber \\ u\left( {x, y} \right)\rightarrow & {} 0,\quad T\left( {x, y} \right) \rightarrow T_\infty \hbox { as } y\rightarrow \infty . \end{aligned}$$

(7)

Here $U_w, T_w$ are the sheet velocity and sheet temperature respectively. Now we transform the system of Eqs. (2)–(5) into a dimensionless form. Let the dimensionless similarity variable be

$$\begin{aligned} \eta =y\sqrt{\frac{U_0 (n+1)}{2\nu }}x^{\frac{n-1}{2}}, \end{aligned}$$

(8)

and the dimensionless stream function $\psi (x, y)$, the dimensionless temperature distribution $\theta \left( \eta \right)$ be

$$\begin{aligned} \psi (x, y)=f(\eta ) \sqrt{\frac{2}{n+1}U_{0}\,\nu \,}\left( x \right) ^{{n+1}/2}, \quad \theta \left( \eta \right) ={\left( {T-T_\infty } \right) }/{\left( {T_w -T_\infty } \right) }, \end{aligned}$$

(9)

where $\psi \left( {x, y} \right)$ identically satisfies the continuity Eq. (2). Using (9), the velocity components can be written as

$$\begin{aligned} u=U_w {f}'(\eta ) \hbox { and } v=-\sqrt{\nu \frac{n+1}{2}U_0}\, x^{\frac{n-1}{2}}\left[ {f(\eta )+\eta {f}'(\eta )\left( {\frac{n-1}{n+1}} \right) } \right] . \end{aligned}$$

(10)

Here a prime denotes differentiation with respect to $\eta$.With the use of Eqs. (8)–(10), Eqs. (3), (6) and (7) reduce to

$$\begin{aligned} \left( {1+\frac{1}{\beta }} \right) {f}'''+f{f}''-\frac{2n}{n+1}{f}'^{2}+\lambda \theta =0, \end{aligned}$$

(11)

$$\begin{aligned} \left[ {\left( {1+\varepsilon \theta } \right) {\theta }'} \right] ^{\prime }+\Pr \left( {f{\theta }'-\frac{2r}{n+1}{f}'\theta } \right) =0, \end{aligned}$$

(12)

where $\lambda =\pm Gr_x /\hbox {Re}_x^2$ is the mixed convection or buoyancy parameter parameter, $\Pr =\mu C_p /K_\infty$ is the Prandtl number, $Gr_x=g\beta _T \left( {T_w -T_\infty } \right) x^{3}/\nu ^{2}$ is the local Grashof number and $\hbox {Re}_x=U_w x/\nu$ is the local Reynolds number. It can be shown that $\lambda$ is independent of x,  if $r=2n - 1$. Hence, the similarity solutions are obtained under this limitation for $\lambda \ne 0$. Here, $\lambda >0 \hbox { and } \lambda <0$ correspond to the assisting flow and opposing flow, respectively, while $\lambda =0\, \left( {\hbox { i.e., } T_w=T_\infty } \right)$ represents the case when the buoyancy force is absent (pure forced convection flow). On other hand, if $\lambda$ is of order greater than one then the buoyancy forces will be predominant and the flow will be due to free convection. Hence, combined convection flow exists for $\lambda =O (1)$. The appropriate boundary conditions in dimensionless form are:

$$\begin{aligned} f\left( 0 \right) =0,\quad {f}'\left( 0 \right) =1,\quad \theta \left( 0 \right) =1,\quad \theta \left( \infty \right) =0,\quad {f}'\left( \infty \right) =0. \end{aligned}$$

(13)

We notice that in the absence of variable thermal conductivity parameter, Casson fluid parameter and when $n=1$ (linear stretching case), the equations reduce to those of Vajravelu [20], while in the absence of Casson fluid parameter and when $n\ne 1$ the equations reduce to those of Vajravelu [12] under different physical situations. Further, with constant thermal conductivity parameter and no Casson fluid parameter equations reduce to those of Ishak et al. [13]. From the engineering point of view, the important physical quantities are the local skin friction $C_{fx}$ and the local Nusselt number $Nu_x$. They are defined as

$$\begin{aligned} C_{f_x}=\frac{\tau _w}{\rho U_w^2}\,\,\hbox { and }\,\,Nu_x=\frac{xq_w}{k\left( {T_w -T_x} \right) }, \end{aligned}$$

where $\tau _w$ is the skin friction and $q_w$ is surface heat flux introduced as

$$\begin{aligned} \tau _w=\mu \left( {\frac{\partial u}{\partial y}} \right) _{y=0},\quad q_w=-k\left( {\frac{\partial T}{\partial y}} \right) _{y=0}. \end{aligned}$$

Applying the non-dimensional transformations (9), we obtain

$$\begin{aligned} C_{f_x}= & {} 2\sqrt{\left( {{n+1}/2} \right) } \left( {1+\frac{1}{\beta }} \right) \left( {\hbox {Re}_x} \right) ^{{-1}/2}{f}''\left( 0 \right) ,\nonumber \\ Nu_x= & {} -\sqrt{\left( {{n+1}/2} \right) } \left( {\hbox {Re}_x} \right) ^{1/2}{\theta }'\left( 0 \right) , \end{aligned}$$

(14)

where $\hbox {Re}_x=U_w x/\nu$ is the local Reynolds number.

Exact Solutions for Some Special Cases

Here we present exact solutions for some special cases. Such solutions are useful, in that they serve as a benchmark for comparison with the solutions obtained via numerical /analytical schemes. In the absence of Casson parameter and when $n \ne 1$, the present results are in good agreement with those of Hsiao [29] for different values of mixed convection parameter in the absence of wedge, magnetic and viscoelastic parameter.

No Free Convective Currents and Linear Stretching $(\lambda =0\hbox { and }n=1)$

In the limiting case of $\lambda =0 \hbox { and } \left( {\lambda =0 \hbox { and } n=1} \right)$ the boundary layer flow and heat transfer problem degenerates. In this case the solution for the velocity field is given by, namely,

$$\begin{aligned} f_\eta \left( \eta \right) =1-e^{-\alpha \eta }\quad \hbox {where }\alpha =\pm 1/\sqrt{1+1/\beta }. \end{aligned}$$

(15)

Perturbation Analysis in the Absence of Free Convection Currents and Linear Stretching $(\lambda =0 \hbox { and } n=1)$ and in the Presence of Variable Thermal Conductivity

We follow a perturbation expansion approach to solve Eq. (12). Suppose

$$\begin{aligned} \theta \left( \eta \right) =\theta _0 \left( \eta \right) +\varepsilon \theta _1 \left( \eta \right) +\varepsilon ^{2}\theta _2 \left( \eta \right) +\cdots \end{aligned}$$

(16)

Substituting this into Eq. (12) and equating like powers of $\varepsilon$ ignoring quadratic and higher order terms in $\varepsilon$, we obtain

$$\begin{aligned} \theta _0^{\prime \prime }+\Pr \left( {f\theta _0^{\prime }- r\, {f}'\theta _0} \right) =0, \end{aligned}$$

(17)

with boundary conditions $\theta _0 \left( 0 \right) =1, \theta _0 \left( \infty \right) =0,$ and

$$\begin{aligned} \theta _1^{\prime \prime }+\Pr \, f\, \theta _1^{'}-\Pr ({\mathrm{r}\, {f}'-\beta }) \theta _1=-\theta _0 \theta _0^{''}-\theta _0^{'2}, \end{aligned}$$

(18)

with the boundary conditions $\theta _1 \left( 0 \right) =0, \theta _1 \left( \infty \right) =0$.

The solution for the Eq. (17) is expressed in terms of Confluent hypergeometric series, namely, Kummer’s function, M, to wit:

$$\begin{aligned} \theta _0 \left( \eta \right) =\exp \left( {-\alpha \frac{\left( {a_0 +b_0} \right) \eta }{2}} \right) \frac{M\left( {a_1, b_1, z} \right) }{M\left( {a_1, b_1, -b_0} \right) }, \end{aligned}$$

(19)

where $z=-\left( {\Pr /\alpha ^{2}} \right) e^{-\alpha \eta }, b_0={\Pr }/{\alpha ^{2}}, a_1=\left( {\Pr +b_0 -2} \right) /2, b_1=1+b_0$. We now analyse Eq. (18), which gives the first-order correction term $\varepsilon \theta _1$. Note that Eq. (12) is linear and inhomogeneous and therefore it is possible to obtain a power series solution for $\theta _1$. However, it becomes very tedious to obtain various values of $\theta _1$ using this power series solution. Instead, we employ the following semi-analytical algorithm based on Optimal Homotopy Analysis Method (OHAM) method to solve the coupled boundary value problem.

Semi-Analytical Solution: Optimal Homotopy Analysis Method

In order to obtain optimal HAM solutions for the system (11)–(13), we assume the following initial guesses for dimensionless velocity $f(\eta )$ and temperature $\theta (\eta ):$ (see for details Refs. [41–43])

$$\begin{aligned} f_0 (\eta )= & {} 1-e^{-\eta }, \end{aligned}$$

(20)

$$\begin{aligned} \theta _0 (\eta )= & {} e^{-\eta }. \end{aligned}$$

(21)

Now we choose linear operators $L_1$ and $L_2$ as

$$\begin{aligned} L_1(\,)=\frac{d^{3}}{d\eta ^{3}}-\frac{d}{d\eta }, \quad L_2 (\,)=\frac{d^{2}}{d\eta ^{2}}+\Pr \frac{d}{d\eta }, \end{aligned}$$

(22)

such that $L_1 \left[ {c_1 +c_2 e^{\eta }+c_3 e^{-\eta }} \right] =0$ and $L_2 \left[ {c_4 +c_5 e^{-\eta }} \right] =0$ where $c_{i} \hbox {'s}\;(i=1, 2, 3, 4, 5)$ are arbitrary constants. Now let us define homotopy operators $H_{1}$ and $H_{2}$ as

$$\begin{aligned} H_1 \left( {\hat{{f}}, q} \right)\equiv & {} \left( {1-q} \right) L_1 \left( {\hat{{f}}\left( {\eta , q} \right) -f_0 (\eta )} \right) -q\bar{{h}}N_1 \left( {\hat{{f}}\left( {\eta , q} \right) , \hat{{\theta }}\left( {\eta , q} \right) } \right) \end{aligned}$$

(23)

$$\begin{aligned} H_2 \left( {\hat{{\theta }}, q} \right)\equiv & {} \left( {1-q} \right) L_2 \left( {\hat{{\theta }}\left( {\eta , q} \right) -\theta _0 (\eta )} \right) -q\bar{{h}}N_2 \left( {\hat{{\theta }}\left( {\eta , q} \right) , \hat{{f}}\left( {\eta , q} \right) } \right) \end{aligned}$$

(24)

and by considering the equations $H_1 \left( {\hat{{f}}, q} \right) =0$ and $H_2 \left( {\hat{{\theta }}, q} \right) =0$, we have the so-called zeroth order deformation equation given by

$$\begin{aligned} (1-q)L_1 \left[ {\hat{{f}}(\eta , q)-f_0 (\eta )} \right]= & {} q{\overline{h}} N_1 \left[ {\hat{{f}}(\eta , q), \hat{{\theta }}(\eta , q)} \right] , \end{aligned}$$

(25)

$$\begin{aligned} (1-q)L_2 \left[ {\hat{{\theta }}(\eta , q)-\theta _0 (\eta )} \right]= & {} q\bar{{h}}N_2 \left[ {\hat{{\theta }}(\eta , q), \hat{{f}}(\eta , q)} \right] , \end{aligned}$$

(26)

with conditions

$$\begin{aligned} \hat{{f}}(0, q)=0, \quad {\hat{{f}}}'(0, q)=1, \quad {\hat{{f}}}'(\infty , q)=0, \quad \hat{{\theta }}(0, q)=1, \quad \hat{{\theta }}(\infty , q)=0. \end{aligned}$$

(27)

where $q\in [0, 1]$ is an embedding parameter, $\bar{{h}}\ne 0$ is the convergence control parameter and $N_1, N_2$ are nonlinear operators defined as

$$\begin{aligned} N_1= & {} \left( {1+\frac{1}{\beta }} \right) \frac{d^{3}\hat{{f}}(\eta , q)}{d\eta ^{3}}+\hat{{f}}(\eta , q)\frac{d^{2}\hat{{f}}(\eta , q)}{d\eta ^{2}}-\left( {\frac{2n}{n+1}} \right) \frac{d\hat{{f}}(\eta , q)}{d\eta }^{2}+\lambda \hat{{\theta }}(\eta , q),\nonumber \\ \end{aligned}$$

(28)

$$\begin{aligned} N_2= & {} \left( {\left( {1+\varepsilon \hat{{\theta }}(\eta , q)} \right) \hat{{{\theta }'}}(\eta , q)} \right) ^{\prime }+\Pr \, \hat{{f}}(\eta , q)\frac{d\hat{{\theta }}(\eta , q)}{d\eta }\nonumber \\&-\left( {\frac{2r}{n+1}} \right) \Pr \frac{d\hat{{f}}(\eta , q)}{d\eta }\hat{{\theta }}(\eta , q). \end{aligned}$$

(29)

From Eqs. (23) and (24), at $q=0$, we have $L_1 [{\hat{{f}}(\eta , 0)-f_0 (\eta )} ]=0$ and $L_2[{\hat{{\theta }}(\eta , 0)-\theta _0 (\eta )} ]=0$, which imply that $\hat{{f}}(\eta , 0)=f_0 (\eta )$ and $\hat{{\theta }}(\eta , 0)=\theta _0 (\eta )$ respectively. Whereas at $q=1,$ we have $N_1 \left[ {\hat{{f}}(\eta , 1), \hat{{\theta }}(\eta , 1)} \right] =0$ and $N_2 [{\hat{{\theta }}(\eta , 1), \hat{{f}}(\eta , 1)} ]=0$, which imply that $\hat{{f}}(\eta , 1)=f(\eta )$, and $\hat{{\theta }}(\eta , 1)=\theta (\eta ),$ respectively. Hence, by defining

$$\begin{aligned} \left. {f_m (\eta )=\frac{1}{m!}\frac{d^{m}f(\eta , q)}{d\eta ^{m}}} \right| _{q=0}, \quad \left. {\theta _m (\eta )=\frac{1}{m!}\frac{d^{m}\theta (\eta , q)}{d\eta ^{m}}} \right| _{q=0}, \end{aligned}$$

(30)

we expand $\hat{{f}}(\eta , q)$, $\hat{{\theta }}(\eta , q)$ by means of Taylor’s series as

$$\begin{aligned} \hat{{f}}(\eta , q)=f_0 (\eta )+\sum _{m=1}^\infty {f_m (\eta )q^{m}}, \quad \hat{{\theta }}(\eta , q)=\theta _0 (\eta )+\sum _{m=1}^\infty {\theta _m (\eta )q^{m}}. \end{aligned}$$

(31)

If the series in Eq. (31) converges at $q=1$, we get the homotopy series solution as

$$\begin{aligned} f(\eta )=f_0 (\eta )+\sum _{m=1}^\infty {f_m (\eta )}, \quad \theta (\eta )=\theta _0 (\eta )+\sum _{m=1}^\infty {\theta _m (\eta )} . \end{aligned}$$

(32)

It should be noted that $f(\eta )\,\,\hbox {and}\,\,\theta (\eta )$ in Eq. (32) contain an unknown convergence control parameter $\bar{{h}}\ne 0$, which can be used to adjust and control the convergence region and the rate of convergence of the homotopy series solution. The mth order deformation equations and the conditions are

$$\begin{aligned}&L_1 \left[ {f_m (\eta )-\chi _m f_{m-1} (\eta )} \right] =\bar{{h}}{R^{f}_m}(\eta ), \nonumber \\&L_2 \left[ {\theta _m (\eta )-\chi _m \theta _{m-1} (\eta )} \right] =\bar{{h}}R_m^\theta (\eta ), \end{aligned}$$

(33)

$$\begin{aligned}&f_m (0)=0, \quad {f}'_m (0)=0, \quad {f}'_m (\infty )=0, \quad \theta _m (0)=0, \quad \theta _m (\infty )=0, \end{aligned}$$

(34)

where

$$\begin{aligned} R_m^f= & {} \left( {1+\frac{1}{\beta }} \right) {f}'''_{m-1} (\eta ) +\sum _{k=0}^{m-1} {f}''_{m-1-k} f_k\nonumber \\&-\left( {\frac{2n}{n+1}} \right) \sum _{k=0}^{m-1} {{f}'_{m-1-k} {f}'_k +\lambda \theta _{m-1} (\eta )} \end{aligned}$$

(35)

$$\begin{aligned} R_m^\theta= & {} {\theta }''_{m-1} (\eta )+\varepsilon \left( {\sum _{k=0}^{m-1} {{\theta }''_{m-1-k} \theta _k} +\sum _{k=0}^{m-1} {{\theta }'_{m-1-k} {\theta }'_k}} \right) +\Pr \sum _{k=0}^{m-1} {\theta }'_{m-1-k} f_k\nonumber \\&-\left( {\frac{2r}{n+1}}\right) \Pr \sum _{k=0}^{m-1} {{f}'_{m-1-k} \theta _k} \end{aligned}$$

(36)

and

$$\begin{aligned} \chi _m=\left\{ {{\begin{array}{ll} 0,&{} \quad m\le 1\\ 1,&{} \quad m>1\end{array}}} \right. \end{aligned}$$

(37)

Appropriate selection of convergence control parameter $\bar{{h}}\ne 0$ plays an important role in determining the convergence region and convergence rate. Here we find optimal value of $\bar{{h}}$ about which the Eq. (32) not only converges but it also ensures the fastest convergence. Now we evaluate squared residual error of governing equation and minimize it over ${\overline{h}}$ in order to obtain optimal value of ${\overline{h}}$ and least possible error.

Table 1 Comparison of ${f}''(0)$ and CPU time (s) incurred to evaluate mth order approximation by exact residual error and average residual error when $\hbox {Pr}=1.0$, $\beta =1.0$, $\lambda =0.5$, $\varepsilon =0.1, n=1$

Error Analysis and CPU Time

In the process of error analyses two different methods are employed, namely, exact residual error and average residual error. For different order approximation, CPU time required for evaluation of ${f}''(0)$ is observed. It is evident that, the values of ${f}''(0)$ evaluated using both the method are almost same (for details see Table 1). As for as CPU time is concerned average residual error needs very less time compared to that of exact residual error. The time required to calculate average residual error is 28.9, 9.1, 14.6, 15.7, 21.0, and 21.2 % for $m=1, 2, 3, 4, 5, 6$ respectively that of CPU time required to calculate exact residual error. Practically, the evaluation of ${\hat{E}}_{m}^{f} ({\bar{h}})$ and ${\hat{E}}_m^\theta ({\bar{h}})$ is time consuming. In order to speed up the calculations we employ average residual error instead of the exact residual error. For the $m^{\hbox {th}}$ order deformation equation, the exact residual error is given by

$$\begin{aligned} \hat{{E}}_m^f (\bar{{h}})=\int \limits _0^\infty {\left( {N_1 \left[ {\sum _{n=0}^m {f_n (\eta )}} \right] } \right) ^{2}} d\eta , \quad \hat{{E}}_m^\theta (\bar{{h}})=\int \limits _0^\infty {\left( {N_2 \left[ {\sum _{n=0}^m {\theta _n (\eta )}} \right] } \right) ^{2}} d\eta \end{aligned}$$

(38)

and the average residual error is given by

$$\begin{aligned} E_m^f (\bar{{h}})=\frac{1}{M+1}\sum _{k=0}^M {\left( {N_1 \left[ {\sum _{n=0}^m {f_n (\eta _k)}} \right] } \right) ^{2}}, \quad E_m^\theta (\bar{{h}})=\frac{1}{M+1}\sum _{k=0}^M {\left( {N_2 \left[ {\sum _{n=0}^m {\theta _n (\eta _k)}} \right] } \right) ^{2}}\nonumber \\ \end{aligned}$$

(39)

where $\eta _k=k\Delta \eta =k/M, k=0, 1, 2, \dots , M$ ($M=20$ for Blasius flow problem). We minimize the error functions $E_m^f (\bar{{h}})$ and $E_m^\theta (\bar{{h}})$ in $\bar{{h}}$ and obtain the optimal values of $\bar{{h}},$ separately for f and $\theta$. Substituting this optimal value of $\bar{{h}}$ into Eq. (32), we get the approximate solutions for Eqs. (11) and (12) satisfying the conditions (13).

Results and Discussion

The system in Eqs. (11)–(12) is highly nonlinear and coupled ordinary differential equations with variable coefficients. The appropriate analytical solutions for these equations with boundary condition (13) are obtained using optimal homotopy analysis method (see for details Liao [6, 41, 42], Fan and You [43]). In order to validate the method used in this study and to judge the accuracy of the present analysis, the wall temperature gradient results are compared with the previously published results of Grubka and Bobba [9], Chen and Char [10], Ali [11], and Mabood et al. [17] for several special cases in which the buoyancy force and thermal conductivity are neglected: The obtained results are found to be in excellent agreement and are shown in Tables 2 and 3. The computations have been carried out by the method of OHAM as described above for different values of the pertinent parameters, such as the mixed convection parameter $\lambda$, the thermal conductivity parameter $\varepsilon$, the velocity power index parameter n,  the Prandtl number Pr and the Casson parameter $\beta$. We present the results graphically for the horizontal velocity profile ${f}'(\eta )$ and the temperature profile $\theta (\eta )$ for several sets of values of the parameters in Figs. 2, 3, 4, 5, 6. It is observed from these figures that both ${f}'(\eta )$ and $\theta (\eta )$ monotonically decreases and tends to zero asymptotically as the distance increases from the boundary. The computed analytical values for the skin friction ${f}''(0)$ and the wall temperature gradient ${\theta }'(0)$ are presented in Table 4.

Table 2 Comparison between exact and analytical solution by HAM for $-f''(0)$ when $n=1, \lambda =0$

Table 3 Comparison of wall temperature gradient ${\theta }'\left( 0 \right)$ for different values of Prandtl number when $\varepsilon =0.0, \lambda =0\hbox { and }\beta =0$

Figure 2a, b elucidate the effects of $\beta$ on ${f}'(\eta )\,\, \hbox {and}\, \,\theta (\eta )$. Here we considered the values of $\beta$ in the range of $1\le \beta \le 5$. It is observed that, for increasing values $\beta$, fluid flow produces resistance, hence ${f}'(\eta )$ decreases. That is, as $\beta$ approach higher values, the momentum boundary layer thickness squeezes and the velocity distribution becomes linear for higher values of n but the impact is quite the opposite in the case of $\theta (\eta )$. Physically, increase in $\beta$ means, a decrease in the yield stress, in this case the fluid behaves like a Newtonian fluid. Further, it is interesting to note that the fluid velocity is prominent for linear stretching $(\hbox {for }n=1)$ than that of nonlinear stretching sheet $(\hbox {for }n=2, n=5)$; where as in the case of the temperature field it is more suppressed for linear stretching than that of the nonlinear stretching sheet; see Fig. 2a, b. Figure 3a, b exhibit the effect of n on ${f}'(\eta )\hbox { and }\theta (\eta )$. It is noticed that both the velocity and the temperature fields decrease as n increases leading to thinning the velocity and thermal boundary layer. The effect of n is negligible: That is, the coefficient $2n/(n+1)$ in Eq. (11) approaches 2 as $n\rightarrow \infty$. This phenomenon is true even in the case of skin friction (see Table 4). The effect of the mixed convection parameter $\lambda$ on ${f}'(\eta )\hbox { and }\theta (\eta )$ is demonstrated in Fig. 4a, b, respectively. The presence of thermal buoyancy effects are revealed by the finite value of $\lambda (\lambda \ne 0)$ which has a propensity to enhance the flow along the surface. It is seen that an increase in the value of $\lambda$ leads to an enhancement in ${f}'(\eta )$. Physically $\lambda >0$ means heating of the fluid or cooling of the surface, $\lambda <0$ means cooling of the fluid or heating of the surface, and $\lambda =0$ corresponds to the absence of the mixed convection parameter. Increase in $\lambda$ means an increase in the temperature difference $(T_w -T_\infty )$ which leads to an enhancement in ${f}'(\eta )$ due to the enhanced convection, and thus an increase in the momentum boundary layer thickness. The effect of $\lambda$ on temperature profile is quite opposite. The effect of $\lambda$ on $\theta (\eta )$ is illustrated in Fig. 4b: With an increase in $\lambda$, the temperature field is suppressed and consequently thermal boundary layer thickness becomes thinner. Hence the magnitude of the rate of heat transfer from the surface increases. This is due to effects of buoyancy force.

Fig. 2

a Horizontal velocity profile for different values of $\beta$ and n with $\epsilon =0.1$, $Pr=1.0$, $\lambda =0.5$ b Temperature profile for different values of $\beta$ and n with $\epsilon =0.1$, $Pr=1.0$, $\lambda =0.5$

Fig. 3

a Horizontal velocity profile for different values of n and $\beta$ with $\epsilon =0.1$, $Pr=1.0$, $\lambda =0.1$ b Temperature distribution profile for different values of n and $\beta$ with $\epsilon =0.1, { Pr=1.0}, \beta =0.1$

Fig. 4

a Horizontal profile for different values of $\lambda$ and n with $\epsilon =0.1$, $Pr=1.0$, $\beta =1.0$. b Temperature profile for different values of $\lambda$ and n with $\epsilon =0.1$, $Pr=1.0$, $\beta =1.0$

Fig. 5

Temperature profile for different values of Pr and n with $\epsilon =0.1, \beta =2.0, \lambda =0.5$

Fig. 6

Temperature profile for different values of $\epsilon$ and n with Pr=1.0, $\beta =1.0$, $\lambda =0.1$

Figures 5 and 6 depict the effects of $\Pr$ and $\varepsilon$ on $\theta (\eta )$ for increasing values of n. Increase in $\Pr$ leads to a decrease in the temperature: This is due to decrease in the thermal conductivity $k_\infty$. That is, as $\Pr$ increases the thermal boundary layer thickness reduces. Hence, cooling of the heated surface can gradually be improved by choosing a proper coolant with a large $\Pr$. Fluid temperature is found to increase with increasing values of $\varepsilon$ which leads to a fall in the rate of heat transfer. That is, the assumption of temperature dependent thermal conductivity suggests a reduction in the magnitude of the transverse velocity by a quantity ${\partial k(T)}/{\partial y}$ which can be seen in Eq. (4). Therefore, the rate of cooling is much faster for the coolant material with low values for the thermal conductivity parameter.

Table 4 is prepared to observe the variations of skin-friction coefficient and wall temperature gradient for various values of pertinent parameters. One can observe that both ${f}''(0)$ and ${\theta }'(0)$ decrease with increasing values of n where as in the case of $\beta$ it is observed that ${f}''(0)$ decreases and quite the opposite in the case of increasing $\lambda$. For increasing values of $\Pr$ there is a decrease in ${\theta }'(0)$ where as in the case of $\varepsilon$ it is reversed.

Conclusions

Heat transfer with variable thermal conductivity in a Casson fluid flow over a vertical stretching sheet is analyzed using an analytical method, namely, the optimal homotopy analyses method. Some of the interesting findings are as follows.

• The velocity boundary layer thickness reduces and the thermal boundary layer thickness increases with increasing values of the Casson parameter.

• The effect of the variable thermal conductivity parameter is to enhance the temperature field; whereas for higher values of the Prandtl number the temperature field decrease and hence the thermal boundary layer thickness is reduced.

• Mixed convection parameter has reverse effects on velocity and temperature fields.

• The effect of the velocity power index parameter is to reduce both the velocity and the thermal boundary layers.

• Average residual error method is less time consuming compared to that of exact residual error method.

Table 4 Values of skin friction and wall temperature gradient for different values of the physical parameters