Introduction

The topic of fractional calculus has gain considerable attention in the last few years. Fractional derivatives and fractional integrals provide more accurate systems’s models in various applications. Analysis and numerical approximate solutions of fractional differential equations with various types of initial and boundary conditions gain interest due to its numerous applications  [1–5]. In this paper, Caputo’s fractional derivative is used. This operator is widely applied in modelling of the material’s mechanical properties  [6], modelling of the viscoelastic behaviour, signal processing  [7], diffusion problems  [8], bioengineering and mathematical finance models  [9] etc. The existence and uniqueness of the solution of two-point boundary value problem of fractional order can be seen in  [10–13]. Akram and Tariq established the exponential spline method to compute approximate solution for FBVP [14].

Many authors used the spline technique to establish the accurate and efficient numerical schemes for solution of boundary value problems (BVPs). For example, Siddiqi and Akram constructed many numerical schemes with help of different spline functions such as polynomial splines and non-polynomial splines for the solution of eighth and tenth order BVPs [15, 16].

In this paper, consider the following FBVP:

$$\begin{aligned} D^{\alpha }y(x)+y(x)= f(x), \quad x\in [a, b] ,\quad 1\le \alpha <2, \end{aligned}$$
(1)

subject to

$$\begin{aligned} y(a)=A , \quad y(b)=B, \end{aligned}$$
(2)

where A and B are real constants. Also f(x) is continuous function on the interval [a, b] and \(D^{\alpha }\) denotes fractional derivative in Caputo’s sense. The left and right sided Riemann-Liouville fractional integral operator of order \(\alpha \) is:

$$\begin{aligned} I^{\alpha }_{a+}y(x)=\frac{1}{\Gamma (\alpha )}\int _{a}^{x}(x-s)^{\alpha -1}y(s)ds, \quad \alpha >0 \end{aligned}$$

and

$$\begin{aligned} I^{\alpha }_{b-}y(x)=-\frac{1}{\Gamma (\alpha )}\int _{b}^{x}(x-s)^{\alpha -1}y(s)ds,\quad \alpha >0, \end{aligned}$$

respectively. The right and left sided Caputo’s fractional derivative of order \(\alpha \) is defined as

$$\begin{aligned} D^{\alpha }_{-b}y(x)=\left\{ \begin{array}{ll} I^{m-\alpha }_{-b}D^{m}y(x), \quad m-1<\alpha <m , m \in \mathbb {N},\\ \frac{D^{m}y(x)}{Dx^{m}}, \quad \alpha =m \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} D^{\alpha }_{a+}y(x)=\left\{ \begin{array}{ll} I^{m-\alpha }_{a+}D^{m}y(x), \quad m-1<\alpha <m , m\in \mathbb {N},\\ \frac{D^{m}y(x)}{Dx^{m}}, \quad \alpha =m, \end{array} \right. \end{aligned}$$

respectively, where \(D^{m}\) is ordinary differential operator.

If \(\alpha >0\), \(m-1\le \alpha <m\), \(\delta >-1\), \(m \in \mathbb {N}\), \(\lambda , \mu \in \mathbb {R}\) and y(x) is continuous function, then the following results hold:

$$\begin{aligned}&D^{\alpha }C=0, \quad C \ is \ constant\\&D^{\alpha }(\lambda y(x) + \mu q(x))=\lambda D^{\alpha }y(x)+\mu D^{\alpha }q(x)\\&I^{\alpha }x^{\delta }= \frac{\Gamma (\delta +1)}{\Gamma (\delta +1+\alpha )}x^{\delta +\alpha } \end{aligned}$$

For more properties of fractional derivatives, we refer to  [17–19].

The main aim of this work is that to establish a numerical scheme using polynomial spline functions. The paper is organized as follows: In section “Polynomial Spline”, cubic polynomial spline functions based methods are developed for the solutions of FBVPs with right Caputo’s operator and left Caputo’s operator. The matrix form of the proposed scheme is discussed in section “Matrix Form of the Method”. In section “Convergence Analysis”, the convergence analysis of method is presented. In section “Numerical Experiments”, two examples are given to illustrate the efficiency of the method. Also the numerical results of suggested scheme is compared with scheme developed in  [20] and find that presented method gives better results.

Polynomial Spline

Derivation of the Methods

Let \(x_{i}=a+il\) \((i=0,1,\ldots ,n, \ \ l=\frac{b-a}{n}, \ n>0)\) be grid points of the uniform partition of [a, b] into the subintervals \([x_{i-1},x_{i}]\). Let y(x) be the exact solution of Eq. (1) and \(S_{i}\) be an approximation to \(y_{i} = y(x_{i})\) obtained by the cubic spline function \(\Psi _{i}\) passing through the points \((x_{i} , S_{i})\) and \((x_{i+1}, S_{i+1})\).

The numerical solution of given FBVP is discussed with left differential operator (first case) and secondly with right differential operator (second case).

Numerical Scheme of FBVP with Left Fractional Operator

In this case, FBVP becomes

$$\begin{aligned} D^{\alpha }_{a+}y(x)+y(x)=f(x), \quad 1 \le \alpha < 2. \end{aligned}$$
(3)

Consider that cubic spline segment has the following form:

$$\begin{aligned} \widehat{\Psi _{i}}(x)= \widehat{a_{i}}(x-x_{i-1})^{3}+\widehat{b_{i}}(x-x_{i-1})^{2}+\widehat{c_{i}}(x-x_{i-1}) +\widehat{d_{i}},\quad i=1,2,\ldots ,n, \end{aligned}$$

where \(\widehat{a_{i}}\), \(\widehat{b_{i}}\), \(\widehat{c_{i}}\) and \(\widehat{d_{i}}\) are undetermined coefficients. These coefficients are expressed in terms of \(S_{i}\) and \(M_{i}\) as

$$\begin{aligned} \widehat{\Psi _{i}}(x_{i-1})= S_{i-1}, \quad \widehat{\Psi _{i}}(x_{i})= S_{i}, \quad \widehat{\Psi _{i}}''(x_{i-1})= M_{i-1}, \quad \widehat{\Psi _{i}}''(x_{i})= M_{i}, \end{aligned}$$

and are calculated, as

$$\begin{aligned} \widehat{a_{i}}= & {} \frac{1}{6l}(M_{i}-M_{i-1}), \quad \widehat{b_{i}}= \frac{M_{i-1}}{2}, \quad \widehat{c_{i}}= \frac{S_{i}}{l}-\frac{S_{i-1}}{l}- \frac{l}{6}(M_{i}-M_{i-1})- \frac{M_{i-1}}{2}l, \\ \widehat{d_{i}}= & {} S_{i-1}. \end{aligned}$$

Applying the derivative continuities of order up to the maximum of 2 and using values of the constants, the following consistency relations are obtained as,

$$\begin{aligned} S_{i+1}-2 S_{i}+ S_{i-1}=\frac{l^{2}}{6}(M_{i+1}+4M_{i}+M_{i-1}), \quad i=1,2,\ldots , n-1. \end{aligned}$$
(4)

The approximations of \(M_{0}\) and \(M_{n}\) in terms of functional values are defined as

$$\begin{aligned} M_{0}\cong \frac{2S_{0}-5S_{1}+4S_{2}-S_{3}}{l^{2}} \end{aligned}$$

and

$$\begin{aligned} M_{n}\cong \frac{2S_{n}-5S_{n-1}+4S_{n-2}-S_{n-3}}{l^{2}}. \end{aligned}$$

For \(i=1\) and \(i=n-1\), the consistency relations can be taken as

$$\begin{aligned}&\frac{1}{6} S_{3}+\frac{1}{3} S_{2}+\frac{-7}{6}S_{1}+\frac{2}{3}S_{0} =\frac{l^{2}}{6}( M_{2}-4M_{1}), \end{aligned}$$
(5)
$$\begin{aligned}&\frac{1}{6} S_{n-3}+\frac{1}{3} S_{n-2}+\frac{-7}{6}S_{n-1}+\frac{2}{3}S_{n} =\frac{l^{2}}{6}( M_{n-2}-4M_{n-1}) \end{aligned}$$
(6)

respectively. Also \(M_{i}\) are taken from Eq. (3), as

$$\begin{aligned} D^{\alpha }_{x_{i-1}}{\widehat{\Psi _i}}(x)\mid _ {x=x_{i}}+S_{i} =f_{i}, \quad i=0,1,\ldots , n, \end{aligned}$$
(7)

where \(f_{i}=f(x_{i})\).

Numerical Scheme of FBVP with Right Fractional Operator

Consider the cubic polynomial spline as,

$$\begin{aligned} \Psi _{i}(x)= a_{i}(x_{i+1}-x)^{3}+b_{i}(x_{i+1}-x)^{2}+c_{i}(x_{i+1}-x) +d_{i},\quad i=0,1,\ldots ,n-1, \end{aligned}$$
(8)

where \(a_{i}\), \(b_{i}\), \(c_{i}\) and \(d_{i}\) are constants. Now the cubic spline is defined by the following relations:

  • \(S(x)=\Psi _{i}\),    \(x\in [x_{i},\ x_{i+1}],\)    \(i=0,1,\ldots ,n-1\)

  • \(S(x) \in C^{2}[a,b]\)

In order to obtain the consistency relations in terms of \(S_{i}\) and \(M_{i}\), let

$$\begin{aligned}&\Psi _{i}(x_{i})= S_{i}, \quad \Psi _{i}(x_{i+1})= S_{i+1},\\&\Psi _{i}''(x_{i})= M_{i}, \quad \Psi _{i}''(x_{i+1})= M_{i+1}. \end{aligned}$$

The coefficients introduced in Eq. (8) have the following form:

$$\begin{aligned}&a_{i}=\frac{1}{6l}(M_{i}-M_{i+1}), \quad b_{i}= \frac{M_{i+1}}{2}, \quad c_{i}= \frac{S_{i}}{l}-\frac{S_{i+1}}{l}- \frac{l}{6}(M_{i}-M_{i+1})- \frac{M_{i+1}}{2}l, \\&d_{i}=S_{i+1}. \end{aligned}$$

Applying derivative continuities of order up to the maximum of 2 and using values of the constants, same relations Eqs. (4)–(6) are obtained. Also,

$$\begin{aligned} D^{\alpha }_{x_{i+1}}{\Psi _{i}}(x)\mid _ {x=x_{i}}+S_{i} =f_{i}, \quad i=0,1,\ldots , n, \end{aligned}$$
(9)

Matrix Form of the Method

Let \(Y=[y_{1},y_{2},\ldots ,y_{n-1}]^{T}\), \(S=[S_{1},S_{2},\ldots ,S_{n-1}]^{T}\), \(M=[M_{1},M_{2},\ldots ,M_{n-1}]^{T}\), \(E = (e_{i})\) and \(T= (\widetilde{t}_{i})\) for \(i=1,2,\ldots ,n-1\) are \((n-1)\) dimensional column vectors.

The Eqs. (4)–(6) in matrix form can be written as,

$$\begin{aligned} ZS=l^{2}BM \end{aligned}$$
(10)

where \(Z=(z_{ij})\), \(B=(b_{ij})\) are \((n-1)\times (n-1)\) matrices and

$$\begin{aligned} z_{ij}=\left\{ \begin{array}{ll} \frac{-7}{6}, &{}\quad i=j=1,n-1,\\ \frac{1}{3}, &{}\quad i=1,j=2,\\ \frac{1}{6}, &{}\quad i=1,j=3, \\ \frac{1}{3}, &{}\quad i=n-1,j=n-2,\\ \frac{1}{6}, &{}\quad i=n-1,j=n-3,\\ -2, &{}\quad i=j=2,3,\ldots ,n-2,\\ 1, &{}\quad |i-j|=1, i,j=2,3,\ldots ,n-2\\ 0, &{}\quad otherwise, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} b_{ij}=\left\{ \begin{array}{ll} \frac{4}{6}, &{}\quad i=j=1,2,\ldots ,n-1,\\ \frac{1}{6}, &{}\quad |i-j|=1,\\ 0, &{}\quad otherwise. \end{array} \right. \end{aligned}$$

The system (9) in matrix form have the following form,

$$\begin{aligned} WM+KS=F, \end{aligned}$$
(11)

where \(W=(w_{ij})\), \(K=(k_{ij})\) are \((n-1)\times (n-1)\) matrices,

$$\begin{aligned} w_{ij}= & {} \left\{ \begin{array}{ll} w_{2},\ \ \ j-i=1,\\ w_{1},\ \ \ i=j=1,2,\ldots ,n-1,\\ 0,\ \ \ \ otherwise, \end{array} \right. \\ k_{ij}= & {} \left\{ \begin{array}{ll} 1,\ \ \ \ \ \ \ \ \ \ \ \ i=j=1,2,\ldots ,n-2,\\ \frac{-w_{2}}{l^{2}}, \ \ \ \ \ \ \ \ i=n-1, j=n-3,\\ \frac{4w_{2}}{l^{2}},\ \ \ \ \ \ \ \ \ i=n-1, j=n-2,\\ \frac{-5w_{2}}{l^{2}}+1,\ \ i=n-1, j=n-1,\\ 0,\ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} w_{1}= & {} \frac{l^{2-\alpha }}{\Gamma (4-\alpha )},\\ w_{2}= & {} \frac{\Gamma (4-\alpha )l^{2-\alpha }-l^{2-\alpha }\Gamma (3-\alpha )}{\Gamma (3-\alpha )\Gamma (4-\alpha )}. \end{aligned}$$

Moreover, \(F = (f_{i})\) is \((n-1)\) dimensional column vector such that

$$\begin{aligned} F =\left\{ \begin{array}{ll} f_{i}, &{}\quad i=1,2,\ldots \,n-2,\\ f_{n-1}-\frac{2w_{2}}{l^{2}}S_{n} , &{}\quad i=n-1. \end{array} \right. \end{aligned}$$

The Eq. (11) can be written as

$$\begin{aligned} M= W^{-1}F-W^{-1} KS, \end{aligned}$$

From Eqs. (10) and (11), it can be written, as

$$\begin{aligned} (Z+l^{2}B W^{-1} K) S =l^{2}B W^{-1}F. \end{aligned}$$
(12)

In order to get a bound on \(\Vert E\Vert _{\infty }\), consider

$$\begin{aligned} (Z+l^{2}B W^{-1} K) Y =l^{2}B W^{-1}F +T. \end{aligned}$$
(13)

From Eqs. (12) and (13),

$$\begin{aligned} (Z+l^{2}B W^{-1} K)E=T. \end{aligned}$$
(14)

From Eq. (14), E can be expressed as

$$\begin{aligned} E=(I+l^{2}Z^{-1}B W^{-1} K)^{-1} Z^{-1} T. \end{aligned}$$
(15)

Order of Trucation Error

Lemma 1

Let \(y \in C^{6}[a,b]\) then the local trucation errors \(\widetilde{t}_{i}, \ i= 0, 1, \ldots , n-1\) associated with the Eqs. (4)–(6) are

$$\begin{aligned} \widetilde{t}_{i}=\left\{ \begin{array}{lll} \frac{5}{72}l^{4}y_{1}^{(4)}+O(l^{5}), &{}\quad i=1,\\ \\ \frac{-1}{12}l^{4}y_{i}^{(4)}+O(l^{6}), &{}\quad i= 2,3,\ldots ,n-2,\\ \\ \frac{5}{72}l^{4}y_{n-1}^{(4)}+O(l^{5}), &{}\quad i=n-1. \end{array} \right. \end{aligned}$$

Moreover,

$$\begin{aligned} ||T||_{\infty }=c_{1} l^{4} J_{4}, \quad J_{4}=max_{x \in [0, 1] }| y^{(4)}(x)|, \end{aligned}$$

where \(c_{1}\) is a constant and also independent of l.

Convergence Analysis

Lemma 2

 [21] If Z is a matrix of order n and \(\Vert Z\Vert <1\), then \((I+Z)^{-1}\) exists and

$$\begin{aligned} \Vert (I+Z)^{-1}\Vert < \frac{1}{ 1-\Vert Z\Vert }. \end{aligned}$$

Lemma 3

The infinite norm of \( W^{-1}\) satisfies the inequality

$$\begin{aligned} \Vert W^{-1}\Vert _{\infty }\le \frac{\Gamma (4-\alpha )}{2\Gamma (4-\alpha )- l^{2-\alpha }}, \end{aligned}$$
(16)

provided that \(\frac{ l^{2-\alpha }}{2\Gamma (4-\alpha )} < 1.\)

Proof

The matrix W can be written, as

$$\begin{aligned} W=I+ l^{2-\alpha } \widetilde{W}, \end{aligned}$$

where matrix \(\widetilde{W}=(\widetilde{w_{ij}}) \) is \((n-1)\times (n-1)\) and

$$\begin{aligned} \widetilde{w}_{ij}=\left\{ \begin{array}{ll} \frac{1}{\Gamma (3-\alpha )}-\frac{1}{\Gamma (4-\alpha )} ,&{}\quad j-i=1,\\ \frac{1}{\Gamma (4-\alpha )}-l^{\alpha -2},&{}\quad i=j=1,2,\ldots ,n-1,\\ 0,&{}\quad otherwise. \end{array} \right. \end{aligned}$$

The matrix \(W^{-1}\) can be written, as

$$\begin{aligned} W^{-1}=(I+l^{2-\alpha } \widetilde{W})^{-1}, \end{aligned}$$

Using the Lemma 2, if

$$\begin{aligned} \Vert l^{2-\alpha } \widetilde{W}\Vert _{\infty }<1, \end{aligned}$$

then

$$\begin{aligned} \Vert W^{-1}\Vert _{\infty } \le \frac{1}{1-\Vert l^{2-\alpha } \widetilde{W} \Vert _{\infty }}, \end{aligned}$$
(17)

where

$$\begin{aligned} \Vert l^{2-\alpha } \widetilde{W}\Vert _{\infty }= \frac{ l^{2-\alpha }-\Gamma (4-\alpha )}{\Gamma (4-\alpha )} \end{aligned}$$
(18)

From Eq. (17),

$$\begin{aligned} \Vert W^{-1}\Vert _{\infty }\le \frac{\Gamma (4-\alpha )}{2\Gamma (4-\alpha )- l^{2-\alpha }}. \end{aligned}$$

\(\square \)

Lemma 4

The matrix \((Z+l^{2}BW^{-1}K)\) in Eq. (14) is nonsingular, provided that:

$$\begin{aligned} \frac{\lambda _{2}}{2\lambda _{1}h^{-\alpha }c_{2}\Gamma (4-\alpha )}< 1, \end{aligned}$$

where \(\lambda _{1}=\frac{1}{8}((b-a)^{2}+l^{2})\), \(\lambda _{2}=2\Gamma (4-\alpha )-l^{2-\alpha }\) and \(c_{2}=\frac{h^{-\alpha }(\Gamma (4-\alpha )-\Gamma (3-\alpha ))}{\Gamma (3-\alpha )\Gamma (4-\alpha )}\). Then

$$\begin{aligned} \Vert E\Vert _{\infty } = O(l^{2}). \end{aligned}$$
(19)

Proof

From Lemma 2,

$$\begin{aligned} \Vert E\Vert _{\infty }=max_{1\le i \le n-1}|e_{i}| \le \frac{ \Vert Z^{-1}\Vert _{\infty }\Vert T\Vert _{\infty }}{1-l^{2}\Vert Z^{-1}\Vert _{\infty }\Vert B\Vert _{\infty }\Vert W^{-1}\Vert _{\infty }\Vert K\Vert _{\infty }}, \end{aligned}$$
(20)

provided that \(l^{2}\Vert Z^{-1}\Vert _{\infty }\Vert B\Vert _{\infty }\Vert W^{-1}\Vert _{\infty }\Vert K\Vert _{\infty }< 1.\)

As, \(\Vert Z^{-1}\Vert _{\infty } = \frac{l^{-2}}{8}((b-a)^{2}+l^{2})\). Also, \(\Vert B\Vert _{\infty }=1\) and \( \Vert K\Vert _{\infty }=\frac{2l^{-\alpha }(\Gamma (4-\alpha )-\Gamma (3-\alpha ))}{\Gamma (3-\alpha )\Gamma (4-\alpha )}.\) Substitute the values of \(\Vert Z^{-1}\Vert _{\infty }\), \(\Vert B\Vert _{\infty }\), \(\Vert W^{-1}\Vert _{\infty }\) and \(\Vert K\Vert _{\infty }\) in Eq. (20),

$$\begin{aligned} \Vert E\Vert _{\infty } \le \frac{c_{1}J_{4}l^{2}\lambda _{1}\lambda _{2}}{\lambda _{2}-2\lambda _{1}c_{2}\Gamma (4-\alpha ) }\cong O(l^{2}). \end{aligned}$$
(21)

\(\square \)

Theorem 1

Let y(x) be the exact solution of the fractional differential equation Eq. (1) with boundary condition Eq. (2) and \(y_{i}, i = 0, 1, 2,\ldots , n-1\), satisfy the discrete BVP Eq. (13). Moreover, if \(e_{i}= y_{i}-S_{i}\), then

$$\begin{aligned} \Vert E\Vert _{\infty } = O(l^{2}). \end{aligned}$$

Numerical Experiments

Two numerical examples are given to check the accuracy, efficiency and validity of the hyperbolic spline method. All calculations are implemented with MATLAB 7.

Example 4.1

Consider the following boundary value problem:

$$\begin{aligned} D^{\frac{199}{100}}y(x)+y(x)=f(x), \ \ \ \ \ \ \ \ x \in [0,1], \end{aligned}$$

with

$$\begin{aligned} y(0)= 0, \ \ y(1)=0, \end{aligned}$$

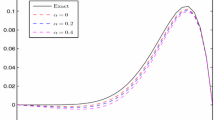
The exact solution of this problem is \(x^{5}-x^{4}.\) The results are shown in Table 1 and Fig. 1.

Table 1 Maximum absolute errors for \(\alpha =\frac{199}{100}\) with left fractional operator
Full size table
Fig. 1
figure 1

Exact and approximate solutions of Example 1

Full size image
Table 2 Absolute errors for \(\alpha =2\)
Full size table
Fig. 2
figure 2

Exact and approximate solutions of Example 2

Full size image

Example 4.2

Consider the boundary value problem for inhomogeneous linear fractional differential equation

$$\begin{aligned} D^{\alpha }y(x)+\frac{3}{57}y(x)=f(x), \quad x \in [0,1], \ 1 < \alpha \le 2, \end{aligned}$$

with

$$\begin{aligned} y(0)= 0, \ \ y(1)=\frac{1}{\Gamma (\alpha +2)}, \end{aligned}$$

The exact solution of this problem is \(\frac{x^{\alpha +1}}{\Gamma (\alpha +2)}.\) The results are shown in Table 2 and Fig. 2. Also, the results of same problem are compared with the numerical scheme in  [20], and found that results of suggested method are more accurate than  [20].

Conclusion

Collocation method is established for the approximate solution of fractional differential equation along with boundary conditions, using cubic spline. The suggested method also utilize the properties of fractional derivatives in order to solve this problem. This numerical scheme is computationally captivate. Descriptive examples show applications of this problem. It is proved that the method is of \(O(l^{2})\).