Fuzzy Portfolio with a Novel Power Membership Function Based on GARCH and Black–Litterman Model

Abstract

We construct a fuzzy mean-semi-absolute deviation portfolio with novel power membership functions. The portfolio return is measured by the Black–Litterman model, which combines the market’s objective information and investors’ subjective preference by the GARCH model. In addition, we use semi-absolute deviation to measure portfolio risk instead of variance, which not only reduces the computational complexity but also considers the corresponding risk lower than the expected return. Considering the investors’ psychological satisfaction with return and risk, we propose two novel power membership functions of return and risk, respectively. We fully demonstrate the shapes of membership functions with different preference parameters and medium satisfaction levels and deeply discuss monotonicity, convexity and concavity using the first- and second-order derivatives by strict mathematical proof. Furthermore, a fuzzy mean-semi-absolute deviation portfolio is proposed based on the satisfaction maximization principle and the absolute value optimization theory. Finally, we give a numerical example and present the results of neutral, pessimistic, and optimistic portfolios. In terms of Sharpe ratio and satisfaction degree, the portfolio model with our proposed novel membership functions is superior to those with S-type membership functions (Watada (2001) Dynamical aspects in fuzzy decision making. Physica, Heidelberg). Moreover, it is more effective than that with standard deviation or absolute deviation to measure risk.

1 Introduction

The portfolio problem is a hot issue in current scientific research. The mean–variance model proposed by Markowitz [1] used mean and variance to measure the return and risk of portfolio, respectively, which laid a foundation for modern portfolio theory. To solve the portfolio model, Markowitz [2] proposed the critical line algorithm, which used the quadratic programming method to solve this problem. Bitran [3] proposed an interval programming. Zadeh [4] first proposed the concept of fuzzy set, and then fuzzy portfolio decision-making had gradually become an important method of the portfolio. Bellman and Zadeh [5] put forward the maximization principle to solve the fuzzy portfolio model. Zimmermann [6] first proposed a fuzzy multi-objective linear programming model, which transformed the multi-objective programming problem into a single objective programming problem. Tanaka and Asai [7] proposed a fuzzy linear programming. Magoč et al. [8] showed how to express the optimal portfolio selection problem from a decision-theoretic perspective and showed how to address this problem using fuzzy measures and fuzzy integrals. Yaakob et al. [9] introduced a novel extension of the technique for ordering of preference by similarity to ideal solution (TOPSIS) method and used fuzzy networks to solve multicriteria decision-making problems where both benefit and cost criteria are presented as subsystems. Ferreira et al. [10] considered legal aspects and investor’s preferences as an input to the novel fuzzy multiple-attribute decision making approach for sorting problems, and used the sorting results for a fuzzy multi-objective optimization model that considers the risk and return associated with the investor’s profile over three objectives. Joshi et al. [11] developed a hesitant probabilistic fuzzy set based MCDM method to completely depict statistical and non-statistical uncertainty in a single framework. He and Zhou [12] established an optimized group decision-making portfolio strategy to better achieve the goal of increasing group decision-making investors’ returns or reducing risks. Mohammed [13] provided and applied the concept and techniques of multi-criteria decision-making under fuzzy environment in the prioritization and selection of projects in a portfolio management, and the preference weights of the criteria were identified using fuzzy AHP.

In view of the fact that the mean–variance model did not consider investors’ psychological satisfaction of return and risk, Bellman and Zadeh used fuzzy sets to define investors’ target levels of return and risk, where the membership function is used to express fuzziness. Leberling [14] defined a tangent-type membership function. Guua and Wu [15] and Tang and Zhao [16] employed a two-phase method to achieve the solutions of the multi-objective programming problem, which used linear membership functions to provide the satisfaction degree to the objectives. Watada [17] proposed nonlinear S-type membership functions, which represented the fuzzy target levels of return and risk. Khanesar et al. [18] proposed a novel type-2 fuzzy membership function, which is an ellipsoidal membership function. De et al. [19] transformed the fuzzy numbers which are the coefficient vectors of the concerned minimization cost function into interval numbers, and transformed the interval objective function into a classical multi-objective EOQ model using intuitionistic fuzzy technique. Liu and Zhang [20] proposed a fuzzy portfolio decision-making model based on the S-type membership function. Kocadağlı and Keskin [21] assumed the portfolio return, risk and beta coefficient as objectives including the possibilistic uncertainties, and constituted specific fuzzy membership functions to define the uncertainty. Rutkowska [22] studied the influence of membership function’s shape on the result of fuzzy portfolio optimization. Kayacan et al. [23] focused on the ellipsoidal membership function to compare and contrast various ways of modeling uncertainty. De [24] considered an EOQ model with fuzzy parameters, and incorporated the concept of possibility theory in the approximated fuzzy membership function. Deng and Chen [25] combined the prospect theory and possibility theory to provide investors with a portfolio strategy that meets investors’ preference for assets. De et al. [26] developed a new set named doubt fuzzy set the real and imaginary parts of which are the membership functions of fuzzy variables, and developed a backlogging economic production quantity (EPQ) model the demand function of which is disrupted due to the presence of shortages. De and Nandi [27] studied a polygonal fuzzy set by means of an interpolating polynomial function due to different membership grades are found by different researchers for a given problem.

When the number of assets in the portfolio is too large, the calculation of the covariance would be difficult. At the same time, investors usually only worried about the part of risk lower than the expected return, but the mean–variance model also took into account the part of risk higher than the expected return. Therefore, Markowitz [28] proposed the mean-semi-variance model, which only considered the part of risk lower than the expected return. Konno and Yamazaki [29] proposed an absolute deviation risk function, which greatly reduced the computational complexity of the portfolio model. To better capture investors’ risk attitudes, Deng et al. [30] extended the downside risk from stochastic environment to hesitant fuzzy environment and define a new hesitant semi-variance. Speranza [31] proposed a semi-absolute deviation risk function, which reduced the complexity of calculation and merely considered the part of risk lower than the expected return. Subsequently, Fang and Wang [32] extended the semi-absolute deviation to an interval case, and proposed an interval semi-absolution deviation model for portfolio selection. Gupta et al. [33] applied multi criteria decision making via fuzzy mathematical programming to develop comprehensive models of asset portfolio optimization by morphing mean–variance optimization portfolio model into semi-absolute deviation model. Zhang [34] presented a new credibilitic multiperiod mean-semi-absolute deviation portfolio selection. Meng and Shan [35] proposed a fuzzy mean semi-absolute deviation–semi-variance-proportional entropy portfolio selection model with transaction costs.

The mean–variance model took the average of historical return rate of assets as the expected return rate and assumed that investors hold identical views, which had certain limitations. Black and Litterman [36] put forward the Black–Litterman model to calculate the expected return rate and covariance matrix combining the market view and subjective view, which was spread in 1992. Later, Black and Litterman [37] and Black and Litterman [38] carried on further research and found that the level of confidence of opinions was not necessarily 100%. In addition, for the definition of the scale factor $\tau$ in the model, He and Litterman [39] set the parameter to a small number of 0.05. Idzorek [40] thought that the parameter could be set according to the number of samples, which is defined as the reciprocal of the number of samples. Some papers applied the Black–Litterman model to portfolio optimization models. For example, Subekti and Rosadi [41] built two portfolios using the Black–Litterman model and found the results of weight allocation are similar. Subekti and Rosadi [42] showed how the Black–Litterman approach to portfolio optimization works. Murtadina et al. [43] applied the Black–Litterman model to portfolio on the liquid index 45 (LQ45) with information ratio assessment. For the quantification of subjective view, Litterman and Winkelmann [44] used the GARCH model to forecast the expected return rate and its volatility to quantify subjective view and uncertainty, respectively. Palomba [45] provided an empirical model for large-scale tactical asset allocation with multivariate GARCH estimates. Arisena et al. [46] formed the weight of the Black–Litterman model portfolio with a single view investor using ARMA–GARCH. Kara et al. [47] used the GARCH model for predicting indicators for the stocks.

In view of the research on portfolio models, some scholars constructed fuzzy portfolio decision-making models with nonlinear membership function and employed semi-absolute deviation to measure the risk of the portfolio, but simply defined the average value of the historical return rate as the expected return rate of assets, others applied the Black–Litterman model to the portfolio model. However, very few studies combined the Black–Litterman model with the fuzzy decision-making method, where the Black–Litterman model is used to calculate the expected return rate with the GARCH model to measure investors’ subjective preference.

In Table 1, we compare this paper with 20 pieces of literature according to 7 criteria (the criterion of risk measurement, whether membership function is used, whether the Black–Litterman model is applied, whether the GARCH model is applied, whether the portfolio is considered in fuzzy environment, whether satisfaction approach is considered and whether it is a single-objective model). The characteristics of our proposed model are as follows:

• (a) Our model considers semi-absolute deviation as portfolio risk, which reduces the computational complexity and only considers the part of risk lower than the expected return.

• (b) Our model proposes two novel power membership functions of portfolio return and risk, and we can change the shape of membership functions by setting the preference parameters.

• (c) Our model applies the Black–Litterman model to the fuzzy portfolio model to calculate the expected return rate by combining the market’s objective information and investors’ subjective perspectives.

• (d) Our model applies the GARCH model to predict the expected return rate of each asset, the result of which is input into the Black–Litterman model as investors’ subjective perspectives.

• (e) Our model is considered in a fuzzy environment, and the proposed membership functions denote the fuzzy target levels of portfolio return and risk, respectively.

• (f) Our model considers a satisfaction approach solving the fuzzy portfolio. Compared to the optimization approach, the satisfaction approach aims to maximize the investors’ psychological satisfaction.

• (g) Our model transforms the multi-objective programming model into the single-objective programming model based on the maximization principle, making the portfolio solution more convenient and effective.

Table 1 Comparison between this paper and previous literatures

This paper aims to construct a fuzzy portfolio model with novel power membership functions based on the GARCH and the Black–Litterman models. The main contributions of this paper are as follows:

• (a) We propose two novel power membership functions to describe the investors’ psychological satisfaction with return and risk, respectively. On one hand, we fully demonstrate the shapes of membership functions with different preference parameters and medium satisfaction levels. Our proposed power membership functions can describe investors’ different preferences by changing the value of the preference parameters. On the other hand, we deeply discuss monotonicity, convexity and concavity using the first- and second-order derivatives by strict mathematical proof.

• (b) We construct a single-objective programming fuzzy portfolio model based on the satisfaction approach, which aims to maximize the investors’ psychological satisfaction.

• (c) We consider semi-absolute deviation as portfolio risk, and the Black–Litterman model as the way to calculate the expected return rate, whereas the GARCH model is used to measure investors’ subjective perspective.

• (d) We compare our proposed model with the other three comparison models (mean-semi-absolute deviation portfolio with S-type membership function, mean-standard deviation portfolio with our proposed membership function, mean-absolute deviation portfolio with our proposed membership function), and show that our proposed model is superior.

The rest of the paper is organized as follows. In Sect. 2, we introduce the theory related to the following sections. In Sect. 3, we propose two novel power membership functions, and construct a fuzzy portfolio model. In Sect. 4, we propose a numerical example and show the result in different cases. In Sect. 5, three comparison models are proposed and solved and the effectiveness of our proposed model is illustrated. Finally, Sect. 6 is the discussions and conclusions of this paper.

2 Preliminaries

This section mainly introduces the theory related to the following sections, including the basic concepts of fuzzy sets, the fuzzy multi-objective programming model, the mini–max solution, and the theory of the Black–Litterman model.

First, the definition of variables which are used in this paper are shown in Table 2.

Table 2 Definition of variables

2.1 The Theory of Fuzzy Sets

Definition 1:

If the membership function of fuzzy number $A$ is $\mu_{{\text{A}}} \left( x \right):U \to \left[ {0,1} \right]$, then $\mu_{{\text{A}}} \left( x \right)$ has the following properties:

• (1) $\mu_{{\text{A}}} \left( x \right)$ is normal, that is $\exists x_{0} \in U,\mu_{A} \left( {x_{0} } \right) = 1$;

• (2) The necessary and sufficient conditions for $\mu_{{\text{A}}} \left( x \right)$ to be convex are as follows: for $\forall x_{1} ,x_{2} \in U,\lambda \in \left[ {0,1} \right]$, there is $\mu_{A} \left[ {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right] \ge \min \left\{ {\mu_{A} \left( {x_{1} } \right),\mu_{A} \left( {x_{2} } \right)} \right\}$;

• (3) $\mu_{{\text{A}}} \left( x \right)$ is bounded upper semicontinuous function and $\left\{ {x \in U|\mu_{{\text{A}}} \left( x \right) \le \varepsilon } \right\}$ is a closed set;

• (4) $\mu_{{\text{A}}} \left( x \right)$ is a compact set.

Definition 2:

If $A$ is a fuzzy number, then the $\gamma$-level set $\left[ A \right]^{\gamma } = \left\{ {x \in U|\mu_{{\text{A}}} \left( x \right) \ge \gamma } \right\}$ of $A$ can be expressed as $\left[ A \right]^{\gamma } = \left[ {a_{1} \left( \gamma \right),a_{2} \left( \gamma \right)} \right]$, where

$$a_{1} \left( \gamma \right) = \min \left\{ {x \in U|\mu_{{\text{A}}} \left( x \right) \ge \gamma } \right\},a_{2} \left( \gamma \right) = \max \left\{ {x \in U|\mu_{{\text{A}}} \left( x \right) \ge \gamma } \right\}.$$

Definition 3:

If $A = \left( {a,b;\alpha ,\beta } \right)$ is a fuzzy number, where $L_{A} ,R_{A}$ are monotone non-increasing continuous functions on $\left[ {0,1} \right] \to \left[ {0,1} \right]$, and $L_{A} \left( 0 \right) = R_{A} \left( 0 \right) = 1,L_{A} \left( 1 \right) = R_{A} \left( 1 \right) = 0$. The membership function of $A$ is expressed as follows:

$$\mu_{A} \left( x \right) = \left\{ \begin{gathered} L_{A} \left( {\frac{a - x}{\alpha }} \right),a - \alpha \le x < a, \hfill \\ 1, \quad \quad \quad \quad \quad a \le x < b, \hfill \\ R_{A} \left( {\frac{x - b}{\beta }} \right),b \le x < b + \beta , \hfill \\ 0,\quad \quad \quad \quad \quad {\text{ other}}. \hfill \\ \end{gathered} \right.$$

(1)

When $A = \left( {a,b;\alpha ,\beta } \right)$ is a trapezoidal fuzzy number, $L_{A} ,R_{A}$ degenerate into linear functions, and the membership function of $A$ is expressed as follows:

$$\mu_{A} \left( x \right) = \left\{ \begin{gathered} 1 - \frac{a - x}{\alpha }, \, a - \alpha \le x < a, \hfill \\ 1, \quad \quad \quad \quad a \le x <; b, \hfill \\ 1 - \frac{x - b}{\beta }, \, b \le x < b + \beta , \hfill \\ 0, \quad \quad \quad \quad {\text{ other}}. \hfill \\ \end{gathered} \right.$$

(2)

When $A = \left( {a;\alpha ,\beta } \right)$ is a triangular fuzzy number, $L_{A} ,R_{A}$ degenerate into linear functions, and the membership function of $A$ is expressed as follows:

$$\mu_{A} \left( x \right) = \left\{ \begin{gathered} 1 - \frac{a - x}{\alpha },a - \alpha \le x < a, \hfill \\ 1 - \frac{x - b}{\beta },b \le x < b + \beta , \hfill \\ 0, \quad \quad \quad {\text{ other}}. \hfill \\ \end{gathered} \right.$$

(3)

When $A = \left[ {a,b} \right]$ is an interval number, $L_{A} ,R_{A}$ degenerate into linear functions and $\alpha = \beta = 0$;

When $A = a$ is a real number,$L_{A} ,R_{A}$ degenerate into linear functions and $a = b,\alpha = \beta = 0$.

2.2 The Theory of Fuzzy Decision and Maximization Decision

Bellman and Zadeh proposed fuzzy decision theory in 1970 to study the uncertainty in decision-making problems. In 1978, Zimmermann first proposed a fuzzy multi-objective linear programming method, which is as follows:

$$\left\{ \begin{gathered} \max Z\left( x \right) = \left[ {\sum\limits_{j = 1}^{n} {c_{1j} x_{j} } ,\sum\limits_{j = 1}^{n} {c_{2j} x_{j} } ,...,\sum\limits_{j = 1}^{n} {c_{nj} x_{j} } } \right] \hfill \\ \min W\left( x \right) = \left[ {\sum\limits_{j = 1}^{n} {d_{1j} x_{j} } ,\sum\limits_{j = 1}^{n} {d_{2j} x_{j} } ,...,\sum\limits_{j = 1}^{n} {d_{nj} x_{j} } } \right] \hfill \\ {\text{s}}{\text{.t}}{. }\sum\limits_{j = 1}^{n} {a_{ij} x_{j} } \le b_{i} ,i = 1,2,...,m, \hfill \\ \, x_{j} \ge 0,j = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(4)

The membership functions of fuzzy targets in the model are linear functions, which are

$$\mu_{k} \left( {z_{k} } \right) = \frac{{z_{k} \left( x \right) - z_{k}^{ - } }}{{z_{k}^{ + } - z_{k}^{ - } }},k = 1,2,...,q,$$

(5)

$$\mu_{s} \left( {w_{s} } \right) = \frac{{z_{s} \left( x \right) - z_{s}^{ - } }}{{z_{s}^{ + } - z_{s}^{ - } }},s = 1,2,...,r,$$

(6)

where $z_{k}^{ + } = \mathop {\max }\limits_{x \in X} z_{k} \left( x \right),z_{k}^{ - } = \mathop {\min }\limits_{x \in X} z_{k} \left( x \right),w_{s}^{ + } = \mathop {\max }\limits_{x \in X} w_{s} \left( x \right),w_{s}^{ - } = \mathop {\min }\limits_{x \in X} w_{s} \left( x \right)$.

Definition 4:

Suppose $G, \, C$ are fuzzy objectives in decision space $X$, then fuzzy decision $D = G \cap C$ is also a fuzzy set, and its membership function is

$$\mu_{D} \left( x \right) = \min \left\{ {\mu_{G} \left( x \right),\mu_{C} \left( x \right)} \right\},\forall x \in X.$$

(7)

From Formula (5), Formula (6) and Definition 4, the fuzzy multi-objective programming problem (4) can be transformed into the following problems:

$$\max \mu_{D} \left( x \right) = \mathop {\min }\limits_{\begin{subarray}{l} k \in \left( {1,2,...,q} \right) \\ s \in \left( {1,2,...,r} \right) \\ x \in X \end{subarray} } \left\{ {\mu_{k} \left( {z_{k} } \right),\mu_{s} \left( {w_{s} } \right)} \right\}.$$

(8)

Let $\lambda = \mu_{D} \left( x \right) = \mathop {\min }\nolimits_{\begin{subarray}{l} k \in \left( {1,2,...,q} \right) \\ s \in \left( {1,2,...,r} \right) \\ x \in X \end{subarray} } \left\{ {\mu_{k} \left( {z_{k} } \right),\mu_{s} \left( {w_{s} } \right)} \right\}$, then Model (8) can be transformed into the following Model (9), and the result of which is the minimax solution proposed by Bellman and Zadeh:

$$\left\{ \begin{gathered} \max \lambda \hfill \\ {\text{s}}{\text{.t}}{. }\lambda \le \frac{{z_{k} \left( x \right) - z_{k}^{ - } }}{{z_{k}^{ + } - z_{k}^{ - } }},k = 1,2,...,q, \hfill \\ \, \lambda \le \frac{{z_{s} \left( x \right) - z_{s}^{ - } }}{{z_{s}^{ + } - z_{s}^{ - } }},s = 1,2,...,r, \hfill \\ \, x \in X. \hfill \\ \end{gathered} \right. \, {.}$$

(9)

2.3 Black–Litterman Model

The Black–Litterman model can be used to calculate the expected return and covariance matrix combining market view and subjective view by Bayes formula.

On the market view, the prior distribution of expected return is

$$r\sim N\left( {\mu ,\Sigma } \right),$$

(10)

where $\mu$ is the expected return rate in equilibrium; $\Sigma$ is the covariance matrix of historical return rate. In the Black–Litterman model, $\mu$ can be expressed by probability and correspond to normal distribution, that is

$$\mu \sim N\left( {\pi ,\tau \Sigma } \right),$$

(11)

where $\pi$ is the estimate of $\mu$; $\tau \Sigma$ denotes the uncertainty, where $\tau = \frac{1}{T}$, $T$ represents the number of samples, then Formula (11) can be transformed into Formula (12):

$$\mu \sim N\left( {\pi ,\frac{\Sigma }{T}} \right).$$

(12)

To measure $\pi$, the Black–Litterman model assumes that the market is equilibrium, which means that the estimation error is zero, so $\tau = 0$ in this case. For any N assets, the return rate follows the following normal distribution:

$$r\sim N\left( {\pi ,\Sigma } \right).$$

(13)

$\pi$ can be calculated by the CAPM theory and the inverse optimization formula, expressed as follows:

$$\pi \equiv 2\lambda \Sigma w_{eq} ,$$

(14)

where $w_{eq}$ denotes the market weight of portfolio and $\lambda$ is the average risk aversion coefficient of the market, which can be derived from the following formula:

$$\lambda = \frac{{E\left( r \right) - r_{f} }}{{\sigma^{2} }},$$

(15)

where $E\left( r \right)$ denotes market expected return, $\sigma^{2} = w_{eq}^{T} \Sigma w_{eq}$ denotes the variance of market return, $w_{eq}^{T}$ represents the transpose of $w_{eq}^{{}}$ and $r_{f}$ denotes the risk-free rate.

On the subjective view, suppose that an expert generates $K$ independent views on $N$ assets, and expresses these views into a $K \times N$ ‘viewpoint selection matrix’ $P$. Then these views obey the normal distribution:

$$V = P\mu \sim N\left( {v,\Omega } \right),$$

(16)

where $v$ is the vector of expected returns of the views and $\Omega$ is the covariance matrix, denoting expert opinion and the uncertainty, respectively. This paper uses the GARCH (1,1) model to estimate $v$ and $\Omega$. The GARCH (1,1) model is expressed as follows:

$$\sigma_{t}^{2} = \omega + \alpha_{1} \varepsilon_{t - 1}^{2} + \beta_{1} \sigma_{t - 1}^{2} .$$

(17)

Function ‘garchfit’ of R software can be used to estimate the parameters $mu, \, omega, \, alphal, \, betal$ of the model, and then predict the return rate of the next period. The predicted value $r_{t + 1,i}$ and volatility $h_{t + 1,i}$ are expressed as the vector $v$ and uncertainty matrix $\Omega$, respectively, then $v$, $\Omega$ and $P$ are expressed as follows:

$$v^{T} = (r_{t + 1,1} ,r_{t + 1,2} ,...,r_{t + 1,k} ),$$

(18)

$$\Omega = diag\left( {h_{t + 1,1} ,h_{t + 1,2} ,...,h_{t + 1,k} } \right),$$

(19)

$$P = diag\left( {1,1,...,1} \right)_{k \times k} ,$$

(20)

where $v^{T}$ represents the transpose of $v$.

By Bayes formula, we can derive the posterior distribution of the expected return:

$$r\sim N\left( {\mu_{BL} ,\Sigma_{BL} } \right),$$

(21)

where $\mu_{BL}$ and $\Sigma_{BL}$ are expressed as follows:

$$\mu_{BL} = \pi + \tau \Sigma P^{T} \left( {\tau \Sigma P^{T} + \Omega } \right)^{ - 1} \left( {v - P\pi } \right),$$

(22)

$$\Sigma_{BL} = \left( {1 + \tau } \right)\Sigma - \tau^{2} \Sigma P^{T} \left( {\tau \Sigma P^{T} + \Omega } \right)^{ - 1} P\Sigma .$$

(23)

3 Fuzzy Portfolio with Novel Power Membership Function Based on GARCH and Black–Litterman Models

In this section, two novel power membership functions are proposed to describe investors’ psychological satisfaction for return and risk of the portfolio, respectively. At the same time, a fuzzy portfolio decision-making model based on the GARCH and the Black–Litterman models is established based on the maximization principle.

3.1 The Proposal of Two Novel Power Membership Functions

Since investors’ psychological satisfaction with return and risk of the portfolio is not necessarily linear, this section will propose two nonlinear power membership functions to describe the changes of investors’ satisfaction for return and risk, respectively.

3.1.1 Membership Function of Portfolio Return

Considering that investors’ psychological satisfaction with return of the portfolio is nonlinear and monotonically increasing, a novel membership function of return of the portfolio is proposed as follows:

$$\mu_{r} (x) = \frac{1}{{1 + \left( {\frac{r(x)}{{\overline{r}}}} \right)^{{ - k_{r} }} }},$$

(24)

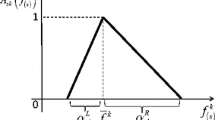
where $r\left( x \right)$ is the return of the portfolio; $k_{r} > 0$ is a parameter about the preference of return, which can be set by investors, and the value of the parameter can reflect the investors’ requirements for the return target. Let $k_{r} = 2,3,4,5,6$, then the image of membership functions is shown in Fig. 1; $\overline{r}$ represents the medium satisfaction level of return of the portfolio, and its membership function value is 0.5. For pessimistic investors, neutral investors and optimistic investors, let the value of $\overline{r}$ be the minimum value $r_{\min } = \min \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \}$, average value $\overline{r} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\overline{r}_{i} }$ and maximum value $r_{\max } = \max \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \}$ of the average historical return $\overline{r}_{i}$ of each alternative asset $i(i = 1,2,...,n)$, and the image of relevant membership functions is shown in Fig. 2.

Fig. 1

Membership functions with different values of $k_{r}$

Fig. 2

Membership functions with different medium satisfaction levels of return

Remark 1:

From Fig. 1, the shape of the membership function can be determined by the value of $k_{r}$. The greater the value of $k_{r}$, the less fuzzy the membership function is.

Remark 2:

According to Fig. 2, when $r_{\min } = \min \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \}$ is taken as the medium satisfaction level of return, a pessimistic investor can achieve a higher satisfaction level when his return is lower than the average historical return; when $r_{\max } = \max \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \}$ is taken, the risk optimistic investors need to obtain more than the maximum average historical return to achieve a greater satisfaction degree; when taking $\overline{r} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\overline{r}_{i} }$, $r_{\min }$ and $r_{\max }$ correspond to lower and higher satisfaction, respectively, which conforms to the psychology of neutral investors.

To further analyze the properties of the membership function, take $k_{r} = 3$ as an example, calculate the first-order derivative and the second-order derivative of $\mu_{r} \left( x \right)$, respectively:

$$\mu^{\prime}_{r} (x) = \frac{{3 \cdot \overline{r}^{3} }}{{\left( {r(x)} \right)^{4} \cdot \left( {1 + \left( {\frac{r(x)}{{\overline{r}}}} \right)^{ - 3} } \right)^{2} }},$$

(25)

$$\mu^{\prime\prime}_{r} (x) = \frac{{18 \cdot \overline{r}^{6} }}{{\left( {r(x)} \right)^{8} \cdot \left( {1 + \left( {\frac{r(x)}{{\overline{r}}}} \right)^{ - 3} } \right)^{3} }} - \frac{{12 \cdot \overline{r}^{3} }}{{\left( {r(x)} \right)^{5} \cdot \left( {1 + \left( {\frac{r(x)}{{\overline{r}}}} \right)^{ - 3} } \right)^{2} }}.$$

(26)

Without losing generality, take the same data as 4.3, assume that the investor is a neutral investor, that is $\overline{r} = 0.0003$, then the images of $\mu_{r}^{\prime } (x)$ and $\mu_{r}^{\prime \prime } (x)$ are shown in Figs. 3 and 4, respectively:

Fig. 3

First derivative of $\mu_{r} \left( x \right)$

Fig. 4

Second derivative of $\mu_{r} \left( x \right)$

Remark 3:

The following conclusions can be derived from Figs. 3 and 4:

• (a) Function $\mu_{r}^{\prime } \left( x \right) > 0 \, \left( {r\left( x \right) > 0} \right)$, that is, when $r\left( x \right) \in \left( {0, + \infty } \right)$, membership function $\mu_{r} \left( x \right)$ increases strictly monotonically, which shows that the investors’ satisfaction increases continuously when the return increases. In addition, when $\mu_{r} \left( x \right) = 1$, it means that investors are very satisfied; when $\mu_{r} \left( x \right) = 0$, it means that investors are very dissatisfied.

• (b) Function $\mu_{r}^{\prime } \left( x \right)$ gets the maximum value at $r\left( x \right) = 0.2381 \times 10^{ - 3}$, and increases strictly monotonically when $r\left( x \right) \in \left( {0,0.2381 \times 10^{ - 3} } \right]$, decreases strictly monotonically when $r\left( x \right) \in \left[ {0.2381 \times 10^{ - 3} , + \infty } \right)$. According to the necessary and sufficient condition of convex function, when $r\left( x \right) \in \left( {0,0.2381 \times 10^{ - 3} } \right]$, function $\mu_{r} \left( x \right)$ is convex. At this time, with the increase of the return, the investors’ satisfaction will increase faster. When $r\left( x \right) \in \left[ {0.2381 \times 10^{ - 3} , + \infty } \right)$, function $\mu_{r} \left( x \right)$ is concave, which shows that when the return exceeds certain level, the increase rate of satisfaction gradually decreases.

• (c) The zero of function $\mu^{\prime\prime}_{r} \left( x \right)$ is $r\left( x \right) = 0.2381 \times 10^{ - 3}$, and when $r\left( x \right) \in \left( {0,0.2381 \times 10^{ - 3} } \right]$, function $\mu^{\prime\prime}_{r} \left( x \right) \ge 0$; when $r\left( x \right) \in \left[ {0.2381 \times 10^{ - 3} , + \infty } \right)$, function $\mu_{r}^{\prime \prime } \left( x \right) \le 0$. According to the sufficient condition of inflection point, point $\left( {0.2381 \times 10^{ - 3} ,0.3333} \right)$ is the inflection point of function $\mu_{r} \left( x \right)$, and the convexity of the function $\mu_{r} \left( x \right)$ changes on both sides of the inflection point.

3.1.2 Membership Function of Portfolio Risk

Considering that investors’ psychological satisfaction with risk of the portfolio is nonlinear and monotonically decreasing, a novel membership function of risk of the portfolio is proposed as follows:

$$\mu_{\omega } (x) = \frac{1}{{1 + \left( {\frac{\omega (x)}{{\overline{\omega }}}} \right)^{{k_{\omega } }} }},$$

(27)

where $\omega \left( x \right)$ is the risk of portfolio; $k_{\omega } > 0$ is a parameter about the preference of risk, which can be set by investors, and the value of the parameter can reflect the investors’ requirements for risk target. Let $k_{\omega } = 2,3,4,5,6$, then the image of membership functions is shown in Fig. 5. $\overline{\omega }$ represents the investors’ medium satisfaction level of risk, and its membership function value is 0.5. For pessimistic investors, neutral investors and optimistic investors, let the value of $\overline{\omega }$ be the minimum value $\omega_{\min } = \min \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \}$, average value $\overline{\omega } = 1/n\sum\nolimits_{i = 1}^{n} {\omega_{i} }$ and maximum value $\omega_{\max } = \max \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \}$ of the semi-absolute deviation of historical return rate with the same weight of each alternative asset $i(i = 1,2,...,n)$, respectively, and the image of the relevant membership functions is shown in Fig. 6.

Fig. 5

Membership functions with different values of $k_{\omega }$

Fig. 6

Membership functions with different values of medium satisfaction levels of risk

Remark 4:

From Fig. 5, the shape of the membership function can be determined by the value of $k_{\omega }$. The greater the value of $k_{\omega }$, the less fuzzy the membership function is.

Remark 5:

From Fig. 6, when the medium satisfaction level of risk is $\omega_{\min } = \min \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \}$, the investors’ satisfaction is low for the risk higher than $\omega_{\min }$; when $\omega_{\max } = \max \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \}$ is taken, optimistic investors are more satisfied with the risk level lower than $\omega_{\max }$; when taking $\overline{\omega } = 1/n\sum\nolimits_{i = 1}^{n} {\omega_{i} }$, $\omega_{\min }$ and $\omega_{\max }$ correspond to higher and lower satisfaction, respectively, which is in line with the psychology of neutral investors.

To analyze the properties of the membership function better, take $k_{\omega } = 3$ as an example, calculate the first derivative and the second derivative of $\mu_{\omega } \left( x \right)$, respectively:

$$\mu_{\omega }^{\prime } \left( x \right) = - \frac{{3 \cdot \left( {\omega (x)} \right)^{2} }}{{\overline{\omega }^{3} \cdot \left( {1 + \left( {\frac{\omega (x)}{{\overline{\omega }}}} \right)^{3} } \right)^{2} }},$$

(28)

$$\mu_{\omega }^{\prime \prime } \left( x \right) = \frac{{18 \cdot \left( {\omega (x)} \right)^{4} }}{{\overline{\omega }^{6} \cdot \left( {1 + \left( {\frac{\omega (x)}{{\overline{\omega }}}} \right)^{3} } \right)^{3} }} - \frac{6 \cdot \omega (x)}{{\overline{\omega }^{3} \cdot \left( {1 + \left( {\frac{\omega (x)}{{\overline{\omega }}}} \right)^{3} } \right)^{2} }}.$$

(29)

Without losing generality, take the same data as 4.3, assume that the investor is a neutral investor, that is, $\overline{\omega } = 0.0063$, then the images of $\mu_{\omega }^{\prime } \left( x \right)$ and $\mu_{\omega }^{\prime \prime } \left( x \right)$ are shown in Figs. 7 and 8, respectively:

Fig. 7

First derivative of $\mu_{\omega } \left( x \right)$

Fig. 8

Second derivative of $\mu_{\omega } \left( x \right)$

Remark 6:

From Figs. 7 and 8, we can derive the following conclusions:

• (a) Function $\mu_{\omega }^{\prime } \left( x \right) < 0 \, \left( {\omega \left( x \right) > 0} \right)$, that is, when $\omega \left( x \right) \in \left( {0, + \infty } \right)$, membership function $\mu_{\omega } \left( x \right)$ decreases strictly monotonically, which shows that the investors’ satisfaction decreases continuously when the risk increases. In addition, when $\mu_{\omega } \left( x \right) = 1$, it means that investors are very satisfied, and when $\mu_{\omega } \left( x \right) = 0$, it means that investors are very dissatisfied.

• (b) Function $\mu_{\omega }^{\prime } \left( x \right)$ gets the minimum value at $\omega \left( x \right) = 0.005$, while decreasing strictly monotonically when $\omega \left( x \right) \in \left( {0,0.005} \right]$ and increasing strictly monotonically when $\omega \left( x \right) \in \left[ {0.005, + \infty } \right)$. According to the necessary and sufficient condition of convex function, when $\omega \left( x \right) \in \left( {0,0.005} \right]$, function $\mu_{\omega } \left( x \right)$ is concave. At this time, with the increase of the risk, the investors’ satisfaction will decrease gradually. When $\omega \left( x \right) \in \left[ {0.005, + \infty } \right)$, function $\mu_{\omega } \left( x \right)$ is convex, which shows that when the risk exceeds a certain level, the rate of decline in investor satisfaction gradually accelerates.

• (c) The zero of function $\mu_{\omega }^{\prime \prime } \left( x \right)$ is $\omega \left( x \right) = 0.005$, and when $\omega \left( x \right) \in \left( {0,0.005} \right]$, function $\mu_{\omega }^{\prime \prime } \left( x \right) \le 0$; when $\omega \left( x \right) \in \left[ {0.005, + \infty } \right)$, function $\mu_{\omega }^{\prime \prime } \left( x \right) \ge 0$. According to the sufficient condition of inflection point, point $\left( {0.005,{0}{\text{.6667}}} \right)$ is the inflection point of function $\mu_{\omega } \left( x \right)$, and the convexity of the function $\mu_{\omega } \left( x \right)$ changes on both sides of the inflection point.

3.2 Fuzzy Portfolio Model with Novel Power Membership Function

Suppose the portfolio of $n$ assets is $x = (x_{1} ,x_{2} ,...,x_{n} )$, where $x_{i}$ is the weight of asset $i$ and satisfies $\sum\nolimits_{i = 1}^{n} {x_{i} = 1}$; $r_{ti}$ is the historical return rate of asset $i$ in period $t$; $r_{i}$ is the expected return rate of asset $i$, which is calculated by Black–Litterman formula (22), that is

$$r_{i} = \mu^{i}_{BL} = \pi + \tau \Sigma P^{T} \left( {\tau \Sigma P^{T} + \Omega } \right)^{ - 1} \left( {v - P\pi } \right),$$

(30)

Then, the return of the portfolio can be expressed as follows:

$$r\left( x \right) = \sum\limits_{i = 1}^{n} {r_{i} x_{i} } \;,i = 1,2,...,n.$$

(31)

In this section, the semi-absolute deviation risk function proposed by Speranza is used to measure the risk of the portfolio, which is expressed as follows:

$$\begin{gathered} \omega \left( x \right) = \frac{1}{T} \cdot \sum\limits_{t = 1}^{T} {\left| {\min \left\{ {0,\sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right\}} \right|} \hfill \\ \, = \frac{1}{T} \cdot \sum\limits_{t = 1}^{T} {\frac{{\left( {\left| {\sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right| - \sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right)}}{2}} \; \hfill \\ \, = \frac{1}{2 \cdot T} \cdot \sum\limits_{t = 1}^{T} {\left( {\left| {\sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right| - \sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right)} \;,\;t = 1,2,...,T \hfill \\ \end{gathered}$$

(32)

3.2.1 Maximization Principle for Satisfaction

According to Definition 4, let $\theta = \min \left\{ {\mu_{r} \left( x \right),\mu_{\omega } \left( x \right)} \right\}$, then we can obtain the following fuzzy portfolio model:

$$\left\{ \begin{gathered} {\text{max}}\;\theta \hfill \\ {\text{s}}{\text{.t}}{. }\mu_{r} \ge \theta , \hfill \\ \, \mu_{\omega } \ge \theta , \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,\; \hfill \\ \, \; \, 0 \le x_{i} \le v_{i} , \hfill \\ \, 0 \le \theta \le 1, \hfill \\ \, i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(33)

where $v_{i}$ denotes the upper limit of investment of asset $i$. Substituting Formula (24) and Formula (27) into model (33), we obtain the following model:

$$\left\{ \begin{gathered} \max \;\theta \hfill \\ {\text{s}}{\text{.t}}{.}\;\; \, \left( {\frac{1}{{\overline{r}}}r\left( x \right)} \right)^{{k_{r} }} \ge \frac{\theta }{1 - \theta }, \hfill \\ \, \left( {\frac{1}{{\overline{\omega }}}\omega \left( x \right)} \right)^{{ - k_{\omega } }} \ge \frac{\theta }{1 - \theta }, \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1\;, \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, 0 \le \theta \le 1,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(34)

Let $\eta = \frac{\theta }{1 - \theta }\;\left( {\eta \ge 0} \right)\;$, then because $\eta$ is proportional to $\theta$, maximizing $\theta$ is also equivalent to maximizing $\eta$. Therefore, Model (34) can be transformed into the following model:

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\;\; \, \left( {\frac{1}{{\overline{r}}}r(x)} \right)^{{k_{r} }} \ge \eta , \hfill \\ \, \left( {\frac{1}{{\overline{\omega }}}\omega \left( x \right)} \right)^{{ - k_{\omega } }} \ge \eta , \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1\;, \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, \eta \ge 0,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(35)

Substituting Formulas (31) and (32) into Model (35), then we obtain the following model:

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\;\; \, \left( {\frac{1}{{\overline{r}}}\sum\limits_{i = 1}^{n} {r_{i} x_{i} } } \right)^{{k_{r} }} \ge \eta , \hfill \\ \, \left( {\frac{1}{{\overline{\omega } \cdot T}}\sum\limits_{t = 1}^{T} {\left| {\min \left\{ {0,\sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } } \right\}} \right|} } \right)^{{k_{\omega } }} \cdot \eta \le 1,\; \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,\; \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, \eta \ge 0,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(36)

3.2.2 Absolute Value Optimization Theory

To make the model more concise, according to the absolute value optimization theory, let

$$d_{t}^{ + } = \frac{{\left| {\sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } } \right| + \sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } }}{2},$$

(37)

$$d_{t}^{ - } = \frac{{\left| {\sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } } \right| - \sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } }}{2},$$

(38)

Then, Model (36) can be further transformed into model (39):

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\;\; \, \left( {\frac{1}{{\overline{r}}}\sum\limits_{i = 1}^{n} {r_{i} x_{i} } } \right)^{{k_{r} }} \ge \eta , \hfill \\ \, \left( {\frac{1}{{\overline{\omega } \cdot T}}\sum\limits_{t = 1}^{T} {\;d_{t}^{ - } } } \right)^{{k_{\omega } }} \cdot \eta \le 1,\; \hfill \\ \, d_{t}^{ + } - d_{t}^{ - } = \sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } , \hfill \\ \, d_{t}^{ + } \cdot d_{t}^{ - } = 0,d_{t}^{ + } \ge 0,d_{t}^{ - } \ge 0, \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,\; \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, \eta \ge 0, \hfill \\ \, i = 1,2,...,n, \hfill \\ \, t = 1,2,...,T. \hfill \\ \end{gathered} \right.$$

(39)

4 A Numerical Example

In this section, we conduct a numerical example, applying our proposed fuzzy mean-semi-absolute deviation portfolio with novel power membership functions [Model (39)].

4.1 Practical Data

This section selects ten industry indexes of CSI 300 index from January 6th, 2020 to February 18th, 2022 for numerical example, with a total of $513 \, \times \, 10$ data. The data source is https://uqer.datayes.com/. To simplify the description, 10 assets are abbreviated as asset $i\left( {i = 1,2,...,10} \right)$ in this example. The codes of the 10 assets are shown in Table 3.

Table 3 Codes of 10 assets

4.2 Application of Black–Litterman Model

On the market view, first, we calculate the logarithmic return rate of price of the assets by the following formula:

$$R_{i,t} = \ln P_{i,t} - \ln P_{i,t - 1} ,$$

(40)

where $P_{i,t}$ denotes the price of asset $i$ in period $t$. The return rate of the risk-free asset in this section uses the Shanghai Interbank Offered Rate ($R_{Shibor,t - 1}$) with a lag of one overnight(O/N), which is the annual return rate calculated by the simple interest during 360 days. Therefore, the excess return rate can be expressed as

$$r_{i,t} = R_{i,t} - \frac{{R_{Shibor,t - 1} }}{360}.$$

(41)

According to Formula (14), we can obtain the return rate on market view. In this numerical example, the average return of CSI 300 index is $E\left( r \right) = 0.0004$; the standard deviation of CSI 300 index is $\sigma = 0.0168$; the return rate of the risk-free asset is $r_{f} = 1.6278 \times 10^{ - 5}$; the market weight vector is $w_{eq}^{T} = \left( {1.32\% ,7.7\% ,19.86\% ,7.92\% ,14.17\% ,8.73\% ,24.61\% ,11.14\% ,2.11\% ,2.44\% } \right)$; the covariance matrix of excess return rate of the 10 assets $\Sigma$ is shown as follows:

$$\Sigma = \left[ {\begin{array}{*{20}c} {2.9164} \\ {1.7337} \\ {0.9552} \\ {0.6831} \\ {0.3254} \\ {0.1732} \\ {1.1968} \\ {0.7105} \\ {0.8807} \\ {0.9806} \\ \end{array} \, \begin{array}{*{20}c} {1.7337} \\ {3.4367} \\ {2.1998} \\ {1.8901} \\ {1.5110} \\ {1.4675} \\ {1.4171} \\ {1.9168} \\ {1.5892} \\ {0.6366} \\ \end{array} \, \begin{array}{*{20}c} {0.9552} \\ {2.1998} \\ {2.3302} \\ {1.9067} \\ {1.5888} \\ {1.5903} \\ {1.2178} \\ {1.9726} \\ {1.5798} \\ {0.5729} \\ \end{array} \, \begin{array}{*{20}c} {0.6831} \\ {1.8901} \\ {1.9067} \\ {2.8085} \\ {2.1919} \\ {1.9999} \\ {1.4117} \\ {2.2357} \\ {1.7723} \\ {0.4650} \\ \end{array} \, \begin{array}{*{20}c} {0.3254} \\ {1.5110} \\ {1.5888} \\ {2.1919} \\ {3.6333} \\ {2.5061} \\ {1.3226} \\ {1.9005} \\ {1.5113} \\ {0.4890} \\ \end{array} \, \begin{array}{*{20}c} {0.1732} \\ {1.4675} \\ {1.5903} \\ {1.9999} \\ {2.5061} \\ {3.5411} \\ {0.9156} \\ {1.9730} \\ {1.3782} \\ {0.3607} \\ \end{array} \, \begin{array}{*{20}c} {1.1968} \\ {1.4171} \\ {1.2178} \\ {1.4117} \\ {1.3226} \\ {0.9156} \\ {2.0371} \\ {1.3272} \\ {1.3060} \\ {0.7322} \\ \end{array} \, \begin{array}{*{20}c} {0.7105} \\ {1.9168} \\ {1.9726} \\ {2.2357} \\ {1.9005} \\ {1.9730} \\ {1.3272} \\ {3.5702} \\ {2.7486} \\ {0.5125} \\ \end{array} \, \begin{array}{*{20}c} {0.8807} \\ {1.5892} \\ {1.5798} \\ {1.7723} \\ {1.5113} \\ {1.3782} \\ {1.3060} \\ {2.7486} \\ {3.3260} \\ {0.5835} \\ \end{array} \, \begin{array}{*{20}c} {0.9806} \\ {0.6366} \\ {0.5729} \\ {0.4650} \\ {0.4890} \\ {0.3607} \\ {0.7322} \\ {0.5125} \\ {0.5835} \\ {1.4902} \\ \end{array} } \right]_{10 \times 10} \times 10^{ - 4}$$

Then, we get the vector of the return rate on market view:

$$\pi = \left( {0.0215\% ,0.0439\% ,0.0415\% ,0.0453\% ,0.0462\% ,0.0417\% ,0.0346\% ,0.0471\% ,0.0393\% ,0.0144\% } \right)^{T} .$$

On subjective view, the traditional Black–Litterman model uses the expert viewpoint in the form of terminology to quantify the subjective view, which is subjective to a certain extent. In this section, the method of time series is used to predict the return rate and volatility in the next period, which measures the subjective views and uncertainties of experts, respectively.

Taking Asset 1 (Code: 000908) as an example, using R software for prediction and analysis. First, the time series diagram of the excess return rate is shown in Fig. 9.

Fig. 9

Time series diagram of the excess return rate

Remark 7:

From Fig. 9, we can find that the series of excess return rate is relatively stable.

Furthermore, the augmented Dickey–Fuller test is carried out, and the result shows that the ADF statistic is $- 8.1771$, and the P value is $0.01 < 0.05$, rejecting the original assumption that there is a unit root, so no further difference is required. The ACF and PACF images of the sample are shown in Figs. 10 and 11, respectively.

Fig. 10

ACF of series of excess return rate

Fig. 11

PACF of series of excess return rate

Remark 8:

As can be seen from Figs. 10 and 11, the sample basically has no sequence correlation, so it meets the mean equation in the GARCH model, that is, the return rate $r_{t}$ is composed of a constant term $c$ and a random disturbance term $\varepsilon_{t}$.

It can be seen from the time series diagram (Fig. 9) that the sample may exist Auto Regressive Conditional Heteroscedasticity (ARCH) effect. If there exists ARCH effect, the GARCH model can be used to forecast. Therefore, the ARCH–LM test in package FinTS is used for the ARCH test. The result of the LM test shows that the Chi-square statistic is 55.799, and the P value is almost zero, that is, the original hypothesis is rejected at the significance level of 1%, which indicates that the sample has the ARCH effect, so the GARCH model can be used. Employ function garchFit in package fGarch to fit the GARCH model. Since GARCH (1,1) is the most suitable model for financial time series modeling, the GARCH (1,1) model is used for estimation first. The estimated result is shown in Table 4.

Table 4 Estimated result of ${\text{GARCH}}\left( {1,1} \right)$ model

Table 4 shows that all coefficients are different from zero at the significant level of 0.05, indicating that the past volatility of the return rate has a significant impact on the current volatility, with a volatility aggregation effect.

To determine the optimal order of the model, overfitting operation is carried out, and the models GARCH (1,2), GARCH (2,1) and GARCH (2,2) are fitted, respectively. The values of information criteria of each model are shown in Table 5.

Table 5 Values of information criteria of each model

It can be seen from Table 5 that the information criterion does not increase significantly with the increase of the order, so GARCH (1,1) is selected for modeling and prediction, and the prediction results are shown in Table 6.

Table 6 Prediction results based on ${\text{GARCH}}\left( {1,1} \right)$ model

Forecast the remaining nine assets, respectively, to obtain the prediction results and standard deviations for the next period, as shown in Table 7, which are used to measure subjective views and uncertainties, respectively.

Table 7 Prediction results and standard deviation for the next period

These views and uncertainties can be expressed in vector and matrix form, then the view vector is $v = (r_{t + 1,1} ,r_{t + 1,2} ,...,r_{t + 1,10} )^{T}$ and the uncertainty matrix is $\Omega = diag\left( {h_{t + 1,1} ,h_{t + 1,2} ,...,h_{t + 1,10} } \right)$. Since absolute opinions have been expressed for 10 assets, the opinion selection matrix is $P = diag\left( {1,1,...,1} \right)_{10 \times 10}$.

Finally, according to Formula (22), Formula (23) and the above data, we can obtain the expected return rate $\mu_{BL}$ and covariance matrix ${\Sigma }_{{{\text{BL}}}}$ combining the market view and subjective view as follows (Table 8).

$${\Sigma }_{{{\text{BL}}}} { = }\left[ {\begin{array}{*{20}c} {2.9221} \\ {1.7370} \\ {0.9570} \\ {0.6844} \\ {0.3260} \\ {0.1735} \\ {1.1991} \\ {0.7119} \\ {0.8824} \\ {0.9825} \\ \end{array} \, \begin{array}{*{20}c} {1.7370} \\ {3.4434} \\ {2.2040} \\ {1.8937} \\ {1.5139} \\ {1.4703} \\ {1.4198} \\ {1.9205} \\ {1.5922} \\ {0.6378} \\ \end{array} \, \begin{array}{*{20}c} {0.9570} \\ {2.2040} \\ {2.3347} \\ {1.9103} \\ {1.5918} \\ {1.5934} \\ {1.2201} \\ {1.9764} \\ {1.5829} \\ {0.5740} \\ \end{array} \, \begin{array}{*{20}c} {0.6844} \\ {1.8937} \\ {1.9103} \\ {2.8139} \\ {2.1961} \\ {2.0038} \\ {1.4144} \\ {2.2400} \\ {1.7757} \\ {0.4659} \\ \end{array} \, \begin{array}{*{20}c} {0.3260} \\ {1.5139} \\ {1.5918} \\ {2.1961} \\ {3.6403} \\ {2.5109} \\ {1.3251} \\ {1.9042} \\ {1.5142} \\ {0.4900} \\ \end{array} \, \begin{array}{*{20}c} {0.1735} \\ {1.4703} \\ {1.5934} \\ {2.0038} \\ {2.5109} \\ {3.5479} \\ {0.9174} \\ {1.9767} \\ {1.3809} \\ {0.3613} \\ \end{array} \, \begin{array}{*{20}c} {1.1991} \\ {1.4198} \\ {1.2201} \\ {1.4144} \\ {1.3251} \\ {0.9174} \\ {2.0410} \\ {1.3298} \\ {1.3085} \\ {0.7336} \\ \end{array} \, \begin{array}{*{20}c} {0.7119} \\ {1.9205} \\ {1.9764} \\ {2.2400} \\ {1.9042} \\ {1.9767} \\ {1.3298} \\ {3.5771} \\ {2.7538} \\ {0.5134} \\ \end{array} \, \begin{array}{*{20}c} {0.8824} \\ {1.5922} \\ {1.5829} \\ {1.7757} \\ {1.5142} \\ {1.3809} \\ {1.3085} \\ {2.7538} \\ {3.3324} \\ {0.5846} \\ \end{array} \, \begin{array}{*{20}c} {0.9825} \\ {0.6378} \\ {0.5740} \\ {0.4659} \\ {0.4900} \\ {0.3613} \\ {0.7336} \\ {0.5134} \\ {0.5846} \\ {1.4931} \\ \end{array} } \right]_{10 \times 10} \times 10^{ - 4}$$

Table 8 Expected return rate

So far, we have obtained the input data of the fuzzy portfolio Model (39).

4.3 Application of Fuzzy Portfolio Model

In this section, we input the above $\mu_{BL}$ into Model (39), and use the LINGO software to solve the fuzzy portfolio model. First, assume the upper limits of investment are $v_{i} = 0.3, \, 0.4, \, 0.5, \, 0.6$_, respectively, and three sets of values of $k_{r} ,k_{\omega }$ are set to describe the preferences of different investors, assuming that:$\left( {k_{r} ,k_{\omega } } \right) = \left( {3,3} \right), \, \left( {k_{r} ,k_{\omega } } \right) = \left( {2,4} \right), \, \left( {k_{r} ,k_{\omega } } \right) = \left( {4,2} \right).$ Next, for neutral, pessimistic and optimistic investors, provide different medium satisfaction levels of return $\overline{r}$ and medium satisfaction levels of risk $\overline{\omega }$, respectively.

• Case 1: For neutral investors, we assume that $\overline{r} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\overline{r}_{i} } = 0.0003$ and $\overline{\omega } = \frac{1}{n}\sum\limits_{i = 1}^{n} {\omega_{i} } = 0.0063$.

• Case 2: For pessimistic investors, we assume that $\overline{r} = \min \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \} = 0.0002$ and $\overline{\omega } = \min \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \} = 0.0044$, since they usually prefer lower risk under certain return.

• Case 3: For optimistic investors, we assume that $\overline{r} = \max \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \} = 0.0009$ and $\overline{\omega } = \max \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \} = 0.0073$, since they usually prefer higher return under certain risk.

Then, the optimal weight $x_{i}$ of the portfolio for 10 assets is shown in Table 9, and the corresponding return, risk, satisfaction and Sharpe ratio of the portfolio are shown in Table 10.

Table 9 Optimal weight of the portfolio under Model (39)

Table 10 Return, risk, satisfaction and Sharpe ratio of the portfolio under Model (39)

From Table 10, we can derive the following similarities between investors with different preferences:

• (a) When $\left( {k_{r} ,k_{\omega } } \right) = \left( {3,3} \right)$, under the same upper limit of investment, the return and risk of the portfolio are at a medium level, and the investors’ satisfaction degree and the Sharpe ratio of the portfolio are higher than the other two cases, which indicates that the portfolio model is better;

• (b) When $\left( {k_{r} ,k_{\omega } } \right) = \left( {2,4} \right)$, the return of the portfolio is higher than the return when $\left( {k_{r} ,k_{\omega } } \right) = \left( {3,3} \right)$, but in turn the risk of the portfolio is higher with the same upper limit of investment. In addition, the investors’ satisfaction degree and the Sharpe ratio of the portfolio are lower than the case when $\left( {k_{r} ,k_{\omega } } \right) = \left( {3,3} \right)$;

• (c) When $\left( {k_{r} ,k_{\omega } } \right) = \left( {4,2} \right)$, the risk of the portfolio is lower than the other two cases, which means that the return in this case is also lower than the others. What’s more, the investors’ satisfaction degree and the Sharpe ratio of the portfolio only have little difference with the case when $\left( {k_{r} ,k_{\omega } } \right) = \left( {2,4} \right)$

We can derive the following differences between investors with different preferences:

• (a) For neutral investors, the return and risk of the portfolio are both at a medium level;

• (b) For pessimistic investors, who are more inclined to obtain less risk under a certain return, the corresponding return and risk of the portfolio are lower;

• (c) For optimistic investors, who tend to get relatively more return under certain risk, the return and risk of the portfolio are higher.

In summary, investors with different preferences can choose different medium satisfaction levels and values of parameter $k_{r} , \, k_{\omega }$ according to their needs, so as to meet their needs to the greatest extent and make reasonable portfolio decisions.

5 Comparative Analysis

In this section, we provide three comparison models to verify the superiority of Model (39).

5.1 Fuzzy Portfolio with S-Type Membership Function

Employ the S-type membership function proposed by Watada, then the membership functions of the objective level of return and risk are

$$\mu_{r} \left( x \right) = \frac{1}{{1 + e^{{ - \alpha_{r} \left( {r(x) - \overline{r}} \right)}} }},$$

(42)

$$\mu_{\omega } \left( x \right) = \frac{1}{{1 + e^{{\alpha_{\omega } \left( {\omega (x) - \overline{\omega }} \right)}} }},$$

(43)

where $r(x)$ is the return of the portfolio; $\omega (x)$ is the risk of the portfolio; $\overline{r}, \, \overline{\omega }$ are the medium satisfaction level of return and risk of portfolio, respectively; $\alpha_{r} , \, \alpha_{\omega }$ are the parameters to reflect investors’ satisfaction with objectives of return and risk, and the larger the value of $\alpha_{r} , \, \alpha_{\omega }$, the less fuzzy the membership functions are.

Combined with Model (33), the following model is obtained after corresponding simplification:

$$\left\{ \begin{gathered} {\text{max}}\;\theta \hfill \\ {\text{s}}{\text{.t}}{.}\;\; \, \alpha_{r} \left( {r(x) - \overline{r}} \right) \ge \ln \frac{\theta }{{\left( {1 - \theta } \right)}}, \hfill \\ \, - \alpha_{\omega } \left( {\omega (x) - \overline{\omega }} \right) \ge \ln \frac{\theta }{{\left( {1 - \theta } \right)}}, \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1\;, \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, 0 \le \theta \le 1,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(44)

Let $\eta = \ln \frac{\theta }{{\left( {1 - \theta } \right)}}\;$ and substitute the return function $r(x)$ [Formula (31)] and risk function $\omega \left( x \right)$ [Formula (32)] with Model (44). Combined with the absolute value optimization theory, Model (44) can be further transformed into Model (45).

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\; \, \alpha_{r} \left( {\sum\limits_{i = 1}^{n} {r_{i} x_{i} } - \overline{r}} \right) \ge \eta , \hfill \\ \, - \alpha_{\omega } \left( {\frac{1}{T}\sum\limits_{t = 1}^{T} {\;d_{t}^{ - } } - \overline{\omega }} \right) \cdot \eta \le 1,\; \hfill \\ \, d_{t}^{ + } - d_{t}^{ - } = \sum\limits_{i = 1}^{n} {(r_{ti} - r_{i} )x_{i} } , \hfill \\ \, d_{t}^{ + } \cdot d_{t}^{ - } = 0, \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,\; \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, d_{t}^{ + } \ge 0\;,\;d_{t}^{ - } \ge 0, \hfill \\ \, i = 1,2,...,n, \hfill \\ \, t = 1,2,...T. \hfill \\ \end{gathered} \right.$$

(45)

Refer to Liu (2015), assume the value of $\alpha_{r} , \, \alpha_{\omega }$ taking the following three cases, respectively: $\left( {\alpha_{r} ,\alpha_{\omega } } \right) = \left( {50,50} \right){, }\left( {\alpha_{r} ,\alpha_{\omega } } \right) = \left( {20,80} \right){, }\left( {\alpha_{r} ,\alpha_{\omega } } \right) = \left( {80,20} \right)$. In addition, the medium satisfaction levels of different investors can be classified as follows:

• Case 1: For neutral investors, we assume that $\overline{r} = 1/n\mathop \sum \nolimits_{i = 1}^{n} \overline{r}_{i} = 0.0003$ and $\overline{\omega } = 1/n\mathop \sum \nolimits_{i = 1}^{n} \omega_{i} = 0.0063$;

• Case 2: For pessimistic investors, we assume that $\overline{r} = \min \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \} = 0.0002$ and $\overline{\omega } = \min \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \} = 0.0044$;

• Case 3: For optimistic investors, we assume that $\overline{r} = \max \{ \overline{r}_{1} ,\overline{r}_{2} ,...,\overline{r}_{n} \} = 0.0009$ and $\overline{\omega } = \max \{ \omega_{1} ,\omega_{2} ,...,\omega_{n} \} = 0.0073$.

Then, the optimal weight $x_{i}$ of the portfolio for 10 assets under Model (45) is shown in Table 11, and the corresponding return, risk, satisfaction and Sharpe ratio of the portfolio are shown in Table 12.

Table 11 Optimal weight of the portfolio under Model (45)

Table 12 Return, risk, satisfaction and Sharpe ratio of the portfolio under Model (45)

5.2 Fuzzy Portfolio with Standard Deviation Risk Function

Employ standard deviation to measure the risk of portfolio, where the risk function is

$$\omega \left( x \right) = \sqrt {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} x_{i} x_{j} } } } .$$

(46)

Then, model (35) can be transformed into Model (47):

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\;\;\;\left( {\frac{1}{{\overline{r}}}\sum\limits_{i = 1}^{n} {r_{i} x_{i} } } \right)^{{k_{r} }} \ge \eta , \hfill \\ \, \left( {\frac{1}{{\overline{\omega }}}\sqrt {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sigma_{ij} x_{i} x_{j} } } } } \right)^{{k_{\omega } }} \cdot \eta \le 1,\; \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,\; \hfill \\ \, 0 \le x_{i} \le v_{i} , \hfill \\ \, \eta \ge 0,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(47)

Take the same input data as in 4.3, then for neutral, pessimistic and optimistic investors, the optimal weight $x_{i}$ of the portfolio for 10 assets under Model (47) is shown in Table 13, and the corresponding return, risk, satisfaction and Sharpe ratio of the portfolio are shown in Table 14.

Table 13 Optimal weight of the portfolio under Model (47)

Table 14 Return, risk, satisfaction and Sharpe ratio of the portfolio under Model (47)

5.3 Fuzzy Portfolio with Absolute Deviation Risk Function

Employ absolute deviation to measure the risk of portfolio, where the risk function is

$$\omega \left( x \right) = \frac{1}{T}\sum\limits_{t = 1}^{T} {\left| {\sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right|} ,t = 1,2,...,T.$$

(48)

Then, Model (35) can be transformed into Model (49):

$$\left\{ \begin{gathered} \max \;\eta \hfill \\ {\text{s}}{\text{.t}}{.}\;\;\;\left( {\frac{1}{{\overline{r}}}\sum\limits_{i = 1}^{n} {r_{i} x_{i} } } \right)^{{k_{r} }} \ge \eta , \hfill \\ \, \left( {\frac{1}{{\overline{\omega }}}\frac{1}{T}\sum\limits_{t = 1}^{T} {\left| {\sum\limits_{i = 1}^{n} {\left( {r_{ti} - r_{i} } \right)x_{i} } } \right|} } \right)^{{k_{\omega } }} \cdot \eta \le 1,\; \hfill \\ \, \sum\limits_{i = 1}^{n} {x_{i} } = 1,0 \le x_{i} \le v_{i} , \hfill \\ \, \eta \ge 0,i = 1,2,...,n. \hfill \\ \end{gathered} \right.$$

(49)

Take the same input data as in 4.3, then for neutral, pessimistic and optimistic investors, the optimal weight $x_{i}$ of the portfolio for 10 assets is shown in Table 15, and the corresponding return, risk, satisfaction and Sharpe ratio of the portfolio are shown in Table 16.

Table 15 Optimal weight of the portfolio under Model (49)

Table 16 Return, risk, satisfaction and Sharpe ratio of the portfolio under Model (49)

5.4 Comparison Results

For Model (39) and the comparison Model (44), Model (47) and Model (49), the investors with different investment preferences are classified according to the upper limit of investment and the value of preference parameters $k_{r} , \, k_{\omega }$, then the Sharpe ratio and satisfaction are compared, which are shown in Figs. 12, 13 and 14, respectively.

Fig. 12

Sharpe ratio and satisfaction degree of neutral portfolio for different parameter values

Fig. 13

Sharpe ratio and satisfaction degree of pessimistic portfolio for different parameter values

Fig. 14

Sharpe ratio and satisfaction degree of optimistic portfolio for different parameter values

Remark 9:

From Figs. 12, 13, and 14, we can find that the Sharpe ratio of Model (39) is higher than the three comparison models, whether the preference of the investors is neutral, pessimistic or optimistic. Compared with Model (44), the Sharpe ratio of the portfolio with different upper limits of investment in Model (39) is closer and more stable. In addition, it can be clearly found that a fuzzy portfolio with semi-absolute deviation risk function is better than with standard deviation risk function or absolute deviation risk function. In neutral and pessimistic cases, the satisfaction degree of the portfolio in Model (39) is relatively high, while in optimistic cases, since the risk of the portfolio is high, the satisfaction degree becomes lower. In conclusion, our proposed Model (39) performs better than the comparison models.

6 Conclusion

6.1 Merits of This Study

This paper proposes two novel power membership functions, which consider the investors’ psychological satisfaction of portfolio return and risk. In addition, Black–Litterman model is used to calculate the expected return rate combining the market’s objective information and investors’ subjective preference where the GARCH model is used to predict the investors’ subjective preference, making the result more reasonable. In terms of the methods of measuring risk, this paper employs the semi-absolute deviation risk function. A numerical example is given based on our proposed model, and we compare our model with three models to demonstrate the superiority.

More specifically, the merits of this study are as follows:

• (a) In view of the fact that the traditional mean–variance model did not consider investors’ psychological satisfaction of return and risk, this paper proposes a fuzzy portfolio model, which can better reflect the subjective preference and attitude of investors in financial market.

• (b) In generally, previous studies have mostly used linear membership functions, which cannot effectively reflect the subjective preferences of investors in financial market. Therefore, this paper explores novel nonlinear membership functions to more comprehensively characterize the nonlinearity of actual financial markets.

• (c) The traditional mean–variance model took the average of historical return rate of assets as the expected return rate. In this paper, Black–Litterman model is used to calculate the expected return rate combining the market’s objective information and investors’ subjective preference where the GARCH model is used to predict the investors’ subjective preference.

• (d) In addition, the mean–variance model also took into account the part of risk higher than the expected return. This paper employs the semi-absolute deviation risk function, and illustrates that the portfolio model with it is better than with standard deviation risk function or absolute deviation risk function.

• (e) A numerical example based on our proposed model shows the optimal weight and the corresponding return, risk, satisfaction and Sharpe ratio of the portfolio with different preferences, upper limits of investment and values of parameters $k_{r} , \, k_{\omega }$.

• (f) By comparing the Sharpe ratio and the satisfaction degree, our proposed model is superior to the three comparison models (mean-semi-absolute deviation portfolio with S-type membership function, mean-standard deviation portfolio with our proposed membership function, mean-absolute deviation portfolio with our proposed membership function).

6.2 Limitations and Possible Future Works

Pointing at the proposed fuzzy portfolio model with novel power membership function, we can further improve it in the future. First, we can continue studying intelligent algorithms (GA, DE and NSGAII), making use of the big data to solve the model more quickly and efficiently. Second, we can further consider cardinality constraint in the fuzzy portfolio model, and make comparisons with the current models shown in this paper. Finally, we can consider other method of measuring risk-like entropy and compare it to our proposed model, to better satisfy investors in real financial market.