Abstract
As an effective tool to show the fuzziness of qualitative information, the probabilistic hesitant fuzzy set (PHFS) can utilize a group of membership degrees with a clear probability distribution to show the opinions of decision-maker (DM). Given this merit, many probabilistic hesitant fuzzy multi-criteria group decision-making (PHF-MCGDM) methods have been designed. However, most of the existing PHF-MCGDM methods have some limitations, including the difficulty of reflecting DMs’ ambiguous and hesitant preferences for criteria weights and the inability to comprehensively show the impacts of DMs’ irrational behaviors. To address these limitations, this paper develops a novel PHF-MCGDM method that integrates the defining interrelationships between ranked criteria (DIBR) approach and tri-reference point (TRP) theory. First, the PHF-DIBR approach is constructed to determine criteria weights by fully expressing DMs’ ambiguous and hesitant preferences for the importance of criteria. Second, the novel probabilistic hesitant fuzzy correlation coefficient (NPHFCC) is developed for deriving the weights of DMs, which remedies the flaws of the existing correlation coefficients (CC). Moreover, TRP theory is used to describe the psychological behavior effects of DMs and derive the order of alternatives. Finally, the applicability of the proposed method is validated by the case about office flooring material selection, while the sensitivity and comparison analyses are also conducted to further prove its advantages and effectiveness.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Multi-criteria group decision making (MCGDM) is an important research field in decision science. Since the evaluation information provided by decision makers (DMs) is usually ambiguous and uncertain in MCGDM, some fuzzy sets have been adopted to express uncertain evaluation information, including fuzzy set [1], intuitionistic fuzzy set [2], and Pythagorean fuzzy set [3]. In actual situations, DMs may give multiple different opinions on the same evaluation object, which cannot be handled through the above fuzzy sets. To conquer this problem, the hesitant fuzzy set, HFS [4] is defined, which contains multiple membership degrees. However, HFSs assumes that the probability of each membership degree is same. In practice, the DM may think that the probability of each membership degree is not necessarily the same. For example, if a DM hesitates between two scores: 0.2 and 0.7 when evaluating the technological level of the sustainable building material, then his/her evaluation information can be represented by a hesitant fuzzy element (HFE) {0.2, 0.7}. However, if the DM prefers 0.2 to 0.7 in his/her evaluation, the HFE {0.2, 0.7} cannot fully represent such an evaluation. Afterwards, Xu et al. [5] proposed the probabilistic hesitant fuzzy set (PHFS), which allows DMs to provide their preference information by using some membership degrees with probability information. For the above example, the evaluation information can be expressed as a probabilistic hesitant fuzzy element (PHFE) {0.2 (0.6), 0.7 (0.4)}, where 0.6 and 0.4 are the probabilities of 0.2 and 0.7 respectively. Obviously, PHFSs can retain more important information than HFSs.
Taking the advantages of PHFS, some probabilistic hesitant fuzzy MCGDM (PHF-MCGDM) methods have been proposed [6,7,8,9,10,11,12,13]. These methods can be divided into three types: (1) The integrated operation-based method, such as probabilistic hesitant fuzzy weighted averaging (PHFWA) operator [6], probabilistic hesitant fuzzy weighted geometric (PHFWG) operator [6] and probabilistic hesitant fuzzy prioritized weighted averaging (PHFPWA) operator [7]; (2) The utility value-based methods, such as the technique for order of preference by similarity to ideal solution (TOPSIS) [8], the vlsekriterijumska optimizacija i kompromisno resenje in serbian (VIKOR) [9], and the combinative distance-based assessment (CODAS) [10]; (3) The outranking-based methods, such as the elimination and choice translating reality (ELECTRE) [11], the preference ranking organization method for enrichment evaluations (PROMETHEE) [12], and qualitative flexible multiple criteria method (QUALIFLEX) [13]. Although the three kinds of methods differ from a mathematical perspective, they assume DMs are completely rational when giving the corresponding evaluations for each alternative. However, in real cases, DMs are rarely completely rational and may provide evaluation information with risk attitudes, which leads them to have bounded rational behaviors. To address this issue, Kahneman et al. [14] proposed prospect theory, which sets the standard as a reference point, and then the evaluated objects are compared with the reference point to capture the influence of bounded rational behavior. Some scholars [15,16,17] have applied prospect theory to solve PHF-MCGDM problems. However, prospect theory belongs to the single reference point (SPR) theory, which has some defects [18, 19]. For example, the three aspects that affect the decision of a risk investor contain his\her capital status, the target income he/she pursues, and the lower limit of the loss he\she can bear. The prospect theory only helps this investor handle one of the three aspects, resulting in information loss. To overcome this shortcoming of prospect theory, Wang and Johnson [20] introduced the tri-reference point (TRP) theory, which sets the status quo (SQ), the minimum requirement (MR), and the goal (G) reference points to depict fully the bounded rational behavior effects. Since then, TRP theory has been widely used to solve a variety of problems. For example, Song and Zhu [21] used TRP theory to construct a decision model for handling the multi-stage risk decision-making problem in cloud model. Liang et al. [22] adopted TRP theory to solve the agricultural project selection under q-rung orthopair fuzzy environment. Tu et al. [23] integrated TRP and ELECTRE III to handle urban flood resilience evaluation. Obviously, TRP theory can describe more important information than prospect theory. However, there are few studies on TRP in PHF-MCGDM problems. Hence, it is valuable to employ TRP to solve PHF-MCGDM problems.
In PHF-MCGDM, different criteria usually have different impacts on the decision results. In other words, different criteria should be assigned with different weights. To derive criteria weights, many approaches have been designed, such as analytic hierarchy process (AHP) [24] and best–worst method (BWM) [25]. However, AHP and BWM have common drawbacks of numerous comparisons and low consistency. To remedy these drawbacks, Pamucar et al. [26] proposed a weight determination approach, namely defining interrelationships between ranked criteria (DIBR), which relies on the preferences of DMs about relations between adjacent criteria to derive criteria weights. Compared with AHP and BWM, DIBR approach can reduce pairwise comparisons between criteria and improve the consistency of results. However, the classical DIBR approach uses crisp numbers to show DMs’ preferences about the importance of criteria, which cannot model DMs' uncertain assessments. To address this issue, many studies have fused uncertain information with DIBR approach. For example, Tešić et al. [27] integrated rough set into DIBR to develop rough DIBR (R-DIBR) approach and applied it to select an anti-tank missile system. Given the merit of fuzzy set, Pamucar et al. [28] extended DIBR to fuzzy environment and presented fuzzy DIBR (F-DIBR) approach. Although these extensions of DIBR employ fuzzy sets or rough numbers to show DMs’ preferences, they cannot accurately show the uncertainty information. For instance, when comparing the criteria “environment” with “economy” in sustainable building material selection, the DM may think the relative weight of “environment” is 0.2 with a ten percent probability and 0.3 with a ninety percent probability. Clearly, previous DIBR approaches cannot handle this type of uncertain information provided by the DM. Given that PHFSs can effectively contain different opinions and the probability distribution of these opinions, it is very meaningful to combine DIBR approach with PHFSs for determining the criteria weights in MCGDM problems.
In PHF-MCGDM, it is almost impossible to have a homogeneous group formed by DMs whose experiences, attitudes, and knowledge are the same. For that reason, the effects of DMs’ opinions on the final decision should be different, which implies that different DMs should be assigned with different weights. Therefore, how to derive the weights of DMs is an urgent problem for PHF-MCGDM. The similarity-based approach [29, 30] is very effective in determining DMs’ weights, which relies on the similarity between DMs’ opinions and the collective evaluation to derive DMs’ weights. Therefore, how to measure the similarity between DMs’ opinions and the collective evaluation is important for implementing the similarity-based approach. In general, if one set of data is closer to another set of data, the correlation coefficient (CC) between them is likely to be greater. On the contrary, the more different the two sets of data are, the smaller the correlation coefficient will be. In other words, the CC can reflect the approximation of the data to some extent. Therefore, it is very effective to combine CC with the similarity-based approach to determine DMs’ weights. The CC has been extended to the probabilistic hesitant fuzzy environment. For example, Song et al. [31] defined the CC based on the mean value of PHFS, but it will be equal to one as long as the mean values of two different PHFSs are equal. In addition, this CC will produce invalid calculation results when each PHFS contains only one PHFE. Subsequently, Liu and Guan [32] proposed a mix CC considering the average, variance, and length ratio of PHFS, but it is still inefficient in dealing with the situation that both two PHFSs have only one PHFE. To avoid the shortcomings of Song et al.’s CC and the mix CC proposed by Liu and Guan, Zhang et al. [33] presented the CC of PHFS based on the closeness coefficient and demonstrated the validity of this CC by an example of an investment decision problem. It is worth mentioning that some scholars [34] have pointed out that the CC for HFSs should have certain degree of hesitant rather than just a fixed value as the HFSs are hesitant and not precise. Inspired by this, the CC between PHFSs also should be hesitant and not just a single value. Specifically, since there may be many possible values for the degree of membership degree of an object in a PHFS, the CC should describe the correlation between different PHFSs in terms of a set of different values with their respective probabilities. However, all the above existing CCs for PHFS select a single value to show the correlation between two PHFSs, which cannot reflect the hesitancy of original data. To address this issue, the novel probabilistic hesitant fuzzy correlation coefficient (NPHFCC) is developed in this paper to measure the correlation between two PHFSs from the viewpoint of hesitancy, which means the proposed CC consists of a series of possible values and their probabilities. In addition, the NPHFCC ensures the calculation result is equal to one if and only if the two PHFSs are the same, and remains valid when each PHFS contains only one PHFE. Therefore, the NPHFCC can not only inherit the merit of Zhang et al.’s CC, but also overcome the flaws of previous CCs. Given this advantage of NPHFCC, it can be combined with the similarity-based approach to derive DMs’ weights in PHF-MCGDM problems, and provides the necessary support for the proposed MCGDM method.
According to the aforementioned discussion, this paper aims to propose a novel PHF-MCGDM method that can fully describe DMs’ ambiguous and hesitant preferences for the importance of criteria and reflect the impacts of DMs’ irrational behaviors. The motivation for the novel PHF-MCGDM method can be listed as follows:
-
(1)
Most existing CCs [31,32,33] of PHFSs are expressed as single values, which cannot reflect the hesitancy of original data.
-
(2)
The classical DIBR approach [26] adopts crisp numbers to express the preferences of DMs about criteria weights, which cannot deal with uncertain information that exists in reality. Although some previous studies [27, 28] have combined fuzzy sets or rough numbers with DIBR, they still cannot adequately show preferences with high uncertainty.
-
(3)
Some existing PHF-MCGDM methods [15,16,17] depict the impacts of DMs’ irrational behaviors from SPR, which leads to information loss.
To address these key issues, the PHF-DIBR-TRP method is designed to solve MCGDM problems. First, the probabilistic hesitant fuzzy DIBR (PHF-DIBR) approach is developed to determine criteria weights, which can assure that DMs’ preferences about the importance of criteria are adequately expressed. Second, the NPHFCC is defined to conquer the flaws of the existing CCs and combined with the similarity-based approaches to derive the weights of DMs. Moreover, the expected values of alternatives are computed to get the order of alternatives with the aid of TRP. In the end, an example of the sustainable building material selection is presented to prove the availability of the proposed method, while the comparative analysis is used to prove the merit of the proposed method. In a summary, the contributions of this paper contain:
-
(1)
The NPHFCC is developed to measure the correlation relationship between two PHFSs from the viewpoint of hesitancy, which is characterized by a series of possible values with their own probabilities to reflect the hesitancy of original data.
-
(2)
The PHF-DIBR approach is proposed to determine criteria weights under each DM, thus ensuring that DMs’ ambiguous and hesitant preferences can be adequately described. Meanwhile, the PHF-DIBR approach reduces pairwise comparisons between criteria and improves the consistency of results.
-
(3)
In the procedure of the proposed method, the expected values of alternatives are computed on the basis of TRP theory, which can capture DMs’ psychological behavior effects in a comprehensive way.
The framework of this paper includes: in Sect. 2, some basic knowledge about PHFS, TRP theory and DIBR approach are recalled. In Sect. 3, the NPHFCC is defined to remedy the shortcoming of the existing CCs. In Sect. 4, a novel MCGDM method is proposed on the basis of PHF-DIBR approach and TRP theory. Section 5 presents an application of the proposed method into an illustrative case. Additionally, the sensitivity and comparison analyses prove the merit of the proposed method. In Sect. 6, some conclusions are given.
2 Preliminaries
In this section, we recall some basic knowledge of PHFS, TRP theory and DIBR approach.
2.1 Some Concepts About PHFS
Definition 1
[5] Let X be a reference set, a PHFS is expressed as:
where \(h_{x} (p) = \{ \gamma_{x}^{\lambda } (p_{x}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{x} \}\) is a PHFE, \(p_{x}^{\lambda }\) is the probability of membership degree \(\gamma_{x}^{\lambda }\), and \(\# h_{x}\) is the total number of elements \(\gamma_{x}^{\lambda } (p_{x}^{\lambda } )\) in \(h_{x} (p)\). Additionally, \(0 \le p_{x}^{\lambda } \le 1\) and \(\sum\nolimits_{\lambda = 1}^{{\# h_{x} }} {p_{x}^{\lambda } } = 1\).
For convenience, we denote the set \(h_{x} (p) = \{ \gamma_{x}^{\lambda } (p_{x}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{x} \}\) as \(h(p) = \{ \gamma^{\lambda } (p^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h\}\). Note that the membership degrees in a PHFE are usually out of order. To facilitate the calculation, all membership degrees of the PHFE \(h(p)\) are arranged in an increasing order, and \(\gamma^{\lambda }\) is the \(\lambda {\text{th}}\) smallest membership degree in \(h(p)\). Moreover, the complement of \(h(p)\) is denoted as \((h(p))^{c} = \{ 1 - \gamma^{\lambda } (p^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h\}\).
Definition 2
[33] Let \(h_{1} (p) = \{ \gamma_{1}^{\lambda } (p_{1}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{1} \}\) and \(h_{2} (p) = \{ \gamma_{2}^{\lambda } (p_{2}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{2} \}\) be two PHFEs. Then, the distance measure between \(h_{1} (p)\) and \(h_{2} (p)\) is expressed as
where \(\Gamma = \left\{ {\nu_{ij} |\sum\nolimits_{j = 1}^{{\# h_{2} }} {\nu_{ij} } = p_{1}^{i} ,\;\sum\nolimits_{i = 1}^{{\# h_{1} }} {\nu_{ij} } = p_{2}^{j} ,\;\nu_{ij} \ge 0,\;\sum\nolimits_{j = 1}^{{\# h_{2} }} {\sum\nolimits_{i = 1}^{{\# h_{1} }} {\nu_{ij} } } = 1} \right\}\).
Definition 3
[5] For a PHFE \(h(p) = \{ \gamma^{\lambda } (p^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h\}\), its score function and deviation function are expressed as respectively
By using Eqs. (3) and (4), the order of two PHFEs can be obtained. For two PHFEs \(h_{1} (p)\) and \(h_{2} (p)\), if \(s(h_{1} (p)) > s(h_{2} (p))\), then \(h_{1} (p) > h_{2} (p)\); if \(s(h_{1} (p)) = s(h_{2} (p))\) and \(v(h_{1} (p)) < v(h_{2} (p))\), then \(h_{1} (p) > h_{2} (p)\); if \(s(h_{1} (p)) = s(h_{2} (p))\) and \(v(h_{1} (p)) = v(h_{2} (p))\), then \(h_{1} (p) \approx h_{2} (p)\).
To decrease the complexity of aggregation and calculation, Lin et al. [35] developed a normalization algorithm to obtain normalized probabilistic hesitant fuzzy element (NPHFE).
Algorithm 1
[35] Input: n PHFEs \(h_{j} (p)\;(j = 1,\;2, \ldots ,n)\), where \(h_{j} (p) = \{ \gamma_{j}^{\lambda } (p_{j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{j} \}\).
Output: n NPHFEs \(\tilde{h}_{j} (p)\;(j = 1,\;2, \ldots ,n)\), where \(\tilde{h}_{j} (p) = \{ \tilde{\gamma }_{j}^{\lambda } (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l\}\).
Step1. Let \(\lambda = 1\), \(sum = 0\) and n empty sets \(\tilde{h}_{j} (p) = \{ \} \;(j = 1,\;2, \ldots ,n)\).
Step2. Compare the probabilities \(p_{j}^{\lambda }\) of elements \(\gamma_{j}^{\lambda } \;(j = 1,\;2, \ldots ,n)\) in the \(\lambda\)th position of each \(h_{j} (p)\), and let \(\tilde{p}^{\lambda } = \mathop {\min }\limits_{j} \{ p_{j}^{\lambda } \}\).
Step3. Let \(j = 1\).
Step4. If \(p_{j}^{\lambda } > \tilde{p}^{\lambda }\), then the element \(\gamma_{j}^{\lambda } (p_{j}^{\lambda } )\) in \(h_{j} (p)\) is divided into two elements \(\gamma_{j}^{\lambda } (\tilde{p}^{\lambda } )\) and \(\gamma_{j}^{\lambda } (p_{j}^{\lambda } - \tilde{p}^{\lambda } )\). \(\gamma_{j}^{\lambda } (\tilde{p}^{\lambda } )\) is the input to \(\tilde{h}_{j} (p)\), named as \(\tilde{\gamma }_{j}^{\lambda } (\tilde{p}^{\lambda } )\), while \(\gamma_{j}^{\lambda } (p_{j}^{\lambda } - \tilde{p}^{\lambda } )\) is used to replace the original element in the \(\lambda\)th position of \(h_{j} (p)\). If \(p_{j}^{\lambda } = \tilde{p}^{\lambda }\), \(\gamma_{j}^{\lambda } (\tilde{p}^{\lambda } )\) is the input to \(\tilde{h}_{j} (p)\), named as \(\tilde{\gamma }_{j}^{\lambda } (\tilde{p}^{\lambda } )\), while \(\gamma_{j}^{\lambda + 1} (p_{j}^{\lambda + 1} )\) is used to replace the original element in the \(\lambda\)th position of \(h_{j} (p)\).
Step5. If \(j < n\), let \(j = j + 1\) and turn to Step 4. Otherwise, turn to the next step.
Step6. Calculate \(sum = sum + \tilde{p}^{\lambda }\).
Step7. Determine that \(sum\) is smaller than or equal to 1. If \(sum = 1\), turn to the next step; otherwise, let \(\lambda = \lambda + 1\), and return to Step 2.
Step8. Output \(\tilde{h}_{j} (p)\;(j = 1,\;2, \ldots ,n)\) as NPHFEs.
Step9. End.
Example 1
For three PHFEs \(h_{1} (p) = \{ 0.2\;(0.6),\;0.6\;(0.4)\}\), \(h_{2} (p) = \{ 0.3\;(0.4),\;0.4\;(0.6)\}\) and \(h_{3} (p) = \{ 0.5\;(1)\}\), we can use Algorithm 1 to obtain the corresponding NPHFEs, denoted as \(\tilde{h}_{1} (p) = \{ 0.2\;(0.4),\;0.2\;(0.2),\;0.6\;(0.4)\}\), \(\tilde{h}_{2} (p) = \{ 0.3\;(0.4),\;0.4\;(0.2),\;0.4\;(0.4)\}\) and \(\tilde{h}_{3} (p) = \{ 0.5\;(0.4),\;0.5\;(0.2),\;0.5\;(0.4)\}\).
As can be seen from Example 1, NPHFEs do not change the original information and ensure that the membership degrees of the same positions of NPHFEs have same probabilities.
Definition 4
[5, 36] For a group of PHFEs \(h_{1} (p),\;h_{2} (p), \ldots ,h_{n} (p)\), in which \(h_{j} (p) = \{ \gamma_{j}^{\lambda } (p_{j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{j} \}\) for \(\forall j \in \{ 1,\;2, \ldots ,n\}\), and \(\alpha > 0\). Then
(1) \(h_{1} (p) \oplus h_{2} (p) \oplus \cdots \oplus h_{n} (p) = \left\{ {1 - \prod\nolimits_{j = 1}^{n} {(1 - \tilde{\gamma }_{j}^{\lambda } )} (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l} \right\}\),
(2) \(h_{1} (p) \otimes h_{2} (p) \otimes \cdots \otimes h_{n} (p) = \left\{ {\prod\nolimits_{j = 1}^{n} {\tilde{\gamma }_{j}^{\lambda } } (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l} \right\}\),
(3) \(\alpha h_{1} (p) = \{ 1 - (1 - \gamma_{1}^{\lambda } )^{\alpha } (p_{1}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{1} \}\),
(4) \((h_{1} (p))^{\alpha } = \{ (\gamma_{1}^{\lambda } )^{\alpha } (p_{1}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{1} \}\).
2.2 TRP Theory
TRP theory [20] holds that people’s psychological perceived values are determined by three different reference points, including SQ, MR, and G. In TRP theory, three points divide the psychological perceived value x into four regions: failure (\(x < MR\)), loss (\(MR \le x < SQ\)), gain (\(SQ \le x < G\)), and success (\(x \ge G\)) [35], while the psychological perceived values are different in four regions.
In risk decision problems, avoiding failure is the most important thing, achieving success is the second most important thing, and loss reduction is the third most important thing, while obtaining gain has the least influence. Thus, DMs are risk-seeking in failure and gain regions, while they are risk-averse in loss and success regions. According to the above analysis, the value function of TRP is double-S shape [37], as shown in Fig. 1.
In Fig. 1, SQ is set as the coordinate origin, and \(V(x)\) denotes the value function. In the first quadrant, the TRP value function is composed of concave part of the gain and convex part of the success. In the third quadrant, the TRP value function is composed of concave part of the failure and convex part of the loss. It is worth noting that the value function of TRP in the third quadrant is more skewed than it in the first quadrant. The reasons for the above results are as follows: (1) if facing the failure, people are willing to take risks for conquering failure. Analogously, when locating in the gain region, people are willing to take risks for achieving goal. (2) If locating in the loss and success region, people are afraid to face failure or fail to achieve their goals, which makes they dislike taking risks.
2.3 DIBR Approach
To determine criteria weights, the DIBR approach is proposed by Pamucar et al. [26]. This approach relies on the preference comparisons between criteria to derive the importance of criteria. In the following, we introduce the process of this approach.
(a) Determine n criteria \(c_{1} ,\;c_{2} , \ldots ,c_{n}\).
(b) Rank the importance of criteria according to the DM’s preferences, and the ranking result is \(c_{1} > c_{2} > \cdots > c_{n}\).
(c) Assess the relative importance between adjacent criteria through the DM’s preferences, and the corresponding assessments are expressed in form of a group of crisp numbers that denote as \(\tau_{(1,2)} ,\;\tau_{(2,3)} , \ldots ,\tau_{(n - 1,n)} ,\;\tau_{(1,n)}\). For example, the crisp number \(\tau_{(1,2)}\) represents the value of the weight coefficient of \(c_{1}\) relative to the weight coefficient of \(c_{2}\). Meanwhile, these crisp numbers should satisfy the condition \(0 < \tau_{(1,2)} ,\;\tau_{(2,3)} , \ldots ,\tau_{(n - 1,n)} ,\;\tau_{(1,n)} \le 0.5\).
(d) Let the weight vector of criteria be \((w_{1} ,\;w_{2} , \ldots ,w_{n} )^{T}\), in which the weight coefficient \(w_{j}\) meets \(w_{j} \ge 0\) and \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\). Then according to the above description, derive the relations among the weight coefficients of criteria:
(e) With the conditions that \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\), derive criteria weight coefficients by the following equations.
(f) Use the derived weight coefficients \(w_{1}\) and \(w_{n}\) to determine the value \(\tau^{\prime}_{(1,n)}\).
Then we can calculate the deviation between \(\tau^{\prime}_{1,n}\) and \(\tau_{1,n}\).
\(de(\tau_{(1,n)} ,\;\tau^{\prime}_{(1,n)} )\) is used to justify whether the derived criteria weight coefficients meet the preferences of DM. If \(de(\tau_{(1,n)} ,\;\tau^{\prime}_{(1,n)} ) \le 0.1\), it indicates that the preferences of DM are satisfied. If \(de(\tau_{(1,n)} ,\;\tau^{\prime}_{(1,n)} ) > 0.1\), the relative relations between criteria weight coefficients need to be adjusted.
3 The CC for PHFSs
In this section, we analyse the shortcoming of previous CCs of PHFS, and define NPHFCC to prepare for the construction of a decision model.
3.1 The Existing CCs and Their Drawbacks
At present, some scholars [31,32,33] have given the CCs of PHFS to measure the correlation between two PHFSs, which are shown as:
Let \(H_{1} = \{ h_{1j} (p)|j = 1,\;2, \ldots ,n\}\) and \(H_{2} = \{ h_{2j} (p)|j = 1,\;2, \ldots ,n\}\) be two PHFSs on the fixed set \(X = \{ x_{j} |j = 1,\;2, \ldots ,n\}\), in which \(h_{1j} (p) = \{ \gamma_{1j}^{\lambda } (p_{1j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{1j} \}\) and \(h_{2j} (p) = \{ \gamma_{2j}^{\lambda } (p_{2j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{2j} \}\).
(1) Song et al.’s CC [31] can be expressed as:
(2) Liu and Guan’s mix CC [32] is defined as:
where \(\rho^{S} (H_{1} ,\;H_{2} )\), \(\rho^{V} (H_{1} ,\;H_{2} )\) and \(\rho^{L} (H_{1} ,\;H_{2} )\) denote the mean, variance and length CC respectively, and \(\alpha_{1}\), \(\alpha_{2}\) and \(\alpha_{3}\) are their corresponding weights that meet \(\alpha_{1} + \alpha_{2} + \alpha_{3} = 1\) and \(0 \le \alpha_{1} ,\;\alpha_{2} ,\;\alpha_{3} \le 1\). Here, \(\rho^{S} (H_{1} ,\;H_{2} )\) is calculated according to Eq. (13). The calculation formulas of \(\rho^{V} (H_{1} ,\;H_{2} )\) and \(\rho^{L} (H_{1} ,\;H_{2} )\) are as follows:
(3) Zhang et al.’s CC [33] is calculated as:
where \(d(h_{1j} (p),\;(h_{2j} (p))^{c} )\) represents the distance measure between \(h_{1j} (p)\) and \((h_{2j} (p))^{c}\), and \((h_{2j} (p))^{c}\) is the complement of \(h_{2j} (p)\).
Although the above CCs have been applied to cluster analysis and decision problems [31,32,33], it sometimes provides the counterintuitive result. Their deficiencies are shown through the following examples.
Example 2
For two PHFSs \(H_{1} = \{ \langle x_{1} ,\;\{ 0.3\;(0.5),\;0.5\;(0.5)\} \rangle ,\;\langle x_{2} ,\;\{ 0.2\;(0.2),\;0.3\;(0.6),\;0.4\;(0.2)\} \rangle \}\) and \(H_{2} = \{ \langle x_{1} ,\;\{ 0.1\;(0.5),\;0.7\;(0.5)\} \rangle ,\;\langle x_{2} ,\;\{ 0.1\;(0.2),\;0.3\;(0.6),\;0.5\;(0.2)\} \rangle \}\), we apply Song et al.’s CC to obtain \(\rho^{S} (H_{1} ,\;H_{2} ) = 1\).
It is clear that \(H_{1} \ne H_{2}\), which indicates the CC cannot be equal to one. Therefore, the calculated result obtained by Song et al.’s CC is unreasonable.
Example 3
For two PHFSs \(H_{3} = \{ \langle x_{1} ,\;\{ 0.3\;(1)\} \rangle \}\) and \(H_{4} = \{ \langle x_{1} ,\;\{ 0.9\;(1)\} \rangle \}\), we apply Song et al.’s CC and the mix CC proposed by Liu and Guan to measure the correlation between \(H_{3}\) and \(H_{4}\). Then we can find the term \(s(h_{1j} (p)) - \frac{1}{n}\sum\nolimits_{j = 1}^{n} {s(h_{1j} (p))} = s(h_{2j} (p)) - \frac{1}{n}\sum\nolimits_{j = 1}^{n} {s(h_{2j} (p))} = 0\). This causes that the Eqs. (13)–(16) are meaningless when calculating the CC between \(H_{3}\) and \(H_{4}\). Therefore, \(\rho^{S}\) and \(\rho^{M}\) are invalid when each PHFS contains only one PHFE.
The main reason for the above drawback is that the Song et al.’s CC and the mix CC uses statistical characterization of data, such as mean, variance and length, to represent a PHFS, which may lose some important information.
Additionally, when using Zhang et al.’s CC to measure correlations among four PHFSs in Examples 2 and 3, we can obtain \(\rho^{Z} (H_{1} ,\;H_{2} ) = 0.4043\) and \(\rho^{Z} (H_{3} ,\;H_{4} ) = - 0.5\). Although Zhang et al.’s CC can avoid the occurrence of invalid results and counter-intuitive, it adopts a single value to express the correlation between two PHFSs, which cannot reflect the hesitancy of original data.
3.2 NPHFCC
According to the ideas of Liu [38] and Liao [34], we propose the NPHFCC to overcome the drawbacks of existing CCs, as follows:
Definition 5
Let \(H_{1} = \{ h_{1j} (p)|j = 1,\;2, \ldots ,n\}\) and \(H_{2} = \{ h_{2j} (p)|j = 1,\;2, \ldots ,n\}\) be two PHFSs on the fixed set \(X = \{ x_{j} |j = 1,\;2, \ldots ,n\}\), in which \(h_{1j} (p) = \{ \gamma_{1j}^{\lambda } (p_{1j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{1j} \}\) and \(h_{2j} (p) = \{ \gamma_{2j}^{\lambda } (p_{2j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{2j} \}\). By using Algorithm 1 to handle \(h_{11} (p),\;h_{12} (p), \ldots ,h_{1n} (p),\;h_{21} (p),\;h_{22} (p), \ldots ,h_{2n} (p)\), two groups of NPHFEs \(\tilde{H}_{1} = \{ \tilde{h}_{1j} (p)|j = 1,\;2, \ldots ,n\}\) and \(\tilde{H}_{2} = \{ \tilde{h}_{2j} (p)|j = 1,\;2, \ldots ,n\}\) are derived, in which \(\tilde{h}_{1j} (p) = \{ \tilde{\gamma }_{1j}^{\lambda } (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l\}\) and \(\tilde{h}_{2j} (p) = \{ \tilde{\gamma }_{2j}^{\lambda } (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l\}\). Then the NPHFCC between \(H_{1}\) and \(H_{2}\) is expressed as:
where
Next, the score of NPHFCC is proposed to rank two NPHFCCs.
Definition 6
Let \(\rho^{N} = \{ CC^{\lambda } (\tilde{p}^{\lambda } )|\lambda = 1,\;2, \ldots ,l\}\) be a NPHFCC, and its score is expressed as:
According to the score of NPHFCC, we give a comparison method to rank two NPHFCCs \(\rho_{1}^{N}\) and \(\rho_{2}^{N}\): (1) if \(score(\rho_{1}^{N} ) > score(\rho_{2}^{N} )\), it implies \(\rho_{1}^{N}\) is bigger than \(\rho_{2}^{N}\), denoted as \(\rho_{1}^{N} > \rho_{2}^{N}\); (2) If \(score(\rho_{1}^{N} ) = score(\rho_{2}^{N} )\), it implies \(\rho_{1}^{N}\) is approximate to \(\rho_{2}^{N}\), denoted as \(\rho_{1}^{N} \approx \rho_{2}^{N}\).
According to Definition 5, the properties about NPHFCC are as follows:
Property 1
Let \(H_{1} = \{ h_{1j} (p)|j = 1,\;2, \ldots ,n\}\) and \(H_{2} = \{ h_{2j} (p)|j = 1,\;2, \ldots ,n\}\) be two PHFSs on the fixed set \(X = \{ x_{j} |j = 1,\;2, \ldots ,n\}\). Then \(\rho^{N} (H_{1} ,\;H_{2} )\) represents the NPHFCC between \(H_{1}\) and \(H_{2}\), and it satisfies the following five properties:
(P1) \(- 1 \le score(\rho^{N} (H_{1} ,\;H_{2} )) \le 1\);
(P2) \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ 1\;(1)\}\) if and only if \(H_{1} = H_{2}\);
(P3) \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ - 1\;(1)\}\) if and only if \(H_{1} = (H_{2} )^{c}\), where \((H_{2} )^{c} = \{ (h_{2j} (p))^{c} |j = 1,\;2, \ldots ,n\}\) and \((h_{2j} (p))^{c} = \{ 1 - \gamma_{2j}^{\lambda } (p_{2j}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{2j} \}\);
(P4) \(\rho^{N} (H_{1} ,\;H_{2} ) = \rho^{N} (H_{2} ,\;H_{1} )\);
(P5) \(\rho^{N} (H_{1} ,\;H_{2} ) = \left\{ {\frac{0}{0}(1)} \right\} \Leftrightarrow H_{1} = H_{2} = (H_{2} )^{c}\).
Proof
(P1) It is easy that we have
Then, we can obtain \(- 1 \le CC^{\lambda } \le 1(\lambda = 1,\;2, \ldots ,l)\).Thus, according to Eq. (20), we can easily derive \(- 1 \le score(\rho^{N} (H_{1} ,\;H_{2} )) \le 1\).
(P2) If \(H_{1} = H_{2}\), we have \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ 1\;(1)\}\). Conversely, if \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ 1\;(1)\}\), we have
Then we can derive
Since \(|\tilde{\gamma }_{1j}^{\lambda } - \tilde{\gamma }_{2j} | \ge 0\) and \(|\tilde{\gamma }_{2j}^{\lambda } - \tilde{\gamma }_{1j} | \ge 0\), we can derive
It implies that \(\tilde{h}_{1j} (p) = \tilde{h}_{2j} (p)\). Therefore we can conclude that \(H_{1} = H_{2}\) when \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ 1\;(1)\}\).
(P3) If \(H_{1} = (H_{2} )^{c}\), we have
Therefore we can obtain \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ - 1\;(1)\}\). Conversely, if \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ - 1\;(1)\}\), we have
Then we can derive
Since \(|\tilde{\gamma }_{1j}^{\lambda } - (1 - \tilde{\gamma }_{2j} )| \ge 0\) and \(|\tilde{\gamma }_{2j}^{\lambda } - (1 - \tilde{\gamma }_{1j} )| \ge 0\), we can derive
Therefore we can conclude that \(H_{1} = (H_{2} )^{c}\) when \(\rho^{N} (H_{1} ,\;H_{2} ) = \{ - 1\;(1)\}\).
(P4) It is straightforward.
(P5) If \(h_{1j} (p) = h_{2j} (p) = \{ 0.5\;(1)\}\) for \(\forall j = 1,\;2, \ldots ,n\), then we can derive \(h_{1j} (p) = h_{2j} (p) = (h_{2j} (p))^{c}\) and \(H_{1} = H_{2} = (H_{2} )^{c}\). Therefore, there must be
Subsequently, we can obtain the calculation result by Eq. (19), as follows:
Moreover, if \(\rho^{N} (H_{1} ,\;H_{2} ) = \left\{ {\frac{0}{0}(1)} \right\}\), we can obtain the simultaneous equations, as follows:
By solving above simultaneous equations, we have
Further, we can derive that \(h_{1j} (p) = h_{2j} (p) = (h_{2j} (p))^{c}\) for \(\forall j = 1,\;2, \ldots ,n\), and \(H_{1} = H_{2} = (H_{2} )^{c}\). At this point, it can be sure that \(h_{1j} (p) = h_{2j} (p) = \{ 0.5(1)\}\).
Remark 1
According to (P5), the Eq. (19) produces 0/0, which by convention is 1. Therefore, we stipulate that \(CC^{\lambda } = \frac{0}{0} = 1\).
The NPHFCC is used again to measure the correlation relationships among four PHFSs in Examples 1 and 2, the calculation results are as follows:
It is clearly that there are some certain gaps between \(H_{1}\) and \(H_{2}\), which means the NPHFCC is more reasonable than Song et al.’s CC. Meanwhile, the NPHFCC can measure the correlation between \(H_{3}\) and \(H_{4}\), which implies the NPHFCC can handle the situation that each PHFS contains one PHFE and remedy the flaws of Song et al.’ CC and the mix CC proposed by Liu and Guan. Additionally, the NPHFCC can be characterized by a series of possible values with different probabilities instead of a single value, which indicates it can more effectively reflect the hesitancy of the original data than the three existing CCs.
4 The Proposed MCGDM Method Integrated PHF-DIBR Approach and TRP Theory
To consider fully the impact of DMs’ irrational behavior and the preferences of DMs about criteria weights, this section proposes a new MCGDM method by integrating PHF-DIBR, TRP, and NPHFCC. First, the PHF-DIBR approach is developed to derive the criteria weights under different DMs. Second, we can divide the criteria values into four regions based on the TRP theory and determine the individual expected value of each alternative. In addition, DMs’ weights are determined by adopting the similarity-based approach [29, 30] and NPHFCC. Finally, the total expected values of alternatives are calculated to rank alternatives.
4.1 Problem Description
Suppose that a PHF-MCGDM problem involves m alternatives \(X = \{ x_{i} |i = 1,\;2, \ldots ,m\}\), n criteria \(C = \{ c_{j} |j = 1,\;2, \ldots ,n\}\), and r DMs \(E = \{ e_{k} |k = 1,\;2, \ldots ,r\}\). Let \(M^{k} = (h_{ij}^{k} (p))_{m \times n}\) be a decision matrix given by DM \(e_{k}\), in which the PHFE \(h_{ij}^{k} (p) = \{ \gamma_{ijk}^{\lambda } (p_{ijk}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{ij}^{k} \}\) denotes the assessment of alternative \(x_{i}\) with respect to the criterion \(c_{j}\) under the DM \(e_{k}\). The decision matrix \(M^{k}\) is shown as:
4.2 The Calculation of Criteria Weights Under Each DM by PHF-DIBR Approach
In this sub-section, the PHF-DIBR approach is developed to derive criteria weights under different DMs, and its process is as follows:
(a) Invite DM \(e_{k} \;(k = 1,\;2, \ldots ,r)\) to give the order of significances of criteria, and the rank of all criteria is \(c_{1} > c_{2} > \cdots > c_{n}\), where “\(>\)” represents criterion \(c_{s} \;(s = 1,\;2, \ldots ,n - 1)\) is more important than criterion \(c_{s + 1}\).
(b) Assess the relative importance between adjacent criteria through the preferences of DM \(e_{k} \;(k = 1,\;2, \ldots ,r)\), and the corresponding assessments are expressed as a group of PHFEs that denotes as \(h_{(1,2) - k} (p),\;h_{(2,3) - k} (p), \ldots ,h_{(n - 1,n) - k} (p),\;h_{(1,n) - k} (p)\). For example, when comparing the criterion \(c_{1}\) with \(c_{2}\), the DM \(e_{k}\) provides a PHFE \(h_{(1,2) - k} (p) = \{ \gamma_{(1,2) - k}^{\lambda } (p_{(1,2) - k}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{(1,2)}^{k} \}\), where the membership degree \(\gamma_{(1,2) - k}^{\lambda } (0 < \gamma_{(1,2) - k}^{\lambda } \le 0.5)\) represents the value of the weight coefficient of \(c_{2}\) relative to the weight coefficient of \(c_{1}\), and \(p_{(1,2) - k}^{\lambda }\) is its corresponding probability.
(c) Derive the following relations among the weight coefficients of criteria under DM \(e_{k} \;(k = 1,\;2, \ldots ,r)\) according the previous description:
where the value \(w_{(j) - k}\) denotes the weight coefficient of criterion \(c_{j}\), and it meets \(0 \le w_{(j) - k} \le 1\) and \(\sum\nolimits_{j = 1}^{n} {w_{(j) - k} } = 1\).
(d) In view of the above relations and the sum of criteria weight coefficients is one, n PHFEs \(h_{(1) - k}^{w} (p),\;h_{(2) - k}^{w} (p), \ldots ,h_{(n) - k}^{w} (p)\;(k = 1,\;2, \ldots ,r)\) are derived by the following Eqs. (25) and (26), where \(h_{(j) - k}^{w} (p)\;(j = 1,\;2, \ldots ,n)\) denotes the probabilistic hesitant fuzzy weight of criterion \(c_{j}\) under DM \(e_{k}\).
(e) Calculate the PHFE \(h^{\prime}_{(1,n) - k} (p)\) by using \(h_{(1) - k}^{w} (p)\) and \(h_{(n) - k}^{w} (p)\), where
By employing Algorithm 1 to handle \(h_{(1,n) - k} (p)\) and \(h^{\prime}_{(1,n) - k} (p)\), two NPHFEs \(\tilde{h}_{1n}^{k} (p)\) and \(\tilde{h}_{1n}^{k} (p)\) can be derived, in which \(\tilde{h}_{(1,n) - k} (p) = \{ \tilde{\gamma }_{(1,n) - k}^{\lambda } (\tilde{p}_{k}^{\lambda } )|\lambda = 1,\;2, \ldots ,l_{k} \}\) and \(\tilde{h}^{\prime}_{(1,n) - k} (p) = \{ \tilde{\gamma }_{(1,n) - k}^{^{\prime}\lambda } (\tilde{p}_{k}^{\lambda } )|\lambda = 1,\;2, \ldots ,l_{k} \}\). Then the deviation between \(h_{(1,n) - k} (p)\) and \(h^{\prime}_{(1,n) - k} (p)\) is calculated by the following equation.
If \(de(h_{(1,n) - k} (p),\;h^{\prime}_{(1,n) - k} (p)) \le 0.1\), it indicates that the preferences of DM \(e_{k}\) are satisfied. If \(de(h_{(1,n) - k} (p),\;h^{\prime}_{(1,n) - k} (p)) > 0.1\), then the relations among criteria weight coefficients need be refined.
4.3 The Calculation of the Individual Expected Values of Alternatives Based on TRP Theory
When adopting TRP theory in PHF-MCGDM, all criteria should have their own three reference points. In TRP theory, \(SQ\) usually represents the current level, thus it is the mean value of all assessments under each criterion [21, 22]. Therefore \(SQ\) can be expressed as:
where \(SQ_{j}^{k}\) denotes the \(SQ\) point of criterion \(c_{j}\) under DM \(e_{k}\).
\(MR\) represents the minimum requirement of DMs, and is determined by the preferences of DMs [21, 22]. By using the score and deviation functions of PHFE, we can obtain the rank order \(h_{1j}^{k} (p),\;h_{2j}^{k} (p), \ldots ,h_{mj}^{k} (p)\). Let \(h_{(i)j}^{k} (p)\) be the rank of \(h_{ij}^{k} (p)\) and \(h_{(i)j}^{k} (p) \le h_{(i + 1)j}^{k} (p)\). Then \(MR\) point can be calculated as:
where \(I^{MR} \;(I^{MR} \in \{ 1,\;2, \ldots ,m - 1\} )\) is adjustment coefficient, and \(MR_{j}^{k}\) means the \(MR\) point of criterion \(c_{j}\) under DM \(e_{k}\).
\(G\) represents the goal of a DM, namely success, which is determined by the preferences of DMs [21, 22]. Let \(h_{{(i)^{\prime}j}}^{k} (p)\) be the other rank of \(h_{ij}^{k} (p)\) and \(h_{{(i)^{\prime}j}}^{k} (p) \ge h_{{(i + 1)^{\prime}j}}^{k} (p)\). Then \(G\) point can be determined as:
where \(I^{G} \;(I^{G} \in \{ 1,\;2, \ldots ,m - 1\} )\) is adjustment coefficient, and \(G_{j}^{k}\) denotes the \(G\) point of criterion \(c_{j}\) under DM \(e_{k}\). Notice that these three reference points are actually PHFEs.
By comparing \(h_{ij}^{k} (p)\) with three reference points, \(h_{ij}^{k} (p)\) can be divided into four regions that contain failure (\(h_{ij}^{k} (p) < MR_{j}^{k}\)), loss (\(MR_{j}^{k} \le h_{ij}^{k} (p) < SQ_{j}^{k}\)), gain (\(SQ_{j}^{k} \le h_{ij}^{k} (p) < G_{j}^{k}\)), and success (\(h_{ij}^{k} (p) \ge G_{j}^{k}\)) regions. According to Wang and Wang [37], the psychological perceived value function is expressed as:
where \(FR_{ij}^{k}\), \(LR_{ij}^{k}\), \(GR_{ij}^{k}\) and \(SR_{ij}^{k}\) denote the psychological perceived values of four regions, respectively.
To accurately show the comparison result between \(h_{ij}^{k} (p)\) and each reference point, we give the TRP value function of \(h_{ij}^{k} (p)\) by prospect theory [14, 39], as follows:
The parameters \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) reflect people’ risk attitudes in different regions. In TRP theory, people’s risk attitudes are risk-seeking when facing the failure or gain, thus the parameters \(\varepsilon_{1}\) and \(\varepsilon_{2}\) should meet \(0 < \varepsilon_{1} < 1\) and \(\varepsilon_{2} > 1\). On the contrary, if locating in the loss and success region, people’s risk attitudes are risk aversion, which implies the parameters \(\theta_{1}\) and \(\theta_{2}\) must satisfy \(\theta_{1} > 1\) and \(0 < \theta_{2} < 1\). In addition, the parameters \(\chi_{1}\) and \(\chi_{2}\) are loss sensitivity coefficient and gain sensitivity coefficient respectively. In view of the fact that people are usually more sensitive to losses than gains, the parameters \(\chi_{1}\) and \(\chi_{2}\) should meet \(\chi_{1} > 1 \ge \chi_{2} > 0\).
In Eq. (33), \(h_{ij}^{k} (p)\) may across two or more regions. At this point, the probabilities of \(h_{ij}^{k} (p)\) to different regions can be expressed as:
Considering \(h_{ij}^{k} (p) = \{ \gamma_{ijk}^{\lambda } (p_{ijk}^{\lambda } )|\lambda = 1,\;2, \ldots ,\# h_{ij}^{k} \}\) is a discrete probability distribution, we use classical probability theory to determine the probabilities of \(h_{ij}^{k} (p)\) to four regions, and the result is shown as:
Then, we can define the expected value of alternative \(x_{i}\) with respect to criterion \(c_{j}\) under DM \(e_{k}\) as:
Finally, the expected value \(EV_{i}^{k}\) of alternative \(x_{i}\) under DM \(e_{k}\) is determined as:
where \(s(h_{(j) - k}^{w} (p))\) denotes the score value of probabilistic hesitant fuzzy weight \(h_{(j) - k}^{w} (p)\).
4.4 The Calculation of Weights of DMs
In PHF-MCGDM, it is almost impossible to have a homogeneous group of DMs with the same experiences, attitudes, and knowledge. For that reason, the influence of DMs’ opinions on the final decision should be different, which means that different DMs should be assigned with different weights. Therefore, how to derive the weights of DMs is an urgent problem for PHF-MCGDM. The similarity-based approach [29, 30] is very effective in determining DMs’ weights, which are based on the similarity of each DM to the collective evaluation. If the similarity is large, then the DM has a larger weight. On the contrary, a small weight is assigned to a DM with less similarity. Thus, we adopt the similarity-based approach and NPHFCC to determine DMs’ weights in PHF-MCGDM method, and the procedure is shown as:
(a) The collective evaluation is taken as the mean of DMs’ evaluations, which is calculated as:
where \(\overline{h}_{ij} (p)\) denotes the collective evaluation of alternative \(x_{i}\) under criterion \(c_{j}\).
(b) The NPHFCC between the collective evaluation of alternative \(x_{i}\) and the opinions of DM \(e_{k}\) can be calculated and denoted as \(\rho_{ki}^{N} = \{ CC_{ki}^{\lambda } (\tilde{p}_{ki}^{\lambda } )|\lambda = 1,\;2, \ldots ,l_{ki} \}\), where
(c) The total correlation measure between DM \(e_{k}\) and the collective evaluation is computed as:
Clearly, a larger \(CM_{k}\) indicates that the opinions of DM \(e_{k}\) are more similar to the collective evaluation.
(d) Inspired by the idea of similarity-based approach, the DMs’ weights can be computed as:
where \(\omega_{k}\) is the weight of DM \(e_{k}\), and it meets \(\omega_{k} \ge 0\) and \(\sum\nolimits_{k = 1}^{r} {\omega_{k} } = 1\).
4.5 The Calculation of Total Expected Values of Each Alternative
According to the simplest and widely known weighted sum model, the total expected values of alternatives can be expressed as:
where \(EV_{i}\) denotes the total expected value of alternative \(x_{i}\).
Then we can rank alternatives on the basis of the order of the total expected values and select the best one.
4.6 The Procedure of the Proposed Method
Based on the above-mentioned discussions, the procedure of the proposed method is follows as:
Stage 1. Collect DMs’ evaluation information.
Step 1.1: Determine m alternatives \(\{ x_{i} |i = 1,\;2, \ldots ,m\}\), n criteria \(\{ c_{j} |j = 1,\;2, \ldots ,n\}\) and r DMs \(\{ e_{k} |k = 1,\;2, \ldots ,r\}\).
Step 1.2: Invite DMs to give their evaluation results of alternatives about criteria, and use PHFS to express these assessments, thus constructing r individual decision matrices \(M^{k} = (h_{ij}^{k} (p))_{m \times n} \, \).
Stage 2. Determine the weights of criteria under each DM by PHF-DIBR approach.
Step 2.1: Each DM gives the order of the importance of criteria by significance.
Step 2.2: Each DM provides the mutual relations between criteria weight coefficients.
Step 2.3: Calculate the probabilistic hesitant fuzzy weights of criteria under each DM by Eqs. (21)–(26).
Step 2.4: Test whether the obtained weights of criteria satisfy the preferences of DMs through Eqs. (27) and (28). If the preferences of DMs are not satisfied, then turn to step 2.2. Otherwise, turn to step 3.1.
Stage 3. Calculate the expected values of alternatives under each DM based on TRP theory.
Step 3.1: Determine three reference points of each criterion under each DM by Eqs. (29)–(31).
Step 3.2: Compare the evaluation values of alternatives with three points to calculate the TRP value in the light of Eq. (32).
Step 3.3: Determine the probabilities of criteria values to each region by Eqs. (33)–(35), and calculate the expected values of alternatives about each criterion under each DM with the help of Eq. (36).
Step 3.4: The individual expected values of alternatives are computed by Eq. (37).
Stage 4. Determine the weights of DMs by similarity-based approach and the proposed NPHFCC.
Step 4.1: Calculate the collective evaluation by using Eq. (38).
Step 4.2: Calculate the individual NPHFCC about each alternative by employing Eq. (39).
Step 4.3: Determine DMs’ weights through Eqs. (40) and (41).
Stage 5. Calculate the total expected values of alternatives.
Step 5.1: Determine the total expected values of alternatives based on weighted sum model and Eq. (42).
Step 5.2: The order of alternatives is consistent with the order of their total expected values.
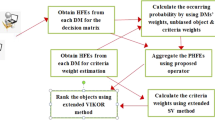
The process of the proposed method is shown in Fig. 2.
5 An Illustrative Example
To prove the effectiveness of the proposed method, this section adopts it to select flooring material and conducts the comparative analyses to prove its merit.
5.1 Background of the Case
Recently, Zhengzhou Municipal People's Government intends to develop an office design to renovate the interior layout of office buildings. The choice of office flooring plays an important role in office design. This is because the flooring can not only provide some basic functions, including avoiding temperature fluctuations and reducing noise, but also meet the requirements of aesthetics and comfort [40]. This means that the choice of office flooring must consider the social factors that affect functionality and comfort, which inevitably increases the complexity of office flooring selection. It is worth mentioning that glue, paint and other materials may be added to the flooring during the production process, which will cause the floor to contain harmful substances such as benzene and formaldehyde. Once these harmful substances are released into air, they will harm human health. Therefore, office flooring material selection should pay attention to environmental protection [41], which also adds to the complexity. Additionally, the level of technology has a deep impact on the performance of the flooring material, such as improving the service life of materials and promoting the ability of materials to withstand fire and explosion, which indicates the technology cannot be ignored in office flooring material selection [42]. Furthermore, to save government expenditures, the initial cost and subsequent maintenance cost of flooring materials need to be emphasized, which implies that office flooring materials need to be evaluated from the perspective of economy [43].
According to the above description, it can be concluded that the relevant evaluation criteria mainly include economy (c1), environment (c2), society (c3) and technology (c4). Subsequently, there are a variety of flooring types that can be identified as alternatives through market research, such as ceramic tiles (x1), terrazzo flooring (x2), solid hardwood flooring (x3), luxury vinyl planks (x4), bamboo flooring (x5), and linen flooring (x6). In view of the above complexities, the government department decides to deal with office flooring material selection by using the scientific MCGDM model. Then a group of experts that contain government official (e1), designer (e2) and construction worker (e3) will participate in evaluating the performances of materials.
5.2 Solving the Case by Using the Proposed Method
The PHF-DIBR-TRP method is used in this subsection to select the optimal suitable flooring material for office buildings.
Stage 1. Collect the assessment information provided by experts.
Step 1.1–1.2: Three experts evaluate six indoor floor materials according to the four criteria, and their evaluation results are collected through interview. In view of experts’ evaluations may be uncertain and ambiguous, all evaluation results are expressed in PHFEs. Then three probabilistic hesitant fuzzy decision matrices \(M^{k} = (h_{ij}^{k} (p))_{6 \times 4} \;(k = 1,\;2,\;3;\;i = 1,\;2, \ldots ,6;\;j = 1,\;2,\;3,\;4)\) are constructed, as shown in Tables 1, 2, and 3.
Stage 2. Determine the weights of criteria under each DM by PHF-DIBR approach.
Step 2.1–2.2: Through interview, all experts give the order of criteria by significance, and provide the pairwise comparisons about the weight coefficients of the ranked criteria, which is displayed in Table 4.
Step 2.3: According to Table 4 and Eqs. (21)–(26), the probabilistic hesitant fuzzy weights of criteria under different experts are derived and shown in Table 5.
Step 2.4: To check whether the obtained weights of criteria satisfy the preferences of DMs, the relations between the weights of the most and least influential criteria under three experts are derived by Eq. (27), as follows:
By using Eq. (28), we can calculate the deviation between the defined and derived relations about the weights of the most and least influential criteria under three experts, the calculation results are as below:
According to the above calculation results, we can conclude that the derived weights of criteria satisfy three experts’ preferences.
Stage 3. Calculate the expected values of alternative under experts based on TRP theory.
Step 3.1: Let the adjustment coefficients be \(I^{MR} = I^{G} = 3\) [21, 22]. Then, with the aid of TRP, three reference points of each criterion under each expert are determined by Eqs. (29)–(31), which are displayed in Table 6.
Step 3.2–3.3: Let \(\chi_{1} = 2.25\), \(\chi_{2} = 1\), \(\theta_{1} = \varepsilon_{2} = 1.21\), and \(\varepsilon_{1} = \theta_{2} = 0.88\) [39] are the parameter values in the TRP value function of in Eq. (33). The criteria values are compared with the three reference points. Then the corresponding expected values of criteria values are determined by using Eqs. (34)–(36) and shown in Table 7.
Step 3.4: By using Eq. (37) and criteria weights, the individual expect values of alternatives are determined, which are displayed in Table 8.
Stage 4. Determine the weights of experts.
Step 4.1: According to Eq. (38), the collective evaluation is obtained and shown in Table 9.
Step 4.2: The NPHFCCs between experts’ opinions and the collective evaluation under alternatives are determined by using Eq. (39) and shown in Table 10.
Step 4.3: According to Table 10 and Eqs. (40) and (41), the weights of experts can be calculated as:
Stage 5. Calculate the total expected values of alternatives.
Step 5.1: The total expect values of alternatives are computed with the help of Eq. (42), as follows:
Step 5.2: According to the total expect values, the order of the six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\). Therefore, we can conclude that bamboo flooring (x5) is the most suitable one.
5.3 Sensitivity Analysis
According to the proposed method, different values of some parameters, including adjustment coefficients \(I^{MR}\) and \(I^{G}\), risk attitude coefficients \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\), and gain–loss sensitivity coefficients \(\chi_{1}\) and \(\chi_{2}\), may lead to different expected values for each alternative, thus affecting the sorting of alternatives. Therefore, this subsection calculates the order of alternatives with different values of \(I^{MR}\), \(I^{G}\), \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\), \(\varepsilon_{2}\), \(\chi_{1}\) and \(\chi_{2}\) to validate their influence on the ranking results.
5.3.1 Sensitive Analysis of the Adjustment Coefficients \(I^{MR}\) and \(I^{G}\)
The adjustment coefficients \(I^{MR}\) and \(I^{G}\) represent the minimum requirement and the goal of people, respectively. In general, a larger value of \(I^{MR}\) means the higher extent of minimum requirement. Analogously, if \(I^{G}\) gets a larger value, it implies the higher goal.
To explore the impact of \(I^{G}\) on the final decision result, we assume that \(\chi_{1} = 2.25\), \(\chi_{2} = 1\), \(\theta_{1} = \varepsilon_{2} = 1.21\), \(\varepsilon_{1} = \theta_{2} = 0.88\), and \(I^{MR} = 3\). Then we set the values of \(I^{G}\) from 1 to 5 in increments of 1 for sensitivity analysis. The corresponding expected values are shown in Fig. 3.
From Fig. 3, we can see that the ranking of six indoor floor materials is always \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\). On the other hand, if we let \(\chi_{1} = 2.25\), \(\chi_{2} = 1\), \(\theta_{1} = \varepsilon_{2} = 1.21\), \(\varepsilon_{1} = \theta_{2} = 0.88\), and \(I^{G} = 3\), the expected values of indoor floor materials can be obtained as the values of \(I^{MR}\) from 1 to 5 in increments of 1, which is shown in Fig. 4.
As shown in Fig. 4, we can find that
(a) When \(I^{MR} = 1\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{1} \succ x_{6} \succ x_{3}\).
(b) When \(I^{MR} = 2\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{6} \succ x_{1} \succ x_{3}\).
(c) When \(I^{MR} = 3\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\).
(d) When \(I^{MR} = 4\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{3} \succ x_{4} \succ x_{1}\).
(f) When \(I^{MR} = 5\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{3} \succ x_{1} \succ x_{4}\).
To illustrate the influence of the joint changes of both parameters \(I^{MR}\) and \(I^{G}\) on the final decision result, we still set \(\chi_{1} = 2.25\), \(\chi_{2} = 1\), \(\theta_{1} = \varepsilon_{2} = 1.21\) and \(\varepsilon_{1} = \theta_{2} = 0.88\). Then Fig. 5 shows the ranking results of six indoor floor materials with different values of \(I^{MR}\) and \(I^{G}\).
From Figs. 3, 4, and 5, we can see that the ranking results may be different with different adjustment coefficients \(I^{MR}\) and \(I^{G}\), but the first-ranked indoor floor material is always \(x_{5}\). Therefore, we can conclude that the order of six indoor floor materials may be influenced by the change of \(I^{MR}\) and \(I^{G}\). Since \(I^{MR}\) and \(I^{G}\) can reflect the people’s subjective requirements, two adjustment coefficients should be derived through questionnaire survey and interview.
5.3.2 Sensitive Analysis of the Risk Attitude Coefficients \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\)
The parameters \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) reflect people’ risk attitudes in different regions. Generally, if the value of parameter \(\varepsilon_{1}\) is smaller, it means a higher extent of risk seeking in failure region. On the other hand, a larger value of \(\varepsilon_{2}\) implies the higher extent of risk seeking in gain region. Moreover, people’s risk attitudes are the higher extent of risk aversion with a larger value of \(\theta_{1}\) or a smaller value of \(\theta_{2}\). According to the above description, we will analyze the influence of the change of any one of the four parameters \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) on the final ranking result.
(1) In the case of other parameters are fixed, the values of \(\varepsilon_{1}\) are set from 0.1 to 1 in increments of 0.1 for sensitivity analysis. Figure 6a shows the impact of different \(\varepsilon_{1}\) values on the rankings of indoor floor materials. From Fig. 6a, we can obtain the following results:
(a) When \(\varepsilon_{1} \in \{ 0.1,\;0.2,\;0.3,\;0.4\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{6} \succ x_{2} \succ x_{4} \succ x_{3} \succ x_{1}\).
(b) When \(\varepsilon_{1} \in \{ 0.5,\;0.6,\;0.7,\;0.8,\;0.9\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\).
(c) When \(\varepsilon_{1} = 1\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{6} \succ x_{3} \succ x_{1}\).
(d) When \(\varepsilon_{1}\) is assigned to a smaller value, the expected values of all indoor floor materials are smaller, and the discrimination among them is larger.
(2) In the case of other parameters are fixed, the values of \(\varepsilon_{2}\) are set from 1.1 to 2 in increments of 0.1 for sensitivity analysis. Figure 6b shows the influence of different \(\varepsilon_{2}\) values on the rankings of indoor floor materials. We can observe that the ranking of six indoor floor materials is still \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\) with different values of \(\varepsilon_{2}\).
(3) In the case of other parameters are fixed, the values of \(\theta_{1}\) are set from 1.1 to 2 in increments of 0.1 for sensitivity analysis. Figure 6c shows the effect of different \(\theta_{1}\) values on the rankings of indoor floor materials. As shown in Fig. 6c, the ranking of six indoor floor materials is still \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\) with different values of \(\theta_{1}\).
(4) In the case of other parameters are fixed, the values of \(\theta_{2}\) are set from 0.1 to 1 in increments of 0.1 for sensitivity analysis. Figure 6d depicts how the change of \(\theta_{2}\) affects the rankings of indoor floor materials. From Fig. 6d, we can see that
(a) When \(\theta_{2} \in \{ 0.1,\;0.2,\;0.3,\;0.4\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{1} \succ x_{3}\).
(b) When \(\theta_{2} \in \{ 0.5,\;0.6,\;0.7,\;0.8,\;0.9\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\).
(c) When \(\theta_{2}\) is assigned to a smaller value, the expected values of all indoor floor materials are larger, and the discrimination among them is larger.
Further, as the values of no less than two risk attitude coefficients synchronously change, the ranking of six indoor floor materials can be obtained and shown in Table 11.
As we can see in Table 11 and Fig. 6, the order of \(x_{1}\), \(x_{3}\) and \(x_{5}\) never changed with different risk attitude coefficients, while the rankings of \(x_{2}\), \(x_{4}\) and \(x_{6}\) did. It indicates the risk attitude coefficients \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) have an impact on the sorting of six indoor floor materials. In view of that \(\theta_{1}\), \(\theta_{2}\), \(\varepsilon_{1}\) and \(\varepsilon_{2}\) can model people’s risk attitudes, we suggest that experimental research and questionnaire survey be used to determine these risk attitude coefficients.
5.3.3 Sensitive Analysis of the Gain–Loss Sensitivity Coefficients \(\chi_{1}\) and \(\chi_{2}\)
The parameters \(\chi_{1}\) and \(\chi_{2}\) show the people’ sensitivity for gain and loss respectively. Generally speaking, a larger value of \(\chi_{1} (\chi_{2} )\) indicates the higher extent of sensitivity for loss (gain). In the followings, we will illustrate the effect of parameters \(\chi_{1}\) and \(\chi_{2}\) on the sorting of indoor floor materials under the conditions of \(\theta_{1} = \varepsilon_{2} = 1.21\), \(\varepsilon_{1} = \theta_{2} = 0.88\), and \(I^{G} = I^{MR} = 3\).
First, let the parameter \(\chi_{2} = 1\), the values of \(\chi_{1}\) are set from 1.1 to 3 in increments of 0.1 for sensitivity analysis. Figure 7 depicts the expected values of indoor floor materials with different \(\chi_{1}\) values.
As shown in Fig. 7, we can find that
(a) When \(\chi_{1} = 1.1\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{1} \succ x_{6} \succ x_{3}\).
(b) When \(\chi_{1} \in \{ 1.2,\;1.3,\;1.4,\;1.5\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{6} \succ x_{1} \succ x_{3}\).
(c) When \(\chi_{1} \in \{ 1.6,\;1.7,\;1.8\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{4} \succ x_{6} \succ x_{3} \succ x_{1}\).
(d) When \(\chi_{1} \in \{ 1.9,\;2, \ldots ,3\}\), the ranking of six indoor floor materials is \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\).
(f) When \(\chi_{1}\) is assigned a larger value, the expected values of all indoor floor materials are smaller, and the discrimination among them is larger.
On the other hand, if we let the parameter \(\chi_{1} = 2.25\), the expected values of indoor floor materials can be obtained as the values of \(\chi_{2}\) from 0.1 to 1 in increments of 0.1, which is shown in Fig. 8.
According to Fig. 8, we can find that the ranking of six indoor floor materials is always \(x_{5} \succ x_{2} \succ x_{6} \succ x_{4} \succ x_{3} \succ x_{1}\) with different values of \(\chi_{2}\).
Additionally, to show the impact of the changes of both parameters \(\chi_{1}\) and \(\chi_{2}\) on the final decision result, we still set \(\theta_{1} = \varepsilon_{2} = 1.21\) and \(\varepsilon_{1} = \theta_{2} = 0.88\), and Fig. 9 describes the corresponding ranking results of six indoor floor materials.
As shown in Figs. 7, 8, and 9, when parameters \(\chi_{1}\) and \(\chi_{2}\) are assigned different values, the first-ranked and the second-ranked indoor floor materials are \(x_{5}\) and \(x_{2}\) respectively, whereas the ranking results of other indoor floor materials are inconsistent. Thus, \(\chi_{1}\) and \(\chi_{2}\) can affect the final decision result. The specific values of \(\chi_{1}\) and \(\chi_{2}\) can be obtained through experimental research, questionnaire survey, and other methods.
5.4 Comparative Analysis
To demonstrate the merits of the proposed method, comparative analyses are conducted at three levels: criteria weight determination method, the correlation measurement method, and the decision-making method.
5.4.1 Comparative Analysis of Different DIBR Approaches
To verify the merit of PHF-DIBR approach, we compare it with crisp DIBR [26] and F-DIBR [28] based on the illustrative case.
At first, crisp numbers are used to represent the relations between the weights of criteria in crisp DIBR approach. Thus, the score values of PHFEs in Table 4 are calculated and used as the relations in crisp DIBR approach. In F-CIBR approach, the weight coefficients obtained from expert estimation are transformed into fuzzy weights by using the following Eq. (43).
The triangular fuzzy number \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{j}\) represents the weight of criterion \(c_{j}\), and \(\hat{w}_{j}^{k}\) denotes the crisp weight of criterion \(c_{j}\) given by DM \(e_{k}\).
Subsequently, the criteria weights are determined by the three DIBR approaches and shown in Table 12.
As we can see in Table 12, the criteria weights derived by the three DIBR approaches are different. This is because there are some gaps between these approaches in modeling uncertain information. The crisp DIBR approach uses crisp numbers to express DMs’ preferences, which may reduce the accuracy of the expression of qualitative information. Moreover, crisp DIBR approach cannot handle the fuzziness and uncertainty of DMs’ cognition. Although F-DIBR approach provides a way to show DMs’ fuzzy and uncertain opinions, the single fuzzy number cannot consider the hesitancy in preference expression. In contrast, PHF-DIBR approach adopts PHFEs to show ambiguity and intangibility of human qualitative judgments, and extracts the DMs’ hesitancy in determining the preference. Thus, compared with crisp DIBR and F-DIBR approaches, PHF-DIBR approach is more capable of handling uncertainties.
5.4.2 Comparative Analysis of NPHFCC and the Existing CCs of PHFS
To prove the merit of NPHFCC, we compare it with the existing CCs of PHFS [31,32,33]. According to Eqs. (13), (14), and (17) and the proposed decision-making procedures in the above case, the CCs between the opinions of experts and the collective evaluation under each alternative are calculated and shown in Table 13, where \(\alpha_{1} = \alpha_{2} = \alpha_{3} = 1/3\).
As we can see in Table 13, Song et al.’s CC [31] of expert e2 is very close to one for the evaluation information of alternative x6. However, there is a relatively large gap between the opinions of expert e2 and the collective evaluation under alternative x6 in the above case, which means the CC should not be close to one. The reason for this unreasonable result is that Song et al.’s CC uses the mean value of information to measure the relationship, which causes the calculation result equal to one when the mean values of two different PHFSs are equal. In contrast, Table 10 shows the correlation between the opinions of expert e2 and the collective evaluation under alternative x6 is a NPHFCC{− 0.3499 (0.2), − 0.1437 (0.1), − 0.1059 (0.2), − 0.0748 (0.1), 0.0126 (0.2), 0.5944 (0.2)}, which is consistent with the actual situation. This is because the NPHFCC is constructed based on the closeness coefficient between two PHFSs, which ensure the calculation result is equal to one if and only if the two PHFSs are exactly the same. Therefore, the NPHFCC can provide more reasonable calculation results than Song et al.’s CC.
Additionally, as we can see from Table 13 that Liu and Guan’s CC [32] produced invalid result when measuring correlations between the experts’ opinions and the collective evaluation information of alternative x1. The reason for this invalid result is that Liu and Guan’s CC adopts the mean variance and length ratio of PHFE to measure the correlations. Specifically, each length ratio of collective evaluations of alternative x1 under each criterion is 0.8333, which causes the denominator term of Eq. (16) is equal to zero. Luckily, Table 10 shows that NPHFCC does not produce invalid results, which implies NPHFCC can overcome the flaw of Liu and Guan’s CC.
Moreover, Table 13 shows that the correlations between the collective evaluations and the opinions of experts are expressed in precise numbers when using the three existing CCs. However, as both experts’ opinions and the collective evaluations are PHFSs, it is not adequate to use just a single value to represent their correlations. Fortunately, in Table 10, the NPHFCCs between experts’ opinions and the collective evaluations are characterized by a series of different values with their own probabilities. Therefore, compared with the existing CCs [31,32,33], the NPHFCC can effectively reflect the hesitancy of the original data.
5.4.3 Comparative Analysis of Single Reference Point (SRP) and the Proposed Method
In the proposed method, TRP theory is utilized to describe experts’ irrational behaviors. Thus, we compare the proposed method with the SRP method. The SRP method evaluates alternatives based on a reference point. If SRP method chooses G as the reference point, the expected values of criteria values are calculated as:
MR can also be set as a reference point. Therefore, the expected values of criteria values are computed as:
When choosing SQ as the reference point, the expected values of criteria values are expressed as:
To be consistent with the previous case, we still assume \(\chi = 2.25\), \(\theta = 0.88\) and \(\varepsilon = 0.88\) in Eqs. (44)–(46). Then we can get the expected values of six types of indoor floor materials by the above three SRP methods, and the calculation results are displayed in Fig. 10.
As shown in Fig. 10, the SPR methods and the proposed method give the same optimal indoor floor material, which proves the effectiveness of the proposed method. Meanwhile, the order of other indoor floor materials obtained by SPR methods is not completely the same as that obtained by the proposed method. The reason for these gaps between SPR methods and the proposed method is that there are some gaps in the selection of reference points. The SRP methods choose one of SQ, MR and G as the reference point, which would lose some of the important information about the effects of DMs’ irrational behaviors. In contrast, the proposed method uses three reference points to simultaneously reflect the influences of irrational behaviors. Thus, the proposed method is more suitable for human decision-making process and produces more comprehensive and rational results than SRP methods.
5.4.4 Comparative Analysis of Other Decision Methods and the Proposed Method
To validate the superiorities of our decision model, we compare it with some existing PHF-MCGDM methods, such as the integrated operation-based method [6], the utility value-based method [8,9,10], and the outranking-based method [11,12,13]. To ensure that the comparison is reasonable, all methods employ the assessments and weights derived by Sect. 5.2.
(1) Compared with the integrated operation-based method
To aggregate evaluation information in PHF-MCGDM, Zhang et al. [6] defined two operators, including PHFWA operator and PHFWG operator, for developing the integrated operation-based method. Then the integrated operation-based method is used to solve the illustrative case for showing the merit of the proposed method.
According to the procedure of the integrated operation-based method listed in [6], we need to obtain the criteria collective weights. Based on experts’ weights and the individual criteria weights, the criteria collective weights in the above case can be determined as:
where \(w_{j}\) denotes the collective weight of criterion \(c_{j}\).
Then the collective weights of criteria, PHFWA and PHFWG are employed to integrate all experts’ assessments under each criterion. Finally, the score function of PHFE and the weights of experts are adopted to obtain the weight score values of alternatives, which are listed in Table 14.
As shown in Table 14, the best indoor floor material obtained from two aggregation operators is the same as that from the proposed method, which means the proposed method is valid. Meanwhile, the ranking results of the other indoor floor materials obtained by two aggregation operators and the proposed method are inconsistent. The reason for these gaps is as follows:
(a) The information integration method is different. The integrated operation-based method uses PHFWA and PHFWG operators to simply aggregate the assessments of three experts, which leads to information loss. The proposed method uses Eq. (37) to fuse the psychological perceived values of alternatives on the three reference points, thus it considers more useful information than two aggregation operators.
(b) The ranking index is different. The integrated operation-based method uses the weighted score value to rank indoor floor materials, which ignores the influences of DMs’ irrational behaviors. In contrast, with the aid of TRP theory, the proposed method employs the expected values to sort indoor floor materials, so that the impacts of irrational behaviors on the final ranking result are considered. Therefore, the proposed method can obtain more realistic results than aggregation operators.
(2) Compared with the utility value-based method
To illustrate the advantage of the proposed method, two kinds of utility value-based methods, namely PHF-TOPSIS and PHF-VIKOR, are utilized to solve the illustrative case. When adopting PHF-TOPSIS method, the relative closeness of alternatives depends on the distances to positive ideal solution (PIS) and negative ideal solution (NIS) (please refer to [8]), which is shown in Table 14. Meanwhile, three measures of alternatives, including group utility measure, individual regret measure, and compromise measure, are calculated by using PHF-VIKOR method (please refer to [9]), which are also shown in Table 15.
As shown in Table 15, there are some gaps between two utility value-based methods and the proposed method about the ranking results. The reasons for these gaps are explained in two ways:
(a) The selected reference points are different. Both PHF-TOPSIS and PHF-VIKOR set PIS and NIS as two reference points to reflect the competitiveness of alternatives in the evaluation system. The proposed method chooses three reference points according to TRP theory, so that both the competitiveness of alternatives and DMs’ subjective requirements are considered. Therefore, compared with PIS and NIS, the reference points set by the proposed method contain more useful information.
(b) The decision context is different. Since both PHF-TOPSIS and PHF-VIKOR simply depend on the gap of alternatives to PIS and NIS to obtain the final ranking result, these methods are suitable for the situation that people are completely rational in decision. In contrast, the proposed method can handle the situation that people are irrational. Therefore, compared with PHF-TOPSIS and PHF-VIKOR, the proposed method can capture the impacts of DMs’ irrational behaviors and provide more realistic results.
(3) Compared with the outranking-based method
To validate the superiority of the proposed method, we compare it with two outranking-based methods, such as PHF-ELECTRE and PHF-QUALIFLEX, by the above illustrative case. The ranking results of alternatives (please refer to [11, 13]) are displayed in Table 16.
In Table 16, the order of indoor floor materials derived from two outranking-based methods is not the same as that derived from the proposed method. The reason for these gaps is that the ranking method is different. Two outranking-based methods rank alternatives by using the preference, indifference, and incomparability relations among six indoor floor materials, and ignore DMs’ psychology and behaviors. Compared to two outranking-based methods, the proposed method derives the order of alternatives by capturing the loss and gain from three reference points. Therefore, we can conclude that the proposed method is a useful bounded rationality behavioral decision method and more practical than the two outranking-based methods.
Additionally, during the process of PHF-ELECTRE, the concordance and discordance sets should be determined by comparing the significance of the criteria in pairs. It means that PHF-ELECTRE generates tedious computations when solving the MCGDM problem with a sufficiently large number of criteria. Moreover, PHF-QUALIFLEX must consider all possible permutations of alternatives, which implies its computation complexity will increase with the increase of number of alternatives. It is gratifying that the computational cost of the proposed method does not increase dramatically with the increase in the number of criteria and alternatives. Therefore, compared with PHF-QUALIFLEX and PHF-ELECTRE, the proposed method is more time-saving and easy to handle MCGDM problems with a large number of criteria and alternatives.
5.5 Discussion
Based on the aforementioned comparison analyses, the proposed method has merits as follows:
(1) In the criteria weight determination procedure, the proposed PHF-DIBR approach can take into account the ambiguous and hesitant comparative judgments of experts on the significances of criteria and derive criteria weights under different experts, which is closer to practical situations. Additionally, compared with crisp DIBR and F-DIBR approaches, PHF-DIBR approach can effectively represent the ambiguity and intangibility of human qualitative judgments and extract the DMs’ hesitancy in determining preferences.
(2) In the correlation measurement methodology, the NPHFCC developed in this paper can effectively measure the correlation between two PHFSs and provide support for determining the weights of experts. Moreover, compared with the existing CCs, NPHFCC can reflect the hesitancy of original data.
(3) In the decision-making methodology, the proposed method computes the expected value of each alternative based on TRP theory so as to rank alternatives, which not only retains more useful information but also overcomes the flaw of some existing PHF-MCGDM methods that ignore the impacts of DMs’ psychology and irrational behaviors on the final result.
6 Conclusions
Since the merit of PHFS in showing the uncertain information, this paper proposes a novel PHF-MCGDM method by integrating DIBR approach, NPHFCC, and TRP theory. First, to remedy the flaws of the previous CC of PHFS, the NPHFCC is defined and combined with similarity-based approach to derive DMs’ weights. Second, PHF-DIBR approach is designed to derive criteria weights under each DM. The results show that the PHF-DIBR approach can consider DMs’ ambiguous and hesitant preferences about the importance of criteria. Finally, TRP theory is adopted to obtain the order of alternatives, which fully shows the effects of DMs’ irrational behaviors on the final decision result. In addition, an illustrative example is conducted to validate the applicability of PHF-DIBR-TRP method, and comparative analyses are performed to prove its validity and merit.
Although the PHF-MCGDM method proposed in this paper has many advantages, there are still some areas worth further research. First, some criteria may be related to other criteria in practical applications, which is difficult to guarantee the independence of each criterion. Therefore, the PHF-MCGDM problem considering interactive characteristics is the focus of the next work. Second, since PHF-DIBR approach can determine the subjective weights, it can be combined with objective weighting methods to comprehensively assess the importance of criteria in the future.
Data availability
The data used to support the findings of this study are included in the article
Abbreviations
- AHP:
-
Analytic Hierarchy Process
- BWM:
-
Best–Worst Method
- CODAS:
-
Combinative Distance-based Assessment
- CC:
-
Correlation coefficient
- ELECTRE:
-
Elimination and Choice Translating Reality
- DIBR:
-
Defining Interrelationships Between Ranked Criteria
- DM:
-
Decision Maker
- F-DIBR:
-
Fuzzy DIBR
- G:
-
Goal
- HFE:
-
Hesitant Fuzzy Element
- HFS:
-
Hesitant Fuzzy Set
- MCGDM:
-
Multi-Criteria Group Decision Making
- MR:
-
Minimum Requirement
- NIS:
-
Negative Ideal Solution
- NPHFCC:
-
Novel Probabilistic Hesitant Fuzzy Correlation Coefficient
- NPHFE:
-
Normalized Probabilistic Hesitant Fuzzy Element
- PHFE:
-
Probabilistic Hesitant Fuzzy Element
- PHF-DIBR:
-
Probabilistic Hesitant Fuzzy DIBR
- PHF-DIBR-TRP:
-
Probabilistic Hesitant Fuzzy Multi-Criteria Group Decision Making Method Integrated DIBR and Tri-reference Point Theory
- PHF-MCGDM:
-
Probabilistic Hesitant Fuzzy MCGDM
- PHF-PROMETHEE:
-
Probabilistic Hesitant Fuzzy PROMETHEE
- PHFPWA:
-
Probabilistic Hesitant Fuzzy Prioritized Weighted Averaging
- PHF-QUALIFLEX:
-
Probabilistic Hesitant Fuzzy QUALIFLEX
- PHFS:
-
Probabilistic Hesitant Fuzzy Set
- PHF-TOPSIS:
-
Probabilistic Hesitant Fuzzy TOPSIS
- PHF-VIKOR:
-
Probabilistic Hesitant Fuzzy VIKOR
- PHFWA:
-
Probabilistic Hesitant Fuzzy Weighted Averaging
- PHFWG:
-
Probabilistic Hesitant Fuzzy Weighted Geometric
- PIS:
-
Positive Ideal Solution
- PROMETHEE:
-
Preference Ranking Organization Method for Enrichment Evaluations
- QUALIFLEX:
-
Qualitative Flexible Multiple Criteria Method
- R-DIBR:
-
Rough DIBR
- SPR:
-
Single Reference Point
- SQ:
-
Status Quo
- TOPSIS:
-
Technique for Order of Preference by Similarity to Ideal Solution
- TRP:
-
Tri-reference Point
- VIKOR:
-
VIse Kriterijumska Optimizacija I Kompromisno Resenja
References
Zadeh, L.A.: Fuzzy sets. Inf. Control. 8, 33 (1965)
Atanassov, K.T.: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96 (1986)
Yager, R.R.: Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 22, 958–965 (2014)
Torra, V.: Hesitant fuzzy sets. Int. J. Intell. Syst. 25, 529–539 (2010)
Xu, Z.S., Zhou, W.: Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim. Decis. Mak. 16, 481–503 (2017)
Zhang, S., Xu, Z.S., He, Y.: Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf. Fusion 38, 1–11 (2017)
Li, J., Wang, Z.X.: Multi-attribute decision making based on prioritized operators under probabilistic hesitant fuzzy environments. Soft. Comput. 23, 3853–3868 (2019)
Qi, Q.S.: TOPSIS methods for probabilistic hesitant fuzzy multiple attribute group decision-making and application to performance evaluation of public charging service quality. J. Intell. Fuzzy Syst. 43, 7317–7328 (2022)
Li, Z.Q.: VIKOR method for evaluating the management quality of teacher education with probabilistic hesitant fuzzy information. Discrete Dyn. Nat. Soc. 2021, 1326202 (2021)
Liao, N.N., Wei, G.W., Xu, X.R., Chen, X.D., Guo, Y.F.: CODAS method with probabilistic hesitant fuzzy information and its application to environmental and economically balanced supplier selection. Technol. Econ. Dev. Econ. 28, 1419–1438 (2022)
Li, J., Chen, Q.X.: An outranking method for multi-criteria decision making with probabilistic hesitant information. Exp. Syst. 37, e12513 (2020)
Li, J., Wang, J.Q.: Multi-criteria outranking methods with hesitant probabilistic fuzzy sets. Cogn. Comput. 9, 611–625 (2017)
Li, J., Wang, J.Q.: An extended QUALIFLEX method under probability hesitant fuzzy environment for selecting green suppliers. Int. J. Fuzzy Syst. 19, 1866–1879 (2017)
Kahneman, D., Tversky, A.: Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291 (1979)
Sha, X.Y., Yin, C.C., Xu, Z.S., Zhang, S.: Probabilistic hesitant fuzzy TOPSIS emergency decision-making method based on the cumulative prospect theory. J. Intell. Fuzzy Syst. 40, 4367–4383 (2021)
Liang, W., Goh, M., Wang, Y.M.: Multi-attribute group decision making method based on prospect theory under hesitant probabilistic fuzzy environment. Comput. Ind. Eng. 149, 106804 (2020)
Liao, N.N., Gao, H., Lin, R., Wei, G.W., Chen, X.D.: An extended EDAS approach based on cumulative prospect theory for multiple attributes group decision making with probabilistic hesitant fuzzy information. Artif. Intell. Rev. 56, 2971–3003 (2022)
Alarie, Y., Dionne, G.: Lottery decisions and probability weighting function. J. Risk Uncertain. 22, 21–33 (2001)
Chung, H.K., Glimcher, P., Tymula, A.: An experimental comparison of risky and riskless choice—limitations of prospect theory and expected utility theory. Am. Econ. J. Microecon. 11, 34–67 (2019)
Wang, X.T., Johnson, J.G.: A tri-reference point theory of decision making under risk. J. Exp. Psychol. Gen. 141, 743–756 (2012)
Song, W., Zhu, J.: Three-reference-point decision-making method with incomplete weight information considering independent and interactive characteristics. Inf. Sci. 503, 148–168 (2019)
Liang, D.C., Cao, W., Xu, Z.S.: Tri-reference point method for q-rung orthopair fuzzy multiple attribute decision making by considering the interaction of attributes with Bayesian network. Eng. Appl. Artif. Intell. 112, 104838 (2022)
Tu, Y., Shi, H.W., Chen, K., Liang, Y.Y., Zhou, X.Y., Lev, B.: Three-reference-point based group ELECTRE III method for urban flood resilience evaluation. Expert Syst. Appl. 210, 118488 (2022)
Liao, N.N., Cai, Q., Garg, H., Wei, G.W., Xu, X.R.: Novel gained and lost dominance score method based on cumulative prospect theory for group decision-making problems in probabilistic hesitant fuzzy environment. Int. J. Fuzzy Syst. 25, 1414–1428 (2023)
Liu, P.D., Wu, Y.F., Li, Y.: Probabilistic hesitant fuzzy taxonomy method based on best–worst-method (BWM) and indifference threshold-based attribute ratio analysis (ITARA) for multi-attributes decision making. Int. J. Fuzzy Syst. 24, 1301–1317 (2022)
Pamucar, D., Deveci, M., Gokasar, I., Işık, M., Zizovic, M.: Circular economy concepts in urban mobility alternatives using integrated DIBR method and fuzzy Dombi CoCoSo model. J. Clean. Prod. 323, 129096 (2021)
Tešić, D., Radovanović, M., Božanić, D., Pamucar, D., Milić, A., Puška, A.: Modification of the DIBR and MABAC methods by applying rough numbers and its application in making decisions. Information 13, 353 (2022)
Pamucar, D., Simic, V., Lazarević, D., Dobrodolac, M., Deveci, M.: Prioritization of sustainable mobility sharing systems using integrated fuzzy DIBR and fuzzy-rough EDAS model. Sustain. Cities Soc. 82, 103910 (2022)
Yue, Z.: Deriving decision maker’s weights based on distance measure for interval-valued intuitionistic fuzzy group decision making. Expert Syst. Appl. 38, 11665–11670 (2011)
Yue, Z.: Approach to group decision making based on determining the weights of experts by using projection method. Appl. Math. Model. 36, 2900–2910 (2012)
Song, C.Y., Xu, Z.S., Zhao, H.: New correlation coefficients between probabilistic hesitant fuzzy sets and their applications in cluster analysis. Int. J. Fuzzy Syst. 21, 355–368 (2019)
Liu, Y., Guan, X.: Mixed correlation coefficient between probability hesitation fuzzy sets and applications. Int. J. Fuzzy Syst. 26, 154–167 (2024)
Zhang, S.S., Liu, X.D., Garg, H., Zhang, S.T.: Investment decision making in the fuzzy context: an integrated model approach. J. Intell. Fuzzy Syst. 44, 3763–3786 (2023)
Liao, H.C., Xu, Z.S., Zeng, X.J.: Novel correlation coefficients between hesitant fuzzy sets and their application in decision making. Knowl. Based Syst. 82, 115–127 (2015)
Lin, M.W., Zhan, Q.S., Xu, Z.S.: Decision making with probabilistic hesitant fuzzy information based on multiplicative consistency. Int. J. Intell. Syst. 35, 1233–1261 (2020)
Li, J., Chen, Q.X., Niu, L.L., Wang, Z.X.: An ORESTE approach for multi-criteria decision-making with probabilistic hesitant fuzzy information. Int. J. Mach. Learn. Cybern. 11, 1591–1609 (2020)
Wang, X.T., Wang, P.: Tri-reference point theory of decision making: from principles to applications. Adv. Psychol. Sci. 21, 1331–1346 (2013)
Liu, X.D., Wang, Z.W., Zhang, S.T., Garg, H.: Novel correlation coefficient between hesitant fuzzy sets with application to medical diagnosis. Expert Syst. Appl. 183, 115393 (2021)
Su, N.N., Zhu, X.Q., Xin, Y.S.: Using improved prospect theory to develop a partner selection method for virtual enterprises with unknown weight. Math. Probl. Eng. 2020, 9608704 (2020)
Chen, Z.S., Martínez, L., Chang, J.P., Wang, X.J., Xiong, S.H., Chin, K.S.: Sustainable building material selection: a QFD- and ELECTRE III-embedded hybrid MCGDM approach with consensus building. Eng. Appl. Artif. Intell. 85, 783–807 (2019)
Reza, B., Sadiq, R., Hewage, K.: Sustainability assessment of flooring systems in the City of Tehran: an AHP-based life cycle analysis. Constr. Build. Mater. 25, 2053–2066 (2011)
Meng, F.Y., Dong, B.H.: Linguistic intuitionistic fuzzy PROMETHEE method based on similarity measure for the selection of sustainable building materials. J. Ambient. Intell. Humaniz. Comput. 13, 4415–4435 (2022)
Hamza, M., Bafail, O., Alidrisi, H.: HVAC systems evaluation and selection for sustainable office buildings: an integrated MCDM approach. Buildings 13, 1847 (2023)
Acknowledgements
The authors would like to thank the Editor-in-Chief, the associated editor and anonymous reviewers for their insightful and constructive comments and suggestions that have led to an improved version of this paper. The work was supported by the National Natural Science Foundation of China (Grant No. U1904211), National Social Science Foundation of China (Grant No. 20BTJ059), Training Program for Young Backbone Teachers in Higher Education Institutions of Henan Province (Grant No. 2021GGJS006), Support Program for Innovative Talents in Philoso phy and Social Science of Henan Province (Grant No. 2023-CXRC-19), Precision Disciplines Support Program of Zhengzhou University (Grant No. XKLMJX202201), and Outstanding Young Research Team in Social Sciences of Zhengzhou University (Grant No. 2023-QNTD-01).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhu, F., Liu, Y., Sun, J. et al. A Probabilistic Hesitant Fuzzy Multi-criteria Group Decision-Making Method Integrated DIBR and Tri-reference Point Theory. Int. J. Fuzzy Syst. (2024). https://doi.org/10.1007/s40815-024-01728-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40815-024-01728-w