1 Introduction

Today, using power electronic devices at various levels has become very popular. Such popularity is due to their high efficiency and controllability; however, these devices are the main source of harmonic generation as well. Harmonics have significantly negative impacts on power systems since they decrease power quality and power factor and increase wastage of power [1,2,3]. Such negative effects can be divided into two categories: short-term and long-term effects. Short-term negative effects include voltage distortion, sensitive loads slippage, and overheating and saturation of the iron cores fitted in the power system (such as electrical machines, transformers, etc.). Long-term negative effects include increased power loss and voltage stress [4].

Each of the aforementioned negative effects involves other problems as well. For instance, voltage stress may result in problems such as relay malfunction and excessive pressure on capacitor dielectrics. One way to reduce harmonics is to use inactive filters (RLC circuits). This is usually used in high-voltage discrete current lines. The inactive filters not only reduce harmonics but also improve the power factor; however, they can correct only a particular power system (i.e., the system for which they have been designed), and they are not capable of adapting to changes in the system [5]. In addition, resonance with system impedance may also occur. Considering the problems mentioned above, developing a design that could tackle such problems seemed indispensable; therefore, Sasaki and Machida proposed the active filter in 1971 [6]. Active filters carry out such actions as reactive power compensation, harmonics reduction, voltage or current negative sequence compensation, and voltage adjustment [7]. There are two types of active filters: series and shunt. Shunt-active filters are used for current compensation while series-active filters are mainly used for voltage compensation [7, 8]. The current control system constitutes an important part of the structure of shunt-active filters, and many methods have been suggested for controlling the inverter current. The main differences among current controllers include response speed, ease of application, maximum current capability, insensitivity to line parameters, and reduction in the number of switches.

The optimization of the structure of active filters can be achieved in different ways. They include changing the inductance which connects the filter to the line LC to LCL and optimizing the same [9, 10], using four-switch three-phase inverters (FSTPI) [11], improved modulation methods [12], fuzzy logic [13], Kalman filter [14], and the sin cosine algorithm [15].

In this paper, total harmonic distortion (THD) of the current is reduced in two steps. First, by phase shifting in load currents, the existing harmonics are reduced. Then, by applying the active filter of which coefficients of the PI controllers, i.e., kp and ki, are adjusted by using the FPSO algorithm, the harmonics are reduced to a level allowed by the IEEE-519 standard.

In Sect. 2, the structure of the shunt-active filter is discussed. The proposed filter is described in Sect. 3. In Sect. 4, the results of the simulations conducted by MATLAB software is discussed in order to show the capabilities of the proposed method. In the end, the conclusions made about this structure are provided.

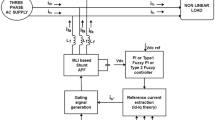
2 Shunt-Active Filter

In the structure of shunt-active filters, as illustrated in Fig. 1, there are three elements. The first element is the identification phase. In this phase, the purpose is to generate the reference signal which needs to be generated by the compensator for reducing the harmonics of the line current. Another essential element is the inverter, which makes the reference signal generated in the identification phase in the form of a power signal to be injected into the line and, thus, reduces harmonics. The inverter control takes place in the modulation phase.

Fig. 1
figure 1

Structure of active filter

Full size image

2.1 Identification Method

The methods of generating reference currents are classified into two groups: temporal and frequency. Temporal methods, like d–q conversion (synchronous rotary reference frame) and p–q conversion (theory of momentary active and reactive powers), are based on three-phase measurements and conversions whereas frequency methods are based on Fast Fourier Transfer [16]. Temporal methods have a higher velocity. In contrast, frequency methods enjoy a higher accuracy. The theory of momentary active and reactive powers is one of the temporal theories that do not yield an appropriate performance with harmonic sources. This fact has been proved with mathematical arguments.

Following this theory, first, the current and voltage are measured using abc coordinates; then, they are transferred to the orthogonal \((\alpha \beta o)\) frame, according to Eqs. (1) and (2).

$$\left[ {\begin{array}{lll} {v_{\alpha } } \\ {v_{\beta } } \\ {v_{o} } \\ \end{array} } \right] = \sqrt {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \left[ {\begin{array}{lll} 1 & { - 0.5} & { - 0.5} \\ 0 & {\frac{ - \sqrt 3 }{2}} & {\frac{\sqrt 3 }{2}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} \\ \end{array} } \right]\left[ {\begin{array}{lll} {v_{a} } \\ {v_{b} } \\ {v_{c} } \\ \end{array} } \right],$$
(1)
$$\left[ {\begin{array}{lll} {i_{\alpha } } \\ {i_{\beta } } \\ {i_{o} } \\ \end{array} } \right] = \sqrt {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \left[ {\begin{array}{lll} 1 & { - 0.5} & { - 0.5} \\ 0 & {\frac{ - \sqrt 3 }{2}} & {\frac{\sqrt 3 }{2}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} \\ \end{array} } \right]\left[ {\begin{array}{lll} {i_{a} } \\ {i_{b} } \\ {i_{c} } \\ \end{array} } \right].$$
(2)

Later on, the powers are calculated in the new space, according to Eq. (3).

$$\left[ {\begin{array}{lll} P \\ q \\ {P_{o} } \\ \end{array} } \right] = \left[ {\begin{array}{lll} {v_{\alpha } } & {v_{\beta } } & 0 \\ { - v_{\beta } } & {v_{\alpha } } & 0 \\ 0 & 0 & {v_{o} } \\ \end{array} } \right]\left[ {\begin{array}{lll} {i_{\alpha } } \\ {i_{\beta } } \\ {i_{0} } \\ \end{array} } \right].$$
(3)

These powers have dc and ac terms. If the purpose is to reduce current harmonics, the compensating power needs to be symmetrical concerning the term ac of the powers mentioned above. Therefore, the reference currents for the compensator follow Eq. (4). Finally, these currents are obtained by getting reversed to abc coordinates, following Eq. (5).

$$\left[ {\begin{array}{lll} {i^{*}_{\alpha } } \\ {i^{*}_{\beta } } \\ {i^{*}_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{lll} {v_{\alpha } } & {v_{\beta } } & 0 \\ { - v_{\beta } } & {v_{\alpha } } & 0 \\ 0 & 0 & {v_{o} } \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{lll} { - P_{ac} } \\ { - q_{ac} } \\ { - P_{{o{}_{ac}}} } \\ \end{array} } \right],$$
(4)
$$\left[ {\begin{array}{lll} {i^{*} a} \\ {i^{*} b} \\ {i^{*} c} \\ \end{array} } \right] = \left\{ {\sqrt {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}} \left[ {\begin{array}{lll} 1 & { - 0.5} & { - 0.5} \\ 0 & {\frac{ - \sqrt 3 }{2}} & {\frac{\sqrt 3 }{2}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 2 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt 2 }$}}} \\ \end{array} } \right]} \right\}^{ - 1} \left[ {\begin{array}{lll} {i^{*}_{\alpha } } \\ {i^{*}_{\beta } } \\ {i^{*}_{0} } \\ \end{array} } \right].$$
(5)

This method yields satisfactory results for sine sources; however, it cannot provide an appropriate response for harmonic sources. To prove such a claim, let us consider the currents and voltages, as shown in harmonic Eqs. (6) and (7).

$$\left\{ \begin{array}{lll} v_{a} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 V_{n} } \sin (n\omega t + \psi_{n} ) \hfill \\ v_{b} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 V_{n} } \sin (n\omega t + 120 + \psi_{n} ) \hfill \\ v_{c} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 V_{n} } \sin (n\omega t - 120 + \psi_{n} ) \hfill \\ \end{array} \right..$$
(6)
$$\left\{ \begin{array}{lll} i_{a} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 I_{n} } \sin (n\omega t - \varphi_{n} ) \hfill \\ i_{b} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 I_{n} } \sin (n\omega t - \varphi_{n} + 120) \hfill \\ i_{c} = \sum\limits_{n = 1}^{\infty } {\sqrt 2 I_{n} } \sin (n\omega t - \varphi_{n} - 120) \hfill \\ \end{array} \right..$$
(7)

Now, if such voltages and currents are transferred to the orthogonal frame and then they are expressed based on positive, negative, and zero sequences, we will have

$$\left\{ \begin{array} {lll}v_{\alpha } = \sqrt 3 \sum\limits_{n = 1}^{\infty } {V_{n}^{ + } } \sin (n\omega t + \psi_{n}^{ + } ) + V_{n}^{ - } \sin (n\omega t + \psi_{n}^{ - } ) \hfill \\ v_{\beta } = \sqrt 3 \sum\limits_{n = 1}^{\infty } { - V_{n}^{ + } } \cos (n\omega t + \psi_{n}^{ + } ) + V_{n}^{ - } \cos (n\omega t + \psi_{n}^{ - } ) \hfill \\ v_{o} = \sqrt 6 \sum\limits_{n = 1}^{\infty } {V_{n}^{o} } \sin (n\omega t + \psi_{{_{n} }}^{0} ) \hfill \\ \end{array} \right.,$$
(8)
$$\left\{ \begin{array}{lll} i_{\alpha } = \sqrt 3 \sum\limits_{n = 1}^{\infty } {(I_{n}^{ + } } \sin (n\omega t - \varphi_{n}^{ + } ) + I_{n}^{ - } \sin (n\omega t - \varphi_{n}^{ - } )) \hfill \\ i_{\beta } = \sqrt 3 \sum\limits_{n = 1}^{\infty } {( - I_{n}^{ + } } \cos (n\omega t - \varphi_{n}^{ + } ) + I_{n}^{ - } \cos (n\omega t - \varphi_{n}^{ - } )) \hfill \\ i_{o} = \sqrt 3 \sum\limits_{n = 1}^{\infty } {(I_{n}^{o} } \sin (n\omega t - \varphi_{n}^{0} )) \hfill \\ \end{array} \right. .$$
(9)

The powers of the new frame are calculated by Eq. (10):

$$\left\{ \begin{array}{lll} P = 3\sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {\left\{ {V_{j}^{ + } I_{i}^{ + } \cos ((i - j)\omega t + \varphi_{i}^{ + } - \psi_{j}^{ + } ) + V_{j}^{ - } I_{i}^{ - } \cos ((i - j)\omega t + \varphi_{i}^{ - } - \psi_{j}^{ - } )} \right.} } \hfill \\ - V_{j}^{ + } I_{i}^{ - } \cos ((i + j)\omega t + \varphi_{i}^{ - } + \psi_{j}^{ + } ) - V_{j}^{ - } I_{i}^{ + } \cos ((i + j)\omega t + \varphi_{i}^{ + } + \psi_{j}^{ - } \left. ) \right\} \hfill \\ q = 3\sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {\left\{ { - V_{j}^{ + } I_{i}^{ + } \sin ((i - j)\omega t + \varphi_{i}^{ + } - \psi_{j}^{ + } ) + V_{j}^{ - } I_{i}^{ - } \sin ((i - j)\omega t + \varphi_{i}^{ - } - \psi_{j}^{ - } )} \right.} } \hfill \\ + V_{j}^{ + } I_{i}^{ - } \sin ((i + j)\omega t + \varphi_{i}^{ - } + \psi_{j}^{ + } ) - V_{j}^{ - } I_{i}^{ + } \sin ((i + j)\omega t + \varphi_{i}^{ + } + \psi_{j}^{ - } \left. ) \right\} \hfill \\ P_{o} = 3\sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {V_{j}^{o} I_{j}^{o} } \left\{ {\cos ((i - j)\omega t + \varphi_{i}^{o} - \psi_{j}^{o} ) - \cos ((i + j)\omega t + \varphi_{i}^{o} + \psi_{j}^{o} )} \right\}} \hfill \\ \end{array} \right. .$$
(10)

dc powers can be extracted from the above equations, as described below:

$$\left\{ \begin{array}{lll} P_{dc} = 3\sum\limits_{n = 1}^{\infty } {V_{n}^{ + } I_{n}^{ + } } \cos (\varphi_{n}^{ + } - \psi_{n}^{ + } ) + V_{n}^{ - } I_{n}^{ - } \cos (\varphi_{n}^{ - } - \psi_{n}^{ - } ) \hfill \\ q_{dc} = 3\sum\limits_{n = 1}^{\infty } { - V_{n}^{ + } I_{n}^{ + } } \sin (\varphi_{n}^{ + } - \psi_{n}^{ + } ) + V_{n}^{ - } I_{n}^{ - } \cos (\varphi_{n}^{ - } - \psi_{n}^{ - } ) \hfill \\ p_{{{o_{dc}}}} = 3\sum\limits_{n = 1}^{\infty } {V_{n}^{o} I_{n}^{o} } \cos (\varphi_{n}^{o} - \psi_{n}^{o} ) \hfill \\ \end{array} \right. .$$
(11)

Equation (11) indicates that harmonics also play a role in transferring dc power from source to the load, so compensating ac powers is insufficient for reducing line harmonics. Therefore, due to the occurrence of voltage harmonics, the efficiency of this theory is weakened. The method used by the authors of the present paper is a frequency method that is based on band-stop filters. In this method, the line current signal is passed through a band-stop filter with a definite frequency equal to the basic frequency in the power system. As a result, the signal gained at the exit of this filter will have all harmonics except the main element. This signal can be considered a suitable reference for compensation.

In addition, band-stop filters only sample the current while the proposed theory samples both the current and the voltage. In other words, this method only needs the current sensor; however, theories of momentary active and reactive powers need both the current sensor and the voltage sensor, which increases the costs of the hardware required. It is needless to say that one end of the experiments is to save costs, and this is in line with the purposes of this study as well. Therefore, using band-stop filters is preferred.

3 Proposed Active Filter

In the proposed active filter, the frequency method mentioned earlier has been used in the identification phase. Then, the current signals gained in this phase are transformed into voltage signals. This method will be explained in the next section. Subsequently, the gained signals will be generated with the inverter and will be injected into the line to reduce current harmonics.

3.1 Transforming Current Signals to Voltage

Since a voltage source inverter was used, first, the current signals generated during the identification phase need to be transformed to voltages. Then, such voltages will be generated by an inverter. The inverter output is connected to the line by a self; hence, there should be some capacitor properties in the compensator so that the effect of the self will not reduce the ability of the filter. On the other hand, since the capacitor voltage is the integral of the capacitor current, the reference signal acquired in the previous phase will go through a PI controller so that this signal will be transformed into a voltage reference signal having capacitor properties. Now, the PI controller coefficients must be adjusted so that the filter efficiency will be maximized. Therefore, these coefficients are determined with the purpose of reducing line current harmonics with the PSO algorithm.

3.2 PSO Algorithm

PSO algorithm is based on group movements of particles. In this algorithm, the time interval is considered. Therefore, as in Eq. (12), the situation of each particle in the new phase will be its location in the previous phase plus velocity.

$$V = \Delta x/\Delta t = \left( {x - x_{0} } \right)/1 \to x = vt + x$$
(12)

Each particle moves in two directions: the direction of the best situation it has had up to now (Pbest,i), and the direction of the best situation of all of the existing particles (gbest). As a result,

$$\Delta v_{i} = \Delta x_{1,i} + \Delta x_{2,i} = \left( {P_{best,i} - x_{i} } \right) + \left( {g_{best} - x_{i} } \right).$$
(13)

It is better to multiply these two expressions by the random coefficients C1 and C2, respectively, so that the nature of random movements will be created in the particles. Therefore,

$$\Delta v_{i} = C_{1} *\left( {P_{{{\text{best}},i}} x_{i} } \right) + C_{2} *\left( {g_{{{\text{best}}}} - x_{i} } \right),$$
(14)
$$v_{i}^{{{\text{new}}}} = v_{i}^{{{\text{old}}}} + C_{1} *\left( {P_{{{\text{best}},i}} x_{i} } \right) + C_{2} *\left( {g_{{{\text{best}}}} - x_{i} } \right).$$
(15)

To gradually reduce the effects of previous velocities, the expression Viold is multiplied by the inertia constant w (w is a coefficient less than 1). As a result,

$$v_{i}^{{{\text{new}}}} = w*v_{i}^{{{\text{old}}}} + C_{1} *\left( {P_{{{\text{best}},i}} x_{i} } \right) + C_{2} *\left( {g_{{{\text{best}}}} - x_{i} } \right),$$
(16)
$$x_{i}^{{{\text{new}}}} = x_{i}^{{{\text{old}}}} + w*v_{i}^{{{\text{old}}}} + C_{1} *\left( {P_{{{\text{best}},i}} x_{i} } \right) + C_{2} * \, \left( {g_{{{\text{best}}}} - x_{i} } \right).$$
(17)

Experientially, the coefficients C1, C2, and w are within the following limits:

C1 + C2 <  = 4.

0.1 < W < 1.

Here, the coefficient w has been considered constant, though it sometimes requires changes. In the next section, a fuzzy method that expresses this coefficient as a variable will be explained.

3.3 PSO Algorithm with Fuzzy Inertia Constant

It is proposed that the inertia is not constant in all iterations. These changes can be linear, according to Eq. (18), but this change only leads to a decrease in inertia [17].

$${w}^{k}={w}_{max}-\frac{{w}_{max}-{w}_{min}}{{k}^{max}}k,$$
(18)

where \({w}_{\text{max}}\) and \({w}_{\text{min}}\) are maximum and minimum values of inertia constant, respectively. k is the number of iterations, \({k}^{\text{max}}\) is the maximum iteration, and \({w}^{k}\) is the inertia in kth iteration.

In PSO algorithm, the change process of the inertia constant is not always decreasing or increasing; rather it occasionally increases or decreases. Also, at times, the changes are not limited to a number of separate points, and the change process is not constant. In such cases, the inertia constant is better defined as fuzzy [17].

In the fuzzy method, first, the objective function must be normalized. Hence, the function f is normalized, according to Eq. (19):

$$f_{{{\text{norm}}}} = \left( {f - f_{\min } } \right)/\left( {f_{\max } - f_{\min } } \right).$$
(19)

Then, the diagram of membership functions for w, fnorm, and Δw will be as illustrated (Fig. 2).

Fig. 2
figure 2

Membership function of a normalized fitness, b inertia weight, and c change in inertia weight

Full size image

The next phase is to define fuzzy rules. This is provided in Table 1.

Table 1 Fuzzy rule for inertia weight correction
Full size table

where, S = Small, M = Medium, and L = large. Moreover, Z = Zero, N = Negative, and P = Positive.

According to Table 1, Δw will be determined at each phase, and it will either increase or decrease w.

3.4 Execution Phases of the PSO Algorithm

The PSO algorithm includes several steps as follows:

(I) Determining control variables and their ranges.

(II) Forming the initial population in a random manner and within the authorized range.

(III) Calculating the cost function for the initial population.

(IV) Determining best,i and gbest.

(V) Selecting i, trustworthy member.

(VI) Selecting a member and updating its situation.

(VII) Calculating the cost function for it.

(VIII) Updating best,i and gbest.

(IX) Considering the selection of all members.

No: Return to phase V.

Yes: Move to phase X.

(X) Controlling the convergence condition.

No: Return to phase V.

Yes: Move to phase XI.

(XI) Selecting gbest as the final response.

4 Simulation Results

To show the capabilities of the proposed active filter for reducing harmonics, we need a non-linear load. For this purpose, we use two diode-bridge rectifiers as the load. The rectifier, as shown in Fig. 3, is connected to the load RL.

Fig. 3
figure 3

Non-linear load, diode-bridge rectifier

Full size image

4.1 Simple Load

If we connect the given loads to a sine source, the diagrams of the changes related to its line current will be like Fig. 4A. The line current frequency spectrum is calculated using the following equations:

$$i_{1} (t) = a_{0} + \sum\limits_{n = 1}^{\infty } {\left[ {a_{n} \cos (n\omega t) + b_{n} \sin (n\omega t)} \right]} \,,$$
(20)
$$a_{0} = I_{dc} = \frac{1}{2\pi }\int\limits_{0}^{2\pi } {i_{1} (t)d(\omega t) = 0\,} ,$$
(21)
Fig. 4
figure 4

Line current without a compensator. a Temporal waveform. b Frequency spectrum.

Full size image
$${a}_{n}=\frac{1}{\pi }\underset{0}{\overset{2\pi }{\int }}{i}_{1}\left(t\right)\mathrm{cos}\left(n\omega t\right)d\left(\omega t\right)=\frac{{I}_{a}}{\pi }\left[\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}\mathrm{cos}\left(n\omega t\right)d\left(\omega t\right)-\underset{\frac{7\pi }{6}}{\overset{11\frac{\pi }{6}}{\int }}\mathrm{cos}\left(n\omega t\right)d\left(\omega t\right)\right]=0,$$
(22)
$${b}_{n}=\frac{1}{\pi }\underset{0}{\overset{2\pi }{\int }}{i}_{1}\left(t\right){\sin}\left(n\omega t\right)d\left(\omega t\right)=\frac{{I}_{a}}{\pi }\left[\underset{\frac{\pi }{6}}{\overset{\frac{5\pi }{6}}{\int }}\sin\left(n\omega t\right)d\left(\omega t\right)-\underset{\frac{7\pi }{6}}{\overset{11\frac{\pi }{6}}{\int }}\sin\left(n\omega t\right)d\left(\omega t\right)\right]\to$$
$${b}_{n}=\left\{\begin{array}{ll}0\,\, if\,\, n=2k\\ 0\,\, if\,\, n=3k\\ \frac{4{I}_{a}}{n\pi }{\sin}\left(\frac{n\pi }{3}\right)\,\, otherwise\end{array}\right. .$$
(23)

It is worth mentioning that, in the above equations, the amplitude of the peak current is equal to (\(\pm I_{a}\)), i.e., the small variations in peak are neglected in the above calculation.

According to Eqs. (21), (22), and (23), the amplitudes of 2nd and 3rd harmonics and their multiples are zero, and there are other harmonics. The line current frequency spectra are shown in Fig. 4b. According to this figure, THD is equal to 20.56%, which is higher than the allowable IEEE-519 standard. Initially, to reduce THD, two diode-bridge rectifiers are linked to the line by two transformers with D–D and Y–D connections. Subsequently, an active filter equipped by FPSO is used for further harmonic reduction.

4.2 Phase Shifting of Load Current

As mentioned, if two diode bridges are connected to a line with two star-triangle and triangle-triangle transformers, the load current of the two rectifiers will have 30 degrees phase difference. The new load current, as shown in Fig. 5, will be less disturbed, and THD will drop below 8%. In fact, harmonics 5, 7 and their multiples are eliminated. However, this value is higher than the standard limit, and it is recommended to use a shunt-active filter and reduce the current THD. It is described in the next section.

Fig. 5
figure 5

Line current with phase shifting of load currents. a Temporal waveform. b Frequency spectrum.

Full size image

4.3 Shunt-Active Filter Trained by FPSO

Since phase shifting in the load currents did not reduce the harmonics by less than 5%, so shunt-active filter (SAF) is employed. SAF with PI controller reduces harmonics. Fundamental to SAF use is to appropriately tune its filters coefficients to enhance their performance. For this purpose, the PSO algorithm of which inertia constant w is determined by the fuzzy method is used in the objective function as follows:

$${\text{Min }}\left( {{\text{THD }}I_{{{\text{line}}}} } \right).$$
(24)

If the FPSO algorithm is used to reduce the harmonic current, kp and ki will be obtained according to Table 2.

Table 2 PI controller coefficient
Full size table

It should be noted that these values are obtained by considering the phase shifting of the current. If the current phase shift is not taken into account, the obtained THD, as shown in Fig. 6, will be greater than 7%, which is not acceptable. Once both the phase shift and the active filter are used together, the harmonics will be reduced to 2.15%, (Fig. 7), which is acceptable by IEEE-519 standard.

Fig. 6
figure 6

Line current with active filter without phase shifting. a Temporal waveform. b Frequency spectrum.

Full size image
Fig. 7
figure 7

Line current with both active filter and phase shifting. a Temporal waveform. b Harmonic spectrum.

Full size image

The FSTPI cannot decrease the current THD to less than 5% [11]. Therefore, it is not an appropriate choice. Moreover, the variable index method [12, 18] not only requires variable switching frequency but also increases switching losses.

5 Conclusion

In this paper, THD initially decreases with load current phase shifting. Next, a trained active filter with the FPSO algorithm was used. The adjustment of the inertia constant w with fuzzy methods yields fairly better results. The utilized active filter not only enjoys some advantages, including simplicity of control algorithm and acceptable performance in the presence of harmonics but also can reduce THD to less than the acceptable value of the IEEE-519 standard.