1 Introduction

With the development of hybrid systems, digital control and network control systems (see [1,2,3,4,5,6]), the importance of quantization methods has increased in recent years. These systems need to transmit information between components via wireless media. Because of the wireless communication network has physical constraints, it is necessary to introduce quantization technology to reduce communication rate. Quantitative control of linear and nonlinear plants has received much attention in the past several years, which result in many fruitful results [4,5,6,7,8,9,10]. Among the above results [4,5,6], are for linear quantized systems [7,8,9,10,11], are for nonlinear quantized systems. Theoretically, the above works merely ensure the expected performance as the time variable approaches infinity. In addition, the above works require the control system is fully known.

Due to the influence of uncertain factors, the actual systems have nonlinearity. The nonlinear system functions, including the bounding functions, may be completely unknown. As we all know, the adaptive fuzzy or neural control approaches are very useful tool to solve unknown nonlinear problems, for instance, see [12,13,14,15]. It is worth mentioning that the above works are realized on the basis of infinite time stability, and the results of the asymptotic stability has been unable to meet people’s needs. Different from asymptotic stability, the good features of finite time control are fast response speed, high tracking accuracy and strong anti-interference ability. Obviously, finite time stability make the systems have better transient performance. In recent years, the researches about finite time control has been well developed. In [16], the terminal sliding mode control method was raised. On that basis [17], established a terminal sliding manifold to surmount the singularity around the equilibrium point. Sliding mode control is a useful tool to stabilize complex nonlinear systems. In [18], the event-triggered fuzzy sliding mode control issue about a networked control system based on a semi-Markov process was studied. The sliding mode control problem of nonlinear stochastic Markov jump systems with uncertain time-varying delays was studied in [19]. The Lyapunov-type finite-time stability theory was established firstly in [20, 21] to solve the chattering phenomenon resulted from the sliding mode controller. On that basis [22, 23], studied the finite-time stability of nonlinear systems. In order to guarantee the capability of the system under low communication rates, the quantization scheme was proposed on basis of finite time stability. In [24], the quantitative control problem of finite-time synthesis of nonlinear semi-Markov switching systems based on T–S fuzzy means was studied. In [25], the issue of finite-time quantitative cost-guaranteed fuzzy control of nonlinear systems was discussed. The issue of finite-time adaptive fuzzy control for nonlinear quantized systems with unknown time delays was discussed in [26]. Even though some works about finite time on basis of nonlinear quantized systems has made some progress, the determination of time relies on the initial state. Therefore, when the initial conditions are unknown, the designer cannot accurately estimate the system stability time, which restricts the application of finite time control. When initial conditions are unknown or uncertain, the finite time control methods described above have been unable to guarantee that the systems achieve the desired performance at a predetermined time.

To solve this problem, a sufficient condition for stability in fixed time was raised for the first time in [27]. From [27], the stability time of the system is connected with a constant that has nothing to do with the initial state, and the constant is only determined by the design parameters. The fixed-time stability is especially important for either hybrid or switching systems [28,29,30] with dwell time. According to the theorem of stability in fixed time in [27], the fixed time controller was constructed for nonlinear systems in [31, 32] respectively. In [33], the issue of fixed-time stability of strict-feedback uncertain nonlinear systems was investigated [34] proposed a fixed-time adaptive control strategy for nonlinear systems by neural network. In [35], a fixed-time terminal sliding mode control means was raised for momentum wheel system. A global fixed-time consistency protocol of second-order multi-agent systems was discussed in [36]. In [35, 36], the sinusoid continuous functions were introduced to eliminate the singularity. In order to suppress chaotic oscillation in power system, a fast fixed time non-singular terminal sliding mode control means was proposed in [37]. However, it should be pointed out that the results in [31,32,33,34,35,36,37] need to meet the hypothesis that the nonlinear function is known. Moreover, since the signals between the factory and the controller are realized remotely through the communication channel with limited bandwidth, the quantization of the control signals cannot be ignored. In [38], the fixed-time attitude tracking control issue of rigid spacecraft with external disturbances and input quantization was investigated. It should be pointed out that the nonlinear function of the system in [38] is known. When the nonlinear terms of uncertain nonlinear systems are completely unknown, the fixed time control schemes mentioned above have been unable to apply. It is a challenge to construct a quantitative feedback controller to avoid chattering and ensure the system is stable at fixed time. Inspired by the above, the adaptive fixed-time control issue of quantized uncertain nonlinear systems is investigated in this paper. The main merits are generalized below.

  1. (1)

    Compared with the existing fixed-time works [31,32,33,34,35,36,37] for nonlinear systems, the quantitative control issue is considered. Compared with [38], the nonlinear function of the system is completely unknown in this paper. By applying the fuzzy logic system to approximate unknown nonlinearities, a novel fixed-time fuzzy control strategy is raised. The proposed control strategy ensures the system performance in fixed time.

  2. (2)

    In the finite-time control schemes [20,21,22,23,24,25,26], the convergence time is dependent on the initial conditions. In practice, the initial condition of the system is not easy to obtain, which makes the schemes in [20,21,22,23,24,25,26] difficult to implement. Instead, by constructing a novel fuzzy fixed-time controller, this limitation can be overcome in this paper. The upper bound of convergence time is merely affected by design parameters. The proposed control strategy is more interesting in application.

This article is organized below. The preliminary knowledge and problem description are introduced in the second part. The third part gives the major research results of this article. Simulation studies are conducted in the fourth part. Finally, the fifth part summarizes the work.

2 Preliminaries and Problem Statement

According to some lemmas and definitions of fixed-time control, important results of this article are obtained in this part.

2.1 Preliminaries

Definition 1

[39] Think about a nonlinear system:

$$\begin{aligned} \dot{x}=f(x,t), x(0)=x_{0} \end{aligned}$$
(1)

where \(x\in R^n\) represents state variable, f(x, t) is unknown smooth nonlinear function and satisfy \(x(0)=0\), \(f(0,0)=0\). Suppose that system (1) is stable in Lyapunov sense. If there exist convergence time T, for \(\forall t \ge T\) , \(x(t)=0\), then system (1) is finite-time stability.

Definition 2

[39] If system (1) is stable in finite time, and convergence time T has a definite upper bound \(T_{m}\) , and the upper bound don’t affect by the initial state, then the system (1) is fixed-time stability.

Lemma 1

[34] If the design constants \(\varsigma ,\epsilon >0\), \(p>1, q\in (0,1),\eta \in (0,\infty )\), one has:

$$\begin{aligned} \dot{V}\le -\varsigma V^{p}(x)-\epsilon V^{q}(x)+\eta ,\forall x\in R^{n} \end{aligned}$$
(2)

the system (1) is globally fixed-time stability, and settling time \(T_{m}\) reckons as:

$$\begin{aligned} T \le T_{m}=\frac{1}{\varsigma \phi (p-1)}+\frac{1}{\epsilon \phi (1-q)} \end{aligned}$$
(3)

the residual set of system (1) solution as follows:

$$\begin{aligned} x\in \left\{ V(x)\le min\left\{ (\frac{\eta }{(1-\phi )\varsigma })^{\frac{1}{p}}, (\frac{\eta }{(1-\phi )\epsilon })^{\frac{1}{q}}\right\} \right\} . \end{aligned}$$
(4)

Lemma 2

[40] For any given \((x,y)\in R^{2},\) \(\alpha> 1, \beta> 1, \varepsilon > 0,\) and \((\alpha -1)(\beta -1)=1,\) the following relation hold:

$$\begin{aligned} xy\le \frac{\varepsilon ^\alpha }{\alpha }|x|^\alpha +\frac{1}{\beta \varepsilon ^\beta }|y|^\beta . \end{aligned}$$

Lemma 3

[41] For any given positive constants \(b_{1},b_{2},b_{3}\), and real variables x and y, we have:

$$\begin{aligned} \left| x\right| ^{b_{1}}\left| y\right| ^{b_{2}}\le \frac{b_{1}}{b_{1}+b_{2}}b_{3}\left| x\right| ^{b_{1}+b_{2}}+\frac{b_{2}}{b_{1} +b_{2}}b_{3}^{-\frac{b_{1}}{b_{2}}}\left| y\right| ^{b_{1}+b_{2}}. \end{aligned}$$
(5)

Lemma 4

[42] For \(\iota k\in R,\) and \(k=1,\cdots ,n,0<\varphi \le 1\), we have:

$$\begin{aligned} \left( \sum _{k=1}^{n}|\iota k|\right) ^{\varphi }\le \sum _{k=1}^{n}|\iota k|^{\varphi }\le n^{1-\varphi }\left( \sum _{k=1}^{n}|\iota k|\right) ^{\varphi }. \end{aligned}$$

2.2 Problem Statement

This article thinks about an uncertain nonlinear quantized system below:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_i=x_{i+1}+f_i(\bar{x}_i),1\le i\le n-1 ,\\ \dot{x}_n=Q(u(t))+f_n(\bar{x}_n),\\ y=x_{1}. \end{array}\right. \end{aligned}$$
(6)

where \(\bar{x}_i=[x_{1}, x_{2}, \ldots , x_i]^T\in R^{i}\) stands for system states, \((i=1,2,\ldots ,n)\), and \(y\in R\) expresses output of system. \(f_{i}(.): R^i\rightarrow R (i=1, 2, \ldots , n)\) is unknown smooth functions. \(u(t)\in R\) and Q(u(t)) denote a controller and a quantizer, respectively.

In this article, according to [43], hysteretic quantizer is presented to avert chattering. It follows from [44] that quantizer Q(u(t)) is described as follows:

$$\begin{aligned} Q(u(t))=\left\{ \begin{array}{ll} u_isgn(u), \frac{u_i}{1+\delta }<|u|\le u_i,\dot{u}<0,or \\ u_i<|u|\le \frac{u_i}{1-\delta },\dot{u}>0 \\ u_i(1+\delta )sgn(u), u_i<|u|\le \frac{u_i}{1-\delta },\dot{u}<0,or \\ \frac{u_i}{1-\delta }<|u|\le \frac{u_i(1+\delta )}{1-\delta },\dot{u}>0\\ 0, ~0\le |u|<\frac{u_{min}}{1+\delta },\dot{u}<0,or \\ \frac{u_{min}}{1+\delta }\le |u|\le u_{min},\dot{u}>0\\ Q(u(t^{-})), \dot{u}=0 \end{array}\right. \end{aligned}$$
(7)
Fig. 1
figure 1

Quantizer Q(u(t))

Full size image

where \(u_i=\rho ^{1-i}u_{min}\), \(i=1,2,\ldots ,n\), \(u_{min}>0\) and \(0<\rho <1\), \(\delta =\frac{1-\rho }{1+\rho }\). Thus, \(Q(u(t))\in U=\{0, \pm u_i,\pm u_i(1+\delta ),i=1,2,\ldots \}\). \(u_{min}\) governs the range of dead-zone. The map of Q(u(t)) displays in Fig 1.

Remark 1

Different from the traditional research about fixed time control of nonlinear systems, the quantization of signals is considered firstly. An fixed-time adaptive control strategy is provided for uncertain nonlinear quantized systems.

Lemma 5

[45] Decomposing the quantized value Q(u(t)) as follows:

$$\begin{aligned} Q(u(t))=\varpi (u)u(t)+d(t) \end{aligned}$$
(8)

where

$$\begin{aligned} 1-\delta \le \varpi (u)\le 1+\delta ,|d(t)|\le u_{\min }. \end{aligned}$$
(9)

2.3 Fuzzy Logic Systems

Since the system (6) contains unknown functions, we need to introduce fuzzy logic system to approximate them. Using the singleton point fuzzifier, the center-average defuzzifier and the product inference, we can obtain fuzzy rules:

\(R^{l}\): IF \(x_{1}\) is \(F_{1}^{l},\ldots , x_{n}\) is \(F_{n}^{l}\),

Then: \(y_{G}\) is \(G^{l}\), \(l=1,2,\ldots ,N\) where \(x=[x_{1},x_{2},...,x_n]^{T}\in R^{n}\) denotes input variable, and \(y_{G}\in R\) stands for fuzzy system output. The membership functions of fuzzy set \(F_{i}^{l}\) are signified by \(\mu _{F_{i}^{l}}(x_i)\). N expresses total amount of the rules.

We can select Gaussian functions with the exponential as the membership functions:

$$\begin{aligned} \mu _{F^{l}_{i}}(x)=exp \left[ -\frac{(x_{i}-a^{l}_{i})}{b^{l}_{i}}\right] \end{aligned}$$

where \(a^{l}_{i}\) and \(b^{l}_{i}\) stands for the center and the width of a fuzzy membership function, respectively.

Applying the singleton function, the center-average defuzzification and the product inference [46], \(y_{G}(x)\) is described as:

$$\begin{aligned} y_{G}(x)=\frac{\sum _{l=1}^{N}\Phi _{l} \prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})}{\sum _{l=1}^{N}[\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})]} \end{aligned}$$
(10)

where

$$\begin{aligned} \Phi _{l}= \max _{y_{G}\in R}\mu _{G^{l}}(y),\Phi =(\Phi _{1},\Phi _{2},\ldots ,\Phi _{N})^{T}. \end{aligned}$$

Let

$$\begin{aligned} \omega _{l}(x)=\frac{\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})}{\sum _{l=1}^{N}[\prod _{i=1}^{n}\mu _{F_{i}^{l}}(x_{i})]} \end{aligned}$$

and \(\omega (x)=(\omega _{1}(x),\omega _{2}(x),\ldots ,\omega _{N}(x))^{T}\). Then, fuzzy logic system is expressed as:

$$\begin{aligned} y_{G}(x)=\Phi ^{T}\omega (x). \end{aligned}$$
(11)

Lemma 6

[47] If \(f(x)\in \Omega\) is a continuous function, for any given \(\varepsilon >0\), fuzzy logic system (11) makes the relational expression true:

$$\begin{aligned} \sup _{x\in \Omega }|f(x)-\Phi ^{T}\omega (x)|\le \varepsilon . \end{aligned}$$
(12)

The purpose of this manuscript is constructed an fuzzy adaptive controller to ensure all closed-loop signals remain stable for a fixed time, and system output signal y follows the reference signal \(y_d\).

3 Adaptive Controller Design

A fixed-time adaptive controller for the system (6) is constructed via backstepping approach in this part. Then, the error variable is defined as follows:

$$\begin{aligned} z_{1}=\,&x_{1}-y_d,\nonumber \\ z_i=\,&x_i-\alpha _{i-1}, i=2, \cdots , n. \end{aligned}$$
(13)

where \(\alpha _{i-1}\) stands for virtual controller. For convenience of symbol operation, the ith time derivative of \(y_d\) is expressed by \(y_d^{(i)}\), and let \(\bar{y}^{(i)}_d=[y_d,y_d^{(1)}, \ldots , y_d^{(i)}]^T\), \(i=1, 2, \ldots , n\).

Remark 2

Based on backstepping technique, approximating unknown nonlinear function \(\bar{f}_i\) by fuzzy logic system \(\Phi _i(X_i)\). To achieve control objectives, we define a constant \(\theta _i=\Vert \Phi _i\Vert ^{2}, i=1, 2, \cdots , n\), \(\hat{\theta }_{1}\) stands for estimate of \(\theta _{1}\), and the parameter estimation error is \(\tilde{\theta }_{1}=\theta _{1}-\hat{\theta }_{1}\).

Step 1. Consider the nonlinear uncertain system (6), according to \(z_{1}=x_{1}-y_d\), we have:

$$\begin{aligned} \dot{z}_{1}=x_{2}+f_{1}(x_{1})-\dot{y}_d. \end{aligned}$$
(14)

Think about the following Lyapunov function:

$$\begin{aligned} V_{1}=\frac{z_{1}^{2}}{2}+\frac{\tilde{\theta }_{1}^{2}}{2\lambda _{1}} \end{aligned}$$
(15)

where \(\lambda _{1}>0\) is a design constant.

By (13), (14), one has:

$$\begin{aligned} \dot{V}_{1}= z_{1}(z_{2}+\alpha _{1}+f_{1}(x_{1})-\dot{y}_d)-\frac{\tilde{\theta }_{1}\dot{\hat{\theta }}_{1}}{\lambda _{1}}. \end{aligned}$$
(16)

Using Young’s inequality, one has:

$$\begin{aligned} z_{1}z_{2}\le \frac{z_{1}^{2}}{2}+\frac{z_{2}^{2}}{2}. \end{aligned}$$
(17)

Substituting (17) into (16) yields:

$$\begin{aligned} \dot{V}_{1}\le z_{1}(f_{1}+\frac{z_{1}}{2}+\alpha _{1}-\dot{y}_d)+\frac{z_{2}^{2}}{2} -\frac{\tilde{\theta }_{1}\dot{\hat{\theta }}_{1}}{\lambda _{1}}. \end{aligned}$$
(18)

Let \(\bar{f}_{1}=f_{1}+z_{1}-\dot{y}_d\), then (18) can be rewritten as:

$$\begin{aligned} \dot{V}_{1}\le \,&z_{1}\alpha _{1}+ z_{1}\bar{f}_{1}+\frac{z_{2}^{2}}{2}-\frac{z_{1}^{2}}{2}- \frac{\tilde{\theta }_{1}\dot{\hat{\theta }}_{1}}{\lambda _{1}}. \end{aligned}$$
(19)

Since \(\bar{f}_{1}\) is unknown, it cannot be obtained. Applying Lemma 6, for \(\forall \varepsilon _{1}>0\), there is a fuzzy logic system \(\Phi _{1}^{T}\omega _{1}(X_{1})\) as follows:

$$\begin{aligned} \bar{f}_{1}=\Phi _{1}^{T}\omega _{1}(X_{1}) +\delta _{1}(X_{1}),|\delta _{1}(X_{1})|\le \varepsilon _{1} \end{aligned}$$
(20)

where \(X_{1}=(x_{1},y_{d},\dot{y}_{d})\).

By applying Young’s inequality, one has:

$$\begin{aligned} z_{1}\bar{f}_{1}\le \,&\frac{1}{2a_{1}^{2}}z_{1}^{2}\theta _{1} \omega _{1}^T\omega _{1}\nonumber \\&\quad +\,\frac{1}{2}a_{1}^{2}+\frac{1}{2}z_{1}^{2}+\frac{1}{2}\varepsilon _{1}^{2}. \end{aligned}$$
(21)

Then, we choose the virtual controller as:

$$\begin{aligned} \alpha _{1}=\,&-c_{1}z_{1}^{2\sigma -1}-k_{1}z_{1}^{2\beta -1}\nonumber \\&-\,\frac{1}{2a_{1}^{2}}\hat{\theta }_{1}z_{1}\omega _{1}^{T}\omega _{1} \end{aligned}$$
(22)

where \(c_{1}>0\), \(k_{1}>0\) and \(a_{1}>0\) are design constants.

Next, we set up the adaptive law as:

$$\begin{aligned} \dot{\hat{\theta }}_{1}=\,&\frac{\lambda _{1}}{2a_{1}^{2}}z_{1}^{2}\omega _{1}^{T}\omega _{1}\nonumber \\&\quad -\,\gamma _{1}\hat{\theta }_{1}-\kappa _{1}\hat{\theta }_{1}, \hat{\theta }_{1}(0)\ge 0 \end{aligned}$$
(23)

where \(\gamma _{1}\) and \(\kappa _{1}\) are positive design constants.

Substituting (21)–(23) into (19), we have:

$$\begin{aligned} \dot{V}_{1}\le \,&-c_{1}z_{1}^{2\sigma }-k_{1}z_{1}^{2\beta }+\frac{z_{2}^{2} }{2}\nonumber \\&\quad +\,\frac{a_{1}^{2}}{2}+\frac{\varepsilon _{1}^{2}}{2} +\frac{\gamma _{1}}{\lambda _{1}}\tilde{\theta }_{1}\hat{\theta }_{1}\nonumber \\&\quad +\,\frac{\kappa _{1}}{\lambda _{1}}\tilde{\theta }_{1}\hat{\theta }_{1}. \end{aligned}$$
(24)

It is noted that:

$$\begin{aligned} \frac{\gamma _{1}}{\lambda _{1}}\tilde{\theta }_{1}\hat{\theta }_{1}\le \,&-\frac{\gamma _{1}}{2\lambda _{1}}\tilde{\theta }_{1}^{2}+\frac{\gamma _{1}}{2\lambda _{1}}\theta _{1}^{2}, \end{aligned}$$
(25)
$$\begin{aligned} \frac{\kappa _{1}}{\lambda _{1}}\tilde{\theta }_{1}\hat{\theta }_{1}\le \,&-\frac{\kappa _{1}}{2\lambda _{1}}\tilde{\theta }_{1}^{2}+\frac{\kappa _{1}}{2\lambda _{1}}\theta _{1}^{2}. \end{aligned}$$
(26)

Equation (24) can be described as:

$$\begin{aligned} \dot{V}_{1}\le \,&-c_{1}z_{1}^{2\sigma }-k_{1}z_{1}^{2\beta }-\frac{\gamma _{1}}{2\lambda _{1}}\tilde{\theta }^{2}_{1}\nonumber \\&\quad -\,\frac{\kappa _{1}}{2\lambda _{1}}\tilde{\theta }_{1}^{2}+\eta _{1}+\frac{z_{2}^{2}}{2} \end{aligned}$$
(27)

where \(\eta _{1}=\frac{a_{1}^{2}}{2}+\frac{\varepsilon _{1}^{2}}{2}+\frac{\gamma _{1}}{2\lambda _{1}}\theta _{1}^{2} +\frac{\kappa _{1}}{\lambda _{1}}{\theta ^{2}_{1}}\).

Step \(i (2\le i\le n-1)\). Based on (13) and Step 1, we have:

$$\begin{aligned} \dot{z}_i=f_i(\bar{x}_i)+x_{i+1}-\dot{\alpha }_{i-1} \end{aligned}$$
(28)

where

$$\begin{aligned} \dot{\alpha }_{i-1}=\,&\sum _{j=1}^{i-1}\frac{\partial \alpha _{i-1}}{\partial x_j}\Big [f_j(\bar{x}_j)+x_{j+1}\Big ]\nonumber \\&\quad +\sum _{j=1}^{i-1} \frac{\partial \alpha _{i-1}}{\partial \hat{\theta }_j}\dot{\hat{\theta }}_j \nonumber \\&\quad +\sum _{j=0}^{i-1}\frac{\partial \alpha _{i-1}}{\partial y_d^{(j)}}y_d^{(j+1)}. \end{aligned}$$
(29)

Now, think about the Lyapunov function:

$$\begin{aligned} V_i=V_{i-1}+\frac{1}{2}z_i^{2}+\frac{1}{2\lambda _i}\tilde{\theta }^{2}_i \end{aligned}$$
(30)

where \(\lambda _i\) is a positive design constant.

Then its derivative can be obtained:

$$\begin{aligned} \dot{V_i}=\,&\dot{V}_{i-1}+z_i(z_{i+1}+\alpha _i+f_i(\bar{x}_i)-\dot{\alpha }_{i-1})\nonumber \\&\quad -\frac{1}{\lambda _i}\tilde{\theta }_i\dot{\hat{\theta }}_i. \end{aligned}$$
(31)

According to Lemma 2, we have:

$$\begin{aligned} z_iz_{i+1}\le \frac{1}{2}z_i^{2}+\frac{1}{2}{z_{i+1}^{2}}. \end{aligned}$$
(32)

Substituting (32) into (31), one has:

$$\begin{aligned} \dot{V_i}\le \,&-\sum _{j=1}^{i-1}(c_jz_j^{2\sigma }+k_jz_j^{2\beta }+\frac{\gamma _j}{2\lambda _j}\tilde{\theta }_j^{2}+\frac{\kappa _j}{2\lambda _j}\tilde{\theta }_j^{2})\nonumber \\&\quad +\sum _{j=1}^{i-1}\eta _j +z_i\bar{f}_i+z_i\alpha _i+\frac{1}{2}z_{i+1}^{2}-\frac{1}{2}z_i^{2}-\frac{1}{\lambda _i}\tilde{\theta }_i\dot{\hat{\theta }}_i \end{aligned}$$
(33)

where

$$\begin{aligned} \bar{f}_i=f_i(\bar{x}_i)-\dot{\alpha }_{i-1}+\frac{3}{2}z_i^{2}. \end{aligned}$$

Similarly, \(\Phi _{i}^{T}\omega _{i}(X_{i})\) is used for approximating \(\bar{f}_i\), and \(X_i=[\bar{x}_i^T, \bar{\hat{\theta }}_{i-1}^T,\) \(\bar{y}_d^{(i)T}]^T\in \Omega _{Z_i} \subset R^{3i}\) with \(\hat{\theta }_{i-1}=[\hat{\theta }_{1}, \hat{\theta }_{2}, \ldots , \hat{\theta }_{i-1}]^T\). Applying Lemma 6, we have:

$$\begin{aligned} \bar{f}_{i}=\Phi _{i}^{T}\omega _{i}(X_{i})+\delta _{i}(X_{i}), |\delta _{i}(X_{i})|\le \varepsilon _{i} \end{aligned}$$
(34)

where \(\varepsilon _i\) is any given positive constant.

Using Young’s inequality, we have:

$$\begin{aligned} z_i\bar{f}_i\le \,\frac{1}{2a_i^{2}}z_i^{2}\theta _i \omega _i^T\omega _i+\frac{1}{2}a_i^{2} +\frac{1}{2}z_i^{2}+ \frac{1}{2}\varepsilon _i^{2}. \end{aligned}$$
(35)

Then, the virtual controller is constructed as:

$$\begin{aligned} \alpha _i=-c_iz_i^{2\sigma -1}-k_iz_i^{2\beta -1} -\frac{1}{2a_i^{2}}\hat{\theta }_iz_i\omega _i^T\omega _i \end{aligned}$$
(36)

where \(c_i>0\), \(k_i>0\) and \(a_i>0\) are design constants.

Next, we set up adaptation law as:

$$\begin{aligned} \dot{\hat{\theta }}_{i}=\frac{\lambda _{i}}{2a_{i}^{2}}z_{i}^{2}\omega _{i}^{T}\omega _{i} -\gamma _{i}\hat{\theta }_{i}-\kappa _i\hat{\theta }_{i}, \hat{\theta }_i(0)\ge 0 \end{aligned}$$
(37)

where \(\gamma _i\) and \(\kappa _i\) are positive design constants.

Much like (25), (26), we have:

$$\begin{aligned} \frac{\gamma _i}{\lambda _i}\tilde{\theta }_i\hat{\theta }_i\le \,&-\frac{\gamma _i}{2\lambda _i}\tilde{\theta }_i^{2}+\frac{\gamma _i}{2\lambda _i}\theta _i^{2}, \end{aligned}$$
(38)
$$\begin{aligned} \frac{\kappa _i}{\lambda _i}\tilde{\theta }_i\hat{\theta }_i\le \,&-\frac{\kappa _i}{2\lambda _i}\tilde{\theta }_i^{2}+\frac{\kappa _i}{2\lambda _i}\theta _i^{2}. \end{aligned}$$
(39)

Substituting (35)–(39) into (33) yields:

$$\begin{aligned} \dot{V_i}\le \,&-\sum _{j=1}^{i}(c_jz_j^{2\sigma }+k_jz_j^{2\beta }+\frac{\gamma _j}{2\lambda _j}\tilde{\theta }_j^{2}+\frac{\kappa _j}{2\lambda _j}\tilde{\theta }_j^{2})\nonumber \\&\quad +\sum _{j=1}^{i}\eta _j+\frac{1}{2}z_{i+1}^{2} \end{aligned}$$
(40)

where \(\eta _j=\frac{\gamma _j}{2\lambda _j}\theta _j^{2}+\frac{\kappa _j}{2\lambda _j}{\theta ^{2}_j} +\frac{1}{2}a_j^{2}+\frac{1}{2}\varepsilon _j^{2}, j=1,2,\cdots ,i\).

Step n. According to the analysis in step i, one has:

$$\begin{aligned} \dot{z}_n=f_n(\bar{x}_n)+Q(u(t))-\dot{\alpha }_{n-1} \end{aligned}$$
(41)

where

$$\begin{aligned} \dot{\alpha }_{n-1}=\,&\sum _{j=1}^{n-1}\frac{\partial \alpha _{n-1}}{\partial x_j}\Big (f_j(\bar{x}_j)+x_{j+1}\Big )+\sum _{j=1}^{n-1}\frac{\partial \alpha _{n-1}}{\partial \hat{\theta }_j}\dot{\hat{\theta }}_{j}\\&\quad +\sum _{j=0}^{n-1}\frac{\partial \alpha _{n-1}}{\partial y_d^{(j)}}y_d^{(j+1)}. \end{aligned}$$

Now, think about the Lyapunov function:

$$\begin{aligned} V_n=V_{n-1}+\frac{1}{2}z_n^{2}+\frac{1}{2\lambda _n}\tilde{\theta }_n^{2} \end{aligned}$$
(42)

where \(\lambda _n\) is a positive design constant.

From its derivative and Lemma 5, one has:

$$\begin{aligned} \dot{V_n}=\,&\dot{V}_{n-1}+z_n(f_n(\bar{x}_n)+\varpi (u)u(t)+d(t)-\dot{\alpha }_{n-1})\nonumber \\&\quad -\,\frac{\tilde{\theta }_n}{\lambda _n}\dot{\hat{\theta }}_n \end{aligned}$$
(43)

Based on Young’s inequality, we have:

$$\begin{aligned} z_nd(t)\le \frac{1}{2}z_n^{2}+\frac{1}{2}u_{\min }^{2}. \end{aligned}$$
(44)

According to (40) with \((i=n-1)\), (44), one has:

$$\begin{aligned} \dot{V}_n\le \,&-\sum _{j=1}^{n-1}(c_jz_j^{2\sigma }+k_jz_j^{2\beta }+\frac{\gamma _j}{2\lambda _j}\tilde{\theta }_j^{2}+\frac{\kappa _j}{2\lambda _j}\tilde{\theta }_j^{2})\nonumber \\&\quad +\sum _{j=1}^{n-1}\eta _j+z_n\bar{f}_n-\frac{1}{2}z_n^{2}+z_n\varpi (u)u(t)\nonumber \\&\quad +\frac{1}{2}u_{\min }^{2}-\frac{1}{\lambda _n}\tilde{\theta }_n\dot{\hat{\theta }}_n \end{aligned}$$
(45)

where

$$\begin{aligned} \bar{f}_n=f_n(\bar{x}_n)-\dot{\alpha }_{n-1}+\frac{3}{2}z_n. \end{aligned}$$
(46)

Similarly, for \(\forall \varepsilon _n>0\), fuzzy logic system \(\Phi _n^{T}\omega _n(X_n)\) is adopted to approximate \(\bar{f}_n\).

From Lemma 6, we have:

$$\begin{aligned} \bar{f}_{n}=\Phi _{n}^{T}\omega _{n}(X_{n}) +\delta _{n}(X_{n}),|\delta _{n}(X_{n})|\le \varepsilon _{n}. \end{aligned}$$
(47)

Applying Young’s inequality, we have:

$$\begin{aligned} z_n\bar{f}_n\le \,&\frac{1}{2a_n^{2}}z_n^{2}\theta _n \omega _n^T\omega _n+\frac{1}{2}a_n^{2}+\frac{1}{2}z_n^{2}+\frac{1}{2}\varepsilon _n^{2}. \end{aligned}$$
(48)

Now, the actual controller is constructed as:

$$\begin{aligned} u=-c_n{z_n}^{2\sigma -1}-k_n{z_n}^{2\beta -1}-\frac{z_n\hat{\theta }_n \omega _n^T\omega _n}{2a_n^{2}} \end{aligned}$$
(49)

where \(k_n>0\),\(c_n>0\) and \(a_n>0\) are design constants.

Next, we set up adaptation law as:

$$\begin{aligned} \dot{\hat{\theta }}_n=\,&\frac{\lambda _n}{2a_n^{2}}z_n^{2}\omega _n^T\omega _n\nonumber \\&-\gamma _n\hat{\theta }_n-\kappa _n\hat{\theta }_n, \hat{\theta }_n(t_0)\ge 0 \end{aligned}$$
(50)

where \(\gamma _n\) is a positive design constant.

Combining (48), (9), we can obtain:

$$\begin{aligned} z_n\varpi (u)u(t)\le \,&-c_n{z_n}^{2\sigma }-k_n{z_n}^{2\beta }\nonumber \\&-\frac{1}{2a_n^{2}}z_n^{2}\hat{\theta }_n \omega _n^T\omega _n. \end{aligned}$$
(51)

Substituting (48)–(51) into (45) gives:

$$\begin{aligned} \dot{V_n}\le \,&-\sum _{j=1}^{n-1}(c_jz_j^{2\sigma }+k_jz_j^{2\beta }+\frac{\gamma _j}{2\lambda _j}\tilde{\theta }_j^{2}+\frac{\kappa _j}{2\lambda _j}\tilde{\theta }_j^{2})+\sum _{j=1}^{n-1}\eta _j\nonumber \\&-c_nz_n^{2\sigma }-k_nz_n^{2\beta }+\frac{1}{2}u_{\min }^{2}+\frac{1}{2}a_n^{2}+\frac{1}{2}\varepsilon _n^{2}+\frac{\gamma _{n}}{\lambda _n}\tilde{\theta }_n\hat{\theta }_n\nonumber \\&\quad +\frac{\kappa _{n}}{\lambda _n}\tilde{\theta }_n\hat{\theta }_n. \end{aligned}$$
(52)

Furthermore, as is the same case of (38) and (39), we have:

$$\begin{aligned} \frac{\gamma _n}{\lambda _n}\tilde{\theta }_n\hat{\theta }_n \le \,&-\frac{\gamma _n}{2\lambda _n}\tilde{\theta }_n^{2}+\frac{\gamma _n}{2\lambda _n}\theta _n^{2}, \end{aligned}$$
(53)
$$\begin{aligned} \frac{\kappa _n}{\lambda _n}\tilde{\theta }_n\hat{\theta }_n \le \,&-\frac{\kappa _n}{2\lambda _n}\tilde{\theta }_n^{2}+\frac{\kappa _n}{2\lambda _n}{\theta }_n^{2} \end{aligned}$$
(54)

Substituting (53), (54) into (52), one has:

$$\begin{aligned} \dot{V}_n\le \,&-\sum _{j=1}^{n}(c_jz_j^{2\sigma }+\frac{\gamma _j}{2\lambda _j}\tilde{\theta }_j^{2})-\sum _{j=1}^{n}(k_jz_j^{2\beta }+\frac{\kappa _j}{2\lambda _j}\tilde{\theta }_j^{2})\nonumber \\&\quad +\tau \end{aligned}$$
(55)

where \(\tau =\sum _{j=1}^{n}\eta _j+\frac{1}{2}u_{\min }^{2}\) and \(\eta _j=\frac{\gamma _j}{2\lambda _j}\theta _j^{2}+\frac{\kappa _j}{2\lambda _j}{\theta ^{2}_j} +\frac{1}{2}a_j^{2}+\frac{1}{2}\varepsilon _j^{2}, j=1,2, \ldots , n\).

So far, the following theorem summarizes the above work.

Theorem 1

Think about the uncertain nonlinear system (6), preceded by hysteresis quantizer (7). Based on controller (49), intermediate virtual controller (36) and adaptive law (37), system (6) is globally fixed-time stability. The tracking error converges to a small neighborhood of the origin. Within a fixed time, the closed-loop system stability is guaranteed and convergence time has a certain upper bound.

Proof

Applying Lemma 3, one has:

$$\begin{aligned} \Big (\sum _{j=1}^{n}\frac{\tilde{\theta }_j^{2}}{2\lambda _j}|Big)^{\sigma }\le \,&\sum _{j=1}^{n}\frac{\tilde{\theta }_j^{2}}{2\lambda _j}+(1-\sigma )\sigma ^{\frac{\sigma }{1-\sigma }}, \end{aligned}$$
(56)
$$\begin{aligned} \Big (\sum _{j=1}^{n}\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\Big )^{\beta }\le \,&\sum _{j=1}^{n}\frac{\tilde{\theta }_j^{2}}{2\lambda _j}+(1-\beta )\beta ^{\frac{\beta }{1-\beta }}. \end{aligned}$$
(57)

Combining (55), (56), (57), we have:

$$\begin{aligned} \dot{V}_n\le \,&-\sum _{j=1}^{n}c_jz_j^{2\sigma }-\sum _{j=1}^{n}\gamma _j\Big (\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\Big )^{\sigma }-\sum _{j=1}^{n}k_jz_j^{2\beta }\nonumber \\&-\sum _{j=1}^{n}\kappa _j\Big (\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\Big )^{\beta }+\varrho \nonumber \\ \le \,&-c\sum _{j=1}^{n}\Big (\frac{1}{2}z_j^{2}\Big )^{\sigma }-c\sum _{j=1}^{n}\Big (\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\Big )^{\sigma }-k\sum _{j=1}^{n}\Big (\frac{1}{2}z_j^{2}\Big )^{\beta }\nonumber \\&-k\sum _{j=1}^{n}\Big (\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\Big )^{\beta }+\varrho \end{aligned}$$
(58)

where \(c=min\left\{ 2^{\sigma }c_{j},\gamma _{j},j=1,\ldots ,n\right\}\), \(k=min\{2^{\beta }k_{j}, \kappa _{j},j=1,\cdots ,n\},\varrho =\sum _{j=1}^{n}\eta _j+\frac{1}{2}u_{\min }^{2}+(1-\sigma )\sigma ^{\frac{\sigma }{1-\sigma }}\gamma _{j} +(1-\beta )\beta ^{\frac{\beta }{1-\beta }}\kappa _{j}\) and \(\eta _j=\frac{\gamma _j}{2\lambda _j}\theta _j^{2}+\frac{\kappa _j}{2\lambda _j}{\theta ^{2}_j} +\frac{1}{2}a_j^{2}+\frac{1}{2}\varepsilon _j^{2}, j=1,2, \ldots , n\).

By using Lemma 4, one has:

$$\begin{aligned} \dot{V}_n\le \,&-c\left( \sum _{j=1}^{n}\left( \frac{z_j^{2}}{2}+\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\right) \right) ^{\sigma }-k\left( \sum _{j=1}^{n}\left( \frac{z_j^{2}}{2}+\frac{\tilde{\theta }_j^{2}}{2\lambda _j}\right) \right) ^{\beta }+\varrho \nonumber \\ \le \,&-cV^{\sigma }(x)-kV^{\beta }(x)+\varrho . \end{aligned}$$
(59)

Applying Lemma 1, we can obtain system (6) is practical fixed-time stable and converges to a compact set

$$\begin{aligned} x\in \left\{ V(x)\le min\left\{ (\frac{\varrho }{(1-\phi )c})^{\frac{1}{\sigma }}, (\frac{\varrho }{(1-\phi )k})^{\frac{1}{\beta }}\right\} \right\} \end{aligned}$$
(60)

Then, the setting time can be obtained:

$$\begin{aligned} T\le T_{m}= \frac{1}{c\phi (\sigma -1)}+\frac{1}{k\phi (1-\beta )}. \end{aligned}$$
(61)

In addition, applying the definition of \(V_{n}\), we have:

$$\begin{aligned} |y-y_{d}|\le 2(\frac{\varrho }{(1-\phi )c})^{\frac{1}{2\sigma }}. \end{aligned}$$
(62)

By choosing appropriate constant parameters, the tracking error can reduce to an ideal range in a fixed time. \(\square\)

Remark 3

From formula (61), the convergence time boundary T is not affected by the initial state. The raised adaptive fixed-time control tactic overcomes the limitation of the finite-time control scheme relies on initial state and guarantees tracking performance within a fixed-time.

Fig. 2
figure 2

Control design process

Full size image

4 Simulation Results

Example 1

The following second-order uncertain nonlinear quantized system is thought about:

$$\begin{aligned} \dot{x}_{1}=\,&x_{2}+f_{1}(\bar{x}_{1}) \nonumber \\ \dot{x}_{2}=\,&Q(u)+f_{2}(\bar{x}_{2})\nonumber \\&y &=x_{1} \end{aligned}$$
(63)

where y stands for system output, \(x_{1}\) and \(x_{2}\) denote the systems states, Q(u) represents hysteretic quantizer as in (7).

Then, the fuzzy membership functions are defined below:

$$\begin{aligned} \mu _{F_{i}^{1}}(x)=\,&\exp \Big (\frac{-(x+2)^{2}}{2}\Big ),\\ \mu _{F_{i}^{2}}(x)=\,&\exp \Big (\frac{-(x+1.5)^{2}}{2}\Big ),\\ \mu _{F_{i}^{3}}(x)=\,&\exp \Big (\frac{-(x+1)^{2}}{2}\Big ),\\ \mu _{F_{i}^{4}}(x)=\,&\exp \Big (\frac{-(x+0.5)^{2}}{2}\Big ),\\ \mu _{F_{i}^{5}}(x)=\,&\exp \Big (\frac{-x^{2}}{2}\Big ),\\ \mu _{F_{i}^{6}}(x)=\,&\exp \Big (\frac{-(x-0.5)^{2}}{2}\Big ),\\ \mu _{F_{i}^{7}}(x)=\,&\exp \Big (\frac{-(x-1)^{2}}{2}\Big ),\\ \mu _{F_{i}^{8}}(x)=\,&\exp \Big (\frac{-(x-1.5)^{2}}{2}\Big ),\\ \mu _{F_{i}^{9}}(x)=\,&\exp \Big (\frac{-(x-2)^{2}}{2}\Big ). \end{aligned}$$

According to Theorem 1, the adaptive law, the virtual controller and the real controller are established as:

$$\begin{aligned} \alpha _{1}=\,&-c_{1}z_{1}^{2\sigma -1}-k_{1}z_{1}^{2\beta -1}-\frac{z_{1}}{2a_{1}^{2}}\hat{\theta }_{1}\omega ^T_{1}(X_{1})\omega _{1}(X_{1}) \end{aligned}$$
(64)
$$\begin{aligned} u=\,&-c_{2}z_{2}^{2\sigma -1}-k_{2}z_{2}^{2\beta -1}-\frac{z_{2}\hat{\theta }_{2}\omega ^T_{2}(X_{2})\omega _{2}(X_{2})}{2a_{2}^{2}} \end{aligned}$$
(65)
$$\begin{aligned} \dot{\hat{\theta }}_i=\,&\frac{\lambda _i}{2a_i^{2}}z_i^{2}\omega _i^T(X_i)\omega _i(X_i)-\gamma _i\hat{\theta }_i-\kappa _i\hat{\theta }_i, i=1, 2 \end{aligned}$$
(66)

where \(\sigma =118/100\), \(\beta =90/101\), \(z_{1}=x_{1}-y_d, z_{2}=x_{2}-\alpha _{1}, X_{1}=[x_{1}, y_d, \dot{y}_d]^T\) and \(X_{2}=[\bar{x}_{2}^T, \hat{\theta }_{1}, \bar{y}_d^{(2)T}]^T\) (Fig. 2).

Fig. 3
figure 3

The tracking performance of y and \(y_{d}\)

Full size image
Fig. 4
figure 4

State variable \(x_{2}\)

Full size image

In simulation, \(f_i(\bar{x}_i)\) is chosen as \(f_{1}(\bar{x}_{1})=(1-\sin ^{2}(x_{1}))x_{1}\), \(f_{2}(\bar{x}_{2})=cos(x_{1})^{2}x_{1}^{2}+sin(x_{1})^{2}x_{2}^{2}-x_{1}x_{2}^{2}.\)

Fig. 5
figure 5

The adaptive parameter \(\hat{\theta }_{1}\) and \(\hat{\theta }_{2}\)

Full size image

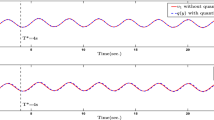
To test the correctness of Theorem 1, we need to let \(y_{d}=sin(0.5t)+0.5sin(t)\). The related parameters can be set to \(\delta =0.5\), \(\mu _{min}=0.2\), \(c_{1}=c_{2}=8\), \(c_{3}=c_{4}=6\), \(a_{1}=0.8, a_{2}=1.2, \lambda _{1}=20, \lambda _{2}=25, \gamma _{1}=1,\) \(\gamma _{2}=2\), \(\kappa _{1}=1\), \(\kappa _{2}=2.\) we choose initial conditions as \([x_{1}(0), x_{2}(0)]^T=[0.05, -0.5]^T,\) and \([\hat{\theta }_{1}(0), \hat{\theta }_{2}(0)]^T =[0.1, 0.2]^T.\) Simulation results are displayed in Figs. 3, 4,5, 6, and 7. From the simulation results, it is shown that all the signals are stabilized in fixed time.

Remark 4

To further demonstrate the suitability and availability of the proposed control tactics, we have compared the results with the control results in [42]. According to Fig. 7, we can know that the proposed fixed time control scheme has faster convergence speed and better tracking performance. In addition, different from [18, 19], the control strategy can guarantee the stability of the system at fixed time. Moreover, the upper bound of the stability time is only influenced by the design parameters.

Fig. 6
figure 6

u and Q(u)

Full size image
Fig. 7
figure 7

The tracking error \(y-y_d\)

Full size image

5 Conclusion

This article provides an adaptive fixed-time control scheme for uncertain nonlinear quantized systems. The fuzzy logic system is used to approximate the unknown nonlinear function. To build the relationship of u(t) and Q(u(t)), a nonlinear decomposition of quantized input is introduced. The fixed time controller is constructed to get over limitation that system convergence time relies on initial state, and ensures tracking error converges to a small neighborhood of the origin within a fixed time. Simultaneously, the closed-loop system signals are bounded, and convergence time has a definite upper bound. Finally, the main result is proved by simulation results. Moreover, the time delay problem is not considered in the proposed control strategy. How to design a quantitative feedback controller to ensure the fixed time stability of nonlinear systems with time delay is our future research direction.