Deep Fuzzy System Algorithms Based on Deep Learning and Input Sharing for Regression Application

Abstract

Although fuzzy system (FS) is highly interpretable, it is difficult to address high-dimensional big data due to the curse of dimensionality. On the contrary, deep neural network (DNN), a fashion deep learning algorithm, can deal with high-dimensional big data with shortcomings of complex model, huge calculation, and poor interpretability. We present a model of random locally optimized deep fuzzy system (RLODFS) and four specific heuristic implementation algorithms, which combines the advantages of high interpretability of FS and great ability of processing high-dimensional big data of DNN. This method takes Wang-Mendel (WM) algorithm as the basic module, to construct a RLODFS by bottom-up parallel structure. Through hierarchical, random group and combination-based learning, and input sharing, it can retain the interpretability and dramatically improve the computational efficiency. The input variables of the low-dimensional FS are randomly grouped by isometric sampling. Four implementation algorithms of RLODFS based on random local search for optimal combination, group learning, and deep structure with 0, 1, 2, and 3 input sharing, respectively, named as RLODFS-S0, RLODFS-S1, RLODFS-S2, and RLODFS-S3, are developed for regression-oriented problems. Using local loops to find the best combination of parameters, our final algorithms, RLODFS, can achieve fast convergence in training phase, and also superior generalization performance in testing. Compared with six classic algorithms in 12 datasets, the proposed RLODFS algorithms are not only highly interpretable with just some fuzzy rules but also can achieve higher precision, less complexity, and better generalization. Furthermore, it can be used for training fuzzy systems on datasets of any size, particularly for big datasets. Relatively, RLODFS-S3 and RLODFS-S2 achieve the best in comprehensive performance. More importantly, the proposed RLODFS is a new promising method of deep learning with good interpretability and high accuracy.

1 Article Highlights

• A random locally optimized hierarchical fuzzy model is proposed and three specific implementation algorithms are developed, which apply deep learning and input sharing to construct the hierarchical RLODFS model.

• The model is constructed by bottom-up layer-by-layer approach and the complexity of the model is reduced through hierarchical, grouping and input sharing learning.

• Compared with some classic and latest algorithms, the proposed algorithms achieved fast convergence, higher precision, better generalization, less time consuming, and the number of rules which is much lower than that of the single-layer fuzzy system.

2 Introduction

Compared with other artificial intelligence methods, i.e., deep belief networks (DBN) [1], deep restricted Boltzmann machines (DBM) [2], and evolutionary algorithms (EAs) [3], one of the outstanding advantages of fuzzy system (FS) is that it is constructed based on a series of IF-THEN rules [4]. Its structure and parameters have clear physical significance and it has the advantages of fastness and flexibility. Despite that, it often suffers from combinatorial rule explosion, so it is crucial for a model to extract fuzzy rules.

Very recently, the generation of rules from data has caused great concern. The main reason is that simple systems can generate fuzzy rules based on expert knowledge, but when the variables increase, the fuzzy rules will increase too many to obtain fuzzy rules only by relying on expert experience. Therefore, automatic generation of fuzzy rules based on the genetic algorithm (GA) [5], fuzzy clustering (FC) [6], neural networks (NNs) [7], and data mining (DM) [8], has been proposed. However, these methods are time-consuming with iterative learning, so it is hard to implement in engineering.

Therefore, it is extremely important to construct a FS with good performance, but it is not an easy task [9]. There are many challenges in designing an optimal FS [10], e.g., too many rules, optimization, interpretability, curse of dimension, generalization performance, etc. FS can be optimized by the EAs [11], gradient descent algorithm (GDA) and combining gradient descent with least square estimation (GDA+LSE) [12]. However, each method has its shortcomings. EAs are too expensive to be suitable for big data analysis [13]. Conventional GDA is very sensitive to learning parameters and LSE is difficult to optimize non-linear parameters [14]. Hence, it is necessary to develop more efficient and fast optimization algorithms for generating FS, especially for big data applications [15].

In addition to the methods aforementioned, Kosko and Wang [13, 14] have proved that both NNs and FS have the ability of non-linear mapping. If the NNs are combined with the fuzzy logic, the advantages of the two can be fully utilized to avoid the shortcomings. The key of fuzzy modeling is the acquisition of fuzzy rules. Wang proved in 1992 that a class of FSs is a universal approximator [8], which opened up the field of fuzzy approximation. In the same year, Wang and Mendel [14] jointly proposed a algorithm of obtaining fuzzy rules from samples, which can obtain a fuzzy rule base from a small-scale sample set. However, there are following weak points in Wang-Mendel (WM) algorithm: (1) lack of good completeness and robustness of its fuzzy rule base, leading to low accuracy of fuzzy model, (2) the efficiency of the algorithm drops rapidly with increasing data,and, (3) rules increase exponentially as dimension increases, which is called as “curse of dimensionality.” To solve these problems, researchers have put forward many improved algorithms, i.e., Leski [16] proposed a fuzzy C-means clustering (FCM) algorithm, which reduces the sample size and improves the completeness and robustness of FS,Fan et al. [17] presented a two-layer WM fuzzy method to improve the approximation ability of the FS and obtain higher robustness and accuracy. EAs have also been used as a new tool for building compact FSs. Both GA [18] and EA [19] have been introduced to reduce the complexity of fuzzy rules. Apart from the above efforts on an efficient rule structure, Wang [20] proposed a deep convolution fuzzy system, which has achieved encouraging results in reducing the amount of computation, but it is not suitable to handle the high-dimensional datasets.

Hierarchical fuzzy systems were original proposed by Raju et al. [21], Wang et al. [22] proved the basic properties of hierarchical fuzzy systems. Then, the study of fuzzy hierarchical system has become prosperous-the same period when Hinton et al. proposed new strategies for deep neural networks in 2006 [23], during which many new methods for designing hierarchical fuzzy systems were proposed [24,25,26,27,28,29]. Since then, hierarchical fuzzy systems were widely applied in many practical problems, such as milling process [26], target tracking [27], climate monitoring [28], and risk assessment [29].

In recent years, the deep convolution neural network (DCNN) [30] has achieved great success in many practical problems [31, 32], which reveals the powerful expressive ability of multi-layer structure in representing complex models. The main problem of DCNN is that the massive network parameters are difficult to explain [33], hence, its applications in the security fields are subject to certain restrictions.

Existing regression methods based on FS mainly use shallow regression models and are still unsatisfying for many real-world applications. This situation inspires us to rethink the regression problems based on deep architecture models with big data. Combined with the advantages of DCNN and FS, the deep structure and learning algorithms of random locally optimized deep fuzzy system modeling(RLODF)were constructed in a bottom-up layer-by-layer fashion.

Based on deep learning and big data, taking AlphaGo as a typical application has set off a third development wave of artificial intelligence (AI) [34,35,36,37], which has achieved a notable momentum. We intend to develop a deep fuzzy modeling for interpretable AI [34, 35] and big data, to develop a new deep learning method with higher precision, lower complexity, and better interpretability, thus adding a new form of implementation to AI.

This paper narrows the gap in efficient and effective training of deep fuzzy modeling, particularly for big data regression problems. The main contributions are as follows: (1) Inspired by the advantages of both DCNN and FS, we construct a RLODFS by bottom-up parallel fashion. (2) We combine three novel techniques ( hierarchical, random group and combination-based learning, and input sharing) specifically for training deep fuzzy systems. (3) Four algorithms, RLODFS-S0, RLODFS-S1, RLODFS-S2, and RLODFS-S3, are developed for regression-oriented problems; 12 real-world datasets from various applications, with varying size and dimensionality, are selected to demonstrate the method’s superiority.

The remainder of this paper is organized as follows: Sect. 2 introduces the structure of the RLODFS. Section 3 describes the implementation details of the four algorithms of RLODFS. Section 4 presents 12 examples on the proposed algorithms. Section 5 draws conclusion and points out some future research directions.

3 The Definition and Structure of RLODFS

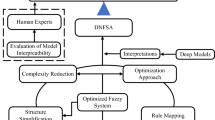
To facilitate description and clarity, here we only consider the case of multi-dimensional inputs and single-dimensional output. The basic structure of a RLODFS is illustrated in Fig. 1, and the whole RLODFS is described as a series of IF-THEN rules, which can be linked together to explain how the results are produced.

Fig. 1

The deep structure of RLODFS based on grouping and input sharing

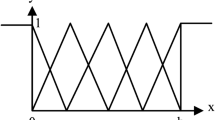
The structure of the FSs ${S}_{i}^{k}(i = {1,2},\cdots ,{n}^{k}, k = {1,2},\cdots ,L)$ is as follows: for each input $x_{i}^{k - 1} , \ldots ,x_{n}^{k - 1} \in F_{i}^{k}$ to the FS, first define $p$ fuzzy sets ${F}_{1},{F}_{2},\cdots ,{F}_{p}$, and the membership functions are shown in the abscissa of Fig. 2. Specifically, suppose $p$ fuzzy sets have p^d rules of (4) in d-dimensional space, there has three input variables $x_{i}$(i =1, 2, 3) ,then the j fuzzy rule is

$$R_{j} :{\text{ IF}}\,\, \,{\text{is}}\,F_{{1j}} ,x_{2} {\mkern 1mu} \,{\text{is}}\,{\mkern 1mu} {\text{ F}}_{{2j}} ,x_{3} \,{\mkern 1mu} {\text{is}}{\mkern 1mu} {\text{ F}}_{{3j}} ,{\text{ THEN}}\,y{\mkern 1mu} \,{\text{is}}{\mkern 1mu} \,{\text{ B}}_{j} ,$$

(1)

Fig. 2

Interpretation of RLODFS

where F_ij (i= 1, 2, 3) are fuzzy sets for input $x_{i}$ in rule j , B_j is a fuzzy set for the output $y$. If no input appears in the antecedent, the rule is removed.

Assume that the FS to be designed is given by

$$y = \sum\nolimits_{{j_{d} = 1}}^{p} { \cdots \sum\nolimits_{{j_{d} = 1}}^{p} {z^{{j_{1} \cdots j_{d} }} } \left[ {\prod\nolimits_{{j_{d} = 1}}^{p} {F^{{j_{d} }} \left( {g_{{j_{d} }} \left( {x_{d + i - 1}^{k - 1} } \right)} \right)} } \right]}$$

(2)

$$g_{j_{d}} ={\exp \left( - \left( {x_{i}-{\overline{x}}_{i}}^{l}/\sigma_{i}^{l}\right)^2 \right)}$$

(3)

where k = 1,2,$\cdots$, L-1, and the top FS^L with n ^L−1 input variables.

The FS is constructed by the following p^d rules.

IF ${x}_{i}^{k-1}$ is $F_{{z_{1} }}$ and  ..., and ${x}_{i+d-1}^{k-1}$ is $F_{{z_{d} }}$, THEN y is

$${B}^{{j}_{1}, \ldots, {j}_{d}}$$

(4)

where $\overline{x}_{i}^{l}$ and $\sigma_{i}^{l}$ are the center and width of the Gauss fuzzy set of the rule premise, respectively, which are determined by gradient descent method [8].$z^{j^{\prime}}$ is the center of the rule consequent,this paper mainly determines $z^{j^{\prime}}$.

Figure 2 depicts an example of $p$=3 and d=2, where a 2-dimensional input space is divided into p^d=3² = 9 fuzzy regions. To ensure the completeness of the rule base, it must contain the following nine rules, and the premise of the nine rules should be composed of all possible combinations of F₁, F_2, and F_3.

For any given input $(x_{1}^{^{\prime}} ,x_{2}^{^{\prime}} )$ in Fig. 2, FS $y(x_{{1}}^{^{\prime}} ,x_{{2}}^{^{\prime}} )$ can be described as the fuzzy rule: IF $x_{1}^{^{\prime}}$ is F₃ and $x_{{2}}^{^{\prime}}$ is F_3, THEN y is $B_{22}$. In other words, FS takes single operation with one rule responsible mainly for one region [20]. So for any given input $(x_{i}^{k - 1} , \ldots ,x_{d + i - 1}^{k - 1} )$, the FS (2) can be represented by a parameter $z{^{{j_{1} \cdots j_{d} }}}$ that represents the fuzzy rule in the form of (4).

The advantage of FS is that there are ways to choose better parameters. Since, each fuzzy subsystem in Fig. 1 can be represented by a single parameter $z{^{{j_{1} \cdots j_{d} }}}$, and thus, the whole action of the RLODFS on any given input can be interpreted by connected $z^{{j_{1} \cdots j_{d} }}$'s. Given a FS of (2), the physical meaning of $z^{j^{\prime}}$,$\overline{x}_{i}^{l}$ and $\sigma_{i}^{l}$ cannot only be used to repair the fuzzy IF-THEN rule of constructing the FS but also it can explain the FS in a user-friendly way. If the RLODFS in Fig. 1 obtains an error output ${x}_{1}^{L}$, we can easily find out which rule causes the error output according to Fig. 2, then we can take corresponding measures to avoid the problem from happening again. On the contrary, the main problem of DCNN is that the input–output transition is a black box with poor interpretability, if something goes wrong, we do not know which part of the DCNN should be corrected. Compared with the RLODFS, the DCNN model is complex, the connections between neurons are complex, and the correlation between features and results is difficult to interpret. In addition, it is difficult to understand what feature selection and why such feature selection is performed in deep learning.

4 The Proposed Algorithm

RLODFS constructs a deep structure by dividing subsystems and grouping learning strategies, learns rules from local data to extract data features, and integrates layer-by-layer to approach the final target. Different from other algorithms, the group operations of RLODFS reduce the complexity of the model. While making the most of the data, data-rule changes become traceable.

4.1 Training Algorithms for RLODFS

This paper mainly discusses the algorithms of deep hierarchical to solve the defect that shallow FS is difficult to deal with high-dimensional with big data.

The basic structure of RLODFS is shown in Fig. 1, where $x_{1}^{{0}} (i), \ldots, x_{n}^{0} (i) \in R^{n}$ input to the features space are usually high-dimensional features, and the output $x_{1}^{L}$ is a vector. $F_{1}^{{1}} , \ldots, F_{{n_{{1}} }}^{{1}}$ and $FS_{1}^{1} , \ldots, FS_{{n_{{1}} }}^{1}$ are the fuzzy sets and fuzzy subsystems of the first Level, respectively (${n}_{1}$ is the number of fuzzy sets or fuzzy subsystems). Once the $F_{1}^{{1}} , \ldots, F_{{n_{{1}} }}^{{1}}$ are input to the $FS_{1}^{1} , \ldots, FS_{{n_{{1}} }}^{1}$, then a new dataset is generated. The k-th Level FS is composed of $n^{k}$ fuzzy subsystems (k=1, 2,…, L), whose input is obtained from the output of the (k-1)-th Level. Suppose the FSs from Level 1 to Level L-1 have been designed, then the final input of the Level L is obtained from the previous L-1 Level’s output.

For a given set of M input–output data pairs,

$$[{x}_{1}^{0}\left(i\right),{x}_{2}^{0}\left(i\right),\cdots ,{x}_{n}^{0}\left(i\right);{y}_{n}^{0}\left(i\right)] \quad i=\mathrm{1,2},\cdots ,M$$

(5)

To design a RLODFS in Fig. 1 to match these data pairs (5). Firstly, the input variables $x_{1}^{{0}} (i), \ldots ,x_{n}^{0} (i)$ are randomly divided into several groups and input them to the $F_{1}^{{1}} , \ldots ,F_{{n_{{1}} }}^{{1}}$ to perform the fuzzification,then input these fuzzy sets to the FSs $FS_{1}^{1} , \ldots ,FS_{{n_{{1}} }}^{1}$, design the Level 1 FS (2). By passing the training data into the first-Level FSs, a new dataset is generated, and then obtain the first Level’s output $x_{1}^{{1}} (i), \ldots ,x_{n}^{1} (i)$. And Level 2 FSs are designed in a similar way as designing the first Level’s. Similarly, through the input of the k-th Level (that is, (k-1)-th Level’s output)$x_{1}^{{k{ - 1}}} (i), \ldots ,x_{n}^{{k{ - 1}}} (i)$, input these variables to the $F_{1}^{{1}} , \ldots ,F_{{n_{k} }}^{{1}}$ and $FS_{1}^{1} , \ldots ,FS_{{n_{{1}} }}^{1}$, the outputs $x_{1}^{k} (i), \ldots ,x_{{n_{k} }}^{k} (i)$ are obtained. Suppose the FSs from Level 1 to Level k have been designed, this process continues, until the whole RLODFS is constructed.

4.2 The Detail Implementation Steps

The implementation steps of RLODFS are as follows:

• Step 1: Determine the structure of RLODFS as shown in Fig. 1. Firstly, select the basic training unit $\theta = {4}$, and the Level k ( k =1, 2,···, L).

• Step 2:2.1) Replace the original data $x_{1}^{{0}} (i), \ldots ,x_{n}^{0} (i)$ by the regularized data $x_{1}^{{0}} {^{\prime}}(i), \ldots ,x_{n}^{0}{^{\prime}}(i)$.

  2.2) Divide the $x_{1}^{{0}} {^{\prime}}(i), \ldots ,x_{n}^{0}{^{\prime}}(i)$ into training set ${T}_{train}$ and test set ${T}_{test}$.

• Step 3: The input variables $x_{1}^{{0}} {^{\prime}}(i), \ldots ,x_{n}^{0} {^{\prime}}(i)$ are randomly grouped by isometric sampling according to the $\theta$.

  3.1) Using correlation coefficients to rank different feature groups, subsystems below the correlation threshold are discarded; otherwise, it will enter the next iteration.

• Step 4: The input–output data pairs (5) are used to design the Level 1 FS in the form of (2).

  4.1) For each region, set the initial values of the weighting factor $\alpha^{{j_{1} , \ldots ,j_{d} }} = {0}$ and the weighting factor of the output layer $\beta^{{j_{1} , \ldots ,j_{d} }} = {0}$.

• Step 5: Define $p$ fuzzy sets $F_{1} , \ldots ,F_{p}$, and select the nodes as follows:

  $$\begin{gathered} \min x_{j}^{k - 1} = min\left( {x_{j}^{k - 1} (i)|i = 1,2, \ldots ,M;j = t,t + 1,t + 2} \right) \hfill \\ \max x_{j}^{k - 1} = max\left( {x_{j}^{k - 1} (i)|i = 1,2, \ldots ,M;j = t,t + 1,t + 2} \right) \hfill \\ \end{gathered}$$

  (6)

  where $\min x_{j}^{k - 1}$ and $\max x_{j}^{k - 1}$ are determined by the training data.

• Step 6: For each data pairs of (5) starting from i = 1, determine the membership value $F_{1}^{^{\prime}} , \ldots ,F_{p}^{^{\prime}}$ of the p fuzzy sets $F_{1}^{{}} , \ldots ,F_{p}^{{}}$ that reach the maximum value.

• Step 7: Each sub-fuzzy system in Level 1 was trained (in parallel ) according to the WM algorithm [26] to get the outputs $x_{1}^{{1}} (i), \ldots ,x_{{n_{1} }}^{1} (i)$, and use the first Level’s output as the second Level’s input.

• Step 8: Repeat steps 3–7 to build the (k+1)-th Level and input $x_{1}^{k} (i), \ldots ,x_{{n_{k} }}^{k} (i)$ to (k+1)-th Level, calculate the each fuzzy set $F_{1}^{k} , \ldots ,F_{{n_{k} }}^{k}$, and then input these fuzzy sets to the corresponding subsystems $FS_{1}^{1} , \ldots ,FS_{{n_{{1}} }}^{1}$.

  8.1) Update $\alpha^{{j_{1} , \ldots ,j_{d} }}$ and $\beta^{{j_{1} , \ldots ,j_{d} }}$ in phase 1.

• Step 9: Using WM algorithm to train and get outputs $x_{1}^{k} (i), \ldots ,x_{{n_{k} }}^{k} (i)$, extracting fuzzy rules and creating fuzzy rule base.

  9.1) Perform a local loop search from Level 1 to Level L−1 to delete feature combinations and corresponding subsystems with low correlation.

  9.2) Determine the parameter $z^{{j_{1} \cdots j_{d} }}$ in the FS of (2), such that $z^{{j_{1} \cdots j_{d} }} = {{\alpha^{{j_{1} \cdots j_{d} }} } \mathord{\left/ {\vphantom {{\alpha^{{j_{1} \cdots j_{d} }} } {\beta^{{j_{1} \cdots j_{d} }} }}} \right. \kern-\nulldelimiterspace} {\beta^{{j_{1} \cdots j_{d} }} }}$.

• Step 10: Repeat steps 5–6, Levels 1 to L-1 are constructed until the final output is only one FS.

  10.1) The final $x_{1}^{L}$ is the output of RLODFS.

  For any given input $(x_{1}^{^{\prime}} ,x_{2}^{^{\prime}} )$, fuzzy system can be represented by a parameter $z^{22}$.

Figure 3 depicts an example of automatic layering from the bottom-up with 8-dimensional input, whose variables are divided into several groups [ namely RLODFS-Sδ (δ = 0, 1, 2, 3) with or without input sharing ] to reduce the data dimension and computation. Fig. 3a–d demonstrates the cases of non-input sharing (RLODF-S0), one input sharing (RLODFS-S1), two input sharing (RLODFS-S2), and three input sharing (RLODFS-S3), respectively.

Fig. 3

Basic structure of RLODFS based on grouping and input sharing (8 dimensions as an example)

Let the grouping scheme θ = 4 ( 3≤θ≤9, user-specified), where the number of levels of RLODFS-S0, RLODFS-S1, RLODFS-S2, and RLODFS-S3 are, respectively, $\left\lfloor {n/4} \right\rfloor$,$\left\lfloor {\left( {n{ - 1}} \right)/{3}} \right\rfloor$,$\left\lfloor {n/{2}} \right\rfloor - 1$, and $n - \left\lceil {n/2} \right\rceil$, where n is the number of features .

Remark

The number of input variables of each fuzzy subsystem θ is set to 4 for the following reasons:

• 1. The accuracy of the model.

• 2. The complexity of the subsystem will increase with more inputs.

• 3. As input variables increase, the number of rules increase exponentially in basic WM algorithm, which will violate the original intention of improving interpretability and reducing model complexity.

5 Case Study

This section presents simulation results to demonstrate the performance of proposed RLODFS-Sδ. By dividing a large-scale problem into several sub-problems to solve, the total rules extracted by the deep fuzzy system is different due to the different sharing strategies among each subsystem. If the input sharing between subsystems is simply required, the influence of several important data characteristics may be diluted, resulting in insufficient extraction rules or weakening the influence of important rules. At the same time, similar inputs will cause the two sub-fuzzy systems to extract the similar partial rules, which will increase computational cost.

5.1 Datasets

To illustrate the proposed method in this paper in an even better fashion, Table 1 presents the 12 real-world datasets with varying size and dimensionality. Their features range from small to large. The original datasets are downloaded from https://archive.ics.uci.edu/ml/datasets.php. For each dataset, we randomly selected 60% examples for training, and the remaining 40% for test. For space limitations, we focus on showing the effect of the test sets. WM was trained in one single pass on all training examples, and then its root mean squared error (RMSE) on the test examples was computed. The other eight algorithms were iterative. The maximum iterations was 450. Since there was randomness involved, each algorithm was repeated 15 times on each dataset, and the average test results are reported next.

Table 1 Summary of the 12 regression datasets used in the simulations.

11 datasets have numerical features. Each numerical feature was mapminmax normalized to have zero mean and unit variance, and the output mean was also subtracted. Classic fuzzy systems have difficulty dealing with high-dimensional data, but owing to the hierarchical and the random grouping structure that we proposed overcome the dimension constrains, we do not constrained the maximum feature dimensionality. Due to the curse of dimensionality, the WM failed to analyze the datasets after Housing in Table 1, so it was removed from the comparison in the following examples and replaced with a better performing GRNN.

Specifically, assuming the MFs is $r$, and the input dimension has 2 and 3, then the system’s rules are as follows:$r^{2} \sum\nolimits_{k = 1}^{L} {level_{2} } \left( k \right) + r^{3} \sum\nolimits_{k = 1}^{L} {level_{3} } \left( k \right)$, where k is the number of layers. We can see from (5) that each system FS_i has p^m free parameters to be designed and stored in the computer memory. The complexity of RLODFS-S0 is approximately $O\left( {N + p^{d} } \right)\sum\nolimits_{k = 1}^{L} {n^{k} }$. The complexity of RLODFS-S1 , RLODFS-S2, and RLODFS-S3 is $\omega \left( {N\sum\nolimits_{k = 1}^{L} {n^{k} + p^{d} L} } \right)$, where $O(N)$ accounts for the one-pass of data in (5)–(6), $O(p^{d} )$ accounts for the computation of $z^{{j_{1} \cdots j_{d} }}$ in steps 7–9, and $\sum\nolimits_{k = 1}^{L} {n^{k} }$ is the number of fuzzy systems in the L level of RLODFS-Sδ .

5.2 Algorithms

To evaluate the proposed RLODFS algorithms, we introduced the classical shallow prediction algorithms, i.e., BP(Back Propagation), RBF(Radial Basis Function), and the commonly used deep neural network algorithms GRNN (Generalized Regression Neural Network), LSTM (Long Short-Term Memory), DBN (Deep Belief Networks), and other algorithms for comparison.

• 1. BP network, the parameters increase dramatically as the number of dimensions increases; therefore, no one can well explain the relationship between the characteristics of a NN and an actual problem. And because of the " black box " nature of the network, people will not know how the network will produce results, let alone why it will produce such results.

• 2. RBF network can approximate arbitrary non-linear functions and has good generalization ability. Unlike BP's activation function sigmoid (or Relu), the former is a radial basis function.

• 3. GRNN is a special form of RBF, which was essentially identical to RBF; it does not have weights, but with good approximation ability, learning speed, and fault tolerance. spread = 0.5 was used.

• 4. LSTM network [38], as one of the deep learning methods, can avoid the problem of gradient vanishing or gradient expansion by increasing the input threshold, forgetting threshold and output threshold. Max epochs = 200, gradient threshold=1, initial rate = 0.005, and drop factor = 0.2 were used.

• 5. DBN network [39], as the most important multi-layer network structure in deep learning, adopts semi-supervised learning algorithm. The network consists of Restricted Boltzmann machine and BP, and the optimal solution can be achieved by fine tuning, but the learning process is slow. LayerMin = 2, 20, 50, and 70 samples per batch, net1Index2 = 0, and the minimum neurons in each layer is 2. The target error and max epochs are 0 and 200, respectively.

• 6. WM method [40], which can extract rules from data and improve rules to construct the input–output mapping, makes the fuzzy system more interpretable than NN, but it often encounters rule explosion.

• 7. RLODFS-Sδ is based on the random local loop optimization strategy and WM algorithm, and cuts into the construction of the deep structure from the perspective of the random division subsystem calculation. Compared with other algorithms that directly complete the input–output mapping from the data as a whole, it starts from the local integration rules and then deduces to the whole. RLODFS-Sδ learns rules from data and completes the mapping between input and output through IF-THEN rules, which is easy to understand and overcome the poor interpretability of DNN.

In addition, once the output is wrong, the later can trace the source according to the IF-THEN rule, and quickly find the wrong rule and correct it, which opens a new way for fuzzy system to solve the problem of high-dimensional big data. Compared with the classical fuzzy systems that directly address the entire dataset, the complexity of this method is greatly reduced, and the accuracy has been significantly improved, on which currently no other efficient training algorithms exist. It can be used for training deep fuzzy systems on datasets of any size.

5.3 Index of Performance

There are some limitations in the analysis of experiments from the perspective of visual effects. In order to avoid artificial subjectivity and empiricism, mean absolute error (MAE), mean squared error (MSE), and standard deviation (STD), are selected as the objective evaluation. They are defined as follows:

$$MSE = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left( {\hat{y}_{i} - y_{i} } \right)^{2} },$$

(7)

$$RMSE = \left( {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left( {\hat{y}_{i} - y_{i} } \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}},$$

(8)

$$MAE = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {\hat{y}_{i} - y_{i} } \right|},$$

(9)

$$STD = \left( {\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left( {x_{i} - u} \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}},$$

(10)

$$Error_{max} = max\left\{ {\hat{y}_{i} - y_{i} \left| {i = 1,2, \ldots ,N} \right.} \right\},$$

(11)

$$Error_{\min } = \min \left\{ {\hat{y}_{i} - y_{i} \left| {i = 1,2, \ldots ,N} \right.} \right\},$$

(12)

$$SMAPE = \frac{100\% }{N}\sum\nolimits_{i = 1}^{N} {\frac{{2\left| {\hat{y}_{i} - y_{i} } \right|}}{{\left( {\left| {\hat{y}_{i} } \right| + \left| {y_{i} } \right|} \right)}}},$$

(13)

where N and $u$ are the size of the dataset and the mean value, respectively. $u = {{\left( {x_{1} + x_{2} + \cdots + x_{N} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{1} + x_{2} + \cdots + x_{N} } \right)} N}} \right. \kern-\nulldelimiterspace} N}$,$\hat{y}_{i} - y_{i}$ is the deviation between the observed value $\hat{y}_{i}$ and the true value $y_{i}$. We define an evaluation system to evaluate each model. The final score of the model is the sum of the scores of each index. The higher the score, the better the comprehensive performance.

The time taken to finish 450 training iterations for the RLODFS-Sδ-based algorithms on the 12 datasets is shown in Table 2. The experimental software and operating environment of all methods are Matlab 2019a(App Designer) and Windows 10 Enterprise 64x, with Intel Core i7-8700K CPU @ 3.70 GHz, 16GB memory, and 512GB solid-state drive. Not surprisingly, RLODFS-S0 was the fastest, one reason is that group learning, layering, and none input sharing, which reduced the number of parameters to be adjusted in each iteration. Although WM just one pass through the data solution, and no iteration was needed, its rules increase exponentially. Among the four RLODFS-based algorithms and WM, feature dimensions and MFs are the most important factors. Additional, combined with Tables 2 and 5, we can observe that the computational cost largely depends on number of MFs, parameters, variables, and samples. From 12 datasets in Table 2, as parameters and features increase, the time required for each algorithm increases exponentially. Furthermore, the features and parameters has a greater impact on running time than samples.

Table 2 Computational cost (seconds) of different algorithms on the 12 regression datasets

5.4 Experimental Results

The performance and the average test RMSEs of each algorithm are shown in Fig. 4 (the horizontal axis and the vertical axis, respectively, represent the sample label and the test output) and 5, respectively. We can see from figure as follows:

Fig. 4

Comparison of the results of eight algorithms in 12 datasets (a)–(l).

• 1. There are several abnormal prediction values that significantly deviate from the target value in the BP and RLODFS-S0, RLODFS-S1( especially Smart watch, Skill Craft and ONP), and the overall performance of each algorithm is good.

• 2. The average test MSE, MAE, STD, SMAPE, Error_min, and Error_max on the 12 datasets are shown in Table 3. From the indicators of STD, MSE, and SMAPE, the gap between DBN, RLODFS-S2 and RLODFS-S3 is small, and the fluctuation between the predicted value and the true value of the model is small and relatively stable. The Error_min and Error_max of WM are the most obvious, meanwhile, we found that WM had the smallest average SMAPE, but its accuracy was not the best. It reflects indirectly SMAPE's failure to characterize the problem well. The LSTM and BP algorithms are relatively close to RLODFS in MAE, reflecting their high overall accuracy in the prediction. We can see from Table 3 that the four algorithms of RLODFS outperformed the other four algorithms (smaller MSE, RMSE and STD), which verifies the effectiveness of the proposed method.

  Table 3 Average test evaluation indexes of 10 algorithms on 12 datasets.

• 3. RLODFS-S1, RLODFS-S2, and RLODFS-S3 had comparable performance with BP, RBF, and LSTM. All of them were worse than the RLODFS on 10 out of the 12 datasets, suggesting that a model with much more parameters and non-linearity does necessarily outperform a simple linear regression model, if properly trained.

• 4. RLODFS-S2 and RLODFS-S3 performed the best among the 10 algorithms. On nine out of the 12 datasets (except Winequality-white, ONP and SUP ), RLODFS’s best test RMSEs were smaller than BP and RBF. On all 12 datasets, RLODFS-S3’s best test RMSEs were smaller than RBF. RLODFS-S2 and RLODFS-S1 also converged much faster than BP, RBF, LSTM, and DBN. As the final RLODFS trained from the four RLODFS-based algorithms had the similar structures and parameters, these results suggest that RLODFS-S2 and RLODFS-S3 were indeed very effective in dealing with high-dimensional data, which in turn helped obtain better learning performances.

• 5. The rules for WM is 3⁸ = 6561, while the RLODFS-S0, RLODFS-S1, RLODFS-S2, and RLODFS-S3 have two Levels, two Levels, three Levels, and four levels, respectively. The rules are 3⁴×2+3² =171, 3⁴×3+3³ = 270, 3⁴×4+3⁴+3² = 414, and 7×3⁴+3² = 576, respectively, which account for 2.606%, 4.115% , 6.310%, and 8.779% of WM’s rules. Herein the rules of four algorithms of the RLODFS are far lower than the WM’s, which thus reflects the advantages of the proposed algorithms in terms of interpretability.

From the evaluation indicators in Table 3, RLODFS-S2 and RLODFS-S3 occupy the main advantage of being the most ideal prediction model, while WM has the worst performance and the lowest score. Based on Fig. 4 and Table 3, RLODFS-S0 and RLODFS-S1 have more advantages in low-dimensional problems. As dimension increases, RLODFS-S2 has certain advantages in prediction accuracy, with few obvious abnormalities. In general, the prediction models of RLODFS-S1, RLODFS-S2, and RLODFS-S3 are more stable than other competing methods.

The average number of layers (levels) of each algorithm on the 12 datasets is shown in Table 4. RLODFS-S3 has 140 layers on the BlogFeedback dataset, with an average of 32 layers. RBF, LSTM, and RLODFS-S0 have a lower average layers, all of which are 3 layers.

Table 4 The average number of layers(levels) of each algorithm in 12 datasets.

The selection of hidden layer nodes not only has a great impact on the established model but also is the direct cause of overfitting [41]. As shown in Table 5, the enumeration method [42] was adopted to determine the optimal number of nodes and iterations among BP, RBF, DBN, and LSTM.

Table 5 The average 12 datasets of the different methods on the quality under tenfold cross-validation.

The results of Tables 2, 3, and 4 objectively illustrate the differences between the various algorithms. We can observe that:

• 1. The complexity of each algorithm is as follows: GRNN < RLODFS-S0 ≤ RLODFS-S1 ≤ RLODFS-S2 < RLODFS-S3 < BP < RBF < DBN < LSTM < WM.

• 2. Although BP and LSTM always achieved the smallest training RMSE, their test RMSE was almost always the largest, and had large oscillations. This suggests that they had significant overfitting.

• 3. The DBN, RLODFS-S2, and RLODFS-S3 show good predicted performance during the test phase, of which DBN and RLODFS-S3 are the most obvious.

• 4. Although LSTM, BP, and RBF all have achieved pretty good prediction, their test errors are not as good as DBN and RLODFS. The superiority of RLODFS-S3 is further revealed as dimension increases. From Fig. 5, the RLODFS-S3 also occupies the commanding heights, which is significant in accuracy and stability. The RLODFS based on IF-THEN rules cannot only guarantee the accuracy and stability of the model but also give full play to the strong interpretability of the FS, which has reference for understanding the mapping relationship between input and output of the model [43].

  Fig. 5

  

  The average test RMSEs of the seven algorithms on the 12 datasets

Figure 5 confirms the observations made from Fig. 4. Particularly, RLODFS-S3, RLODFS-S2, RLODFS-S1, and DBN converged much faster and to smaller values than BP, LSTM, RBF, and RLODFS-S0. Although RLODFS-S1 and RLODFS-S2 may not always outperform RLODFS-S3, their performance were more stable than RLODFS-S3, which explain indirectly that RLODFS-S1 and RLODFS-S2 have better generalization performance.

The tenfold cross-validation method [44] was used to further verify the proposed method. The results of the test sets are shown in Table 5.

Milton Friedman [45, 46] developed a non-parametric statistical test to detect the differences in multiple tests. Here, we performed the Friedman ranking test on all data sets listed in Table 1. Figures 6 and 7 present the ranking results of these 10 algorithms on all datasets in the Friedman ranking test. We can see from Table 5 and Figs. 6 and 7, RLODFS-S2 and RlODFS-S3 have the best rankings. RBF and RLODFS-S1 rank second in scores only after RLODFS-S1, and the score and ranking of WM are the lowest. Simulation results demonstrate that the proposed method outperforms other enhancement methods in terms of Error_max, SMAPE, MSE, and rankings.

Fig. 6

Non-parametric statistical analysis

Fig. 7

Non-parametric statistical analysis

In conclusion, these results also show that RLODFS is significantly superior to other competing models. The difference being statistically significant.

6 Conclusion

Interpretability decreases rapidly as the rules increase. Therefore, based on the interpretability of FS and the advantages of DCNN, a hierarchical RLODFS and algorithms were developed to overcome the input–output transition black box of DCNN, and evaluations show the method’s superiority.

• It is highly interpretability. A FS can be described by a series of fuzzy IF-THEN rules, whose structure and parameters have clear physical significance. If there are errors in the FS, they can be corrected directly by finding the corresponding fuzzy rules and changing it.

• It is simple in representation, fast in running, easy to use, and has the ability to effectively construct models for massive datasets. The FS has overlapping and parallel structure which overcome the curse of dimension and local loop search has been increased the opportunity of finding better combination of different variables.

• Its correctness verification is flexible and easy to be implemented. The system is constructed by a bottom-up fashion and trained in a layerwise to speed up the computation.

The selection of grouping unit θ, input sharing δ, the number of fuzzy sets, and layers can be easily adjusted to improve the performance: (1) does not take up too much memory; (2) suitable for datasets of varying size and dimensionality.

In the future, intelligent algorithms will be adopted to optimize the structure and parameters of RLODFS, further reducing the rules and improving the performance of the system. Additionally, a post hoc test [46, 47] will be applied to verify our algorithms,we believe that fuzzy systems can be combined with deep learning to become deep fuzzy systems, so as to obtain a new idea and solution with high interpretability and strong robustness in dealing with complex high-dimensional systems. Some preliminary studies on deep fuzzy modeling we have done show that this idea has great development potential and may become a new deep learning algorithm.