1 Introduction

The objective of inverse reinforcement learning (IRL) is to learn a task using an approximation of an unknown reward by observing an expert demonstration [1, 2]. Many IRL methods offer frameworks for estimating a reward function, which is then used to derive an optimal policy [3, 4]. A Bayesian model provides a higher reward to the states that are close to the goal so there is greater adaptability to changes of task, such as the assignment of a new target or variations in parameters [5, 6]. A fuzzy comprehensive evaluation method is proposed to extract the features utilized in fuzzy Bayesian reinforcement learning and classifies the situations into a set of features. The factors defined for them can be used to calculate the weights [7]. These methods learn a mapping by observing an input to state values/costs using margin maximization techniques and minimize the cost function using gradient descent or game-theoretic approach [8]. The residual gradient fuzzy reinforcement learning algorithm uses the residual gradient algorithm with fuzzy actor–critic structure to tune the input and output parameters of its function approximation systems [9]. The maximum entropy algorithm [10, 11] uses a Markov decision process (MDP) model to calculate a probability distribution for the state actions. These IRL methods assume that a MDP model of a system is either given a priori or can be accurately learned using the demonstrated trajectories, in terms of a state space. Nevertheless, the IRL concept by matching of a defined feature expectation is ambiguous. Each policy can be optimal for many reward functions, and many policies lead to the same feature counts.

A notable exception is the projection algorithm, whereby the trajectories that are generated by the learning agent are compared with the demonstrated trajectories using state features, in order to minimize the worst-case loss in the value of the learned policy. This guarantees that the correct reward function is learned if the feature counts are properly estimated. The algorithms regard an IRL problem as an approximation of a linear combination function with constraints. Using the orthogonal projection method to calculate the weights for the linear reward function, the method estimates the linear combination function and derives an optimal policy faster and with less effort [2]. From the viewpoint of supervised learning, this type of IRL uses supervised learning techniques to acquire the reward function. Supervised learning uses labeled data to approximate a mapping between inputs and outputs. If labeled data (features) are used to derive a reward function, an agent must explore the features space and derive an optimal action policy. The human reinforcement learning links direct policy evaluation and human reinforcement to autonomous robots, accordingly shaping the reward function by combining both reinforcement signals [12]. Besides, the architecture of adaptive heuristic critic combined with action bias allows agents to solve the problem of continuous action system [13]. Unfortunately, it is likely for this simple method to become trapped by problems or failures [6].

Using ensemble learning techniques, the proposed approach inputs the compared trajectories for IRL into a boosting classification problem and provides a faster and more flexible method of adjusting the weights of the approximated reward function comparing with the aforementioned methods [14, 15]. Besides, in order to improve the performance of RL algorithm, fuzzy-based methods were proposed for tuning the learning rate [16, 17]. In this paper, the proposed approach also uses a fuzzification technique to accelerate the updating process. The remainder of this paper is organized as follows. Section 2 briefly introduces the relative research background, including reinforcement learning, inverse reinforcement learning and the boosting classifier. The proposed ensemble inverse reinforcement learning technique that uses boosting and fuzzification techniques is introduced in Sect. 3. In Sect. 4, the simulation results for a labyrinth and a robotic soccer are used to demonstrate the validity of the proposed method. The final section draws conclusions.

2 Background

2.1 Inverse Reinforcement Learning

In some IRL algorithms, the reward function is represented by a linear combination of useful features as [14]:

$$R(s) = \omega \cdot \phi (s)$$
(1)

where \(\phi (s) = \left[ {\phi_{1} (s), \, \phi_{2} (s), \ldots , \, \phi_{k} (s)} \right]^{T}\) is a function mapping from a state space to a feature vector that is predefined as 0 or 1, k is the number of features in the reward function, and \(\omega (s) = \left[ {\omega_{1} , \, \omega_{2} , \ldots , \, \omega_{k} } \right]\) is an unknown vector to be tuned during the learning process. The value function of policy \(\pi\) is shown below. The expected discounted accumulated feature value is defined as a vector of feature expectations in Eq. (3):

$$\begin{aligned} E_{{s_{0} \sim D}} \left[ {V^{\pi } (s_{0} )} \right] =& E\left[ {\sum {_{t = 0}^{\infty } \gamma^{t} R} (s_{t} )\left| \pi \right.} \right] \hfill \\ \, =& E\left[ {\sum {_{t = 0}^{\infty } \gamma^{t} \omega \cdot \phi } (s_{t} )\left| \pi \right.} \right] \hfill \\ \, =& \omega \cdot E\left[ {\sum {_{t = 0}^{\infty } \gamma^{t} \phi } (s_{t} )\left| \pi \right.} \right] \hfill \\ \end{aligned}$$
(2)
$$\mu (\pi ) = E\left[ {\sum {_{t = 0}^{\infty } \gamma^{t} \phi } (s_{t} )\left| \pi \right.} \right]$$
(3)

IRL estimates a reward function that allows the agent to generate the same trajectory as the demonstrated trajectory using a policy under this approximate reward function.

2.2 Boosting Classifier

Ensemble methods are learning algorithms that construct a set of classifiers and then classify new data points by taking a weighted vote of their predictions. Some common ensemble methods use Bayesian averaging and error-correcting output coding. Boosting algorithms, which correct the error in output coding, and convert weak learners to proficient learners, improve the accuracy of prediction in a machine learning model when they are combined with a learning algorithm. A boosting algorithm constructs a strong classifier that is a linear combination of weak classifiers with adaptive weights for training data, as defined below, where αt denotes the weight of the selected weak classifier at iteration t, and ht(x) denotes the output of the selected weak classifier at iteration t using training data x.

$$F_{T} \left( x \right)\; = \;\sum\limits_{t = 1}^{T} {\alpha_{t} h_{t} \left( x \right)}$$
(4)

At each iteration, t, the boosting algorithm selects a weak classifier and adjusts weight αt for this weak classifier to minimize the sum of training error, Et, for the boosted classifier that is defined in Eq. (5). |X| denotes the number of samples in the training dataset, Ft−1(x) is the boosted classifier that constructed by iteration t-1, and E(F) denotes some error function.

$$E_{t} \; = \;\sum\limits_{i = 1}^{\left| X \right|} {E\left( {F_{t - 1} \left( {x_{i} } \right) + \alpha_{t} h_{t} \left( {x_{i} } \right)} \right)}$$
(5)

2.3 The AdaBoost Algorithm and the Concept of Dissimilarity

AdaBoost is an abbreviation for adaptive (adjust the error rate) and boost (improve the classification accuracy). It is implemented in the framework of boosting algorithm [18, 19]. AdaBoost calculates the adjustment parameter α using the error rate of each classifier and combines the weak classifiers into a strong classifier [20]. Figure 1 shows a simple schematic diagram of AdaBoost. The classifiers decide to which category the data belong, and the parameter, α, defines the classifiers’ credibility. By combining the classifiers and the parameter, α, data are classified sequentially.

Fig. 1
figure 1

A schematic diagram of an AdaBoost

Full size image

The original AdaBoost algorithm and the AdaBoost.M1 algorithm are slightly different. AdaBoost.M1 updates the weights via a training process. The input data have m points, x1, x2, …, xm. Each point corresponds to classification labels y1, y2, …, ym, yk∈{1,2,…,g}. After i iterations, the value for the weight of sample xk∈{x1,x2,…,xm} is expressed as Di(k). The initialized weight values are all the same at 1/m. After training, the values of the weights for correct classifications are reduced and the weights for incorrect classifications are increased. If hi represents the classifier that is selected at the ith iteration and hi(xk) ≠ yk denotes that the output is not the same as actual yk, the classification is incorrect. The samples are individually checked in the classifier to determine the correctness of each classification. The error rate Ei is added all of the weight values of the incorrectly classified samples, as shown in formula (6). The parameter, αi, is defined in formula (7).

$$E_{i} = \sum\limits_{{k:h_{i} (x_{k} ) \ne y_{k} }} {D_{i} (k)}$$
(6)
$$\alpha_{i} = \ln \left( {\frac{{1 - E_{i} }}{{E_{i} }}} \right)$$
(7)

The larger the error rate Ei, the smaller is the parameter αi and the less reliable is the classifier.

The iterative and regularized formulation of Di(k) is depicted as:

$$\begin{aligned} & Z_{i} = \sum\limits_{m} {D_{i + 1} (k)} \\ & D_{i + 1} (k) = \frac{{D_{i} (k)}}{{Z_{i} }} * \left\{ {\begin{array}{*{20}c} {1\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{if}}\,y_{k} \ne h_{i} (x_{k} )} \\ {e^{{ - \alpha_{i} }} \;i{\text{f}}{\kern 1pt} \,y_{k} = h_{i} (x_{k} )} \\ \end{array} } \right\} \\ \end{aligned}$$
(8)

3 Proposed Method

IRL establishes a reward function, R, which can generate a policy that is similar to the expert’s policy. The difference between the expert’s behaviors and the agent’s behaviors is used to update the reward function over many iterations. When the reward function has been adjusted, the agent learns a policy that is similar to the expert’s behavior.

3.1 Ensemble Techniques for Inverse Reinforcement Learning

If an ensemble method is used for inverse reinforcement learning, the feature expectations defined in (9) are regarded as a set of week classifiers and the trajectories acquired from demonstrations are used as class labels for the training sample, i.e., the desired outputs. To calculate the coefficients for the weak classifiers, the proposed approach uses the framework of an ensemble method for IRL, to determine the importance of the distribution of features that causes policy value errors in a search for iterative policy [21, 22]. Therefore, the parameters for a linear combination of feature functions are updated using the importance distribution as the step size and the errors as the direction for each iteration. In other words, the proposed method uses the difference between the expert behaviors and the agent behaviors to determine the degree of importance for features and adjusts the weights for the weak classifier. During successive learning iterations, the parameters for the linear combination of the reward function are updated as:

$$\omega_{i + 1} = \omega_{i} + D_{i + 1} \times \Delta \mu_{i}$$
(9)

where ωi is the value of the weight, i is the number of iterations, and D is the ensemble voting weight, as previously defined before. The difference between the expert trajectory and that which is generated using the learned policy that is based on the transiently approximated reward function is \(\Delta \mu_{t} \; = \;\mu \left( {\pi_{E} } \right)\; - \;\mu \left( {\pi_{t} } \right)\). μ(πE) is the target feature expectation vector for the corresponding sample inputs from the demonstration, and μ(πt) is the contemporary feature expectation vector, which is acquired from the policy that uses a transiently approximated reward function at iteration t.

Equations (1) and (9) define the optimum weight value \(\omega^{*}\) as a set of linear combinations. The proposed ensemble method for determining the values of parameters using this method is listed in Algorithm 1 [2]. The algorithm shows the step for updating the value of ω and for finding the value of μ in IRL methods. Ei represents the error rate, which is calculated by adding all of the categorization errors. The error rate is used to adjust each element of the value of the weight. If the error rate is high, the value of the weight is decreased. If the error rate is small, the value of the weight is increased.

figure e

3.2 Inverse Reinforcement Learning Using Dissimilarity

Since the ensemble method requires many learning iterations, this paper proposes an ensemble method that uses dissimilarity to adjust the value of ω in the vicinity of a specific future using batch learning [23]. In the first step, the weight for the reward is generated at a random value, ω0, to calculate the expected characteristic value μi using the policy πi which is generated by Eq. (1) in the IRL. The characteristic expected value μE is the expert behavior.

Comparing μi with μE, the following three conditions are possible:

  1. 1.

    An element in μi is larger than that in the corresponding position in μE, which means that the route that is learned by the agent passes earlier than the expert route.

  2. 2.

    An element in μi is smaller than that in the corresponding position in μE, which means that the route that is learned by agent passes later than the expert route.

  3. 3.

    All elements in μi are as the same as those in the corresponding position in μE, which means that the route that is learned by the agent passes at the same time as the expert route.

The difference between the agent’s behaviors and expert’s behaviors is calculated as:

$$\Delta \mu_{i} = \mu_{E} - \mu_{i}$$
(10)

This paper uses the concept of dissimilarity to update the learning rate for the elements in ωi. Because the goal is to emulate the expert exactly, adjustments are made using the dissimilarity between the expert’s and the agent’s paths.

The relevant equation is:

$$S_{j} = \sqrt {\frac{{\left( {\frac{{D_{{1,e_{1} }} - D_{{1,a_{1} }} }}{{D_{1,range} }}} \right)^{2} + \cdots + \left( {\frac{{D_{{j,e_{j} }} - D_{{j,a_{j} }} }}{{D_{j,range} }}} \right)^{2} + \cdots + \left( {\frac{{D_{{n,e_{n} }} - D_{{n,a_{n} }} }}{{D_{n,range} }}} \right)^{2} }}{n}}$$
(11)

where \({\text{S}}_{\text{j}}\) means the reward features, j = 1, 2,…, n. Dj,e is the experts’ weight in dimension i, Dj,a represents the learning agent’s weight in dimension i, and Dj,range represents the maximum range of the weights in dimension i.

Equation (11) allows the agent’s behaviors to emulate the expert’s using fewer learning iterations. The weight for the reward is:

$$\omega_{i + 1} = \omega_{i} + S_{i + 1} \times \Delta \mu_{i}$$
(12)

If the dissimilarity Si is high, the weight for the reward must be significantly adjusted, and if it is low, little adjustment is required.

3.3 IRL with Fuzzification

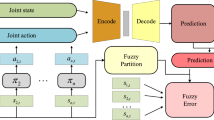
In IRL, the policy updates the reward feature ωi using Eq. (12). The value for ∆μi represents the difference between the expert’s and the agent’s behaviors. The learning process is illustrated in Fig. 2.

Fig. 2
figure 2

The learning process of IRL

Full size image

IRL adjusts the weight for the reward ωi, which is based on μi. This is then used to establish a new policy. The learning agent uses the policy to learn behaviors. To accelerate learning further, fuzzification and dissimilarity are used to learn the expert’s behaviors quickly. An example of a robotic soccer game, which is shown in Fig. 3, is used to illustrate the implementation of dissimilarity and fuzzification of the state space. In a robotic soccer game, the state space is composed of the two-dimensional one-spanned angle between the robot and the ball and the distance between the robot and ball. The dimension of the angle is divided into four portions, {(0°, 90°), (90°, 180°), (180°, 270°), (270°, 360°)}, and the distance is partitioned into four ranges, {(0, 1), (1, 2), (2, 3), (2, 3)}, so the cardinality of state space is 16; that is, there are 16 discrete states. Triangular membership functions are used for fuzzification, as shown in Fig. 4. If the current sensory input is (1.3°, 99°), the weight of the current state containing (1.3°, 99°) is updated with the sum of the weights for the active vicinity: the top left four grids on the table in Fig. 5; i.e., 0.08 × ω1 + 0.12 × ω2+ 0.32 × ω5 + 0.48 × ω6.

Fig. 3
figure 3

An example of a soccer robot

Full size image
Fig. 4
figure 4

The fuzzification example for robotic soccer games where the receptive field receives sensory data (1.3°, 99°)

Full size image
Fig. 5
figure 5

Weighted averages for the updated parameters in defuzzification

Full size image

There are two possible outcomes when the value for ∆μi is calculated over the state space. If ∆μi is negative, i.e., the expert’s expected feature μE is smaller than the agent’s value for μi on the state i along the trajectory that is generated using the currently learned policy, the learning agent visits this state earlier using its own trajectory than if it is uses the expert’s trajectory and vice versa. If \(\Delta \mu_{\text{i}} = 0\), the learning agent and the expert either visit that state during the same time sequence or neither visits that state. The algorithm is more complex so the latter is the most common for an IRL process. There is no reward value of ωi, and time is wasted in RL learning process. The fuzzification process allows an agent to update its own ωi about rarely visited states by referring to a neighbor’s experience, and learning is accelerated.

4 Simulations and Discussion

Three simulations were conducted to demonstrate the proposed method: a mountain car, a mobile robot in a maze and a robotic soccer game. The first three experiments compare the methods for this paper to verify the performance: the method used in [3] and the proposed IRL. The robotic soccer game simulation verifies that using fuzzy theory for the IRL algorithm improves the reinforcement learning rate.

4.1 Maze

In this simulation, a robot tries to determine a reward function, which is used to learn the demonstrator’s strategy and approach the goal in a maze, as shown in Fig. 6. The simulation of maze problem shows the performance of the proposed IRL in discrete environments.

Fig. 6
figure 6

The agent’s path after learning

Full size image

The maze has 20 × 20 grids, which are surrounded by walls. The yellow part in the maze is starting point for the mobile robot. The goal is the red rectangle in the maze. The gray parts represent the obstacles. The robot can move up, down, left or right. The robot can move only one grid at one time. The learning rate α was set to 0.7, and the ε-greedy action selection implemented in the simulation, that the exploration rate, was set to 5%. The other setting of parameters is listed in Table 1. After learning, the agent can imitate the expert’s demonstration shown in Fig. 6.

Table 1 Parameters of maze
Full size table

The average iteration round time is listed in Table 2 to show the proposed IRL efficiency. It takes less time than the method in [3]. This demonstrates that the proposed method learns the demonstrated path more quickly. The proposed IRL’s variance is smaller than its counterpart’s, so that the proposed IRL is demonstrably more stable.

Table 2 Comparison of Number of Iteration between Two Methods in Maze
Full size table

4.2 Mountain Car

This simulation, a standard testing domain in reinforcement learning, an under-powered car must drive up a steep hill, as shown in Fig. 7. Since gravity is stronger than the car’s engine, even at full throttle, it must learn to leverage potential energy by driving up the opposite hill before the car is able to make it to the goal at the top of the rightmost hill. The dynamic equation is:

$$\begin{aligned} & x_{t + 1} = x_{t} + \dot{x}_{t + 1} \\ & \dot{x}_{t + 1} = \dot{x}_{t} + 0.001a_{t} - 0.0025\cos (3x_{t} ) \\ \end{aligned}$$
(13)

where xt is the position of the car and \(\dot{x}_{t + 1}\) is its velocity. The state space for the problem has two dimensions: its position and its velocity. The position interval is [− 1.2, 0.5], and the velocity interval is [− 0.07, 0.07]. In each state, three actions are allowed: throttle forward (+1), throttle reverse (−1) or zero throttles (0). The end of the simulation is when position ≥ 0.6.

Fig. 7
figure 7

Mountain car

Full size image

The results in Table 3 show that after 100 rounds, the proposed IRL takes less time than its counterpart to complete the mountain car simulation. This demonstrates that the proposed method learns the path that expert demonstrates more quickly. The proposed IRL’s variance is smaller than its counterpart’s, which demonstrates that the proposed IRL is more stable.

Table 3 Comparison of number of iteration between two methods in mountain car
Full size table

4.3 Robotic Soccer Game Simulation

The simulation environment is the same as that shown in Fig. 3. Two-wheeled robot soccer must kick the ball into the goal in the same way as the expert. As shown in Fig. 8, the state space includes two dimensions: the angle of 18 ranges between the robot and ball, and the distance of 10 ranges between the robot and ball. The robot can move forward and backward and can rotate clockwise and anti-clockwise.

Fig. 8
figure 8

Definition of state space

Full size image

The results in Table 4 show that after 100 rounds, the proposed IRL requires fewer learning iterations than its counterpart. Table 4 shows that the proposed IRL also exhibits a smaller variance for the learning process than its counterpart, so it is more stable than its counterpart. The performance of the proposed IRL for behavior learning is validated in continuous environment, even though it is more difficult to design the reward function than in a discrete environment.

Table 4 Comparison of number of iteration between two methods in robot soccer
Full size table

4.4 Robotic Soccer Simulation with Fuzzy Theory

The simulation environment is the same as shown in Fig. 2. This simulation experiment verifies whether the proposed IRL-fuzzy can learn more quickly the same path as an expert. Table 5 shows the average number of iterations for the proposed IRL with and without fuzzy theory after 100, 200, 300, 400 and 500 rounds. It is seen the proposed IRL with fuzzy theory finds the reward R more quickly and saves much time.

Table 5 Comparison of number of iteration between the proposed IRL with and without fuzzy theory
Full size table

5 Conclusions

This paper has proposed inverse reinforcement learning that uses the ensemble and fuzzy logic method. Using an approximated reward function, the agent learns the policy akin to the expert’s demonstration. The learned policy that is derived from the approximated reward function can also accommodate stronger derivations, even though the agent may temporarily stray from the expert’s demonstrated trajectory during exploration. The evolving policy leads the agent back to the trajectory. The proposed method relies on the concept of boosting methods for classification. In addition, a more advanced version of this method, using fuzzification, is introduced. The proposed fuzzy-based IRL method adjusts the weight for the reward to decrease the number of learning iterations. The method is implemented in robotic soccer simulation to verify the performance. Even if a state space is complex, the feature weights are still updated to ensure more precise correction. Therefore, this method is particularly well suited for learning scenarios in the context of robotics.