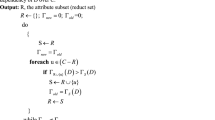1 Introduction

Data size has increased explosively not only due to increase in samples but also due to attributes in many real-life applications such as text mining, biomedical and bioinformatics. The high-dimensional dataset not only makes the machine learning algorithm very slow but also can corrupt the actual performance due to the presence of redundant, irrelevant and noisy informations. It is necessary to learn how to handle these large size data for knowledge extraction. Feature selection or attribute reduction is one of the dimensionality reduction techniques, which is capable of selecting a small subset of relevant and non-redundant features from the original information systems [1,2,3].

Rough set theory, proposed by Pawlak, is a key tool to tackle high-dimensional datasets in a much efficient manner [4,5,6,7]. However, this method is applicable to discrete data only. Therefore, discretization is required in order to tackle the real-valued information system before feature selection, but this may lead to information loss. Zadeh’s fuzzy set concept is very much useful in handling vagueness and uncertainty available in datasets [8]. Dubois and Prade combined fuzzy set with rough set and proposed fuzzy rough set by approximating a set by its lower and upper approximations [9, 10]. Further many researchers extended this idea for feature selection and classification problems of high-dimensional datasets [11,12,13,14].

In variable precision rough set (VPRS) model, Ziarko presented a generalization of the rough set concept by introducing quantifiers at least 100 * u per cent and more than 100 * l per cent to replace the universal and existential quantifiers, respectively [15]. Further, in vaguely quantified rough set (VQRS) model, Cornelis et al. extended the concept of VPRS model by introducing vague quantifiers most (an object x belongs to the lower approximation of \(X \subseteq U\), if most of the object related to \(X\) are included in \(X)\)) and some (an object x belongs to the upper approximation of \(X \subseteq U\), if some of the object related to \(X\) are included in \(X\)) into the model [16]. They used fuzzy quantifiers based on Zadeh’s notion [17]. They also discussed vaguely quantified fuzzy rough set (VQFRS) model by using a fuzzy relation in place of crisp relation.

An intuitionistic fuzzy set is an extension of a fuzzy set as it considers positive as well as negative and hesitancy degree of an object to belong to a set [18]. So, it has a strong ability in better describing the vagueness when compared to the traditional fuzzy set theory. Some researchers proposed different kinds of intuitionistic fuzzy rough sets by combining rough set with an intuitionistic fuzzy set [19,20,21,22,23,24]. The intuitionistic fuzzy rough set theory is evolving as a successful and powerful tool to deal with uncertainty and implemented for decision-making to take care of numerous genuine issues of the real world. However, not much research works have been published for attribute reduction based on intuitionistic fuzzy rough set [25,26,27,28,29,30,31,32,33,34]. Intuitionistic fuzzy rough set-based approaches for attribute reduction are much better than fuzzy rough set-based approaches when hesitancy is involved in an information system, but it may drastically change lower and upper approximations on addition or rejection of a single object.

To overcome the above issue, intuitionistic fuzzy quantifier-based feature selection approach is needed. However, some researchers defined intuitionistic fuzzy quantifier, but they did not apply it on the problem of feature selection of high-dimensional datasets. Atanassov [35] defined intuitionistic fuzzy quantifier. Szmidt and Kacprzyk [36] proposed the concept of intuitionistic fuzzy linguistic quantifiers to find the degree of truth of intuitionistic fuzzy linguistic quantified statements. Cui represented an intuitionistic fuzzy linguistic quantifier by a family of intuitionistic fuzzy-valued fuzzy measures and provided a method for calculating the intuitionistic fuzzy truth value of a quantified proposition [37]. Recently, Atanassov proposed the basic concept of intuitionistic fuzzy quantifier and discussed multi-dimensional intuitionistic fuzzy quantifiers along with level operators [38, 39].

We present an intuitionistic fuzzy quantifier-based rough set method for attribute reduction using the degree of dependency approach to overcome above mentioned issues. In this paper, we first define intuitionistic fuzzy quantifiers most and some and compared their effects with already existed VPRS and VQRS through an example. Lower and upper approximations are constructed by using intuitionistic fuzzy quantifiers. A method for attribute reduction in a decision system is presented via the degree of dependency approach. Algorithm and illustrative examples are given for a better understanding of the proposed method.

By using intuitionistic fuzzy linguistic quantifier in the definition of lower approximation, we get extra information about the degree of non-involvement (non-membership grade) of objects in the lower approximation together with involvement degree (membership grade). Proposed model contributes in finding close-to-minimal reduct set and improves classification accuracy of real benchmark datasets. Our approach also works on the fuzzy and intuitionistic fuzzy decision systems, and hence, it is a generalized approach. Moreover, the proposed approach provides better results in terms of classification accuracy for reduced datasets.

The rest of the paper is structured as follows. In this paper, some preliminaries are discussed in Sect. 2. In Sect. 3, intuitionistic fuzzy quantifier and intuitionistic fuzzy quantified rough set (IFQRS) are defined. An approach for feature selection of a decision system is presented by using IFQRS model in Sect. 4. In Sect. 5, an algorithm for the proposed method is presented. Illustrative examples based on proposed model are given for demonstration in Sect. 6. In Sect. 7, we conclude our work.

2 Preliminaries

In this section, an overview of proposed models like VPRS, VQRS and VQFRS is given.

2.1 Variable Precision Rough Sets (VPRS) [15]

Traditional lower and upper approximations of a set \(A\) proposed in Pawlak’s rough set can be redefined as follows [4]:

$$y \in R \uparrow A \, \quad {\text{iff}}\quad \, R_{A} (y) > 0 \,$$
(1)
$$y \in R \downarrow A\quad {\text{ iff}}\quad \, R_{A} (y) = 1 \,$$
(2)

where \(R_{A} \left( y \right) = \frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}\) represents the degree of involvement of \(R_{y}\) into \(A\).

However, a small change in the involvement of \(R_{y}\) into \(A\) may discard the entire class from the lower approximation.

Example 2.1

Let us consider a collection of reports \(R = \left\{ {r_{1} ,r_{2} , \ldots ,r_{16} } \right\}\) in any manufacturing company. The reports are characterized into four categories: \(R_{1} = \left\{ {r_{1} ,r_{2} ,r_{3} ,r_{4} } \right\}, \;R_{2} = \left\{ {r_{5} ,r_{6} ,r_{7} ,r_{8} } \right\},\;R_{3} = \left\{ {r_{9} ,r_{10} ,r_{11} ,r_{12} } \right\}\) and \(R_{4} = \left\{ {r_{13} ,r_{14} ,r_{15} ,r_{16} } \right\}\). These grouping form an equivalence relation \(R\) in \(X.\) If any query was launched which is relevant to the report set \(A = \left\{ {r_{2} ,r_{3} , \ldots ,r_{10} } \right\}\), then it is clear that information retrieval system has all documents from \(R_{1}\) are in \(A\) except \(r_{1}\). Moreover, only \(r_{9}\) and \(r_{10}\) are recaptured from \(R_{3}\), showing the fact that these reports from \(R_{3}\) are less relevant to the query, than the reports of \(R_{2} ,\) which all comprised in A. Pawlak’s notion of rough sets does not pay attention to these nuances, since using Eqs. (1) and (2) we get, \(R \downarrow A = R_{2}\) and \(R \uparrow A = R_{1} \cup R_{2} \cup R_{3} ,\) putting \(R_{1}\) and \(R_{3}\) at the same level.

In many practical situations, classification analysis in datasets is not easy due to the inadequacy of available information. Ziarko [15] dealt with classification error problem by introducing parameters into Eqs. (1) and (2) to get the definitions:

$$y \in R \uparrow_{l} A\quad {\text{iff}}\quad \, R_{A} (y) > l$$
(3)
$$y \in R \downarrow_{u} A\quad {\text{iff}}\quad R_{A} (y) \ge u \,$$
(4)

Using quantifiers, the above-defined formulas (3) and (4) can be interpreted as:

$$y \in R \uparrow_{l} A\quad {\text{iff}}\quad {\text{at}}\;{\text{least}}\;100*u\% \;{\text{elements}}\;{\text{of}}\;R_{y} \;{\text{are}}\;{\text{in}}\;A$$
(5)
$$y \in R \downarrow_{u} A\quad {\text{iff}}\;{\text{more}}\;{\text{than}}\;100*l\% \;{\text{elements}}\;{\text{of}}\;R_{y} \;{\text{are}}\;{\text{in}}\;A$$
(6)

Both above-defined threshold quantifiers \(> 100*l\%\) and \(\ge 100*u\%\) are crisp. Despite the fact that VPRS model permits a measure of tolerance towards errors, but it obeys old-fashioned manner of a binary system. Due to its dependency on particular values of \(l\) and \(u,\) any element either fully belongs to lower or upper approximations or does not belong at all.

Example 2.2

In the information retrieval problem from Example 2.1, Ziarko’s VPRS model proposes a more flexible way to differentiate between the roles of \(R_{1}\) and \(R_{3}\) as described in Eqs. (5) and (6), but the choice of the threshold value is very vital. If we choose \(u = 0.7\) and \(l = 1 - u = 0.3\), in a symmetric VPRS model [15], this provides \(R \downarrow_{.7} = R_{1} \cup R_{2}\) and \(R \uparrow_{.3} = R_{1} \cup R_{2} \cup R_{3}\). However, for \(u = 0.8\), it gives the same outcome as in Example 2.1.

2.2 Vaguely Quantified Rough Sets (VQRS) [16]

The definitions of upper and lower approximations in the VPRS model can be relaxed by presenting vague quantifiers, deliberating the fact that \(y\) belongs to the lower and upper approximations of \(A\) to the extent that most and some elements of \(R_{y}\) are in \(A\), respectively. It is assumed that approximations used in the approach are fuzzy sets. A fuzzy quantifier is used to model quantifier \(Q\) suitably [17]. \(Q\) is an increasing mapping from \(\left[ {0,1} \right]\) to \(\left[ {0,1} \right]\) which fulfils the boundary conditions \(Q\left( 0 \right) = 0\) and \(Q\left( 1 \right) = 1\).

With the notion of Zadeh’s concept of s-number, a fuzzy quantifier [17] that takes values in-between 0 and 1 is given by the parameterized formula, for \(0 \le \alpha < \beta \le 1,\) and \(x\) in \(\left[ {0,1} \right],\)

$$Q_{{\left( {\alpha ,\beta } \right)}} \left( x \right) = \left\{ {\begin{array}{l} {0, \, x \le \alpha } \\ {\frac{{2\left( {x - \alpha } \right)^{2} }}{{\left( {\beta - \alpha } \right)^{2} }}, \, \alpha \le x \le \frac{\alpha + \beta }{2}} \\ {1 - \frac{{2\left( {x - \beta } \right)^{2} }}{{\left( {\beta - \alpha } \right)^{2} }}, \, \frac{\alpha + \beta }{2} \le x \le \beta \, } \\ {1, \, \beta \le x} \\ \end{array} } \right.$$
(7)

In this example, quantifiers \(Q_{{\left( {0.2,0.6} \right)}}\) and \(Q_{{\left( {0.3,1} \right)}}\) could be chosen to reveal vague quantifiers some and most from natural language, respectively.

If \(Q_{l}\) and \(Q_{u}\) are fixed fuzzy quantifiers, the \(Q_{l}\)-upper and \(Q_{u}\)-lower approximations of any set \(A\) can be defined as

$$R \uparrow_{{Q_{l} }} A(y) = Q_{l} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right) = Q_{l} (R_{A} (y)) \,$$
(8)
$$R \downarrow_{{Q_{u} }} A(y) = Q_{u} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right) = Q_{u} (R_{A} (y)) \,$$
(9)

where \(Q_{l} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right)\) and \(Q_{u} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right),\) respectively, quantify the truth values of the statement “\(Q_{l}\) and \(Q_{u} R_{y}^{'} s\) are also \(A^{'} s\)”.

Example 2.3

Continuing Examples 2.1 and 2.2, on applying VQRS model with fuzzy quantifiers \(Q_{u} = Q_{{\left( {0.3,1} \right)}}\) and \(Q_{l} = Q_{{\left( {0.2,0.6} \right)}} ,\) results the lower approximation \(R \downarrow_{{Q_{u} }} A = \{ \left( {r_{5} ,1} \right),\left( {r_{6} ,1} \right), \ldots ,\left( {r_{8} ,1} \right),\left( {r_{1} ,0.74} \right),\left( {r_{2} ,0.74} \right), \ldots ,\left( {r_{4} ,0.74} \right),\left( {r_{9} ,0.16} \right), \ldots ,\left( {r_{12} ,0.16} \right)\}\). In this list, a report will have a higher grade if most of its elements relevant to query report set \(A\). With this reason, category \(R_{3}\) appears at the bottom of the list. Therefore, different roles of the categories in the search process can be determined in a desirable way by assigning membership grades through this model. Similarly, upper approximation can be found as \(R \downarrow_{{Q_{u} }} A = \left\{ {\left( {r_{1} ,1} \right),\left( {r_{2} ,1} \right), \ldots ,\left( {r_{8} ,1} \right),\left( {r_{9} ,0.87} \right), \ldots ,\left( {r_{12} ,0.87} \right)} \right\}\).

2.3 Vaguely Quantified Fuzzy Rough Sets (VQFRS) [16]

In VQFRS, the \(Q_{l} { - }\)upper and \(Q_{u} { - }\)lower approximations of \(A\) are same as defined in Eqs. (8) and (9) by using the following fuzzy convention.

If \(P\) and \(Q\) are two fuzzy sets in \(X\), then

  1. (1)

    \(\left( {P \cap Q} \right)\left( x \right) =\) min \(\left( {P\left( x \right),Q\left( x \right)} \right)\),

  2. (2)

    Cardinality of \(P, \left| P \right| = \mathop \sum \nolimits_{x \in X} P\left( x \right)\)

  3. (3)

    \(R_{y} \left( x \right) = R\left( {x,y} \right),\) where \(R\left( {x,y} \right)\) is a fuzzy relation.

3 Intuitionistic Fuzzy Quantifier

Intuitionistic fuzzy sets, a generalization of fuzzy sets, are more effective to handle uncertainty as it contains hesitancy degree together with membership and non-membership degree. Combining VQRS model to intuitionistic fuzzy sets, we can better deal with the complexity of vague (uncertain) problems.

Definition 3.1

[18] Let \(U\) be a finite non-empty set. A set \(A\) on the universe \(U\) of the form \(A = \left\{ {\left\langle {x,\mu_{A} \left( x \right),\vartheta_{A} \left( x \right)} \right\rangle |x \in U} \right\}\) is said to be an intuitionistic fuzzy set (IFS), where \(\mu_{A} :U \to \left[ {0,1} \right]\) and \(\vartheta_{A} :U \to \left[ {0,1} \right]\) satisfy the condition \(0 \le \mu_{A} \left( x \right) + \vartheta_{A} \left( x \right) \le 1\) for all \(x\) in \(U.\)\(\mu_{A} \left( x \right)\) and \(\vartheta_{A} \left( x \right)\) are the membership degree and non-membership degree of the element \(x\) in \(A\), respectively, and \(\pi_{A} \left( x \right) = 1 - \mu_{A} \left( x \right) - \vartheta_{A} \left( x \right)\) is the degree of hesitancy (or non-determinacy) of the element \(x\) in IFS \(A.\)

Any fuzzy set \(A = \left\{ {\left\langle {x,\mu_{A} \left( x \right)} \right\rangle |x \in U} \right\}\) can be characterized by an IFS having the form \(\left\{ {\left\langle {x,\mu_{A} \left( x \right),1 - \mu_{A} \left( x \right)} \right\rangle |x \in U} \right\}.\) Thus, every fuzzy set is an IFS.

Definition 3.2

[18] An ordered pair \(\langle\mu ,\vartheta\rangle\) is called an intuitionistic fuzzy value, where \(0 \le \mu ,\vartheta \le 1\) and \(0 \le \mu +\vartheta \le 1\).

Definition 3.3

[40] Let \(A = \left\{ {\left\langle {x,\mu_{A} \left( x \right),\vartheta_{A} \left( x \right)} \right\rangle |x \in U} \right\}\) be an IFS on the real line \(R.\) It is called an intuitionistic fuzzy number (IFN) if

  1. (a)

    \(A\) is normal,

    i.e. there exist at least two points \(x_{1} ,x_{2} \in X\) such that \(\mu_{A} \left( {x_{1} } \right) = 1,\vartheta_{A} \left( {x_{2} } \right) = 1,\)

  2. (b)

    \(A\) is convex,

    i.e. \(\forall x_{1} ,x_{2} \in R,\forall \lambda \in \left[ {0,1} \right], \mu_{A} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \ge \mu_{A} \left( {x_{1} } \right) \wedge \mu_{A} \left( {x_{2} } \right)\) and \(\vartheta_{A} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \le \vartheta_{A} \left( {x_{1} } \right) \vee \vartheta_{A} \left( {x_{2} } \right)\),

  3. (c)

    \(\mu_{A}\) is upper semi-continuous and \(\vartheta_{A}\) is lower semi-continuous,

  4. (d)

    supp \(A = \left\{ {x \in U|\vartheta_{A} \left( x \right) < 1} \right\}\) is bounded.

Definition 3.4

[41, 42] Let \(A = \left\{ {\left\langle {x,\mu_{A} \left( x \right),\vartheta_{A} \left( x \right)} \right\rangle |x \in U} \right\}\) be an IFS, its cardinality is given by \(\left| A \right| = \mathop \sum \nolimits_{x \in A} \frac{{1 + \mu_{A} \left( x \right) - \vartheta_{A} \left( x \right)}}{2}.\)

We generalize the concept of Zadeh’s fuzzy quantifiers, which rely on fuzzy cardinality, into the notion of the intuitionistic fuzzy quantifier. We propose two quantifiers in natural language with imprecise meaning such as most and some in order to find a degree of truth of intuitionistic fuzzy linguistically quantified statements as follows:

$$\mu_{Q} (x) = Q_{{\left( {a_{1} ,a_{2} } \right)}} (x) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & { \, x \le a_{1} } \hfill \\ {\frac{{2\left( {x - a_{1} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }},} \hfill & {a_{1} \le x \le \frac{{a_{1} + a_{2} }}{2}} \hfill \\ {1 - \frac{{2\left( {x - a_{2} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }},} \hfill & {\frac{{a_{1} + a_{2} }}{2} \le x \le a_{2} } \hfill \\ {1,} \hfill & { \, x \ge a_{2} } \hfill \\ \end{array} } \right.$$
(10)
$${\text{and}}\quad \, \nu_{Q} (x) = Q_{{\left( {b_{1} ,b_{2} } \right)}} (x) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {x \le b_{1} } \hfill \\ {1 - \frac{{2\left( {x - b_{1} } \right)^{2} }}{{\left( {b_{2} - b_{1} } \right)^{2} }} ,} \hfill & {{\text{b}}_{1} \le x \le \frac{{b_{1} + b_{2} }}{2}} \hfill \\ {\frac{{2\left( {x - b_{2} } \right)^{2} }}{{\left( {b_{2} - b_{1} } \right)^{2} }},} \hfill & {\frac{{b_{1} + b_{2} }}{2} \le x \le b_{2} } \hfill \\ {0,} \hfill & {x \ge b_{2} } \hfill \\ \end{array} } \right.$$
(11)

where \(a_{1} ,a_{2} ,b_{1} ,b_{2} \in \left[ {0,1} \right]\) are parameters such that \(0 \le b_{1} \le a_{1} \le b_{2} \le a_{2} \le 1.\) These parametric values are expert dependent/user oriented. \(Q = \left\{ {\left\langle {x,\mu_{A} \left( x \right),\vartheta_{A} \left( x \right)} \right\rangle |x \in U} \right\}\) is an intuitionistic fuzzy quantifier and \(\left\langle {\mu_{Q} ,\vartheta_{Q} } \right\rangle\) interprets the quantifiers most and some. For example, \(\left\langle {Q_{{\left( {0.3,1} \right)}} ,Q_{{\left( {0.2,0.8} \right)}} } \right\rangle\) and \(\left\langle {Q_{{\left( {0.2,0.6} \right)}} ,Q_{{\left( {0.1,0.55} \right)}} } \right\rangle\) could be used to express the intuitionistic quantifiers most and some from natural language.

These mathematical formulae can be interpreted as follows for the quantifier most: if less than \(a_{1} *100\)% of some elements \(x \in X\) satisfy a property P and less than \(b_{1} *100\)% do not satisfy it, then we say most of them certainly do not satisfy it (satisfy to degree \(\left\langle {0,1} \right\rangle\)). If at least \(a_{2} *100\)% of them satisfy it and also at least \(b_{2} *100\)% do not satisfy it, then most of them certainly satisfy it (to degree \(\left\langle {1,0} \right\rangle\)). For rest of the cases, we will get some values in-between \(\left\langle {0,1} \right\rangle\) and \(\left\langle {1,0} \right\rangle\), which means the more of them satisfy it, the higher the degree of satisfaction by most of the elements. Similarly, the quantifier some can be interpreted. The geometrical interpretation of the intuitionistic fuzzy quantifier is illustrated in Fig. 1.

Fig. 1
figure 1

Intuitionistic fuzzy quantifiers

Full size image

Lemma 3.1

$$0 \le \mu_{Q} (x) + \nu_{Q} (x) \le 1.$$

Proof

From Eqs. (10) and (11),

$$\mu_{Q} (x) + \nu_{Q} (x) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {x \le b_{1} ,x \ge a_{2} } \hfill \\ {1 - \frac{{2(x - b_{1} )^{2} }}{{(b_{2} - b_{1} )^{2} }},} \hfill & {b_{1} \le x \le a_{1} } \hfill \\ {1 + \frac{{2\left( {x - a_{1} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }} - \frac{{2(x - b_{1} )^{2} }}{{(b_{2} - b_{1} )^{2} }}, \, } \hfill & {a_{1} \le x \le \frac{{b_{1} + b_{2} }}{2}} \hfill \\ {\frac{{2\left( {x - a_{1} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }} + \frac{{2(x - b_{2} )^{2} }}{{(b_{2} - b_{1} )^{2} }},} \hfill & {\frac{{b_{1} + b_{2} }}{2} \le x \le \frac{{a_{1} + a_{2} }}{2}} \hfill \\ {1 + \frac{{2(x - b_{2} )^{2} }}{{(b_{2} - b_{1} )^{2} }} - \frac{{2\left( {x - a_{2} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }},} \hfill & {\frac{{a_{1} + a_{2} }}{2} \le x \le b_{2} } \hfill \\ {1 - \frac{{2\left( {x - a_{2} } \right)^{2} }}{{\left( {a_{2} - a_{1} } \right)^{2} }},} \hfill & { \, b_{2} \le x \le a_{2} } \hfill \\ \end{array} } \right.$$

It is clear from the above expression and Fig. 1 that \(0 \le \mu_{Q} (x) + \nu_{Q} (x) \le 1.\) □

Lemma 3.2

An Intuitionistic fuzzy quantifier is an intuitionistic fuzzy number.

Proof

For the intuitionistic fuzzy quantifier defined in Eqs. (10) and (11),

  1. (1)

    Normality Since \(\mu_{Q} (x) = 1,\forall x \ge a_{2} {\text{ and }}\nu_{Q} (x) = 1,\forall x \le b_{1}\) , Q is normal.

  2. (2)

    Convexity Let \(x_{1} ,x_{2} \in {\mathbb{R}},\lambda \in [0,1].\)

    Since \(\mu_{Q}\) is an increasing function. It implies \(\mu_{Q} (x_{1} ) \ge \mu_{Q} (x_{2} ){\text{ when }}x_{1} \ge x_{2}\), and \(\nu_{Q}\) is a decreasing function. It implies \(\nu_{Q} (x_{1} ) \le \nu_{Q} (x_{2} ){\text{ when }}x_{1} \ge x_{2}\)

    • Case 1 If \(x_{1} \ge x_{2} \Rightarrow \lambda x_{1} + (1 - \lambda )x_{2} \ge x_{2} \Rightarrow \mu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \ge \mu_{Q} (x_{2} )\) and \(\mu_{Q} (x_{1} ) \ge \mu_{Q} (x_{2} ) \Rightarrow \mu_{Q} (x_{1} ) \wedge \mu_{Q} (x_{2} ) = \mu_{Q} (x_{2} )\) hence, \(\mu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \ge \mu_{Q} (x_{1} ) \wedge \mu_{Q} (x_{2} ).\) Similarly, \(x_{1} \ge x_{2} \Rightarrow \lambda x_{1} + (1 - \lambda )x_{2} \ge x_{2} \Rightarrow \nu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \le \nu_{Q} (x_{2} )\) and \(\nu_{Q} (x_{1} ) \ge \nu_{Q} (x_{2} ) \Rightarrow \nu_{Q} (x_{1} ) \vee \nu_{Q} (x_{2} ) = \nu_{Q} (x_{2} )\) hence, \(\nu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \ge \nu_{Q} (x_{1} ) \vee \nu_{Q} (x_{2} ).\)

    • Case 2 If \(x_{2} \ge x_{1} \Rightarrow \lambda x_{1} + (1 - \lambda )x_{2} \ge x_{1}\). With the similar process, \(\mu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \ge \mu_{Q} (x_{1} ) \wedge \mu_{Q} (x_{2} )\) and \(\nu_{Q} (\lambda x_{1} + (1 - \lambda )x_{2} ) \ge \nu_{Q} (x_{1} ) \vee \nu_{Q} (x_{2} ).\)

  3. (3)

    Semi-continuity

    Since \(\mu_{Q}\) and \(\nu_{Q}\) are continuous, \(\mu_{Q}\) is upper semi-continuous and \(\nu_{Q}\) is lower semi-continuous also.

  4. (4)

    Boundedness

    \({\text{supp (}}Q ) { = }\{ x \in X|\nu_{Q} (x) < 1\} = [b_{1} ,b_{2} ] \subseteq [0,1]\) is bounded. □

The definition of lower and upper approximations in VQFRS model can be more generalized by presenting intuitionistic fuzzy quantifiers, expressing the fact that \(y\) belongs to the lower approximations of \(A\) to the extent that most = \(\left\langle {Q_{l} ,Q_{{l^{\prime}}} } \right\rangle\) elements of \(R_{y}\) are in \(A\) and \(y\) belongs to the upper approximations of \(A\) to the extent that some = \(\left\langle {Q_{u} ,Q_{{u^{\prime}}} } \right\rangle\) elements of \(R_{y}\) are in \(A\).

If we fix couples \(\left\langle {Q_{l} ,Q_{{l^{\prime}}} } \right\rangle\), \(\left\langle {Q_{u} ,Q_{{u^{\prime}}} } \right\rangle\) of intuitionistic fuzzy quantifiers, the \(Q_{{\left( {l,l^{\prime}} \right)}}\)-upper and \(Q_{{\left( {u,u^{\prime}} \right)}}\)-lower approximations of an approximation set \(A\) in \(X\) are defined as

$$R \uparrow_{{Q_{{\left( {l,l^{'} } \right)}} }} A\left( y \right) = \left\langle {Q_{l} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right),Q_{{l^{'} }} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right)} \right\rangle = \left\langle {Q_{l} (R_{A} (y)),Q_{{l^{'} }} (R_{A} (y))} \right\rangle$$
(12)
$$R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A\left( y \right) = \left\langle {Q_{u} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right),Q_{{u^{'} }} \left( {\frac{{\left| {R_{y} \cap A} \right|}}{{\left| {R_{y} } \right|}}} \right)} \right\rangle = \left\langle {Q_{u} (R_{A} (y)),Q_{{u^{'} }} (R_{A} (y))} \right\rangle$$
(13)

Here, \(Q_{l} ,Q_{u}\) are determined by Eq. (10) and \(Q_{{l^{\prime}}} ,Q_{{u^{\prime}}}\) are determined by Eq. (11). \(l,u\) and \(l^{\prime},u^{\prime}\) are parameters in tuple form \(\left( {a_{i} ,a_{j} } \right)\) and \(\left( {b_{i} ,b_{j} } \right)\), respectively. Pair \(\left( {R \downarrow_{{Q_{{\left( {u,u^{\prime}} \right)}} }} A\left( y \right),R \uparrow_{{Q_{{\left( {l,l^{\prime}} \right)}} }} A\left( y \right)} \right)\) is called intuitionistic fuzzy quantified rough set.

Example 3.1

In the continuation of Example 2.1, we have applied the proposed IFQRS model on the above information retrieval problem. We have chosen intuitionistic fuzzy quantifiers \(\left\langle {Q_{u} ,Q_{{u^{\prime}}} } \right\rangle\) and \(\left\langle {Q_{l} ,Q_{{l^{\prime}}} } \right\rangle\) with \(Q_{u} = Q_{{\left( {0.3,1} \right)}} , Q_{{u^{\prime}}} = Q_{{\left( {0.2,0.8} \right)}} ,\)\(Q_{l} = Q_{{\left( {0.2,0.6} \right)}}\) and \(Q_{{l^{\prime}}} = Q_{{\left( {0.1,0.55} \right)}}\). We get, the lower approximation \(R \downarrow_{{Q_{u} }} A = \left\{ {\left( {r_{5} ,1,0} \right),\left( {r_{6} ,1,0} \right), \ldots ,\left( {r_{8} ,1,0} \right),\left( {r_{1} ,0.74,0.01} \right),\left( {r_{2} ,0.74,0.01} \right), \ldots ,\left( {r_{4} ,0.74,0.01} \right),\left( {r_{9} ,0.16,0.5} \right), \ldots ,\left( {r_{12} ,0.16,0.5} \right)} \right\}\). Here, we are assigning membership grade together with non-membership grade to reports in each category so that we can get extra information to choose any category relevant to the query by choosing desirable parameters. We can see, the reports which are highly related to the query report set have high membership grade and low non-membership grade. On the similar manner, we get upper approximation \(R \downarrow_{{Q_{u} }} A = \left\{ {\left( {r_{1} ,1,0} \right),\left( {r_{2} ,1,0} \right), \ldots ,\left( {r_{8} ,1,0} \right),\left( {r_{9} ,0.87,0.05} \right), \ldots ,\left( {r_{12} ,0.87,0.05} \right)} \right\}\).

Now, we extend the results on lower and upper approximations similar to Dubois and Prade [10] for our approach.

Let \(\left\langle {Q_{l} ,Q_{{l^{\prime}}} } \right\rangle\), \(\left\langle {Q_{u} ,Q_{{u^{\prime}}} } \right\rangle\) be intuitionistic fuzzy quantifiers with \(Q_{l} ,Q_{{l^{\prime}}} ,Q_{u} ,Q_{{u^{\prime}}} \in \left[ {0,1} \right]\)

Theorem 3.1

\({\text{If }}Q_{u} \subseteq Q_{l} {\text{ and }}Q_{{l^{\prime}}} \subseteq Q_{{u^{\prime}}} ,\) \({\text{i}} . {\text{e}} .\;Q_{u} (x) \le Q_{l} (x)\;{\text{and}}\;Q_{{l^{\prime}}} (x) \le Q_{{u^{\prime}}} (x), \, \forall x \in [0,1] \,\) \(R \downarrow_{{Q_{{(u,u^{\prime})}} }} A(y) \subseteq R \uparrow_{{Q_{{(l,l^{\prime})}} }} A(y)\)

Proof

$${\text{If }}Q_{u} (x) \le Q_{l} (x){\text{ and }}Q_{{l^{\prime}}} (x) \le Q_{{u^{\prime}}} (x),\forall x \in [0,1]$$

Replacing x by \(R_{A} (y),\)

$$Q_{u} (R_{A} (y)) \le Q_{l} (R_{A} (y))$$
(14)
$$Q_{{l^{\prime}}} (R_{A} (y)) \le Q_{{u^{\prime}}} (R_{A} (y))$$
(15)

Using Eqs. (14) and (15), we get

$$\left\langle {Q_{u} (R_{A} (y)),Q_{{u^{'} }} (R_{A} (y))} \right\rangle \, \leq \, \left\langle {Q_{l} (R_{A} (y)),Q_{{l^{'} }} (R_{A} (y))} \right\rangle$$

Hence, \(R \downarrow_{{Q_{{(u,u^{\prime})}} }} A(y) \subseteq R \uparrow_{{Q_{{(l,l^{\prime})}} }} A(y).\) □

Theorem 3.2

If \(A_{1} \subseteq A_{2} \subseteq X,\)

$$\begin{aligned} & R \downarrow_{{Q_{{(u,u^{\prime})}} }} A_{1} (y) \subseteq R \downarrow_{{Q_{{(u,u^{\prime})}} }} A_{2} (y) \\ & R \uparrow_{{Q_{{(l,l^{\prime})}} }} A_{1} (y) \supseteq R \uparrow_{{Q_{{(l,l^{\prime})}} }} A_{2} (y) \\ \end{aligned}$$

Proof

Since \(A_{1} \subseteq A_{2}\)

$$\begin{aligned} & \therefore\; R_{y} \cap A_{1} \subseteq R_{y} \cap A_{2} \Rightarrow \left| {R_{y} \cap A_{1} } \right| \le \left| {R_{y} \cap A_{2} } \right| \\ & \quad \Rightarrow \frac{{\left| {R_{y} \cap A_{1} } \right|}}{{\left| {R_{y} } \right|}} \le \frac{{\left| {R_{y} \cap A_{2} } \right|}}{{\left| {R_{y} } \right|}} \Rightarrow R_{{A_{1} }} (y) \le R_{{A_{2} }} (y) \\ \end{aligned}$$

Since Qu and Ql are increasing functions,

$$Q_{u} (R_{{A_{1} }} (y)) \le Q_{u} (R_{{A_{2} }} (y))$$
(16)
$$Q_{l} (R_{{A_{1} }} (y)) \le Q_{l} (R_{{A_{2} }} (y))$$
(17)
$${\text{and}}\;Q_{{u^{\prime}}} \;{\text{and}}\;Q_{{l^{\prime}}} \;{\text{are}}\;{\text{decreasing}}\;{\text{functions}},$$
$$Q_{{u^{\prime}}} (R_{{A_{1} }} (y)) \le Q_{{u^{\prime}}} (R_{{A_{2} }} (y)) \,$$
(18)
$$Q_{{l^{\prime}}} (R_{{A_{1} }} (y)) \le Q_{{l^{\prime}}} (R_{{A_{2} }} (y))$$
(19)

By Eqs. 16–19, we get the required result. □

4 Feature Selection by IFQRS

Feature selection has become center of the attention of much research in application areas for which datasets with tens or hundreds of thousands of features are available. Feature selection for the information systems with the help of the proposed model is done in this section. Here, the degree of dependency method for the feature selection is used.

Definition 4.1

[43] A quadruple \({\text{IS}} = \left( {U,{\text{AT}},V,h} \right)\) is called an information system, where \(U = \left\{ {u_{1} ,u_{2} , \ldots ,u_{n} } \right\}\) is a non-empty finite set of objects, called the universe of discourse, \({\text{AT}} = \left\{ {a_{1} ,a_{2} , \ldots ,a_{m} } \right\}\) is a non-empty finite set of attributes. \(V = \mathop {\bigcup }\nolimits_{a \in AT} V_{a}\), where \(V_{a}\) is the set of attribute values associated with each attribute \(a \in AT\) and \(h:U \times AT \to V\) is an information function that assigns particular values to the objects against attribute set such that \(\forall a \in {\text{AT}}, \forall u \in U, h\left( {u,a} \right) \in V_{a}\).

An information system is called an intuitionistic fuzzy information system if attribute values associated with objects are intuitionistic fuzzy numbers.

Definition 4.2

[43] An information system \({\text{IS}} = \left( {U,{\text{AT}},V,h} \right)\) is said to be decision system if \({\text{AT}} = C \cup D\) where \(C\) is a non-empty finite set of conditional attributes and \(D\) is a non-empty collection of decision attributes with \(C \cap D = \emptyset\). Here, \(V = V_{C} \cup V_{D}\) with \(V_{C}\) and \(V_{D}\) as the set of conditional attribute values and decision attribute values, respectively. \(h\) be a mapping from \(U \times C \cup D\) to \(V,\) such that \(h:U \times C \to V_{C}\) and \(h:U \times D \to V_{D}\). For example, Table 1 represents real-valued decision system, while Table 2 represents intuitionistic fuzzy decision system.

Table 1 Real-valued decision system
Full size table
Table 2 An information systems security risk judgment decision table
Full size table

Different similarity relations for different type of information systems are available in the literature. We consider following fuzzy similarity relation between two objects of the information system with respect to a conditional attribute \(c \in C\) as given in [12].

$$S_{c} \left( {u_{i} ,u_{j} } \right) = { \hbox{max} }\left( {{ \hbox{min} }\left( {\frac{{(\mu (u_{j} ) - (\mu (u_{i} ) - \sigma_{c} ))}}{{(\mu (u_{i} ) - (\mu (u_{i} ) - \sigma_{c} ))}},\frac{{\left( {(\mu (u_{i} ) + \sigma_{c} ) - \mu (u_{j} )} \right)}}{{\left( {(\mu (u_{i} ) + \sigma_{c} ) - \mu (u_{i} )} \right)}}} \right),0} \right)$$
(20)

where \(\sigma_{c}^{2}\) is the variance of feature c and \(\mu \left( {u_{i} } \right)\) is membership grade of object \(u_{i}\).

And following intuitionistic fuzzy similarity relation as in [41] is used

$$S_{c} \left( {u_{i} ,u_{j} } \right) = 1 - \sqrt {\left( {\mu \left( {u_{i} } \right) - \mu \left( {u_{j} } \right)} \right)^{2} + \left( {\nu \left( {u_{i} } \right) - \nu \left( {u_{j} } \right)} \right)^{2} + \left( {\pi \left( {u_{i} } \right) - \pi \left( {u_{j} } \right)} \right)^{2} }$$
(21)

where \(u_{i}\) and \(u_{j}\) are objects. \(\mu \left( {u_{i} } \right)\),\(\nu \left( {u_{i} } \right)\) and \(\pi \left( {u_{i} } \right)\) are membership, non-membership and hesitancy degree of \(u_{i} ,\) respectively.

For partitioning the universe of discourse, we define \(R\)-foreset of the object \(u_{i} ,\) i.e. \(R_{{u_{i} }}\) with respect to attribute \(c \in C\) as:

$$R_{{u_{i} }} = [T_{c}^{\alpha } ](u_{i} ) = \left\{ {u_{j} :s_{c} \left( {u_{i} ,u_{j} } \right) \ge \alpha } \right\}$$
(22)

where \(\alpha \in \left( {0,1} \right)\) is a similarity threshold, which provides a degree of similarity for addition of objects within tolerance classes.

With the help of lower approximation defined in terms of quantifiers, the positive region of decision attribute \(D\) over set of conditional attributes \(C\) can be calculated as:

$$\begin{aligned} {\text{POS}}_{C} \left( D \right) = & \mathop {\sup }\limits_{A \in U/D} R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A\left( {u_{i} } \right) \\ = & \left\langle {\mathop {\sup }\limits_{A \in U/D} Q_{u} (R_{A} (u_{i} )),\mathop { \inf }\limits_{A \in U/D} Q_{{u^{'} }} (R_{A} (u_{i} ))} \right\rangle \\ \end{aligned}$$
(23)

where \(R \downarrow_{{Q_{{\left( {u,u^{\prime}} \right)}} }} A\left( {u_{i} } \right)\) is defined in Eq. (13) and \(U{\backslash }D\) contain sets of objects having same decision values.

After calculating positive region, the degree of dependency of decision attribute \(D\) over set of conditional attributes \(C\) can be computed as:

$$\Gamma _{C} \left( D \right) = \frac{{\left| {{\text{POS}}_{C} \left( D \right)} \right|}}{\left| U \right|}$$
(24)

where \(\left| . \right|\) in the numerator is the cardinality of an intuitionistic fuzzy set, while \(\left| . \right|\) in the denominator is the cardinality of a crisp set and \(\Gamma _{C} \left( D \right) \in \left[ {0,1} \right].\)

Definition 4.3

[11] A subset \(R\) of the conditional attribute set \(C\) is said to be reduct set of a decision system if

$$\begin{aligned} &\Gamma _{R} \left( D \right) =\Gamma _{C} \left( D \right) \\ &\Gamma _{{R - \left\{ {c_{i} } \right\}}} \left( D \right) <\Gamma _{R} \left( D \right),\forall c_{i} \in C \, \\ \end{aligned}$$
(25)

Required reduct set can be obtained by comparing the degree of dependencies of decision attribute over sets of conditional attributes. Attributes are selected one by one until the reduct set gives the same degree of dependency value as the original set.

5 Algorithm for Intuitionistic Fuzzy Rough Set Approach

In this section, a quick reduct algorithm for feature selection of a decision system based on intuitionistic fuzzy quantifier approach is presented by using degree of dependency method. Initially, the reduct set is an empty set. We add conditional attributes one by one in reduct set and calculate degree of dependencies of decision attribute over obtained reduct set. The proposed algorithm selects only those conditional attributes, which causes a maximum increase in the degree of dependency of decision attribute. The proposed algorithm is given as follows:

  • Step 1 Take an intuitionistic fuzzy information system/fuzzy information system.

  • Step 2 Calculate similarity relations between objects with respect to set of conditional attributes.

  • Step 3 On the basis of similarity relations, tolerance class of each object with respect to conditional attributes can be determined by introducing a similarity threshold between object.

  • Step 4 Compute the lower approximations of each object with respect to \(U{{\backslash }}D\) by using quantifier \(Q_{{\left( {u,u^{\prime}} \right)}} .\)

  • Step 5 Evaluate the degree of dependency of decision attribute over set of conditional attributes by calculating positive region.

  • Step 6 Select the conditional attribute that has the highest degree of dependency (Select any one if there are more than one conditional attributes having the highest and same degree of dependencies). That will be the first member of reduct set.

  • Step 7 Add other conditional attributes to obtained conditional attribute and again calculate the degree of dependencies of such coupled conditional attributes.

  • Step 8 Apply the same process for so obtained attributes as in Step 6 and 7.

  • Step 9 The process will terminate until the newly obtained subset of conditional attributes causes no increment in the degree of dependency than the previous one.

In the proposed algorithm, for a dataset with dimension \(n\), we require \(n\) evaluations in calculating degrees of dependency of decision attribute over \(n\) conditional attributes. After selecting the conditional attribute with the highest degree of dependency, we need \(\left( {n - 1} \right)\) evaluations and repeating this process one more time, we need \(\left( {n - 2} \right)\) evaluations and so on. Hence, time complexity of proposed approach is \(n + \left( {n - 1} \right) + \left( {n - 2} \right) + \cdots + 3 + 2 + 1\) for the worst-case dataset. Therefore, the proposed intuitionistic fuzzy quantified rough set-based algorithm requires \(\left( {n^{2} + n} \right)/2\) evaluations of the dependency function.

6 Experimental Analysis

In this section, proposed algorithm is implemented on two different types of example datasets and on eight real datasets for feature selection and classification.

Example 6.1

Consider a decision system as given in Table 1, which contains real-valued conditional attributes \(\left\{ {c_{1} ,c_{2} ,c_{3} } \right\}\) and a decision attribute \(\left\{ d \right\}\left[ {11} \right]\).

The similarity degree between objects with respect to each conditional attributes is calculated by using Eq. (20) and presented in Table 3.

Table 3 Similarity relation between objects
Full size table

Here, \(D = \{ d\} , \, U{{\backslash }}D = \left\{ {A_{1} ,A_{2} } \right\}, \, A_{1} = \left\{ {u_{1} ,u_{3} ,u_{6} } \right\}, \, A_{2} = \{ u_{2} ,u_{4} ,u_{5} \}\)

Taking \(\alpha = 0.7\), R-foreset of each object corresponding to attribute \(c_{1}\) is calculated by Eq. (22),

$$\begin{aligned} & R_{{u_{1} }} = \left\{ {u_{1} ,u_{2} } \right\},\quad R_{{u_{2} }} = \left\{ {u_{1} ,u_{2} } \right\},\quad R_{{u_{3} }} = \left\{ {u_{3} } \right\}, \\ & R_{{u_{4} }} = \left\{ {u_{4} } \right\}, \, \quad R_{{u_{5} }} = \left\{ {u_{5} ,u_{6} } \right\},\quad \, R_{{u_{6} }} = \left\{ {u_{5} ,u_{6} } \right\}. \\ \end{aligned}$$

By using Eq. (13), intuitionistic fuzzy lower approximations of objects over \(U{{\backslash }}D\) are given as:

$$\begin{aligned} & R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{1} } \right) = \left\langle {0.16,0.5} \right\rangle ,\quad \, R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{2} } \right) = \left\langle {0.16,0.5} \right\rangle , \, \quad R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{3} } \right) = \left\langle {1,0} \right\rangle \\ & R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{4} } \right) = \left\langle {0,1} \right\rangle ,\quad \, R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{5} } \right) = \left\langle {0.16,0.5} \right\rangle , \, \quad \, R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{1} \left( {u_{6} } \right) = \left\langle {0.16,0.5} \right\rangle \\ & R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{1} } \right) = \left\langle {0.16,0.5} \right\rangle , \, \quad R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{2} } \right) = \left\langle {0.16,0.5} \right\rangle ,\quad \, R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{3} } \right) = \left\langle {0,1} \right\rangle \\ & R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{4} } \right) = \left\langle {1,0} \right\rangle ,\quad R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{5} } \right) = \left\langle {0.16,0.5} \right\rangle , \, \quad R \downarrow_{{Q_{{\left( {u,u^{'} } \right)}} }} A_{2} \left( {u_{6} } \right) = \left\langle {0.16,0.5} \right\rangle \\ \end{aligned}$$

After calculating fuzzy lower approximation, the positive region of decision attribute over conditional attributes computed by Eq. (23) results

$$\begin{aligned} & {\text{POS}}_{{c_{1} }} \left( D \right)(u_{1} ) = \left\langle {0.16,0.5} \right\rangle ,\quad {\text{POS}}_{{c_{1} }} \left( D \right)(u_{2} ) = \left\langle {0.16,0.5} \right\rangle ,\quad {\text{POS}}_{{c_{1} }} \left( D \right)(u_{3} ) = \left\langle {1,0} \right\rangle , \\ & {\text{POS}}_{{c_{1} }} \left( D \right)(u_{4} ) = \left\langle {1,0} \right\rangle ,\quad {\text{POS}}_{{c_{1} }} \left( D \right)(u_{5} ) = \left\langle {0.16,0.5} \right\rangle ,\quad {\text{POS}}_{{c_{1} }} \left( D \right)(u_{6} ) = \left\langle {0.16,0.5} \right\rangle . \\ \end{aligned}$$

Now, the degree of dependency of decision attribute \(D\) over conditional attribute \(c_{1}\) can be calculated by Eq. (24) as follows:

$$\Gamma _{{c_{1} }} \left( D \right) = 0.554$$

In a similar manner, \(\Gamma _{{c_{2} }} \left( D \right) = 0.854,\Gamma _{{c_{3} }} \left( D \right) = 0.854\).

The degrees of dependency of \(c_{2}\) and \(c_{3}\) are equal and highest. Any one of them can be taken as the first candidate of reduct set of given information system, say \(c_{2} .\) Now, combining \(c_{1}\) and \(c_{3}\) to \(c_{2}\) one by one and calculating the corresponding degrees of dependency, we get

$$\Gamma _{{\left\{ {c_{1} ,c_{2} } \right\}}} \left( d \right) = 1, \,\Gamma _{{\left\{ {c_{2} ,c_{3} } \right\}}} \left( d \right) = 1$$

Since degree of dependency cannot exceed 1, the reduct set of this dataset is either \(\left\{ {c_{1} ,c_{2} } \right\}\) or \(\left\{ {c_{2} ,c_{3} } \right\}.\)

Example 6.2

An intuitionistic fuzzy decision system is chosen which is a judgment problem of CISA’s information systems security audit risk [44]. In this dataset, the object set \(U = \left\{ {u_{1} ,u_{2} , \ldots ,u_{10} } \right\}\) comprises 10 audited objects. Five conditional attributes \(C = \left\{ {c_{1} ,c_{2} ,c_{3} ,c_{4} ,c_{5} } \right\}\) are there in conditional attribute set, where \(c_{1}\) = “Better Systems Total Security”, \(c_{2}\) = “Better Systems Operation Security”, \(c_{3}\) = “Safer Data Centre”, \(c_{4}\) = “Credible Hardware Device”, and \(c_{5}\) = “Credible Network Security”. Every value which condition attribute is taken on has special actual meaning. For example, \(f\left( {x_{1} ,c_{1} } \right) = \left\langle {0.2,0.4} \right\rangle\) means that the membership degree of systems total security is 0.2, and non-membership degree of systems total security is 0.4. The decision attribute set, d = “Risk Judgement Order of Information Systems Security Audit”. The domain of d is \(\left\{ {1,2,3} \right\},\) where 1 means “Complete Examination”, 2 means “Major Examination”, and 3 means “No Examination”.

Here, \(D = \{ d\} ,U{{\backslash }}D = \left\{ {A_{1} ,A_{2} ,A_{3} } \right\},A_{1} = \left\{ {u_{1} ,u_{3} ,u_{4} ,u_{6} } \right\},A_{2} = \{ u_{2} ,u_{5} ,u_{7} ,u_{8} \} ,A_{3} = \left\{ {u_{9} ,u_{10} } \right\}\)

Calculating fuzzy similarity relation between two intuitionistic fuzzy numbers with respect to attribute \(c_{1} \in C\) by using Eq. (21), we get Table 4.

Table 4 Fuzzy similarity relation \(S_{{c_{1} }} \left( {u_{i} ,u_{j} } \right)\) with respect to \(c_{1}\)
Full size table

Taking \(\alpha = 0.8,\)R-foreset of each object with respect to attribute \(c_{1}\) is given as:

$$\begin{aligned} & R_{{u_{1} }} = \left\{ {u_{1} } \right\},\quad R_{{u_{2} }} = \left\{ {u_{2} ,u_{3} ,u_{6} } \right\},\quad R_{{u_{3} }} = \left\{ {u_{2} ,u_{3} ,u_{4} } \right\},\quad R_{{u_{4} }} = \left\{ {u_{3} ,u_{4} } \right\},\quad R_{{u_{5} }} = \left\{ {u_{5} } \right\}, \\ & R_{{u_{6} }} = \left\{ {u_{2} ,u_{6} } \right\},\quad R_{{u_{7} }} = \left\{ {u_{7} } \right\},\quad R_{{u_{8} }} = \left\{ {u_{8} } \right\},\quad \, R_{{u_{9} }} = \left\{ {u_{9} } \right\},\quad R_{{u_{10} }} = \left\{ {u_{10} } \right\} \\ \end{aligned}$$

Now, proceeding in a similar manner as in Example 6.1, degree of dependencies of decision attribute D over conditional attributes are given as:

$$\Gamma _{{c_{1} }} \left( D \right) = 0.875,\quad\Gamma _{{c_{2} }} \left( D \right) = 0.469,\quad\Gamma _{{c_{3} }} \left( D \right) = 0.846,\quad\Gamma _{{c_{4} }} \left( D \right) = 0.808,\quad\Gamma _{{c_{5} }} \left( D \right) = 0.799$$

The degree of dependency in case of \(c_{1}\) is highest; therefore, we add other attributes \(c_{2} ,c_{3 \, } {\text{and }}c_{4}\) to \(c_{1}\). After applying the same process as above, we calculate degree of dependencies of decision attribute with respect to each pair of conditional attributes, we get

$$\Gamma _{{\left\{ {c_{1} ,c_{2} } \right\}}} \left( D \right) = 1,\quad\Gamma _{{\left\{ {c_{1} ,c_{3} } \right\}}} \left( D \right) = 0.86,\quad\Gamma _{{\left\{ {c_{1} ,c_{4} } \right\}}} \left( D \right) = 1,\quad\Gamma _{{\left\{ {c_{1} ,c_{5} } \right\}}} \left( D \right) = 0.86$$

Therefore, reduct set of above intuitionistic fuzzy information system is \(\left\{ {{\mathbf{c}}_{{\mathbf{1}}} ,{\mathbf{c}}_{{\mathbf{2}}} } \right\}\) or \(\left\{ {{\mathbf{c}}_{{\mathbf{1}}} ,{\mathbf{c}}_{{\mathbf{4}}} } \right\}.\)

We have examined the proposed approach for feature selection on two example datasets. In Example 6.1, we have taken a decision system having three real-valued conditional attributes and one decision attribute. \(R\)-foreset of each object based on fuzzy similarity relation are calculated. Using quantifier-based lower approximation formula, positive region has been computed and it has been found that the degrees of dependency for attribute set \(\left\{ {c_{1} ,c_{2} } \right\}\) and \(\left\{ {c_{2} ,c_{3} } \right\}\) are highest amongst \(\left\{ {c_{1} ,c_{2} ,c_{3} } \right\}.\) Therefore,\(\left\{ {c_{1} ,c_{2} } \right\}\) or \(\left\{ {c_{2} ,c_{3} } \right\}\) is the reduct set of the given decision system. After proceeding with the similar process, we have dealt with an intuitionistic fuzzy decision system in Example 6.2 and got \(\left\{ {c_{1} ,c_{2} } \right\}\) or \(\left\{ {c_{1} ,c_{4} } \right\}\) as the reduct set.

Example 6.3

In this example, proposed algorithm is applied on real datasets and classification accuracies are evaluated.

6.1 Experimental Setup

In this section, we apply proposed algorithm on eight benchmark datasets: Column_2C, Ionosphere, Iris, Glass, Hepatitis, Lung cancer, Soybean_small, Zoo [45]. First, we calculate reduct of these datasets by intuitionistic fuzzy quantified rough set approach. Reducts of different datasets are calculated by assigning different values to the parameters \((a_{1} , a_{2} ), \left( {b_{1} ,b_{2} } \right)\), and then, classification analysis is performed for unreduced as well as reduced datasets. For classification part, eight different classifiers are used, namely JRip, PART, J48, Random Tree, IBK, Bayes Net, KSTAR, LMT. Classification accuracies for original and reduced datasets are calculated with these classifiers. Effects of the parameters on classification accuracies are also shown. All the experiments are performed in MATLAB 2017a.

6.2 Experimental Results

In Table 5, the reduct size of different datasets for different parametric values is compared. Table 6 shows the average classification accuracy for eight classifiers in the form of percentage obtained using 10-fold cross-validation. Initially, the classification process was performed on the unreduced (original) datasets and then on the reduced datasets obtained using the proposed technique. It can be observed that classification accuracies are either improving or remaining the same for most datasets. Effect of parametric values on classification accuracy is presented in Tables 6, 7 and 8. For dataset “Glass”, classification accuracies are mostly decreasing for the parametric value (0.3, 1), (0.2, 0.8) and mostly increasing for the parametric value (0.2, 0.9), (0.1, 0.7) or (0.3, 0.9), (0.1, 0.8). For dataset Zoo, parametric value (0.2, 0.9), (0.1, 0.7) classification accuracy increases for all classifiers except Naïve Bayes and decreases for parametric value (0.3, 0.9), (0.1 ,0.8) for all classifiers except JRip. A slight change in parametric value can differ in accuracy a lot. So assigning values to the parameters plays an important role and can be chosen carefully for particular data domain.

Table 5 Reduct sets for different parametric values
Full size table
Table 6 Classification accuracies (in percentage) for parametric value (0.3, 0.1), (0.2, 0.8)
Full size table
Table 7 Classification accuracies (in percentage) for parametric value (0.2, 0.9), (0.1, 0.7)
Full size table
Table 8 Classification accuracies (in percentage) for parametric value (0.3, 0.9), (0.1, 0.8)
Full size table

7 Conclusion

In this paper, we have proposed a new approach for attribute reduction in an information system based on intuitionistic fuzzy quantified rough set. We have defined intuitionistic fuzzy quantifiers most and some and associated them with intuitionistic fuzzy rough set. Some results on lower and upper approximations are proven for justification of proposed rough set. Degree of dependency concept has been used for attribute reduction in a decision system with our model. Stepwise algorithm has been presented with two examples for better understanding of proposed work. Proposed algorithm has been implemented on some real benchmark datasets, and classification accuracies for different classifiers have been evaluated. It has been found that reduced datasets outperform unreduced datasets in terms of resulting classification performance.

In future, we intend to use intuitionistic fuzzy quantified rough set for attribute reduction in high-dimensional datasets by using discernibility matrix approach. We wish to define new intuitionistic fuzzy linguistic quantifier based on relational logic, and we will combine this with rough set to propose a new robust approach for attribute reduction in real datasets.