1 Introduction

As a new granulation of hesitant fuzzy sets (HFSs) [14, 22, 23, 34], hesitant fuzzy linguistic term sets (HFLTSs) were introduced by Rodríguez et al. [20]. The HFLTSs are a very useful and flexible way to represent the qualitative judgments of experts [8]. Nowadays, it has attracted much attention in the field of multi-criteria decision-making (MCDM). For example, in the hesitant fuzzy decision-making, Gou et al. [8] introduced two aggregation operators for HFLTSs. Liao et al. [16] developed the distance and similarity measures for HFLTSs. Then, Liao et al. [17] also discussed the correlation coefficients of HFLTSs. With respect to the qualitative MCDM, Liao et al. [18] designed a hesitant fuzzy linguistic VIKOR method. Wang [24] proposed extended hesitant fuzzy linguistic term sets (EHFLTSs). Wang and Xu [25] deeply studied the total orders of EHFLTSs. Rodríguez et al. [21] constructed a group decision-making model dealing with comparative linguistic expressions based on HFLTSs. In most of the current studies about HFLTSs, all possible values provided by the decision-makers (DMs) have equal importance. In the some practical problems, the DMs may prefer some of the possible linguistic terms so that the set of possible values may have different importance degrees [6, 19]. To overcome this question, Pang et al. [19] extended HFLTSs and proposed a new concept of probabilistic linguistic term sets (PLTSs). Then, under the multi-criteria group decision-making (MCGDM), He et al. [11] discussed the probabilistic interval reference ordering sets and the application. Considering the multi-granular linguistic information, Zhai et al. [35] proposed a probabilistic linguistic vector-term set and applied it into the group decision-making (GDM). Zhang et al. [36] discussed the consistency-based risk assessment with probabilistic linguistic preference relation. Under the hesitant probabilistic fuzzy environment, Zhou and Xu [37] analysed the consensus building of GDM. As mentioned above, PLTSs recently have became a hot topic in the area of HFLTSs. With the PLTSs, the DMs can not only provide several possible linguistic values over an object (alternative or attribute), but also reflect the probabilistic information of the set of values [19]. The PLTSs have strong ability to express the information vagueness and uncertainty in the real-world applications. In the existing literature, most aggregation operators developed for PLTSs are based on the independence assumption.

During the information aggregation, the Bonferroni mean (BM) proposed by Bonferroni [4] takes into account the interrelationship between the input arguments [32, 33, 15] and has been successfully applied in the MCDM. The research works of BM have been developed in the last decades. For instance, Xu and Yager [31] extended the BM to the intuitionistic fuzzy decision environments. Then, Xu [32] further enriched the results of intuitionistic fuzzy BM. Beliakova et al. [2] generalized the BM and presented a composed aggregation operator. Beliakova and James [3] introduced the generalized BMs into Atanassov orthopairs. He et al. [9] and He and He [10] developed some intuitionistic fuzzy interaction BM operators. Wei et al. [28] designed some uncertain linguistic BM operators. Xia et al. [29] proposed some generalized intuitionistic fuzzy BMs. Xia et al. [30] applied the well-known geometric mean (GM) to the BM and introduced the geometric Bonferroni mean (GBM) to the intuitionistic fuzzy information. Yager [33] elaborated the BM and suggested some generalizations that can enhance their modelling capability. Zhu et al. [38] and Zhu and Xu [39] extended BM and GBM to the hesitant fuzzy environment. For the PLTSs, it also encounters the interrelationship phenomenon and needs to depict the interrelationship between the input arguments. Therefore, considering the special characters of GBM [38], we introduce it into the probabilistic linguistic environment.

Under the novel probabilistic linguistic environment, we develop two new aggregation operators based on GBM, i.e. probabilistic linguistic geometric BM (PLGBM) and weighted probabilistic linguistic geometric BM (WPLGBM). On the basis of group decision-making (GDM), we utilize the WPLGBM operator to fuse the information and design the corresponding approach for the probabilistic linguistic multi-criteria group decision-making (PLMCGDM). With respect to the decision procedure of PLMCGDM, we further develop an extended grey relational analysis method based on PLTSs. Grey relational analysis method originally developed by Deng [5] is a decision-making approach under conditions of uncertainty and has been found to be superior to comparable methods in the mathematical analysis of systems with incomplete information [12, 13]. As a complement of the existing generalization of GBM, this paper expands the applied field of GBM to the probabilistic linguistic situations and designs the corresponding aggregation operators. Meanwhile, we improve the grey relational analysis method to make it adapt to the probabilistic linguistic environment.

To accomplish this, the remainder of the paper is organized as follows. In Sect. 2, we briefly review some basic concepts of PLTSs and GBM. Under the probabilistic linguistic environment, we develop some aggregation operator-based GBM in Sect. 3, i.e. PLGBM and WPLGBM. Besides, some special properties of them are explored. With the aid of grey relational analysis method, Sect. 4 proposes a new extension model and design an approach for the application of PLMCGDM by employing the WPLGBM operator. In Sect. 5, we give an illustrative example to elaborate and verify our proposed method. Section 6 concludes the paper and elaborates on future studies.

2 Preliminaries

Basic concepts of PLTSs and GBM are briefly reviewed in this section [1, 4, 19].

2.1 Probabilistic Linguistic Term Sets (PLTSs)

The concept of PLTSs [19] is an extension of the concepts of HFLTSs [1, 16]. In the following, we review some basic concepts of PLTSs and the corresponding operations.

Definition 1

Let \(S=\{s_{t}|t=-\tau , \ldots , -1, 0, 1, \ldots , \tau \}\) be a linguistic term set. Then a probabilistic linguistic term set (PLTS) is defined as:

$$\begin{aligned} L(p)=\left\{ L^{(k)}(p^{(k)})|L^{(k)} \in S, r^{(k)} \in t, p^{(k)} \ge 0, k=1, 2, \ldots , \#L(p), \sum _{k=1}^{\#L(p)} p^{(k)} \le 1\right\} , \end{aligned}$$
(1)

where \(L^{(k)}(p^{(k)})\) is the linguistic term \(L^{(k)}\) associated with the probability \(p^{(k)}\), \(r^{(k)}\) is the subscript of \(L^{(k)}\) and \(\#L(p)\) is the number of all linguistic terms in L(p).

In order to facilitate the information aggregation and keep the consistency, Gou et al. [7] defined two novel transformation functions between the HFLTS and the HFS. For the PLTSs, Bai et al. [1] also came up with the corresponding transformation functions:

Definition 2

Let \(S=\{s_{t}|t=-\tau , \ldots , -1, 0, 1, \ldots , \tau \}\) be a linguistic term set. L(p) is a PLTS. The equivalent transformation function of L(p) is defined as:

$$\begin{aligned} g(L(p))=\left\{ \left[ \frac{r^{(k)}}{2\tau }+\frac{1}{2}\right] \left( p^{(k)}\right) \right\} =L_{\gamma }(p), \end{aligned}$$
(2)

where \(g: [-\tau , \tau ]\rightarrow [0, 1]\) and \(\gamma \in [0, 1]\). Additionally, we can obtain the transformation function of \(L_{\gamma }(p)\) as follows:

$$\begin{aligned} g^{-1}(L_{\gamma }(p))=\left\{ s_{(2\gamma -1)\tau }(p^{(k)})|\gamma \in [0, 1]\right\} =L(p), \end{aligned}$$
(3)

where \(g^{-1}: [0, 1]\rightarrow [-\tau , \tau ]\).

Definition 3

Let \(S=\{s_{t}|t=-\tau , \ldots , -1, 0, 1, \ldots , \tau \}\) be a linguistic term set. Given three PLTSs L(p), \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\), their basic operations are summarized as follows [1]:

  1. (1)

    \(L_{1} (p_{1} ) \oplus L_{2} (p_{2} ) = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{1}^{{(i)}} \in g(L_{1} ),\eta _{2}^{{(j)}} \in g(L_{2} )}} {\left\{ {\left( {\eta _{1}^{{(i)}} + \eta _{2}^{{(j)}} - \eta _{1}^{{(i)}} \eta _{2}^{{(j)}} } \right)\left( {p_{1}^{{(i)}} p_{2}^{{(j)}} } \right)} \right\}} } \right)\);

  2. (2)

    \(L_{1} (p_{1} ) \otimes L_{2} (p_{2} ) = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{1}^{{(i)}} \in g(L_{1} ),\eta _{2}^{{(j)}} \in g(L_{2} )}} {\left\{ {\left( {\eta _{1}^{{(i)}} \eta _{2}^{{(j)}} )(p_{1}^{{(i)}} p_{2}^{{(j)}} } \right)} \right\}} } \right)\);

  3. (3)

    \(\lambda L(p)=g^{-1}\left( \bigcup _{\eta ^{(k)} \in g(L)}\left\{ (1-(1-\eta ^{(k)})^{\lambda })(p^{(k)})\right\} \right)\) and \(\lambda \ge 0\);

  4. (4)

    \((L(p))^{\lambda }=g^{-1}\left( \bigcup _{\eta ^{(k)} \in g(L)}\left\{ (\eta ^{(k)})^{\lambda }(p^{(k)})\right\} \right)\), where \(\lambda \in \mathbf {R}\) and \(\lambda \ge 0\).

In order to compare the PLTSs, Pang et al. [19] defined the score and the deviation degree of a PLTS:

Definition 4

Let \(L(p)=\{L^{(k)}(p^{(k)})|k=1, 2, \ldots , \#L(p)\}\) be a PLTS, and \(r^{(k)}\) is the subscript of linguistic term \(L^{(k)}\). Then, the score of L(p) is defined as follows:

$$\begin{aligned} E(L(p))=s_{\bar{\alpha }}, \end{aligned}$$
(4)

where \(\bar{\alpha }=\sum _{k=1}^{\#L(p)} r^{(k)}p^{(k)}/\sum _{k=1}^{\#L(p)}p^{(k)}\). The deviation degree of L(p) is:

$$\begin{aligned} \sigma (L(p))=\frac{\sum _{k=1}^{\#L(p)}(p^{(k)}(r^{(k)}-\bar{\alpha }))^{0.5}}{\sum _{k=1}^{\#L(p)}p^{(k)}}. \end{aligned}$$
(5)

Based on the score and the deviation degree of a PLTS, Pang et al. [19] further proposed the following laws to compare them:

Definition 5

Given two PLTSs \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\). \(E(L_{1}(p_{1}))\) and \(E(L_{2}(p_{2}))\) are the scores of \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\), respectively. \(\sigma (L_{1}(p_{1}))\) and \(\sigma (L_{2}(p_{2}))\) denote the deviation degrees of \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\). Then, we have:

  1. (1)

    If \(E(L_{1}(p_{1})) > E(L_{2}(p_{2}))\), then \(L_{1}(p_{1})\) is bigger than \(L_{2}(p_{2})\), denoted by \(L_{1}(p_{1}) > L_{2}(p_{2})\);

  2. (2)

    If \(E(L_{1}(p_{1})) <\,E(L_{2}(p_{2}))\), then \(L_{1}(p_{1})\) is smaller than \(L_{2}(p_{2})\), denoted by \(L_{1}(p_{1}) <L_{2}(p_{2})\);

  3. (3)

    If \(E(L_{1}(p_{1})) = E(L_{2}(p_{2}))\), then we need to compare their deviation degrees:

    1. (a)

      If \(\sigma (L_{1}(p_{1})) = \sigma (L_{2}(p_{2}))\), then \(L_{1}(p_{1})\) is equal to \(L_{2}(p_{2})\), denoted by \(L_{1}(p_{1}) \sim L_{2}(p_{2})\);

    2. (b)

      If \(\sigma (L_{1}(p_{1})) > \sigma (L_{2}(p_{2}))\), then \(L_{1}(p_{1})\) is smaller than \(L_{2}(p_{2})\), denoted by \(L_{1}(p_{1}) < L_{2}(p_{2})\);

    3. (c)

      If \(\sigma (L_{1}(p_{1})) < \sigma (L_{2}(p_{2}))\), then \(L_{1}(p_{1})\) is bigger than \(L_{2}(p_{2})\), denoted by \(L_{1}(p_{1}) > L_{2}(p_{2})\).

2.2 Geometric Bonferroni Mean (GBM)

Considering the interrelationships among the input arguments and the BM [4], Xia et al. [30] proposed the geometric Bonferroni mean (GBM) as follows:

Definition 6

Let \(p, q \ge 0\), and \(a_{i} (i=1, 2, \ldots , n)\) be a collection of non-negative numbers. Then the geometric Bonferroni mean (GBM) is defined as:

$${\text{GBM}}^{{p,q}} (a_{1} ,a_{2} , \ldots ,a_{n} ) = \frac{1}{{p + q}}\prod\limits_{{i,j = 1;i \ne j}}^{n} {(pa_{i} + qa_{j} )^{{\frac{1}{{n(n - 1)}}}} } .$$
(6)

3 Probabilistic Linguistic Geometric Bonferroni Mean Aggregation Operators

In this section, we mainly study the GBM aggregation operators under the probabilistic linguistic environment. In practical terms, we propose two aggregation operators of PLGBM and WPLGBM based on GBM, respectively.

3.1 PLGBM

Under the probabilistic linguistic environment, we discuss that the input arguments of GBM reported in Ref. [30] are PLTs and then propose the PLGBM operator. Based on the results of Definitions 1 and 6, we give the definition of probabilistic linguistic geometric Bonferroni mean (PLGBM) operator as follows:

Definition 7

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs. Then, for any \(p, q \ge 0\), we define the probabilistic linguistic geometric Bonferroni mean (PLGBM) as:

$$\begin{aligned} & {\text{PLGBM}}^{{p,q}} (L_{1} (p_{1} ),L_{2} (p_{2} ), \ldots ,L_{n} (p_{n} )) \\ \quad &=\frac{1}{{p + q}}\left( {\mathop \otimes \limits_{{i,j = 1;i \ne j}}^{n} (pL_{i} (p_{i} ) \oplus qL_{j} (p_{j} ))^{{\frac{1}{{n(n - 1)}}}} } \right). \\ \end{aligned}$$
(7)

According to the operational laws of the PLTSs, we can derive the following results from Definition 5:

Proposition 1

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs and \(p, q \ge 0\). Then for any i, j and \(i\ne j\), we have:

$$\begin{aligned}&pL_{i}(p_{i})\oplus qL_{j}(p_{j})\nonumber \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})(p_{i}^{(k)}p_{j}^{(d)})\right\} \right) , \end{aligned}$$
(8)

where \(g(L_{i})=\left\{ \left[ \frac{r^{(k)}}{2\tau }+\frac{1}{2}\right] \right\}\) and \(g(L_{j})=\left\{ \left[ \frac{r^{(d)}}{2\tau }+\frac{1}{2}\right] \right\}\).

Proof

With respect to the two PLTSs \(L_{i}(p_{i})\) and \(L_{j}(p_{j})\), we have:

$$\begin{aligned} pL_{i} (p_{i} ) & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} )}} {\left\{ {(1 - (1 - \eta _{i}^{{(k)}} )^{p} )(p_{i}^{{(k)}} )} \right\}} } \right), \\ qL_{j} (p_{j} ) & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{j}^{{(d)}} \in g(L_{j} )}} {\left\{ {(1 - (1 - \eta _{j}^{{(d)}} )^{q} )(p_{j}^{{(d)}} )} \right\}} } \right). \\ \end{aligned}$$

By operational law (1) described in Definition 3, \(pL_{i}(p_{i})\oplus qL_{j}(p_{j})\) is calculated as:

$$\begin{aligned} pL_{i}(p_{i})\oplus qL_{j}(p_{j})= & {} g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i})}\left\{ (1-(1-\eta _{i}^{(k)})^{p})(p_{i}^{(k)})\right\} \right) \\&\oplus g^{-1}\left( \bigcup _{\eta _{j}^{(d)} \in g(L_{j})}\left\{ (1-(1-\eta _{j}^{(d)})^{q})(p_{j}^{(d)})\right\} \right) \\=\,& {} g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})(p_{i}^{(k)}p_{j}^{(d)})\right\} \right) . \end{aligned}$$

Thus, we complete the proof of Proposition 1. \(\square\)

Proposition 2

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs and \(p, q \ge 0\). Then for any i, j and \(i\ne j\), we have:

$$\begin{aligned}&(pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)}\nonumber \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}(p_{i}^{(k)}p_{j}^{(d)})\right\} \right) . \end{aligned}$$
(9)

Proof

In light of the results of Proposition 1 and operational law (4) of Definition 3, we have:

$$\begin{aligned} (pL_{i} (p_{i} ) \oplus qL_{j} (p_{j} ))^{{\frac{1}{{n(n - 1)}}}} & = \left( {g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} )}} {\left\{ {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} } \right)} \right\}} } \right)} \right)^{{\frac{1}{{n(n - 1)}}}} \\ & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} )}} {\left\{ {\left( {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} } \right)} \right\}} } \right). \\ \end{aligned}$$

Hence, the statement of Proposition 2 holds. \(\square\)

Proposition 3

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs and \(p, q \ge 0\). For any i, j and \(i\ne j\), we have:

$$\begin{aligned} & (pL_{i} (p_{i} ) \oplus qL_{j} (p_{j} ))^{{\frac{1}{{n(n - 1)}}}} \otimes (pL_{j} (p_{j} ) \oplus qL_{i} (p_{i} ))^{{\frac{1}{{n(n - 1)}}}} \\ & \quad = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} ),\eta _{i}^{{(k^{\prime})}} \in g(L_{i} ),\eta _{j}^{{(d^{\prime})}} \in g(L_{j} )}} {\left\{ {\left| {\left( {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} } \right)} \right|^{{\frac{1}{{n(n - 1)}}}} \left( {1 - \left( {1 - \eta _{j}^{{(d^{\prime})}} } \right)^{p} \left( {1 - \eta _{i}^{{(k^{\prime})}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} p_{i}^{{(k^{\prime})}} p_{j}^{{(d^{\prime})}} } \right)} \right\}} } \right) \\ \end{aligned}$$
(10)

Proof

According to the result of Proposition 2, we can obtain:

$$\begin{aligned} (pL_{i} (p_{i} ) \oplus qL_{j} (p_{j} ))^{{\frac{1}{{n(n - 1)}}}} & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} )}} {\left\{ {\left( {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} } \right)} \right\}} } \right), \\ (pL_{j} (p_{j} ) \oplus qL_{i} (p_{i} ))^{{\frac{1}{{n(n - 1)}}}} & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k^{\prime } )}} \in g(L_{i} ),\eta _{j}^{{(d^{\prime } )}} \in g(L_{j} )}} {\left\{ {\left( {1 - \left( {1 - \eta _{j}^{{(d^{\prime } )}} } \right)^{p} \left( {1 - \eta _{i}^{{(k^{\prime } )}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k^{\prime } )}} p_{j}^{{(d^{\prime } )}} } \right)} \right\}} } \right). \\ \end{aligned}$$

With the aid of operational law (2) presented in Definition 3, we have:

$$\begin{aligned} & (pL_{i} (p_{i} ) \oplus qL_{j} (p_{j} ))^{{\frac{1}{{n(n - 1)}}}} \otimes (pL_{j} (p_{j} ) \oplus qL_{i} (p_{i} ))^{{\frac{1}{{n(n - 1)}}}} \\ & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} )}} {\left\{ {\left| {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} } \right|^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} } \right)} \right\}} } \right) \\ & \quad\quad \otimes g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k^{\prime } )}} \in g(L_{i} ),\eta _{j}^{{(d^{\prime } )}} \in g(L_{j} )}} {\left\{ {\left( {1 - \left( {1 - \eta _{j}^{{(d^{\prime } )}} } \right)^{p} \left( {1 - \eta _{i}^{{(k^{\prime } )}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k^{\prime } )}} p_{j}^{{(d^{\prime } )}} } \right)} \right\}} } \right) \\ & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} ),\eta _{j}^{{(d)}} \in g(L_{j} ),\eta _{i}^{{(k^{\prime } )}} \in g(L_{i} ),\eta _{j}^{{(d^{\prime } )}} \in g(L_{j} )}} {\left\{ {\left( {1 - \left( {1 - \eta _{i}^{{(k)}} } \right)^{p} \left( {1 - \eta _{j}^{{(d)}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {1 - \left( {1 - \eta _{j}^{{(d^{\prime } )}} } \right)^{p} \left( {1 - \eta _{i}^{{(k^{\prime } )}} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} \left( {p_{i}^{{(k)}} p_{j}^{{(d)}} p_{i}^{{(k^{\prime } )}} p_{j}^{{(d^{\prime } )}} } \right)} \right\}} } \right). \\ \end{aligned}$$

Thus, we complete the proof of Proposition 3. \(\square\)

Based on the result of Proposition 3 and operational law (2) of Definition 3, we can deduce the following proposition:

Proposition 4

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs and \(p, q \ge 0\). Then for any i, j and \(i\ne j\), we have:

$$\begin{aligned}&\bigotimes _{i, j=1; i\ne j}^{n}(pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)}\nonumber \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( \prod ^{n}_{i, j=1, i\ne j}(1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) . \end{aligned}$$
(11)

Proof

According to the definition of PFGBM, suppose that there are two different cases: (1) i, j and \(i\ne j\); (2) u, v and \(u\ne v\). Following the result of Proposition 3, we have:

$$\begin{aligned}&(pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)} \otimes (pL_{j}(p_{j})\oplus qL_{i}(p_{i}))^\frac{1}{n(n-1)}\\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j}), \eta _{i}^{(k')} \in g(L_{i}), \eta _{j}^{(d')} \in g(L_{j})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{j}^{(d')})^{p}(1-\eta _{i}^{(k')})^{q})^\frac{1}{n(n-1)}\right. \right. \\&\quad \left. \left. (p_{i}^{(k)}p_{j}^{(d)}p_{i}^{(k')}p_{j}^{(d')})\right\} \right) ,\\&\quad (pL_{u}(p_{u})\oplus qL_{v}(p_{v}))^\frac{1}{n(n-1)} \otimes (pL_{v}(p_{v})\oplus qL_{u}(p_{u}))^\frac{1}{n(n-1)}\\&\quad =g^{-1}\left( \bigcup _{\eta _{u}^{(f)} \in g(L_{u}), \eta _{v}^{(h)} \in g(L_{v}), \eta _{u}^{(f')} \in g(L_{u}), \eta _{v}^{(h')} \in g(L_{v})}\left\{ (1-(1-\eta _{u}^{(f)})^{p}(1-\eta _{v}^{(h)})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{v}^{(h')})^{p}(1-\eta _{u}^{(f')})^{q})^\frac{1}{n(n-1)}\right. \right. \\&\quad \left. \left. (p_{u}^{(f)}p_{v}^{(h)}p_{u}^{(f')}p_{v}^{(h')})\right\} \right) . \end{aligned}$$

By using operational law (2) of Definition 3, \(\left( (pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)} \otimes (pL_{j}(p_{j})\oplus qL_{i}(p_{i}))^\frac{1}{n(n-1)}\right) \bigotimes \left( (pL_{u}(p_{u})\oplus qL_{v}(p_{v}))^\frac{1}{n(n-1)} \otimes (pL_{v}(p_{v})\oplus qL_{u}(p_{u}))^\frac{1}{n(n-1)}\right)\) is calculated as follows:

$$\begin{aligned}&\left( (pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)}\right. \left. \otimes (pL_{j}(p_{j})\oplus qL_{i}(p_{i}))^\frac{1}{n(n-1)}\right) \\&\quad \bigotimes \left( (pL_{u}(p_{u})\oplus qL_{v}(p_{v}))^\frac{1}{n(n-1)} \otimes (pL_{v}(p_{v})\oplus qL_{u}(p_{u}))^\frac{1}{n(n-1)}\right) \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j}), \eta _{i}^{(k')} \in g(L_{i}), \eta _{j}^{(d')} \in g(L_{j})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{j}^{(d')})^{p}(1-\eta _{i}^{(k')})^{q})^\frac{1}{n(n-1)}\right. \right. \nonumber \\&\left. \left. \quad (p_{i}^{(k)}p_{j}^{(d)}p_{i}^{(k')}p_{j}^{(d')})\right\} \right) \bigotimes \\&\quad g^{-1}\left( \bigcup _{\eta _{u}^{(f)} \in g(L_{u}), \eta _{v}^{(h)} \in g(L_{v}), \eta _{u}^{(f')} \in g(L_{u}), \eta _{v}^{(h')} \in g(L_{v})}\left\{ (1-(1-\eta _{u}^{(f)})^{p}(1-\eta _{v}^{(h)})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{v}^{(h')})^{p}(1-\eta _{u}^{(f')})^{q})^\frac{1}{n(n-1)}\right. \right. \nonumber \\&\quad \left. \left. (p_{u}^{(f)}p_{v}^{(h)}p_{u}^{(f')}p_{v}^{(h')})\right\} \right) \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j}), \eta _{i}^{(k')} \in g(L_{i}), \eta _{j}^{(d')} \in g(L_{j}), \eta _{u}^{(f)} \in g(L_{u}), \eta _{v}^{(h)} \in g(L_{v}), \eta _{u}^{(f')} \in g(L_{u}), \eta _{v}^{(h')} \in g(L_{v})}\left\{ (1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}\right. \right. \nonumber \\&\quad \left. \left. (1-(1-\eta _{j}^{(d')})^{p}(1-\eta _{i}^{(k')})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{u}^{(f)})^{p}(1-\eta _{v}^{(h)})^{q})^\frac{1}{n(n-1)}(1-(1-\eta _{v}^{(h')})^{p}(1-\eta _{u}^{(f')})^{q})^\frac{1}{n(n-1)}\right. \right. \nonumber \\&\quad \left. \left. (p_{i}^{(k)}p_{j}^{(d)}p_{i}^{(k')}p_{j}^{(d')}p_{u}^{(f)}p_{v}^{(h)}p_{u}^{(f')}p_{v}^{(h')})\right\} \right) . \end{aligned}$$

In this case, the result of \(\left( (pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)} \otimes (pL_{j}(p_{j})\oplus qL_{i}(p_{i}))^\frac{1}{n(n-1)}\right) \bigotimes \left( (pL_{u}(p_{u})\oplus qL_{v}(p_{v}))^\frac{1}{n(n-1)} \otimes (pL_{v}(p_{v})\oplus qL_{u}(p_{u}))^\frac{1}{n(n-1)}\right)\) can be extended into any situation. Therefore, the statement of Proposition 4 holds. \(\square\)

On the basis of the results of Definition 7, Proposition 4, and operational law (3) of Definition 3, we deduce the following theorem:

Theorem 1

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) be n PLTSs and \(p, q \ge 0\), then the aggregated value by using the PLGBM operator is also an PFN, and

$$\begin{aligned}&\text{PLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n})) \nonumber \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( 1-\left( 1-\left( \prod ^{n}_{i, j=1, i\ne j}\left( 1-\left( 1-\eta _{i}^{(k)}\right) ^{p}\left( 1-\eta _{j}^{(d)}\right) ^{q}\right) ^\frac{1}{n(n-1)}\right) \right) ^{\frac{1}{p+q}}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) . \end{aligned}$$
(12)

Proof

In light of operational law (3) of Definition 3, \(\text{PLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))\) can be computed as follows:

$$\begin{aligned}&\text{PLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))=\frac{1}{p+q}\left( \bigotimes _{i, j=1; i\ne j}^{n}(pL_{i}(p_{i})\oplus qL_{j}(p_{j}))^\frac{1}{n(n-1)}\right) \\&\quad =\frac{1}{p+q}\left( g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( \prod ^{n}_{i, j=1, i\ne j}(1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) \right) \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( 1-\left( 1-\left( \prod ^{n}_{i, j=1, i\ne j}(1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}\right) \right) ^{\frac{1}{p+q}}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) . \end{aligned}$$

Therefore, the statement of Theorem 1 holds. \(\square\)

With respect to \(\text{PLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))\) of Theorem 1, we can further deduce the following corollaries based on the results of Ref. [30].

Corollary 1

Commutativity. If \(L'_{i}(p'_{i})\) is any permutation of \(L_{i}(p_{i})\,(i=1, 2, \ldots , n)\), then we have the relationship:

$$\begin{aligned} \text{PLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))=\text{PLGBM}^{p, q}(L'_{1}(p'_{1}), L'_{2}(p'_{2}), \ldots , L'_{n}(p'_{n})). \end{aligned}$$

Corollary 2

Monotonicity. Let \(\varepsilon _{ij}=1-(1-(\prod ^{n}_{i, j=1, i\ne j}(1-(1-\eta _{i}^{(k)})^{p}(1-\eta _{j}^{(d)})^{q})^\frac{1}{n(n-1)}))^{\frac{1}{p+q}}\). When the values of n, p , and q are constant, \(\varepsilon _{ij}\) is monotonously increasing with the increase of \(\eta _{i}^{(k)}\) and \(\eta _{j}^{(d)}\).

3.2 WPLGBM

Considering the importance of the aggregated arguments [30, 32], we further define a weighted probabilistic linguistic geometric Bonferroni mean (WPLGBM) operator as follows:

Definition 8

Let \(L_{i}(p_{i})=\{L_{i}^{(k)}(p_{i}^{(k)})|k=1, 2, \ldots , \#L_{i}(p_{i})\}\,(i=1, 2, \ldots , n)\) and \(p, q \ge 0\). \(w=(w_{1}, w_{2}, \ldots , w_{n})^{T}\) is the weight vector of \(L_{i}(p_{i})\), where \(w_{i}\) indicates the importance degree of \(L_{i}(p_{i})\), satisfying \(w_{i} \in [0, 1]\) and \(\sum _{i}^{n}w_{i}=1\). Given the value of the weight vector \(w=(w_{1}, w_{2}, \ldots , w_{n})^{T}\) , the WPLGBM is defined as:

$$\begin{aligned} \text{WPLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))=\frac{1}{p+q}\left( \bigotimes _{i, j=1; i\ne j}^{n}(p(L_{i}(p_{i}))^{w_{i}}\oplus q(L_{j}(p_{j}))^{w_{j}})^\frac{1}{n(n-1)}\right) . \end{aligned}$$
(13)

On the basis of Theorem 1 and the operational laws of Definition 3, we can deduce the following theorem:

Theorem 2

Let \(\beta _{i}=P(\mu _{\beta _{i}}, \nu _{\beta _{i}})\,(i=1, 2, \ldots , n)\) be the set of PFNs and \(p, q \ge 0\). \(w=(w_{1}, w_{2}, \ldots , w_{n})^{T}\) is the weight vector of \(\beta _{i}\), where \(w_{i}\) indicates the importance degree of \(\beta _{i}\), satisfying \(w_{i} \in [0, 1]\) and \(\sum _{i}^{n}w_{i}=1\). Based on these results, the aggregated value by using the WPFGBM is also an PFN, and

$$\begin{aligned}&\text{WPLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))\nonumber \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( 1-\left( 1-\left( \prod ^{n}_{i, j=1, i\ne j}(1-(1-(\eta _{i}^{(k)})^{w_{i}})^{p}(1-(\eta _{j}^{(d)})^{w_{j}})^{q})^\frac{1}{n(n-1)}\right) \right) ^{\frac{1}{p+q}}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) . \end{aligned}$$
(14)

Proof

In light of the result of Definition 8 and operational law (4) of Definition 3, the elements \((L_{i}(p_{i}))^{w_{i}}\) and \((L_{j}(p_{j}))^{w_{j}}\) are calculated as follows:

$$\begin{aligned} (L_{i} (p_{i} ))^{{w_{i} }} & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{i}^{{(k)}} \in g(L_{i} )}} {\left\{ {(\eta _{i}^{{(k)}} )^{{w_{i} }} (p_{i}^{{(k)}} )} \right\}} } \right), \\ (L_{j} (p_{j} ))^{{w_{j} }} & = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{j}^{{(k)}} \in g(L_{j} )}} {\left\{ {(\eta _{j}^{{(k)}} )^{{w_{j} }} (p_{j}^{{(k)}} )} \right\}} } \right). \\ \end{aligned}$$

Then, by utilizing the results of Definition 8 and Theorem 1, we can get:

$$\begin{aligned}&\text{WPLGBM}^{p, q}(L_{1}(p_{1}), L_{2}(p_{2}), \ldots , L_{n}(p_{n}))\\&\quad =\frac{1}{p+q}\left( \bigotimes _{i, j=1; i\ne j}^{n}(p(L_{i}(p_{i}))^{w_{i}}\oplus q(L_{j}(p_{j}))^{w_{j}})^\frac{1}{n(n-1)}\right) \\&\quad =g^{-1}\left( \bigcup _{\eta _{i}^{(k)} \in g(L_{i}), \eta _{j}^{(d)} \in g(L_{j})}\left\{ \left( 1-\left( 1-\left( \prod ^{n}_{i, j=1, i\ne j}(1-(1-(\eta _{i}^{(k)})^{w_{i}})^{p}(1-(\eta _{j}^{(d)})^{w_{j}})^{q})^\frac{1}{n(n-1)}\right) \right) ^{\frac{1}{p+q}}\right) \left( \prod ^{n}_{i, j=1, i\ne j}p_{i}^{(k)}p_{j}^{(d)}\right) \right\} \right) . \end{aligned}$$

Thus, we complete the proof of Theorem 2. \(\square\)

From Theorems 1 and 2, the results of the PLGBM operator and the WPLGBM operator are PLTSs. Besides, WPLGBM also has considered the importance of the aggregated arguments and is the extension of PLGBM.

4 Grey Relational Analysis Method for PLMCGDM with WPLBM

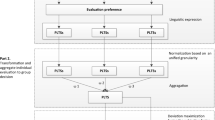
In this section, we firstly present the PLMCGDM problem. Then, we adopt the WPLGBM aggregation operator to collect the individual evaluations and obtain an integrated evaluation for each alternative. By introducing grey relation analysis method, we further order the collective evaluations to obtain the best alternative(s). Finally, we summarize the decision-making procedure and propose the corresponding approach.

4.1 The Problem Description of PLMCGDM

For the PLMCGDM problem, it has multiple decision matrices whose elements denote the evaluations with PLTSs of all alternatives with respect to each criterion [19]. Let \(X=\{x_{1}, x_{2}, \ldots , x_{m}\}\) be a discrete set of alternatives, \(C=\{c_{1}, c_{2}, \ldots , c_{n}\}\) be the set of criteria, and \(\lambda =(\lambda _{1}, \lambda _{2}, \ldots , \lambda _{n})^{T}\) be the weight vector of the criteria. Suppose that \(E=\{e_{1}, e_{2}, \ldots , e_{y}\}\) is the set of experts with the corresponding weight information \(W=(w_{1}, w_{2}, \ldots , w_{y})^{T}\), which satisfies \(0 \le w_{z} \le 1\) and \(\sum _{z=1}^{y}w_{z}=1\). Let \(D^{z}=(L^{z}_{ij}(p^{z}_{ij}))_{m \times n}\) be the probabilistic linguistic decision matrix provided by the expert \(e_{z}\) \((z=1, 2, \ldots , y)\). Hence, the probabilistic linguistic decision matrix \(D^{z}\) can be written as:

$$\begin{aligned} D^{z}=\begin{bmatrix} \beta ^{z}_{11}=L^{z}_{11}(p^{z}_{11})&\beta ^{z}_{12}=L^{z}_{12}(p^{z}_{12})&\cdots&\beta ^{z}_{1n}=L^{z}_{1n}(p^{z}_{1n})\\ \beta ^{z}_{21}=L^{z}_{21}(p^{z}_{21})&\beta ^{z}_{22}=L^{z}_{22}(p^{z}_{22})&\cdots&\beta ^{z}_{2n}=L^{z}_{2n}(p^{z}_{2n})\\ \vdots&\vdots&\cdots&\vdots \\ \beta ^{z}_{m1}=L^{z}_{m1}(p^{z}_{m1})&\beta ^{z}_{m2}=L^{z}_{m2}(p^{z}_{m2})&\cdots&\beta ^{z}_{mn}=L^{z}_{mn}(p^{z}_{mn}) \end{bmatrix}. \end{aligned}$$

In this matrix \(D^{z}\), the element \(\beta ^{z}_{ij}=L^{z}_{ij}(p^{z}_{ij})\) denotes the evaluation value of the alternative \(x_{i}\) with respect to the criterion \(c_{j}\) provided by the expert \(e_{z}\) \((i=1, 2, \ldots, m;\,j=1, 2, \ldots , n)\).

4.2 The Fusion Analysis with the Aid of WPLBM and the Grey Relational Analysis Method

With the help of the WPLGBM operator, the collective outcome of the alternative \(x_{i}\) with respect to the criterion \(c_{j}\) is aggregated based on (13) and (14) \((i=1, 2, \ldots , m; j=1, 2, \ldots , n)\). The result is shown as follows:

$$\begin{aligned} L_{{ij}} (p_{{ij}} ) & = {\text{WPLGBM}}^{{p,q}} \left( {\beta _{{ij}}^{1} ,\beta _{{ij}}^{2} , \ldots ,\beta _{{ij}}^{y} } \right) = {\text{WPLGBM}}^{{p,q}} \left( {L_{{ij}}^{1} (p_{{ij}}^{1} ),L_{{ij}}^{2} (p_{{ij}}^{2} ), \ldots ,L_{{ij}}^{y} (p_{{ij}}^{y} )} \right) \\ & \quad = \frac{1}{{p + q}}\left( {\mathop \otimes \limits_{{z,l = 1;z \ne l}}^{y} \left( {p(L_{{ij}}^{z} (p_{{ij}}^{z} )} \right)^{{w_{z} }} \oplus q\left( {L_{{ij}}^{l} (p_{{ij}}^{l} ))^{{w_{l} }} } \right)^{{\frac{1}{{n(n - 1)}}}} } \right) \\ & \quad = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{{ijz}}^{{(k)}} \in g(L_{{ij}}^{z} ),\eta _{{ijl}}^{{(d)}} \in g(L_{{ij}}^{l} )}} {\left\{ {\left( {1 - \left( {1 - \left( {\prod\limits_{{z,l = 1,z \ne l}}^{y} {\left( {1 - \left( {1 - (\eta _{{ijz}}^{{(k)}} )^{{w_{z} }} } \right)^{p} \left( {1 - (\eta _{{ijl}}^{{(d)}} )^{{w_{l} }} } \right)^{q} } \right)^{{\frac{1}{{n(n - 1)}}}} } } \right)} \right)^{{\frac{1}{{p + q}}}} } \right)} \right.} } \right. \\ & \quad \left. {\left. {\left( {\prod\limits_{{z,l = 1,z \ne l}}^{y} {p_{{ijz}}^{{(k)}} } p_{{ijl}}^{{(d)}} } \right)} \right\}} \right). \\ \end{aligned}$$
(15)

Then, we eventually obtain an integrated group decision matrix \(D=(L_{ij}(p_{ij}))_{m \times n}\). The decision matrix D can be written as:

$$\begin{aligned} D=\begin{bmatrix} \beta _{11}=L_{11}(p_{11})&\beta _{12}=L_{12}(p_{12})&\cdots&\beta _{1n}=L_{1n}(p_{1n})\\ \beta _{21}=L_{21}(p_{21})&\beta _{22}=L_{22}(p_{22})&\cdots&\beta _{2n}=L_{2n}(p_{2n})\\ \vdots&\vdots&\cdots&\vdots \\ \beta _{m1}=L_{m1}(p_{m1})&\beta _{m2}=L_{m2}(p_{m2})&\cdots&\beta _{mn}=L_{mn}(p_{mn}) \end{bmatrix}. \end{aligned}$$

For the matrix D, the element \(\beta _{ij}=L_{ij}(p_{ij})\) is the group evaluation of the alternative \(x_{i}\) with respect to the criterion \(c_{j}\). Based on the matrix D, the evaluation of the alternative \(x_{i}\) is denoted as \(x_{i}=(\beta _{i1}, \beta _{i2}, \ldots , \beta _{in})\). According to the results of Refs. [13, 26, 27], we need to determine the positive ideal solution based on the matrix D. Note that we only utilize the score of Definition 4 when we compare the PLTSs in the application [14] and assume that all criteria are benefit. Inspired by the idea, the positive ideal solution \(x^{+}\) can be determined by the following formula:

$$\begin{aligned} x^{+}=(\beta _{1}, \beta _{2}, \ldots , \beta _{n}), \end{aligned}$$
(16)

where \(\beta _{j}=\arg \max _{i=1}^{m} E(\beta _{ij})=L_{j}(p_{j})\) \((j=1, 2, \ldots , n)\). Meanwhile, \(\beta _{j}\) is a PLTS. In light of the grey relational analysis method, we calculate the grey relational coefficient of each alternative from the positive ideal solution using the following equation:

$$\begin{aligned} \varepsilon ^{+}_{ij}=\frac{\min _{1\le i \le m}\min _{1\le j \le n}d(\beta _{ij}, \beta _{j})+\rho \max _{1\le i \le m} \max _{1\le j \le n} d(\beta _{ij}, \beta _{j})}{d(\beta _{ij}, \beta _{j})+\rho \max _{1\le i \le m} \max _{1\le j \le n} d(\beta _{ij}, \beta _{j})}, \end{aligned}$$
(17)

where \(\rho\) is the identification coefficient. The value of \(\rho\) normally is 0.5 [27]. \(d(\beta _{ij}, \beta _{j})\) denotes the deviation degree between \(\beta _{ij}\) and \(\beta _{j}\). Fortunately, Pang et al. [19] defined the deviation degree between PLTSs. Considering the results of Definition 2, the deviation degree between two PLTSs can be defined as:

Definition 9

Let \(L_{1}(p_{1})=\{L_{1}^{(k)}(p_{1}^{(k)})|k=1, 2, \ldots , \#L_{1}(p_{1})\}\) and \(L_{2}(p_{2})=\{L_{2}^{(k)}(p_{2}^{(k)})|k=1, 2, \ldots , \#L_{2}(p_{2})\}\) be two PLTSs, then the deviation degree between \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\) is computed as:

$$\begin{aligned} d(L_{1}(p_{1}), L_{2}(p_{2}))=\sqrt{\frac{\sum _{k=1}^{\#L_{1}(p_{1})}(p_1^{k}g(L_1^k)-p_2^{k}g(L_2^k))^2}{\#L_{1}(p_{1})}}, \end{aligned}$$
(18)

where \(\#L_{1}(p_{1})=\#L_{2}(p_{2})\), \(g(L_1^k)=\frac{r_1^{k}}{2\tau }+\frac{1}{2}\), \(g(L_2^k)=\frac{r_2^{k}}{2\tau }+\frac{1}{2}\). \(r_1^{(k)}\) and \(r_2^{(k)}\) are the subscript of \(L_1^{(k)}\) and \(L_2^{(k)}\), respectively.

When we analyse the comparison of PLTSs, we encounter that the number of their corresponding number of the linguistic terms may not be equal. In order to solve this problem, Pang et al. [19] normalized the PLTSs by increasing the numbers of linguistic terms for PLTSs. The normalized definition of PLTSs is:

Definition 10

Let \(L_{1}(p_{1})=\{L_{1}^{(k)}(p_{1}^{(k)})|k=1, 2, \ldots , \#L_{1}(p_{1})\}\) and \(L_{2}(p_{2})=\{L_{2}^{(k)}(p_{2}^{(k)})|k=1, 2, \ldots , \#L_{2}(p_{2})\}\) be any two PLTSs. \(\#L_{1}(p_{1})\) and \(\#L_{2}(p_{2})\) are the numbers of the linguistic terms in \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\). If \(\#L_{1}(p_{1})>\#L_{2}(p_{2})\), then we will add \(\#L_{1}(p_{1})-\#L_{2}(p_{2})\) linguistic terms to \(L_{2}(p_{2})\) so that the numbers of linguistic terms in \(L_{1}(p_{1})\) and \(L_{2}(p_{2})\) are identical. The added linguistic terms are the smallest ones in \(L_{2}(p_{2})\), and the probabilities of all the linguistic terms are zero. Analogously, if \(\#L_{1}(p_{1})<\#L_{2}(p_{2})\), we can use the similar method.

Based on (17) and (18), we further calculate the degree of grey relational coefficient of each alternative from the positive ideal solution using the following equation:

$$\begin{aligned} \varepsilon ^{+}_{i}=\sum _{j=1}^{n}\lambda _{j}\varepsilon ^{+}_{ij}. \end{aligned}$$
(19)

The basic principle of the grey relational analysis method is that the chosen alternative should have the largest degree of grey relation from the positive ideal solution [27]. Obviously, given the weight vector of the criteria \(\lambda =(\lambda _{1}, \lambda _{2}, \ldots , \lambda _{n})^{T}\), the larger the value of \(\varepsilon ^{+}_{i}\), the better the alternative \(x_{i}\) is \((i=1, 2, \ldots , m)\).

4.3 The Decision Procedure

With the above-mentioned results, we develop an approach of the application for PLMCGDM with WPLBM and grey relational analysis method. On the one hand, we utilize the WPLBM to fuse the information of GDM. On the other hand, the grey relational analysis method can help us to make the decision. The new approach is designed as follows:

Step 1 :

In light of the practical decision-making problem, we determine the discrete set of alternatives \(X=\{x_{1}, x_{2}, \ldots , x_{m}\}\) and the set of criteria \(C=\{c_{1}, c_{2}, \ldots , c_{n}\}\). Meanwhile, we obtain the weight vector of the criteria \(\lambda =(\lambda _{1}, \lambda _{2}, \ldots , \lambda _{n})^{T}\). Suppose that \(E=\{e_{1}, e_{2}, \ldots , e_{y}\}\) is the set of experts with the corresponding weight information \(w=(w_{1}, w_{2}, \ldots , w_{y})^{T}\). By using the linguistic term set \(S=\{s_{t}|t=-\tau , \ldots , -1, 0, 1, \ldots , \tau \}\), the probabilistic linguistic decision matrix provided by the expert \(e_{z}\) is constructed as \(D^{z}=(L^{z}_{ij}(p^{z}_{ij}))_{m \times n}\) \((i=1, 2, \ldots , m;\,j=1, 2, \ldots , n; z=1, 2, \ldots , y)\).

Step 2 :

Given the values of p and q, we utilize the WPLGBM operator to integrate the individual evaluations into the group opinion. In light of (15), the collective evaluation value of the alternative \(x_{i}\) with respect to the criterion \(c_{j}\) is aggregated as follows:

$$\begin{aligned} \beta _{ij} & = {} L_{ij}(p_{ij})\\= & {} g^{-1}\left( \bigcup _{\eta _{ijz}^{(k)} \in g(L^{z}_{ij}), \eta _{ijl}^{(d)} \in g(L^{l}_{ij})}\left\{ \left( 1-\left( 1-\left( \prod ^{y}_{z, l=1, z\ne l}\left( 1-\left( 1-\left( \eta _{ijz}^{(k)}\right) ^{w_{z}}\right) ^{p}\left( 1-(\eta _{ijl}^{(d)})^{w_{l}}\right) ^{q}\right) ^\frac{1}{n(n-1)}\right) \right) ^{\frac{1}{p+q}}\right) \left( \prod ^{y}_{z, l=1, z\ne l}p_{ijz}^{(k)}p_{ijl}^{(d)}\right) \right\} \right) . \end{aligned}$$

Thus, the integrated group decision matrix \(D=(\beta _{ij})_{m \times n}=(L_{ij}(p_{ij}))_{m \times n}\) is obtained \((i=1, 2, \ldots , m; \,j=1, 2, \ldots , n)\).

Step 3 :

With respect to each criterion, we normalize the evaluation with PLTSs of the matrix D by using the result of Definition 10.

Step 4 :

On the basis of (16) and the integrated decision matrix D, we identify the positive ideal solution \(x^{+}=(\beta _{1}, \beta _{2}, \ldots , \beta _{n})\).

Step 5 :

In light of (17)–(18), the positive ideal solution \(x^{+}\) and the identification coefficient \(\rho\), we calculate the grey relational coefficient of each alternative with each criterion, i.e. \(\varepsilon ^{+}_{ij}\) \((i=1, 2, \ldots , m; j=1, 2, \ldots , n)\).

Step 6 :

For each alternative \(x_{i}\), we compute its corresponding degree of grey relational coefficient based on (19), i.e. \(\varepsilon ^{+}_{i}\,(i=1, 2, \ldots , m)\).

Step 7 :

We finally rank all the alternatives in accordance with \(\varepsilon ^{+}_{i}\,(i=1, 2, \ldots , m)\).

5 An Illustrative Example

In this section, we illustrate the proposed approach of Sect. 4 by evaluating the personalized healthcare system of some domestic hospitals in China. Due to the increasingly serious environmental pollution in China and limited medical resources, several domestic hospitals have to be evaluated to search for the optimal one [1], especially their personalized healthcare system [7, 8]. According to the study of Gou et al. [8], we invite three professional experts to aid the evaluation, denoted as \(E=\{e_{1}, e_{2}, e_{3}\}\). We also assume that the weights of experts are \(w=(w_{1}, w_{2}, w_{3})^{T}=(0.3, 0.3, 0.4)^{T}\). In light of the results of Refs. [1, 7], the criteria considered for the assessment of the decision problem are summarized as follows: (1) the environmental factor of medical and health service (\(c_{1}\)); (2) personalized diagnosis and treatment optimization (\(c_{2}\)); (3) social resource allocation optimization under the pattern of wisdom medical and health services (\(c_{3}\)). The weight vector of the criteria is given by experts as \(\lambda =(\lambda _{1}, \lambda _{2}, \lambda _{3})^{T}=(0.2, 0.1, 0.7)^{T}\). There are four hospitals to be evaluated, i.e. \(X=\{x_{1}, x_{2}, x_{3}, x_{4}\}\). Let \(S=\{s_{t}|t=-3, -2, -1, 0, 1, 2, 3\}\) be the linguistic term set. Then, the assessments of the alternatives with respect to each criterion provided by the experts are assumed to be represented by PLTSs. Their results are given in the probabilistic linguistic decision matrices, see Tables 1, 2, and 3.

Table 1 The probabilistic linguistic decision matrix \(D^{1}\) provided by the expert \(e_{1}\)
Full size table
Table 2 The probabilistic linguistic decision matrix \(D^{2}\) provided by the expert \(e_{2}\)
Full size table
Table 3 The probabilistic linguistic decision matrix \(D^{3}\) provided by the expert \(e_{3}\)
Full size table

5.1 Decision Analysis with the Proposed Approach

Based on the proposed approach of Sect. 4, we fuse the information presented in the decision matrices \(D^1-D^3\). Following the results of Ref. [8], we assume that the values of p and q are 1. With the aid of the WPFGBM operator, the collective evaluation value of the alternative \(x_{i}\) with respect to the criterion \(c_{j}\) can be derived from (13) \((i=1, 2, 3, 4; j=1, 2, 3)\). In order to illustrate the calculation procedure, we take the alternative \(x_{4}\) as an example. In light of the results of Tables 1,  2, and 3 and (14), the collective evaluation value of the alternative \(x_{4}\) with respect to the criterion \(c_{3}\) is calculated as:

$$\begin{aligned} \beta _{{43}} & = L_{{43}} (p_{{43}} ) \\ & \quad = g^{{ - 1}} \left( {\bigcup\limits_{{\eta _{{43z}}^{{(k)}} \in g(L_{{43}}^{z} ),\eta _{{43l}}^{{(d)}} \in g(L_{{43}}^{l} )}} {\left\{ {\left( {1 - \left( {1 - \left( {\prod\limits_{{z,l = 1,z \ne l}}^{3} {\left( {1 - \left( {1 - \left( {\eta _{{43z}}^{{(k)}} } \right)^{{w_{z} }} } \right)^{p} \left( {1 - \left( {\eta _{{43l}}^{{(d)}} } \right)^{{w_{l} }} } \right)^{q} } \right)^{{\frac{1}{{3(3 - 1)}}}} } } \right)} \right)^{{\frac{1}{{1 + 1}}}} } \right)\left( {\prod\limits_{{z,l = 1,z \ne l}}^{3} {p_{{43z}}^{{(k)}} } p_{{43l}}^{{(d)}} } \right)} \right\}} } \right) \\ & \quad = \{ s_{{2.1048}} (0.0001),s_{{2.1624}} (0.0081),s_{{2.1816}} (0.0081),s_{{2.2458}} (0.6561)\} . \\ \end{aligned}$$

Analogously, we can calculate the other collective evaluation values and construct the integrated group decision matrix \(D=(\beta _{ij})_{4 \times 3}=(L_{ij}(p_{ij}))_{4 \times 3}\). With respect to each criterion, we normalize the evaluation with PLTSs of the matrix D by using the result of Definition 10. On the basis of (16) and the integrated decision matrix D, we then identify the positive ideal solution \(x^{+}=(\beta _{1}, \beta _{2}, \beta _{3})\). With respect to (17), we compute the deviation degree between the alternative and the positive ideal solution under the each criterion. The result is shown in Table 4.

Table 4 The deviation degree between the alternative and the positive ideal solution under the each criterion
Full size table

From Table 4, the row denotes the alternative and the column represents the deviation degree. Suppose that the identification coefficient \(\rho\) is 0.5. In light of (17)–(18), we calculate the grey relational coefficient of each alternative with each criterion, see Table 5.

Table 5 The grey relational coefficient of each alternative with each criterion
Full size table

Based on (19) and the weight vector of the criteria, we further compute the degree of grey relational coefficient for each alternative. The result is shown in Table 6.

Table 6 The degree of grey relational coefficient for each alternative
Full size table

In accordance with the results of Table 6, we finally rank the alternatives, that is, \(x_2>x_1>x_3 >x_4\). Therefore, the best candidate is \(x_2\).

5.2 Comparison Analysis and Discussion

Based on the multi-attribute group decision-making with PLTSs, Pang et al. [19] developed an extended TOPSIS method. On the basis of the evaluations of four hospitals of Tables 1, 2, and 3, we compute the decision results by this method and compare it with our proposed method. The decision results of different methods are shown in Table 7.

Table 7 The decision results of different methods
Full size table

From Table 7, we can find the rank result of the method proposed in Ref. [19] is: \(x_2>x_3>x_4 >x_1\). Compared with the decision results of our proposed method, the extended TOPSIS with PLTSs can select the same best candidate, i.e. \(x_2\). However, the desirable advantages of our proposed method are summarized as follows: (1) it not only involves the probabilistic information, but also considers the interrelationship of the individual evaluation; (2) it utilizes the subscript-symmetric additive linguistic term set, which is more convincing in the calculation process [8]. (3) Our proposed method measures the relationship between the alternative and two reference points. Thus, our proposed method takes the decision information into account as much as possible.

6 Conclusions

Considering the interrelationship between input arguments with PLTSs, we extend the GBM to the probabilistic linguistic environment. In this paper, we develop the PLGBM and WPLGBM operators, respectively. Based on the PLMCGDM problems, we present a new extension of the grey relational analysis method and design the corresponding approach for the application by employing the WPLGBM. By introducing GBM, this paper expands the applied field of PLTSs and designs the corresponding aggregation operators. In addition, we improve the grey relational analysis method and GBM to make them adapt to the new probabilistic linguistic environment. Our proposed method can be useful in dealing with many operational research problems in the qualitative assessment, such as the selection of project investments and the evaluation of P2P platform. Future research work may focus on developing some new generalized aggregation operators of PLTSs in the complex decision scenarios.