Exponential Stability and Asynchronous Stabilization of Nonlinear Impulsive Switched Systems via Switching Fuzzy Lyapunov Function Approach

Abstract

In this paper, the Takagi–Sugeno (T-S) fuzzy model is first used to deal with the exponential stability and asynchronous stabilization problem of a class of continuous-time nonlinear impulsive switched systems with asynchronous behaviors. In order to reduce the conservativeness resulting from the quadratic Lyapunov functions (QLFs) and nonlinearity, the switching fuzzy Lyapunov functions (FLFs) are proposed using the switching information and structural information of membership function in the rule base. Using the switching FLFs approach and the mode-dependent average dwell time (MDADT) technique, we obtain stability conditions for the open-loop nonlinear impulsive switched systems and stabilization conditions for the closed-loop nonlinear impulsive switched systems. Moreover, the stability and stabilization results are formulated in the form of LMIs. Finally, a numerical example and a chemical process example are given to demonstrate the advantage and applicability of the proposed method.

1 Introduction

Switched systems are an important class of hybrid systems encountered in numerous practical circumstances. The stability problem is a main concern in the field of switched systems [1–6]. Up to now, two stability issues have been addressed in the literature, i.e., the stability under arbitrary switching and the stability under constrained switching. As for the arbitrary switching issue, the study is mainly based on a common Lyapunov function for all subsystems [1, 6]. As for the constrained switching issue, the multiple Lyapunov functions play an important role in the stability analysis [7–9]. As one typical example of the constrained switching, the average dwell time (ADT) logic is proposed in [3]. The ADT is widely used to investigate the problems of stability and stabilization of switched systems [10–12]. However, most works assumed that the ADT is independent of the system models. Thus, the acquired results have more or less conservativeness compared with the case if the ADT can be extended to the mode-dependent average dwell time (MDADT) [13]. Recently several, though not many, works have studied the control problem for switched systems with MDADT [14, 15].

It is well known that many practical systems exhibit impulsive dynamical behaviors because of sudden changes at certain instants during the dynamical process. The switched systems with impulsive effect can be modeled as impulsive switched systems [16]. Due to the existence of the impulsive effect, the traditional pure continuous or pure discrete models cannot well describe these systems, so it is important and necessary for us to study the impulsive switched systems. As for such systems, some useful results on stability and stabilization have been achieved [16–18].

In this paper, we are interested in investigating the asynchronous stabilization problem of nonlinear impulsive switched systems. As is well known, due to the existence of nonlinearity, it is difficult to analyze the nonlinear systems directly. The T-S fuzzy model is proven to be an effective tool in approximating most complex nonlinear systems [19], which utilizes local linear system description for each rule. The issue of stability and controller synthesis of T-S fuzzy systems has been studied extensively [20–28]. Similar to [27, 28], we use the T-S fuzzy model to represent each nonlinear subsystem of nonlinear impulsive switched systems in this paper.

It is well known that the results based on a common quadratic Lyapunov function might be conservative. By taking into consideration the information of membership functions, the authors in [29] presented the fuzzy Lyapunov functions (FLFs) which are defined by fuzzily blending multiple quadratic Lyapunov functions (QLFs). Stability analysis and controller synthesis results based on FLFs can be seen in [29–31]. The FLFs method only needs to search for a local common positive matrix in fuzzy model. In this paper, we investigate the nonlinear impulsive switched systems by employing the T-S fuzzy model. The switching FLFs are proposed using the switching information and structural information of membership function in the rule base. The candidate Lyapunov function is switching according to the system switching among several FLFs, which is based on premise membership functions to reduce conservativeness introduced by nonlinearity. Due to the above advantages, we consider nonlinear impulsive switched systems based on switching FLFs method.

In practice, when the systems are switching among the subsystems, the switching of the matched controller of each subsystem has a lag to the switching of the corresponding subsystem, which results in asynchronous switching in the switched systems. The asynchronous behaviors usually bring unsatisfactory performance or even make the switched systems out of control. Recently, several works have explored the effect of asynchronous behaviors on the switched systems [11, 12, 15, 32].

To the best of our knowledge, there is very little work on the use of the T-S fuzzy model to study the nonlinear impulsive switched systems, not to mention the nonlinear impulsive switched systems with asynchronous behaviors. In this paper, we fully considered the effects of various factors on the systems and used the T-S fuzzy model to study the nonlinear impulsive switched systems with asynchronous behaviors. Furthermore, the results obtained in this paper can also apply to the nonlinear switched systems without impulsive behaviors or asynchronous switching.

The main contributions of this paper are as follows: (i) The previous work studied the asynchronous switching problem mainly focused on the switched linear systems. In our work, the T-S fuzzy model is first used to study the nonlinear impulsive switched systems with asynchronous switching. (ii) In order to further reduce the conservativeness resulting from the nonlinearity and the quadratic Lyapunov functions approach, the switching fuzzy Lyapunov functions approach is proposed, and this approach can also be applied to study other nonlinear switched systems. (iii) The case $\beta _p < 0$ is also considered in this paper, which means that the Lyapunov functions can still decrease in the asynchronous state, so the results obtained in this paper can be much looser compared with the results in [11].

The remainder of the paper is organized as follows: System descriptions and preliminaries are presented in Sect. 2. The main results are given in Sect. 3. In Sect. 4, a numerical example and a chemical process example are presented. Finally, some conclusions are obtained in Sect. 5.

Notations: The notations used in this paper are fairly standard. N and N ⁺ denote the set of the natural numbers and the set of positive integers, respectively. I represents the identity matrix. The symbol “*” in a matrix stands for the transposed elements in the symmetric positions. The superscript “T” is the matrix transposition. R ⁿ denotes the n-dimensional Euclidean space. The notation $\left\| {\;}\cdot {\;} \right\|$ refers to the Euclidean vector norm. ${\mathcal{C}}^1$ denotes the space of continuously differentiable functions. ${L_2}[0,\infty )$ is the space of square-integrable, and for $v(t) \in {L_2}[0,\infty )$ its norm is given by ${\left\| {v(t)} \right\| _2} = \sqrt{\int _0^\infty {v{{(t)}^T}v(t)dt}}$. We use $P > 0\, ( \ge , < , \le )$ to denote a positive definite (semi-positive definite, negative definite, semi-negative definite) matrix P. We use ${\lambda _{\max }}(P)$ and ${\lambda _{\min }}(P)$, respectively, to denote the maximum and minimum eigenvalues of P. If not explicitly stated, matrices are assumed to have compatible dimensions. Throughout this paper, $(p, q) \in S \times S$, $p \ne q$, and $(m, n, u, v) \in \left\{ 1,2, \ldots , k\right\}$.

2 System Descriptions and Preliminaries

In this paper, let us consider the following class of nonlinear impulsive switched systems:

$$\left\{ \begin{array}{ll} \dot{x}(t) = {f_{\sigma (t_i)}}(x(t),u(t)), &\quad t \ne {t_i} \\ \Delta x(t) = {D_{\sigma (t_i)}}x(t) + g(t,x(t)), &\quad t = {t_i} \\ x(t_0^ + ) = {x_0} \end{array} \right.,$$

(1)

where $x(t) \in R^{n}$ and $u(t) \in R^{m}$ denote the state vector and input vector, respectively. $D_{\sigma (t_i)}$ is a known matrix. $f_{\sigma (t)}$ and $g(t, x(t))$ are nonlinear functions, and $g(t,0) \equiv 0$ for all $t \in \left[ {{t_0},\infty } \right)$. $\sigma (t)$ is defined as a switching signal, which is a piecewise constant function of time and takes its values in the finite set $S = \left\{ 1, 2,\ldots , M\right\}$, where M is the number of subsystems. For a switching sequence $0 < {t_0} < {t_1} < \cdots < {t_i} < {t_{i + 1}} < \cdots$, $\sigma (t)$ is continuous from right everywhere. When $t \in [{t_i},{t_{i + 1}})$, we say that the $\sigma (t_i)$ subsystem is activated, and $\sigma (t_i) = p$, $p \in S$. $\Delta x(t_i) = x(t_i^+) - x(t_i^-) = x(t_i^+) - x({t_i})$, with $x(t_i^+) = \mathop{\lim }\limits _{\;\;h \rightarrow {0^+}} x({t_i} + h)$, $x(t_i^-) = \mathop {\lim }\limits _{\;\;h \rightarrow {0^-}} x({t_i} + h)=x(t_i)$, meaning that the solution of the nonlinear impulsive switched systems (1) is left continuous. This implies that the impulses will affect the state x(t) at the switching instant.

The T-S fuzzy model which is described by fuzzy IF-THEN rules [19] is employed here to represent each subsystem of systems (1). By introducing the T-S fuzzy model, the subsystem p of the nonlinear impulse switched systems (1) is described in the following form:

Rule m for the subsystem p: IF $z_{p1}(t)$ is $M_{p1m}$ and $\cdot \cdot \cdot$ and $z_{pg}(t)$ is $M_{pgm}$, THEN

$$\left\{{\begin{array}{ll} \dot{x}(t) = A_{pm}x(t) + B_{pm}u(t), &\quad t \ne t_i \\ \Delta x(t) = {D_p}x(t) + g(t,x(t)), &\quad t = t_i \\ x(t_0^ + ) = x_0 \end{array}}\right.,$$

(2)

where $z_{pl}(t)$ are some measurable premise variables and $M_{plm}$ are fuzzy sets $(l=1, 2, \ldots , g)$. $A_{pm}$ and $B_{pm}$ are constant real matrices of the mth local model of the pth subsystem.

Using “fuzzy blending”, the final output of the pth subsystem is inferred as follows:

$$\left\{ {\begin{array}{ll}\dot{x}(t)= \sum \limits_{m = 1}^{k} h_{pm}(t) [A_{pm}x(t) + B_{pm}u(t)], &\quad t \ne {t_i} \\ \Delta x(t) = {D_p}x(t) + g(t,x(t)), &\quad t = {t_i} \\ x(t_0^ + ) = x_0 \end{array}} \right.,$$

(3)

where $h_{pm}(t) = w_{pm}(t)/ \sum \limits _{m = 1}^{k} w_{pm}(t), w_{pm}(t) = \prod \limits _{l = 1}^g M_{plm}(z_{pl}(t))$, k is the number of IF-THEN rules, and $M_{plm}(z_{pl}(t))$ is the grade of the membership function of $z_{pl}$ in $M_{plm}$. It is assumed that $w_{pm}(t) \ge 0$ for all t, $m = 1, 2, \ldots , k$. Therefore, the normalized membership function $h_{pm}(t)$ satisfies

$$h_{pm}(t) \ge 0, \quad \sum \limits _{m = 1}^{k} h_{pm}(t) = 1.$$

(4)

In this paper, we design a fuzzy controller for the system (3) via parallel distributed compensation (PDC) [20]. In the PDC design, the designed fuzzy controller shares the same premise variables with the fuzzy model (3). In view of the asynchronous behaviors, the controller u(t) is divided into two parts $\bar{u}(t)$ and $\hat{u}(t)$, where $\bar{u}(t)$ denotes the unmatched controller, and $\hat{u}(t)$ represents the matched controller. For the fuzzy model (3), we can construct the following fuzzy controller via the PDC:

$$\left\{ \begin{array}{ll} \bar{u}(t) = \sum \limits _{n = 1}^{k} h_{qn}(t) K_{qn}x(t), &\quad t \in (t_i, {\bar{t}}_i] \\ \hat{u}(t) = \sum \limits _{n = 1}^{k} h_{pn}(t) K_{pn}x(t), &\quad t \in ({\bar{t}}_i, t_{i + 1}] \end{array} \right.,$$

(5)

where notation $\bar{t}_i$ (${t_i} \le {\bar{t}_i} < {t_{i + 1}}$) denotes the starting-operating instant of the matched controller, and $K_{qn}$ and $K_{pn}$ are constant matrices. Substituting (5) into (3), we can obtain the following closed-loop nonlinear impulsive switched system:

$$\left\{ \begin{array}{ll} \dot{x}(t) = \bar{A}_p(t)x(t),&\quad t \in ({t_i},{{\bar{t}}_i}] \\ \dot{x}(t) = \hat{A}_p(t)x(t),&\quad t \in ({{\bar{t}}_i},{t_{i + 1}}] \\ \Delta x(t) = {D_p}x(t) + g(t,x(t)),&\quad t = {t_i} \\ x(t_0^ + ) = {x_0} \end{array} \right.,$$

(6)

where the $\bar{A}_p(t)$ and $\hat{A}_p(t)$ are defined as follows:

$$\begin{aligned}\bar{A}_p(t) &= A_p(t) + B_p(t)K_q(t)\\ &= \sum \limits _{m = 1}^{k} \sum \limits _{n = 1}^{k} {h_{pm}(t)h_{qn}(t)}(A_{pm} + B_{pm}K_{qn}), \\ \hat{A}_p(t) &= A_p(t) + B_p(t)K_p(t)\\ &= \sum \limits _{m = 1}^{k} \sum \limits _{n = 1}^{k} {h_{pm}(t)h_{pn}(t)}(A_{pm} + B_{pm}K_{pn}). \end{aligned}$$

We assume that there is no impulsive and asynchronous effects at the initial instant.

Now, we introduce the following assumptions, definitions and lemmas, which are useful in the following derivation.

Assumption 1

Let the nonlinear function $g(t, x(t))$ satisfy the following inequality:

$$\left\| {g(t,x(t))} \right\| \le {\eta }\left\| {x(t)} \right\|$$

for all $t \in \left[ {{t_0},\infty } \right)$, where ${\eta }$ is a positive constant.

Definition 1

Suppose that a switching signal $\sigma (t)$ is given. The nonlinear impulsive switched systems (1) with $u(t) \equiv 0$ are exponentially stable under the switching signal $\sigma (t)$ if for any initial conditions $x(t_0)$

$$\Vert x(t)\Vert \le \Gamma \Vert x(t_0)\Vert e^{-\gamma (t - t_0)}, \quad \forall t \ge t_0,$$

where $\Gamma > 0$ and $\gamma > 0$ are constants.

Definition 2

[13] For switching signal $\sigma (t)$ and each $T \ge t \ge 0$. Let $N_{\sigma _p}(T,t)$ be the switching numbers such that the pth subsystem is activated over the interval [t, T], and $T_p(T,t)$ denotes the total running time of the pth subsystem over the interval [t, T], $\forall p\in S$. We say that $\sigma (t)$ has a mode-dependent average dwell time (MDADT) $T_{ap}$ if there exist positive numbers $N_{0p}$ ($N_{0p}$ denotes mode-dependent chatter bounds here) and $T_{ap}$ such that

$$N_{\sigma _p}(T,t) \le N_{0p} + T_p(T,t)/T _{ap}, \quad \forall T \ge t \ge 0.$$

Definition 3

[29] Equation (7) is said to be a fuzzy Lyapunov function for the pth subsystem of the T-S fuzzy system (3) if there exists a positive definite matrix $P_{pu}$ and the time derivative of $V_p(x(t))$ is always negative at $x(t) \ne 0$.

$$V_p (x(t)) = x(t)^T P_{p}(t)x(t),$$

(7)

where $P_p(t) = \sum \nolimits _{u=1}^{k} h_{pu}(t) P_{pu}$ and $\dot{P}_p(t) = \sum \nolimits _{u=1}^{k} \dot{h}_{pu}(t) P_{pu}$.

Lemma 1

[33] Let $P \in {R^{n \times n}}$ be a given symmetric positive definite matrix and let $Q \in {R^{n \times n}}$ be a given symmetric matrix. Then

$${\lambda _{\min }}({P^{ - 1}}Q)\Omega (t) \le x{(t)^T}Qx(t) \le {\lambda _{\max }}({P^{ - 1}}Q)\Omega (t)$$

for all $x(t) \in {R^{n}}$, where $\Omega (t)\; = x{(t)^T}Px(t)$, ${\lambda _{\max }}( \cdot )$ and ${\lambda _{\min }}( \cdot )$ denote, respectively, the largest and the smallest eigenvalues of the matrix inside the brackets.

Lemma 2

[34] Given matrices M, E, and F with compatible dimensions and F satisfying ${F^T}F \le I$, the following inequality holds for any $\varepsilon > 0$:

$$MFE + {E^T}{F^T}{M^T} \le \varepsilon M{M^T} + {\varepsilon ^{ - 1}}{E^T}E.$$

3 Main Results

In this paper, to deal with the asynchronous switching of switched systems, the Lyapunov function is allowed to increase with a bounded rate. Here, the parameter $\alpha _p$ represents the decaying rate of the Lyapunov function, which corresponds to the convergence rate of the system in synchronous state. And the parameter $\beta _p$ denotes the increasing rate of the Lyapunov function, which corresponds to the divergence rate of the system in asynchronous state. In a sense, the purpose of controller design is to design the appropriate $\alpha _p$ and $\beta _p$ parameters to make the systems reach the desired control performance.

For concise notation, let $T({t_{i + 1}},{t_i}) = {t_{i + 1}} - {t_i}$ represent the length of the running time interval of each subsystem. By (6), we can see that $T({t_{i + 1}},{t_i})$ is divided into two parts, ${T_{ \uparrow }}({t_i},{t_{i + 1}})$ and ${T_ \downarrow }({t_i},{t_{i + 1}})$, where ${T_ \uparrow }({t_{i + 1}},{t_i}) = {{\bar{t}}_i} - {t_i}$ and ${T_ \downarrow }({t_{i + 1}},{t_i}) = {t_{i + 1}} - {{\bar{t}}_i}$. During ${T_{ \uparrow }}({t_i},{t_{i + 1}})$ the Lyapunov function may increase or decrease, which represents the running time of the unmatched controllers in $({t_i},{t_{i + 1}}]$, while during ${T_ \downarrow }({t_i},{t_{i + 1}})$ the Lyapunov function is strictly decreasing with the matched controllers.

For brevity, we introduce the following notations: $\sigma _i = \sigma (t_i)$ and

$$\begin{aligned}{Q_p} &= {(I + {D_p})^T}{\left( \sum \limits _{m = 1}^{k}P_{pm}\right) }(I + {D_p}) + \left( \frac{\eta }{\varepsilon } + \eta \lambda _{\max } \left( \sum \limits _{m = 1}^{k}P_{pm}\right) \right) I \\ &\quad+ \varepsilon {(I + {D_p})^T}{\left( \sum \limits _{m = 1}^{k}P_{pm}\right) }{\left( \sum \limits _{m = 1}^{k}P_{pm}\right) }(I + {D_p}), \end{aligned},$$

where the parameters $\eta$ and $\varepsilon$ are given in assumption 1 and lemma 2. The parameter $\mu _p$ used in the following lemmas and theorems is ${\mu _p} = \max \limits _q \{{\mu _{qp}},1\}$, $\forall q \in S$, $q \ne p$, with $\mu _{qp} = {\lambda _{\max }}\left( \left( \sum \nolimits _{n = 1}^{k} P_{qn}\right) ^{-1}{Q_p}\right)$.

3.1 Stability Analysis

In this section, we consider the stability analysis problem of the nonlinear impulsive switched systems. Without control input, the open-loop system for (6) is listed as follows:

$$\left\{ {\begin{array}{ll}\dot{x}(t) = \sum \limits _{m = 1}^{k} h_{pm}(t) A_{pm}x(t), &\quad \forall t \in (t_i,t_{i+1}] \\ \Delta x(t) = {D_p}x(t) + g(t,x(t)), &\quad t = {t_i} \\ x(t_0^ + ) = {x_0} \\ \end{array}} \right. .$$

(8)

Lemma 3

Consider the open-loop nonlinear impulsive switched system (8), and let $\eta > 0$, $\varepsilon > 0$, and $\alpha _p < 0$ be given constants. If there exists positive definite ${\mathcal{C}}^1$ function ${V_{\sigma ({t_i})}}:{R^n} \rightarrow R, \sigma ({t_i})\in S$ with $V_{\sigma (t_0)}(x(t_0)) \equiv 0$ satisfying

$${\dot{V}_p}(t) \le \alpha _p {V_p}(t), \quad t \in (t_i, t_{i + 1}],$$

(9)

then the system (8) is exponentially stable for any switching signal satisfying

$$\tau _{op} \ge \tau _{op}^{*} = \frac{\ln {\mu _p}}{-\alpha _p}.$$

(10)

Proof

From definition 3, at the switching instant ${t_i}$, we can obtain

$$\begin{aligned}{V_p}(x(t_i^+)) &= {\left[ {(I + {D_p})x(t_i) + g(t_i, x(t_i))} \right] ^T}{P_p}(t_i)\left[ {(I + {D_p})x(t_i) + g(t_i,x(t_i))} \right] \\&= x{(t_i)^T}{(I + {D_p})^T}{P_p}(t_i)(I + {D_p})x(t_i) \\ &\quad+ 2x{(t_i)^T}{(I + {D_p})^T}{P_p}(t_i)g(t_i) + g{(t_i, x(t_i))^T}{P_p(t_i)} g(t_i, x(t_i)). \\ \end{aligned}$$

Then, by Assumption 1, Lemmas 1 and 2, we have

$$\begin{aligned}{V_p}(x(t_i^+)) &\le x{(t_i )^T}{(I + {D_p})^T}{P_p(t_i)}(I + {D_p})x(t_i) + \varepsilon x{(t_i)^T}{(I + {D_p})^T}{P_p(t_i)}{P_p(t_i)}(I + {D_p})x(t_i)\\ &\quad + \frac{1}{\varepsilon }g(t_i, x(t_i))^T g(t_i, x(t_i)) + \lambda_{\max }({P_p(t_i)})g(t_i, x(t_i))^T g(t_i, x(t_i)) \\ &\le x{(t_i )^T}\left[ {(I + {D_p})^T}\left( \sum \limits _{m = 1}^{k}P_{pm}\right) (I + {D_p})\right.\\ &\left. \quad + \varepsilon {(I + {D_p})^T}\left( \sum \limits _{m = 1}^{k}P_{pm}\right) \left( \sum\limits _{m = 1}^{k}P_{pm}\right) (I + {D_p}) \right. \\&\quad\left. + \left( \frac{\eta }{\varepsilon } + \eta \lambda_{\max }\left( \sum \limits _{m = 1}^{k}P_{pm}\right) \right)\right] x(t_i) \\ &= x{(t_i)^T}{Q_p}x(t_i).\end{aligned}$$

(11)

By Lemma 1 and (11), we have

$${V_p}(x(t_i^+)) \le x{(t_i)^T}{Q_p}x(t_i)\le \lambda _{\max }\left( {P_q^{-1}(t_i)}{Q_p}\right) {V_q}(x(t_i)).$$

(12)

Due to ${P_q^{-1}(t_i)} = \left( \sum \nolimits _{n = 1}^{k} h_{qn}(t_i) P_{qn}\right) ^{-1}$, we can conclude that the inequality (12) holds if the following inequality (13) holds

$${V_p}(x(t_i^+)) \le x{(t_i)^T}{Q_p}x(t_i)\le \lambda _{\max }\left( {\left( \sum \nolimits _{n = 1}^{k} P_{qn}\right) ^{-1}}{Q_p}\right) {V_q}(x(t_i)).$$

(13)

Let ${\mu _p} = \max \limits _q \{{\mu _{qp}},1\}$, $\forall q \in S$, $q \ne p$ with $\mu _{qp} = {\lambda _{\max }}\left( \left( \sum \nolimits _{n = 1}^{k} P_{qn}\right) ^{-1}{Q_p}\right)$, then we get

$${V_p}(x(t_i^+)) \le \mu _p {V_q}(x(t_i)).$$

(14)

By integrating (9) we have

$$V_p(t) \le {e^{\alpha _p (t - t_i )}}V_p(t_i).$$

(15)

Combining (14) and (15), $t \in (t_i, t_{i + 1}]$, we have

$$\begin{aligned}{V_{\sigma _i}}(x(t)) &\le \mu _{\sigma _i} e^{{\alpha _{\sigma _i}}(t-{t_i})}{V_{\sigma _{i-1}}}({x(t_i)}) \\ &\le \mu _{\sigma _i} e^{{\alpha _{\sigma _i}}(t-{t_i}) + {\alpha _{\sigma _{i-1}}}(t_i -{t_{i-1}})}{V_{\sigma _{i-1}}}({x(t_{i-1}^+)}) \\ &\le \cdots \\ &\le \mu _{\sigma _i}\mu _{\sigma _{i-1}}\cdots \mu _{\sigma _1} e^{\alpha _{\sigma _i}(t-{t_i}) + \cdots + \alpha _{\sigma _0}(t_1 -t_0)}{V_{\sigma _0}(x(t_0)}). \end{aligned}$$

From definition 2, let $N_{\sigma _i}$ denote $N_{\sigma _i}(t,t_0)$ for simplicity. The following inequality holds

$$V(t) \le \exp \left\{ \sum \nolimits _{p = 1}^M {N_{\sigma _i} (\alpha _p \tau _{op} + \ln \mu _p)}\right\} V(t_0).$$

If supposing

$$\alpha _p \tau _{op} + \ln \mu _p \le 0,$$

(16)

we obtain a sufficient condition that guarantees the exponential stability of the system (8). The inequality (16) is equivalent to

$${\tau _{op}} \ge \tau _{op}^{*} = \frac{\ln \mu _p }{-\alpha _p}.$$

$\square$

The stability conditions for the system (8) can be summarized in the following theorem.

Theorem 1

Assume that

$$\left| \dot{h}_{ps}(t)\right| \le \varepsilon _{ps}, \quad s = 1,2, \ldots , k,$$

(17)

where $\varepsilon _{ps} \ge 0$. Let $\eta > 0$, $\varepsilon > 0$, and $\alpha _p < 0$ be given constants. The system (8) is exponentially stable for any switching signal satisfying (10), if there exist matrices $P_{pu} > 0$ satisfying

$$P_{pl} \ge P_{pk}, \quad l = 1, 2, \ldots , k-1,$$

(18)

and

$$\Theta _{pmu} + \Theta _{pum} <0, \quad m \le u,$$

(19)

where $\Theta _{pmu} = A_{pm}^T{P_{pu}} + {P_{pu}}A_{pm} + \sum \nolimits _{s = 1}^{k-1}{\varepsilon _{ps}}(P_{ps}-P_{pk}) - {\alpha _p}P_{pu}.$

Proof

Differentiating (4) implies $\dot{h}_{pk}(t) = -\sum \nolimits _{m=1}^{k-1}\dot{h}_{pm}(t)$, so we have

$$\dot{P}_p(t) = \sum \limits _{u=1}^{k-1}\dot{h}_{pu}(t)(P_{pu}-P_{pk}).$$

(20)

Combining (17), (18) with (20) implies

$$\dot{P}_p(t) \le \sum \limits _{u=1}^{k-1}\varepsilon _{pu} (P_{pu}-P_{pk}).$$

(21)

Along with the solution of the system (8), we have

$${{\dot{V}}_p}(t) - {\alpha _p}{V_p}(t) = x(t)^T\left[ A_p(t)^T{P_p}(t) + {P_p}(t){A_p}(t) + {{\dot{P}}_p}(t) - {\alpha _p}{P_p}(t)\right] x(t).$$

Since ${A_p}(t) = \sum \nolimits _{m = 1}^{k} {h_{pm}(t)} A_{pm}$, $P_p(t) = \sum \nolimits _{u = 1}^{k} h_{pu}(t) P_{pu}$ and ${\dot{P}_p}(t) = \sum \nolimits _{s = 1}^{k} {\dot{h}}_{ps}(t) P_{ps}$, then

$${{\dot{V}}_p}(t) - {\alpha _p}{V_p}(t) \le {\sum \limits _{m = 1}^{k} {h_{pm}^2}}(t){x}(t)^T \Theta _{pmm} x(t) + {\sum \limits _{m < u}^{k} {h_{pm}}(t){h_{pu}}(t)} {x}(t)^T \left[ \Theta _{pmu} + \Theta _{pum} \right] x(t).$$

From (19) we can conclude that

$${\dot{V}_p}(t) - {\alpha _p}{V_p}(t) \le 0.$$

So the system (8) is exponentially stable for any switching signal satisfying (10). This completes the proof. $\square$

Remark 1

By setting $P_{pu} = P_p$, we get Corollary 1 where the QLFs are used. Compared with the QLFs method, the computational complexity of the results based on the FLFs method will be greater. But the results based on the FLFs method have less conservativeness than the results based on the QLFs method.

Corollary 1

Let $\eta > 0$, $\varepsilon > 0$, and $\alpha _p < 0$ be given constants. The system (8) is exponentially stable for any switching signal satisfying (10), if there exist matrices $P_p > 0$ satisfying

$$A_{pm}^T{P_p} + {P_p}A_{pm} - \alpha _p{P_p} \le 0.$$

(22)

Proof

The proof is similar to that of Theorem 1, with the function $V_p(t)$ given by

$${V_p}(t) = {x}(t)^T{P_p}x(t).$$

It is omitted here. $\square$

3.2 Controller design

In this section, our objective is to design a set of model-dependent controllers and find a set of admissible switching signal such that the closed-loop nonlinear impulsive switched system (6) is exponentially stable with asynchronous switching.

Lemma 4

Consider the closed-loop nonlinear impulsive switched system (6), and let $\eta > 0$, $\varepsilon > 0$, $\alpha _p < 0$ and $\beta _p$ be given constants. If there exists positive definite ${\mathcal{C}}^1$ function ${V_{\sigma ({t_i})}}:{R^n} \rightarrow R, \sigma ({t_i})\in S$ with $V_{\sigma (t_0)}(x(t_0)) \equiv 0$ satisfying

$${{\dot{V}}_p}(t) \le \left\{ \begin{array}{l} \beta _p {V_p}(t), \quad t \in {T_ \uparrow }({t_i},{t_{i + 1}}) \\ \alpha _p {V_p}(t), \quad t \in {T_ \downarrow }({t_i},{t_{i + 1}}) \end{array} \right. ,$$

(23)

then the system is exponentially stable for any switching signal satisfying

$$\left\{\begin{array}{ll} \tau_{p} \ge \tau_{p}^{\ast} =\frac{\ln{\mu_{p}}}{-\alpha_{p}}, &\beta_{p} < \alpha_{p}\\ \tau_{p} \ge \tau_{p}^{*} = \frac{T_{pM}(\beta_{p} -\alpha_{p}) + \ln {\mu_{p}}}{-\alpha_{p}}, &\beta_{p} \ge\alpha_{p} \end{array} \right.,$$

(24)

where $T_{{p}M} \buildrel \Delta \over = \max T_{p\uparrow }(t_{i+1},t_i), \forall i \in N^+$.

Proof

Let ${S_1} = \{0, 1, \ldots ,{r}\}$, ${S_2} = \{ r+1, \ldots ,{M}\}$, $r \ge 0$. Now based on the value of ${\beta _p}$, all the subsystems are divided into two parts. If the unmatched controller can stabilize the current subsystem, i.e., $\beta _p < 0$, then the subsystem is contained in set ${S_1}$, otherwise, it is contained in set ${S_2}$. For any $T > 0$, let ${t_0} = 0$ and denote the switching times on the interval [0, T] as ${t_1},{t_2}, \ldots {t_i},{t_{i + 1}},\ldots {t_{{N_\sigma }(T,0)}}$, then

$${N_\sigma }(T,0) = \sum \nolimits _{p = 1}^{r} {N_p}(T,0) + \sum \nolimits _{p = r+1}^{M} {N_p}(T,0).$$

Let ${T_{p \downarrow }}(T,0)$ denote the total running time of the pth subsystem controlled by the matched controller and ${T_{p \uparrow }}(T,0)$ denote the total running time of the pth subsystem controlled by the unmatched controller. We get ${T_p}(T,0) = {T_{p \downarrow }}(T,0) + {T_{p \uparrow }}(T,0)$.

Since $T_{{p}M} \buildrel \Delta \over = \max T_{p\uparrow }(t_{i+1},t_i)$, by Definition 2, we have

$${T_{{p} \uparrow }}(T,0) \le {T_{{p}M}}{N_{{p}}}(T,0) \le {T_{{p}M}}\left({N_{0p}} + \frac{{{T_{p}}(T,0)}}{{{\tau _{p}}}}\right).$$

(25)

By integrating (23) and together with (14) for $t \in ({t_i},{t_{i + 1}}]$, we have

$$\begin{aligned}{V_{\sigma _i}}(x(t)) \\ &\le {e^{{\alpha_{\sigma _i}}{T_ \downarrow }(t,{t_i}) + {\beta _{\sigma _i}}{T_\uparrow }(t,{t_i})}}{\mu _{\sigma _i}}{V_{\sigma_{i-1}}}({x(t_i)}) \\ &\le \exp \{ {\alpha _{\sigma _i}}{T_\downarrow }(t,{t_i}) + {\beta _{\sigma _i}}{T_ \uparrow}(t,{t_i})+ {\alpha _{\sigma _{i-1}}}{T_ \downarrow }({t_i},{t_{i- 1}})+ {\beta _{\sigma _{i-1}}}{T_ \uparrow }({t_i},{t_{i -1}})\} {\mu _{\sigma _i}}{V_{\sigma _{i-1}}}\left(x\left(t_{i -1}^+\right)\right)\\ &\le \cdots \\ &\le \prod \limits _{n = 1}^i {{\mu _{{\sigma_n}}}\exp \left\{ {{\alpha _{{\sigma _i}}}{T_ \downarrow}(t,{t_i}) + \beta _{\sigma _i}{T_ \uparrow }(t,{t_i}) + \sum\limits _{n = 1}^i {{\alpha _{{\sigma _{n - 1}}}}{T_ \downarrow}({t_n},{t_{n - 1}})}} \right. }\\ &\left.\quad+ {\sum \limits _{n= 2}^i {{\beta _{\sigma _{n - 1}}}{T_ \uparrow }({t_n},{t_{n -1}})} } \right\} {V_{\sigma _0}}(x(t_0)) \\ &= \prod \limits _{p =1}^M \mu _p^{{N_p}(T,0)} \exp \left\{ \sum \limits _{p = 1}^M{\left[ \alpha _p{T_{p\downarrow }}(T,0) + \beta _p{T_{p\uparrow}}(T,0) \right] }\right\} V_{\sigma _0}(x(t_0)) \\ &= {\Omega_1}{\Omega _2}{V_{\sigma _0}}(x(t_0)),\end{aligned},$$

(26)

where

$${\Omega _1} = \prod \limits _{p = 1}^r {\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = 1}^r {\left[ {{\alpha _p}{T_{p \downarrow }}(T,0) + {\beta _p}{T_{p\uparrow }}(T,0)} \right] }}\right\} ,$$

$${\Omega _2} = \prod \limits _{p = r + 1}^M {\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = r + 1}^M {\left[ {{\alpha _p}{T_{p \downarrow }}(T,0) + {\beta _p}{T_{p\uparrow }} (T,0)}\right] }}\right\} .$$

As for ${\Omega _1}$, we introduce the following notations:

$${\Omega _{11}} = \prod \limits _{p = 1}^{{r_1}}{\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = 1}^{{r_1}}{\left[ {{\alpha _p}{T_{p \downarrow }}(T,0) + {\beta _p} {T_{p \uparrow }}(T,0)}\right] }}\right\} ,$$

where ${\beta _p} < {\alpha _p}$, $0 \le {r_1} \le r$;

$${\Omega _{12}} = \prod \limits _{p = {r_1} + 1}^r {\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = {r_1} + 1}^r{\left[ {{\alpha _p}{T_{p \downarrow }}(T,0) + {\beta _p} {T_{p \uparrow }}(T,0)} \right] } } \right\},$$

where ${\alpha _p} \le {\beta _p} \le 0$, $0 \le {r_1} \le r$.

As for $\Omega _{11}$, we have

$$\begin{aligned} {\Omega _{11}}&\le \prod \limits _{p = 1}^{{r_1}}{\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = 1}^{{r_1}}{\left[ {{\alpha _p}{T_{p\downarrow }}(T,0) + {\alpha _p}{T_{p \uparrow }} (T,0)} \right] } } \right\} \nonumber \\&= \exp \left\{ {\sum \limits _{p = 1}^{{r_1}} {\left[ {{N_{p}}(T,0)\ln {\mu _p} + {\alpha _p}{T_p}(T,0)} \right] } } \right\} \nonumber \\&\le \exp \left\{ {\sum \limits _{p = 1}^{{r_1}} {\left[ {{N_{0p}}\ln {\mu _p} + {T_p}(T,0)({\alpha _p} + \frac{{\ln {\mu _p}}}{{{\tau _p}}})} \right] } } \right\} \nonumber \\&= {\hat{\Omega }}_{11} \end{aligned}$$

(27)

As for $\Omega _{12}$, we get

$$\begin{aligned} \Omega _{12}&= \prod \limits _{p = {r_1} + 1}^r {\mu _p^{{N_p}(T,0)}} \exp \left\{ {\sum \limits _{p = {r_1} + 1}^r {\left[ {{\alpha _p}{T_p}(T,0) + (-{\alpha _p} + {\beta _p}) {T_{p \uparrow }}(T,0)} \right] }} \right\} \nonumber \\&= \exp \left\{ \sum \limits _{p = {r_1} + 1}^r {\left[ {{N_p}(T,0)\ln {\mu _p} + {\alpha _p}{T_p}(T,0) + (-{\alpha _p} + {\beta _p}){T_{p \uparrow }}(T,0)} \right] }\right\} \nonumber \\&\le \exp \left\{ \sum \limits _{p = {r_1} + 1}^r {\left[ {{N_{0p}}\ln {\mu _p} + {\alpha _p}{T_p}(T,0) + (-{\alpha _p} + {\beta _p}){T_{p \uparrow }}(T,0) + \frac{T_p(T,0) \ln {\mu _p}}{\tau _p}} \right] }\right\} . \end{aligned}$$

(28)

Substituting (25) into (28), we have

$$\begin{aligned} \Omega _{12} &\le \exp \left\{ {\sum \limits _{p = {r_1} + 1}^r {\left[ {{N_{0p}}\left( {\ln {\mu _p} +{T_{pM}}(-{\alpha _p} + {\beta _p})} \right) +\,{T_p}(T,0)\left({\alpha _p} + \frac{\ln {\mu _p}}{\tau _p}\right)}\right. } } \right. \\ &\quad\left. {\left.+ {(-{\alpha _p} +{\beta _p}){T_{pM}}\frac{{T_p}(T,0)}{\tau _p}} \right] } \right\}= {\hat{\Omega }_{12}}. \end{aligned}$$

(29)

Combining (27) and (29), we can obtain

$${{\Omega _1} = {\Omega _{11}}{\Omega _{12}} \le {{\hat{\Omega }}_{11}}{{\hat{\Omega }}_{12}}}.$$

(30)

As for ${\Omega _2}$, similar to the derivations of (28) and (29), and letting

$$\begin{aligned} \hat{\Omega }_{2} = \exp \left\{ \sum \limits _{p = {r} + 1}^M {\left[ {{N_{0p}}\left( {\ln {\mu _p} + {T_{pM}}( - {\alpha _p} + {\beta _p})} \right) + {T_p}(T,0)({\alpha _p} + \frac{{\ln {\mu _p}}}{{{\tau _p}}}) + } {(-{\alpha _p} + {\beta _p}){T_{pM}}\frac{{{T_p}(T,0)}}{{{\tau _p}}}} \right] } \right\} , \end{aligned}$$

we have

$${\Omega _2} \le {{\hat{\Omega }}_2}.$$

(31)

By (26), (30), and (31), we have

$$\begin{aligned} V_{\sigma _i}(x(t)) &\le {{\hat{\Omega}}_{11}}{{\hat{\Omega }}_{12}}{{\hat{\Omega }}_2}{V_{\sigma_0}}(x(t_0))\\ &=\exp \left\{ \sum \limits _{p = 1}^{r_1}N_{0p}\ln{\mu _p} + \sum \limits _{p={r_1}+1}^M \left[ N_{0p}\left( \ln \mu_p + T_{pM}(-\alpha _p + \beta _p)\right) \right] \right\} \\&\quad \times \exp \left\{ \sum \limits _{p = 1}^{r_1}\left[T_p(T,0)\left( \alpha _p + \displaystyle \frac{\ln \mu _p}{\tau_p}\right) \right] + \sum \limits _{p = r_1+1}^{M}\left[T_p(T,0)\left( \alpha _p + \displaystyle \frac{\ln \mu _p}{\tau_p}\right) \right. \right. \\ &\quad+\left. \left. (-\alpha _p +\beta _p)T_{pM} \displaystyle \frac{T_p(T,0)}{\tau _p}\right]\right\} {V_{\sigma _0}}(x(t_0)). \end{aligned}$$

(32)

If (24) holds, we conclude that ${V_{\sigma _i}}(x(t))$ converges to zero as $T \rightarrow \infty$. Let

$$\Gamma _1 = \exp \left\{ \sum \limits _{p = 1}^{r_1}N_{0p}\ln {\mu _p} + \sum \limits _{p={r_1}+1}^M \left[ N_{0p}\left( \ln {\mu _p} + T_{pM}(-{\alpha _p} + {\beta _p})\right) \right] \right\}$$

(33)

and

$$\begin{aligned} -\gamma _1 = \max \left\{ \max \limits _{p\in \{1,\ldots ,r_1\}}\left\{ \alpha _p + \frac{\ln \mu _p}{\tau _p}\right\} , \max \limits _{p\in \{r_1+1,\ldots ,M\}} \left\{ \alpha _p + \frac{\ln \mu _p}{\tau _p} + \frac{(-\alpha _p + \beta _p)T_{pM}}{\tau _p}\right\} \right\} . \end{aligned}$$

(34)

By (32)–(34), we have

$${V_{\sigma _i}}(x(t)) \le \Gamma _1 e^{-\gamma _1 t}{V_{\sigma _0}}(x(t_0)).$$

(35)

Letting $\gamma = \gamma _1/2$ and $\Gamma = \Gamma _1^{1/2}\left[ \min _{p \in S}\left\{ \lambda _{\min }\left( \sum \limits _{m = 1}^{k}P_{pm}\right) \right\} \right] ^{-\frac{1}{2}}\left[ \max _{p \in S}\left\{ \lambda _{\max }\left( \sum \limits _{m = 1}^{k}P_{pm}\right) \right\} \right] ^{\frac{1}{2}}$, by Lemma 1 and together with (35), we get

$$\Vert x(t)\Vert \le \Gamma e^{-\gamma t}\Vert x(t_0)\Vert.$$

By Definition 1, we can conclude that the system is exponentially stable for any switching signal satisfying (24). This completes the proof. $\square$

Remark 2

Although the main method in the proof of Lemma 4 is literally similar to that of [32], there is an essential difference between these two methods. The Lyapunov function $V_p(x(t))$ in [32] is $V_p(x(t)) = x(t)^T P_p x(t)$, which is a quadratic form. However, the Lyapunov function used in our work is a fuzzy Lyapunov function to treat the nonlinearity, which is given by $V_p(x(t)) = x^T(t)P_{p}(t)x(t)$, where $P_p(t) = \sum \nolimits _{m=1}^{k} h_{pm}(t) P_{pm}$. Moreover, we will show that the quadratic Lyapunov function is a special case of the fuzzy Lyapunov function.

Lemma 5

Let $\eta > 0$, $\varepsilon > 0$, $\alpha _p < 0$ and $\beta _p$ be given constants. The closed-loop nonlinear impulsive switched system (6) is exponentially stable for any switching signal satisfying (24), if there exist matrices $P_p(t) > 0$ satisfying

$${P_p}(t){\bar{A}_p}(t) + {\bar{A}_p}^T(t){P_p}(t) + {\dot{P}_p}(t) - {\beta _p}{P_p}(t) < 0,$$

(36)

$${P_p}(t){\hat{A}_p}(t) + {\hat{A}_p}^T(t){P_p}(t) + {\dot{P}_p}(t) - {\alpha _p}{P_p}(t) < 0.$$

(37)

Proof

Suppose pth subsystem is activated and the former one is qth subsystem. Considering $t \in {T_ \uparrow }(t_i,t_{i + 1})$, from the system (6) and definition 3, we have

$${\dot{V}_p}(t) - {\beta _p}V_p(t) = x(t)^T \left[ {P_p}(t){\bar{A}_p}(t) + {\bar{A}_p}^T(t){P_p}(t) + {\dot{P}_p}(t) - {\beta _p}{P_p}(t)\right] x(t).$$

(38)

Similarly, for $t \in {T_ \downarrow }(t_i,t_{i + 1})$, we obtain

$${\dot{V}_p}(t) - {\alpha _p}V_p(t) = x(t)^T \left[ {P_p}(t){\hat{A}_p}(t) + {\hat{A}_p}^T(t){P_p}(t) + {\dot{P}_p}(t) - {\alpha _p}{P_p}(t)\right] x(t).$$

(39)

Inequalities (36) and (37) imply (38)$<0$ and (39) $<0$. So we obtain the following inequality:

$${{\dot{V}}_p}(t) \le \left\{ \begin{array}{l} \beta _p {V_p}(t), \quad t \in {T_ \uparrow }({t_i},{t_{i + 1}}) \\ \alpha _p {V_p}(t), \quad t \in {T_ \downarrow }({t_i},{t_{i + 1}}) \\ \end{array} \right. .$$

According to Lemma 4, the system (6) is exponentially stable for any switching signal satisfying (24). This completes the proof.

Lemma 5 provides a sufficient condition for the controller design. However, the matrix variables $P_p(t)$ are coupled with system parameter matrices in (36) and (37), and thus it is difficult to design the controller directly. To overcome this difficulty, a decoupling technique is needed. In such a way, the following lemma is introduced. $\square$

Lemma 6

Let $\eta > 0$, $\varepsilon > 0$, $\alpha _p < 0$ and $\beta _p$ be given constants. If there exist matrices ${\bar{P}}_p(t) > 0$, $L_p(t)$ and X satisfying

$$\left[ {\begin{array}{cc} {\mathop{\Pi}} _{p1} & {\mathop{\Pi}} _{p2}\\ * & {-X - {X^T}} \end{array}} \right] < 0,$$

(40)

$$\left[ {\begin{array}{cc} {\mathop{\Pi}} _{p3} & {\mathop{\Pi}} _{p4}\\ * &{-X - {X^T}} \end{array}} \right] < 0,$$

(41)

where

$$\begin{aligned}{\mathop{\Pi}} _{p1} &= A_p(t)X + {X^T}A_p(t)^T + {B_p(t)}{L_q(t)} + L_q(t)^TB_p(t)^T - {\beta _p} {\bar{P}}_p(t)+ \dot{\bar{P}}_p(t), \\ {\mathop{\Pi}}_{p2} &= {{{\bar{P}}_p(t)} - X + {X^T}A_p(t)^T + L_q(t)^TB_p(t)^T}, \\ {\mathop{\Pi}}_{p3} &= A_p(t)X + {X^T}A_p(t)^T + {B_p(t)}{L_p(t)} + L_p(t)^TB_p(t)^T - {\alpha _p} {\bar{P}}_p(t)+ \dot{\bar{P}}_p(t), \\ {\mathop{\Pi}}_{p4} &= {{{\bar{P}}_p(t)} - X + {X^T}A_p(t)^T + L_p(t)^TB_p(t)^T}, \end{aligned}$$

we can conclude that the inequalities (36) and (37) hold.

Proof

In order to decouple the matrix variables $P_p(t)$ and system parameter matrices, we introduce a slack matrix H. Moreover, introducing slack matrices can also reduce the design conservativeness [35]. By introducing a slack matrix H, we introduce the following inequalities:

$$\left[ {\begin{array}{cc} {\bar{A}_{p}(t)^TH + {H^T}{{\bar{A}}_{p}(t)} - {\beta _p}{P_p(t)} + \dot{P}_p(t)} &{{P_p(t)} - {H^T} + \bar{A}_{p}(t)^TH}\\ * &{-H - {H^T}} \end{array}} \right] < 0,$$

(42)

$$\left[ {\begin{array}{cc} {\hat{A}_{p}(t)^TH + {H^T}{{\hat{A}}_{p}(t)} - {\alpha _p}{P_p(t)} + \dot{P}_p(t)} &{{P_p(t)} - {H^T} + \hat{A}_{p}(t)^TH}\\ * &{-H - {H^T}} \end{array}} \right] < 0.$$

(43)

Multiplying (42) from the left and right, respectively, by ${\hat{\Lambda}_{p}} = \left[{\begin{array}{cc} I & {\bar{A}_{p}(t)^T} \\ \end{array}}\right]$ and its transpose, and multiplying (43) from the left and right, respectively, by ${{\bar{\Lambda }}_p} = \left[ {\begin{array}{cc} I & {\hat{A}_p(t)^T} \\ \end{array}}\right]$, we can conclude that (36) and (37) hold. Notice that if the conditions in (42) and (43) hold, the matrix H is nonsingular. Now, we define the following matrices:

$$X = {H^{ - 1}}, \quad {L_p(t)} = {K_p(t)}X, \quad {{\bar{P}}_p(t)} = {X^T}{P_p(t)}{X}.$$

(44)

Multiplying (42) from the left and right, respectively, by diagonal matrix diag(${H^{-T}}$,${H^{-T}}$) and its transpose, we can obtain

$$\left[ {\begin{array}{cc} {\mathop{\Pi}}_{p5} &{\mathop{\Pi}}_{p6}\\ * &{-{H^{-1}} - {H^{-T}}} \end{array}} \right] < 0,$$

(45)

where

$$\begin{aligned}{\mathop{\Pi}}_{p5} &= {H^{-T}}\bar{A}_{p}(t)^T + {{\bar{A}}_{p}(t)}{H^{-1}} - {\beta _p}{H^{-T}}{P_p(t)}{H^{-1}} + {H^{-T}}{\dot{P}_{p}(t)}{H^-}, \\ {\mathop{\Pi}}_{p6} &= {H^{-T}}{P_p(t)}{H^{-1}} - {H^{-1}} + {H^{-T}}\bar{A}_{p}(t)^T\end{aligned}.$$

Similarly, for (43), we have

$$\left[{\begin{array}{*{20}c}{\Pi _{{p7}} } & {\Pi _{{p8}} } \\ * & { - H^{{ - 1}} - H^{{ - T}} } \\ \end{array} } \right]\, < \,0$$

(46)

where

$$\begin{array}{l} {\mathop{\Pi}}_{p7} = {H^{-T}}\hat{A}_{p}(t)^T + {{\hat{A}}_{p}(t)}{H^{-1}} - {\alpha _p}{H^{-T}}{P_p(t)}{H^{-1}} + {H^{-T}}{\dot{P}_{p}(t)}{H^-}, \\ {\mathop{\Pi}}_{p8} = {H^{-T}}{P_p(t)}{H^{-1}} - {H^{-1}} + {H^{-T}}\hat{A}_{p}(t)^T \end{array}.$$

LMIs (40) and (41) imply (45) and (46), respectively. Thus, if (40) and (41) hold, we can conclude that (36) and (37) hold. This completes the proof. $\square$

Remark 3

With the introduction of some new additional matrices $L_p(t)$ and X, we obtain the linear matrix inequalities in which the Lyapunov matrix $P_p(t)$ is not involved in any product with the state matrices $A_p(t)$. This feature enables us to derive conditions with less conservativeness due to the extra degrees of freedom.

Based on the above lemmas, the asynchronous stabilization problem can be addressed by the following theorem.

Theorem 2

Assume that

$$\left| \dot{h}_{ps}(t)\right| \le \varepsilon _{ps}, \quad s = 1,2, \ldots , k,$$

(47)

where $\varepsilon _{ps} \ge 0$. Let $\eta > 0$, $\varepsilon > 0$, $\alpha _p < 0$ and $\beta _p$ be given constants. If there exist matrices $\bar{P}_{pu} > 0$, $L_{pn}$ and X satisfying

$${\bar{P}}_{pl} \ge {\bar{P}}_{pk}, \quad l = 1, 2, \ldots , k-1$$

(48)

$${\bar{\Theta }}_{pmnu} + {\bar{\Theta }}_{punm} < 0 , m \le u$$

(49)

$$\left\{\begin{array}{ll} {\hat{S}}_{pmmm} ={\hat{\Theta}}_{pmmm} &< 0 \\ {\hat{S} }_{pmmn} =\displaystyle\frac{1}{3}\left[ {\hat{\Theta }}_{pmmn} +{\hat{\Theta }}_{pmnm}+ {\hat{\Theta }}_{pnmm}\right] & < 0, m \neq n \\ {\hat{S} }_{pmnu}= \displaystyle \frac{1}{6}\left[{\hat{\Theta }}_{pmnu} +{\hat{\Theta }}_{pmun} + {\hat{\Theta}}_{pnmu} + {\hat{\Theta}}_{pnum} + {\hat{\Theta }}_{punm} + {\hat{\Theta }}_{pumn}\right] & < 0, m < n < u \end{array} \right.$$

(50)

for all $m, n, u \in \left\{ 1,2, \ldots , k\right\}$, where

$${\bar{\Theta }_{pmnu}} = \left[ {\begin{array}{cc} {\mathop{\Phi}}_{p1} & {\mathop{\Phi}}_{p2}\\ * &{ - X - {X^T}} \end{array}} \right] , \; {\hat{\Theta }_{pmnu}} = \left[ {\begin{array}{cc} {\mathop{\Psi}}_{p1} & {\mathop{\Psi}}_{p2}\\ * &{ - X - {X^T}} \end{array}} \right]$$

and

$$\begin{aligned} {\mathop{\Phi}}_{p1} &= A_{pm}X + {X^T}A_{pm}^T + {B_{pm}}{L_{qn}} + L_{qn}^TB_{pm}^T - {\beta _p}{\bar{P}}_{pu} + \sum \limits _{s=1}^{k-1} {\varepsilon _{ps}}({\bar{P}_{ps}}-{\bar{P}_{pk}}), \\ {\mathop{\Phi}}_{p2} &= {{{\bar{P}}_{pu}} - X + {X^T}A_{pm}^T + L_{qn}^TB_{pm}^T}, \\ {\mathop{\Psi}}_{p1} &= A_{pm}X + {X^T}A_{pm}^T + {B_{pm}}{L_{pn}} + L_{pn}^TB_{pm}^T - {\alpha _p}{\bar{P}}_{pu} + \sum \limits _{s=1}^{k-1} {\varepsilon _{ps}}({\bar{P}_{ps}}-{\bar{P}_{pk}}), \\ {\mathop{\Psi}}_{p2} &= {{{\bar{P}}_{pu}} - X + {X^T}A_{pm}^T + L_{pn}^TB_{pm}^T}, \end{aligned}$$

The system (6) is exponentially stable for any switching signal satisfying (24). Moreover, if a feasible solution exists, the admissible controller gains can be given by

$$\left\{ \begin{aligned} K_{qn} &= L_{qn}X^{-1}, \quad t \in (t_i, {\bar{t}}_i]\\ K_{pn} &= L_{pn}X^{-1}, \quad t \in ({\bar{t}}_i, t_{i + 1}].\end{aligned}\right.$$

(51)

Proof

Denote the left side of (40) and (41) as ${\bar{\Theta }_p}(t)$ and ${\hat{\Theta }_p}(t)$, respectively. If the conditions in Theorem 2 are satisfied, we can obtain

$$\begin{aligned}{{\bar{\Theta }}_i}(t) &\le \sum \limits _{m = 1}^{k} \sum \limits _{n = 1}^{k} \sum \limits _{u = 1}^{k}h_{pm}(t) h_{qn}(t) h_{pu}(t) \bar{\Theta }_{pmnu} \\ &= \sum\limits _{n = 1}^{k} h_{qn}(t) \left[ \sum \limits _{m = 1}^{k}h_{pm}^2(t) \bar{\Theta }_{pmnm} + \sum \limits _{m = 1}^{k} \sum\limits _{m < u}^{k} h_{pm}(t)h_{pu}(t) (\bar{\Theta }_{pmnu} + \bar{\Theta }_{punm}) \right] < 0 \end{aligned}$$

and

$$\begin{aligned}{{\hat{\Theta }}_p}(t) &\le \sum \limits _{m = 1}^{k} \sum \limits _{n = 1}^{k} \sum \limits _{u = 1}^{k}h_{pm}(t) h_{pn}(t) h_{pu}(t) \hat{\Theta }_{pmnu}\\ &= \sum\limits _{m = 1}^{k} h_{pm}^3(t) \hat{S}_{pmmm} + 3\sum \limits_{m = 1}^{k} \sum \limits _{\begin{array}{c} n = 1\\ n \ne m \end{array}}^{k} h_{pm}(t) h_{pn}(t) \hat{S}_{pmmn} \\ &\quad +\,6\sum \limits _{m = 1}^{k} \sum \limits _{n > m} \sum \limits _{u > n} h_{pm}(t) h_{pn}(t) h_{pu}(t) \hat{S}_{pmnu} < 0.\end{aligned}$$

From Lemmas 4, 5, and 6, we know that the controller design problem is solved. By (44), we can conclude that the gains in (5) can be constructed by (51). This completes the proof. $\square$

Remark 4

Theorem 2 provides a sufficient condition to guarantee the exponential stability of the system (6) with asynchronous switching. This theorem can also be used to study other nonlinear switched systems. For example, if ${T_ {pM}} = 0$, the results obtained above can be used to study the nonlinear impulsive switched systems without asynchronous switching. And if $\Delta x(t) = 0$, the above theorem can be applicable to the asynchronous control of nonlinear switched systems without impulsive behaviors.

Remark 5

By setting $\bar{P}_{pu} = \bar{P}_{p}$, we get Corollary 2 where the QLFs are used.

Corollary 2

Let $\eta > 0$, $\varepsilon > 0$, $\alpha _p < 0,$ and $\beta _p$ be given constants. If there exist matrices $\bar{P}_{p} > 0$, $L_{pn}$ and X satisfying

$$\left\{ \begin{array}{l} {{\bar{\Lambda }}_{pmn}} + {{\bar{\Lambda }}_{pnm}} < 0\\ {{\hat{\Lambda }}_{pmn}} + {{\hat{\Lambda }}_{pnm}} < 0 \end{array} \right. , \quad m \le n,$$

(52)

for all $m, n \in \{1,2, \ldots , k\}$, where

$${\bar{\Lambda }_{pmn}} = \left[ {\begin{array}{cc} {\mathop{\phi}}_{p1} & {\mathop{\Phi}}_{p2}\\ * &{ - X - {X^T}} \end{array}} \right] , \quad {\hat{\Lambda }_{pmn}} = \left[ {\begin{array}{cc} {\mathop{\psi}}_{p1} & {\mathop{\psi}}_{p2}\\ * &{ - X - {X^T}} \end{array}} \right]$$

and

$$\begin{aligned}{\mathop{\phi}}_{p1} &= A_{pm}X + {X^T}A_{pm}^T + {B_{pm}}{L_{qn}} + L_{qn}^TB_{pm}^T - {\beta _p}{\bar{P}}_{p}, \quad {\mathop{\phi}}_{p2} = {{{\bar{P}}_{p}} - X + {X^T}A_{pm}^T + L_{qn}^TB_{pm}^T}, \\ {\mathop{\psi}}_{p1} &= A_{pm}X + {X^T}A_{pm}^T + {B_{pm}}{L_{pn}} + L_{pn}^TB_{pm}^T - {\alpha _p}{\bar{P}}_{p}, \quad {\mathop{\psi}}_{p2} = {{{\bar{P}}_{p}} - X + {X^T}A_{pm}^T + L_{pn}^TB_{pm}^T}, \end{aligned}$$

then the system (6) is exponentially stable for any switching signal satisfying (24). Moreover, if a feasible solution exists, the admissible controller gains can be given by

$$\left\{ \begin{aligned} K_{qn} &= L_{qn}X^{-1}, \quad t \in (t_i, {\bar{t}}_i]\\ K_{pn} &= L_{pn}X^{-1}, \quad t \in ({\bar{t}}_i, t_{i + 1}] \end{aligned}.\right.$$

Proof

The proof is similar to that of Theorem 2 with the function $V_{p}(t)$ given by

$$V_p(t) = x(t)^T{P_p}x(t).$$

It is omitted here. $\square$

4 Example

Example 1

Here, a numerical example is given to illustrate the effectiveness and advantage of our results obtained above. Consider the following continuous-time nonlinear impulsive switched system consisting of two subsystems: Subsystem 1:

$$\left\{ \begin{array}{l} \dot{x}_1(t) = \left( -0.2 +0.03z_{11}(t)\right) x_1(t) + \left( 0.01 + 0.04z_{11}(t)\right)x_2(t) + \\ \qquad \qquad \left( -0.21 + 0.09z_{11}(t)\right)u_1(t) + \left( 0.01 - 0.02z_{11}(t)\right) u_2(t)\\ \dot{x}_2(t)= \left( 0.16 - 0.06z_{11}(t)\right) x_2(t) + \left( 0.22 +0.03z_{11}(t)\right) u_2(t) \end{array},\right.$$

Subsystem 2:

$$\left\{ \begin{array}{l} \dot{x}_1(t) = \left( 0.04 + 0.01z_{21}(t)\right) x_1(t) - \left( 0.02 - 0.01z_{21}(t)\right) x_2(t) + \\ \qquad \quad \left( 0.3 -0.1z_{21}(t)\right) u_1(t) - 0.01u_2(t)\\ \dot{x}_2(t) = 0.02 x_1(t) + \left( 0.05z_{21}(t) - 0.35 \right) x_2(t) - \left( 0.3 + 0.1z_{21}(t)\right) u_2(t) \end{array}\right.,$$

where

$$\left\{\begin{array}{l} z_{11}(t) = \frac{\sin ^2(x_1(t)+0.5) e^{\sin ^2(x_1(t)+0.5)}}{e}\\ z_{21}(t) = \cos ^2(x_2(t)+0.5) \end{array}.\right.$$

Using the local sector nonlinearity method [20], we obtain the fuzzy model as follows:

Subsystem 1:

Rule 1: IF $z_{11}(t)$ is 0, THEN $\dot{x}(t) = A_{11} x(t) + B_{11} u(t)$,

Rule 2: IF $z_{11}(t)$ is 1, THEN $\dot{x}(t) = A_{12} x(t) + B_{12} u(t)$,

Subsystem 2:

Rule 1: IF $z_{21}(t)$ is 0, THEN $\dot{x}(t) = A_{21} x(t) + B_{21} u(t)$,

Rule 2: IF $z_{21}(t)$ is 1, THEN $\dot{x}(t) = A_{22} x(t) + B_{22} u(t)$,

where

$$\begin{array}{l} A_{11} = \left[ {\begin{array}{cc} -0.2 & 0.01 \\ 0 & 0.16 \\ \end{array}} \right], \quad A_{12} = \left[ {\begin{array}{cc} -0.17 & 0.05 \\ 0 & 0.1 \\ \end{array}} \right], \quad B_{11} = \left[ {\begin{array}{cc} -0.21 & 0.01 \\ 0 & 0.22 \\ \end{array}} \right] ,\\ B_{12} = \left[ {\begin{array}{cc} -0.12 & -0.01 \\ 0 & 0.25 \\ \end{array}} \right], \quad A_{21} = \left[ {\begin{array}{cc} 0.04 & -0.02 \\ 0.02 & -0.35 \\ \end{array}} \right], \quad A_{22} = \left[ {\begin{array}{cc} 0.05 & -0.01 \\ 0.02 & -0.3 \\ \end{array}} \right] ,\\ B_{21} = \left[ {\begin{array}{cc} 0.3 & -0.01 \\ 0 & -0.3 \\ \end{array}} \right], \quad B_{22} = \left[ {\begin{array}{cc} 0.2 & -0.01 \\ 0 & -0.4 \\ \end{array}} \right] . \end{array}$$

The normalized membership functions are calculated as follows:

$$\left\{ \begin{array}{ll} h_{11}(x_1(t)) = 1- \frac{\sin ^2(x_1(t)+0.5) e^{\sin ^2(x_1(t)+0.5)}}{e}, &\quad h_{12}(x_1(t)) = 1 - h_{11}(x_1(t))\\ h_{21}(x_2(t)) = 1 - \cos ^2(x_2(t)+0.5), &\quad h_{22}(x_2(t)) = 1 - h_{21}(x_2(t)) \end{array}.\right.$$

The nonlinear functions $g_p(t, x(t))$ and the parameters $D_p$ are given as

$${g_1} = {g_2} = \left[ {\begin{array}{c} {0.01\sin ({x_1(t)})} \\ {0.01\sin ({x_2(t)})} \\ \end{array}} \right],\quad {D_1} = {D_2} = \left[ {\begin{array}{cc} {0.3} & 0 \\ 0 & {0.3} \\ \end{array}} \right].$$

By the method of [29], we can calculate the parameters $\varepsilon _{ps}$ as $\varepsilon _{11} = \varepsilon _{12} = 1$ and $\varepsilon _{21} = \varepsilon _{22} = 0.5$. The initial conditions are assumed to be $x(t_0)=[1, 2]^T$. The state response of subsystem 1 and subsystem 2 is shown in Fig. 1. As we see from Fig. 1 that both of these two subsystems are unstable.

Fig. 1

State response of subsystem 1 and subsystem 2

We will use our results to design a set of model-dependent controllers such that the system (6) is exponentially stable. In practice, the asynchronous switching between the system models and the controllers generally exists. First, we study the asynchronous switching between the system models and the controllers, while the controllers are designed by only considering the synchronous conditions. Given $\eta = 0.01$, $\varepsilon = 0.01$, ${\alpha _1} = -0.12$, ${\alpha _2} = -0.2$, ${\beta _1} = 0.08$, ${\beta _2} = 0.045$ and $T_M = 8$, with these parameters, we can obtain $\mu _1=2.1892$, $\mu _2=2.2699$, $\tau _1^{*}=19.8626$ and $\tau _2^{*}=13.8987$. Using the LMI toolbox in Matlab to solve (48) and (50), the controller gains can be obtained as

$$\begin{array}{l} K_{11} = \left[ {\begin{array}{cc} 7.9722 & -0.4578 \\ -0.1675 & -9.1560 \\ \end{array}} \right],\quad K_{12} = \left[ {\begin{array}{cc} 8.3959 & 0.5866 \\ 0.0438 & -6.5639 \\ \end{array}} \right],\\ K_{21} =\left[ {\begin{array}{cc} -7.3636 & 0.2791 \\ 0.1263 & 5.0258 \\ \end{array}} \right], \quad K_{22} = \left[ {\begin{array}{cc} -6.3776 & 0.2231 \\ 0.0955 & 2.7234 \\ \end{array}} \right] \end{array}.$$

The state response for this case is shown in Fig. 2. As shown in Fig. 2, the system becomes unstable if we ignore the effects of asynchronous behaviors on the controllers design.

Fig. 2

State response of the closed-loop asynchronous switched system with controllers designed by synchronous conditions

Then, we investigate the situation that the asynchronous switching between the system models and the controllers, and the controllers are designed by considering the asynchronous conditions. We get $\mu _1=9.7281$, $\mu _2=13.0302$, $\tau _1^{*}=32.2918$ and $\tau _2^{*}= 22.6363$ with the above parameters. Using the LMI toolbox in Matlab to solve (48), (49), and (50), the controller gains are listed as follows:

$$\begin{array}{l} K_{11} = \left[ {\begin{array}{cc} 0.1450 & 6.3475 \\ 0.1332 & -0.3805 \\ \end{array}} \right], \quad K_{12} = \left[ {\begin{array}{cc} -0.1433 & 4.2655 \\ 0.0626 & -0.5197 \\ \end{array}} \right] ,\\ K_{21} =\left[ {\begin{array}{cc} -0.6258 & 1.7423 \\ 0.0695 & -0.4502 \\ \end{array}} \right], \quad K_{22} = \left[ {\begin{array}{cc} -0.5616 & 3.7148 \\ 0.0886 & -0.2252 \\ \end{array}} \right] \end{array}.$$

The state response for this situation is shown in Fig. 3. As is shown in Fig. 3,the states of the system converge to zero. It means that the designed controllers by considering asynchronous conditions are effective. Since the asynchronous switching is very common in real world, it is necessary for us to consider this effect on the controller design. Through comparing Fig. 2 with Fig. 3, we can conclude if we ignore the effects of asynchronous behaviors on the controller design when there exists asynchronous switching, the controllers designed cannot meet the actual requirements.

Fig. 3

State response of the closed-loop asynchronous switched system with controllers designed by considering asynchronous conditions

Next, we give some comparisons to show the advantage of our methods. We firstly compare the closed-loop nonlinear impulsive switched system under two different switching schemes MDADT and ADT. The parameters and computation results are shown in Table 1. It is clearly shown in Table 1 that ${\tau ^{*}} > \tau _1^{*}$ and ${\tau ^{*}} > \tau _2^{*}$. Therefore, any switching signals which satisfy the ADT of the closed-loop nonlinear impulsive switched system will satisfy the MDADT of all subsystems of that system, that is, $\tau _{p}^{*} \le \tau ^{*}$, $\forall p \in S$.

Table 1 Parameters and computation results for the closed-loop system under two different switching schemes

Secondly, we give a comparison between Theorem 2 and Corollary 2. Given the parameters $T_M = 8$, $\beta _1=0.08$ and $\beta _2=0.045$ for Theorem 2 and Corollary 2, by changing $\alpha _1$ with a step of 0.01, the lower bounds of $\alpha _2$ for Theorem 2 and Corollary 2 are plotted in Fig. 4. As is shown in Fig.  4, the lower bounds of $\alpha _2$ of Theorem 2 are smaller than those of Corollary 2. As we see from (23) and (24), a smaller $\alpha _p$ leads to a quicker decay of Lyapunov functions and a smaller $\tau _p^{*}$. It is because that the QLFs method is a special case of the FLFs method.

Fig. 4

The lower bounds of $\alpha _2$ for Theorem 2 and Corollary 2 by changing $\alpha _1$ with a step of 0.01

Example 2

Here, we give a practical example to show the validity of our method. Consider a continuous stirred tank reactor (CSTR) where an exothermic, irreversible reaction of the form $A \rightarrow B$ happens. As shown in [36], there are two different feeding streams to feed the reactor, and these two feeding streams are selected by a selector. Source 1 feeds pure species A at the flow rate $F_1 = 50$ L/min, concentration $C_{A_1} = 1.5$ mol/L and temperature $T_{A_1} = 350$ K, and source 2 feeds pure species A at the flow rate $F_2 = 200$ L/min, concentration $C_{A_2} = 0.75$ mol/L and temperature $T_{A_2} = 350$ K. In other words, the reactor has two modes with respect to the feeding stream. For each mode of operation, the mathematical model for the process has the following differential equations [27, 36]:

$$\begin{aligned}&\dot{C_A} = \frac{F_\sigma }{V}(C_{A \sigma } - C_A) - k_{0}e^{-E/R T_R}C_{A}, \nonumber \\&\dot{T_R} = \frac{F_\sigma }{V}(T_{A \sigma } - T_R) + \frac{-\triangle H}{\rho c_{p}} k_{0}e^{-E/R T_R}C_{A} + \frac{Q_{\sigma }}{\rho c_{p} V}, \end{aligned},$$

(53)

where $C_A$ represents the concentration of the species A, $T_R$ denotes the temperature of the reactor, $Q_{\sigma }$ is the heat removed from the reactor, V is the volume of the reactor, $k_0, E, \triangle H$ are the pre-exponential constant, the activation energy, and enthalpy of the reaction, $c_p$, $\rho$ are the heat capacity and fluid density in the reactor, and $\sigma (t) \in \{1, 2\}$ is the switching signal which is a discrete variable. The values of all process parameters can be found in [27].

The system (53) is a switched nonlinear system. Substituting all the process parameters into equation (53), we can get the following two subsystems:

Subsystem 1: $(\sigma = 1)$

$$\begin{aligned}&\dot{C_A} = -0.0334 C_A - 1.2 \times 10^{9} e^{-10,000T_{R}}C_{A} + 0.026386, \\&\dot{T_R} = -0.0334 T_R + 2.4 \times 10^{11} e^{-10,000T_{R}}C_{A} + 11.77684 +\frac{Q_{\sigma }}{23.9}, \end{aligned}$$

Subsystem 2: $(\sigma = 2)$

$$\begin{aligned}&\dot{C_A} = -0.0167 C_A - 1.2 \times 10^{9} e^{-10,000T_{R}}C_{A} + 0.0167, \\&\dot{T_R} = -0.0167 T_R + 2.4 \times 10^{11} e^{-10,000T_{R}}C_{A} + 5.177 +\frac{Q_{\sigma }}{23.9}. \end{aligned}$$

When $Q_{\sigma } = 0$, the two steady-states can be easily obtained as $(C_{A}, T_{R})_1 = (0.57, 395.3)$ and $(C_{A}, T_{R})_2 = (0.738, 509.12)$.

Using the T-S fuzzy model [19] and from [27], the nonlinear system (53) can be approximated by the following subsystem $S_\sigma$:

Subsystem $S_\sigma$:

Rule 1: IF the concentration of the species A is $M_{\sigma 1}(x1)$ (i.e., $x_1(t)$ is 0.57). THEN

$$\delta \dot{x}_{\sigma }(t) = A_{\sigma 1} \delta x(t) + B_{\sigma 1} \delta u(t),$$

Rule 2: IF the concentration of the species A is $M_{\sigma 2}(x1)$ (i.e., $x_1(t)$ is 0.738). THEN

$$\delta \dot{x}_{\sigma }(t) = A_{\sigma 2} \delta x(t) + B_{\sigma 2} \delta u(t),$$

where $\sigma \in \{1, 2\}$ represents the subsystem subscript, $x_{\sigma }(t) = [x_{\sigma 1}(t) \quad x_{\sigma 2}(t)]^T = [C_A \quad T_R]^T$, $\delta x_{\sigma }(t) = x_{\sigma }(t) - x_{\sigma }^d$, and $x_{\sigma }^d$ is the stationary point of the subsystem $\sigma$. It was shown in [27] that the $A_{\sigma 1}$ and $A_{\sigma 2}$ have the following values:

$$\begin{array}{l} A_{11} = \left[ {\begin{array}{cc} -4.5803\times 10^{-2} & 6.6748\times 10^{-5} \\ 2.4807 & -3.61\times 10^{-3} \\ \end{array}} \right], \quad A_{12} = \left[ {\begin{array}{cc} -3.5728 & 5.1826\times 10^{-5} \\ 707.89 & -0.010268 \\ \end{array}} \right] ,\\ A_{21} =\left[ {\begin{array}{cc} -0.029103 & 5.1833\times 10^{-5} \\ 2.4807 & -0.0036045 \\ \end{array}} \right], \quad A_{22} = \left[ {\begin{array}{cc} -3.564 & 5.1826\times 10^{-5} \\ 706.13 & -0.010265 \\ \end{array}} \right]\end{array}.$$

The parameters $B_{\sigma 1}$ and $B_{\sigma 2}$ are set as $B_{11}=B_{12}=B_{21}=B_{22}=[-0.000005; 0.0030]$. The nonlinear functions $g_{\sigma }(t, x(t))$ used here are the same as in Example 1. Based on different properties of the source 1 and source 2, the matrices $D_{\sigma }$ are given as

$${D_1} = \left[ {\begin{array}{cc} {0.02} & 0 \\ 0 & {-0.02} \\ \end{array}} \right], \quad {D_2} = \left[ {\begin{array}{cc} {0.01} & 0 \\ 0 & {-0.02} \\ \end{array}} \right].$$

If $g_{\sigma }(t, x(t))$ and $D_{\sigma }$ can be measured in practice, we can use these practical values to replace the values used in this example.

The normalized membership functions for Rule 1 and Rule 2 of the two subsystems are taken as

$$\left\{ \begin{aligned} h_{11}(x_1) &= h_{21}(x_1) = \frac{\arctan (50\, \times\,(x_1-0.654)) + \pi /2}{\pi }, \\ h_{12}(x_1) &= 1- h_{11}(x_1), h_{22}(x_1) = 1- h_{21}(x_1). \end{aligned}\right.$$

By the method of [29], the parameters $\varepsilon _{ps}$ used in this example are calculated as $\varepsilon _{11} = \varepsilon _{12} = \varepsilon _{21} = \varepsilon _{22} = 2$. Given $\eta = 0.01$, $\varepsilon = 0.01$, $T_M=200$, $\alpha _1 = -0.02$, $\alpha _2 = -0.015$, $\beta _1=0.01$ and $\beta _2=0.015$, substituting above parameters into (48), (49), and (50), we find these LMIs are feasible. A set of feasible controller gains can be given as follows:

$$\begin{aligned} K_{11} &= \left[ \begin{array}{cc} 6.9574&4.2107 \end{array}\right], \quad K_{12} = \left[ \begin{array}{cc} -18.3518 & 2.483 \end{array}\right] , \\ K_{21} &= \left[ \begin{array}{cc} 7.9568 & -1.2109 \end{array} \right], \quad K_{22} = \left[ \begin{array}{cc} -20.3518&5.4854 \end{array} \right] . \end{aligned}$$

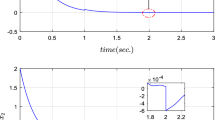
By assuming the initial conditions to be $x(t_0)=[0.5, 404.9]^T$, and setting $\tau _{1}^{*} = 765.2733$, $\tau _{2}^{*} = 681.3643$, the simulation results are shown in Figs. 5 and 6. As we see from these two figures, although there exist effects of impulsive behaviors and asynchronous switching, the system (53) can still be stable, which illustrates the validity of our method.

Fig. 5

The state trajectory of $x_1(t)$

Fig. 6

The state trajectory of $x_2(t)$

5 Conclusion

In this paper, the T-S fuzzy model is first used to study the exponential stability and asynchronous stabilization problem of the continuous-time nonlinear impulsive switched systems with asynchronous switching. Based on the switching FLFs approach and the MDADT technique, the stability conditions and asynchronous stabilization conditions are obtained. Moreover, the state-feedback fuzzy controllers are designed to guarantee the closed-loop systems to be exponentially stable. Besides, we remark that the obtained results can also apply to the nonlinear switched systems without the effects of asynchronous switching or impulsive behaviors. Finally, a numerical example and a chemical process example are given to illustrate the advantage and applicability of the results obtained.