1 Introduction

There always exist unnoticeable and unknown aspects of the real system in the dynamic model which captures prominent features of the mechanical system. Researches on mechanical system control have always been very active, especially on handling uncertainties in the system. Exploring uncertainty and determining what is known and what is unknown about the uncertainty is very important. Once the bound information of the uncertainty is clearly identified, we can use this known bound information to develop deterministic control approaches. The well-known H 2/ H ∞ control [17, 20], the Lyapunov-based control [6, 19], the sliding mode control [24], and so on contribute to this deterministic approach. When the known portion cannot be completely isolated from the unknown, one may take the stochastic control approach. The classic Linear–Quadratic–Gaussian control [23] is in such domain.

The stochastic dynamical system merges the probability theory with system theory and has been the most outstanding since 1950s. Kalman initiated the effort of looking into the estimation problem and control problem [11, 12] in the state space framework when a system is under stochastic noise. Although the stochastic approach is quite self-contained and an impressive arena of practitioners, concerns on the probability theory’s validity in describing the real world does exist. That is to say, the link between the stochastic mathematical tool and the physical world might be loose. Kalman, among others, despite his early devotion to stochastic system theory now contends that the probability theory might not be all that suitable to describe the majority of randomness [13].

The uncertainty in engineering is often acquired via observed data and then analyzed by the practitioner. However, the observed data are, by nature, always limited and the uncertainty is unlikely to be exactly repeated many times. The earthquake data can be an example for interpretation [22]. Hence, any interpretation via the frequency of occurrence, which requires a large number of repetitions, might sometimes be limited due to a lack of basis. As a result, the fuzzy view via the degree of occurrence may be considered as an alternative in certain applications. We can find more discussions on the relative advantages of fuzziness versus probability in Bezdek [2].

Fuzzy theory was initially introduced to describe information (for example, linguistic information) that is in lack of a sharp boundary with its environment [26]. Most interest in fuzzy logic theory is attracted to fuzzy reasoning for control, estimation, decision-making, etc. Therefore, the merge between the fuzzy theory and system theory (fuzzy dynamical system) has been less focused on. Past efforts on fuzzy dynamical systems can be found in Hanss [9], Bede et al. [1], Lee et al. [15], Huang et al. [10], and Xu et al. [25]. We stress that these are different from the very popular Takagi–Sugeno model or other fuzzy if–then rules-based models. In this paper, from a different angle, we employ the fuzzy theory to describe the uncertainty in the mechanical system and then propose optimal robust control design of fuzzy mechanical systems.

The main contributions are fourfold. First, we not only guarantee the deterministic performance (including uniform boundedness and uniform ultimate boundedness), but also explore fuzzy description of system performance should the fuzzy information of the uncertainty be provided. Third, we propose a robust control which is deterministic and is not the usual if–then rules-based. The resulting controlled system is uniformly bounded and uniformly ultimately bounded proved via the Lyapunov minimax approach. Fourth, a performance index (the combined cost, which includes average fuzzy system performance and control effort) is proposed based on the fuzzy information. The optimal design problem associated with the control can then be solved by minimizing the performance index. In the end, the unique closed-form solution of optimal gain and the cost are explicitly presented. The resulting control design is systematic and is able to guarantee the deterministic performance as well as minimizing the cost.

2 Fuzzy mechanical systems

Consider the following uncertain mechanical system:

$$ M(q(t),\sigma (t),t) {\ddot{q}}(t) + V(q(t),\dot{q}(t),\sigma (t),t) + G(q(t),\sigma (t),t) + T(q(t),\dot{q}(t),\sigma (t),t) = \tau (t). $$
(2.1)

Here \( q_{0} \) is the time (i.e., the independent variable), \( q \in R^{n} \) is the coordinate, \( \dot{q} \in R^{n} \) is the velocity, \( {\ddot{q}} \in R^{n} \) is the acceleration, \( \sigma \in R^{p} \) is the uncertain parameter, and\( \tau \in R^{n} \) is the control input. \( M(q,\sigma ,t) \in R^{n \times n} \) is the inertia matrix, \( V(q,\dot{q},\sigma ,t) \in R^{n} \) is the Coriolis/centrifugal force vector, \( G(q,\sigma ,t) \in R^{n} \) is the gravitational force vector, and \( T(q,\dot{q},\sigma ,t) \in R^{n} \) is the friction force and external disturbance or force (we omit arguments of functions where no confusions may arise).

Assumption 1

The functions M(·), V(·), G(·), and T(·) are continuous (Lebesgue measurable in t). Furthermore, the bounding set Σ is known and compact.

Assumption 2

(i) For each entry of \( q_{0i} \), namely \( q_{0i} \), i = 1, 2,…, n, there exists a fuzzy set \( Q_{0i} \) in a universe of discourse \( \varXi i \subset R \) characterized by a membership function \( \mu \varXi i:\varXi i \to \left[ {0,1} \right] \). That is,

$$ Q_{0i} = \left\{ {(q_{0i} ,\mu \varXi i\left( {q_{0i} } \right))|q_{0i} \in \varXi i} \right\}. $$
(2.2)

Here \( \varXi i \) is known and compact. (ii) For each entry of the vector σ(t), namely \( \sigma_{i} \left( t \right) \), i = 1, 2,…, p, the function \( \sigma_{i} \left( \cdot \right) \) is Lebesgue measurable. (iii) For each \( \sigma_{i} \left( t \right), \) there exists a fuzzy set \( S_{i} \) in a universe of discourse \( \varSigma i \subset R \) characterized by a membership function \( \mu_{i} :\varSigma_{i} \to \left[ {0,1} \right] \). That is,

$$ S_{i} = \, \{ (\sigma_{i} ,\mu_{i} (\sigma_{i} ))|\sigma_{i} \in \varSigma_{i} \} . $$
(2.3)

Here \( \varSigma_{i} \) is known and compact.

Remark

Assumption 2 imposes fuzzy restriction on the uncertainty \( q_{0} \) and \( \sigma \left( t \right) \). We employ the fuzzy description on the uncertainties in the mechanical system. This fuzzy description earns much more advantage than the probability avenue which often requires a large number of repetitions to acquire the observed data (always limited by nature).

Assumption 3

The inertia matrix \( M\left( {q,\sigma ,t} \right) \) in mechanical systems is uniform positive definite, that is, there exists a scalar constant \( r > 0 \) such that

$$ M(q,\sigma ,t) \ge \gamma I $$
(2.4)

for all \( q \in R^{n} . \)

Remark

We emphasize that this is an assumption, not a fact. There are cases that the inertia matrix may be positive semi-definite (hence, γ = 0). One example is documented in McKerrow [18] where the generalized inertia matrix

$$ M = \left[ {\begin{array}{*{20}c} {ml_{2}^{2} \cos^{2} \theta_{2} } & 0 \\ 0 & {ml_{2}^{2} } \\ \end{array} } \right]. $$
(2.5)

Thus \( det\left[ M \right] = 0 \) if \( \theta_{2} = \, \left( {2n \, + \, 1} \right)\frac{\pi }{2},\quad n = 0, \pm 1, \pm 2, \ldots \). That is to say, the generalized inertia matrix M is singular. When \( \theta_{2} = \, \left( {2n \, + \, 1} \right)\frac{\pi }{2},\quad n = 0, \pm 1, \pm 2, \ldots \), the kinetic energy \( \frac{1}{2}\dot{q}{}^{T}M\dot{q} = 0,\quad \forall \,\dot{\theta }_{1} \) which means the rotation does not bring up kinetic energy.

Assumption 4

There is a constant \( \mathop \gamma \limits^{\_} \), such that for all \( \left( {q,t} \right) \in R^{n} \times R,\sigma \in \varSigma , \) the inertial matrix \( M\left( {q,\sigma ,t} \right) \) is bounded as

$$ k_{M} (q,\sigma ,t)k \le \overline{\gamma }. $$
(2.6)

Unless otherwise stated, \( \left\| {\; \cdot \;} \right\| \) always denotes the Euclidean norm (i.e., \( \left\| {\; \cdot \;} \right\|_{2} \)). The l 1-norm are sometimes used and indicated by subscript 1.

Theorem 1

There always exists the factorization

$$ V \, \left( {q,\dot{q},\sigma ,t} \right) \, = \, C\left( {q,\dot{q},\sigma ,t} \right)\dot{q} $$
(2.7)

such that \( \dot{M}\left( {q,\dot{q},\sigma ,t} \right) - 2C\left( {q,\dot{q},\sigma ,t} \right) \) is skew symmetric [21]. Here \( \dot{M}\left( {q,\dot{q},\sigma ,t} \right) \) is the time derivative of \( M\left( {q,\sigma ,t} \right) \).

Remark

To satisfy \( V = C\mathop q\limits^{.} \), the matrix C may not be unique. But if you also want \( \mathop M\limits^{.} - 2C \) to be skew symmetric, then the particular choice of C should be defined as

$$ c_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{n} {\frac{{\partial m_{ij} }}{{\partial q_{k} }}} \dot{q}_{k} + \frac{1}{2}\sum\limits_{k = 1}^{n} {\left( {\frac{{\partial m_{ik} }}{{\partial q_{j} }} - \frac{{\partial m_{jk} }}{{\partial q_{i} }}} \right)} \dot{q}_{k}, $$
(2.8)

where \( c_{ij} \) is the ij-element of matrix C.

3 Robust control design of fuzzy mechanical systems

We wish the mechanical system to follow a desired trajectory \( q^{d} \left( t \right),t \in \left[ {t_{0} ,t_{1} } \right] \), with the desired velocity \( \dot{q}^{d} \left( t \right) \). Assume \( q^{d} (\cdot) \, : \, [t_{0} ,\infty ] \to R^{n} \) is of class \( C^{2} \) and \( \dot{q}^{d} \left( t \right) \),\( {\ddot{q}}^{d} \left( t \right) \), and \( {\ddot{q}}^{d} \left( t \right) \) are uniformly bounded. Let

$$ e\left( t \right) = \, q\left( t \right) \, - \, q^{d} \left( t \right), $$
(3.1)

and hence \( {\dot{\text{e}}}\left( t \right) = \, \dot{q}\left( t \right) \, - \, \dot{q}^{d} \left( t \right),\,{{{\ddot{e}}}}\left( t \right) = \, {\ddot{q}}\left( t \right) \, - \, {\ddot{q}}^{\text{d}} \left( t \right)\). The system (2.1) can be rewritten as

$$ M\left( {e \, + \, q^{d} ,\sigma ,t} \right)\left( {{\ddot{e}} \, + {{ {\ddot{q}}}}^{\text{d}} } \right) \, + \, C\left( {e \, + \, q^{d} , \, \dot{e} \, + {\dot{\text{q}}}^{\text{d}} ,\sigma ,t} \right)\left( {\dot{e} \, + {\dot{\text{q}}}^{\text{d}} } \right) + G\left( {e \, + \, q^{d} ,\sigma ,t} \right) \, + \, T\left( {e \, + \, q^{d} , \, \mathop e\limits^{.} \, + {\dot{\text{q}}}^{\text{d}} ,\sigma ,t} \right) \, = \, \tau . $$
(3.2)

The functions M(·), C(·), G(·), and T(·) can be decomposed as

$$ . \begin{aligned} & M\left( {e \, + \, q^{d} ,\sigma ,t} \right) \, = \overline{M}\left( {e \, + \, q^{d} ,t} \right) \, + \Delta M(e \, + \, q^{d} ,\sigma ,t), \\ & C(e \, + \, q^{d} ,\dot{e} \, + \dot{q}^{d} ,\sigma ,t) \, = \overline{C}(e \, + \, q^{d} , \, \dot{e} \, + \, \dot{q}^{d} ,\sigma ,t) \\ & \quad + \,\Delta C(e \, + \, q^{d} , \, \dot{e} \, + \dot{q}^{d} ,\sigma ,t), \\ & \quad G(e \, + \, q^{d} ,\sigma ,t) \, = \overline{G}\left( {e \, + \, q^{d} ,t} \right) \, + \Delta G(e \, + \, q^{d} ,\sigma ,t), \\ & \quad T(e \, + \, q^{d} , \, \dot{e} \, + \, \dot{q}^{d} ,\sigma ,t) \, = \mathop T\limits^{\_\_} (e \, + \, q^{d} , \, \dot{e} \, + \, \mathop {\dot{q}^{d} }\limits^{{}} ,\sigma ,t) \, \\ & \quad + \,\Delta T(\dot{e} \, + \, q^{d} , \, \dot{e} \, + \, \dot{q}^{d} ,\sigma ,t), \\ \end{aligned} , $$
(3.3)

where \( \overline{M},\overline{C},\overline{G}, \) and \( \overline{T} \) are the nominal terms of corresponding matrix/vector and \( \Delta M,\Delta C,\Delta G, \) and \( \Delta{\text{T}} \) are the uncertain terms which depend on \( \sigma \). We now define a vector

$$ \varPhi \left( {e, \, \dot{e},\sigma ,t} \right) \, : = - \Delta M\left( {e + q^{d} ,\sigma ,t} \right)\left( {{\ddot{q}}^{d} - S\dot{e}} \right) \, - \Delta C\left( {e + q^{d} ,\dot{e} + \dot{q}^{d} ,\sigma ,t} \right)\left( {\dot{q}^{d} - \, Se} \right) - \Delta G(e + q^{d} ,\sigma ,t) - \Delta T\left( {e + q^{d} , \, \dot{e} + \dot{q}^{d} ,\sigma ,t} \right), $$
(3.4)

where \( S = diag\left[ {si} \right]_{n \times n} \), \( s_{i} > 0 \) is a constant, i = 1, 2,…, n. Obviously \( \varPhi \equiv \, 0 \) if all uncertain terms vanish.

Assumption 5

There are fuzzy numbers \( \zeta_{K} \left( {\dot{q}d, \, {\ddot{q}}d,e, \, \dot{e},\sigma ,t}\right)\) ’s and scalars \( \rho_{K} \left( {\dot{q}d, \, {\ddot{q}}d,e, \, \dot{e},\sigma ,t} \right) \)’s, k = 1, 2,…, r, such that

$$ \left\| \varPhi \right\| \le \left[ {\begin{array}{*{20}c} {\hat{\varsigma }_{1} } & {\hat{\varsigma }_{2} } & {\cdot\cdot\cdot} & {\hat{\varsigma }_{r} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{\rho }_{1} } \\ {\hat{\rho }_{2} } \\ \vdots \\ {\hat{\rho }_{r} } \\ \end{array} } \right] = :\hat{\zeta }^{T} \left( {e, \, \dot{e},\sigma ,t} \right)\hat{\rho }\left( {e, \, \dot{e},t} \right). $$
(3.5)

From (3.5), we have

$$ \parallel \varPhi \parallel \le \parallel \hat{\zeta }\parallel \parallel \hat{\rho }\parallel = :\zeta \rho. $$
(3.6)

Remark

One can employ fuzzy arithmetic and decomposition theorem (see the Appendix) to calculate the fuzzy number ζ based on the fuzzy description of \( \sigma_{i} \)’s (Assumption 2).

We introduce the following desirable deterministic dynamical system performance.

Definition 1

Consider a dynamical system

$$ \dot{\xi }\left( t \right) \, = \, f\left( {\xi \left( t \right),t} \right),\xi \left( {t_{0} } \right) = \xi_{0} . $$
(3.7)

The solution of the system (suppose it exists and can be continued over \( [t_{0} ,\infty ) \)) is uniformly bounded if for any \( r > 0 \) with \( \left\| {\xi_{0} } \right\| \le r \), there is \( d\left( r \right) > 0 \) with \( \left\| {\xi_{0} } \right\| \le d\left( r \right) \) for all \( t \ge t_{0} \). It is uniformly ultimately bounded if for \( \left\| {\xi_{0} } \right\| \le r \) there are \( \overline{d}\left( r \right) > 0 \) and \( T(\overline{d}\left( r \right),r) \ge 0 \) such that \( \left\| {\xi_{0} } \right\| \le \overline{d}\left( r \right) \) for all \( t \ge t_{0} + \, T(\overline{d}\left( r \right),r) \).Let

$$ e\left( t \right): = \left[ {e\left( t \right) \, \dot{e}\left( t \right)} \right]T. $$
(3.8)

The control design is to render the tracking error vector e(t) to be sufficiently small. We propose the control as

$$ \tau \left( t \right) \, = \overline{M}\left( {{\ddot{q}}^{d} - S\dot{e}} \right) \, + \overline{C}\left( {\dot{q}d - Se} \right) + \overline{G} + \overline{T} - Pe - D\dot{e} - \gamma \left( {\dot{e} + Se} \right)\rho^{2}, $$
(3.9)

where P, D are positive definite diagonal matrices and the scalar \( \overline{\gamma }: = \, \gamma^{r} > 0. \) The scalar \( \gamma \) is a constant design parameters.

Theorem 2

Subject to Assumptions 1–5, the control (3.9) renders \( {\text{e}}\left( t \right) \) of the system (3.2) to be uniformly bounded and uniformly ultimately bounded. In addition, the size of the ultimate boundedness ball can be made arbitrarily small by suitable choices of the design parameters.

Remark

The control \( \tau (t) \) is based on the nominal system, the tracking error e(t), the bound of uncertainty, and the design parameters. Therefore, this proposed control is deterministic and is not if–then rules-based.

4 Proof of Theorem 2

The mechanical system with the proposed control is proved to be stable in this section. The chosen Lyapunov function candidate is shown to be legitimate and then the proof of stability follows via Lyapunov minimax approach [7, 16].

The Lyapunov function candidate is chosen as

$$ V \, \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right) \, = \frac{1}{2}\left( {\dot{e} + Se} \right)^{T} M\left( {\dot{e} + Se} \right) + \frac{1}{2}e^{T} \left( {P \, + \, SD} \right)e.\quad {\text{V(e)}} = 1. $$
(4.1)

To prove \( V \, \) is a legitimate Lyapunov function candidate, we shall prove that \( V \, \) is (globally) positive definite and decrescent. By (2.4), we have

$$ \begin{aligned} V \, \left( e \right) \ge \frac{1}{2}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma } \parallel \dot{e} + Se\parallel^{2} + \frac{1}{2}e^{T} \left( {P + SD} \right)e \hfill \\ \quad = \frac{1}{2}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma } \sum\limits_{i = 1}^{n} {\dot{e}_{i}^{2} + 2s_{i} \dot{e}_{i} e_{i} + s_{i}^{2} e_{i}^{2} } \hfill \\ \quad \quad + \,\frac{1}{2}\sum\limits_{i = 1}^{n} {(p_{i} + s_{i} d_{i} )e_{i}^{2} } = \frac{1}{2}\sum\limits_{i = 1}^{n} {\left[ {\begin{array}{*{20}c} {e_{i} } & {\dot{e}_{i} } \\ \end{array} } \right]} \varPsi_{i} \left[ {\begin{array}{*{20}c} {e_{i} } \\ {\dot{e}_{i} } \\ \end{array} } \right] \hfill \\ \end{aligned}, $$
(4.2)

where \( s_{i} \), \( p_{i} \)’s, and \( d_{i} \)’s are from (3.4) and (3.9), \( e_{i} \) and \( \dot{e}_{i} \) are the i-th components of e and \( \dot{e} \), respectively, and

$$ \varPsi_{i} = \left[ {\begin{array}{*{20}c} {\gamma s_{i}^{2} + po_{i} + \, s_{i} do_{i} } & {\gamma s_{i} } \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma } s_{i} } & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\gamma } } \\ \end{array} } \right]. $$
(4.3)

It can be easily verified that \( \varPsi_{i} > 0\quad \forall \;i \). Thus, by letting \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } = min\left( {\frac{1}{2}\lambda_{m} \left( {\varPsi_{1} } \right),\cdot\cdot\cdot \, ,\frac{1}{2}\lambda_{m} \left( {\varPsi_{n} } \right)} \right) \) (hence λ > 0), V is shown to be positive definite:

$$ V \ge \frac{1}{2}\sum\limits_{i = 1}^{n} {\lambda_{m} \left( {\varPsi_{i} } \right)} (e_{i}^{2} + \dot{e}_{i}^{2} ) \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } \left\| e \right\|^{2} . $$
(4.4)

By Assumption 4, we have

$$ V \le \parallel \dot{e} + Se\parallel^{2} \overline{\gamma } + e^{T} \left( {P \, + \, SD} \right)e. $$
(4.5)

For the first term on the right-hand side,

$$ \overline{\gamma }\left\| {\dot{e} + Se} \right\|^{2} = \overline{\gamma }\left\| {\dot{e} + Se} \right\|^{T} (\dot{e} + Se) = \overline{\gamma }\left[ {\begin{array}{*{20}c} e & {\dot{e}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {S^{2} } & S \\ S & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} e \\ {\dot{e}} \\ \end{array} } \right] \le \overline{\gamma }\,\lambda_{M} \left[ {\begin{array}{*{20}c} {S^{2} } & S \\ S & I \\ \end{array} } \right]\parallel e\parallel^{2} = : \, \overline{\gamma }\overline{s}\left\| e \right\|^{2} . $$
(4.6)

For the second term on the right-hand side, by Rayleigh’s principle,

$$ e^{T} \left( {P \, + \, SD} \right)e \le \lambda_{M} \left( {P \, + \, SD} \right)\left\| e \right\|^{2} . $$
(4.7)

With (4.6) and (4.7) into (4.5), we have

$$ V \le \overline{\gamma }\overline{s}\left\| e \right\|^{2} + \lambda_{M} \left( {P + SD} \right)\left\| e \right\|^{2} = :\overline{\lambda }\left\| e \right\|^{2} , $$
(4.8)

where \( \overline{\lambda } = \overline{\gamma }\overline{s} \, + \, \lambda_{M} \left( {P \, + \, SD} \right). \) Note that \( \overline{\lambda } \) in (4.8) is a strictly positive constant, which implies that V is decrescent. From (4.4) and (4.8), V is a legitimate Lyapunov function candidate.

Now, we prove the stability of the mechanical system with the proposed control. For any admissible \( \xi \left( \cdot \right) \), the time derivative of V along the trajectory of the controlled mechanical system of (3.2) is given by

$$ \dot{V} = \left( {\dot{e} \, + Se} \right)^{T} M\left( {{\ddot{e}} + S\dot{e}} \right) + \frac{1}{2}\left( {\dot{e} + Se} \right)^{T} \dot{M}\left( {\dot{e} + Se} \right) + e^{T} \left( {P + SD} \right)\dot{e}. $$
(4.9)

By applying \( {\ddot{e}} = {\ddot{q}} - {\ddot{q}}^{d} \) and Eq. (2.1), the first two terms become

$$ \left({\dot{e} + Se} \right)^{T} M\left({{\ddot{e}} + S\dot{e}} \right) + \frac{1}{2}\left({\dot{e} + Se} \right)^{T} \dot{M}\left({\dot{e} + Se} \right) = \left({\dot{e} + Se} \right)^{T} (M{\ddot{q}} - M{\ddot{q}}^{d} + MS\dot{e} + \frac{1}{2}\dot{M}\left({\dot{e} + Se} \right)) = \left({\dot{e} + Se} \right)^{T} (\tau - C\left({\dot{e} + \dot{q}^{d}} \right) - G - T - M{\ddot{q}}^{d} + MS\dot{e} + \frac{1}{2}\dot{M}\left({\dot{e} + Se} \right)) = \left({\dot{e} + Se} \right)^{T} (\tau - C\left({\dot{q}^{d} - Se} \right) - G - T - M{\ddot{q}}^{d} + MS\dot{e} - C\left({\dot{e} + Se} \right) + \frac{1}{2}\dot{M}\left({\dot{e} + Se} \right)) = \left({\dot{e} + Se} \right)^{T} \left({\tau - C\left({\dot{q}^{d} - Se} \right) - G - T - M{\ddot{q}}^{d} + MS\dot{e}} \right) + \left({\dot{e} + Se} \right)^{T} \left({\frac{1}{2}\dot{M} - C} \right)(\dot{e} + Se). $$
(4.10)

With Theorem 1, (3.3) and (3.9), we can get

$$ \left({\dot{e} + Se} \right)^{T} M\left({{\ddot{e}} + S\dot{e}} \right) + \frac{1}{2}\left({\dot{e} + Se} \right)^{T} \dot{M}\left({\dot{e} + Se} \right) = \left({\dot{e} + Se} \right)^{T} \left({\tau - C\left({\dot{q}^{d} - Se} \right) - G - T - M{\ddot{q}}^{d} + MS\dot{e}} \right) = \left({\dot{e} + Se} \right)^{T} \{\overline{M}\left({{\ddot{q}}^{d} - S\dot{e}} \right) - M\left({{\ddot{q}}^{d} - S\dot{e}} \right) + \overline{C}\left({\dot{q}^{d} - Se} \right) - C\left({\dot{q}^{d} - Se} \right) + \overline{G} - G + \overline{T} - T - \gamma \rho^{2} \left({\dot{e} + Se} \right) - Pe - D\dot{e}\} = \left({\dot{e} + Se} \right)^{T} \{- \Delta M\left({{\ddot{q}}^{d} - S\dot{e}} \right) - \Delta C\left({\dot{q}^{d} - Se} \right) - \Delta G - \Delta T - \gamma \rho^{2} \left({\dot{e} + Se} \right) - Pe - D\dot{e}\}. $$
(4.11)

By (3.4)–(3.6),

$$ \left({\dot{e} + Se} \right)^{T} M\left({{\ddot{e}} + S\dot{e}} \right) + \frac{1}{2}\left({e + Se} \right)^{T} \dot{M}\left({\dot{e} + Se} \right) = \left({\dot{e} + Se} \right)^{T} \left[{\varPhi - \gamma \rho^{2} \left({\dot{e} + Se} \right) - Pe - D\dot{e}} \right] \le \left\| {\dot{e} + Se} \right\| \left\| {\varPhi} \right\| - \gamma \rho^{2} \left\| {\dot{e} + Se} \right\|^{2} - \left({\dot{e} + Se} \right)^{T} \left({Pe + D\dot{e}} \right) \le \zeta \rho \left\| {\dot{e} + Se} \right\| - \gamma \rho^{2} \left\| {\dot{e} + Se} \right\|^{2} - \left({\dot{e} + Se} \right)^{T} \left({Pe + D\dot{e}} \right) \le \tfrac{{\zeta^{2}}}{4\gamma} - \left({\dot{e} + Se} \right)^{T} \left({Pe + D\dot{e}} \right). $$
(4.12)

Since

$$ - \left( {\dot{e} + Se} \right)^{T} \left( {Pe \, + \, D\dot{e}} \right) = - e^{T} PSe - \dot{e}^{T} D\dot{e} - e^{T} \left( {P + SD} \right)e, $$
(4.13)

we have

$$ \left( {\dot{e} + Se} \right)^{T} M\left( {{\ddot{e}} + S\dot{e}} \right) + \frac{1}{2}\left( {\dot{e} + Se} \right)^{T} \dot{M}\left( {\dot{e} + Se} \right) \le \frac{\zeta 2}{4\gamma } - e^{T} PSe - \dot{e}^{T} D\dot{e} - e^{T} \left( {P + SD} \right)e. $$
(4.14)

Substituting (4.14) into (4.9), we get

$$ \dot{V} \le \frac{\delta }{\gamma } - e^{T} PSe \, - \dot{e}^{T} D\dot{e} - e^{T} \left( {P + SD} \right)e + e^{T} \left( {P + SD} \right)e = \frac{{\zeta^{2} }}{4\gamma } - e^{T} PSe - \dot{e}TD\dot{e} \le \frac{{\zeta^{2} }}{4\gamma } - \, \lambda \left\| e \right\|^{2} , $$
(4.15)

where \( \lambda = \hbox{min} \left\{ {\lambda \hbox{min} \left( {PS} \right), \, \lambda \hbox{min} \left( D \right)} \right\}. \) This in turn means that\( \dot{V} \) is negative definite for all \( \left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\| \) such that

$$ \frac{\delta }{\gamma } - \lambda \parallel \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \parallel^{2} < 0, $$
(4.16)

where \( \delta = \frac{{\zeta^{2} }}{4} \). Since all universes of discourse \( \varSigma_{i} \)’s are compact (hence closed and bounded), δ is bounded. In addition, both \( \gamma \) and \( \lambda \) are crisp. Thus, \( \dot{V} \) is negative definite for sufficiently large \( \parallel e\parallel \). The uniform boundedness performance follows [6]. That is, given any r > 0 with \( \parallel e\left( {t_{0} } \right)\parallel \le r, \) where \( t_{0} \) is the initial time, there is a d(r) given by

$$ d\left( r \right) \, = \left\{ {\begin{array}{*{20}c} {r\left[ {\overline{\lambda }/\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } } \right]} \\ {R\left[ {\overline{\lambda }/\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } } \right]^{1/2} } \\ \end{array} } \right.^{1/2} \begin{array}{*{20}c} \quad{if \, r \, > \, R,} \\ \quad{if \, r \, \le \, R,} \\ \end{array} $$
(4.17)
$$ R = \left[ {\frac{\delta }{\lambda r}} \right]^{1/2} , $$
(4.18)

such that \( \parallel \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \left( t \right)\parallel \le d\left( r \right) \) for all \( t \ge t_{0} . \) Uniform ultimate boundedness also follows. That is, given any d with

$$ \overline{d} > R\parallel \overline{\lambda }/\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } \parallel^{\frac{1}{2}} , $$
(4.19)

we have \( \parallel \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \left( t \right)\parallel \le d,\forall t \ge t_{0} + \, T\left( {d,r} \right) \), with

$$ T\left( {d,r} \right) \, = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\frac{{\overline{\lambda }r^{2} - \lambda \overline{R}^{2} }}{{\lambda \overline{R}^{2} - \delta /\gamma }}} \\ \end{array} } & {\begin{array}{*{20}c} {if \, r \le \overline{R},} \\ {otherwise,} \\ \end{array} } \\ \end{array} } \right. $$
(4.20)
$$ \overline{R} = \overline{d}\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } /\overline{\lambda }} \right]^{1/2} . $$
(4.21)

The stability of the mechanical system is guaranteed and tracking error \( \parallel \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} \parallel \) can be made arbitrarily small by choosing large λ and/or γ. □

Remark

We have shown that fundamental properties explored in Sect. 3 are quite useful in constructing the legitimate Lyapunov function. The first five terms of the control scheme (3.9) are only for the nominal system (i.e., the system without uncertainty) while the last term is to compensate the uncertainty. For the last term, the magnitude γ is still free for we still have freedom on designing γ to determine the size of the ultimate boundedness. The larger the value of γ is, the smaller the size. This stands for a trade-off between the system performance and the cost which suggests an interesting optimal quest for the control design. We will pursue the optimal design in the following section.

5 Optimal gain design

Sections 3 and 4 show that a system performance can be guaranteed by a deterministic control scheme. By the analysis, the size of the uniform ultimate boundedness region decreases as γ increases. As γ approaches to infinity, the size approaches to 0. This rather strong performance is accompanied by a (possibly) large control effort, which is reflected by γ (assuming r has been chosen). From the practical design point of view, the designer may be interested in seeking an optimal choice of γ for a compromise among various conflicting criteria. This is associated with the minimization of a performance index.

We first explore more on the deterministic performance of the uncertain mechanical system. Define

$$ \kappa = \frac{{\overline{\lambda }}}{\lambda }, $$
(5.1)

where \( \overline{\lambda } \) is from (4.8) and λ is from (4.15) and κ > 0. Then by (4.8) and (4.15), we get

$$ \dot{V} \le \frac{\delta }{\gamma } - \lambda \left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\|^{2} = \frac{\delta }{\gamma } - \frac{1}{\kappa }\overline{\lambda }\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\|^{2} \le \frac{\delta }{\gamma } - \frac{1}{\kappa }V $$
(5.2)

with \( V_{0} = V\left( {t_{0} } \right) = V\left( {e\left( {t_{0} } \right)} \right) \). This is a differential inequality [8] whose analysis can be made according to Chen [4] as follows.

Definition 2

If \( w\left( {\psi ,t} \right) \) is a scalar function of the scalars ψ, t in some open connected set D, we say a function \( \psi \left( t \right), \, t_{0} \le t \le \overline{t},\overline{t} > t_{0} \) is a solution of the differential inequality [8]

$$ \dot{\psi }\left( t \right) \le w(\psi \left( t \right),t) $$
(5.3)

on \( \left[ {t_{0} ,\overline{t}} \right) \) if ψ(t) is continuous on \( \left[ {t_{0} ,\overline{t}} \right) \) and its derivative on \( \left[ {t_{0} ,\overline{t}} \right) \) satisfies (5.3).

Theorem 3

Let w(φ(t), t) be continuous on an open connected set D ∈ R 2 and such that the initial value problem for the scalar equation [8]

$$ \dot{\phi }\left( t \right) \le w(\dot{\phi }\left( t \right),t),\quad \varphi \left( {t_{0} } \right) \, = \, \phi_{0} $$
(5.4)

has a unique solution. If φ(t) is a solution of (5.4) on \( t_{0} \le t \le \overline{t} \) and ψ(t) is a solution of (5.3) on \( t_{0} \le t \le \overline{t} \) with \( \psi \left( {t_{0} } \right) \le \varphi \left( {t_{0} } \right) \), then \( \psi \left( {t_{0} } \right) \le \varphi \left( {t_{0} } \right) \) for \( t_{0} \le t \le \overline{t} \).

Instead of exploring the solution of the differential inequality, which is often non-unique and not available, the above theorems suggest that it may be feasible to study the upper bound of the solution. The reason is, however, based on that the solution of (5.4) is unique.

Theorem 4

Consider the differential inequality (5.3) and the differential Eq. (5.4). Suppose that for some constant L > 0, the function w(·) satisfies the Lipschitz condition [4]

$$ \left| {w\left( {v_{1} ,t} \right) \, - \, w\left( {v{}_{2},t} \right)} \right| \le L\left| {v_{1} - \, v_{2} } \right| $$
(5.5)

for all points \( \left( {v_{1} ,t} \right),\left( {v_{2} ,t} \right) \in D. \) Then any function ψ(t) that satisfies the differential inequality (5.3) for \( t_{0} \le t \le \overline{t} \) satisfies also the inequality

$$ \psi \left( t \right) \le \varphi \left( t \right) $$
(5.6)

for \( t_{0} \le t \le \overline{t} \).

We consider the differential equation

$$ \dot{r}\left( t \right) = - \frac{1}{\kappa }r\left( t \right) \, + \frac{\delta }{\gamma },r\left( {t_{0} } \right) = V_{0} . $$
(5.7)

The right-hand side satisfies the global Lipschitz condition with L = 1/κ. We proceed with solving the differential Eq. (5.7). This result in

$$ r\left( t \right) = \left( {V_{0} - \frac{\kappa \delta }{\gamma }} \right)exp\left[ { - \frac{1}{\kappa }\left( {t \, - \, t_{0} } \right) + \frac{\kappa \delta }{\gamma }} \right]. $$
(5.8)

Therefore,

$$ V \, \left( t \right) \le r\left( t \right) $$
(5.9)

or

$$ V\left( t \right) \le (V_{0} - \frac{\kappa \delta }{\gamma })exp\left[ { - \frac{1}{\kappa }\left( {t \, - \, t_{0} } \right)} \right] + \frac{\kappa \delta }{\gamma } $$
(5.10)

for all \( t \ge t_{0} \). By the same argument, we also have, for any \( t_{\rm s} \) and any \( \tau \ge t_{\rm s} , \)

$$ V(\tau ) \le \left( {V_{\text{s}} - \frac{\kappa \delta }{\gamma }} \right){ \exp }\left[ { - \frac{1}{\kappa }\left( {\tau \, - \, t_{\text{s}} } \right)} \right] + \frac{\kappa \delta }{\gamma }, $$
(5.11)

where \( V_{\text{s}} = V\left( {t_{\text{s}} } \right) = V\left( {e\left( {t_{\text{s}} } \right)} \right) \). The time \( t_{\text{s}} \) is when the control scheme (3.9) starts to be executed. It does not need to be \( t_{0} \).

By (4.4) \( V\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right) \ge \lambda \left\| e \right\|^{2} \), the right-hand side of (5.11) provides an upper bound of \( \lambda \left\| e \right\|^{2} \). This in turn leads to an upper bound of \( \left\| e \right\|^{2} \). For each \( \tau \ge t_{\text{s}} , \) let

$$ \eta \left( {\delta ,\gamma ,t,t_{\text{s}} } \right): = \left( {V_{\text{s}} - \frac{\kappa \delta }{\gamma }} \right){ \exp }\left[ { - \frac{1}{\kappa }\left( {\tau \, - \, t_{\text{s}} } \right)} \right]. $$
(5.12)
$$ \eta_{\infty } (\delta ,\gamma ): = \frac{\kappa \delta }{\gamma }. $$
(5.13)

Notice that for each \( \delta ,\gamma ,t_{\rm s} ,\eta (\delta ,\gamma ,\tau ,t_{\rm s} ) \to 0 \) as \( \, \tau \to \infty . \)

One may relate \( \eta (\delta ,\gamma ,t,t_{0} ) \) to the transient performance and \( \eta_{\infty } (\delta ,\gamma ) \) the steady-state performance. Since there is no knowledge of the exact value of uncertainty, it is only realistic to refer to \( \eta (\delta ,\gamma ,t,t_{0} ) \) and \( \eta_{\infty } (\delta ,\gamma ) \) while analyzing the system performance. We also notice that both \( \eta (\delta ,\gamma ,t,t_{0} ) \) and \( \eta_{\infty } (\delta ,\gamma ) \) are dependent on \( \delta \). The value of \( \delta \) is not known except that it is characterized by a membership function.

Definition 3

Consider a fuzzy set [5]

$$ N = \left\{ {(v,vN(v))|v \in N} \right\}. $$
(5.14)

For any function f: N → R, the D-operation \( D[f(\nu )] \) is given by

$$ D[f(\nu )] = \frac{{\int_{N} {f\left( \nu \right)\mu_{N} (v){\text{d}}v} }}{{\int_{N} {\mu_{N} (v){\text{d}}v} }} . $$
(5.15)

Remark

In a sense, the D-operation \( D\left[ {f\left( \nu \right)} \right] \) takes an average value of f(ν) over \( \mu N\left( \nu \right) \). In the special case that \( f\left( \nu \right) = \nu , \) this is reduced to the well-known center-of-gravity defuzzification method [14]. Particularly, if N is crisp (i.e., \( \mu N(\nu ) \, = \, 1 \) for all \( \nu \in N \)), \( D[f(\nu )] \, = \, f(\nu ). \)

Lemma 1

For any crisp constant a ∈ R,

$$ D\left[ {f(\nu )} \right] = \frac{{\int_{N} {af\left( \nu \right)\mu_{N} (v){\text{d}}v} }}{{\int_{N} {\mu_{N} (v){\text{d}}v} }} = a\frac{{\int_{N} {f\left( \nu \right)\mu_{N} (v){\text{d}}v} }}{{\int_{N} {\mu_{N} (v){\text{d}}v} }} = D[f(\nu )]. $$
(5.16)

We now propose the following performance index: For any \( t_{\rm s} \), let

$$ J\left( {\gamma ,t_{\text{s}} } \right): = D\left[ {\int_{{t_{\text{s}} }}^{\infty } {\eta^{2} \left( {\delta ,\gamma ,\tau ,t_{\text{s}} } \right){\text{d}}\tau } } \right] + + \, \alpha D\left[ {\eta_{{_{\infty } }}^{2} (\delta ,\gamma )} \right] \, + \beta \gamma^{2} = : \, J_{1} \left( {\gamma ,t_{\text{s}} } \right) \, + \, \alpha J_{2} \left( \gamma \right) \, + \, \beta J_{3} \left( \gamma \right), $$
(5.17)

where α, β > 0 are scalars. The performance index consists of three parts. The first part \( J_{1} \left( {\gamma ,t_{\text{s}} } \right) \) may be interpreted as the average (via the D-operation) of the overall transient performance (via the integration) from time \( t_{\text{s}} \). The second part \( J_{2} \left( \gamma \right) \) may be interpreted as the average (via the D-operation) of the steady-state performance. The third part \( J_{3} \left( \gamma \right) \) is due to the control cost. Both α and β are weighting factors. The weighting of \( J_{1} \) is normalized to be unity. Our optimal design problem is to choose γ > 0 such that the performance index \( J\left( {\gamma ,t_{\rm s} } \right) \) is minimized.

Remark

A standard LQG (i.e., linear-quadratic-Gaussian) problem in stochastic control is to minimize a performance index, which is the average (via the expectation value operation in probability) of the overall state and control accumulation. The proposed new control design approach may be viewed, loosely speaking, as a parallel problem, though not equivalent, in fuzzy mechanical systems. However, one cannot be too careful in distinguishing the differences. For example, the Gaussian probability distribution implies that the uncertainty is unbounded (although a higher bound is predicted by a lower probability). In the current consideration, the uncertainty bound is always finite. Also, LQG does not take parameter uncertainty into account.

One can show that

$$ \int_{{t_{\text{s}} }}^{\infty } {\eta^{2} \left( {\delta ,\gamma ,\tau ,t_{\text{s}} } \right)d\tau } = \left( {V_{\rm s} - \frac{\kappa \delta }{\gamma }} \right)^{2} \int_{{t_{\text{s}} }}^{\infty } {\exp \left[ { - \frac{2}{\kappa }\left( {\tau - t_{\text{s}} } \right)} \right]d\tau } = \left. {\left( {V_{\rm s} - \frac{\kappa \delta }{\gamma }} \right)^{2} \left( { - \frac{2}{\kappa }} \right)\exp \left[ { - \frac{2}{\kappa }\left( {\tau - t_{\rm s} } \right)} \right]d\tau } \right|_{{t_{\text{s}} }}^{\infty } = \left( {V_{\text{s}} - \frac{\kappa \delta }{\gamma }} \right)^{2} \frac{2}{\kappa } . $$
(5.18)

Taking the D-operation yields

$$ D\left[ {\smallint_{{_{{t_{\rm s} }} }}^{\infty } \eta^{2} \left( {\delta ,\gamma ,\tau ,t_{\rm s} } \right)d\tau } \right] = \left[ {\left( {V_{\text{s}} - \frac{\kappa \delta }{\gamma }} \right)^{2} \frac{2}{\kappa }} \right] = D\left[ {\left( {V_{\rm s}^{2} - 2V_{\rm s} \frac{\kappa \delta }{\gamma } + \left( {\frac{\kappa \delta }{\gamma }} \right)^{2} } \right)\frac{2}{\kappa }} \right] = \left( {D\left[ {V_{\rm s}^{2} } \right] - 2\frac{\kappa }{\gamma }D\left[ {V_{\rm s} \delta } \right] + \frac{{\kappa^{2} }}{{\gamma^{2} }}D\left[ {\delta^{2} } \right]} \right)\frac{\kappa }{2}. $$
(5.19)

The last equality is due to Lemma 1. Next, we analyze the cost \( {\text{J}}_{ 2} \left( \gamma \right). \) Again by Lemma 1, we have

$$ D\left[ {\eta_{\infty }^{2} \left( {\delta ,\gamma } \right)} \right] = D\left[ {\left( {\frac{\kappa \delta }{\gamma }} \right)^{2} } \right] = \frac{{\kappa^{2} }}{{\gamma^{2} }}D\left[ {\delta^{2} } \right] . $$
(5.20)

With (5.19) and (5.20) into (5.17), we also have

$$ J\left( {\gamma ,t_{\rm s} } \right): = \left( {D\left[ {V_{\rm s}^{2} } \right] - 2\frac{\kappa }{\gamma }D\left[ {V_{\rm s} \delta } \right] + \frac{{\kappa^{2} }}{{\gamma^{2} }}D\left[ {\delta^{2} } \right]} \right)\frac{\kappa }{2} + \alpha \frac{{\kappa^{2} }}{{\gamma^{2} }}D\left[ {\delta^{2} } \right] + \beta \gamma^{2} = :\kappa_{1} - \frac{{\kappa_{2} }}{\gamma } + \frac{{\kappa_{3} }}{{\gamma^{2} }} + \alpha \frac{{\kappa_{4} }}{{\gamma^{2} }} + \beta \gamma^{2}, $$
(5.21)

where \( \kappa_{1} = \, \left( {\kappa /2} \right)D\left[ {V_{\rm s}^{2} } \right],\quad \kappa_{2} = \, \kappa^{2} D\left[ {V_{\rm s} \delta } \right],\quad \kappa_{3} = \left( {\kappa^{3} /2} \right)D\left[ {\delta^{2} } \right],\quad \kappa_{4} = \kappa^{2} D\left[ {\delta^{2} } \right] \).

The optimal design problem is then equivalent to the following constrained optimization problem: For any t s,

$$ \mathop {\hbox{min} }\limits_{\gamma } J\left( {\gamma ,t_{\text{s}} } \right)\quad {\text{subject to}}\quad \gamma > 0. $$
(5.22)

By using the performance index in (5.21), we will then pursue the optimal solution in the next section.

6 The closed-form solution of optimal gain

For any \( t_{\text{s}} \), taking the first-order derivative of J with respect to γ

$$ \frac{\partial J}{\partial \gamma } = \frac{{\kappa^{2} }}{{\gamma^{2} }} - 2\frac{{\kappa_{3} }}{{\gamma^{3} }} - 2\alpha \frac{{\kappa_{4} }}{{\gamma^{3} }} + 2\beta \gamma = \frac{1}{{\gamma^{3} }}\left( {\kappa_{ 2} \gamma - 2\kappa_{ 3} - 2\alpha \kappa_{ 4} + 2\beta \gamma^{ 4} } \right).\quad \partial {\text{J}}. $$
(6.1)

That

$$ \frac{\partial J}{\partial \gamma } = 0 $$
(6.2)

leads to

$$ \kappa_{ 2} \gamma \, - { 2}\kappa_{ 3} - { 2}\alpha \kappa_{ 4} + { 2}\beta \gamma^{ 4} = \, 0 $$
(6.3)

or

$$ \kappa_{ 2} \gamma \, + { 2}\beta \gamma^{ 4} = { 2}\left( {\kappa_{ 3} + \, \alpha \kappa_{ 4} } \right). $$
(6.4)

Equation (6.4) is a quartic equation.

Theorem 6

Suppose \( {\text{D}}\left[ \delta \right] \ne 0 \) . For given \( \kappa_{ 1} ,\kappa_{ 2} ,\kappa_{ 3} ,\kappa_{ 4} , \) the solution γ > 0 to (6.4) always exists and is unique, which globally minimizes the performance index (5.21).

Proof

Let \( \theta \left( \gamma \right) \, : = \, \kappa_{ 2} \gamma + 2\beta \gamma^{ 4} . \) Then \( \theta \left( 0 \right) \, = \, 0 \) and \( \theta \left( \cdot \right) \) is continuous in γ. In addition, since \( \kappa_{ 2} \ge 0 \) and \( \beta > 0,\theta ( \cdot ) \) is strictly increasing in γ. Since \( {\text{D}}\left[ \delta \right] \ne 0 \), we have \( {\text{D}}\left[ \delta \right] > 0,\;{\text{D}}\left[ {\delta^{2} } \right] > 0,\kappa 3,\kappa 4> \, 0, \) and therefore \( 2\left( {\kappa_{ 3} + \, \alpha \kappa_{ 4} } \right) > 0 \, \) (notice that α, κ > 0). As a result, the solution γ > 0 to (6.4) always exists and is unique. For the unique solution γ > 0 that solves (6.4),

$$ \frac{{\partial^{ 2} {\text{J}}}}{{\partial \gamma^{ 2} }} = - \frac{1}{{\gamma^{4} }}\left( {\kappa_{ 2} \gamma - 2\kappa_{ 3} - 2\alpha \kappa_{ 4} + 2\beta \gamma^{ 4} } \right) + \frac{1}{{\gamma^{ 3} }}\left( {\kappa_{ 2} + { 8}\beta \gamma^{ 3} } \right) $$
$$ = \frac{1}{{\gamma^{ 3} }}\left( {\kappa_{ 2} + { 8}\beta \gamma^{ 3} } \right) > 0. $$
(6.5)

Therefore, the positive solution γ > 0 of the quartic Eq. (6.4) solves the constrained minimization problem (5.22).□

Remark

In the special case that the fuzzy sets are crisp, D[δ] = δ, D[δ 2] = δ 2. The current setting still applies. The optimal design can be found by solving (6.4).The solutions of the quartic Eq. (6.4) depend on the cubic resolvent [3]

$$ z^{3} + \left( { - 4r_{1} } \right)z - r_{2}^{2} = 0 , $$
(6.6)

where

$$ r_{1} = - \frac{1}{\beta }\left( {\kappa_{3} + \, \alpha \kappa_{4} } \right), $$
(6.7)
$$ r_{2} = \frac{{\kappa_{2} }}{2\beta }. $$
(6.8)

Let \( p_{1} : = - 4r_{1} ,p_{2} : = - r_{2}^{2} \). The discriminant H of the cubic resolvent is given by

$$ H = \left( {\frac{{p_{1} }}{3}} \right)^{3} + \left( {\frac{{p_{2} }}{2}} \right)^{3} . $$
(6.9)

Since r < 0, H > 0. The solutions of the cubic resolvent are given by

$$ z_{1} = u + w, $$
(6.10)
$$ z_{2} = - \frac{(u + w)}{2} + (u - w)i\sqrt{\frac{3}{2}}, $$
(6.11)
$$ z_{3} = - \frac{(u + w)}{2} - (u - w)i\sqrt{\frac{3}{2}} , $$
(6.12)

where

$$ u = \left( { - \frac{{p_{2} }}{2} + \sqrt H } \right)^{\frac{1}{3}} , $$
(6.13)
$$ w = \left( { - \frac{{p_{2} }}{2} - \sqrt H } \right)^{\frac{1}{3}} . $$
(6.14)

The cubic resolvent possesses one real solution and two complex conjugate solutions. This in turn implies that the quartic equation has two real solutions and one pair of complex conjugate solutions. The maximum real solution, which is positive and is therefore the optimal solution to the constrained optimization problem, of the quartic equation is given by

$$ \gamma_{\text{opt}} = \frac{1}{2}(\sqrt {{\text{z}}_{ 1} } + \sqrt {{\text{z}}_{2} } + \sqrt {{\text{z}}_{3} } ) . $$
(6.15)

By using (6.4), the cost J in (5.21) can be rewritten as

$$ \begin{aligned} J = & \;\kappa_{1} - \frac{{\kappa_{2} }}{\gamma } + \frac{{\kappa_{3} }}{{\gamma^{2} }} + \alpha \frac{{\kappa_{4} }}{{\gamma^{2} }} + + \, \beta \gamma^{2} \\ = & \;\kappa_{1} - \frac{1}{{\gamma^{2} }}\left( {\kappa_{2} \gamma + 2\beta \gamma^{4} } \right) + \frac{{\kappa_{3} }}{{\gamma^{{_{2} }} }} + \alpha \frac{{\kappa_{4} }}{{\gamma^{{_{2} }} }} + 3\beta \gamma^{2} \\ = & \;\kappa_{1} - \frac{1}{{\gamma^{{_{2} }} }}\left[ {2\left( {\kappa_{3} + \, \alpha \kappa_{4} } \right)} \right] + \frac{{\kappa_{3} }}{{\gamma^{{_{2} }} }} + \alpha \frac{{\kappa_{4} }}{{\gamma^{2} }}\gamma 2 + \, 3\beta \gamma^{2} \\ = & \;\kappa_{1} - \frac{1}{{\gamma^{{_{2} }} }}\left( {\kappa_{3} + \, \alpha \kappa_{4} - 3\beta \gamma^{4} } \right). \\ \end{aligned} $$
(6.16)

With (6.15), the minimum cost is given by

$$ J_{\hbox{min} } = \,\kappa_{1} - \frac{4}{{\left( {\sqrt {z_{1} } + \sqrt {z_{2} } + \sqrt {z_{3} } } \right)}}\left( {\kappa_{3} + \, \alpha \kappa_{4} - \frac{3}{16}\beta \left( {\sqrt {z_{1} } + \sqrt {z_{2} } + \sqrt {z_{3} } } \right)^{4} } \right) . $$
(6.17)

Remark

Combining the results of Sects. 4, 5, 6, and 7, the robust control scheme (3.9) using the optimal design of γ > 0 renders the tracking error e of the closed-loop mechanical system uniformly ultimately bounded (with the initial state \( e(t_{\text{s}} ) \)). In addition, the performance index \( {\text{J}} \) in (5.21) is globally minimized.

The optimal design procedure is summarized as follows:

  • Step 1 For a given inertia matrix M, obtain γ and \( \overline{\gamma } \).

  • Step 2 According to \( \left\| \varPhi \right\| \) in (3.4), obtain ζ and ρ in (3.6).

  • Step 3 Based on the \( {\text{V }}\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\text{e}}} \right) \) \( {\text{e}}\left( {{\text{t}}_{\text{s}} } \right)). \) V (e) in (4.1), solve for the \( \overline{\lambda}\) in (4.8). For given S, P’s, and D’s, solve for the λ in (4.15). Thus, κ is given in (5.1).

  • Step 4 Using the ζ obtained in Step 2 and the \( V_{\rm s} \) in (5.11), calculate \( \kappa_{ 1} ,\kappa_{ 2} ,\kappa_{ 3} ,\kappa_{ 4} \) in (5.21) based on the D-operation.

  • Step 5 For given α and β, solve for the \( \gamma_{\text{opt}} \) in (6.15) and the minimum cost given in (6.17).

  • Step 6 The optimal robust control scheme is given in (3.9).

7 Some limiting performance

As was shown earlier, the tracking error e of the controlled system enters the uniform ultimate boundedness region after a finite time and stays within the region thereafter. Thus, it is interesting to consider, in the limiting case, only the cost associated with this portion of performance.

In the limiting case, the transient performance cost \( J_{1} \left( {\gamma ,t_{\text{s}} } \right) \) is not considered. The cost is then dictated by that of the steady-state performance and the control gain:

$$ J\left( \gamma \right) = \, \alpha J_{2} \left( \gamma \right) + \beta J_{3} \left( \gamma \right) = \alpha \frac{{\kappa_{4} }}{{\gamma^{2} }} + \beta \gamma^{2} . $$
(7.1)

The quartic Eq. (6.4) is reduced to

$$ \beta \gamma^{4} = \alpha \kappa_{4} . $$
(7.2)

Its positive solution is given by

$$ \gamma_{opt} = \left( {\frac{\alpha }{\beta }\kappa_{4} } \right)^{\frac{1}{4}} . $$
(7.3)

With (7.2) into (7.1),

$$ J = \frac{1}{{\gamma^{2} }}\left( {\alpha \kappa_{4} + \, \beta \gamma^{4} } \right) = \frac{{2\alpha \kappa_{4} }}{{\gamma^{2} }}. $$
(7.4)

Using (7.3), the minimum cost is then

$$ J_{ \hbox{min} } = 2\sqrt {\alpha \beta \kappa_{ 4} } . $$
(7.5)

If the weighting \( \alpha \to \infty , \) then in the quartic equation, the positive solution \( \gamma \to \infty . \) This simply means that the relative cost of the ultimate boundedness region (as is given by \( \alpha J_{ 2} \left( \gamma \right)) \) is high and the control gain, which is relatively cheap, is turned high.

If \( \beta \to \infty , \) then in the quartic equation, the positive solution \( \gamma \to 0, \) this shows the other extreme case when the control is very expensive.

8 Application

Consider the two-link planar manipulator on a vertical plane as shown in Fig. 1. This manipulator is used to convey the load to a designated place. The load may be parts in the factory, solid waste after an earthquake, or packages in the storehouse. Considering the cost, humans first sort out the light, medium, and heavy things based on their own fuzzy judge. Therefore, the load is uncertain and should be described in a fuzzy way.

Fig. 1
figure 1

Planar manipulator with fuzzy uncertain load

Full size image

Friction is not considered. The masses of links one and two are \( m_{1} \) and \( m_{2} \), respectively. The lengths are \( l_{1} \) and \( l_{2} \). The load mg is uncertain. External torques \( \tau = [\mu_{1} \mu_{2} ]^{T} \) (the control) are imposed on the joints.

We choose two generalized coordinates \( q: = [q_{1} ,q_{2} ]^{T} = [\theta_{1} ,\theta_{2} ]^{T} \) to describe the system. The two coordinates are independent of each other. The equation of motion can be written in matrix form using Lagrange’s equation as

$$ M(q){\ddot{q}} + C(q,\dot{q})\dot{q} + G(q) + T(q,\dot{q}) = \tau, $$
(8.1)

where

$$ \begin{aligned} q = & \left[ \begin{aligned} \theta_{1} \hfill \\ \theta_{2} \hfill \\ \end{aligned} \right],\quad \dot{q} = \left[ \begin{aligned} \dot{\theta }_{1} \hfill \\ \dot{\theta }_{2} \hfill \\ \end{aligned} \right],\quad {\ddot{q}} = \left[ \begin{aligned} \ddot{\theta }_{1} \hfill \\ \ddot{\theta }_{2} \hfill \\ \end{aligned} \right],\quad \tau = \left[ \begin{aligned} u_{1} \hfill \\ u_{2} \hfill \\ \end{aligned} \right] \\ M(q) = & \left( {\begin{array}{*{20}c} {\frac{1}{3}(m_{1} l_{1}^{2} + m_{2} l_{2}^{2} ) + m_{2} l_{1}^{2} + m_{2} l_{1} l_{2} \cos \theta_{2} } & {\frac{1}{3}m_{2} l_{2}^{2} + \frac{1}{2}m_{2} l_{1} l_{2} \cos \theta_{2} } \\ {\frac{1}{3}m_{2} l_{2}^{2} + \frac{1}{2}m_{2} l_{1} l_{2} \cos \theta_{2} } & {\frac{1}{3}m_{2} l_{2}^{2} } \\ \end{array} } \right) \\ C(q,\dot{q}) = & \left( {\begin{array}{*{20}c} { - m_{2} l_{1} l_{2} \sin \theta_{2} \dot{\theta }_{2} } & { - \frac{1}{2}m_{2} l_{1} l_{2} \sin \theta_{2} \dot{\theta }_{2} } \\ {\frac{1}{2}m_{2} l_{1} l_{2} \sin \theta_{2} \dot{\theta }_{1} } & 0 \\ \end{array} } \right) \\ G(q) =& \left( \begin{array}{l} \frac{1}{2}m_{1} gl_{1} \cos \theta_{1} + m_{2} gl_{1} \cos \theta_{1} + \frac{1}{2}m_{2} gl_{2} \cos (\theta_{1} + \theta_{2} ) \hfill \\ \frac{1}{2}m_{2} gl_{2} \cos (\theta_{1} + \theta_{2} ) \hfill \\ \end{array} \right) \\ T(q,\dot{q}) = & \left( \begin{array}{l} mg(l_{1} \cos \theta_{1} + l_{2} \cos (\theta_{1} + \theta_{2} )) \hfill \\ mgl_{2} \cos (\theta_{1} + \theta_{2} ) \hfill \\ \end{array} \right). \\ \end{aligned} $$
(8.2)

The desired trajectory \( q^{d} (t) \), the desired velocity and acceleration \( \dot{q}^{d} (t) \), \( {\ddot{q}}^{d} (t) \) are given by

$$ q^{d} (t) = \left[ \begin{aligned} \theta_{1}^{d} \hfill \\ \theta_{2}^{d} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} \cos t \hfill \\ \sin t \hfill \\ \end{aligned} \right],\quad \dot{q}^{d} (t) = \left[ \begin{aligned} \dot{\theta }_{1}^{d} \hfill \\ \dot{\theta }_{2}^{d} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} - \sin t \hfill \\ \cos t \hfill \\ \end{aligned} \right],\quad {\ddot{q}}^{d} (t) = \left[ \begin{aligned} \ddot{\theta }_{1}^{d} \hfill \\ \ddot{\theta }_{2}^{d} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} - \cos t \hfill \\ - \sin t \hfill \\ \end{aligned} \right]. $$
(8.3)

By using \( q = e + q^{d} ,\dot{q} = \dot{e} + \dot{q}^{d} ,{\ddot{q}} = {\ddot{e}} + {\ddot{q}}^{d} \), Eq. (8.1) can be rewritten as

$$ H(e + q^{d} ){\ddot{e}} + H(e + q^{d} ){\ddot{q}}^{d} + C(e + q^{d} ,\dot{e} + \dot{q}^{d} )(\dot{e} + \dot{q}^{d} ) + G(e + q^{d} ) = u, $$
(8.4)

where

$$ \begin{aligned} M(e + q^{d} ) = & \left( {\begin{array}{*{20}c} {\frac{1}{3}(m_{1} l_{1}^{2} + m_{2} l_{2}^{2} ) + m_{2} l_{1}^{2} + m_{2} l_{1} l_{2} \cos (e_{2} + \sin t)} & {\frac{1}{3}m_{2} l_{2}^{2} + \frac{1}{2}m_{2} l_{1} l_{2} \cos (e_{2} + \sin t)} \\ {\frac{1}{3}m_{2} l_{2}^{2} + \frac{1}{2}m_{2} l_{1} l_{2} \cos (e_{2} + \sin t)} & {\frac{1}{3}m_{2} l_{2}^{2} } \\ \end{array} } \right) \\ C(e + q^{d} ,\dot{e} + \dot{q}^{d} ) = & \left( {\begin{array}{*{20}c} { - m_{2} l_{1} l_{2} \sin (e_{2} + \sin t)(\dot{e}_{2} + \cos t)} & { - \frac{1}{2}m_{2} l_{1} l_{2} \sin (e_{2} + \sin t)(\dot{e}_{2} + \cos t)} \\ {\frac{1}{2}m_{2} l_{1} l_{2} \sin (e_{2} + \sin t)(\dot{e}_{2} - \sin t)} & 0 \\ \end{array} } \right) \\ G(e + q^{d} ) = & \left( \begin{array}{l} \frac{1}{2}m_{1} gl_{1} \cos (e_{1} + \cos t) + m_{2} gl_{1} \cos (e_{1} + \cos t) + \frac{1}{2}m_{2} gl_{2} \cos (e_{1} + \cos t + e_{2} + \sin t) \hfill \\ \frac{1}{2}m_{2} gl_{2} \cos (e_{1} + \cos t + e_{2} + \sin t) \hfill \\ \end{array} \right) \\ T(e + q^{d} ,\dot{e} + \dot{q}^{d} ) = & \left( \begin{array}{l} mg(l_{1} \cos (e_{1} + \cos t) + l_{2} \cos (e_{1} + \cos t + e_{2} + \sin t)) \hfill \\ mgl_{2} \cos (e_{1} + \cos t + e_{2} + \sin t) \hfill \\ \end{array} \right). \\ \end{aligned} $$
(8.5)

The masses \( m_{1} \),\( m_{2} \) are known. Therefore, \( M = \overline{M},C = \overline{C},G = \overline{G} \) and \( \Delta M =\Delta C =\Delta G = 0 \). The mass \( m \) is uncertain with \( m = \overline{m} + \Delta m(t) \), where \( \overline{m} \) is the constant nominal value and \( \Delta m \) is the uncertainty. The nominal matrix \( \overline{T} \) and the uncertainty matrix ΔT are given by

$$ \begin{aligned} & \overline{T} = \left( {\begin{array}{*{20}l} {\overline{m}g(l_{1} \cos (e_{1} + \cos t) + l_{2} \cos (e_{1} + \cos t + e_{2} \sin t))} \hfill \\ {\overline{m}gl_{2} \cos (e_{1} + \cos t + e_{2} \sin t)} \hfill \\ \end{array} } \right) \\ & \Delta T = \left( {\begin{array}{*{20}l} {\Delta mg(l_{1} \cos (e_{1} + \cos t) + l_{2} \cos (e_{1} + \cos t + e_{2} \sin t))} \hfill \\ {\Delta mgl_{2} \cos (e_{1} + \cos t + e_{2} \sin t)} \hfill \\ \end{array} } \right) \\ \end{aligned}. $$
(8.6)

We choose S to be a 2 × 2 identity matrix. Therefore, we can get

$$ \varPhi : = - \Delta M({\ddot{q}}^{d} - S\dot{e}) - \Delta C(\dot{q}^{d} - S\dot{e}) - \Delta G - \Delta T $$
(8.7)
$$ \left\| \varPhi \right\| \le {\hat{\zeta }}^{T} (e,\dot{e},\upsigma,t)\hat{\rho }(e,\dot{e},t) \le \left\| {\hat{\zeta }} \right\|\left\| {\hat{\rho }} \right\| = \zeta \rho, $$
(8.8)

where

$$ \zeta = \left\| {\Delta m} \right\| $$
(8.9)

and

$$ \rho = \left\| {gl_{1} \cos (e_{1} + \cos t)} \right\| + \left\| {2gl_{2} \cos (e_{1} + \cos t + e_{2} + \sin t)} \right\|. $$
(8.10)

For the system, we choose \( m_{1} = m_{2} = 10,\;m = 1,\;l_{1} = l_{2} = 1,\;g = 10 \) and assume the uncertainty \( \Delta m \) is “close to 0.5,” or “close to 0.3” or “close to 0.1” corresponding to “heavy,” or “medium” or “light” and governed by three corresponding membership functions

$$ {\text{heavy}}:\mu \Delta m = \left\{ {\begin{array}{*{20}l} {2\nu ,} \hfill & {0 \le \nu \le 0.5} \hfill \\ {2 - 2\nu ,} \hfill & {0.5 \le \nu \le 1} \hfill \\ \end{array} } \right. $$
(8.11)
$$ {\text{medium}}:\mu \Delta m = \left\{ {\begin{array}{*{20}l} {\frac{10}{3}\nu ,} \hfill & {0 \le \nu \le 0.3} \hfill \\ {2 - \frac{10}{3}\nu ,} \hfill & {0.3 \le \nu \le 0.6} \hfill \\ \end{array} } \right. $$
(8.12)
$$ {\text{light}}:\mu \Delta m = \left\{ {\begin{array}{*{20}l} {10\nu ,} \hfill & {0 \le \nu \le 0.1} \hfill \\ {2 - 10\nu ,} \hfill & {0.1 \le \nu \le 0.2} \hfill \\ \end{array} } \right. $$
(8.13)

Set the design parameters P, and D to be the identity matrix \( I_{2 \times 2} \). Follow the design procedure, we have \( \overline{\lambda } = 60.68 \), \( \lambda = 1 \) , and \( \kappa = 60.68 \). If the load is “heavy”, by using the fuzzy arithmetic and decomposition theorem, we obtain \( \kappa_{1} = 1.7386 \times 10^{5} \), \( \kappa_{2} = 3.4842 \times 10^{4} \), \( \kappa_{3} = 893.71 \), \( \kappa_{4} = 29.46 \). By selecting five sets of weighting α and β, the optimal gain \( \gamma_{\text{opt}} \) and the corresponding minimum cost \( J_{\hbox{min} } \) are summarized in Table 1. If the load is “medium,” we obtain \( \kappa_{1} = 1.7386 \times 10^{5} \), \( \kappa_{2} = 2.0914 \times 10^{4} \), \( \kappa_{3} = 145.23 \), \( \kappa_{4} = 4.79 \). By selecting five sets of weighting α and β, the optimal gain, \( \gamma_{\text{opt}} \) and the corresponding minimum cost \( J_{\hbox{min} } \) are summarized in Table 2. If the load is “light,” we obtain \( \kappa_{1} = 1.7386 \times 10^{5} \), \( \kappa_{2} = 6.700 \times 10^{3} \), \( \kappa_{3} = 1.4348 \), \( \kappa_{4} = 0.0474 \). By selecting five sets of weighting α and β, the optimal gain \( \gamma_{\text{opt}} \) and the corresponding minimum cost \( J_{\hbox{min} } \) are summarized in Table 3.

Table 1 Weighting/optimal gain/minimum cost for heavy load
Full size table
Table 2 Weighting/optimal gain/minimum cost for medium load
Full size table
Table 3 Weighting/optimal gain/minimum cost for light load
Full size table

For numerical simulation, we choose \( t_{\text{s}} = 0 \) and the initial condition \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} (0) = [1111]^{T} \). We choose the uncertainty as \( \Delta m = 0.5 + \cos (10t) \) for the heavy load, \( \Delta m = 0.3 + \cos (10t) \) for the medium and \( \Delta m = 0.1 + \cos (10t) \) for the light.

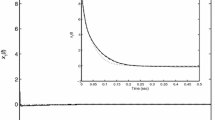
Figure 2 shows comparison of the tracking error norm \( \left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\| \) trajectory with the proposed control (for the heavy load, \( \gamma_{\text{opt}} = 29.6119 \) when \( \alpha = \beta = 1 \)) and with the nominal PD control (without the part of control that governs the uncertainty i.e., \( \gamma = 0 \)). The trajectory \( \left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\| \) with the proposed control enters a much smaller region around 0 after some time (hence ultimately bounded) than the trajectory only with the nominal PD control. For the medium and light load, the figures are similar and also show that the trajectory \( \left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} } \right\| \) with the proposed control is ultimately bounded, so we do not include the figures here.

Fig. 2
figure 2

Comparison of fuzzy mechanical system performances

Full size image

9 Conclusions

Fuzzy description of uncertainties in mechanical systems is employed and we incorporate fuzzy uncertainty and fuzzy performance into the control design. A new robust control scheme is proposed to guarantee the deterministic performance (including uniform boundedness and uniform ultimately boundedness). The control is deterministic and is not if–then rules-based. The resulting controlled system is stable proved via the Lyapunov minimax approach. A performance index is proposed and by minimizing the performance index, the optimal design problem associated with the control can be solved. The solution of the optimal gain is unique and closed-form. The resulting control design is systematic and is able to guarantee the deterministic performance as well as minimizing the cost.