Introduction

Groundwater modelling plays a major role in proper management and conservation of groundwater resources. The accuracy of the model prediction depends upon the input parameters such as transmissivity, dispersivity and boundary conditions. Hence, an accurate determination or estimation of these parameters is crucial. The field measurement of most of these parameters are cumbersome, costly and have large uncertainties. Therefore, these parameters to be indirectly determined and groundwater models need to be calibrated with respect to the parameters, using inverse modelling.

A groundwater flow model is technically a forward problem that predicts the state variables by solving the appropriate governing equations when the system parameters, boundary conditions and control variables are known (Sun 1999). An inverse or backward modelling technique on the other hand is used to estimate the unknown system parameters (e.g., transmissivity, dispersivity, storage coefficient etc.), control variables (e.g., discharge, recharge etc.), boundary conditions of a system when the state variables (e.g., head, concentration) are known or given. The system parameters used in the model are iteratively adjusted in an inverse model so that the model reproduces actual measurements of the state variables as closely as possible. Existing methods for performing inverse modelling are the hit and trial method, direct method and indirect method (Sun 1999). Among the methods mentioned above, the indirect method is advantageous as it can optimally determine aquifer parameters independently of the governing equation and the initial and boundary conditions (De Filippis et al. 2016). Simulation–optimization (SO) approach is an indirect inverse modelling method that employs a forward simulation model (namely flow or transport model) and estimates the model parameters using an optimization technique. The SO-based model is least affected by intermediary processes and is scalable to actual field conditions with complex domain. It also avoids the complicated mathematical formulations associated with direct inversion.

The simulation model component of the SO approach evaluate the groundwater heads and contaminant concentrations in the aquifer. It can be achieved with the help of forward groundwater modeling. Groundwater modeling can be carried out with conventional numerical techniques namely, the finite difference method and the finite element method (Desai et al 2011). These conventional techniques require mesh construction, which can be computationally expensive. Remeshing is required in the case of adaptive analysis, which is further adds to the computational efforts. In order to address the above-mentioned issues, the meshless method has been proposed. In the meshless method, the problem area and its bounds are described using a collection of nodes. The solution is obtained by solving the governing equation without requiring how the nodes are related and connected (Liu and Gu 2005).

Several types of meshless methods were described by Liu and Gu (2005). Meshless methods are grouped into two categories: strong form and weak form, depending on the formulation. Some of the meshless methods commonly used to solve the groundwater flow and contaminant transport problems include point collocation method (PCM), element-free Galerkin method (EFG), meshless local Petrov Galerkin method (MLPG), etc. In strong form methods, point collocation method (PCM) (Meenal and Eldho 2011) or radial point collocation method (RPCM) (Singh et al. 2016) has been used in groundwater studies. Whereas in weak form methods, element-free Galerkin (EFG) (Kumar and Dodagoudar 2008a, b; Pathania et al. 2018), meshless local Petrov–Galerkin (MLPG) (Swathi and Eldho 2013; Mohtashami et al. 2017a, b; Das and Eldho 2022; Khalilabad et al. 2022; Sahranavard et al. 2023) and local radial point interpolation method (LRPIM) (Wang et al. 2005; Saeedpanah and Jabbari 2009; Saeedpanah et al. 2011; Swetha et al. 2022a, b) have been used in solving groundwater problems. Moreover, the shape function consistency needed by weak form meshless methods is lesser than strong form. The discretization in weak form reduces the order of the governing equation, which makes it simpler to apply Neumann boundary conditions (Liu and Gu 2005).

The optimization algorithms used in the indirect methods may be grouped into three categories namely, a search method which uses the values of objective functions, a gradient method which utilizes the gradient of the objective functions and a second-order method which makes use of the second derivative of objective function (Sun 1999).

SO models optimize/minimize the difference between the predicted and the observed data. SO approaches were first proposed by Gorelick et al. (1983) using linear programming and regression for optimization. Other optimization methods used in SO model are the non-linear optimization model (Mahar and Datta 2000; Datta et al. 2009), artificial neural network (ANN) (Zio 1997; Singh and Datta 2004; Singh et al. 2004; Garcia and Shigidi 2006; Das et al. 2023), genetic algorithm (GA) (El Harrouni et al. 1996; Singh and Datta 2006) etc. Swarm intelligence-based optimization techniques such as particle swarm optimization (Sudheer and Shashi 2012; Anshuman and Eldho 2019), cat swarm optimization (Thomas et al. 2018) were linked with the meshless simulation models like RPCM and MLPG to estimate the aquifer parameters.

In this study, the TLBO technique is coupled with the meshless LRPIM to develop the SO model (an indirect inverse method) for parameter estimation. The PSO based SO model is also developed to compare the solutions obtained from the SO model based on TLBO. The application of the developed SO model is demonstrated using a hypothetical and real field problems for estimating the aquifer parameters.

Methods

Governing equations and boundary conditions

Groundwater flow

The governing equation of groundwater flow in a two-dimensional heterogeneous confined aquifer is given as (Bear 1979):

$$\frac{\partial }{\partial x}\left[{T}_{x}\frac{\partial h}{\partial x}\right] + \frac{\partial }{\partial y}\left[{T}_{y}\frac{\partial h}{\partial y}\right]=S\frac{\partial h}{\partial t}+\sum_{w=1}^{n}{Q}_{w}\delta \left({\varvec{r}}-\boldsymbol{ }{{\varvec{r}}}_{{\varvec{w}}}\right)- f$$
(1)

The initial condition used for unsteady state (transient) analysis is,

$$h\left(x,y,0\right)=h_0\left(x,y\right)\;where\;x,y\;\in\Omega$$
(2)

There are two types of boundary conditions namely, Dirichlet boundary and Neumann boundary. These boundary conditions can be written as:

$$h\left(x,y,t\right)=h_1\left(x,y,t\right)\;where\;x,y\;\in\partial\Omega_1\;\left(\mathrm{Dirichlet}\;\mathrm{boundary}\right)$$
(3)
$$T\frac{\partial h}{\partial n} = q(x,y,t)\;{\space}where{\space}\;x,y\; \in \;\partial\Omega_2 \;(Neumann{\space}boundary)$$
(4)

where, \(h\left(x,y,t\right)\) is the piezometric head (m); \({h}_{0}\left(x,y\right)\) is the initial head in the flow domain (m); \(S\) is the storage coefficient; \(T\) is the transmissivity (m2/d); \({T}_{x}\), \({T}_{y}\) are the transmissivities (m2/d) in x and y directions; \({Q}_{w}\) is the source or sink term (m3/d/m2); \(q\left(x,y,t\right)\) is the known inflow rate (m3/d/m); \(f\) is a recharge rate (m/d); The flow domain is represented by Ω while the boundary is denoted by ∂Ω; \(\frac{\partial }{\partial n}\) represent the normal derivative to the boundary; \({h}_{1}\left(x,y,t\right)\) is the known head value at the boundary (m); \(\left({\varvec{r}}-\boldsymbol{ }{{\varvec{r}}}_{{\varvec{w}}}\right)\) is equal to \(\left(x- {x}_{w}\right) \left(y- {y}_{w}\right)\); δ is the Dirac-delta function.

Contaminant transport

The governing equation for contaminant transport in groundwater is given as (Freeze and Cherry 1979; Wang and Anderson 1995; Desai et al. 2011):

$$R\frac{\partial C}{\partial t}=\frac{\partial }{\partial x}\left[{D}_{xx}\frac{\partial C}{\partial x}\right]+\frac{\partial }{\partial y}\left[{D}_{yy}\frac{\partial C}{\partial y}\right]-\frac{\partial }{\partial x}\left({V}_{x}C\right)-\frac{\partial }{\partial y}\left({V}_{y}C\right)-\frac{{c}{\prime}w}{nb}-RC\lambda +\frac{{q}_{w}C}{n}$$
(5)

where R = 1 + \(\left[\frac{{\rho }_{b}{K}_{d}}{n}\right]\). Here, \({\rho }_{b}\) is the media bulk density; \({K}_{d}\) is the sorption coefficient; \({q}_{w}\) is the volumetric rate of pumping from source; \({D}_{xx}\), \({D}_{yy}\) are the dispersion coefficients along the x and y directions, [m2/d]; \({V}_{x}\), \({V}_{y}\) are the seepage velocity along the x and y directions, [m/d]; \(C\) is the concentration of the dissolved species [mg/l]; \(w\) is the elemental recharge rate with solute concentration \({c}{\prime}\); b is the aquifer thickness [m]; R is the retardation factor; n is the porosity; \(\lambda\) is the reaction rate constant [per day];

The boundary conditions considered are as follows:

$$C={C}_{O}$$
(6)
$$\begin{array}{c}D\frac{\partial C}{\partial n}=g\\ D\frac{\partial C}{\partial n} = 0\end{array}$$
(7)

where \({C}_{O}\) is known concentration at the boundary and \(g\) is gradient of concentration.

Simulation model

In this study, the meshless LRPIM is utilized to model the groundwater flow and contaminant transport. It employs the point interpolation method using the multi-quadrics radial basis functions (MQ-RBF) as the basis function for shape function (\(\varphi\)) interpolation and the local weak form discretization for the governing equations (Liu and Gu 2005). The MQ-RBF with optimized shape parameter values is used for the interpolation of shape functions. The MQ-RBF expression is as follows:

$${R}_{i}\left(x, y\right) = {\left[{r}_{i}^{2} + {C}_{s}^{2}\right]}^{q} = {\left[{\left(x- {x}_{i}\right)}^{2}+{\left(y- {y}_{i}\right)}^{2}+ {C}_{s}^{2}\right]}^{q}$$
(8)
$${C}_{{\text{s}}}= {\alpha }_{{\text{c}}}{d}_{{\text{c}}}$$
(9)

where \(q\) and \({C}_{{\text{s}}}\) are the shape parameters of the MQ-RBF and i is the node considered. In this study, the parameter q has been kept at 1.03, as in Liu and Gu (2005). \({C}_{{\text{s}}}\) is usually defined in terms of a characteristic length (\({d}_{{\text{c}}}\)) (Liu and Gu 2005). The optimized value of \({C}_{{\text{s}}}\) is kept at 4 \(\times {d}_{{\text{c}}}\) (Swetha et al. 2022a). The derivatives of the state variables \(h\left(x,y\right) {\text{and}} C(x,y)\) at any point \((x, y)\) are estimated using the procedure given in Swetha et al. (2022a) as below:

$$\frac{\partial h}{\partial x}= \frac{\partial {\Phi }^{T}}{\partial x}{h}_{i}= \sum\nolimits_{i=1}^{N}\frac{\partial {\Phi }_{i}}{\partial x}{h}_{i} ; \frac{\partial C}{\partial x}= \frac{\partial {\Phi }^{T}}{\partial x}{C}_{i}= \sum\nolimits_{i=1}^{N}\frac{\partial {\Phi }_{i}}{\partial x}{C}_{i}$$
(10)
$$\frac{\partial h}{\partial y}= \frac{\partial {\Phi }^{T}}{\partial y}{h}_{i}= \sum\nolimits_{i=1}^{N}\frac{\partial {\Phi }_{i}}{\partial y}{h}_{i} ; \frac{\partial C}{\partial y}= \frac{\partial {\Phi }^{T}}{\partial y}{C}_{i}= \sum\nolimits_{i=1}^{N}\frac{\partial {\Phi }_{i}}{\partial y}{C}_{i}$$
(11)

Here N is the number of nodes in the support domain.

LRPIM formulation for groundwater flow equation using the weighted residual method (Liu and Gu 2005) is given below:

$${\int }_{{\Omega }_{{\text{s}}}}\nabla \cdot \left(T\cdot \nabla h\right)v.d\Omega = {\int }_{{\Omega }_{{\text{s}}}}\sum\nolimits_{w=1}^{N}{Q}_{{\text{w}}}\delta \left(r- {r}_{{\text{w}}}\right)v.d\Omega -{\int }_{{\Omega }_{{\text{s}}}}fv.d\Omega +{\int }_{{\Omega }_{{\text{s}}}}{S}_{{\text{y}}}\frac{\partial h}{\partial t}v.d\Omega$$
(12)

where, \(v\) is the Heaviside step function (weight function). The matrix form of Eq. (12) is obtained by simplifying it as detailed in Swetha et al. (2022a).

$$\left[K\right]\left\{{h}^{t+\Delta t}\right\}=\left[F\right]$$
(13)

where,

$$\left[K\right]= \left({\theta T}_{j}{\int }_{{\partial \Omega }_{s}}\left[\frac{\partial {\varphi }_{i}\left(r\right)}{\partial x}{n}_{x}+\frac{\partial {\varphi }_{i}\left(r\right)}{\partial y} {n}_{y}\right]d\Omega - {\int }_{{\Omega }_{s}}\left[\frac{S }{\Delta t}\right]d\Omega \right)$$
(14)
$$\left[F\right]= {\int }_{{\Omega }_{s}}\sum\nolimits_{w=1}^{n}{Q}_{w}\delta \left(r- {r}_{w}\right)d\Omega - {f}_{j}{A}_{\Omega }-\left(\left(1-\theta \right){T}_{j}{\int }_{{\partial \Omega }_{s}}\left[\frac{\partial {\varphi }_{i}\left(r\right)}{\partial x}{n}_{x}+\frac{\partial {\varphi }_{i}\left(r\right)}{\partial y}{n}_{y}\right]d\Omega -{\int }_{{\Omega }_{s}}\left[\frac{S }{\Delta t}\right]d\Omega \right){h}_{i}^{t}$$
(15)

Similar formulation is followed for the contaminant transport equation in an aquifer (Swetha et al. 2022b).

For contaminant transport, the K and F matrix are given as

$$\left[K\right]\left\{{C}^{t+\Delta t}\right\}=[F]$$
(16)

where,

$$\left[K\right]=\left(\left({D}_{j}\left( {\int }_{{\partial \Omega }_{s}}\left(\frac{\partial {\Phi }_{i}\left(r\right)}{\partial x}{n}_{{\text{x}}}+\frac{\partial {\Phi }_{i}\left(r\right)}{\partial y} {n}_{{\text{y}}}\right)d\Omega \right)-V\left( {\int }_{{\Omega }_{s}}\left(\frac{\partial {\Phi }_{i}\left(r\right)}{\partial x}+\frac{\partial {\Phi }_{i}\left(r\right)}{\partial y} \right)d\Omega \right)\right)\uptheta -{\int }_{{\Omega }_{{\text{s}}}}\frac{R}{\Delta t}d\Omega \right)$$
(17)
$$\left[F\right]=\left(\left(\left({-D}_{j}\right)\left({\int }_{{\partial \Omega }_{s}}\left(\frac{\partial {\Phi }_{i}\left(r\right)}{\partial x}{n}_{{\text{x}}}+\frac{\partial {\Phi }_{i}\left(r\right)}{\partial y} {n}_{{\text{y}}}\right) d\Omega \right)+V \left({\int }_{{\Omega }_{s}}\left(\frac{\partial {\Phi }_{i}\left(r\right)}{\partial x}+\frac{\partial {\Phi }_{i}\left(r\right)}{\partial y} \right)d\Omega \right) \right)\left(1-\theta \right)-{\int }_{{\Omega }_{{\text{s}}}}\frac{R}{\Delta t}d\Omega +{\int }_{{\Omega }_{{\text{s}}}}R\lambda d\Omega -{\int }_{{\Omega }_{{\text{s}}}}\frac{{q}_{w}}{\varepsilon }d\Omega \right){C}_{i}^{t} +{\int }_{{\Omega }_{{\text{s}}}}\frac{{c}{\prime}w}{\varepsilon b}d\Omega$$
(18)

where \(i\) is the number of nodes within the support domain and \(j\) is the index of the node considered.

The unknown state variables namely, head and concentration values in the aquifer domain were computed using the forward simulation model. The values of head/concentration values obtained at the observation wells were noted down. These values obtained were treated as the predetermined/observed values in the simulation–optimization model.

Optimization technique

Optimization of parameters is carried out by minimizing the error between the observed and simulated values which is defined using an objective function. Two variants of swarm optimization techniques namely, TLBO and PSO are used to minimize the objective function and thereby estimate the aquifer parameters.

Teaching learning-based optimization (TLBO)

TLBO is based on the effect of a teacher's influence on the achievement of students in a class (Rao et al. 2011). The two most important components of the algorithm are teachers and students. Implementation of TLBO is divided into two phases: the teacher and learner phase. The teacher phase simulates the student’s (i.e., learner’s) learning through the teacher. During this phase, a teacher shares knowledge with students and works to improve the average performance of the class. The learner phase simulates student’s learning by allowing them to communicate with one another. Students can also obtain information through conversing and connecting with their peers. If another learner has greater knowledge, the learner will learn the new information from him or her.

Particle swarm optimization (PSO)

The PSO algorithm has been inspired by the flocking behavior of birds in nature (Kennedy and Eberhart 1995). In this approach, each particle is assumed as a solution to an optimization problem. It is composed of two vectors: position and velocity. Position vectors are used to represent the variables in problems. For example, if the problem has two parameters, the particles will have two-dimensional position vectors. The magnitude and direction of each particle are defined by the velocity vector. The next iteration of the velocity (\({V}_{t+1}\)) and position (\({Position}_{t+1}\)) of each particle is given in Eq. (19) and Eq. (20), respectively.

$${V}_{t+1}=\left(w \times {V}_{t}\right)+\left[{c}_{1} \times rand(\mathrm{0,1}) \times \left({p}_{best}-position\right)\right]+ \left[{c}_{2} \times rand(\mathrm{0,1}) \times \left({g}_{best}-position\right)\right]$$
(19)
$$Position_{t+1}= Position_t + V_{t+1}$$
(20)

where, \(w\) is the inertia weight, \({c}_{1}\) and \({c}_{2}\) are acceleration factor, \({p}_{best}\) is the personal/individual best solution of each particle and \({g}_{best}\) is the global best solution.

TLBO and PSO comparison

The optimization model developed using the two optimization techniques is verified using standard or benchmark functions as given in Table 1. Convergence graphs obtained from the optimization model are shown in Fig. 1. The computational time taken by two different optimization models for 100 iterations is found to be less than 1 s. The model is able to predict the global minimum accurately.

Table 1 Expression of test function for optimization models
Full size table
Fig. 1
figure 1

Convergence graph for test function at the end of 100 iterations (a) Rastrigin (b) Goldstein-price

Full size image

In case of Rastrigin function both PSO and TLBO techniques take more iteration for convergence whereas, in Goldstein-price function convergence occurs faster.

Simulation–optimization model

The process of simulation–optimization typically involves defining the problem and objective function, developing a simulation model and applying optimization algorithms to find the optimal solution. The state variables (namely head and concentration) in an aquifer were determined with the forward simulation model. The solutions obtained from the forward model were compared with the observed/measured data. The optimization model uses an objective function to select a set of parameter values such that the differences between the observed and the simulated values of state variables in the observation wells are minimal. The mathematical formulation of an optimization model for parameter estimation can be given as

$$Minimize\left(\sum\nolimits_{i}{W}_{i}F({C}_{i}^{predicted}-{C}_{i}^{observed})\right)$$
(21)
$$Minimize\left(\sum\nolimits_{i}{W}_{i}F({h}_{i}^{predicted}-{h}_{i}^{observed})\right)$$
(22)

which is subject to a constraint,

$${K}^{L}\le K\le {K}^{U}$$
(23)

where \({W}_{i}\) is some weighing function. \({h}_{i}^{predicted}\), \({C}_{i}^{predicted}\) are the head and concentration values obtained from the simulation model at ith observation well. The \({h}_{i}^{observed}\), \({C}_{i}^{observed}\) are the observed head and concentration data at ith observation well. \({K}^{L}\) is the lower boundary limit for the unknown aquifer parameter and \({K}^{U}\) is the upper boundary limit for the unknown aquifer parameter. The objective function \(F\left(x\right)\) is usually defined as the sum of the squared differences between the observed and the simulated values of state variables in the observation wells considered for the study (\(n\) is the total number of observation wells).

$$F\left(h\right)={\sum }_{i=1}^{n}{({h}_{i}^{predicted}-{h}_{i}^{observed})}^{2}$$
(24)
$$F\left(C\right)={\sum }_{i=1}^{n}{({C}_{i}^{predicted}-{C}_{i}^{observed})}^{2}$$
(25)

The set of parameter values at which the objective function is found to be the minimum is taken as the solution or the best estimates of the parameters. The detailed procedure of the simulation–optimization model developed with LRPIM-TLBO and LRPIM-PSO model are given in the following sections.

LRPIM-TLBO model

Steps involved in LRPIM-TLBO SO model are:

  • Step 1: Input values such as number of parameters (\({N}_{P})\) to be estimated, lower and upper limit for each parameter, number of particles/students (\({N}_{S}\)) to be used and maximum number of iterations.

  • Step 2: Defining the objective function as given in Eq. (21) to Eq. (25).

  • Step 3: The initial population is generated using Eq. (26)

    $$X = {K}^{L}+\left({K}^{U}-{K}^{L}\right)\times rand ({N}_{S}, {N}_{P})$$
    (26)

  • Step 4: Select the teacher (\({X}_{best}\)), which is the solution corresponding to the best fitness value f(x), mean, teaching factor (\({T}_{f}\)).

    $${T}_{f} =round (1+ rand)$$
    (27)

where \({T}_{f}\) is rounded to take the value as 1 or 2.

  • Step 5: Teacher Phase: Generate a new solution with the above parameters using the equation given below.where Xmean is the mean/average of the positions of the population.

    $${X}_{new} =X+ \left\{rand(\mathrm{0,1}) \times \left[{X}_{best}- \left({T}_{f} \times {X}_{mean}\right)\right]\right\}$$
    (28)

Check whether the new solution is bound within the prescribed limits (if not regenerate the population). Obtain the fitness value for the new solution generated and accept the solution if the selection criteria are met (if \({f}_{new}\) <\({f}_{old}\)).

Learner Phase: Select the partner p randomly and generate a new solution with (\({X}_{p}\)).

For minimization

$$X_{new}=X+\left[rand(0,1)\times\left({X-X}_p\right)\right]\;if\;f<f_p$$
(29)
$$X_{new}=X-\left[rand(0,1)\times\left({X-X}_p\right)\right]\;if\;f>f_p$$
(30)

where \({X}_{p}\) is the position of the partner, \({f}_{p}\) is the fitness of the partner.

Check whether the new solution is bound within the prescribed limits. The new solution is updated if \({f}_{new}\) < \({f}_{old}\), otherwise not.

  • Step 6: Memorize the best solution and repeat the procedure (step 4 to 5) until the stopping criteria are met or till the maximum number of iterations.

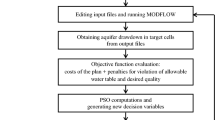
In the present study, the parameter setting for TLBO are: population size = 30, teaching factor (\({T}_{f}\)) = 1 or 2 is chosen randomly(Rao et al. 2011). The steps involved in LRPIM-TLBO model development is described in Fig. 2.

Fig. 2
figure 2

Flowchart for LRPIM-TLBO model

Full size image

LRPIM-PSO SO model

Steps involved in LRPIM-PSO SO model are:

  • Step 1: Define the objective function as given in Eq. (21) to Eq. (25).

  • Step 2: PSO parameters such as population size, the number of variables to be estimated, an upper and lower bound of the parameter, inertia weight, acceleration factor and a maximum number of iterations are fixed.

  • Step 3: Initialization of position and velocity using the following equations:

    $$Positions=lower\;limit+\lbrack random\left(N_S,N_p\right)\times\left(upper\;limit-lower\;limit\right)\rbrack$$
    (31)
    $$Velocity=+\lbrack random\left(N_S,\;N_P\right)\times\left(upper\;limit-lower\;limit\right)\rbrack$$
    (32)

  • Setp 4: With the position generated the objective function is evaluated.

  • Step 5: The position of a particle at which the objective function is minimum is the personal/individual best solution. The minimum value among the particle/individual best solution is taken as the global best solution and the position corresponding to the global best solution is taken as the global best position. Compute the particle/individual best (\({p}_{best}\)) for every particle and the global best (\({g}_{best}\)) value.

  • Step 6: Update the position of the particle using Eq. (33) and Eq. (34). Check whether the values are within the boundary limits (if not regenerate the population).

    $${V}_{t+1}=\left(w \times {V}_{t}\right)+\left[{c}_{1} \times random ({N}_{S}, {N}_{P})\times \left({p}_{best}-position\right)\right]+ \left[{c}_{2} \times random ({N}_{S}, {N}_{P})\times \left({g}_{best}-position\right)\right]$$
    (33)
    $${Position}_{t+1}= {Position}_{t}+ {V}_{t+1}$$
    (34)

  • Step 7: Retain the best value and repeat the procedure till the convergence or maximum number of iterations.

In the present study, the parameters settings for PSO are: population size = 30, \({c}_{1}\) = 1.2, \({c}_{2}\)= 1.1, and \(w\) = 0.9 to 0.4 varies linearly (decreasing with respect to the iteration number) (Thomas et al. 2018; Anshuman and Eldho 2019).

Here the developed LRPIM-TLBO and LRPIM-PSO SO models are used for estimating the parameters for hypothetical and real field problems.

Parameter estimation – Case studies

Case study 1– Flow parameter estimation

Here a hypothetical confined aquifer of size 6000 m × 6000 m with 9 zones of transmissivity is considered (Swathi and Eldho 2013) as shown in Fig. 3(a). A constant head boundary of 100 m is applied at the bottom side of the aquifer domain. The no flow boundary is applied on the top and right sides of the aquifer domain. The Neumann flux boundary with an inflow rate of 0.25 m2/day is applied on the left side of the aquifer domain. The value of transmissivity ranges from 5 to 150 m2/day (as shown in Fig. 3). Two recharge zones recharging at a rate of 0.00015 m/day and 0.00025 m/day are present as shown in Fig. 3(a). There are two wells; one is injecting water at a rate of 500 m3/day whereas the other well is withdrawing water at a rate of 1200 m3/day. The storage coefficient of the aquifer is assumed to be 0.001.

Fig. 3
figure 3

(a) Aquifer configuration for the hypothetical case (b) Nodal representation for the hypothetical case (c) Groundwater head contours

Full size image

Nodes were uniformly distributed at a nodal spacing of 500 m in both x and y directions. The nodal distribution in the aquifer domain is as shown in Fig. 3(b). Observation wells are considered at nodes 7, 33, 59, 85, 111, 137 and 163.

The shape parameters of the MQ-RBF and the size of the local support domain were optimally chosen, and the groundwater flow model (forward model) was constructed with given boundary conditions. The model is run for a total simulation period of 1000 days with a time step size of 1 day to determine the groundwater head contours. The groundwater head values obtained in the observation wells of all the zones are given in Table 2. The head values obtained were compared with the results obtained from the FEM model (Swathi and Eldho 2013) and found to be satisfactory.

Table 2 Comparison of head values obtained from observation wells at the end of 100 days
Full size table

The groundwater head values evaluated by the model are used as the observed values for inverse modeling (taken as an input into the optimization model). The aquifer parameter (transmissivity) was estimated by linking the simulation model with the optimization model to construct the SO model. The maximum number of iterations, the number of populations and other SO model parameters are set. The particles were generated randomly within the upper and lower bound of each parameter. Using the random population generated, the SO model is run iteratively. The model is run till the maximum number of iterations is reached to minimize the value of the fitness function. The value of transmissivities at which the fitness value is minimum is taken as the best estimate of transmissivities. The values of transmissivity obtained from the LRPIM-TLBO and LRPIM-PSO models are given in Table 3. Computational times taken by these models are also given in Table 3. It was found that PSO executes faster than TLBO. The root means square error (RMSE) calculated between the true values and the predicted values show that both methods give good results with an RMS error of less than 7. Zone 2 value has a higher percentage deviation of 12.9. The convergence graph obtained between the fitness value and number of iterations for LRPIM-TLBO and LRPIM-PSO is given in Fig. 4. As can be seen, the convergence of LRPIM-TLBO happens in a few iterations than LPIM-PSO model, though more computational time is required.

Table 3 Comparison of parameters estimated by PSO and TLBO with the true values
Full size table
Fig. 4
figure 4

Convergence graph for the hypothetical case using TLBO and PSO

Full size image

Case study 2 – Flow and transport parameter estimation

In this case study, the groundwater flow (transmissivity) and transport (dispersivity) parameter estimation of a confined aquifer is studied. The groundwater flow and contaminant transport model is constructed with the LRPIM technique for an aquifer with an area of 45 km2 as given in Fig. 5(a) (Singh et al. 2016). For the initial forward modeling, aquifer parameters and flow model simulations were taken from Swetha et al. (2022a). The flow model is executed to obtain the head values in the problem domain. In the case of contaminant transport, the longitudinal dispersivity (\({\propto }_{L}\)) for this problem is 20 m and the transverse dispersivity (\({\propto }_{T}\)) is taken as 10% of the longitudinal dispersivity. An area pollutant source is assumed to be a leaking contaminant of concentration 1000 mg/l as shown in Fig. 5(a). The nodes were established at an interval of 49.6 m along the length and 42.8 m along the width of the aquifer. The total number of nodes distributed throughout the problem domain is 1008. The optimized MQ-RBF shape parameter αc and the support domain size are 4 and 4 × dc, respectively (Swetha et al. 2022a). For time-stepping, the Crank–Nicholson method (\(\uptheta =0.5\)) was implemented. The time step size (Δt) used is 5 days and it is assumed that the whole area was pristine when the simulation started i.e., zero pollutant concentration as the initial condition. The contaminant transport model was constructed and run to track the contaminant plume movement in the aquifer. The transport model is run till the end of 5th year and the results (Table 4) were compared with a FEM model developed by Singh et al. (2016) and found to be satisfactory. Table 4 gives the contaminant concentration values (\({C}_{i}^{obs}\)) obtained from the models in various observation wells with percentage deviations.

Fig. 5
figure 5

(a) Aquifer domain with the TDS source (b) Concentration plume obtained after 500 days

Full size image
Table 4 Observed concentration values from observation wells at the end of the 5th year
Full size table

The SO model is constructed using the optimization algorithms of TLBO and PSO to estimate the groundwater flow and transport parameters. The values obtained from LRPIM- TLBO are compared with the LRPIM- PSO. Here, the groundwater flow parameters (transmissivity) are estimated as unknown parameters in the study area using the SO model (in Case A) and the transport parameters (dispersivity) are estimated along with the flow parameters as unknown in the study area (in Case B). The concentration values obtained at the observation wells were treated as the observed values and is used as input to the inverse model. The total simulation period was 500 days corresponding to 100-time steps. The concentration plume or spreading obtained after 500 days is shown in Fig. 5(b). The model is run for 100 iterations (the number of iterations were finalized based on the computational efficiency) for both cases. The population has the best fitness value at the end of the 100th iterations and the result obtained is taken as the best-predicted solution.

The simulated concentration values at the observation wells obtained using the transport model is used as an input to the optimization model. Maximum number of iterations and the number of populations are present for the developed SO model. The populations are generated randomly with the upper and lower bound of each parameter. The simulated values are compared with the observed values in the SO model to minimize the fitness value. The value of the aquifer parameters at the end of the 100th iteration is taken as the best value. The values of parameters obtained from LRPIM-TLBO and LRPIM-PSO are given in Table 5 and Table 6. The computational time taken by these models is also given in the same tables. The convergence graph for LRPIM-TLBO and LRPIM-PSO are given in Fig. 6(a) and Fig. 6(b), respectively. The model run was increased from 100 to 300 iterations to check for further improvement in predicted values. The result shows that there is a slight improvement in the predicted values. The root means square error (RMSE) calculated between the true values and the predicted values show that both models gave good results with an RMS error of less than 10.

Table 5 Comparison of parameters estimated by TLBO and PSO with the true values (for flow parameter estimation/ Case A)
Full size table
Table 6 Comparison of parameters estimated by TLBO and PSO (for flow and transport parameter estimation/ Case B)
Full size table
Fig. 6
figure 6

Convergence graph for real field problem using TLBO and PSO (a) flow parameter estimation / Case A (b) flow and transport parameter estimation / Case B

Full size image

As shown in Figures and Tables, the LRPIM-TLBO model converges in a few iterations than the LRPIM-PSO model, though the computational time is higher.

Discussion

Here, meshless LRPIM is used for groundwater flow and contaminant transport simulation. LRPIM has be used to simulate the flow and transport in groundwater. LRPIM has the advantage of not using any background cells for integration purposes as in other weak-form meshless methods such as EFGM. It does not need any meshing or re-meshing as in other conventional numerical methods. For inverse modeling and parameter estimation, two optimization models namely TLBO and PSO are used. The ability of the optimization model to predict the global minimum is verified using the two different standard test functions. The aquifer parameter (transmissivity, longitudinal and transverse dispersivity) was estimated using the developed SO model for hypothetical and real field cases. In the hypothetical case, the SO model is able to reproduce the transmissivity values very closely in all the zones except in zone 2 where a maximum deviation of 12.9 percent from the true value was observed. In the real field problem while estimating the transmissivity (case A) the value of transmissivity at zone 1 shows a maximum deviation of 16.9 percent from the actual value. It is observed that TLBO is able to produce better solution than PSO in all the zones. When the flow and transport parameters are estimated simultaneously (case B), the value of transmissivity at zone 9 and 10 shows a maximum deviation of 17 percent from the actual value.

The effectiveness of the optimization algorithm depends upon the algorithm parameter values used. The TLBO requires a lesser number of algorithm parameters whereas, many of the optimization techniques such as PSO require a proper selection of parameter to get the optimal solution of the problem. Thus, TLBO is easy to implement and results in rapid convergence within a smaller number of iterations. The LRPIM model used for the purpose of flow and transport simulation does not require any nodal connectivity information. Coupling LRPIM with TLBO to form LRPIM-TLBO makes use of these advantages to give good results with rapid convergence.

The convergence rate with respect to the number of objective function evaluations is studied in case study 2. The number of iterations was increased from 100 to 300 in case study 2 to check for any further improvement in the predicted values of both TLBO and PSO. It shows that even after increasing the number of iterations, only a slight improvement was observed from both the TLBO and PSO models. The RMSE values were calculated for case study 2 (for both case A and case B) at the end of the 100th and 300th iterations. It is found that the RMSE value is less than 10 percent for case A and is less than 5 percent for case B.

The computational time was observed for computations made on a computer having two Intel 2.0Ghz Broadwell cores and 10 GB RAM. It is found that PSO iterations runs around 2 times faster than TLBO. However, TLBO was able to converge in few iterations for the real field problem considered in this study.

The limitation of the study is that the accuracy of the parameter estimated depends upon the accuracy in the measured values from observation wells. Hence, the values have to be observed with low measurement error. The PSO model parameters such as inertial weight, and acceleration coefficients, which are to be fixed or optimized before coupling it with simulation models whereas TLBO requires lesser number of parameters to be fixed or optimized. On the other hand, LRPIM-TLBO requires more computational time. The present study has explored the applicability of the LRPIM-TLBO SO model as a tool for calibrating / estimating unknown aquifer parameters.

Conclusions

In this study, a simulation–optimization model is presented using the meshless LRPIM method and TLBO. The developed SO model is used for parameter estimation of a confined aquifer. The LRPIM-TLBO SO model results are compared with the LRPIM-PSO SO model. RMSE is used to quantify the error between the true values and predicted values of transmissivity and dispersivity. It is found that for the hypothetical case, the RMS error is less than 7, whereas for the real field case, the RMS error is less than 10. The TLBO model is coupled with LRPIM to estimate the flow and transport parameters and it was demonstrated that it can be used effectively in solving groundwater problems. The effectiveness of the developed LRPIM-TLBO SO model was tested by comparing the results with the LRPIM-PSO SO model. The number of unknown parameters affects the convergence rate of the models developed. The LRPIM-PSO was found to be computationally faster. The LRPIM-TLBO is found to give better accuracy and convergence rate than the LRPIM-PSO model for the problems considered. However, the computational time in LRPIM-TLBO is higher because of calculating the objective function in the teacher phase and the learner phase. The developed SO models may be applied to any complex/irregular aquifer for estimating the parameters and with suitable modifications.