Introduction

Indonesia is a country that is prone to natural disasters such as earthquakes, volcano eruptions, tsunamis, floods, and landslides. An earthquake is one of the frequent natural disasters in Indonesia. Earthquake zones on the southern coast of West Java and southeast Sumatra are known to be very active due to the confluence of the Indo-Australian plate and subduction under the Sunda plate (Supendi et al. 2022). In addition, earthquake events in Sumur Banten, which happened on January 2022, and Cianjur, which happened on November 2022, triggered megathrust issues. The Meteorology, Climatology, and Geophysics Agency of Indonesia (BMKG) also predicts the potential for a megathrust earthquake on the Sunda Plate with a magnitude of 8.7. These catastrophes cause significant damage to infrastructure, homes, and businesses, leading to substantial economic losses. As a mitigation effort, many studies have been conducted to identify the potential for an earthquake. Farid and Mase (2020) provided a seismic hazard mapping based on a shear strain indicator that may cause an earthquake in Bengkulu City, Indonesia, by performing microtremor measurements that observe the geophysical characteristics. Jena et al. (2020) estimated the earthquake risk based on probability and hazard as a mitigation effort of the earthquake occurrence in Palu, Indonesia. They used earthquake probability assessment (EPA), earthquake hazard assessment (EHA), susceptibility to seismic amplification (SSA), and earthquake vulnerability assessment (EVA) to generate the risk of earthquake occurrence. They also clustered the earthquake-prone areas using hierarchical and pure locational clustering. Fuady et al. (2021) summarized several disaster events in Indonesia as one of the disaster mitigation efforts to minimize disaster risk, especially in urban areas. They concluded three major disasters in 2018, including earth-shaking in West Nusa Tenggara, earthquake, tsunami, and liquefaction in Central Sulawesi, and tsunamis in Sunda Strait.

One of the quantities commonly used to measure earthquake risk is peak ground acceleration. The peak ground acceleration (PGA), also known as the acceleration value in the ground, can be used to calculate the earthquake danger and its link to the destruction of building infrastructure (Irwansyah et al. 2013). This measure builds a catastrophic model through the probabilistic seismic hazard analysis (PSHA), which can probabilistically estimate the ground movement events that could result in damage. Tavakoli and Ghafory-Ashtiany (1999) used historical earthquake data, geology, tectonics, fault activity, and seismic source models in Iran to build a probabilistic seismic hazard computation. They provided an Iranian seismic hazard map and probabilistic PGA estimates for 75 and 475 years of return periods. In those studies, they used the maximum expected parameter, \(M_{\max }\), the activity rate, \(\lambda\), and the b value of Gutenberg–Richter relation, and used the probabilistic method of maximum likelihood estimation adopted from Kijko and Sellevoll (1989). One of the assumptions held by this method is that the occurrence of earthquakes is assumed to be independent from time and space domains to conform with the Poisson distribution. This means that there is no mutual connection between the locations affected by the earthquake. A similar study has also been done by Ghodrati Amiri et al. (2003) and Hamzehloo et al. (2012). Ghodrati Amiri et al. (2003) and Hamzehloo et al. (2012) used the same approach as Tavakoli and Ghafory-Ashtiany (1999). Crowley and Bommer (2006) performed independent probabilistic seismic hazard assessment calculations simultaneously at several locations and combined the losses at each site for each annual frequency of exceedance to create loss exceedance curves. They calculated the PSHA hazard curves at a single site and assumed that there was no need to produce a correlated random field of ground motion.

All of the studies mentioned above assume that the occurrence of earthquakes calculated from the PGA value is independent of each other between locations. However, several studies have shown that the link between locations cannot be ruled out. Amendola et al. (2000) proposed a spatial-dynamic, stochastic optimization model that considers the complexities and dependencies of catastrophic hazards. The risk management model is tailored for this goal, explicitly incorporating the location’s geological characteristics, seismic risks, and the built environment’s sensitivity. Ansari et al. (2015) conducted a recent study that combined fuzzy clustering analysis and Monte Carlo simulation to determine and model the seismic sources. They compared the observed PGA on a grid of points and the simulation values and found that the definition of seismic sources and the distribution of earthquakes within each source are better consistent with seismological and seismotectonic observations when the findings of clustering analysis are used. The results showed that the clustered areas produced a higher estimated PGA value. This shows that the relationship between locations in the PGA calculation cannot be ignored because the clustered areas generally have similar characteristics. Cheng et al. (2020) also proved that ground motion parameters are interconnected.

PGA calculations generally involve several parameters, such as the earthquake’s magnitude, the horizontal distance to the epicenter, and the depth of the epicenter. Hence, the PGA calculation is univariate at each location point. However, intuitively, the movement of the ground in a specific area can be influenced by the movement of the ground in nearby locations. Therefore, the assumption of dependencies between locations must be addressed. This assumption has also been demonstrated by Amendola et al. (2000), Ansari et al. (2015), and Cheng et al. (2020), as mentioned before. Consequently, the univariate PGA calculations are considered less representative of the actual conditions. Using this basis, we propose a catastrophic model that assumes dependencies between the locations around the subject area of the calculation using a D-vine copula. A D-vine copula is an innovative mathematical technique that can model the probability distribution of the joint occurrence of multivariate events as an extension of the conventional bivariate copula (Bedford and Cooke 2001; Kurowicka and Cooke 2005; Aas et al. 2009; Brechmann and Czado 2013). Compared to conventional techniques such as linear regression models, the advantage of the D-vine copula model is that it can model the dependencies of multivariate events, both having linear and nonlinear relationships, which are not found in conventional models. In addition, the D-vine copula is also more flexible to use because the probability density function of multivariate events is decomposed into a bivariate function so that the dependency structures between locations that may vary can be identified. Therefore, this paper aims to develop an earthquake model based on simultaneous peak ground acceleration occurrences using the D-vine copula.

We also develop the model computationally using an open-source framework to facilitate the computation process. We take the following steps: First, we identify and determine the earthquake sources. Then we determine the peak ground acceleration (PGA) for the given epicenter using probabilistic seismic hazard analysis (PSHA). Subsequently, we determine the dependencies between locations in the area that contains the earthquake epicenter using a D-vine copula. Finally, we determine the exceedance probability of the original and D-vine copula-based PGA, compare the results, and draw conclusions. This model would support the development of all needs related to catastrophic models, such as disaster mitigation, catastrophic insurance, and so on.

Methodology

In this section we provide an in-depth discussion about the original model of the univariate PGA calculation through the use of the ground motion prediction equation and the basic concept of the D-vine copula in modeling the dependence of PGA between the quake-affected areas.

Ground motion prediction equation (GMPE)

The development and testing of earthquake models requires the use of accurate and thorough earthquake catalog data. The International Seismological Centre (ISC) is one such source of earthquake catalog data. The ISC keeps track of earthquakes that happened all around the world from 1904 to the present. In order to concentrate primarily on earthquakes that happened in and close to the Banten Region, we have filtered the ISC earthquake database for this study. We also added updated data found from several other sources. Banten is a seismically active area situated in the western portion of Indonesia’s Java Island. We can learn more about the seismic activity and features of the Banten Region by restricting the earthquake catalog data to this area.

Ground motion is a crucial element in earthquake modeling that must be precisely observed and accounted for in models. The term “ground motion" describes the trembling that takes place at a specific location when an earthquake occurs. Peak ground acceleration (PGA), a popular gauge of ground motion, is the highest acceleration a particle on the ground experiences during an earthquake (GEM Foundation 2021).

Ground motion sensors, often positioned at key points in earthquake-prone areas, can be used in practice to assess PGA. The models that are created to estimate PGA values for places without sensors can subsequently be built using the recorded ground motion data.

In order to predict the shaking that might happen at a location when an earthquake of a specific magnitude occurs, ground motion prediction equations (GMPEs) are utilized. GMPEs are empirical models that forecast the anticipated ground motion for future earthquakes of comparable magnitude and distance using recorded ground motion data from prior earthquakes.

The selection of GMPEs is extremely reliant on the local environment in one place. The equality of the geological and tectonic conditions in the region where GMPE is created is the basis for selecting GMPE (Irsyam et al. 2008). We have chosen GMPE for this study from Youngs et al. (1997), which is used by Irwansyah et al. (2013) to model earthquake hazards in Aceh. The formula is as follows:

$$\begin{aligned} \ln Y_i= & \, 0.2418 + 1.414 M + C_1 + C_2 (10-M)^3 \nonumber \\{} & {} + C_3 \ln \left( r_{rup,i} + 1.7818 e^{0.554 M}\right) \nonumber \\{} & {} + 0.00607 H + 0.3845 Z_T \end{aligned}$$
(1)

where \(Y_i\) is the PGA value of location i, M is the earthquake magnitude, \(r_{rup, i}\) is the horizontal distance of location i from the epicenter, H is the depth of the earthquake center, and \(Z_T\) is the indicator function identifying whether it is an interface (0) or intraslab (1) earthquake. These are the output and four input parameters for the GMPE. All earthquakes from the catalog data are assumed to be interface earthquakes.

Based on the GMPE formula defined in Eq. 1, the PGA value can be calculated as follows.

$$\begin{aligned} Y_i= & \, \exp \left\{ 0.2418 + 1.414 M + C_1 + C_2 (10-M)^3\right. \nonumber \\{} & {} + C_3 \ln \left( r_{rup,i} + 1.7818 e^{0.554 M}\right) \nonumber \\{} & {} \left. + 0.00607 H + 0.3845 Z_T\right\} \end{aligned}$$
(2)

The PGA formula defined in Eq. 2 is used to calculate the ground motion in a single site, overriding any links to other sites. Through the D-vine copula, we accommodate the dependence assumption of the joint occurrence of the ground motion in the affected locations (Table 1).

The United States Geological Survey developed the shake maps based on the value of the PGA which characterize the range value of the PGA with its perceived shaking and potential damage as presented in Table 1 (U.S. Geological Survey 2011).

Table 1 Shake maps
Full size table

D-vine copula

The calculation of the PGA using GMPE in Eq. 2 is a univariate and deterministic calculation. Meanwhile, as we have previously explained, the acceleration of ground motion in an area is very likely to be affected by ground motion in the surrounding areas so univariate calculations that are independent of each other between locations become less relevant. In addition, even though the PGA calculation is deterministic, earthquake events that result in accelerated ground motion are probabilistic, so PGA events are also indirectly probabilistic. Based on these two reasons, it is necessary to have a PGA calculation that considers the influence or interdependence between PGA events in adjacent locations. In this paper, we propose the use of the copula function, specifically the D-vine copula, to evaluate the dependency of multivariate PGA events.

Suppose \(Y_1, Y_2, \ldots , Y_n\) is a set of random variables representing the PGA values of each location and have a joint probability function \(f(y_1, \ldots , y_n)\) for the joint occurrence of the PGA events. This joint probability function can be factorized as.

$$\begin{aligned}{} & {} f(y_1, \ldots , y_n) \nonumber \\{} & {} \quad = f(y_n) f(y_{n-1}|y_n) f(y_{n-2}|y_{n-1},y_n) \cdots f(y_1|y_2, \ldots , y_n). \end{aligned}$$
(3)

The joint probability function of the PGA occurrences implicitly describes both the marginal behavior of individual variables of PGA in each location and the structure of their dependencies. Copula, a multivariate distribution function, describes their dependence structure (Aas et al. 2009). Based on Sklar’s theorem (Sklar 1959), the multivariate distribution function of the joint occurrences of PGA events can be expressed as a copula function.

$$\begin{aligned} F(y_1, \ldots , y_n) = C(F_1(y_1), \ldots , F_n(y_n)). \end{aligned}$$
(4)

The joint probability function in Eq. 3 can also be expressed in the copula function by deriving the multivariate distribution function of Eq. 4 such that.

$$\begin{aligned} f(y_1, \ldots , y_n)= & {} \frac{\partial ^n}{\partial y_1 \ldots \partial y_n} F(y_1, \ldots , y_n) \nonumber \\= & {} \frac{\partial ^n}{\partial y_1 \ldots \partial y_n} C(F_1(y_1), \ldots , F_n(y_n)) \nonumber \\= & {} c_{1, \ldots , n}(F_1(y_1), \ldots , F_n(y_n)) f_1(y_1) \cdots f_n(y_n) . \end{aligned}$$
(5)

The multivariate density copula \(c_{1, \ldots , n}(F_1(y_1), \ldots , F_n(y_n))\) in Eq. 5 is quite complex; however, we can decompose it into the bivariate density copula. To do so, we can express the conditional probability function provided in Eq. 3 in the bivariate copula function so that later we can get the pair copula decomposition form of the multivariate density copula defined in Eq. 5. First, for the bivariate case, we have the following formula.

$$\begin{aligned} f(y_1, y_2) = c_{12} (F_1(y_1), F_2(y_2)) f_1(y_1) f_2(y_2). \end{aligned}$$
(6)

Therefore, the conditional probability function of \(f(y_1|y_2)\) can be written as

$$\begin{aligned} f(y_1|y_2) = c_{12}(F_1(y_1),F_2(y_2)) f_1(y_1) \end{aligned}$$
(7)

We can also decompose the other conditional probability provided in Eq. 3. For example, for the second conditional probability \(f(y_1|y_2,y_3)\) we have

$$\begin{aligned} f(y_1|y_2,y_3) = c_{12|3}(F(y_1|y_3), F(y_2|y_3)) f(y_1|y_3) \end{aligned}$$
(8)

or

$$\begin{aligned} f(y_1|y_2,y_3) = c_{13|2}(F(y_1|y_2), F(y_3|y_2)) f(y_1|y_2) \end{aligned}$$
(9)

By substituting Eq. 7 to Eq. 9, we have

$$\begin{aligned} f(y_1|y_2,y_3)= & {} c_{13|2}(F(y_1|y_2), F(y_3|y_2))\nonumber \\{} & {} c_{12}(F_1(y_1), F_2(y_2)) f_1(y_1) \end{aligned}$$
(10)

Therefore, the general formula for the conditional probability of the multivariate density function defined in Eq. 3 is

$$\begin{aligned} f(y_i|\textbf{y}) = c_{y_i \mathbf {y_j}|\mathbf {y_{-j}}} (F(y_i|\textbf{y}_{-j}), F(\mathbf {y_j|\textbf{y}_{-j}})) f(y_i|\textbf{y}_{-j}) \end{aligned}$$
(11)

where \(\textbf{y}_j\) is an arbitrarily chosen variable of \(\textbf{y}\) and \(\textbf{y}_{-j}\) is the \(\textbf{y}\)-vector excluding \(\textbf{y}_j\).

For multivariate distribution with higher dimensionality, many possible copula pairs exist. Bedford and Cooke (2001) introduced a Regular vine (R-vine) copula to help organize the copula pairs. Kurowicka and Cooke (2005) and Aas et al. (2009) provided special cases of R-vine copula, known as canonical (C-) and drawable (D-) vine copula. The vine copula decomposes the multivariate copula into bivariate copula through the nested set of trees which consist of nodes and edges. If we have n variables, then we will have \(n-1\) trees, each tree consists of n nodes and \(n-1\) edges. Specifically, for the C-vine copula, the tree structure is constructed into a star structure with a key node connecting to all other modes (Kurowicka and Cooke 2005; Aas et al. 2009; Cheng et al. 2020). While for the D-vine copula, the tree structure is constructed into a path, where each node is connected to no more than two other nodes (Aas et al. 2009; Cheng et al. 2020). In this paper, we focus on utilizing the D-vine copula because the pair of locations to be checked for dependencies are considered to have the same position; in other words, there is no specific location as a key variable as is commonly described in the C-vine copula. The pair structure of the D-vine copula for four variables is provided in Fig. 1.

Fig. 1
figure 1

Example of the tree structure of the D-vine copula for four variables

Full size image

Based on the pair decomposition, the multivariate density function of n variables of PGA events defined in Eq. 3 can be written as.

$$\begin{aligned} f(y_1, \ldots , y_n)= &\, \Pi _{k=1}^{d} f_k(y_k) \times \nonumber \\{} & {} \Pi _{i=1}^{d-1} c_{j,i+j|j+1, \ldots , (i+j-1)}(F(y_j|y_{j+1}, \nonumber \\{} & {} \ldots , y_{i+j-1}), F(y_{i+j}|y_{j+1}, \ldots , y_{i+j-1})) \end{aligned}$$
(12)

Parameter estimation of the D-vine copula is conducted using the two procedures of maximum likelihood estimation method: (1) parameter estimation for the marginal distribution and (2) for the copula function (Patton 2006; Jondeau and Rockinger 2006; Aas et al. 2009). Suppose \(\Psi\) and \(\Theta\) are the parameter spaces of the marginal distributions and the copula functions.

$$\begin{aligned} {\hat{\Psi }}= & {} \arg \max {\mathcal {L}}(\Psi |\tilde{\textbf{y}_i}) \end{aligned}$$
(13)
$$\begin{aligned} {\hat{\Theta }}= & {} \arg \max {\mathcal {L}}(\Theta |{\tilde{u}}, {\tilde{v}}) \end{aligned}$$
(14)

where \(\tilde{\textbf{y}}\) is the vector of the PGA values in location i, \({\tilde{u}} = F_i(y_i)\) and \({\tilde{v}} = F_j(y_j)\) are the cumulative distribution functions of the PGA values at location i and j, \(i \ne j\), and \({\mathcal {L}}(\Psi |\tilde{\textbf{y}})\) and \({\mathcal {L}}(\Theta |{\tilde{u}}, {\tilde{v}})\) are the log-likelihood functions of the marginal distributions and the copula functions, respectively.

Several popular copula families can be used, in Table 2 we provide some popular copula families.

Table 2 Copula families (Scholzel and Friederichs 2008; Weber 2015; Embrechts et al. 2003; Taillon and Miyagawa 2019; Buike 2018; Brechmann and Schepsmeier 2013)
Full size table

For the case of pairing PGA for several locations, suppose that \(Y_i\) be the PGA values of \(i = 1, 2, \ldots , n\) location. We can calculate the D-vine copula-based PGA by the following procedures. First, calculate the original PGA value using the GMPEs equation provided in Eq. 2. To identify which locations, have a strong relationship, calculate the correlation between each location using the three popular dependence measures: Pearson correlation coefficient, Spearman’s rho, and Kendall’s tau. Then pair the subject locations using the D-vine copula and estimate the parameters of the marginal distribution and the copula function using Eqs. 13 and 14. Last, estimate the PGA values of location i which already involves dependencies from PGA events in the surrounding areas using the D-vine copula regression, which is defined as the following conditional expectation.

$$\begin{aligned} E(Y_i|\textbf{Y})= & {} \int _{-\infty }^{\infty } y_i f(y_i|\textbf{y}) dy_i \nonumber \\= & {} \int _{-\infty }^{\infty } y_i c_{y_i \mathbf {y_j}|\mathbf {y_{-j}}} (F(y_i|\textbf{y}_{-j}), F(\mathbf {y_j|\textbf{y}_{-j}})) f(y_i|\textbf{y}_{-j}) dy_i \end{aligned}$$
(15)

where \(f(y_i|\textbf{y})\) is the conditional density function of a PGA event in location i given the occurrences of the PGA events in all other locations, which is obtained from the D-vine copula decomposition such derived in Eq. 11.

Probability of exceedance

The last part of the catastrophic model built using the D-vine copula is calculating the probability of exceedance (POE). POE is the probability that a random variable exceeds a certain amount of value. In probabilistic terminology, it is the survival function of the random variable (Casualty Actuarial Society 2021). In seismic hazard analysis, we calculate the exceedance probability to estimate the probability that, in any given year, the condition will exceed a certain value of PGA (Aslani and Miranda 2005; Bradley et al. 2009). In this paper, we use two approaches to calculate exceedance probabilities: (1) empirical POE and (2) parametric megathrust POE.

Empirical POE is calculated based on historical PGA values, i.e. PGA calculations resulting from original calculations and based on D-vine copulas. Empirical POE calculations are carried out to estimate how big the probability is that if one day an earthquake occurs, the event will cause ground motions that exceed the historical ground motion values. Dotson (2020) presents an empirical formula to calculate POE as follows.

$$\begin{aligned} P(Y_i > y_{i,j}) = \frac{m_j}{n+1} \end{aligned}$$
(16)

where \(P(Y_i > y_{i,j})\) is the probability of exceeding historical PGA value of epicenter j at location i, \(m_j\) is the rank of the PGA value j, and n is the number of observations.

Furthermore, the parametric megathrust POE is calculated to obtain the description of at what probability level the estimated PGA, both original and D-vine copula-based, will exceed the PGA value of the possibility of a megathrust event where the magnitude of the earthquake reaches 8.7 SR. First, we assume that the probability of the PGA of a megathrust event in location i is normally distributed (Septianusa and Ahdika 2015).

$$\begin{aligned} P(y_{i,m}) = \frac{1}{\sigma _{m} \sqrt{2 \pi }} \exp \left\{ -\left( \frac{y_{i,m} - \mu _{m}^2}{2 \sigma _{m}}\right) \right\} \end{aligned}$$
(17)

where \(y_{i,m}\) is the PGA value of a megathrust event in location i, \(\mu _{m}\) and \(\sigma _{m}\) are the mean and standard deviation of PGA of megathrust event. Then, we obtain the parametric megathrust POE by integration.

$$\begin{aligned} P (Y_i > y_{i,m})= & {} \frac{1}{\sigma _m \sqrt{2 \pi }} \int _{y_{i,m}}^{\infty } \exp \left\{ -\left( \frac{y_{i,m} - \mu _m^2}{2 \sigma _m}\right) \right\} d y_{i,m} \nonumber \\= & {} 1 - \phi \left( \frac{y_{i,m} - \mu _m}{\sigma _m}\right) \end{aligned}$$
(18)

Algorithm of the proposed model

All these procedures are encapsulated in the algorithm that we run on the following open-source framework, particularly in R software.


PGA Calculation Algorithm


Initialization Phase

  1. 1.

    Load the required package.

  2. 2.

    Load the earthquake catalog data.

Main Phase

  1. 1.

    Prepare the longitude and latitude data for each epicenter.

  2. 2.

    Prepare the grid points or the location coordinates where the PGA value will be calculated.

  3. 3.

    Calculate the distance between the location and the epicenter using the Haversine distance.

    $$\begin{aligned} hav(\theta ) = hav(\phi _2 - \phi _1) + \cos (\phi _1) \cos (\phi _2) hav (\lambda _2 - \lambda _1) \end{aligned}$$
    (19)

    where \(\theta\) is the central angle between any two points on a sphere, \(\phi _1\) and \(\phi _2\) are the latitude of locations 1 and 2, and \(\lambda _1\) and \(\lambda _2\) are the longitude of the location 1 and 2.

  4. 4.

    Calculate the PGA value using Eq. 2.

Additional Phase

  1. 1.

    Load the map data for Indonesia.

  2. 2.

    Create the map providing the PGA value of each location.

After calculating the PGA value, hereinafter referred to as Original PGA, we estimate the D-vine copula-based PGA value, which is provided in the following algorithm.


D-vine copula-based PGA


Initialization Phase

  1. 1.

    Load the required package.

  2. 2.

    Load the Original PGA that has been calculated in the first algorithm.

  3. 3.

    Plot the correlation between the Original PGA in several locations.

Main Phase

  1. 1.

    Estimate the marginal distribution function of the Original PGA of each location.

  2. 2.

    Estimate the parameter of the D-vine copula.

  3. 3.

    Estimate the D-vine copula-based PGA using Eq. 15.

  4. 4.

    Calculate the empirical and parametric megathrust POE (Eqs. 16 and 18).

Results

Data used in this study is Earthquake Catalogue Data taken from International Seismological Centre (1904–2019) (International Seismological Center 2023). In this study, the data is filtered to earthquakes that happened around the Banten Region with additional latest data from Wikipedia up to 2022. The data consist of 60 earthquake epicenters. The variables used are the magnitude of the earthquake in each epicenter, M, the depth of the earthquake epicenter, H, and latitude and longitude of the subject locations i, \(\phi _i\) and \(\lambda _i\). Most of the epicenters were located in the Indian Ocean area (located to the left and below Banten Region) and the Java Sea (water area above Banten Region).

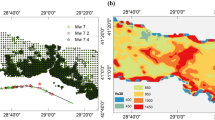
In this study, we build the catastrophe model for 12 major areas in the Banten–Jakarta Region, two provinces close to the center of the Indonesian government, based on earthquake epicenters located in the Banten Region. The 12 major areas include Ujung Kulon, Lebak, Cilegon, Pandeglang, Serang City, Tangerang City, West Jakarta, South Tangerang, South Jakarta, North Jakarta, Central Jakarta, and East Jakarta. However, the PGA calculation involving the D-vine copula was only carried out in the seven areas with the strongest dependencies, among others. Figure 2 provides the maximum value of the original PGA from 60 epicenters at each of 12 major areas in the Banten–Jakarta Region, ranging from, approximately, 0.10–0.25 g. The farther the subject location is from the epicenter, the smaller the PGA value.

Fig. 2
figure 2

Maximum PGA values of the 12 major areas in Banten Region. Calculations were performed univariately

Full size image

Based on Fig. 2, we assume that the clustered locations at the top right of the map have very strong dependencies because the distance between the locations is quite close. However, to strengthen the assumption, we calculate the dependencies of the original PGA between locations. Figure 3 provides the PGA correlation pairs.

Fig. 3
figure 3

PGA correlation pairs of the 12 major areas in Banten–Jakarta Region. The areas in the red box are the ones with the strongest relationships

Full size image

Based on Fig. 3, very strong dependencies are shown by the areas closer to Jakarta (provided by the bottom right of the pairs), including Tangerang City, West Jakarta, South Tangerang, South Jakarta, North Jakarta, Central Jakarta, and East Jakarta. As supporting evidence, Fig. 4 provides the Pearson correlation coefficient, Spearman’s rho, and Kendall’s tau rank correlation, whose absolute values are greater than 0.50. The three measures are used to accommodate all possible dependency structures of the PGA events between locations, both linear and nonlinear.

The darker the circle color in the correlation plot, the stronger the dependency. From the three dependence measures, we obtain some areas having very strong dependencies (greater than 0.90), consisting of Tangerang City, West Jakarta, South Tangerang, South Jakarta, North Jakarta, Central Jakarta, and East Jakarta. This proves our previous hypothesis. Therefore, we limit our analysis to these seven areas as this study focuses on showing that ground motions due to earthquake events are interrelated between adjacent locations, which have so far been assumed to be independent of each other.

To simplify the analysis, we assign a number to each area as follows: (1) Tangerang City, (2) West Jakarta, (3) South Tangerang, (4) South Jakarta, (5) North Jakarta, (6) Central Jakarta, and (7) East Jakarta.

Fig. 4
figure 4

Dependency measures of original PGA values of some locations with a dependency value of more than 0.50; i.e. those with a fairly strong relationship

Full size image

Following the next step in our proposed modeling, the marginal distribution of the PGA in each location can be identified by evaluating the shape of its histogram. Figure 5 shows the histogram of the PGA for the seven major areas.

Fig. 5
figure 5

Histogram of original PGA values of seven major areas

Full size image

The histograms show that the data are not normally distributed. Therefore, we further perform the marginal distribution fitting process and obtain the results of the marginal distribution for each location along with the parameter estimates which are provided in Table 3. The results show that the marginal distribution that best fits the PGA value for all locations is the log-normal distribution. These results are consistent with the histogram which shows the data pattern tends to be positively skewed, where those kind of data pattern is more of a log-normal distribution.

Table 3 Marginal distribution fit
Full size table

Furthermore, the tree structure and the parameter estimates of the D-vine copula are provided in Fig. 6 and Table 4.

Fig. 6
figure 6

Tree structure of the PGA values

Full size image
Table 4 Parameter estimates of the D-vine copula for PGA values
Full size table

The tree structure of the D-vine copula formed arranges the sequence of locations with the strongest dependencies. Based on Fig. 6, we obtain the following information. Location pairs that have strong dependencies formed in the first tree are (6) Central Jakarta and (5) North Jakarta, (5) North Jakarta and (3) South Tangerang, (3) South Tangerang and (2) West Jakarta, (2) West Jakarta and (1) Tangerang City, (1) Tangerang City and (4) South Jakarta, (4) South Jakarta and (7) East Jakarta. Each has Kendall’s tau values of 0.93, 0.90, 0.88, 0.93, 0.86, and 0.93, respectively. For the second to sixth trees, conditional marks indicate the dependency between the original PGA of two locations given the PGA values from other locations. For example, 6, 3|5 indicates the dependence between the PGA of (6) Central Jakarta and (3) South Tangerang given the PGA values of (5) North Jakarta and so on up to the sixth tree, which shows the dependency between the PGA values of (6) Central Jakarta and (7) East Jakarta given the PGA values of the other five locations. The tree structure shows that the D-vine copula can provide an overview of the dependencies of PGA events between locations, for all location pairs, conditionally or not.

An interesting fact shows that in the first tree, the most suitable copula for all pairs is the Joe copula, which has upper tail dependence, with values greater than 0.95. In addition, Kendall’s tau values for all pairs in the first tree are more than 0.85, indicating a very strong dependency among related location pairs. The upper tail dependence can be interpreted as the relationship between the large PGA values in each area. Meanwhile, for the second to sixth trees, the dependency structure among the pairs is more varied with fewer pairs having tail dependencies.

Using the parameter estimates of the marginal distribution and the D-vine copula model, we then construct the multivariate density functions of the PGA values of the seven areas (see Eq. 12). The multivariate density functions are used to estimate the D-vine copula-based PGA values using Eq. 15, whose results are compared to the original PGA and are provided in Fig. 7.

Fig. 7
figure 7

Original and D-vine copula-based PGA

Full size image

The black and red circles in Fig. 7 indicate the original and D-vine copula-based PGA, respectively. In general, there are several differences in the original PGA and D-vine copula-based PGA values at several epicenters. Even though it seems not so significant, the difference in value cannot be ignored due to uncertain natural conditions. In addition, the range of PGA values is not large, even small differences must be considered. Based on Fig. 7, the difference in PGA values that occurred the most is in the three areas farthest from the epicenters of the earthquake, covering North Jakarta, Central Jakarta, and East Jakarta. This is presumably because the area farthest from the epicenter is the area that gets the most influence from land shifts from other locations closer to the epicenter. Meanwhile, the areas where the original and the D-vine copula-based PGA value are not too different are Tangerang City, West Jakarta, South Tangerang, and South Jakarta because these areas are closer to the epicenter than the other four areas. Ground movement at a location closer to the epicenter is more influenced by its proximity to the epicenter but is less affected by ground movement from the surrounding areas. Therefore, the estimated value of the D-vine copula-based PGA is not much different from the original PGA which involves the influence of the distance to the epicenter rather than the influence of other locations. As a comparison, Table 5 provides the summary statistics of the original PGA and D-vine copula-based PGA for the seven areas which are calculated from 60 epicenters.

Table 5 Summary statistics of the original and D-vine copula-based PGA values
Full size table

Based on Table 5, generally, the maximum and average values of the PGA based on D-vine copula are greater than the original PGA values, especially for the last three areas farther from the epicenter. This indicates that ground motions in areas far from the epicenter are likely to be affected by ground motions in areas closer to the epicenter. In addition, modeling using the D-vine copula also provides a more varied PGA value indicated by a larger standard deviation value and a wider range of minimum and maximum values. After obtaining the original and D-vine copula-based PGA, we analyze the results of the empirical and parametric megathrust POE using original and D-vine copula-based PGA, respectively for the seven areas which are provided in Figs. 8 and 9.

Fig. 8
figure 8

Empirical POE

Full size image
Fig. 9
figure 9

Parametric megathrust POE

Full size image

Based on the result provided in Figs. 8 and 9, the same POE value corresponds to different values for original and D-vine copula-based PGA. Both POE approaches indicate similar characteristics, which show that the farther an area is from the epicenter, the greater the influence of ground motions in surrounding areas that are located closer to the epicenter. Although the POE values are the same vertically, the PGAs are affected by area dependencies the further they are from the epicenter. As we can see from the graphs, East Jakarta is more affected by the dependencies of neighboring areas than Tangerang. If we take a closer look at the empirical and parametric megathrust POE values, especially in the three areas further from the epicenter, we can see that for the same POE values, the D-vine copula-based PGA has smaller values than the original PGA.

Discussion

Earthquake modeling through the calculation of the peak ground acceleration (PGA) has been carried out by embedding the assumption of dependency on events that cause ground motion for adjacent areas. Unlike the previous similar studies which assumed that the calculation of PGA is univariate because the occurrence of earthquake is independent of time and space domain (Kijko and Sellevoll 1989; Tavakoli and Ghafory-Ashtiany 1999; Ghodrati Amiri et al. 2003; Hamzehloo et al. 2012), we have proven that the occurrence of earthquakes impacting on PGA events to be dependent on the space domain. This is identical to the results of the study conducted by Cheng et al. (2020). Study shows that there are very strong dependencies between the geographically close areas, where dependency measures show a very strong dependency value between these regions, which is above 0.90. First, we obtained univariate PGA values from each study location in Banten Region from 60 epicenters. The results show that the PGA values due to these earthquakes is included in the moderate and strong vibrations, with very light and light potential damage (U.S. Geological Survey 2011). Next, the PGA values were checked for dependence and it was found that areas that were close to each other had a very strong correlation. These areas are Tangerang City, West Jakarta, South Tangerang, South Jakarta, North Jakarta, Central Jakarta, and East Jakarta.

To develop our model, we employ the D-vine copula to model earthquake events resulting in simultaneous PGA events. We obtained some findings as follows. There are some differences in the PGA values between the original and D-vine copula-based PGA. The PGA values based on D-vine copula vary more with a wider range, as evidenced by a larger range of minimum and maximum values, and a larger standard deviation. In addition, the maximum and average value of PGA based on D-vine copula in areas far from the epicenter of the earthquake is greater than the value of the original PGA. This shows that PGA values in areas farther from the epicenter get more influence from the ground motion of locations closer to the epicenter. While the areas closer to the epicenter are more influenced by its proximity to the epicenter.

Although numerically the difference between the original and D-vine copula-based PGA is not very significant, this difference cannot be ignored because the range of different values is still in the moderate category. Meanwhile, the results of the exceedance probability show that for the same POE values, the D-vine copula-based PGA values are smaller than the original PGA. This indicates that if an earthquake occurs, the probability of the event causing damage is greater if the PGA is estimated using the D-vine copula, especially for areas farther from the epicenter. In these areas, the PGA values obtained were not only based on pure PGA calculations but also influenced by the occurrence of PGA in surrounding locations that were closer to the epicenter.

Conclusions

In earthquake disaster modeling, peak ground acceleration (PGA) is a crucial variable that must be precisely observed. The PGA calculation may not only be affected by the magnitude of the earthquake, the horizontal distance to the epicenter, and the depth of the epicenter but also by the ground motion in the surrounding areas, so the assumption of dependencies between locations is required. Vine copula can be used to calculate the joint probability of land movement events in adjacent areas. In this paper, we estimate the PGA value and its corresponding probability of exceedance using a D-vine copula-based probabilistic seismic hazard analysis.

Although it seems not so significant, there is a discrepancy in the result obtained between the original PGA and D-vine copula-based PGA for seven major areas in Banten–Jakarta provinces, with differences of 4.7069e\(-\)07 to 0.06998 g (see Table 5). This difference, in earthquake disaster modeling, cannot be ignored because it is included in the moderate category for perceived shaking.

Overall, this proposed earthquake model is able to capture dependencies among areas to support better quality development of catastrophe modeling for the use of mitigation toward catastrophe events, especially earthquakes.