Prediction of karst spring discharge using LSTM with Bayesian optimisation hyperparameter tuning: a laboratory physical model approach

Abstract

Estimating spring discharge in karst aquifers is challenging due to non-linear and non-stationary hydrological processes caused by spatial and temporal variations. This study mimicked the phenomenon by simulating spring discharge using a laboratory physical model. The hydrological processes adopted in the simulation include systems such as infiltration, fissure-conduit, and drainage. We then recorded spring discharge and precipitation values from the simulated model along side the corresponding air temperature and humidity—in order to analyse the time series behaviour of the system. To estimate spring discharge from the simulation, a deep learning algorithm is developed taking temperature, humidity and precipitation as the input. In this work, the Bayesian optimisation was used to sweep through a range of hyperparameter values to search for the top 5 optimal training options for a Long Short Term Memory (LSTM) neural network. In addition, XGBoost was employed to identify the key predictors of spring discharge, resulting in enhanced predictability. The results show that LSTM-1, LSTM-2, LSTM-3, and LSTM-4 are the recommended recurrent neural network designs for predicting spring discharge using all three input parameters. LSTM-1, LSTM-2, and LSTM-3 network architectures are optimal for utilising two input variables: precipitation intensity and temperature. LSTM-5 has shown that a single parameter is inadequate for estimating spring discharge. The LSTMs yielded an RMSE value of ∼0.04, as well as a ${R}^{2}$ value of ∼98.01%. The study showed that using different input parameters, the suggested LSTM model can effectively simulate spring discharge in a karst environment.

Introduction

Karst springs are naturally occurring formations that serve as a principal water source for local communities around the world. The hydrological disposition of a karst system is mostly identified by the complex spatial and temporal variable processes of recharge, such as precipitation, surface runoff, infiltration, groundwater flow, conduits and fissure zones, as well as anthropogenic factors (Telesca et al. 2013; Yu et al. 2018). Figure 1 presents a 3D illustration of the hydrological behaviour of a karst aquifer. Generally, karst springs are a direct reflection of the state of groundwater in the aquifers that feed them, reflect the variability of groundwater storage in the basins, and have a direct impact on the streams and other surface water bodies into which they discharge, as well as all dependent ecosystems. Additionally, spring water replenishes the majority of rivers. These springs have significance for the survival of microhabitats in river systems (Hartmann et al. 2021; Ikard and Pease 2019; Kareem et al. 2022).

Fig. 1

A schematic drawing of a heterogeneous karst aquifer system showing the primary source of aquifer recharge (rainfall) and recharge from runoff from non-karst rocks (surface runoff), infiltration, spring discharge outlet, porosity, and flow (characterised by conduits and fissures) (Ding et al. 2020; Williams 2009)

When the world’s population distribution is compared to the distribution of carbonate rocks, karst groundwater accounts for approximately 20% of the Earth’s land surface and can be accountable for about a quarter of the world’s water supplies (Ding et al. 2020; Ford and Williams 2007; Parise et al. 2004). Carbonate rocks underlie 3 × 10⁶ km² of the land surface in Europe and provide water for major cities, including Bristol, London, Paris, Montpellier, Rome, and Vienna (Andreo 2012; Biondić et al. 1998). In addition, karst water is crucial for the survival of more than 100 million individuals in South China (Ding et al. 2020).

Predicting spring flow in karstic aquifers is challenging due to their heterogeneous nature and non-linear relationship. Furthermore, insufficient observational data on spring flow hinders prediction studies and analysis. Overexploitation and inadequate water resource management have caused a spring dry-up. The discharge of springs has decreased due to increased abstraction to meet domestic, industrial, and agricultural water supply demands (Mohammed et al. 2022). The drying up of particular springs underscores the need for improved comprehension of regional groundwater systems and efficient management strategies to ensure the uninterrupted supply of groundwater resources and restore spring flow (An et al. 2019). Karst aquifers exhibit a range of conduits, cracks, and pores that possess hierarchical permeability structures and flow pathways. The Niangziguan Springs in China serve as an instance of aquifers (An et al. 2019, 2020).

Human activities, on the other hand, have decreased karst spring discharge. Previous research discovered that anthropogenic effects influenced or impacted karst hydrological processes in the Niangziguan Springs catchment more than climate change effects (An et al. 2019, 2020). However, it is still unclear how human activity affects the magnitude and periodicity of spring discharge due to the strong non-linear trend and non-stationary fluctuations (An et al. 2019, 2020; Hao et al. 2016).

Physical-based numerical models are commonly used to forecast spring discharge. The governing equations are applied to compute spring flow, considering relevant assumptions and boundary conditions. These models require significant amounts of accurate data for parameter calibration. In certain uncharted regions, acquiring precise and adequate data presents challenges, leading to suboptimal model efficacy and increased uncertainty (Hassanzadeh et al. 2020; Khorrami et al. 2019; Milly et al. 2008; Tavakol-Davani et al. 2019). However, owing to the complexities caused by random uncertain boundary conditions of precipitation, extreme karst aquifer heterogeneity, hydrological modelling errors such as initial conditions, model parameterisation, structure, and anthropogenic impacts, interpreting and predicting spring discharge data using only a physical model is a challenge for understanding the contributions of each component (Khorrami et al. 2019; Quan et al. 2022; Tavakol-Davani et al. 2019; Hartmann et al. 2021; Jeannin et al. 2021).

Various prediction models, including statistical learning, artificial neural networks (ANNs), and grey systems have been developed and applied to address uncertainties in spring flow simulation and solve practical issues (Alameer et al. 2020; Quan et al. 2022). Therefore, in this work, the prediction model adopted the techniques in ANN.

ANNs are training based-models designed to have a functional mapping between input predictor and output prediction variables when relevant historical big data is processed (Anand and Oinam 2022; Roshani et al. 2022). This approach has proven to produce more accurate predictions of hydrological events than the traditional calibrated numerical hydrological models (Sharafati et al. 2020; Akano and James 2022), although they are unable to explain the underlying processes, being data-driven rather than process-driven models. This provides an opportunity for improving prediction accuracy by coupling with other robust schemes such as Bayesian optimisation.

ANNs have been employed by several researchers to model and forecast non-stationary hydrological processes (He et al. 2020; Meng et al. 2019; Niu and Feng 2021; Singh et al. 2023; Xie et al. 2019; Yan et al. 2021; Khorram and Jehbez 2023; Haggerty et al. 2023). Optimal use of ANNs in karst aquifer systems can improve model prediction accuracy. An ANN typically consists of two primary components: The network comprises numerous interconnected artificial neurons. These links extract relevant parameters from a dataset. An artificial neural network (ANN) model does not require a data distribution assumption prior to feature engineering. ANN finds applications in diverse domains. RNNs are more appropriate for modelling dynamic systems than feed-forward neural networks, as Bailer-Jones et al. (1998) and Tsung (2010) suggested. The issue frequently encountered when training RNNs with numerous hidden layers is the exploding gradient problem, as Hochreiter identified in 1998. The problem arises during the weight adjustment of the RNN for gradient computation through backpropagation (Hochreiter 1998).

To address the problem of exploding gradient in RNN, long short-term memory (LSTM) network was developed using the activation functions of the forget gate in addition to the cell state (Sahar and Han 2018; Thonglek et al. 2019). LSTM, a type of artificial neural network, has feedback connections, making it ideal for data processing and prediction. Recent studies by hydrologists (Yang et al. 2019; Yin et al. 2021) have exhibited the potential of LSTM in the application of hydrological sciences. For example, Kratzert et al. (2018) used LSTM to model rainfall-runoff because of its ability to learn and store long-term dependencies between the provided input and output of the network. Using the forget gate and cell state activation functions, long-short-term memory (LSTM) networks were developed to limit gradient explosion in RNNs (Sahar and Han 2018; Thonglek et al. 2019).

LSTM is an artificial neural network with feedback connections, making it ideal for data processing and prediction. Recent studies by hydrologists (Yang et al. 2019; Yin et al. 2021) have exhibited the potential of LSTM in applying hydrological sciences. For example, Kratzert et al. (2018) used LSTM to model rainfall-runoff because of its ability to learn and store long-term dependencies between the provided input and output of the network. They found that LSTM produced better model performance than the traditional RNNs. Like other machine learning (ML) models, RNN models may have several vital hyperparameters that must be optimised to improve model performance (Cheng et al. 2019). As a result, hyperparameter optimisation is a critical step (Ma et al. 2020). Therefore, Bayesian Optimisation (BO) was used in this study to set the network size. BO is more appropriate when objective functions are computationally expensive to calculate due to its higher efficiency compared to alternatives such as genetic algorithms (Alizadeh et al. 2021; He et al. 2019; Lin et al. 2020).

This study aimed to achieve two objectives to comprehend the karst spring discharge in the Jinan basin. A 3D physical laboratory model was put up to replicate the Jinan spring basin (see Fig. 2). Subsequently, rainfall-runoff experiments were performed to collect data on spring discharge. Second, LSTM coupled with BO was used to produce the best LSTM-RNN model that predicts the spring discharge in the simulated area using precipitation intensity, temperature, and humidity. Statistical metrics (the root mean square error (RMSE), the mean absolute error (MAE), the mean absolute percentage error (MAPE), Pearson product-moment correlation coefficients ($\rho$), and the coefficient of determination (${R}^{2}$)) were used to assess the performance of the top 5 LSTM models developed with different input combinations.

Fig. 2

A geographical map of the Jinan spring basin showing the four main spring groups (Baotu, Heihu, Five Dragon, and Pearl) and the Dongwu and Mashan Faults

Materials and methods

Study area

The Jinan Karst System shown in Fig. 2, is located in the midwestern Shandong Province of Northern China. The springs are important historical sites in China. Jinan City has been known as “Spring City” since ancient times due to its fractured-karst springs. However, due to Jinan’s social and economic development, urbanisation and over-exploitation have negatively impacted the level of karst groundwater in recent years, leading to a substantial decrease in the spring flow rate (Zhu et al. 2020).

Jinan is abundant in easily dissolvable Cambrian and Ordovician carbonate rocks. Because of the geological structure, lithology, climate, and other factors, many karst fractures and pipelines have been produced, offering a favourable conduit for groundwater transport and ample storage area. Despite safeguards such as limited mining and artificial groundwater recharge in Jinan, the spring is still in danger of drying out (Zhang et al. 2018).

The main problem is the difficulty in the prediction of spring flow in the field. Hence, there is not enough observation data on spring flow data. Even the data available is insufficient to make any meaningful inference. This is due to the highly heterogeneous nature and non-linear relationship of karstic aquifers (Mohammed et al. 2022). Therefore, this work used the physical model to aid in the simulation of karstic spring flow predictions.

The laboratory physical model

The 3D physical model can simulate surface runoff, pore water runoff, and fissure karst water runoff in karst areas. The model comprised a test sand tank, precipitation replenishment system, mulch, rift karst zone medium, water level monitoring system, and flow monitoring system. The upper infiltration system represented the unsaturated zone, while the lower fissure-conduit system represented the saturated zone. Figure 3 displays a schematic representation of the physical model. The labelled parts are shown in Table 1.

Fig. 3

Schematic diagram of the physical laboratory model

Table 1 The parts of the schematic diagram of the laboratory physical model

Experimental set-up

The physical model can investigate surface runoff, pore water runoff, and spring discharges in the karst region. The study enhances the theoretical understanding of karst water flow and establishes a scientific basis for practically analysing complex karst groundwater resources. It is crucial for developing and utilising water resources in karst areas. Figure 4a–k illustrates the sequential process for setting up the laboratory experiment.

Fig. 4

Experimental set-up of the physical model: a shows the sand tank with multiple outflow holes; b–f are the fissure conduit system at various layers; g–j describes the infiltration systems to mimic the vegetation cover and the soil profile, and k is the complete lab set-up for the experiment

Figure 4a displays the test sand tank. The sand tank is a micro-sloped box that acts as the model domain and is inclined at a 2° tilt. To control the initial conditions, allow all the water to drain thoroughly after each experiment. The tank has multiple outflow holes with no flux boundaries for monitoring runoffs and water levels. The inside and outside of the tank walls are coated with impermeable waterproof paint, preventing water seepage outside the tank’s domain. It also has a surface flow outlet at the top of the sidewall to measure surface runoff and a spring discharge hole at the bottom, connected by conduits.

The fissure-conduit system is constructed of 10 cm concrete cube bricks. Layer one (see Fig. 4b) contains two connected conduits with a cross-sectional area of 30 cm² serving as the fracture zone and a hydraulic conductivity of $0.05$ m/d. The bricks are arranged systematically with a small gap of $2.5$ mm in between them. Construction consists of the pore, fissure, and pipe layers. These segments simulate the flow as it passes through a series of water-conducting fissure zones and is then eventually discharged through two large fissures at the bottom. The second layer in Fig. 4c, showcases the fissure zone designed to aid flow movement. For the third layer (in Fig. 4d) two conduits with dimensions of $5.2\times 146\times 10\,\mathrm{ cm}$ and $5.4\times 153\times 10\,\mathrm{ cm}$ are designed to mimic the fracture zone. As depicted in Fig. 4e multiple conduits were constructed to improve the drainage system in the installation. In layer $5$ (refer to Fig. 4f), a piece of cloth is added to the set-up to block sand from filling up the space created.

The experiment also included an infiltration system to simulate vegetation cover and the soil profile. Figure 4g shows how the soil layer is loamy and sandy. The loamy soil has an average particle size of 57 μm, and that of the sand is 753 μm. The hydraulic conductivity of this layer is approximately 24 m/d, and the specific yield is 0.24. Additionally, the state of saturation was measured using the pressure sensor probes in layer 6.1. Layer 6.2 in Fig. 4h shows how the soil layer with buried pressure tubes is wholly covered. The vegetation cover is simulated using a cloth designed with cotton-like material to cover the soil layer with buried pressure tubes. Figure 4i displays the set-up of the simulated vegetation cover. Figure 4j shows the various positions of the passage for measuring surface runoff and pore water runoff conduits for the developed physical model.

Figure 4k shows the complete experimental set-up for this study. The precipitation recharge system comprises a water tank, a variable frequency pump, hosepipes, and four nozzles to simulate the process of natural rainfall supplying the surface karst region of the area. The flow rate is recorded at different times to measure the intensity of the rain.

Data description

Data from the unsaturated test scenario was used for the analysis of this study. Short-term rainfall was performed in the sand tank area utilising a frequency pump and a spraying apparatus (mimicking rainfall). Using the pump, the intensity of the rain varied at different rates. Surface runoff and fissure karst water runoff (spring discharge) were measured using measuring cups, stop clocks, and a flux flow metre.

The descriptive statistics of the research laboratory simulation are shown in Table 2. 3968 measurement points were obtained in total. The discharge rate, which was used as a response variable in this study, had a mean value of about 37.59 mL/s and ranged between $(0.42, 153.51)$ mL/s. To understand the fluctuations in recorded discharge levels, hydrological parameters such as precipitation intensity, temperature, and humidity were investigated. The expected values for these stated variables were $0.024$ mm/s (precipitation intensity), 31.21 °C (temperature), and 0.61% (humidity).

Table 2 Descriptive statistics of spring discharge and independent variables (i.e., precipitation intensity, temperature, and humidity)

Also, as shown in Fig. 5, at a precipitation intensity of $0.01755$ mm/s, the maximum spring discharge rate was about $78$ mL/s, with a median of about $36$. Also, at $0.02017$ mm/s, the maximum spring discharge rate was about $96$ mL/s with a median value of about $9$. Furthermore, at a precipitation intensity of $0.02279$ mm/s, the maximum spring discharge rate was about $115$ mL/s with a median of about $51,$ while $0.02632$ mm/s gave a maximum spring discharge rate of about 152 and a median of about $36$. The highest precipitation intensity of $0.02925$ mm/s had a maximum spring discharge of about $74$ with a median of about $37$, less than the values recorded by the least precipitation intensity rate. This was due to the material composition of the porous layer (loam and sand), which showed that not all Rainfall could infiltrate the system and further percolate into the aquifer, owing to the high rainfall intensity. The porous layer got fully saturated quickly, and therefore, overland flow (i.e., surface runoff) was higher because the porous layer could not absorb all the water coming to it instantly for this particular test.

Fig. 5

A univariate box and whisker plot to show the data distribution in a single graph

The horizontal axis is the precipitation intensity in mm/s, and the vertical axis is the spring discharge rate in mL/s. The different colours represent different pump set values [$1.2, 1.4, 1.6, 1.8$ and $2.0$ ($\mathrm{kgf}/{\mathrm{cm}}^{2}$)] which gave rise to the respective precipitation intensities, which can be read on the vertical axis.

Due to this phenomenon, data collected on spring discharge with the highest precipitation intensity of $0.02925$ mm/s was minimal and had the lowest peak, as shown in the spring hydrograph, as compared to the other precipitation intensity values of $0.01755$, $0.02017$, $0.02279$, and $0.02632$ mm/s; because less Rainfall infiltrated into the system due to rate of infiltration as a result of material composition. Hence, a threshold value must be set to manage the spring’s inflow and outflow to have a perennial flow, if possible.

The correlation matrix presented in Fig. 6 assesses the strength and direction of the linearity between the two explanatory variables. Strong positive linearity values show that the explanatory variables measure the same characteristics. Figure 6 shows a moderate to low correlation—indicating that the selected variables may measure different characteristics.

Fig. 6

The correlation matrix of all independent variables is depicted as a heat map

Feature importance using extreme gradient boosting

The concept behind a decision-tree-based algorithm is to build a sequential-like tree diagram, where each inner node depicts a test on a feature, each subdivision denotes a test score, and each terminal node holds the regressor target value. The main idea is to generate a regressor using input features $({f}_{1},{f}_{2},{f}_{3},\dots ,{f}_{i})$ and at least one target feature $(\Upsilon)$. In this study, the input features were precipitation intensity, temperature, and humidity, and the output feature was the spring discharge rate. The learning pattern of a decision tree was developed by splitting the data set into multiple sets based on the feature value test. The splitting method was done recursively on each multiple set. The recursive partitioning process was completed when all of the different sets at a node recorded the exact score of the output feature. When recursive splitting on many sets does not improve the prediction score, the learning process may be discontinued.

The algorithms mostly adopted to create ensemble decision trees included bagging and boosting methods (Galar et al. 2012; Quan et al. 2022; Zhou et al. 2010). The former method uses a uniform weak learner by splitting the training set into multiple sets using the bootstrap sampling technique and combining the individual sub-sample based on a deterministic averaging process. The latter method integrates many weak learners to produce a robust learner iteratively. Each weak learner after that is taught using a new sub-sample of data that includes measurements that were not effectively addressed by the previous learners. The ultimate goal is to reduce the regressor’s bias by encouraging the weak learner to rely on more difficult data.

The XGBoost is a supervised learning technique based on the boosting algorithm (Chen and Guestrin 2016), which approximates a function through optimisation and regularisation. The unique nature of this method is how well it can distinguish the relevant features between selected variables and the ability to perform hyper-threading of a computer processor to improve the computational cost. It has been utilised successfully in a variety of practical applications, including stock selection (Li and Zhang 2018), disease diagnosis (Bao 2020), and time series forecasting (Zhai et al. 2020). The decision-tree-based model used in the XGBoost method adopts an iterative approach until the stopping criteria are satisfied. The following equations are used to produce the predicted test values:

$$\hat{\Upsilon } = \sum\limits_{\omega = 1}^{\kappa } {g_{\omega } (f_{i} ),\quad g_{\omega } \in S}$$

(1)

where $\widehat{\Upsilon}$ denotes the predicted test value, ${g}_{\omega }$ represents an individual regression tree, ${f}_{i}$ is the input feature, $\kappa$ is the number of regression functions, and $S$ is the space of all possible cases of ${g}_{\omega }s$.

Figure 7 shows the basic architecture of the XGBoost supervised learning method. The regression model can be optimised by identifying the optimal node for subdivision to minimise the objective function described in Eq. (2). It is imperative to determine the most favourable node to sub-divide to minimise the objective function defined in Eq. (2) to fine-tune the regression model as;

$${\mathcal{Q}}^{t}=\sum_{j=1}^{n}l({\Upsilon }_{j},{\widehat{\Upsilon }}_{j}^{t-1}+{g}_{t}({f}_{j}))+{\Theta }^{*}({g}_{t})$$

(2)

where $l(.)$ represents the loss expression depicting how well the estimated test value approximates the actual test value, ${g}_{t}(.)$ is the predicted outcome of the decision tree at the tth iteration and ${\Theta }^{*}(.)$ denotes the model regularisation function. The regularisation function consists of the number of leaf nodes $T$ and the corresponding weights $w$ such that:

Fig. 7

The principal decision-tree design of the XGBoost algorithm

$${\Theta }^{*}({g}_{t})=\beta T+0.5\varphi \parallel w{\parallel }^{2} ;$$

(3)

The parameter $\beta$ represents the complexity cost of adding more leaves to the decision tree, whilst that of $\varphi$ is the regularisation coefficient. The coefficients are modulated using the L2 norm.

Concerning this work, the specific hydrological features that influence spring discharge was determined using the XGBoost. Therefore, the bar chart in Fig. 8 indicates that precipitation intensity has a higher impact on the model in predicting spring discharge than temperature and humidity. Thus, in this work, we looked at three significant scenarios:

• 1. Estimation of the spring discharge rate using all three hydrological features as input variables;

• 2. Estimation of the spring discharge rate using only the top two features as input variables; and

• 3. Estimation of the discharge rate using only the highest feature as an input variable.

Fig. 8

A plot of the feature importance of input variables using the XGBoost Regressor

LSTM with respective gates

The LSTM is an improved model of the conventional RNN. It was initially introduced by Hochreiter and Schmid Huber (1997) and operates using a cell and three gates (the input, the output, and the forget gates). These memory components regulate the message inflow inside the network unit. Figure 9 illustrates how a typical LSTM unit processes information using the input gate (${i}_{t}$), the forget gate (${f}_{t}$), the output gate (${\rho }_{t}$), and the cell state (${\xi }_{t}$). The mathematical formulations of the LSTM unit of these memory parts are expressed as:

$${i}_{t}=\sigma ({z}_{t}{\Lambda }^{i}+{\eta }_{t-1}{\Omega }^{i})$$

(4)

$${f}_{t}=\sigma ({z}_{t}{\Lambda }^{f}+{\eta }_{t-1}{\Omega }^{f})$$

(5)

$${\rho }_{t}=\sigma ({z}_{t}{\Lambda }^{\rho }+{\eta }_{t-1}{\Omega }^{\rho })$$

(6)

$${\widetilde{\xi }}_{t}=tanh({z}_{t}{\Lambda }^{g}+{\eta }_{t-1}{\Omega }^{g})$$

(7)

$${\xi }_{t}=\sigma ({f}_{t}*{\xi }_{t-1}+{i}_{t}*{\widetilde{\xi }}_{t})$$

(8)

$${\eta }_{t}=tanh({\xi }_{t})*{\rho }_{t}$$

(9)

where, $\sigma$ is the standard deviation, $\Lambda$ and $\Omega$ are weight vectors for $f$, $\xi$, $i$, and $\rho$ for a given time-step $t$. The hidden unit ($\eta$) studies which info to store and which to discard.

Fig. 9

The general architecture of the LSTM model

The input gate process is described in Eq. (4). Given new input data (${z}_{t}$) and the preceding hidden state (${\eta }_{t-1}$), the process here is to search for new information to add to the model’s long-term memory (also known as the cell state). The forget gate presented in Eq. (5) is used to decide which part of the information in the cell state is useful when you are provided with both the preceding hidden state and the new input data. To achieve this, the preceding hidden state and the current input data are supplied into the model network to generate a series of elements using the sigmoid activation function.

The network considers the elements that are close to $0$ as insignificant whilst, those close to $1$ as relevant. The activated values are then multiplied element-wise with the preceding cell state such that the numbers close to $0$ will have less effect on the following processes. The output gate is presented in Eq. (6), and it decides on the new hidden state. The expressions above show that the LSTM structure uses a set of gates to modulate how a sequence of instructions flows into the system, how they are gathered and eventually, how they leave the network.

Hyperparameter selection based on Bayesian optimisation (BO)

One of the key challenges in designing a neural network is knowing the right number of network sizes to use for a specific task. The network size includes the number of layers in the network architecture, the number of nodes in every layer, and even the number of connections to be adopted in the design. A neural network is mostly designed to map a target variable $\varkappa$ onto a non-linear function $\psi (\upsilon )$. The non-linear function $\psi (\upsilon )$ is gleaned during the training phase where the network tries to study the appropriate way to link the input variables $\upsilon$ to the output variables $\varkappa$.

However, building a proper network entail fine-tuning the hyperparameters. The common hyperparameter tuning techniques are the grid search (Ghawi and Pfeffer 2019; Quijano et al. 2021; Shekar and Dagnew 2019) and the random search (Bergstra and Bengio 2012; Mantovani et al. 2015) algorithms. The former search algorithm works by setting up a framework of hyperparameter values such that for every combination in the framework, the network is trained and evaluated on the test data. This makes the searching approach in selecting the best network to be very exhaustive. By contrast, the framework set in the latter search works by choosing random combinations to train the network and evaluate. Nevertheless, even though the latter approach allows for explicit control in selecting the number of parameters to use, there is the possibility of not finding an accurate model.

One state-of-the-art hyperparameter optimisation algorithm introduced by Li et al. (2018) is the hyperband. This optimisation algorithm is based on a successive halving technique known as the bandit method (Li et al. 2018), where more credits are assigned to hyperparameter configurations with very high performance. Here, the configurations with low performance are less likely to predict the best model and are removed in the process to allocate more weights to hyperparameter configurations with good performance. Furthermore, this algorithm ensures early stopping in a principled way–making it more robust than the regular grid and random search schemes.

One major drawback in the previous optimisation techniques is that the hyperparameter settings are treated independently. Meanwhile, the space for these settings is mostly even; therefore, prior knowledge of the previous performance might help improve the performance of the next space. The Bayesian optimisation (BO) method addressed this issue and ensured homogeneity in the hyperparameter space. BO is a probability distribution model that tries to understand complex objective functions based on prior observations. As a result, in this work, an LSTM model was generated using BO to set the network size. Recent studies (Bergstra et al. 2011, 2013; Greenhill et al. 2020; Shahriari et al. 2016; Turner et al. 2021) show the potential and robustness of the BO method compared to the previously mentioned algorithms.

Bayesian optimisation for a classic LSTM

In the prediction of spring discharge values, a simple classic LSTM neural network might be adequate, but this same network can perform poorly if parameters such as the learning rate, the momentum term, the number of layers, the number of hidden units for different layers, and even the batch size are not set correctly. As a result, the units for the LSTM and dropout, the activation type and the learning rate of the model optimiser were chosen as hyperparameters for optimisation in this work. Fine-tuning these parameters was essential because the LSTM units handle the dimensionality of the output vector, whereas the activation function adds complexity to the model, making it non-linear. Also, to improve the performance of the LSTM model and avoid over-fitting, the learning rate must be optimised and some network dropouts must be performed. Table 3 shows the parameter sets for fine-tuning.

Table 3 Tabular description of hyperparameters (LSTM units, dropout units, activation function and learning rate) used in the learning algorithm with their respective min, max, step size and type functions

By fine-tuning, the aim was to discover the appropriate hyperparameter for the proposed LSTM algorithm to produce the best performance when measured on the test data. Additionally, during the tuning process, the objective function usually becomes very complex to compute (Doke et al. 2020). This is because, to obtain a new set of hyperparameters, the neural network must be trained from scratch to determine its performance. Furthermore, calculating the weights of the hyperparameters may be difficult, leaving retraining the model as the only option. As a result, the BO algorithm was used to solve the problem and ensure that the model network learns from the hyperparameter settings. Based on the hyperparameter settings provided, this algorithm generates a probability distribution function (also known as a surrogate model) to compute the probability of obtaining the best score for the objective function.

$D$ was considered to be the independent input data in predicting the spring water discharge, $f$ to be the performance model, $\xi$ to be the hyperparameter sets displayed in Table 3, and ${\widehat{\xi }}_{\theta }$ to be the optimal parameter, then from Bayesian inference (Matsubara et al. 2021) (Dempster 1968), the likelihood function of the sample data is given as;

$$L(\xi )=f(D| \xi )={\prod }_{j=1}^{n}f({D}_{j}| \xi ),$$

(10)

Note that Eq. (10) holds based on the assumption that $D$ obeys a certain probability density distribution with parameter say $\theta$. Therefore, the maximum likelihood estimation in Eq. (10) becomes;

$${\widehat{\xi }}_{\theta }=argma{x}_{\theta \in \xi } f(D| \theta )$$

(11)

where $argmax$ is an operation that finds the argument that gives the maximum value from a target function. Assuming the surrogate model obeys a Gaussian process ($GP$) prior, then the operation of Bayesian optimisation is depicted below:

• (a) Define an objective using a $GP$ prior model: The $GP$ is normally an acceptable model to estimate a non-linear regression output which is exactly the purpose of this work. The model assumes that input data sampled from a distribution with unknown parameters produces an output similar to that distribution, resulting in a continuous objective function. As a result, because the hyperparameter settings in Table 3 are non-parametric, using the $GP$ as a prior model for this analysis was the ideal choice. Following that, a brief review of $GP$ for non-linear regression was provided. For an in-depth discussion on $GP$ theory, refer to these studies (Rasmussen 2004; Rasmussen and Williams 2005; Snelson 2007).

  Typically, a GP regression uses a joint Gaussian density function to map an input observation onto its corresponding target variable. It is characterised by an expectation function $m(\upsilon )$ and covariance function $\Sigma (\upsilon ,\upsilon^{\prime})$ such that $f(\upsilon )\sim GP(m(\upsilon ),\Sigma (\upsilon ,\upsilon^{\prime}))$. Let define $\Lambda =\{{\upsilon }_{j},{\Phi }_{j}{\}}_{j=1}^{K}$ to be a set of measurements, where, ${\upsilon }_{j}\in {R}^{n}$ are $n$ measurement points in $n$-dimensions and ${\Phi }_{j}\in R$ are the matching targets. Mathematically, we can express this measurement as a supervised learning model to have;

  $${\Phi }_{j}=\Phi ({\upsilon }_{j})=f({\upsilon }_{j})+\epsilon , \epsilon \sim N(0,{\sigma }_{k}^{2})$$

  (12)

  Taking $f({\upsilon }_{j})$ as a $GP$ regression, then from (Boyle 2007) we can represent $f$ as;

  $$\begin{array}{ll}{f}_{gp}& =\left[\begin{array}{l}f({\upsilon }_{1})\\ \vdots \\ f({\upsilon }_{K})\end{array}\right]\sim \mathcal{N}\,\left(0,\left[\begin{array}{lll}\Sigma ({\upsilon }_{1},{\upsilon }_{1})& \dots &\Sigma ({\upsilon }_{1},{\upsilon }_{K})\\ \vdots & \ddots & \vdots \\\Sigma ({\upsilon }_{K},{\upsilon }_{1})& \dots &\Sigma ({\upsilon }_{K},{\upsilon }_{K})\end{array}\right]\right)\end{array}$$

  (13)

  Note that in Eq. (12), $\Phi (.)$ is also $GP$, since $\Phi =f+\epsilon$ and adding two random variables that are separate but exactly distributed is also a Gaussian. Therefore, to build a $GP$ model using a training dataset then, Eq. (12) becomes;

  $${\Phi }_{y}\sim N(0,\Sigma (\upsilon ,\upsilon )+{\sigma }_{\tau <k}^{2}I).$$

  (14)

  Equation (14) does not hold a definite parameter and is depicted as non-parametric.

  Finally, to perform a prediction, we identify the joint distribution of the original target label ${\Phi }_{y}$ of the train points $(\upsilon )$ and the latent target label ${\widehat{\Phi }}_{y}$ of the test observation $(\widehat{\upsilon })$. Under the $GP$, the joint distribution of ${\Phi }_{y}$ and ${\widehat{\Phi }}_{y}$ is defined as

  $$\begin{array}{l}\left[\begin{array}{l}{\Phi }_{y}\\ {\widehat{\Phi }}_{y}\end{array}\right]\sim N\left(0,\left[\begin{array}{ll}\Sigma ({\varvec{\upupsilon}},{\varvec{\upupsilon}})+{\sigma }_{\tau <k}^{2}\mathbf{I}&\,\,\,\,\Sigma ({\varvec{\upupsilon}},\widehat{{\varvec{\upupsilon}}})\\\Sigma (\widehat{{\varvec{\upupsilon}}},{\varvec{\upupsilon}})&\,\,\,\,\Sigma (\widehat{{\varvec{\upupsilon}}},\widehat{{\varvec{\upupsilon}}})+{\widehat{\sigma }}_{k-\tau }^{2}\mathbf{I}\end{array}\right]\right).\end{array}$$

  (15)

  By the conditional probability property of Gaussian (Roberts et al. 2013), we have

  $$p({\widehat{\phi }}_{y}|\widehat{\upsilon },\upsilon ,{\Phi }_{y})=N(\widehat{\mu },\widehat{\Sigma }),$$

  (16)

  where the predicted mean is

  $$\widehat{\mu }=\Sigma (\widehat{\upsilon },\upsilon )(\Sigma (\upsilon ,\upsilon )+{\widehat{\sigma }}^{2}I{)}^{-1}{\Phi }_{y, }$$

  (17)

  and variance is

  $$\widehat{\Sigma }=\Sigma (\widehat{\upsilon },\widehat{\upsilon })+{\widehat{\sigma }}^{2}I-\Sigma (\widehat{\upsilon },\upsilon )(\Sigma (\upsilon ,\upsilon )+{\widehat{\sigma }}^{2}I{)}^{-1}\Sigma (\upsilon ,\widehat{\upsilon }).$$

  (18)

  Therefore, we can estimate the posterior on the testing set given the expected and the covariance kernel functions of the $GP$. With this, we can generate a confidence level of $95 \%$ to obtain a Bayesian stochastic model on the objective function.

• (b) Compute the hyperparameter values that boost the acquisition function: The surrogate function described in Step (1) provides an assay of the objective function, making it useful for direct sampling. The sampling uses the posterior in Step (1) to choose the subsequent sample from the search space. This technique helps us to account for the areas in the domain space that are worth exploiting and the ones that are worth exploring. Analytically, we can utilise this acquisition function by considering a posterior function $\Psi$ models the loss such that after $k$ evaluations, the lower bound of this posterior becomes ${\Psi }^{*}$ at some measured point, ${\omega }^{*}$. Performing more evaluations will alter the posterior values and the objective function values at, let us say $\Psi (\omega )$. The result of this optimisation problem becomes $min({\Psi }^{*},\Psi (\omega ))$ and the expected difference distinguishing ${\Psi }^{*}$ and the latter produces Eq. (19), (Doke et al. 2020);

  $${\mathcal{E}}_{I}={E}_{k}\left[{\Psi }^{*}-min\left({\Psi }^{*},\Psi \left(\omega \right)\right)\right].$$

  (19)

• (c) Evaluate the optimal function and insert the outputs into the Gaussian process posterior: In this Step, we determine the objective function using the optimal parameters gathered from the acquisition function. This approach improves the performance of the objective we aim to model by taking the Gaussian process posterior from $k$ measurements to $k+1$.

• (d) Reproduce Steps 2 and 3 until the maximum number of iterations is attained.

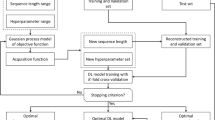
  This work used the BO method to perform a hyperparameter search by taking the set of hyperparameter values presented in Table 3 as inputs and producing the evaluation accuracy for the Bayesian optimiser. New models are constructed with specific hyperparameters during the search process and then trained for several epochs. Note that these new models are evaluated against a set of metrics. Table 4 lists the top $5$ new models (described in this work as LSTM-1, LSTM-2, LSTM-3, LSTM-4, and LSTM-5) adopted to measure the spring discharge.

  Table 4 A summary report displaying the top 5 hyperparameters used to build the LSTM model via BO

  To ensure that a robust LSTM is produced for this work, the BO approach was used to fine-tune the hyperparameters of the neural network. This was achieved by creating a training pipeline for the LSTM with the simulated measurement set and then customising the hyperparameters into an objective function as depicted in Table 4. The hyperparameter optimisation was used to develop and train 5 new models, that is, LSTM-1 to LSTM-5. A flowchart illustrating the procedure for implementing the LSTM model developed in conjunction with Bayesian Optimisation hyperparameter tuning for spring discharge estimation is shown in Fig. 10.

  Fig. 10

  

  Flowchart showing the implementation procedure of the LSTM model developed coupled with Bayesian Optimisation hyperparameter tuning for spring discharge estimation

Performance evaluation

For training the top 5 LSTMs, the mean squared error (MSE) of the training dataset was selected as a benchmark to calibrate the recurrent networks, and their corresponding optimal values of the MSEs were acquired using the Adam optimisation scheme. This optimiser is an improved function of the stochastic gradient descent, and it was designed to update network weights in the training pipeline.

In addition to the above, the prediction performances of the five LSTMs were evaluated using the root mean square error (RMSE), the mean absolute error (MAE), the mean absolute percentage error (MAPE), Pearson product–moment correlation coefficients ($\rho$), and the coefficient of determination (${R}^{2}$). The statistical metrics are defined as follows:

$$MSE=\frac{1}{N}\sum_{j=1}^{N}({d}_{j}-{d}_{j}^{*}{)}^{2}$$

(20)

$$RMSE=\sqrt{\frac{1}{N}\sum_{j=1}^{N}({d}_{j}-{d}_{j}^{*}{)}^{2}}$$

(21)

$$MAE=\frac{1}{N}\sum_{j=1}^{N}|{d}_{j}-{d}_{j}^{*}|$$

(22)

$$MAPE=\frac{1}{N}\sum_{j=1}^{N}\left|\frac{{d}_{j}-{d}_{j}^{*}}{{d}_{j}}\right|\times 100\mathrm{ \%}$$

(23)

$$\rho =\frac{\sum_{j=1}^{N}({d}_{j}-\overline{d })({d}_{j}^{*}-{\overline{d} }^{*})}{\sqrt{\sum_{j=1}^{N}({d}_{j}-\overline{d }{)}^{2}({d}_{j}^{*}-{\overline{d} }^{*}{)}^{2}}}$$

(24)

$${R}^{2}={\rho }^{2}$$

(25)

where $N$ is the sample size of the measured data (that is, the real spring discharge data), $({d}_{j},{d}_{j}^{*})$ are the actual and predicted data, respectively, $\overline{d }$ is the mean of the values of the ${d}_{j}$, and ${\overline{d} }^{*}$ is the mean of the values of the ${d}_{j}^{*}$. The RMSE which is also referred to as the standard error, reports on the dispersion of the prediction errors. MAE denotes the average of absolute errors, and it is used to compute how far the predicted values deviate from the test data. MAPE measures model accuracy as a percentage, and it works best if there are no extremes in the data. As such, MAPE is primarily used to determine any irregularity in the test data (Swanson et al. 2011). The computed values of RMSE, MAE, and MAPE are all within the range of $[0, \infty ]$. Usually, a small value of RMSE indicates a small deviation between the predicted and the observed test data. Therefore, the smaller the value (that is, $RMSE <1$), the better the model design. On the other hand, the correlation coefficient measures the strength of the relationship between the predicted values and the original test data. The metric measure ranges from $[-\mathrm{1,1}]$. The extreme values of $-1$ and $1$ indicate a perfectly linear relationship between the predicted values and the original test data. Meanwhile, as the coefficient approaches $-1$ or $1$, the strength of the relationship increases and the data points tend to draw closer to a reference line. Lastly, the coefficient of determination measures the extent to which the predicted values explain the original test data.

Results and discussions

Generally, three primary methods are used in groundwater research to analyse hydrological behaviours; mathematical models, numerical simulations, and the use of laboratory-scaled experiments (Ding et al. 2020; Suresh Kumar 2014). Mathematical models and numerical simulations have gained much attention recently (Chang et al. 2015). Initially, laboratory-scaled experiments had some limitations when complex geological conditions needed to be studied due to the limited use of materials (Ding et al. 2020). However, with the advancement of technology, the use of laboratory-scaled experiments in conjunction with other methods, such as machine learning approaches, has made tremendous progress in simulating complex geological processes such as karst formations.

The hydrological cycle process in karst environments is so complex that a single linear input–output model cannot properly explain it (Song et al. 2022). This complexity was also evident in research conducted by Labat et al. (2000), who created a linear stochastic rainfall-runoff model and performed a Fourier analysis on three karst springs in France. They concluded that linear input–output models could not accurately represent the hydraulic behaviours of karst springs. Additionally, research by Tao et al. (2022) revealed the importance of humidity in the hydrological cycle processes and further use in water resources planning and management.

Therefore, this work built a 3D physical model based on the conceptual model of a karst aquifer and predicted spring discharge by combining three factors, precipitation intensity, temperature, and humidity. A novel hybrid LSTM-RNN model coupled with BO was employed to model the multivariate time series behaviour of the input parameters. The study’s findings demonstrated the capability of a deep learning model for simulating spring discharge with various input parameters in a karst environment, which validates the findings of previous studies (Hu et al. 2018; Kratzert et al. 2018; Song et al. 2022) that demonstrated the ability of neural networks in solving non-linear relationships in karst terrains.

Influence of rainfall intensity on spring discharge

Examining the influence of rainfall intensity on spring discharge is critical for assessing its impacts and the non-linearity trends in karst environments. The spring hydrograph was used to investigate the effect of varied precipitation intensities on spring flow. The findings revealed that the lower the intensity of the rainfall, the lower the peak flow of the spring hydrograph, and vice versa. Figures 11a–c and 12a–c demonstrate this. However, an intriguing result was found in ‘d’ of both Figs. 11 and 12, which deviated from the previous trend. At the high precipitation intensity of 0.02925 mm/s for 30 min duration of simulated rainfall, the peak flow for spring discharge was very low compared to the other precipitation intensities which had the highest peak flow for the longest duration rainfall of 30 min. The deviation shown in ‘d’ of both Figs. 11 and 12, could be explained by the heterogeneous nature of the soil (sand and loam), which comprised the porous layer.

Fig. 11

Spring hydrographs showing the peak flows for different precipitation intensities and different duration of 15, 20, 25, and 30 min. The precipitation intensities are 0.02017, 0.02279, 0.02632, and 0.02925 mm/s

Fig. 12

Spring hydrographs showing the peak flows for different precipitation intensities with the same duration. The precipitation intensities are 0.02017, 0.02279, 0.02632, and 0.02925 mm/s corresponding to times of 15, 20, 25, and 30 min

The porous layer is a layer of soil that has interconnected pore spaces through which water can flow. Porosity refers to the total amount of pore space available in the soil or rock, while permeability refers to how easily water can flow through that pore space. When the rainfall intensity is high, such as during a heavy rainstorm, the amount of water that falls onto the porous layer can exceed the capacity of the soil to absorb it. If the porosity and permeability of the porous layer are low, the excess rainwater will not be able to infiltrate into the system and will instead accumulate on the surface as overland flow The infiltration rate is affected by the nature of the soil, i.e., its physico-chemical properties (Djukem Fenguia and Nkouathio 2023).

The degree of permeability and porosity of the porous layer showed that not all the simulated Rainfall could infiltrate into the system and further percolate into the aquifer, owing to the high rainfall intensity. The porous layer became fully saturated quickly, and overland flow (i.e., surface runoff) was higher. This led to a shorter peak of the spring hydrograph, as shown in Figs. 11d and 12d. This deviation is also analogous to findings by Djukem Fenguia and Nkouathio (2023), whose results identified the nature of the soil as one major cause of flooding.

With respect to this study, the porous layer quickly reaches its maximum capacity to hold water and becomes saturated at a precipitation intensity of 0.02925 mm/s for 30 min duration of simulated rainfall. This means that any additional rainwater will simply run off the surface of the soil and contribute to surface runoff. This can lead to increased soil erosion, flooding, and decreased groundwater recharge. Therefore, it is important to consider the permeability and porosity of the porous layer when designing and managing water systems for effective water management and sustainability. It is also imperative to pay attention to other physico-chemical properties of the soil, such as grain size, moisture, pH, compactness, and organic matter in water resources planning and management (Ansar and Naima 2021; Djukem Fenguia and Nkouathio 2023).

Predictive models

Furthermore, to determine the variance of the proposed model, the regression models, i.e., LSTM-1 to LSTM-5, were diagnosed and the results are presented in Fig. 13a–e. Figure 13a–c shows the prediction plot generated from LSTM-1, whilst Fig. 13d, and Fig. 13e were produced from LSTM-5. A detailed description of the performance of these 5 models using 3, 2, or 1 input parameter(s) is presented in Table 5. The plots in Fig. 13a–c were predicted using three input parameters (precipitation intensity, temperature, and humidity), two input parameters (precipitation intensity and temperature), and only one input parameter (precipitation intensity), respectively.

Fig. 13

Prediction error plots depicting 20% of the actual discharge from the simulated dataset against the predicted values generated by the proposed model: a the best-optimised model using precipitation intensity, temperature and humidity as input parameters; b the best-optimised LSTM model using precipitation intensity and temperature as input parameters; c the best-optimised LSTM model using only precipitation intensity as an input parameter; d the 5th-ranked-optimised LSTM model using precipitation intensity, temperature and humidity as input parameters; e the 5th-ranked-optimised LSTM model using precipitation intensity and temperature as input parameters

Table 5 Comparison of the true mean value (μ) and the 95% confidence interval (2σ) of the five (5) different LSTM models using three input parameters (precipitation intensity, temperature, and humidity), two input parameters (temperature and humidity), and one input parameter (precipitation intensity)

The left side of the prediction plots presents the original targets from the test data versus the predicted values generated from the trained LSTM models. It can be observed from the residual plots on the right-hand side that plots with 3 and 2 input parameters produced symmetric distributions with mean errors of $0.003\pm 0.036$ and $0.001\pm 0.037$, respectively.

The results indicate an acceptable prediction performance of LSTM-1, LSTM-2, LSTM-3, and LSTM-4. It also validated the established models’ ability to construct a robust and dependable learning process. However, based on the results, it was discovered that including more climate parameters in the prediction, matrix improved prediction performance. This can be seen from the results tabulated in Table 5 which is also confirmed by studies conducted by Tao et al. (2022) on the integration of extreme gradient boosting features with machine learning models on relative humidity prediction. His results showed that an increase in climatic parameters as input parameters improved the model performance. Furthermore, studies conducted by Fiorillo et al. (2021) revealed that a decrease in spring discharge does not appear to be solely dependent on precipitation changes but that temperature fluctuations play a vital role. This shows that in studying the hydrodynamic characteristics of the karst aquifers, particularly pertaining to spring discharge prediction, it is imperative to consider at least precipitation intensity and temperature in the analysis, as evident in Fig. 8 on the feature importance using the XGB regressor. However, using only precipitation intensity as an input variable in the LSTM model (refer to Fig. 13c), is not sufficient to predict spring discharge.

To investigate areas within the target that may be prone to more or less error, the residual plots displayed in Fig. 14a–c capture the disparities between errors on the y-axis and the dependent variable on the x-axis.

Fig. 14

Residual plots showing irregularities between the simulated and fitted response values

In Fig. 14a, b, a fairly random, uniform distribution of the residuals against the target in two dimensions—indicating that our non-linear LSTM-1 model is very robust in predicting the spring discharge using at least 2 input variables is seen. The ${R}^{2}$ values for adopting 3 input variables are $97.2 \mathrm{\%}$ (for the training set) and $97.1 \mathrm{\%}$ (for the testing set). In addition, the histograms show that the errors obtained are symmetrically distributed around zero, which also generally indicates a well-fitted model when we consider at least 2 input variables. However, the scenario is not the same when a single input variable is used as shown in Fig. 14c. The ${R}^{2}$ values, in this case, are $4.7 \mathrm{\%}$ (for the training set) and $2.3 \mathrm{\%}$ (for the testing set).

Additionally, a two-dimensional graphical presentation i.e., “Taylor Diagram (Ansar and Naima 2021)” was generated for the proposed LSTM models 1–5 for the estimation of spring discharge in karst terrains and this is shown in Fig. 15.

Fig. 15

Taylor’s Diagram of the prediction LSTM model developed using three input variables (left panel) and two input variables (right panel), respectively

Taylor’s Diagram is normally used to justify the degree of agreement between the model developed and the measurement set used (the commonly used precision indexes are the Pearson correlation coefficient, the root-mean-square error (RMSE), and the standard deviation) to aid in evaluating the accuracy of the model. In this study (refer to Fig. 15), the same statistical metrics were adopted to assess the performance of the 5 LSTM models produced from the Bayesian optimisation tuning approach.

The five colours in the plot represent the 5 LSTM models developed. The black star on the horizontal axis is the observed or reference point. When the simulation point is close to the observed point, it means they are similar in terms of standard deviation, with a high correlation and a centred root mean square error (CRMSE) value close to zero. The black dashed lines represent the standard deviation of the observed time series. Values above the black dashed line mean the simulated data set has a higher variation, and values below mean the data set has a lower variation. The contour lines on the polar plot show the values of CRMSE.

Figure 15 (left panel), models 1, 2, 3, and 4 are similar in terms of their standard deviation, which is close to the reference or observed point and also falls on or close to the black dashed line with a correlation above $99\mathrm{ \%}$ and a CRMSE of about 0.04. Model 5, on the other hand, has a lower standard deviation (below the black dashed line) with a correlation of around $91 \mathrm{\%}$, and the CRMSE is close to 0.16. On the other hand, Fig. 15 (right panel) shows models 1, 2, and 3 to be slightly below the black dashed line even though their respective standard deviations were closer to the reference or observed point. All three models had a correlation above $99 \mathrm{\%}$ and a CRMSE of about 0.04. Model 4 had a lower deviation than the referenced black dashed line (standard deviation of the observed data set). It also had a correlation of about $98 \mathrm{\%}$, and the CRMSE was very close to the lowest deviation among all with a correlation of about $78 \mathrm{\%}$ and a CRMSE of about 0.22. From the performance metrics of $\rho$ and ${R}^{2}$, LSTM-1 with three input parameters performed better in estimating spring discharge than LSTM-2 and LSTM-3, even though the deviation was not much, in estimating spring discharge. LSTM-4 and LSTM-5 performed relatively poorly in comparison.

Conclusions

Predicting spring flow is very important for management of water demand especially in cities. In this study, the LSTM-RNN model of deep learning coupled with the BO hyperparameter tuning is identified, trained and tested to predict spring flow in karst environment using climatic variables, based on data gathered from a physical laboratory experiment. Different combinations of model input parameters are considered in this study to predict spring flow.

The experimentation revealed in the results section that model performance is primarily determined by input variables and combinations of parameter selection. Model accuracy improves significantly when the number of neurons and epochs are optimised; the Bayesian Optimizer was employed in this study. The Bayesian Optimiser significantly improved the efficiency of the top 5 hybrid versions and gave a stronger prediction ability of the model. The parameter optimisation using the BO was used to determine the top 5 high-precision LSTM models (LSTM-1, LSTM-2, LSTM-3, LSTM-4, and LSTM-5). Also, the use of epochs and hidden layer neurons improves computation speed as well.

This study has proven that the LSTM-RNN model can be used to predict spring flow and can also predict other variables such as rainfall and temperature. It also proved that when the input variables of the model are more, the output of prediction is better. The advantage of this LSTM model is that it may require a smaller training data set to train the model to predict input variables. It is also beneficial for water resources managers to understand the relationship between spring discharge and climatic variables.

Overall, the development of the physical model, the experimental results, and the deep learning models will serve as valuable reference for future research and investigations in the Jinan Spring Basin and also as useful guidelines for other areas.