Introduction

Rock mass is a highly desirable foundation material owing to its exceptional strength to withstand the applied load, making it the preferred choice for foundation construction. However, accurate determination of the ultimate bearing capacity (UBC) of the foundation is critical for designing engineering structures such as dams, bridges, piers, and tunnels. Furthermore, rock masses pose various challenges in construction activities such as tunnelling and pipeline laying due to micro-scale imperfections including cavities and flaws that result from long-term geological processes such as weathering and erosion (Fam et al. 2002; Waltham et al. 2005). The existence of underground structures such as tunnels, pipelines, shafts, caverns, and voids, whether natural or man-made, can pose significant safety risks for adjacent or nearby foundations. Such structures can cause settlement and reduce the ultimate bearing capacity of nearby foundations. In cases where rock masses contain tunnels or cavities, accurately determining their location in relation to the loaded area is crucial. This is because even if the tunnel or cavity is located at significant depths and horizontal distances from the foundation, it can still substantially decrease the foundation’s load-carrying capacity. Previous studies have demonstrated the impact of underground structures on foundation design, making it essential to account for their interaction during design and accurately evaluate the ultimate bearing capacity of the foundation to ensure safe construction of structures above it or in the vicinity (Xiao et al. 2018, 2019; Wu et al. 2020a; Kumar and Chauhan 2022a; Kiyosumi et al. 2011; Ukritchon and Keawsawasvong 2018; Wang and Badie 1985; Wu et al. 2020a; Zhao et al. 2021) have examined these effects.). Previous research has extensively investigated the detrimental effects of various unlined tunnel/cavity cross-sectional shapes, such as rectangular, square, circular, or irregular, on the ultimate load-carrying capacity (UBC) and stability of shallow foundations. While some studies have focused on the impact of a single unlined rectangular cavity/tunnel (Kiyosumi et al. 2011; Wang and Badie 1985), many others have investigated the effects of dual cavities/tunnels on the UBC of shallow foundations (Xiao et al. 2019; Wu et al. 2020a).

Numerous studies in the field have shown that advanced numerical techniques can be highly effective in analyzing the interaction between cavities and footings in rock masses. For instance (Badie and Wang 1984), utilized the Finite Element Method (FEM) and the Upper-Bound (UB) theorem to initially evaluate the load-bearing capacity of footings positioned above cavities. Since then, many studies have tackled the problem of cavity/tunnel–footing interaction in rock masses by employing FEM under various conditions (e.g., Hoek and Brown 1980; Carranza-Torres 1998; Fraldi and Guarracino 2010).

The determination of the bearing capacity of a strip footing using Finite Element Method (FEM) has become subjective due to the deceptive load-settlement curve resulting from substantial displacement of the footing (Wong and Wu 2015; Lee et al. 2014; Lai et al. 2022a, b, c, d, e). To overcome the limitations of FEM, Finite Element Limit Analysis (FELA) is considered a viable method to determine the ultimate bearing capacity (UBC) of a foundation resting on a rock mass (Jaiswal and Chauhan 2021). FELA has been extensively employed for accurate determination of UBC of footings resting over cavities/tunnels in rock mass under various loading considerations (Chauhan et al. 2022; Kumar and Chauhan 2022a, b, c). The stability of the footing is also affected by changes in the shape, location, and rock mass parameters of the tunnel (Xiao et al. 2018, 2019; Wu et al. 2020a; Zhao et al. 2021; Kumar and Chauhan 2022a). The presence of natural structural discontinuities in rock masses such as joints, cracks, and bedding planes, particularly with significant voids, poses challenges to engineering investigations. In such cases, advanced numerical techniques, including the Generalized Hoek Brown (GHB) criterion (Hoek et al. 1980, 2002), a widely recognized nonlinear failure criterion for rock failures, are beneficial in understanding the issue and identifying progressive failure.

Recent advancements in shield technology have facilitated the excavation of various types of tunnels, including circular and non-circular configurations such as elliptical, rectangular, and horseshoe-shaped tunnels, in practical engineering. Among these, non-circular tunnels are preferred due to their superior section utilization and lower construction costs compared to circular tunnels. Horseshoe-shaped tunnels, in particular, are commonly used in tunnel and subway construction, especially in mountainous areas where rock excavation is necessary. These tunnels feature a semi-circular roof and two vertical wall and a horizontal bottom, offering load distribution benefits similar to those of circular tunnels, while allowing for effective section utilization. Consequently, horseshoe-shaped tunnels are considered more efficient than circular, square, and rectangular tunnels.

While several studies have investigated the effects of footings resting above single or multiple unlined tunnels of various shapes, including circular and square, no research has yet explored the impact of footings resting above a horseshoe-shaped unlined tunnel. However, limited exploration into the stability analysis of horseshoe-shaped tunnels in soil or rock mass subjected to gravity or surcharge loading is evident from the literature (Zang et al. 2018; Rehman and Kumar 2022; Liu et al. 2022; Lowongkerd et al. 2022; Jearsiripongkul et al. 2022a). Additionally, a recent study by Ahmadi et al. (2023) examined the impact of a horseshoe-shaped tunnel and metro station on adjacent deep bridge foundations in cohesive soil.

This study aims to investigate the response of a strip footing subjected to a uniformly distributed load in the presence of an unlined horseshoe-shaped tunnel within a rock mass. Accurately evaluating the ultimate bearing capacity (UBC) of the footing and understanding the interaction between the foundation and the underground structures are crucial for ensuring the secure construction of any nearby or on-top structures. Therefore, designers require data on the reduction in UBC resulting from voids or tunnels, as this information significantly impacts the project’s safety and overall cost. The primary objective of this research is to provide such data to designers to ensure the secure construction of structures above or near unlined horseshoe-shaped tunnels.

Soft computing, specifically the use of artificial neural networks (ANNs), has emerged as a promising alternative to traditional analytical and numerical methods for solving problems. ANNs can generate large datasets and construct black-box predictive models using simple equations. This approach has been effective in predicting the bearing capacity of foundations in rock masses, as demonstrated by various studies. However, there are no studies available on the stability of foundations laid over a rock mass with an unlined horseshoe-shaped tunnel. To address this gap, a stability equations and stability charts were derived using Adaptive Finite Element Limit Analysis (AFELA), Artificial Neural Network (ANN), and Multiple Linear Regression Analysis (MLR). These equations and stability charts enable a comprehensive assessment of the stability of a footing in this particular condition, which is valuable for geotechnical engineers for safe and cost-effective design practices. The analysis considered the positional variation of the footing with respect to the horseshoe-shaped tunnel and varying critical rock parameters, including Geological Strength Index (GSI), material constant (mi), uniaxial compressive strength (σci), and disturbance factors (DF), all following the generalized Hoek–Brown failure criterion.

The investigation aimed to examine the influence of these parameters on the stability of a footing situated above a horseshoe-shaped tunnel. Furthermore, the potential failure mechanism of the strip footing in the presence of a horseshoe tunnel was also examined to demonstrate the effect of the positional variation of the footing with respect to tunnel and rock mass parameters on the development of failure patterns.

Problem definition

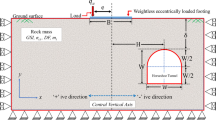
Figure 1 depicts an overview of the problem considered in the present study, which shows a weightless, rigid strip footing of width B resting on a rock mass with unit weight, γ. A horizontal ground overlays a rock mass containing an unlined horseshoe-shaped tunnel. The horseshoe tunnel’s geometry can be described completely by two distinct segments: a flat bottom floor beneath the ceiling with a width of W and vertical walls with a height of W/2, and a semi-circular tunnel ceiling with a diameter of W. The relative position of the tunnel in relation to the footing is indicated by two parameters: the vertical depth, D, and the horizontal offset distance, H. D represent the depth of the tunnel’s crest from the horizontal ground surface, and H represents the horizontal distance of the tunnel’s crest from the footing’s central vertical axis. The strip footing is subjected to a uniformly distributed load, qu. To simplify the representation of the tunnel’s dimensions and its position with respect to the footing, the distances and dimensions are normalized by the width of the footing, which is referred to as the normalized tunnel width (W/B), the normalized depth of the tunnel (D/B), and the normalized horizontal distance of the tunnel (H/B). Additionally, to study the positional variation of the tunnel with respect to the footing, the variation of the horizontal position of the tunnel is considered to be unidirectional, namely in the leftward direction of the footing’s symmetry axis, to avail the advantage of the symmetry of the system.

Fig. 1
figure 1

Uniformly loaded strip footing supported by rock mass over a horseshoe shaped tunnel

Full size image

In the present study, it is assumed that the rock mass follows the Generalized Hoek–Brown (GHB) failure criterion, which was proposed by Hoek et al. (2002) to account for the complex non-linear strength properties of rock masses. This criterion serves as a fundamental tool for accurately estimating the stability of a footing by incorporating the inherent non-linear properties of the underlying rock formations. The GHB failure criterion expresses a mathematical formula that enables one to determine the maximum load capacity (effective major principal stress) that a foundation can withstand before experiencing structural failure and is shown in Eq. (1).

$${\sigma }_{1}^{^{\prime}}={\sigma }_{3}^{^{\prime}}+{\sigma }_{ci}({m}_{b}\frac{{\sigma }_{3}^{^{\prime}}}{{\sigma }_{ci}}+s{)}^{a}$$
(1)

The variables \({\sigma }_{1}^{^{\prime}}\) and \({\sigma }_{3}^{^{\prime}}\), represent the effective major and minor principal stresses at point, respectively and σci represents uniaxial compressive strength of intact rocks. The GSI (geological strength index) utilizes the inherent characteristics of rock types, structural arrangements, and the conditions of discontinuity substrates (Soleiman et al. 2019) present in the rock mass to determine the material parameters mb, s, and a, via the implementation of the following empirically derived relationships shown in Eqs. (2–4).

$${m}_{b}= {m}_{i}\mathrm{exp}\left(\frac{GSI-100}{28-14 DF}\right)$$
(2)
$$s=\mathrm{exp}\left(\frac{GSI-100}{9 - 3DF}\right)$$
(3)
$$a = \frac{1}{2} + \frac{1}{6} ({\mathrm{exp}}^{\frac{-GSI}{15}}- {\mathrm{exp}}^{\frac{-20}{3}})$$
(4)

The material constant for rock mass strength is denoted as mb, whereas the constants s and a represent the Generalized Hoek–Brown failure criterion constants for the rock mass. The material constant of the intact rock, mi is determined by the frictional properties of the minerals comprising the intact rock mass and has a significant impact on the rock's strength characteristics. The disturbance factor, DF, quantifies the amount of disturbance caused by blast damage, impact loading and stress relaxation on the rock mass. To evaluate the effect of an unlined horseshoe-shaped tunnel on the stability of the footing, this study proposes a stability number Nv, which is the ratio of the ultimate bearing capacity of the footing, qu, to the unconfined compressive strength of the intact rock mass, σci. This study further assumes that Nv is a function of various parameters as shown in Eq. (5).

$${N}_{v} = \frac{{q}_{u}}{{\sigma }_{ci}} = f\left(\frac{D}{B},\frac{H}{B}, DF,GSI, {m}_{i},\frac{{\sigma }_{ci}}{\gamma B}\right)$$
(5)

Figure 2 presents the relevant GHB rock mass parameters and their corresponding values, which fall well within the recommended ranges outlined by Hoek et al. (2002). Furthermore, it portrays the intervals of D/B and H/B that were investigated in the parametric analysis.

Fig. 2
figure 2

Details of parameters used in the present study

Full size image

Methodology

Adaptive Finite Element Limit Analysis (AFELA)

The present study developed a numerical model using finite element limit analysis with adaptive mesh refinement techniques for simulating the behavior of a strip footing in the presence of a horseshoe tunnel under uniform distributed load OPTUM G2 (Optum G2 2020) software was employed for the simulation, and to ensure accuracy, a six-noded triangular element and Gaussian integration rule were used, based on the recommendations of a previous study (Lai et al. 2022a; Kumar and Chauhan 2022a). Figure 3 shows the adaptive mesh used in the simulation comprised 8534 number of edges and 5595 triangular elements, with a finer mesh around the footing and tunnel areas where maximum changes in stress and strain occurred. The computational mesh size was set to 15B and 30B in the vertical and horizontal directions, respectively, to prevent adverse effects on the results caused by domain size and minimize the possibility of failure plane development under the footing with the mesh boundaries. The interface between the foundation material and rigid foundation was assumed to be a perfectly rough interface (Jaiswal and Chauhan 2021), and the interface factor was assigned a value of one. A sensitivity analysis was carried out by varying the total number of elements in the mesh within a range of 1500 to 19,000, and it was determined that 13,000 elements provided an optimal level of accuracy for the numerical model, as shown in Fig. 4.

Fig. 3
figure 3

Adaptive finite element mesh arrangement for the strip footing overlaying unlined horseshoe shaped tunnel in rock mass that is obtained from OPTUM G2 (2020)

Full size image
Fig. 4
figure 4

Variation of collapse multiplier load with the total number of elements in the mesh

Full size image

Machine learning

Database

The study employed AFELA solution to generate large datasets, as shown in Fig. 2. The dataset was meticulously segregated into three distinct subsets: namely, the training, validation, and testing by 70%, 15%, and 15%, respectively. The training dataset was utilized to augment the learning process by adjusting weights. Meanwhile, the validation dataset was judiciously employed to finetune the model selection process, such as optimizing the number of hidden neurons and layers and culminating in the ultimate model determination. Finally, the testing set was employed exclusively to expound the generalizability of the trained models with remarkable proficiency.

Multiple linear regression

Linear regression is a statistical technique used for modelling the relationship between a dependent variable and one or more independent variables. The dependent variable is a single response variable, while the independent variables, also called explanatory variables, can be one or more. In the case of multiple independent variables, it is called multiple linear regression. This equation can be used to predict the value of the dependent variable based on the values of the independent variables. The equation that is used to calculate the output, which is dependent on the input or independent variables, is a linear combination of the defined variables. This is done by employing a mathematical formula, such as Eq. (6), which specifies how the independent variables should be combined to obtain the predicted value of the dependent variable.

$${y}_{i}={\beta }_{0}+{\beta }_{1}{x}_{i1}+...+{\beta }_{p}{x}_{ip}+\epsilon$$
(6)

where \({y}_{i}=\) dependent variable (output), \({x}_{i1},{x}_{i2},\dots {x}_{ip}=\) independent variable (input), \({\beta }_{1}\), \({\beta }_{2}\dots ,{\beta }_{p}\)= slope coefficients, \(\epsilon\) = residual error.

Artificial Neural Network (ANN)

This paper employs an Artificial Neural Network (ANN) to provide a data interpretation platform based on the inherent characteristics of the human brain’s composition. Several studies (Azarafza et al. 2021; Jearsiripongkul et al. 2022a; Lai et al. 2022a, c, d; Sirimontree et al. 2022; Jearsiripongkul et al. 2022b; Ngamkhanong et al. 2022; Yodsomjai et al. 2022) demonstrate that the use of Artificial Neural Networks (ANNs) is a highly effective soft-computing approach in civil engineering. ANNs are machine learning algorithms that can recognize patterns and make predictions based on input data (Ansari et al. 2023). The neural network is composed of many interconnected nodes, or neurons, which create a computer model. The ANN model is made up of three layers: the output layer, the hidden layer, and the input layer. The input layer transmits the feature vector. During the learning process, the network’s weights are incrementally modified until they achieve an appropriate level of accuracy to predict the target with reasonable precision. This technique is particularly effective in addressing nonlinear problems, as stated by Park and Lek (2016).

This investigation uses an input layer comprising of four sets of five input nodes each, which correspond, respectively, to the parameters D/B, H/B, GSI, mi, and σci/γB. The second layer is known as the hidden layer, which consists of one or multiple threshold logic unit layers. The optimal configuration of hidden layers and neurons is usually obtained through trial and error, starting with a single hidden layer, followed by varying the number of hidden neurons from one to the maximum value that yields an accurate model. The primary function of the hidden layer is to process the input information and transform it into a format that can be efficiently used by the output layer to generate predictions. The hidden layer computes weighted sums of inputs and applies a step function to them using the rectified linear unit (ReLU) activation function, which adds nonlinearity to the network. The output layer presents dependent variables, and in this paper, it consists of a single node that predicts the Nv.

Additionally, LM back-propagation algorithm is utilized to determine output parameters, achieving second-order training speeds without the need to compute the Hessian matrix. The LM algorithm modifies weight and bias values and provides the advantages of both the Gauss–Newton technique and gradient descent algorithm, addressing the limitations of other algorithms. The LM algorithm is an improved Newton approach, as demonstrated by Eq. (7).

$${x}_{k+1}= {x}_{k}-[{J}^{T}J+uI{]}^{-1}{J}^{T}e$$
(7)

where xk = weight, J = Jacobian matrix, I = identity matrix, e = vector, k and u = damping factor. By adjusting damping, the accuracy and performance of the supervised algorithm can be improved based on stage outcome. Although this may require additional storage, it is recommended as the first-choice algorithm. The effectiveness of the ANN model is evaluated in this study using two statistical indicators: Mean Squared Error (MSE) and the coefficient of determination (R2). The MSE is the average value of a function used to construct a regression model that minimizes the sum of squared errors (SSE), which measures the difference between predicted and actual values. Atici (2011) describes the calculation of MSE and RMSE in Eqs. (8) and (9). Furthermore, Mean Squared Error (MSE) is commonly used, but Root Mean Squared Error (RMSE) is occasionally preferred as it provides a similar error scale to the predicted value. MSE is easy to alter mathematically and frequently used in mathematical approaches. RMSE is used more often than MSE to compare regression model performance against random models. Lower MSE and RMSE values indicate higher model accuracy. where ‘n’ and \({(y}_{i}^{^{\prime}}- {y}_{i})\) represent the number of samples and the difference between predicted and actual values on testing datasets, respectively.

$$MSE=\frac{1}{n}\sum_{i=1}^{n}({y}_{i}^{^{\prime}}- {y}_{i}{)}^{2}$$
(8)
$$RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}({y}_{i}^{^{\prime}}- {y}_{i}{)}^{2}}$$
(9)

In this study, the effectiveness of trained models is assessed by utilizing the coefficient of determination (R2), as defined in Eq. (10).

$${R}^{2}=1-\frac{\sum_{i=1}^{n}({y}_{i}^{^{\prime}}- {y}_{i}{)}^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y } {)}^{2}}$$
(10)

R2 is a measure of the proportion of real-value fluctuations that can be explained by changes in the predicted value, with a range of values between 0 and 1. The numerator and denominator of the equation mentioned above represent the difference between actual and predicted values on testing datasets and the sum of squared differences between true values and the mean, respectively (Bilim et al. 2008). A higher R2 value indicates a better fitting effect, implying that the model can explain a larger proportion of the variability in the data.

Validation of AFELA model

In this study, the accuracy and effectiveness of a numerical model based on AFELA is evaluated by comparing it to the results of a former study conducted by Kumar and Chauhan (2022a). The behavior of a strip footing on an unlined circular tunnel in rock mass is analyzed using the proposed model and compared to the results of the previous study. The ultimate bearing capacity (UBC) values obtained from finite element limit analysis with a six-noded Gaussian element are compared and presented in Fig. 5, with the reduction factor (Rf) used to quantify the effect of the tunnel on the UBC. The results show (Fig. 5a) that the trends in the variation of the simulated model are similar to those reported in the previous study, with a difference in the magnitude of Rf of approximately 4% at H/B = 1 and D/B = 3.5.

Fig. 5
figure 5

Comparison of reduction factor, \({R}_{f}\) obtained from present study and former study (Kumar and Chauhan 2022) for different values of a \(D/B\); and b \(H/B\)

Full size image

Similarly, Fig. 5b shows that the trends in the variation of Rf in this model are slightly lower than those reported in the previous study, with a maximum deviation in the magnitude of Rf of less than 3.3%. Additionally, potential failure envelopes for the strip footing with the tunnel/void located at various positions are compared in Fig. 6, and the results obtained from the numerical model used for validation are similar to those of the previous study. Based on the comparison of the findings and discussion, it can be concluded that the proposed model is suitable for conducting further investigations.

Fig. 6
figure 6

Potential failure envelopes of strip footing resting above circular tunnel for various position-validation study

Full size image

Results and discussion

This section presents the results related to the impact of geometrical parameters, such as the normalized horizontal distance (H/B) and normalized depth (D/B) of a horse-shoe shaped unlined tunnel relative to the centre of a footing, as well as the influence of rock mass strength parameters, such as the geological strength index (GSI), the material constant of rock mass (mi), and the normalized uniaxial compressive strength (σci/γB), on the stability of the footing as measured by stability number, Nv. The analysis also presents the impact of various governing parameters on the potential failure envelope of a strip footing caused by the presence of a tunnel in the rock mass.

Effect of D/B on N v for different H/B

The effect of D/B on the bearing capacity factor (Nv) for various H/B is presented in four distinct scenarios, namely, low GSI-low mi, low GSI-high mi, high GSI-low mi, and high GSI-high mi, in Fig. 7a–d, respectively. The results indicate that Nv increases rapidly with an increase in the offset distance of the tunnel from the footing for depth ratios less than 3. This can be attributed to the fact that as the depth of the tunnel from the footing increases, the impact of the tunnel on the footing’s ultimate bearing capacity decreases rapidly, thereby increasing Nv. However, beyond a specific threshold depth of tunnel, i.e., D/B ≥ 3, the Nv becomes almost constant, and all values of Nv coincide irrespective of horizontal offset distance. This threshold depth is referred to as the critical depth. Beyond this depth, the effect of the tunnel on the footing's bearing capacity is negligible, and the scenario is similar to that of a footing resting on rock mass without any tunnel.

Fig. 7
figure 7

Effect of D/B on Nv for varying H/B for a low GSI, low mi (GSI = 40, mi = 5); b low GSI, high mi (GSI = 40, mi = 35); c high GSI, low mi (GSI = 100, mi = 5); and d high GSI, high mi (GSI = 100, mi = 35)

Full size image

The pattern of all curves in Fig. 7a–d is almost identical for any given values of mi and GSI. However, it is observed that the magnitude of Nv increases with an increase in mi, irrespective of the GSI values. This trend is supported by a comparison of Fig. 7a–d, which reveal that the percentage increases in the magnitude of Nv for mi = 35 is approximately 3.6 times and 2.5 times greater than that for mi = 5, for GSI values of 40 and 100, respectively.

This suggests that the stability of a footing is more significantly influenced by mi for rock masses with lower GSI values compared to those with higher GSI values. Hence, the effect of mi on the stability of the footing is more prominent when the rock mass exhibits lower strength characteristics, as indicated by lower GSI values.

Moreover, a comparing Fig. 7a–d reveals that the maximum difference in the magnitude of Nv, between minimum and maximum values of H/B (i.e., H/B = 0 to 5) for D/B = 1, 2, and 3, is approximately 2.25 times, 1.4 times, and 1.01 times, respectively. This indicates that the change in Nv is not solely dependent on H/B and D/B because the percentage difference in Nv remains constant for a given tunnel depth among all the cases presented in Fig. 7. However, the change in the magnitude of Nv is influenced by varying the rock parameters such as GSI and mi.

Effect of H/B on N v for different D/B

Figure 8a–d illustrate the effect of the tunnel’s horizontal offset distance from the footing, H/B, on Nv for different values of D/B and rock mass properties (Low GSI-Low mi, Low GSI-High mi, High GSI-Low mi, and High GSI-High mi, respectively). The analysis reveals that Nv increases with an increase in H/B, and this effect is more prominent at smaller values of D/B. However, for D/B ≥ 3, the effect of H/B on Nv becomes negligible, and the trend lines for all H/B values merge with each other.

Fig. 8
figure 8

Effect of H/B on Nv for varying D/B for a low GSI, low mi (GSI = 40, mi = 5); b low GSI, high mi (GSI = 40, mi = 35); c high GSI, low mi (GSI = 100, mi = 5); and d high GSI, high mi (GSI = 100, mi = 35)

Full size image

Furthermore, a comparison between the curves for H/B = 0 and 1 shows a similar trend for Nv, except for D/B = 2, where Nv for H/B = 1 is marginally lower than Nv for H/B = 0. This deviation might be due to the non-uniform loading on the tunnel caused by the unsymmetrical position of the tunnel at H/B = 1, leading to a lower load-bearing capacity of the footing compared to the case of symmetrical loading at H/B = 0.

Effect of GSI on N v for different H/B

Figures 9 and 10 display the plots of Nv versus GSI for two different values of mi (i.e., 5 and 35) and varying H/B (0–5) while maintaining σci/γB = 100 constant for D/B (1, 2, 3, and 5). The plots demonstrate a nonlinear relationship between Nv and GSI, with Nv increasing for all values of H/B, D/B, and mi. The increase in Nv with GSI is more significant for higher values of H/B, especially for a tunnel located at a shallow depth from the horizontal ground (i.e., D/B = 1 and 2). However, for tunnels situated at D/B ≥ 3, Nv does not vary with change in H/B for any given value of GSI. As the tunnel depth increases, the impact of H/B diminishes in relation to higher GSI. This observation is explained by the fact that the stability of the footing is primarily controlled by GSI when the tunnel is situated far enough vertically and horizontally from the centre of the footing. Higher GSI values represent a stronger and less fractured rock mass, resulting in an increase in the magnitude of Nv and improved stability of the footing. The effect of GSI is more pronounced for larger values of H/B, with changes in Nv ranging from 3.5 to 8.5 times as GSI increases from 40 to 100 for D/B = 1.

Fig. 9
figure 9

Effect of GSI on Nv for high mi (mi = 35) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image
Fig. 10
figure 10

Effect of GSI on Nv for low mi (mi = 5) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image

Figures 9 and 10 also compare the impact of GSI on Nv for extreme values of mi (i.e., 5 and 35). It is noted that as mi decreases, the magnitude of Nv also decreases. For low mi values, the curves of Nv versus GSI are identical for all ranges of H/B beyond D/B ≥ 3, indicating that GSI has no effect on Nv for a tunnel in a rock mass with low mi. However, for high mi values, a marginal variation of Nv versus GSI is noted for various values of H/B, even at D/B ≥ 3.

Effect of m i on N v for different H/B and D/B

Figures 11 and 12 depict the effect of the parameter mi on Nv for two distinct values of GSI, 40 and 100, respectively. An increasing linear correlation is observed between mi and Nv, throughout the range of H/B corresponding to D/B. This phenomenon can be attributed to the diverse factors that influence mi, such as mineralogy, composition, degree of interlocking, and grain size of the intact rock. As mi increases, the rock mass’s governing parameters, including grain packing patterns, interlocking degree between rock particles, and angularity, also increase. These factors contribute to an increased rock strength, leading to a higher value of Nv. In addition, for low values of mi, the Nv—GSI curves are similar for all H/B ranges beyond D/B ≥ 3, indicating that the rock mass has low mi. Moreover, the stability of a footing resting over a tunnel is not affected by the variation of H/B when the tunnel is located at D/B ≥ 3, given a particular mi and GSI value.

Fig. 11
figure 11

Effect of mi on Nv for low GSI (GSI = 40) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image
Fig. 12
figure 12

Effect of mi on Nv for high GSI (GSI = 100) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image

Effect of σ ci /γB on N v for different H/B and D/B

Figures 13 and 14 illustrate plots of σci/γB versus Nv for two different GSI values of 40 and 100, respectively, while mi is kept constant at 35. It is observed that the trend of Nv for a given H/B and D/B remains unchanged, regardless of the variation in σci/γB. This results in all the curves being parallel to the x-axis. It is noted that the authors assumed σci/γB = ∞, which is not physically possible for rocks in a weightless state (i.e., γ = 0) (Keawsawasvong and Shiau 2022). However, the outcomes obtained by assuming σci/γB = ∞ indicate that the rock is very strong. In numerical simulations, σci/γB = ∞ can be achieved by assigning a very large value of UCS or a very light rock mass to produce valid numerical results. It is interesting to note that the observed trends are independent of the GSI value, as demonstrated in the cases of low (Fig. 13) and high (Fig. 14) GSI values of the rock mass.

Fig. 13
figure 13

Effect of σci/γB on Nv for low GSI (GSI = 40) and low mi (mi = 5) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image
Fig. 14
figure 14

Effect of σci/γB on Nv for high GSI (GSI = 100) and high mi (mi = 35) with varying H/B for a D/B = 1; b D/B = 2; c D/B = 3; and d D/B = 5

Full size image

Multiple linear regression

In this study, the WEKA software is used to create a multiple regression model to examine the relationship between predictor variables and a response variable. The fitted regression weights or coefficients to the model using sophisticated algorithms that minimized the difference between the predicted and actual values of the response variable. These coefficients represent the influence of each predictor variable on the response variable. As a result of this optimization process, authors derived Eq. (11) for multiple linear regression, which expresses the complex relationship between the predictor variables and the response variable in mathematical terms.

$${N}_{v} = (0.187 {\sigma }_{ci}/(\gamma B) + (12.249 GSI) + (2.148 D/B) + (0.6208 H/B) + (6.2637 {m}_{i}) - 5.0749$$
(11)

Figure 15 compares stability factor assessed by FELA with predicted values obtained from MLR. Statistical tests such as coefficient of determination (R2) and Root Mean Square Error (RMSE), which yield corresponding values of 0.86 and 3.1247, respectively, can be used to evaluate the effectiveness of the Eq. (10). Whereas the sensitivity analysis results are presented in Fig. 16, highlighting the relative importance of five dimensionless parameters. The Relative Importance Index (RII) is used to quantify the significance of each parameter, with a value of 100% denoting the highest importance. The Geological Strength Index (GSI) is identified as the most critical parameter with an RII value of 100%. The other parameters, including (mi), (D/B), (H/B), (σci/γB), are of lesser importance with RII values of 70.4%, 50.11%, 17.54%, and 1.52%, respectively.

Fig. 15
figure 15

Comparison of predicted value of Nv from MLR versus actual values of Nv obtained AFELA results

Full size image
Fig. 16
figure 16

Variation of relative importance index, (RII) on all dimensionless input variables

Full size image

Artificial Neural Network (ANN)

Optimizing the number of hidden layers and neurons is crucial for improving the predictive power of an artificial neural network (ANN) model. This study demonstrates that an ANN model can accurately predict stability factor by utilizing a single hidden layer with varying numbers of neurons. The results presented in Fig. 17 show a clear relationship between the number of hidden neurons and the model’s performance, indicating a significant improvement in performance when the number of neurons exceeds a certain threshold. It is expected that once this threshold is reached, the performance of the ANN model becomes stable.

Fig. 17
figure 17

Performance evaluation of square shaped tunnels versus the number of hidden neurons

Full size image

Among the evaluated models, the “5-11-1” ANN model (consisting of 5 input variables, 11 hidden neurons, and 1 output) was found to be the most effective, displaying the lowest mean squared error (MSE), Root mean square value (RMSE) and the highest coefficient of determination (R2) are as 1.1067, 1.051 and 0.992, respectively. Additionally, Fig. 18 demonstrates good agreement between the results obtained from the proposed ANN model and the finite element limit analysis (FELA) model.

Fig. 18
figure 18

Comparison of predicted value of Nv from ANN versus Nv obtained from AFELA results for the optimal ANN architecture (Model: 5-11-1) for horseshoe shaped tunnel

Full size image

Comparing the performance of the multiple linear regression (MLR) and ANN models, the latter demonstrated superior results, as indicated in Table 1. Therefore, the optimal ANN model with the “5-11-1” architecture can be utilized for predicting the stability factor from the ANN model.

Table 1 Evaluation Metrics for Multiple Linear Regression (MLR) and Artificial Neural Networks (ANN) Performance
Full size table

The function can be used to generate output by considering weighted inputs and transfer function with an optimal ANN architecture. This network can simulate general functions and accurately predict functions with a finite number of discontinuities if the hidden layer has enough neurons. Weights for each parameter determine their impact on stability factor, and Eq. (12) represents the prediction equation using matrices from the ANN model.

$$Predicted value=\left[\sum_{i=1}^{N}I{W2}_{i}tansig (\sum_{j=1}^{J}IW{1}_{ij}{x}_{j}+{b}_{1i})+{b}_{2}\right]$$
(12)

The proposed ANN models represent x as input variables, J as the number of input variables, and N as the number of hidden neurons. Weight matrices IW1 and IW2 represent the hidden and output layers, while b1i and b2 represent the associated biases. The hidden weight matrix IW1 is selected based on N and J, resulting in an output matrix with a single column. The input weight matrix IW2 has the same number of rows as N and the same number of columns as the output neurons (k), with one column per neuron in the output layer.

Table 2 illustrates the utilization of weight and bias matrices, as constants within an optimized Artificial Neural Network (ANN) model, for the determination of the stability factor of strip footing over a horseshoe tunnel. The values obtained from the optimal ANN network can be leveraged to construct predictive equation functions, which can subsequently undergo rigorous testing on novel datasets, varying in data ranges, to enhance their accuracy and applicability.

Table 2 Neural network constants of the optimal model for stability prediction of strip footing laying over horseshoe tunnel
Full size table

Associated potential failure mechanism

This section describes the failure mechanisms of a strip footing under various scenarios where a tunnel is located at different distances and depths from the footing. The impact of governing parameters on the potential failure planes is also highlighted. The velocity field contours for the footing under different H/B ratios and depth ratios (D/B = 1, 2.5, and 3) are shown in Figs. 19, 20 and 21 to illustrate the failure mechanisms.

Fig. 19
figure 19

Comparison of shear dissipation contours of footing above horseshoe shaped tunnel for various H/B with D/B = 1

Full size image
Fig. 20
figure 20

Shear dissipation contours of footing above horseshoe shaped tunnel for various H/B with D/B = 2.5

Full size image
Fig. 21
figure 21

Shear dissipation contours of footing above horseshoe shaped tunnel for various H/B with D/B = 3

Full size image

In Fig. 19, for the case where D/B = 1 and H/B = 0, the tunnel experiences a combined failure of the roof and both sides of the vertical edge due to the high-stress concentration caused by the tunnel's placement directly below the footing at shallow depth. As the tunnel is situated away from the central vertical axis of the footing (H/B = 1, 2, and 3), two failure planes originate from both corners of the footing, converging at the crest of the roof and the left bottom corner of the edge, affecting the entire periphery of the left edge. An additional failure plane extends from the crest of the tunnel's roof to the horizontal ground, resulting in the squeezing of the rock mass above this failure plane. For H/B = 4 and 5, there is limited interaction between the tunnel edge and the footing, and an extra failure plane originates from the tunnel's roof, extending outwards until it intersects with the horizontal ground surface. The zone of influence of the failure plane in the rock mass increases as the distance between the footing and tunnel increases horizontally. The maximum influence zone is 8.5B in the horizontal direction and 2B in the vertical direction from the central vertical axis of the footing and ground level, respectively for a given magnitude of H/B and D/B.

In Fig. 20, for the scenario where D/B = 2.5 and H/B = 0, 1, 2, and 3, the failure mode behaves similarly to the previous scenario. However, the maximum extent of the influence zone in the vertical direction enlarges to 3.5B due to the increased depth of the tunnel. For H/B = 4 and 5, the roof and left vertical edge of the tunnel interact with both corners of the footing through the failure plane, and the influence zone of the failure plane remains nearly constant at approximately 11B.

In Fig. 21, for the scenario where D/B = 3, the failure plane depicts a typical general shear failure below the footing, similar to Terzaghi's failure mechanism for strip footing resting on semi-infinite soil mass (Craig 2004). The presence of the tunnel beyond the depth, D/B ≥ 3, has no impact on the generated failure plane. The zone of influence within rock mass, which is affected by the failure plane, exhibits symmetry. Additionally, this zone extends to a distance of 3.5 times the width of footing on both sides for the given value of H/B (except H/B = 0). This failure plane that has been observed in this study is similar to the one reported by Kumar and Chauhan (2022a), where a footing was situated above a circular unlined tunnel in a rock mass. The findings suggest that the presence of the tunnel beyond a depth ratio of D/B ≥ 3 does not have any significant impact on the generated failure plane. As a result, the influence zone of the rock mass affected by the failure plane is symmetrical and extends up to a distance of 3.5B on both sides of the footing, for a given value of H/B (except when H/B = 0).

Conclusions

In this study, the stability number (Nv) for a strip footing subjected to uniformly distributed loading above a horseshoe-shaped tunnel in rock mass was analysed using adaptive finite element limit analysis (AFELA) and dependability of Nv with of various positional and rock mass parameters, including the depth of the tunnel (D/B), the horizontal distance of the tunnel (H/B), the geological strength index (GSI), the normalized uniaxial compressive strength of the rock mass (σci/γB), and the material constant of the rock mass (mi) was investigated. Generally, the magnitude of Nv increases with increasing D/B and H/B, but when D/B ≥ 3, the magnitude of Nv remains constant for any given value of H/B, indicating that the presence of the tunnel has no impact on the stability of the footing. Increasing GSI and mi tends to increase the magnitude of Nv, but the impact of σci/γB on Nv is negligible. The failure mechanisms of tunnels can be classified into three categories based on the horizontal and vertical positions of the tunnels. These categories are as follows: (1) the combined failure of the roof and vertical edge of the tunnel, (2) vertical edge failure only, and (3) general shear failure below the footing, which is similar to the one described in Terzaghi's failure mechanism for strip footings resting on semi-infinite soil mass. In the third category, there is no interaction between the tunnel and the footing is observed. A stable and high-performing neural network model with a single hidden layer of fifteen neurons was constructed and validated for evaluating the stability factor of the strip footing. These models and equation are specifically customized for the ranges outlined in the present study and can be employed for assessing new data with great assurance. The combination of AFELA with artificial neural network (ANN) and multiple linear regression (MLR) models is proposed as a reliable tool for geotechnical engineers to assess the stability of strip footing in inference of tunnel. The ANN and MLR models offer faster prediction of tunnel stability compared to AFELA.