Introduction

Uncertainty is an integral part of modelling and it is a pointer to insufficient knowledge about the reliability of measurements (Wang and Chen 2012; Wang et al. 2006; Refsgaard et al. 2007; Fu and Rich 1999; Wechsler 1999). It arises as a result of spatial and temporal variations in measured data as well as the non-uniqueness of parameters and processes associated with the resulting models (Brimicombe 2010; Refsgaard et al. 2007; Wang and Chen 2012). In groundwater study, incomplete knowledge of the random and spatial distribution of hydrogeological or aquifer parameters give rise to uncertainty (Raaflaub and Collins 2006; Wechsler 1999; Şen 1999; Hunter and Goodchild 1997). The aquifer parameters may include but not limited to depth to the aquifer, thickness, hydraulic conductivity, resistivity, transmissivity, anisotropy among others. If this uncertainty is quantified, it can aid in robust decision making process (Harrison et al. 2010) on the optimal exploitation and management of groundwater resource. There are several and different algorithms that have been developed to quantify uncertainties which are more or less based on probability distribution.

The aim of this study, therefore, is to quantify the uncertainties and assess the risk associated with six aquifer parameters in a basement complex environment using variogram-constrained ordinary kriging estimates and a stochastic conditional Gaussian simulations algorithm. This is with a view to providing quantifiable risk-based distribution of the parameters and their influence on exploitation and management of the groundwater resource. Variogram provides spatial autocorrelation and geologic continuity model whose outputs serve as inputs to constrain the deterministic kriging estimates and stochastic models (Ivits-Wasser 2004; Deutsch 2002; Gringarten and Deutsch 2001; Isaaks and Srivastava 1989). Kriging is usually referred to as a best linear unbiased estimate interpolation technique (Deutsch 2002; Goovaerts 1997; Isaaks and Srivastava 1989). While the stochastic conditional Gaussian simulations algorithm is a Monte Carlo (probabilistic) procedure that makes use of the inverse normal distribution (Karlis 2002; Banks 1998) to calculate several equally probable outcomes conditioned to the variogram which are then used for uncertainty analysis (Vann et al 2002). Uncertainty analysis (Wang and Chen 2012; Refsgaard et al. 2007) tests the reliability of the outcomes and provides a measure of risk to be considered in the process of exploitation and management decision-making. This research therefore, would serve as a contribution to groundwater uncertainty study especially in the basement complex.

Location characteristics and main aquifer types

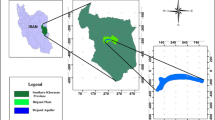
The study location is in Osun State, southwestern Nigeria (Fig. 1), within latitude 7.81°N to 8.05°N (UTM 864,281.40 mN and 890,385.30 mN) and longitude 4.62°N to 4.91°N (UTM 678,806.80 mE and 711,081.40 mE). It is an area dissected by the presence of many rivers and streams characteristic of tropical rain forest environment. The topography is uneven and characterized by ridges, hills and valleys. Regionally, the area is underlain by crystalline basement rocks categorized by Rahaman (1988, 1976) as grey/banded gneiss, granite gneiss, undifferentiated schist, porphyritic granite and pegmatite with evidence of multiple deformations and metamorphisms (Fig. 1). Typical subsurface layers within the basement from bottom to the top are the fresh basement, fractured basement, weathered layer and topsoil (Olorunfemi and Fasuyi 1993; Olayinka and Olorunfemi 1992; Olorunfemi et al. 1991). The target aquifers are usually the weathered and fractured basements but in most cases, the weathered basement occurs more frequently than the fractured basement (Olorunfemi and Fasuyi 1993). So the main consideration in this study, is the weathered basement aquifer.

Fig. 1
figure 1

The study area (Modified after Nigeria Geological Survey Agency 2006)

Full size image

Methodology

The methodology follows the workflow described in Fig. 2. The original data consist of six aquifer parameters (Table 1) distributed as regionalized variables over 39 locations in the study area. The parameters are (1) depth to the aquifer, (2) resistivity, (3) thickness, (4) coefficient of anisotropy, (5) transmissivity and (6) yield. Each parameter is subjected to semivariogram analysis which serves as geologic constraint to produce a deterministic model (ordinary kriging estimate () and standard deviation ()). The kriging estimate and standard deviation are subjected to stochastic process by the application of randomized normal inverse function to produce 100 equally probable realizations which are used for uncertainty analysis.

Fig. 2
figure 2

Methodology workflow

Full size image
Table 1 The original regionalized six aquifer parameters
Full size table

Semivariogram analysis

A semivariogram investigates and quantifies the degree of spatial variableness of the parameter of interest and serves as critical input in geostatistical estimation and simulation algorithms (Gringarten and Deutsch 2001). This is achieved by measuring the mean difference between sample points at a displacement vector (h) from each other. Its value increases as samples become more dissimilar. For a pair of sample points, it is simplified as:

$$\upgamma \left(\mathrm{h}\right)=\frac{1}{2\mathrm{N}\left(\mathrm{h}\right)}\sum_{\propto =1}^{\mathrm{N}\left(\mathrm{h}\right)}{\langle \mathrm{w}\left({\mathrm{x}}_{\propto }\right)-\mathrm{w}\left({\mathrm{x}}_{\propto }+\mathrm{h}\right)\rangle }^{2}$$
(1)

where γ(h) = semivariogram; N(h) = the number of sample pairs in a lag interval; xα = the vector of spatial coordinates of the αth individual; w(xα) and w(xα + h) are values of the attribute at two points at an interval displacement vector (h) (Ivits-Wasser 2004).

The exponential semivariogram model defined mathematically by Eq. 2 was adopted for analysis of the aquifer parameters.

$$\upgamma \left(\mathrm{h}\right)=\mathrm{Cov}(0)\left[1-{\mathrm{e}}^{\left(-\frac{3\mathrm{h}}{\mathrm{a}}\right)}\right]$$
(2)

where Cov(0) = sill—a measure of maximum variance, a = range of correlation, h = lag. The semivariogram analysis was done using Surfer™ software package.

Ordinary kriging (ODK)

The ODK is one of the variants of the linear regression estimator W*(x) defined by Eq. 3. It estimates the value of a random variable at a location from a set of nearby random variables W(xα) (Goovaerts 1997; Isaaks and Srivastava 1989). A group of (n(x) + 1) linear equations combine with (n(x) + 1) unknowns such that kriging weights can be obtained by Eq. 4.

$${\mathrm{W}}^{*}(\mathrm{x}) -\mathrm{ m}(\mathrm{x})=\sum_{\propto =1}^{n\left(x\right)}{\lambda }_{\alpha }\left[W({x}_{\alpha })-m({x}_{\alpha })\right]$$
(3)

where (x) is the estimation point location vector; n(x) is the number of data points used for the estimation of W*(u); xα represents one of the neighboring data points; m(x) is the mean of W(u); while m(xα) is the mean of W(xα). λα(x) is the kriging weight for estimation location (x) assigned to datum W(xα).

$$\left\{\begin{array}{c}{\sum }_{\mathrm{\alpha },\upbeta =1}^{\mathrm{n}(\mathrm{x})}{\uplambda }_{\upbeta }^{\mathrm{ODK}}\left(\mathrm{x}\right)\mathrm{Cov}\left({\mathrm{x}}_{\mathrm{\alpha }}-{\mathrm{x}}_{\upbeta }\right)+{\upmu }_{\mathrm{OK}}\left(\mathrm{x}\right)=\mathrm{Cov}\left({\mathrm{x}}_{\mathrm{\alpha }}-\mathrm{x}\right)\\ {\sum }_{\upbeta =1}^{\mathrm{n}(\mathrm{x})}{\uplambda }_{\upbeta }^{\mathrm{ODK}}\left(\mathrm{x}\right) = 1\end{array}\right.$$
(4)

Equation 4 can be summarized as ODK(x) * T = t; such ODK(x) = T−1 * t. Where T, with elements Tα, β = Cov(xα—xβ) represents covariance matrix between surrounding data points, while t, with elements tα = Cov(xα—x), is the covariance vector between point of estimation and the surrounding data points; and ODK (x) is the vector of the location-by-location ordinary kriging weights for the surrounding data points with respect to the estimation location (x) (Goovaerts 1997; Bohling 2005). The relationship between covariance function Cov(h) and the input semivariogram γ(h) model is as defined by Eq. 5.

$$\mathrm{Cov}(\mathrm{h})=\mathrm{Cov}(0)-\upgamma (\mathrm{h}) =\mathrm{Sill}-\upgamma (\mathrm{h})$$
(5)

Simulation and uncertainty analysis

Given a value of probability, the NORM.INV function simulates an equally probable random value W specified by a random probability generator RAND() for a given average (µ) and standard deviation (σ) (Eq. 6). The probability range is usually between 0 and 1.

$$\mathrm{W} = \mathrm{NORMINV}(\mathrm{RAND}(), \mu , \sigma )$$
(6)

The RAND() will generate a random probability related to normal distribution for which the inverse function is to be obtained. The average and standard deviation values are obtained from the ordinary kriging estimates and kriging standard deviation, respectively. The Gaussian function (NIST/SEMATECH 2012; Karlis 2002) which represents the continuous probability density function of the normal distribution relates the standard normal random variable (W = (x−)/), mean () and standard deviation () by

$$\upphi \left(\mathrm{W},\upmu ,\upsigma \right)=\frac{1}{\upsigma \sqrt{2\uppi }}{e}^{-\frac{{\mathrm{W}}^{2}}{2}}$$
(7)

This is achieved by picking a random deviate from the normal distribution of the estimated location-specific kriged and equivalent standard deviation values using the randomized inverse-normal distribution function. Several random deviates which represent equiprobable realizations are simulated by repeating the process one hundred times. The uncertainties associated with the realizations are then assessed using the cumulative distribution functions (cdfs) and probability maps.

Results and discussions

Semivariogram characteristics of the aquifer parameters

Figure 3 describes the semivariogram characteristics for the six aquifer parameters. They all measure the spatial or the geologic continuity of the parameters using the exponential variography based on the same number of lags of 25 and lag width of 553.46 m. But the sill and range values are mostly different and are represented in Table 2. They are the two most important parameters that serve as inputs to the deterministic and stochastic algorithms.

Fig. 3
figure 3

Variogram model for the each parameter

Full size image
Table 2 Semivariogram characteristics of aquifer parameters
Full size table

The sill for depth is 150 m and the range is 3000 m; while those for thickness are 100 and 5430 m, respectively. Resistivity has a sill of 3000 and a range of 4660 m; while the sill and range for anisotropy are 0.065 and 3000 m, respectively. The sill of hydraulic conductivity is 3.2 × 10–10 at a range of 3000 m; while sill of transmissivity is 1.4 × 10–7 at a range 3000 m. Finally, the yield has a sill of 0.016 at a range of 1170 m.

Deterministic estimates of aquifer parameters

Figure 4 is the resulting deterministic (kriging) estimate distributions which amounted to eight thousand, one hundred (8100) estimated data points for each of the six aquifer parameters. Figure 4a is the map of the depth to the top of the aquifer which varies between 0 and 50 m. The deepest portions are associated with banded and granite gneiss in the northwest and porphyritic granite and pegmatite towards the northeast. The aquifer depth is mostly shallower (less than 20 m) at the southern end of the study area. The thickest portion of the aquifer (Fig. 4b) are similarly associated with the banded and granite gneiss in the northwest as well as the porphyritic granite and pegmatite towards the northeast. The thickness varies between 0 and 42 m. The aquifer resistivity (Fig. 4c) varies between 0 and greater than 270 m. Resistivity values below 150 m are concentrated towards the western parts while above 150 m are more towards the eastern part. The higher the resistivity, the less the conductivity, the fresher the groundwater. The anisotropy distribution (Fig. 4d) varies between 1 and 21. Most parts have anisotropy values less than 1.6 while the remaining parts have values of more than 1.6 particularly on the porphyritic granite towards the north and the granite-gneiss towards west-central parts. Anisotropy indicates degree of heterogeneity that has an index of 1 for a fresh rock but increases with exposure to weathering and fracturing (Akintorinwa et al. 2020).

Fig. 4
figure 4

Kriged estimates for a depth b thickness c resistivity d coefficient of anisotropy e transmissivity and f yield

Full size image

The aquifer transmissivity (Fig. 4e) which is a measure of the rate of fluid flow varies between 0 and 14 × 10–4 m2/s in the study area. The presence and movement of groundwater would increase with degree of fracturing or weathering of the rock. Its distribution is such that the higher the transmissivity, the higher the rate of fluid flow (Akintorinwa et al. 2020). So parts of the study area around the northeast (with porphyritic granite, pegmatite and undifferentiated schist) and northwest (granite-gneiss and banded gneiss) have higher transmissivity values compared to other areas. The yield map (Fig. 4f) indicates a variation between 1.04 and 1.50 L/second which seems to be increasing towards the eastern part. It is worthy of note, that a relative high or low yield is not necessarily associated with any rock units but is most likely related to the degree of weathering, fracturing, connected spaces and potential recharge available in the study area. Yield is of paramount importance in groundwater search and it is a reflection of the combination of multiple groundwater controlling parameters. In all the maps, it appears the distribution patterns of the groundwater parameters are likely influenced by the NE-SW geological/structural trend typical of the basement complex in Nigeria.

Simulated aquifer parameters and associated uncertainty

The kriged maps (Fig. 4) are smoothened or average maps and so are not sufficient to capture the variabilities, heterogeneities or uncertainties associated with the distributions of the estimated parameters (Goovaerts 1997). However, the conditional stochastic simulation algorithm-based maps reveal variabilities, heterogeneities and uncertainties in the distribution of the parameters. Figures 5, 6, 7, 8, 9 and 10 are some six simulations out of the 100 simulations for each parameter of depth, thickness, resistivity, anisotropy, transmissivity and yield, respectively.

Fig. 5
figure 5

Selected six realizations of depth

Full size image
Fig. 6
figure 6

Selected six realizations of thickness

Full size image
Fig. 7
figure 7

Selected six realizations of resistivity

Full size image
Fig. 8
figure 8

Selected six realizations of coefficient of anisotropy

Full size image
Fig. 9
figure 9

Selected six realizations of transmissivity

Full size image
Fig. 10
figure 10

Selected six realizations of yield

Full size image

The cumulative distribution functions (cdfs) of the realizations used to quantify the risk/uncertainty in the distributions of each of the aquifer parameters are summarized into minimum, average and maximum (Figs. 11 and 12). They display a representative range of useful data between 0 and 70% risk/uncertainty for all parameters. The upper images are plots of the cdfs that have red dot for minimum, blue line for average and black dot for maximum while the equivalent tables of the figures are displayed below them. For example, 0% risk represents maximum available to be exploited at no risk, all things being equal while above 70% risk, the expected values are extremely low. Values above 70% uncertainty/risk are not likely to be useful at all. The varying characteristics of the realizations reflect risk which is a function of the potential uncertainty associated with the distribution of these parameters in the subsurface. In Fig. 11a, at 0%, depth has a minimum of about 51 m, maximum of about 66 m and average of about 57 m. However, at 70%, the minimum value of depth is 2.6 m, maximum of 3.3 m and average of 3.0 m. In Fig. 11b for thickness at 0% risk, it has about 45 m at the minimum, 56 m at the maximum and 48 m at the average. At 70% risk, it is just 2.4 m at the minimum, 3.2 m at the maximum and 2.7 m at the average. The resistivity (Fig. 11c) at 0% risk is about 308 m at the minimum, 378 m at the maximum and 342 m at the average. However, at 70% risk, it about 55 m at the minimum, 58 m at the maximum and 56 m at the average. This anisotropy risk distribution values are shown in Fig. 12a. At 0% risk, It has 2.13 for minimum, 2.61 for maximum and 2.28 for average. At 70% risk, it has 1.11 for minimum, 1.13 for maximum and 1.12 for average. Figure 12b, is the risk associated with the distribution of transmissivity. The values of transmissivity at 0% risk in m2/s are 15 × 10–4 at the minimum, 22 × 10–4 at the maximum and 18 × 10–4 at the average. At 70% risk, however, it is 0 × 10–4 at the minimum, 1 × 10–4 and 1 × 10–4 at the average. Moreover, from Fig. 12c, the yield values available at no risk (0%) vary between 1.71 L/second for minimum, 1.93 L/second for maximum and 1.78 L/second for the average. At 70% risk, the yield is 1.21 for minimum, 1.22 for maximum and 1.215 for average. In all, it is clear that the higher the risk, the higher the uncertainty and the less the expected average, minimum, and maximum value for each of the parameters. The simulation allows for the quantification of risk/uncertainty to give a more robust outlook of the distribution of the parameters than just the original data and the kriged estimates.

Fig. 11
figure 11

Risk profile -cumulative distribution functions for a depth b thickness and c resistivity

Full size image
Fig. 12
figure 12

Risk profile -cumulative distribution functions for a coefficient of anisotropy b transmissivity and c yield

Full size image

Implication for groundwater exploitation in the study area

The probability maps (Fig. 13) indicate the risk associated with distribution of the parameters. They can be divided grossly into low risk (< than 30%); mid-risk (between 30 and 60%) and high risk (> than 60%) areas and are expected to have a significant influence on the sustainable exploitation and management of groundwater in the study area. For example, it can be deduced from the depth risk map (Fig. 13a), that part of the granite-gneiss and banded gneiss to the west and the pegmatite and the undifferentiated schist to the east are low-risk areas. About the same patterns can be observed on the thickness risk map (Fig. 13b) and the transmissivity risk map (Fig. 13e). But, it is slightly different for the resistivity risk map (Fig. 13c) as well as the anisotropy risk map (Fig. 13d). Moreover, the yield risk is not the same everywhere (Fig. 13f). It appears that the study area is more of a mid-risk yield (30–60% risk) area interspersed by low and high risk yield regions. With this assessment and quantification, it is easier to project tolerable risk and uncertainty into the search for groundwater and associated decision on its exploitation in this area based on prevailing conditions.

Fig. 13
figure 13

Risk maps for a depth b thickness c resistivity d coefficient of anisotropy e transmissivity and f yield

Full size image

Conclusion

The study describes the analysis of the uncertainties associated with the six aquifer parameters of depth, thickness, resistivity, coefficient of anisotropy, transmissivity and yield to produce risk-based assessment of their distribution. The focus is to glean their potential influence on exploitation and management decision of groundwater resource in the region. The analysis was based on the use of variogram-constrained ordinary kriging estimates and a conditional stochastic simulation algorithm which is a Monte Carlo procedure that makes use of the inverse normal distribution. The resulting several equally probable outcomes form the basis of the uncertainty analysis in the form of cdfs and probability maps. There are evident varying uncertainties in the distribution of the aquifer parameters across rock units and the study area has between 30 and 60% groundwater yield risk. These results, therefore, provide a basis for risk-based decision on groundwater exploitation in the region as well as serves as a contribution to the application of deterministic and stochastic algorithms in groundwater uncertainty study.