Introduction

Typically, in hydraulic structures such as dams, and canals water flows out with high energy and can endanger the stability of downstream structures. So, it is necessary to dissipate excess energy of high-velocity flow at the outlet of a conduit or tunnel. Nowadays, one of the most important energy dissipators in hydraulic structures is stilling basins. Therefore, many researchers are looking for the best optimal stilling basin to increase the energy dissipation of the water flow. Stilling basins dissipate the energy of the outlet flow of channels, chutes, and culverts. The most common form of the impact type energy dissipator is USBR VI stilling basin in which the energy is dissipated by the incoming jet striking the baffle [1]. The efficiency of the USBR VI stilling basin in accomplishing energy losses, for the same Froude number, is higher than a hydraulic jump stilling basin [2]. This basin looks like a box with the intermediate baffle. The USBR VI stilling basin can dissipate the energy of the incoming flow without tailwater. Suitable tailwater; however, will decrease the velocity of the outlet flow from the basin and the scouring of the downstream channel bed. Also, tailwater more than the recommended limit causes some flow passes over the baffle.

Several researchers have studied the efficiency improvement of energy dissipation in the USBR VI stilling basin by using physical models. Aleyasin et al. [3] investigated the flow field experimentally. Their tests were performed for the basin with \(\frac{W}{D}=7.3\) and Froude number of incoming flow 6. Basin width and inlet pipe diameter were 40 and 5.5 cm, respectively. They suggested installing a splitter in the upstream of the baffle and a cellular wall between the baffle and the endsill for improving the efficiency. Verma and Goel [4, 5], Tiwari [6], and Tiwari and Goel [7] studied the scour downstream of this basin for various geometry modifications of the basin experimentally. Their studies were performed for \(\frac{W}{D}=6\) (basin width to incoming flow depth) and the various Froude numbers. The inlet pipe diameters were 7.5 and 10 cm. They presented some suggestions for parameters of the location of the baffle wall, its dimensions, the length of the basin, and the shape of the endsill. All investigations related to USBR VI stilling basin have a common point that outlet flow from the basin should minimize damage to the downstream river bed of the basin. Due to the complexity of the flow field in this basin, they did not evaluate the flow field in different conditions in their physical models. However, the flow field can be studied by numerical simulation accurately. Numerical simulation of the flow field can provide useful information about the mechanism of the energy dissipation of the flow and the optimal stilling basin. Review of previous researches demonstrated that the mechanism of the energy dissipation of the flow in the USBR VI stilling basin has not been studied until now.

The flow field in stilling basins is usually simulated numerically by various methods. One of the most common methods is the finite volume method which is used in the present study [8]. Also, the energy dissipation phenomenon of the flow is often done by using the mean flow characteristics or by the entropy generation (EG) analysis. Recently, the analysis of the flow field by the EG index has been very much considered. In energy systems, the less EG indicates more efficiency.

Most of These researches had been conducted on energy systems such as power plants. Bejan, firstly, was the first researcher that studied convective fluid flow with EG analysis [9, 10]. Several studies have been conducted by EG analysis such as concentric annulus [11], solar collector [12, 13],twisted U-tube [14], a solar heat exchanger [15,16,17], latent heat storage [18], steam turbines efficiency [19, 20], power plant efficiency analysis [21], cavity [22,23,24,25], diesel engine efficiency [26, 27], boiling phenomenon [28, 29], Wells turbine [30, 31] and stretching cylinder [32]. Saghi and Lakzian [33] analyzed the sloshing phenomenon using the EG index. Nazeryan and Lakzian [34] studied the details of the turbulent and viscous EG rate in a Wells turbine based on the blade thickness. Lakzian et al. [35] by simulating an air ejector pump showed that the maximum entrainment ratio and the minimum total EG occur in the same geometry of the ejector.

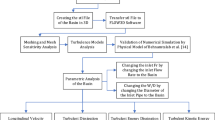
Energy dissipators or stilling basins have different performance comparisons with cases that are presented. In stilling basins, if EG increases, this condition is better than before. Although numerous studies by using EG analysis, this method has not been used to study the energy dissipation mechanism of the stilling basins and their optimization. Hence, in this study, for the first time, we investigated energy dissipation in a hydraulic structure sing entropy generation analysis. Therefore, in the present paper, we numerically simulated the USBR VI stilling basin to analyze the dissipation mechanism by using the EG method. First, the numerical model is validated by the experimental data. Then, the flow field, the EG rate, and the total EG in the basin are calculated for the various \(\frac{W}{D}\) ratios. Finally, the best \(\frac{W}{D}\) ratio and the optimal basin are introduced.

Numerical Method and Procedure

In this research, Reynolds Averaged Navier–Stokes (RANS) is implemented to model the flow field. These RANS equations, which are time-averaged equations of motion for fluid flow, are used to describe turbulent flows of incompressible Newtonian fluid [30]. They are based on Reynolds decomposition in which an instantaneous quantity decomposes into its time-averaged and fluctuating quantities. The following equations show RANS equations, governing the conservation of mass and momentum [36]:

$$\frac{\partial \rho }{\partial t}+\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$
(1)
$$\frac{\partial {u}_{i}}{\partial t}+u\frac{\partial {u}_{i}}{\partial x}+v\frac{\partial {u}_{i}}{\partial y}+w\frac{\partial {u}_{i}}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+\frac{\partial g}{\partial {x}_{i}}+\frac{\mu }{\rho }\left(\frac{{\partial }^{2}{u}_{i}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{i}}{\partial {y}^{2}}+\frac{{\partial }^{2}{u}_{i}}{\partial {z}^{2}}\right)$$
(2)

In the above equations \(\rho\) is the fluid density, \(\mu\) is the dynamic viscosity, \(g\) is the gravity acceleration, \(p\) is the pressure and \(u\), \(v\), \(w\), are local velocity components in \(x\), \(y\), \(z\) directions, respectively. The RNG k-epsilon model equations are given in Eqs. (3) and (4) in which \(K\) and \(\varepsilon\) are turbulent kinetic energy and dissipation rate, respectively and P shows turbulence production given by [37]:

$$\frac{\partial K}{\partial t}+{\overline{u}}_{i}\frac{\partial K}{\partial {x}_{i}}=P-\varepsilon +\frac{\partial }{\partial {x}_{i}}\left(\frac{{\upnu }_{T}}{{\sigma }_{K}}\frac{\partial K}{\partial {x}_{i}}\right)$$
(3)
$$\frac{\partial \varepsilon }{\partial t}+{\overline{u}}_{i}\frac{\partial \varepsilon }{\partial {x}_{i}}={C}_{\varepsilon 1}\frac{\varepsilon }{K}P-{C}_{\varepsilon 2}\frac{{\varepsilon }^{2}}{K}+\frac{\partial }{\partial {x}_{i}}\left(\frac{{\upnu }_{T}}{{\sigma }_{\varepsilon }}\frac{\partial \varepsilon }{\partial {x}_{i}}\right)$$
(4)
$${\upnu }_{T}={C}_{\mu }\frac{{K}^{2}}{\varepsilon }$$
(5)
$$\begin{array}{ccc}K=\frac12\overline{u'_iu'_i}&,&\varepsilon=\nu\overline{\frac{\partial u'_i}{\partial x_j}\frac{\partial u'_i}{\partial x_j}}\end{array}$$
(6)
$$P=2{\nu }_{T}{\overline{S}}_{ij}{\overline{S}}_{ij} and {\overline{S}}_{ij}=\frac{1}{2}\left(\frac{\partial {\overline{u}}_{i}}{\partial {x}_{j}}+\frac{\partial {\overline{u}}_{j}}{\partial {x}_{i}}\right)$$
(7)

The coefficients of above equations are presented in Table 1.

Table 1 Coefficients for RNG k-epsilon turbulence model [37]
Full size table

In CFD modelling, the volume of fluid (VOF) is used to identify the free surface level and its angle among the solution domain, by defining a specified value for the fluid surface cells which are semi-full and show their water-filled proportion [36]. The transport equations for the VOF function are as:

$$\frac{{V}_{f}}{\rho }\frac{\partial \rho }{\partial t}+\frac{1}{\rho }\nabla .\left(\rho .\overline{u }.{A}_{f}\right)=-\frac{\partial {V}_{f}}{\partial t}$$
(8)
$$\frac{\partial \overline{u}}{\partial t }+\frac{1}{{V}_{f}}\left(\overline{u }.{A}_{f}.\nabla \overline{u }\right)=-\frac{1}{\rho }\left[\nabla P+\nabla .\left(\tau {A}_{f}\right)\right]+G$$
(9)
$$\frac{\partial F}{\partial t}+\frac{1}{{V}_{f}}\nabla .\left(F.\overline{u }.{A}_{f}\right)=-\frac{F}{{V}_{f}}\frac{\partial {V}_{f}}{\partial t}$$
(10)

In the above equations \({V}_{f}\) is the volume fraction, \(\tau\) is the viscous stress tensor, \(G\) is the body acceleration and \(F\) is the fluid fraction. Symbol \(G\) denotes the gravity vector.

In order to study the effect \(\frac{W}{D}\) parameter of USBR VI stilling basin on energy dissipation rate, EG analysis is performed, and it is assumed that the viscous heating is very insignificant. \(\frac{W}{D}\) is an important parameter on the USBR VI stilling basin design.

In the modeling, the EG rate is determined by the following equation [21] in which \(S_{gen}^{'''}\) is EG rate (\(\frac{W}{{m}^{3}K}\)) and \(T\), \(k\), \(\mu\) and \(\varphi\) are temperature, thermal conductivity, dynamic viscosity and viscous dissipation function, respectively:

$$S_{gen}^{'''}=\frac k{T^2}\left(\nabla T\right)^2+\frac\mu T\varphi>0$$
(11)

The equation of EG rate has two terms of the thermal dissipation and viscous dissipation and since fluid flow in stilling basins is isothermal, the term of the thermal dissipation can be neglected. As a result, Eq. (11) can be re-written in three-dimensional coordinates as [38] as follow:

$${S}_{gen}=\iiint \left(\frac{\mu }{T}\varphi \right)dxdydz$$
(12)
$$\varphi =2\left[{\left(\frac{\partial u}{\partial x}\right)}^{2}+{\left(\frac{\partial v}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial z}\right)}^{2}\right]+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^{2}+{\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)}^{2}+{\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)}^{2}$$
(13)

In this study the calculation of the total hydraulic head (\(THH\)) of the flow in the beginning and at the end of the basin is performed by determining the value of the mean velocity in the inlet pipe, the depth of the incoming flow, the mean depth and the mean velocity of the flow on the endsill (Eq. (14)). Then, the value of the head decreasing ratio (\(HDR\)) of the basin is drawn by Eq. (15):

$$THH=\frac{{P}_{0}}{\gamma }+Z+\frac{{U}^{2}}{2g}$$
(14)

Where \({P}_{0}\) and \(U\) are the mean pressure and mean velocity in the desired section.

$$HDR \left(\%\right)=\frac{\left({THH}_{at Begining}\right)-\left({THH}_{at End}\right)}{\left({THH}_{at Begining}\right)}\times 100$$
(15)

Model Implementation and Boundary Condition

Physical Model

In general, the most important factor to design a basin is its width which can be calculated from Fig. 1 [2] by the depth and the Froude number of the incoming flow. In this study, it is assumed that the cross-section of the incoming jet to the basin has the shape of a square [2]; therefore, it is calculated by the following equation, in which \(Q\) and \(V\) are the inlet flow rate and mean velocity of the incoming flow, respectively.

Fig. 1
figure 1

Design width of the USBR VI Stilling Basin [2]

Full size image
$$D=\sqrt{A}=\sqrt{\frac{Q}{V}}$$
(16)

Also, Froude number of the incoming flow is calculated from the following equation:

$$Fr=\frac{V}{\sqrt{g.D}}$$
(17)

In CFD modeling, five different models of the stilling basin are chosen as 3D computational domains to cover the best performance of the basin in the \(\frac{W}{D}\) range from 3 to 10 [2].

All the dimensions of these models are considered constant except for the inlet pipe diameter (\({D}_{o}\)) and its length. As a result, five different \(\frac{W}{D}\) ratios with value 9.23, 7.81, 5.97, 4.84, and 3.50, which are in the upper, middle, and lower range of Fig. 1 curve, are achieved. The schematic of the computational domains is depicted in Fig. 2 and their fixed dimensions are presented in Table 2.

Fig.2
figure 2

The schematic model of the stilling basin. (a) Schematic basin [3], (b) Perspective view of the basin, (c) Coordinate system, (d) Longitudinal section and important dimensions

Full size image
Table 2 Dimensions of the USBR VI stilling basin model (in centimeter)
Full size table

Numerical Models and Methods

The physical characteristics of each 3D model are summarized in Table 3. The computational domains from upstream and downstream are extended sufficiently to confirm the fully developed flow condition and uniformity of the flow. Thus, the length of the inlet pipes in the A, B, C, D, and E models are defined as 2, 2.5, 3, 4, and 5 m respectively, to ensure that the incoming flow is fully developed. The tailwater dimension with a value of 16 cm is calculated from the recommended relation of \(d+\frac{b}{2}\), for the best performance of the USBR VI stilling basin [2].

Table 3 Characteristics of simulations for investigating the \(\frac{W}{D}\) effect
Full size table

It can be seen from Fig. 2(c) that the origin of the Cartesian coordinate system is set at the end of the inlet pipe floor; besides, the coordination of each point in the computational domains is normalized with equations of \({x}^{*}=\frac{x}{L}\), \({y}^{*}=\frac{y}{W}\) and \({z}^{*}=\frac{z}{H}\).

A structured meshing is set up to discretize the computational domains. The total number of cells on the computational domain is about 1.1 × 106. The mesh independency analyses are performed, and it is presented in the next section. Simulations with finer grids showed that the quality of prediction is not enhanced by improving the number of cells used. In Fig. 3, the computational domain with the cell distribution is depicted. It can be seen that each model is divided into two blocks to ease the meshing procedure of the inlet pipe to the basin, and the basin itself and its downstream channel. The computational domain contained six boundaries: inlet, outlet, wall surfaces, and symmetry surface at \(Zmax\) in the second block to simulate the atmospheric pressure on the free surface. The location of each boundary is presented in Table 4. The flow is uniformly entered into the computational domain from volume flow rate boundary condition with the turbulent intensity (I) of 5% and it leaves the computational domain with outflow boundary condition. At the wall surfaces, no-slip condition for the flow is assumed. The flow is entered into the A, B, C, D, and E models with a velocity of 5.31, 4.31, 3.10, 2.38, and 1.60 m/s, respectively. The density of the water and its dynamic viscosity are considered 1000 kg/m3 and 0.001 kg.s/m, respectively. The water temperature is assumed to be 20 °C.

Fig. 3
figure 3

Schematic view of the mesh used for simulating the USBR VI stilling basin

Full size image
Table 4 Boundary conditions of the numerical model
Full size table

Mesh Independency

To investigate the mesh independency in the CFD study, the domains of the model E have meshed to five different sizes over a range from 2 × 105 to 1.6 × 106. In all cases, total EG in the stilling basin is considered as a criterion for choosing the optimum meshing size. The result of the meshing size effect on the CFD prediction accuracy is summarized in Table 5 and Fig. 4. It presents that the EG for Mesh 1 and Mesh 2 is completely different from the three other meshes, but there is a little difference between predicted EG of the Mesh 4 and Mesh 5. Therefore, for reducing the simulation time, Mesh 4 is selected as an optimum one. In this mesh setup, the computational domain is meshed into 1,072,566 cells.

Table 5 Total EG in the stilling basin for different meshes
Full size table
Fig. 4
figure 4

Variation of the total EG for different number of cells

Full size image

Solving Method

In this study, the finite volume method (FVM) is employed to discretize and solve governing equations of the flow in the three-dimensional domains. Flow3D software package is applied to simulate steady-state and incompressible flow in the stilling basin.

The momentum advection algorithm is a first-order upwind differencing method. It is sufficiently accurate in most situations.

GMRES method (generalized minimum residual), which is a highly accurate and efficient method for a wide range of problems, is implemented as pressure–velocity implicit solver to couple pressure and velocity fields. This method possesses good convergence, symmetry, and speed properties and does not require any over or under relaxation to achieve good convergence; however, it does use more memory than the other methods [36].

In order to determine the suitable turbulence model in USBR VI stilling basin, the numerical model A (from Table 3) was simulated with three different turbulence models k-ε, k-ω and RNG Turbulence Models, with same conditions. Comparison between these simulation's results and the results of the physical models shows that the average error is 21, 7 and 9 percent, respectively for k-ε, k-ω and RNG turbulence models. This indicates that k-ε turbulence model cannot provide good results compared to the other turbulence models. Therefore, k-ω and RNG turbulence models can be used to simulate the turbulence in this stilling basin. Besides, Previous studies of proposed RNG turbulence model for simulation of turbulence in free surface flows [39,40,41,42,43,44,45]. The numerical computation is considered converged whenever the residual of velocity, Reynolds stress, and continuity equations are below 10–6.

Validation of the Numerical Simulation Method

In order to validate the numerical model, results are compared with experiments conducted by Schlichting [46] and Behnamtalab et al. [47]. The experimental apparatus is depicted in Fig. 5 and more details about this experimental apparatus can be found in the references [47]. A comparison of the experimental results and the acquired data from CFD simulation are shown in Figs. 6 , 7 and 8. In Fig. 6 a line is along the inlet pipe cross-section, and the comparison of velocity profiles of the numerical model and experimental study by Schlichting [46] are depicted. In Fig. 6, \({u}_{P-Max}\) is the maximum velocity at the inlet pipe and it can be seen that numerical prediction has a similar tendency with the experimental results and the mean error of the numerical model is almost 1.2 percent.

Fig. 5
figure 5

Physical model of USBR VI stilling basin [47]

Full size image
Fig. 6
figure 6

Velocity profile in the inlet pipe (\(r\) and \({D}_{o}\) are radius direction and inlet pipe diameter, respectively)

Full size image

In Fig. 7, the stagnation point on the baffle, which is opposite of the central axis of the inlet pipe, is depicted and the pressure at this point is presented in Table 6. The table shows that the measured normalized pressure (\(\frac{p}{\frac{\rho {V}^{2}}{2}}\)) in numerical and experimental studies is 1.16 and 1.22, respectively.

Fig. 7
figure 7

Location of the stagnation point on the baffle

Full size image
Table 6 Pressure on the stagnation point on the baffle wall
Full size table

In Fig. 8, a cross-sectional plate in the endsill is drawn and the simulated normalized flow depth in this plate is compared with the experimental data.

Fig. 8
figure 8

Flow depth on the endsill

Full size image

The results of the comparison in the above Figs. show that the numerical results are in an acceptable agreement with the experiments, and this agreement demonstrates the reliability of the numerical model.

Results and Discussion

In this part, first, the hydrodynamic characteristics of the five simulations are evaluated. Then, the EG of the models is studied. One of the most important features of a stilling basin is the protection of the downstream river bed. Therefore, characteristics of the outlet flow of the stilling basin are very important. Therefore, the variation of the total hydraulic head along the basin, characteristics of the flow on the endsill, shear velocity near the downstream channel bed, and finally the EG will be studied.

\(\frac{W}{D}\) Effect on Total Hydraulic Head (\(THH\))

Total hydraulic head variation between the beginning and the end of the basin is calculated by using Eq. (14). Results show that the total hydraulic head decreases in the basin by 89, 84, 72, 57, and 39 percent for \(\frac{W}{D}\)= 9.23, 7.81, 5.97, 4.84, and 3.50, respectively.

These results demonstrate that the total hydraulic head reduction for \(\frac{W}{D}\)=9.23 is more than twice of the case with \(\frac{W}{D}\)=3.50. It can be concluded that the larger \(\frac{W}{D}\) leads to greater total hydraulic head. In Table 7, the kinetic energy head and piezometric head is presented for various \(\frac{W}{D}\) ratios. Data of this table shows that for \(\frac{W}{D}\)=9.23, a large percentage of the total hydraulic head of the inlet flow to the basin, is the kinetic energy head and it is vice versa for the outlet flow of the basin. In this case, the kinetic energy head at the beginning and the end of the basin are 96 and 3 percent of the total hydraulic head, respectively. The contribution of the kinetic energy to the \(THH\) in the inlet flow to the basin declines significantly, by decreasing the \(\frac{W}{D}\) ratio. For all cases of \(\frac{W}{D}\) ratio at the outlet flow of the basin, the contribution of kinetic energy to the \(THH\) is insignificant. Therefore, USBR VI stilling basin for large \(\frac{W}{D}\) ratio has more capability for decreasing the kinetic energy of the incoming flow (Fig. 9).

Table 7 Total hydraulic head in the beginning (\({x}^{*}=0\)) and the end (\({x}^{*}=1\)) of the basin
Full size table
Fig. 9
figure 9

Head decreasing ratio (\(HDR\)) at different \(\frac{W}{D}\)

Full size image

\(\frac{W}{D}\) Effect on Velocity Field in the Outlet of the Basin

One of the most important characteristics of the flow field at the outlet of the basin is the velocity. The mean velocity, maximum velocity, and shear velocity near the downstream channel bed have a direct effect on the scouring of the downstream of the basin. Therefore, the study of the velocity field on the endsill and near the downstream channel bed can determine the level of outlet flow influence of the basin on the downstream of the basin for various \(\frac{W}{D}\) ratios. In Fig. 10, x-direction velocity contours on the endsill are depicted for various \(\frac{W}{D}\) ratios. The range of the velocity in figures (a) to (e) is between zero to 1.6 \(\frac{m}{s}\).

Fig. 10
figure 10

X-velocity contours on the endsill (\({x}^{*}=1\)). (a) W/D=9.23, (b) W/D=7.81, (c) W/D=5.97, (e) W/D=4.84, (f) W/D=3.50

Full size image

As it can be seen from the above figure, the high velocity contours cover a bigger length of the endsill by decreasing the \(\frac{W}{D}\) ratio. In Fig. 10(a) (\(\frac{W}{D}\)=9.23), velocities more than 1 \(\frac{m}{s}\) are distributed in the ranges of \({y}^{*}\)=0.41 to 0.5 and \({y}^{*}\)=-0.5 to -0.41. In Fig. 10(c) (\(\frac{W}{D}\)=5.97), velocities more than 1 m/s are distributed in the ranges of \({y}^{*}\)=0.28 to 0.5 and y* = -0.5 to -0.28. Figure 10(e) (\(\frac{W}{D}\)=3.50) shows that all widths of outlet velocity on the endsill have velocities more than 1 \(\frac{m}{s}\). On the other hand, by reducing the \(\frac{W}{D}\) ratio, the velocity distribution of outlet flow from the basin on the endsill is converted from vertical to horizontal distribution. Therefore, velocity will increase by moving away from the water surface for lower \(\frac{W}{D}\) ratios on the endsill. Besides, velocity will increase by moving away from the water surface for larger \(\frac{W}{D}\) ratios. These conditions would considerably increase the probability of the scouring in the downstream bed of the basin.

In Fig. 11, normalized x-velocity in \(z\) direction is presented for two \({y}^{*}\), \({y}^{*}\)=0 is for the middle of the basin and \({y}^{*}\)=0.45 is for the location near the sidewall. It can be seen in Fig. 11(a), x-velocity near the top surface of the endsill is high while it is lower toward the water surface. Also, by decreasing \(\frac{W}{D}\) ratio, normalized x-velocity near the top surface of the endsill can be increased, considerably. It is shown that the lower the x-velocity near the bed leads to the lower the scouring downstream of the basin. Figure 11(b) depicts that maximum x-velocity, near the sidewall of the basin, is diverged from the bed. Also, the maximum x-velocity for \(\frac{W}{D}\)=3.50 is more than the others.

Fig. 11
figure 11

Normalized x-velocity on the endsill at different \(y^\ast.\) (a) y*= 0.0, (b) y*= 0.45

Full size image

In Table 8, the mean and maximum real velocity and normalized mean and maximum velocity on the endsill are presented. Normalized velocities are normalized with the mean velocity of incoming flow (\(V\)) to the basin. In this table, umean and umax are mean and maximum velocity on the endsill, respectively. As previously presented in Table 3, the mean velocity of the incoming flow is 5.30, 4.31, 3.10, 2.38 and 1.60 for \(\frac{W}{D}\)=9.23, 7.81, 5.97, 4.84 and 3.50, respectively.

Table 8 Velocity field on the endsill
Full size table

According to Table 8, the mean velocity on the endsill (\({u}_{mean}\)) is decreased by increasing the \(\frac{W}{D}\) ratio. It shows that, although the mean velocity of incoming Flow (\(V\)) for higher \(\frac{W}{D}\) ratio, is greater, outlet mean velocity from the basin (\({u}_{mean}\)) for this \(\frac{W}{D}\) ratio is smaller. This means that higher the \(\frac{W}{D}\) ratio cause lower outlet mean velocity from the basin. Also, maximum velocity (\({u}_{max}\)) on the endsill has a similar trend as mean velocity on the endsill (\({u}_{mean}\)). Normalized velocities are quite similar to real velocities. According to Table 8, normalized mean velocity on the endsill (\(\frac{{u}_{mean}}{V}\)) for \(\frac{W}{D}\) =9.23, 7.81, 5.97, 4.84, and 3.50 are 0.059, 0.086, 0.141, 0.210, and 0.350, respectively. It means that normalized mean velocity on the endsill for \(\frac{W}{D}\) =9.23, 7.81, 5.97, 4.84, and 3.50 is decreased by 94, 91, 86, 79, and 65 percent, respectively. Therefore, by increasing the \(\frac{W}{D}\) ratio, higher percentage of the mean velocity of the inlet flow to the basin is dissipated when it leaves the basin.

In Fig. 12, shear velocity distribution near the bed in the downstream channel of the basin is presented for various \(\frac{W}{D}\) ratios, and the shear velocity distribution is depicted from the beginning of the channel (\({x}^{*}=1\)) to twice of basin length (\({x}^{*}=2\)). It can be seen that, the shear velocity near the downstream channel bed for \(\frac{W}{D}\)=3.50 is higher than other ratios. Therefore, by decreasing the \(\frac{W}{D}\) ratio, shear stress on the channel bed is increased.

Fig. 12
figure 12

Shear velocity distribution near the downstream channel bed. (a) W/D=9.23, (b) W/D=7.81, (c) W/D=5.97, (d) W/D=4.84, (e) W/D=3.50

Full size image

\(\frac{W}{D}\) Effect on Entropy Generation Rate

Technically, the EG analysis can show how to dissipate the energy of flow in the USBR VI stilling basin. Therefore, in this section, the EG rate and the total EG is evaluated for various \(\frac{W}{D}\) ratios in the stilling basin. In Fig. 13, the EG rate in two planes, normal to the z-axis and normal to the y-axis for \(\frac{W}{D}\)=9.23 are presented and it is shown that the EG rate is high near the jet boundaries. As mentioned before, the incoming jet to the basin is fully developed and the boundary layer is formed completely in the incoming jet. In the boundary layer, the EG rate is higher because of the severe variation of the velocity. Besides, incoming jet to the basin is spread in the yz-plane and boundary layer thickness is increased while the incoming jet is undergone deflection considerably near the vertical part of the baffle and it became almost parallel to the vertical part of the baffle. In this case, the incoming jet is converted to a wall jet. This wall jet is moved parallel to the vertical and horizontal parts of the baffle and is vanished gradually.

Fig. 13
figure 13

EG rate on the xz-plane (\({y}^{*}=0\)) and xy-plane (\({z}^{*}=0\)) for W/D = 9.23

Full size image

In Fig. 14, the EG rate on the xz-plane at \({y}^{*}=0\) is presented for various \(\frac{W}{D}\) ratios. It is seen that the maximum velocity in the incoming jet for \(\frac{W}{D}\)=9.23 is much higher than others, so the variation of velocity in the boundary layer is higher in \(\frac{W}{D}\)=9.23 ratio. Figure 14 shows that the EG rate variations are completely in accordance with the distribution of the velocity in the jet boundary layer. After the incoming jet to the basin is passed under the baffle, the distribution of discharge has become uniform in the basin width gradually and the variation of velocity in all directions is declined. In Fig. 14, the EG rate after the baffle is almost negligible. It can be concluded that a major part of the energy dissipation of the incoming jet occurs upstream of the baffle in the basin.

Fig. 14
figure 14

EG rate on the xz-plane at \({y}^{*}=0\)  (a) W/D=9.23, (b) W/D=7.81, (c) W/D=5.97, (d) W/D=4.84, (e) W/D=3.50

Full size image

The EG rate details for various \(\frac{W}{D}\) ratios are presented in Fig. 15. Figure 15(a) depicts the EG rate average in yz-plane along the basin length. The yellow dashed lines show the vertical part of the baffle. The maximum of the average EG rate is happened in the upstream of the baffle and very close to the baffle. Also, after the baffle, the average EG rate is decreased and became uniform. The curve related to \(\frac{W}{D}\)=9.23 had more values than others at any point. Figure 15(b) presents the variation of the EG rate average in xz-plane along the basin width. The dashed lines show the incoming pipe boundaries for any \(\frac{W}{D}\) ratio. The maximum of the EG rate average is almost occurred near the boundaries of the incoming jet to the basin where there is a turbulent shear layer. Also, by increasing the \(\frac{W}{D}\) ratio, the EG rate average is risen. Figure 15(c) presents the variation of the EG rate average in xy-plane along with the basin height. It can be seen that the maximum of the EG rate average is in the \({z}^{*}>0\), and the maximum dissipation is placed behind the baffle.

Fig. 15
figure 15

Average of EG rate in the basin in various directions. (a) yz-Plane in x-direction, (b) xz-Plane in y-direction, (c) xy-Plane in z-direction

Full size image

Figure 16 presents the total EG and its time variation for various \(\frac{W}{D}\) ratios. Results show that the total EG is increased by the increase of \(\frac{W}{D}\) ratio. It can be concluded that in the USBR VI stilling basin, the higher the \(\frac{W}{D}\) ratio is, the higher the energy dissipation will be. Time variation of the total EG shows that the curve has reached a steady-state sooner, at lower \(\frac{W}{D}\) ratios.

Fig. 16
figure 16

Total EG and its time variation for various W/D ratios. (a) Time variation of total EG, (b) Total EG

Full size image

\(\frac{W}{D}\) Effect on Total Entropy Generation

In this section, the results of the total EG for various \(\frac{W}{D}\) ratios in the USBR VI stilling basin are compared with hydrodynamic results of the flow field. As mentioned above, in stilling basins, having higher EG is more satisfactory while the probable damage of the downstream river bed of the basin, because of the outlet flow from the basin, should be minimized. As a result, the variation of the total EG is compared with the velocity characteristics of outlet flow from the basin for various \(\frac{W}{D}\) ratios.

In Fig. 17, the total EG for various \(\frac{W}{D}\) ratios is compared with the total hydraulic head loss. It shows that both the total EG and total hydraulic head loss is increased with the increase of the \(\frac{W}{D}\) ratio. Therefore, the total EG and the total hydraulic head loss are in good agreement.

Fig. 17
figure 17

Total EG with total hydraulic head loss for various W/D ratios

Full size image

In Fig. 18, variations of the total EG for various \(\frac{W}{D}\) ratios are compared with the variations of the normalized mean velocity on the endsill, the normalized mean velocity near the bed on the endsill, the normalized maximum velocity on the endsill, and the normalized shear velocity near the downstream channel bed of the basin. As it is presented, by increasing the \(\frac{W}{D}\) ratio, the total EG is increased and the normalized mean velocity on the endsill is declined. Due to the lower mean velocity on the endsill, the outlet flow from the basin causes less damage on downstream river bed; therefore, improvement of the total EG and the decrease of the mean velocity on the endsill which are occurred for higher \(\frac{W}{D}\) ratio, is a satisfactory condition for the basin and downstream river bed.

Fig. 18
figure 18

Total EG with normalized mean and maximum velocity on endsill, normalized mean velocity near the bed on endsill and normalized shear velocity near the downstream channel bed for various \(\frac{W}{D}\) ratios. (a) Normalized mean velocity on Endsill, (b) Normalized mean velocity near the Bed on Endsill, (c) Normalized maximum velocity on Endsill, (d) Normalized shear velocity near downstream bed

Full size image

In addition, the normalized mean velocity near the bed on the endsill, the normalized maximum velocity on the endsill, and the normalized shear velocity near the downstream channel bed of the basin have similar conditions with the normalized mean velocity on the endsill.

Therefore, it seems, if there are suitable conditions and enough space for the construction of the USBR VI stilling basin, it is better to increase the \(\frac{W}{D}\) ratio as much as possible.

Conclusion

In this paper, the EG and flow field analysis for the USBR VI stilling basin is studied numerically. In this study, for the first time, energy dissipation in a hydraulic structure was investigated using EG analysis. This research has been conducted by solving the RANS equations in the incompressible and steady flow with the RNG k-epsilon turbulence model. A good agreement between the experimental data and the present numerical results has been achieved using mesh cell size and the turbulence models sensitivity analysis. The results are as follows:

By increasing \(\frac{W}{D}\) ratios, the total hydraulic head loss along with the basin is increased. For \(\frac{W}{D}\)=9.23, 7.81, 5.97, 4.84, and 3.50, total hydraulic head losses (Head decreasing ratio, HDR (%)) are 89, 84, 72, 57, and 39 percent, respectively.

  • By decreasing \(\frac{W}{D}\) ratios, the kinetic energy contribution from the total hydraulic head in the inlet flow to the basin is decreased significantly.

  • On the endsill, by moving away from the water surface, the velocity is improved for lower \(\frac{W}{D}\) ratios, while for higher \(\frac{W}{D}\) ratios, the velocity is increased just close to the side walls of the basin.

  • By increasing \(\frac{W}{D}\) ratios, the mean velocity of outlet flow from the basin is decreased. Also, normalized mean velocity by the mean velocity of incoming flow to the basin is declined by increasing the \(\frac{W}{D}\) ratio. For \(\frac{W}{D}\)=9.23, 7.81, 5.97, 4.84, and 3.50. Normalized mean velocities on the endsill are 0.059, 0.086, 0.141, 0.210, and 0.350, respectively.

  • The maximum of the EG rate is happened at the upstream and very close to the baffle, above the incoming pipe floor level. Also near the incoming jet boundaries, the EG rate was high. After the baffle, the EG rate average is declined and became uniform. The maximum of the EG rate average occurred near the boundaries of the incoming jet to the basin.

  • By increasing the \(\frac{W}{D}\) ratios, the total EG is enhanced.

  • Increasing the total EG and the total hydraulic head loss, decreasing the normalized mean and the maximum velocity on the endsill, the normalized mean velocity near the bed on the endsill and decreasing the normalized shear velocity near the downstream bed of the basin occur for higher \(\frac{W}{D}\) ratios which are all satisfactory for the basin and the downstream river bed.

  • In this research, the EG analysis was proposed as a design criterion for the USBR VI stilling basin and according to this criterion, it is suggested that the \(\frac{W}{D}\) ratio increases as much as possible because this situation is completely in accordance with the principles of the stilling basin design criteria. Therefore, the EG criterion can be used by designers.