Introduction

Characterization of shear moduli of the composite lamina is relatively difficult in comparison with that of Young’s modulus. Several techniques are applied for characterization of shear moduli of composite lamina including tension test using [±45]ns angle-ply specimen, tension test using off-axis specimen, three-rail shear test, modified three-rail shear test, Arcan shear test, Iosipescu shear test, torsion test, etc. [1,2,3,4,5]. However, the tension test using [±45]ns angle-ply specimen or off-axis specimen applies a tension force to create shear stress in 45° or off-axis shear stress is an efficient technique, but involves coupled effects from Young’s moduli and Poisson’s ratios which are not yet verified to be negligible. Rail shear test and modified rail shear test are always haunted by the slip problems on the edges of the griped specimen. Arcan shear test and Iosipescu shear test are based on the same assumption that uniform shear stress is applied to the specimen. However, the shear stress is not uniform. Among them, the torsion test could be the most direct and pure shear test.

Tsai et al. [4] published an exact closed-form solution for the case of a unidirectional composite laminate under torsion. The solution takes into consideration the in-plane and also the out-of-plane shear moduli, known as one of the thick plate theories. The solution is almost exactly equal to the series form solution published by Lekhnitskii numerically, except that when the specimen is too thick to be considered as a plate but a rod with rectangular cross-Sects. [4, 6]. Assumptions of both solutions become not realistic when the specimen is a rectangular rod rather than a thick plate. Based on the solution, Tsai and Daniel [5] developed the unique torsion test. By relating the 45° strains at the center of the specimen surface and the center of specimen edge to the torque, the in-plane and out-of-plane shear moduli can be calculated. The torsion test offers a novel, relatively pure, and more direct technique to characterize both in-plane and out-of-plane shear moduli in comparison with other tests. In the process, attaching a strain gauge to the surface center of a specimen with a 45° angle is not difficult at all. However, since the edge of a specimen is mostly merely a couple of millimeters thick, it is not easy to attach a strain gauge to the edge center of a specimen with a 45° angle. Very small strain gauges, very good eyes, a lot of practice, and extreme patience are needed. Because of this reason, the torsion test seems not popular, and researchers still try to find other easier ways.

In 1999, Tsai and Daniel [7] developed the unique torsional pendulum test for characterizing the shear modulus of single fibers. A length of single fiber suspended from one end and with a weight attached at the other end was used as a torsional pendulum. When the weight is twisted and released, it twistingly oscillates with a very steady period, which is inversely proportional to the squire root of the shear modulus of the fiber. By measuring the period, the shear modulus can easily be calculated. This could be the easiest and probably the only way for direct characterization of the shear modulus of a single fiber.

In this work, the authors apply the technique of torsional pendulum to composite laminae. A composite specimen of unidirectional laminate clamped and suspended from one end and with a rod weight attached horizontally at the lower end was tested by twisting and releasing as a torsional pendulum. The rod weight is a copper round bar. A steel bar that may have a magnet and can easily be affected by the magnet field of the earth cannot be used. The period of the twisting oscillation is very steady and can easily be measured, which is related to the shear moduli of the laminate through the solution derived by Tsai et al. [4]. The shear moduli can be calculated theoretically. However, because the effect of the out-of-plane shear modulus, G13, on the period is small but not negligible. A very small measuring error of the period may result in a tremendously large error of G13 numerically. In this work, the material is assumed to be transversely isotropic, meaning that G13 is the same as G12 which is the case with unidirectional carbon/epoxy, aramid/epoxy, and glass/epoxy composites with relatively high fiber volume ratios [1]. A cell phone is good enough to be used to record the motion of the twisting oscillation for calculating the period. Unidirectional specimens with different widths were tested. Rod weights with different lengths were used to challenge the algorithm. A reasonable value was obtained for the shear modulus.

Theory

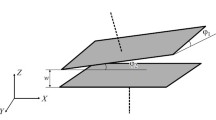
Figure 1 shows that the upper end of a composite specimen of 0° unidirectional laminate is fixed by a clamp, and the specimen is suspended vertically. Rod weight is attached horizontally to the lower end of the specimen. When the rod weight is twisted, the torque, T, causes a twist angle, Φ, and the proportional relationship between them [4, 5] is.

$$T=\frac13a\frac\Phi LG_{12}h^3\lbrack1-\frac{tanh\left(\beta\right)}\beta\rbrack=k\Phi,k=\frac13a\frac1LG_{12}h^3\lbrack1-\frac{tanh\left(\beta\right)}\beta\rbrack$$
(1)

T: torque

Φ: twist angle

a: width of the specimen

h: thickness of the specimen

L: length between clamped end and glued end of the specimen

G12: in-plane shear modulus of the laminate

G13: out-of-plane shear modulus of the laminate

β: β=\(\frac{a}{2 h}\sqrt{10{G}_{13}/{G}_{12}}\)

k: torsional rigidity of the specimen

The frequency, f, of the torsion pendulum [4, 5] is:

$$f = \frac{1}{2\pi }\sqrt{\frac{k}{J}}, J= M(\frac{{D}^{2}}{16}+\frac{{L}_{w}^{2}}{12})$$
(2)

J: inertia of the rod weight with respect to the axis perpendicular to the rod at its center (Fig. 1)

M: mass of the rod weight

D: diameter of the rod weight

Lw: length of the rod weight

Period, p, is the inverse of frequency.

$$p=\frac{1}{f}=2\pi \sqrt{\frac{J}{k}}$$
(3)

Experiments were conducted on specimens with different widths, and rod weights and different lengths were used to challenge the algorithm. The periods of each specimen were measured. The data of period were used to obtain shear moduli by least-square fitting through equations (1)-(3).

Fig. 1
figure 1

Torsional pendulum for a unidirectional composite laminate with a copper rod weight attached horizontally to its lower end

Full size image

Experimental Procedure and Results

16 specimens with different widths were tested which are cut from an 8-ply unidirectional laminate made of TAIRYFIL TC-36P carbon fiber and FTCRITE-EC775001-SA37 epoxy offered by Formosa Plastics Corporation. Data of each test are tabulated in Table 1. The theoretical period of each specimen is calculated via equation (3) which depends on the geometry and mass of the weight, dimensions of the specimen, and its shear modulus. The average thickness of the laminate is 1.02 mm. The length of each specimen is roughly 250 mm, and the width is between 4.1 mm and 25.6 mm. The weight is a copper solid round bar with a diameter of 16 mm, a mass of 518.42 g, and 304 mm long. To challenge the theory, two rods with different lengths and mass, 380 mm-647.85 g, 461 mm-784.23 g, were used randomly in six tests, and their results were mixed with others in the analysis.

Table 1 Diameter, length, and mass of the rod weight, dimensions of the tested specimen and its corresponding experimental and theoretical periods of each test when G12=G13=5.52 GPa which minimize the summation of square of errors between experimental and theoretically periods
Full size table

In each test, the specimen was clamped and suspended from one end, and with the rod weight glued horizontally at the lower end was twisted slightly and released. The rod weight oscillated periodically with a very steady period. For each test, three to six times of twisting and releasing were conducted and filmed simply by a cell phone. The period of each twisting was calculated and the average period corresponding to each specimen was obtained. The deviation of all measured periods is less than 1% of their average. Based on least square data fitting, let G12=G13=5.52 GPa, the errors between the theoretical period and experimental one are less than 4%, and the summation of square of the errors is minimized.

From equations (1)-(3), a normalized period is derived as

$$\frac{p{h}^{2}}{\sqrt{JL}}=2\pi {\left\{\frac{1}{3}\frac{a}{h}{G}_{12}\right[1-{tanh}(\frac{a}{2 h}\sqrt{10\frac{{G}_{13}}{{G}_{12}})}/(\frac{a}{2 h}\sqrt{10\frac{{G}_{13}}{{G}_{12}}})\left]\right\}}^{-1/2}$$
(4)

Figure 2 shows the relationship between the normalized period and aspect ratio, a/h, when the shear moduli are given as G12=G13=5.52 GPa.

Fig. 2
figure 2

Relationship between the normalized period, ph2/, and the aspect ratio, a/h, of the specimen when G12=G13=5.52GPa

Full size image

Discussion

Combination of equations (1)-(3) is

$$p=\frac{1}{f}=2\pi \sqrt{\frac{J}{\frac{1}{3}a\frac{1}{L}{G}_{12}{h}^{3}[1-\frac{{tanh}\left(\beta \right)}{\beta }]}}$$
(5)

The problem is the tanh(β)/β in equation (1) is 0.15-0.06 which is small in comparison with the 1 in front of it but not negligible. As a result, the sensitivity of the period, p, with respect to G13 is very small. In this case, it is between 0.0001 and 0.004.

$$\frac{\partial p/p}{\partial G_{13}/G_{13}}=\pi J^{1/2}k^{-2/3}\frac16\frac{ah^3}L\frac{G_{12}}p\left\{1-tanh^2\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)-\frac{tanh\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)}{\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}}\right\}$$
(6)

This sensitivity decreases when the width, a, increases, meaning that when the specimen becomes wider, this “thick” plate becomes more unsuitable, and the role of the out-of-plane shear modulus, G13, becomes negligible.

Reversely, the sensitivity of G13 with respect to the period, p, is very large.

$$\frac{\partial G_{13}/G_{13}}{\partial p/p}=\frac1{\pi J^{1/2}k^{-3/2}\frac16\frac{ah^3}L\frac{G_{12}}p\left\{1-{tanh}^2\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)-\frac{tanh\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)}{\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}}\right\}}$$
(7)

In this case, it is 250-9000 meaning that 1% measurement error of the period may cause 250-9000% error of calculated G13, which is unacceptable. As a result, fitting the data of period to obtain G13 is not practical in this case. However, tanh(β)/β is not negligible in comparison with 1 and should be kept. Luckily, the material is carbon/epoxy with a high fiber volume ratio, which is transversely isotropic, G13=G12 [1].

The major target in this case is G12. The sensitivity of the period, p, with respect to G12 is.

$$\frac{\partial p/p}{\partial G_{12}/G_{12}}=-\pi J^{1/2}k^{-3/2}\frac13\frac{ah^3}L\frac{G_{12}}p\left\{1-\frac32\frac{tanh\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)}{\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}}+\frac12\left[1-tanh^2\left(\frac a{2h}\sqrt{10\frac{G_{13}}{G_{12}}}\right)\right]\right\}$$
(8)

which is around 0.5. Reversely, the sensitivity of G12 with respect to the period, p, is.

$$\frac{\partial {G}_{12}/{G}_{12}}{\partial p/p}=\frac{1}{-\pi {J}^{1/2}{k}^{-3/2} \frac{1}{3}\frac{a{h}^{3}}{L}\frac{{G}_{12}}{p}\{1-\frac{3}{2}\frac{{tanh}\left(\frac{a}{2 h}\sqrt{10\frac{{G}_{13}}{{G}_{12}}}\right)}{\frac{a}{2 h}\sqrt{10\frac{{G}_{13}}{{G}_{12}}}}+\frac{1}{2}[1-{tanh}^{2}\left(\frac{a}{2 h}\sqrt{10\frac{{G}_{13}}{{G}_{12}}}\right)\left]\right\}}$$
(9)

which is around 1.75-1.95, meaning that 1% measurement error of the period causes less than 2% error of calculated G12, which is acceptable.

For this case, the camera of a cell phone is good enough to record the motion of the copper bar for calculating the period of oscillation to the resolution of 0.01 s, which is around 0.4-1% of the period and induces roughly 0.8-2% error of G12. The resolution is acceptable for the sensitivity of this experimental work. If the specimen is stiff and the period is too short to be measured by a cell phone, more delicate equipment is needed.

Conclusions

The shear modulus is obtained as G12=G13=5.52 GPa in this work, which has only a 3% difference from the value offered by the manufacturer, 5.69 GPa, obtained by tension test using [±45]ns angle-ply specimen [8]. Based on the torsional rigidity of the specimen, the period can be easily related to the shear modulus of the material and the geometry of the specimen. As long as the torsional rigidity of the specimen is derived, the shear modulus can be calculated from the measured period. This work presents the technique of a torsional pendulum, a very simple and efficient technique for measuring the torsional period to calculate shear modulus.