1. Introduction

Composite laminates are widely preferred structures due to their high stiffness and strength-to-weight ratio. Besides, these structures have a high fatigue strength and good corrosion resistance. To investigate the structural and mechanical properties of these types of materials, studies on their static and dynamic behavior are needed. They include the analysis of inplane/out-of-plane stress vs. strain, load vs. displacement, buckling vs. postbuckling, and free and forced vibration relations.

The initial development of beam and plate theories started in the beginning of the 17th century. Daniel Bernoulli and Leonhard Euler were the first who proposed a beam theory including all kinematic and static assumptions. This theory later became known as the Euler–Bernoulli beam theory and paved a way for the development of various theories for plates and shells. In the middle of the 18th century, Kirchhoff [1] formulated a theory purely devoted to plates. Chladni experimentally verified the theory, and S. Germain was the first to propose an equation for vibrations of plates, as reported in [2].

Kirchhoff reduced the 3-D equations of motion of plates to 2-D ones, derived using Navier and Poisson power series and introducing the assumption that the normal to plate midplane remains unchanged after bending of plates. The central deflection w of a plate under the action of a uniform surface load q is determined by the equation

$$ \varDelta \varDelta w=\frac{q}{D},D=\frac{E{h}^3}{12\left(1-{\gamma}^2\right)}, $$

where Δ is the Laplace operator.

Later, Strutt [3] approximated the results of boundary value problems using a direct method. In 1908, Ritz [4] reformulated an approximation technique to obtain a generalized solution, which is currently known as the Rayleigh–Ritz method. An analogical approach for shells was suggested by Love [5] and is known as the Kirchhoff–Love shell theory.

For the first time, the shear deformation effect was introduced into deformation equation by Timoshenko [6]. He used it for beams and reformulated beam vibration equations. This theory is now known as the Timoshenko first-order shear beam theory. The interpretations of nonlinear deformation of thin plates were first addressed by von Karman [7]. He assumed that the strains of thin plates are nonlinear due to large deflections and accordingly formulated his beam theory. Later on, other refined theories of shells and plates were proposed [8,9,10,11,12,13]. The concept of asymptotic integration was first introduced by Gol’denveizer [12, 13]. This expansion method was then used by Heijden [14] in the elasticity equation to obtain 2-D equations of boundary conditions. Meantime, several modifications of Kirchhoff’s plate theory was proposed, among which Reissner’s modification became widely popular. Reissner [15] introduced 3-D statically admissible fields, which set an extra boundary condition, and a sixth-order equation instead of Kirchhoff’s fourth-order one was obtained. A number of other works on this topic were also published by him [16,17,18,19,20] and other researchers [21,22,23,24,25,26,27,28,29]. The modified deflection equation for plates has the form

$$ K\varDelta \varDelta w=p-\frac{h^22-v}{10\;1-v}\varDelta p. $$

Mindlin [30] extended Kirchhoff’s plate theory to dynamic problems using shear stress assumptions. The modified deflection equation of plates is

$$ K\varDelta \varDelta w+ ph-\frac{\partial^2w}{\partial {t}^2}=q. $$

Later on, many works [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68] were published in this field. Most of researchers have concluded that Reissner’s and Mindlin’s formulations are very similar in the finite-element formulation, and this theory now is commonly known as the Reissner–Mindlin plate theory or the first-order shear deformation theory (FSDT).

These theories were modified into higher-orders ones (HSDTs), based on various assumptions, by many researchers [21,22,23, 26, 27, 29, 39, 43, 47, 69,70,71,72,73,74]. In [24, 38, 61,62,63, 75], plate bending theories and Reissner’s theory and analyzed, the disadvantages of FSDT and CLPT are revealed and removed with the use of a sixth-order equation of motion for practically applicable end conditions.

According to the literature information, the different plate theories used can be classified as the classical laminated plate theory (CLPT), the first-order shear deformation theory (FSDT), and higher-order shear deformation theories (HSDTs). They will be discussed more fully in what follows.

1.1. Classical laminated plate theory (CLPT)

This theory is useful to analyze thin laminated composite plates. It is simple, but disregards shear deformations. The midplane is assumed to represent the 3-D plate in the 2-D form, because plate thickness and the position of its midplane remain unchanged during deformation. As a result, the shear deformation and stress are neglected in the transverse direction. Some of the modern conceptions using Kirchhoff’s approach to the plate theory are assigned to the CLPT. Reddy and Robbins [76] presented a displacement-field-based comparative study of CLPT. Liu and Li [77] presented shear deformation, layer-wise, and zig-zag theories in their study. They developed global local double-superposition theories. The progress in theories laminated composite plates (LCPs) and sandwiched plates was assessed by Altenbach [2]. A review of displacement- and stress-based modified FSDTs of LCPs is given by Ghugal and Shimpi [52], where various refined shear deformation theories for LCPs are discussed. A study on the zig-zag theory for LCPs and shells was presented by Carrera [53]. The development of FSDT for plates and shells was analyzed by Reddy and Arciniega [54]. A selective survey and evaluation of the transverse/interlaminar stress in LCPs was given by Kant and Swaminathan [56]. The account of the effect of free edge since 1967 was reviewed by Mittelstedt and Becker [57]. Liew et al. [58] employed the general theory of thin plates, including surface effects, to study their static and dynamic responses. Shimpi and Patel [78] redefined the plate theory by using two variables to study the natural frequencies of plates and showed its closeness to the CLPT. Ebrahimi and Rastgo [79] examined the vibration parameters of thin functionally graded (FG) circular plates by using the CLPT and verified its results by comparing them with 3D finiteelement (FE) calculations. Carrera and Brischetto [80] discussed the Poisson locking mechanism by using simplified kinematic assumptions for isotropic, orthotropic, and multilayered composite plates. Mohammadi et al. [81] presented an analytical Levy solution for a buckling analysis of thin FG plates based on the CLPT for different end conditions, power factors, and aspect ratios of the plates. Ansari et al. [82] reformulated the CLPT by using an interatomic potential and Eringen’s nonlocal equation to study the biaxial buckling and vibration of graphene sheets. Malekzadeh and Shojaee [83] employed the differential quadrature method with two variables to refine the CLPT and applied it to a dynamic analysis of nanoplates. Mahi et al. [84] formulated a new plate theory using Hamilton’s principle and the Navier-type technique to obtain the natural frequencies of different plates. Reddy et al. [85] presented FE models using nonlinear theories for axisymmetric bending of circular plates. Zhang et al. [86] presented an improvised form of CLPT in an element-free KP-Ritz framework for a buckling analysis of graphene sheets. Do and Thai [87] reformed Kirchhoff’s plate theory for a thermomechanical analysis of FG materials and compared the results found with FSDT calculations. Joshi et al. [88] presented a nonclassical analytical model for studying the free vibrations of FG plates in thermal environments by modifying couple stresses. The thermal buckling was found to depend on the buckling temperature and the fundamental frequency. Li and Lee [89] analyzed a circular plate subjected to concentrated and uniformly distributed transverse loads to obtain the deflection, rotation, and stresses at the plate center using Bessel functions and explicit expressions.

1.2. First-order shear deformation theory

The first conception of rotary inertia and shear deformation was introduced into the plate equation by Reissner [15]. Later on, for dynamic problems, Mindlin [30] improved the theoretical model of plate deformation. Since both the theories consider the shear deformation effect on plate deformation, they are named the first-order shear deformation theory. However, the concept of shear deformation is not unique — it is an extension of Timoshenko work of beam vibration [6]. The effect of shear is introduced by shear correction factors. This factor is chosen considering various aspects — the energy of shear deformation, material constants, the assembling pattern of laminate, geometry, configuration, loading, and end conditions. The FSDT is generally employed to analyze thin and moderately thick plates.

Whitney and Pagano [90] presented shear deformation theories for heterogeneous laminated plates considering local transverse shear deformations. This work was extended to LCPs [91]. Noor [73] used both 2-D Kirchhoff’s and FSDT theories to determine the vibration frequencies of multilayer plates. He presented an improved CLPT theory to represent the 3-D elasticity equations by using higher-order functions. Liew et al. [92] presented an extensive appraisal on vibrations of thick plates. Reddy and Kuppusamy [93] employed 3-D elasticity equations and a shear-deformable plate theory to analyze vibration parameters of anisotropic plates. Reddy [94] presented a generalized 2-D FSDT of LCPs in lieu of displacement field approximation across the plate thickness. Later, [95], he generalized the laminate theory based on displacements of 2-D plates. In [96], a theory of shear deformation of LCPs with the use of Reissner variational principle is presented by Murakami. In [97], Chandrashekhara et al. presented a theory of shear-deformable LCPs using Reissner’s variational principle to calculate their inplane response. Averill et al. [98] proposed an exact solution for symmetric laminated composites beams using the FSDT and considering the rotary inertia. Touratier [99] carried out a finite-element analysis (FEA) for plates with great side-to-thickness ratios to get an exact value for shear constraints. Jonnalagadda et al. [100] used the FSDT by neglecting shear correction factors to analyze shear stresses at the bottom and top surface of plates. Eisenberger et al. [101] used the FSDT for a graphite/epoxy LCPs to determine shear deformations at different their aspect ratios. Qi et al. [102] analyzed the exact vibration frequency of a laminated beam considering the effect of rotary inertia and shear deformations. Wang [103] proposed a modified form of the conventional FSDT assuming that inplane displacements varied linearly and the transverse deflection remained constant across the plate thickness. KnightJr et al. [104] studied the free vibration response of a fiber-reinforced skew LCP by the FSDT assuming two shear strains in the place of two rotational displacements to overcome shear locking. Rolfes et al. [105] reformulated the conventional Reissner’s and Mindlin’s theory assuming a variable distribution of the transverse shear strain across the plate thickness. Tanov et al. [106] formulated a FSDT using a single-field displacement FE model to analyze the transverse thermal stresses in laminated plates. Auricchio et al. [107] modified the shell-type FE in the FSDT and eliminated the correction factor to calculate the actual distribution of shear strain and stress in the thickness direction. Wen et al. [108] presented a new mixed variational formulation considering the out-of-plane stress as the factor for variation to obtain an analytical solution neglecting the shear correction factor. Yu [109] studied large deflections of Reisner’s plates using the boundary element method and presented a numerical model based on 2-D elasticity equations to analyze the geometrical nonlinearity in bending and verified the results obtained. Shimpi et al. [110] modified the FSDT without altering the kinematic assumptions. He used the variational asymptotic technique assuming 2-D plate displacements instead of 3-D displacement fields to find an exact solution and compared results with those obtained from the CLPT and FSDT. Nguyen et al. [111] developed two new FSDTs assuming two unknown functions instead of three ones to calculate the modal parameters of simply supported plates. Reddy [112] derived the transverse shear stresses from membrane stresses and equilibrium equations of plates using the FSDT. Ma et al. [113] modified and reformulated the CLPT and FSDT using the nonlinear Eringen and von Karman strains to integrate the bending response of plates. Zhu et al. [114] developed a nonclassical Mindlin plate with a reformed couple-stress theory to determine the natural frequency of a plate with a varying of thickness. Thai et al. [115] conducted a FEA to study the free vibration of a LCP based on the FSDT. Thai et al. [116] have used four unknown variables in the FSDT instead of two ones to obtain displacement equations. Mantari et al. [117] presented closed-form of solutions by reducing the number of unknowns and using Hamilton’s principle to find the natural frequency of a simply supported plate. Liu et al. [118] presented a simple FSDT incorporating Hamilton’s principle to obtain a Navier-type analytical solution for predicting the fundamental frequencies. Rikards et al. [119] presented a model for analyzing the static bending, buckling, and natural frequency of a moderately thick micro-FG plate with account of shear locking and shear deformation.

1.3. Higher-order shear deformation theory (HSDT)

The FSDT is efficient and accurate for a total structural analysis of thin and moderately thick LCPs. However, the accuracy of the interlaminar stress distribution, delamination, and local strains is unpredictable. Further, the FSDT is limited to simply supported plates. Thus, a HSDT was formulated to overcome the difficulties of CLPT and FSDT. The first work in this direction was published by Reddy [69]. His findings are summarized in book [47]. Setoodeh et al. [120] studied vibrations of plates by a FEA with triangular elements. Hull et al. [121] analyzed the vibration parameter of LCPs resting on elastically restrained edges by the FEA. Ahmadian et al. [122] performed a FEA of vibration of orthotropic square stepped plates. Desai et al. [123] conducted a forced vibration analysis for rectangular plates using the FEA. An accurate 3-D higher-order 18-node element was implemented in the FEA by Sheikh et al. [124] to study the free vibration of a LCP. Chakrabarti [125] modified the FSDT using a triangular element to overcome the shear locking by considering the transverse and shear displacements to obtain vibration parameters of a plate. A nonconforming C1-FEA (triangular element) was used by Chakrabarti and Sheikh [126,127,128] to calculate the natural frequencies of LCPs. Latheswary et al. [129] investigated the nonlinear dynamic response of a thin skew LCP using a FEA with von Karman’s assumption for large amplitudes. The free vibration frequencies for a LCP were derived from the TSDT (third-order) using the FEA by Batra [130]. Batra et al. [131] used the Langrange shape function in the FEA for a static and dynamic analysis of a thick isotropic plate with the help of HSDT. Shiau [132] calculated the natural frequencies of thick square plates made from different materials. Moleiro et al. [133] used a highly accurate triangular plate element in a FEA to study free vibrations of a thermally buckled sandwich LCP. Soares et al. [134] and Tanveer 135] developed mixed least-square FE models to study the free-vibration of an LCP. A nonlinear displacement field was developed by Kuo [136] considering the shear strain in the forced vibration response of a piezo-laminated composite. The vibration analysis of an LCP with an inconsistent fiber spacing was studied by Van et al. using the FEA [137]. Taj [138] modeled the vibration response of LCPs/shells by the FEA with a smooth quadrilateral flat shell element allowing inplane rotations. Manna [139] presented a FEA formulation based on the TSDT for static and dynamic responses of FG plates subjected to external loads. Natarajan [140] modified the FSTD to a HSDT by using 18-node 51-DOF element to study the vibration of tapered isotropic plates with a linearly varying thickness. A quad-8 FE based on the HSDT was used in the FEA by Li et al. [141] to investigate the free vibration behavior of sandwich FG plates. Ribeiro [142] proposed a layerwise model in the FEA with an 8-node element to study the free vibration of sandwich composite plates. Kucukrendeci [143] developed a hierarchical FEA model for studying nonlinear vibrations of geometrically nonlinear thick plates. Thai et al. [144] applied the FEA to studying the vibration of LCPs on an elastic foundation. Carrera et al. [145] formulated a NS-DSG3 method neglecting the shear correction factor in static, free vibration, and buckling analyses of LCPs. Chakraverty et al. [146] refined the HSDT using single and layerwise theories to study free vibrations of simple supported square anisotropic plates. The Gram-Schmidt technique was employed by Watkins et al. [147] to calculate the fundamental frequencies of plates made from different inhomogenous materials. Honda [148] used the Mauclarin series for calculating the natural frequencies of plates on an elastic foundation. An analytical formulation incorporating spline functions was developed by Iurlaro et al. [149] to determine the parameters of free vibration of curvilinear reinforcing fibers in an LCP. Fazzolari [150] rederived the nonlinear equation of motion included in the refined zig-zag theory to study the statics and dynamics of layered composites. The Ritz formulation and Carerra’s unified formulas were used to study the free vibration response of LCP and FG plates in thermal environments [151,152,153,154]. Xiang and Wei [155] and Shen et al. [156] used Levy’s solution to exactly calculate the buckling and vibration parameters of rectangular multiply spanned Mindlin plates. Chen et al. [157] reformulated Reddy’s HSDT for a dynamic analysis of LCPs with predominant shear deformations in a thermal environment. The 3-D approach and DQEM were used by Malekzadeh et al. [158] to study the free vibrations of cross-ply rectangular LCPs. The DQEM was employed in the FEA in [159, 160] for studying free vibrations of LCPs resting on Winkler’s foundation. Neves et al. [161] made use of Careera’s formulation and a radial basis function for a static and dynamic analysis of thin and thick LCPs. Rodrigues et al. [162] modeled a modified HSDT for FG plates to analyze their static and dynamic responses. Rodrigues et al. [163] and Liu et al [164] used the finite-difference method on the basis of local collocation and radial basis functions and involved Murakami’s zig-zag theory for a vibration analysis of LCPs. Qian et al. [165] used the Fourier series and Galerkin’s approach for determining the free vibration of sandwich panels with square honeycomb cores. Zhu [166] used the meshless local Petroc–Galerkin technique for investigating free and forced vibrations of plates. Wang et al. [167] and Aydogdu [168] used the discrete singular convolution method in the HSDT for an analysis of free vibration of thin plates at different boundary conditions. Amabili [169] put forward a HSDT for bending and stress analysis for LCPs with up to five degrees of freedom. Aghababei [170] presented a comparative analysis of nonlinear forced vibrations of isotropic and LC plates by using the CLPT, FSDT, and HSDT. Zhang et al. [171] formulated a third-order HSDT using Eringen’s nonlocal linear elasticity theory to examine the minor and quadratic variations of shear strains and shear stresses across the plate thickness. Karama et al. [172] presented an overview of FEAs for LCPs. Thai [173] presented a model for multilayered composite materials based on a kinematic approach to study their bending, vibration, and buckling. Kant [174] presented a Levy-type solution based on the principle of minimum total potential energy to study the buckling of orthotropic plates. Pandya [175] and Levy [176] proposed a FE model for a stress analysis of LCPs using the shear deformation theory and found that the displacement field was quadratic in nature. Stein [177], Touratier [178], Shimpi [179], and Soldatos [180] expressed the displacement as the component of a trigonometric function of shear strain. Shimpi [181] assumed that the displacement field is hyperbolic in nature, but the displacement in the thickness direction was assumed constant. Shimpi et al. [78] modified the FSDT and excluded the shear strain. Later, they considered the shear strain [182] to calculate the bending and shearing displacements [183, 184] for thick plates. Improved and generalized models for the displacement field using trigonometric functions (only in the length and width directions) are presented in [59, 185,186,187,188]. Xiang et al. [189] used the displacement as a sine function of shear strains in the longitudinal and lateral directions. Later, the displacement field was assumed to be hyperbolic [186]. In the first case, the displacements in the thickness direction were assumed as constant and integral parts of bending and shear deformations. More recently, the displacement in the thickness direction has been taken quadratic. Daouadji et al. [190] simplified the displacement field for calculating an n th-order shear deformation of plates. Zenkour et al. [191] again modified the trigonometric displacement function in the length and width directions using four variables (longitudinal and transverse displacements). Bessaim [192] used the displacement as a sine function of shear strain and a cosine function of displacement in the thickness direction. The field to hyperbolic sinusoidal and cosinusoidal forms was used by Thai [193]. Thai et al. [194] used a discrete model of HSDT to define the displacement field. Later, the shear deformation field was modified to a hyperbolic sinusoidal form by incorporating bending [195]. They simplified the displacement field to a cubic form [194]. Trigonometric sine and cosine function were used to express displacement fields in [192, 196]. Zhang [197] used HSDTs to study the dynamic behavior of damaged LCPs. Song et al. [198], Mahi et al. [199], and Phung-Van et al. [200] modified Reddy’s theory to a cubic form for studying the vibration of CNT-reinforced composites, graphene nanoplatelets, FG composite plates, and isotropic sandwiched composite plates, respectively. An isogeometric analysis with a modified HSDT approach was used to study LCPs [199, 201] and FG plates [200]. Bousahla et al. [202] employed a refined hyperbolic form of HSDT to analyze vibrations of LCPs. Choe et al. [203] generalized the displacement equations of HSDT by considering the local force vectors. Sayyad and Ghugal [60] proposed a simple form of HSDT along with a numerical calculation. Narayan et al. [204] used the multisegment partitioning technique in the HSDT to simplify the boundary condition of a shell for a relevant formulation of the displacement field. Abdelmalek et al. [205] considered the variable stiffness of a LCP by a spatial distribution model in the FEA for studying its thermal buckling behavior. Kumar et al. [206] formulated a temperature- and moisture-dependent micromechanical model for an n th-order HSDT taking into account the parabolic distribution of the transverse shear strain. Khiloun et al. [207] proposed two new HSDTs for FGMs using a meshless technique in the FEA. Mohammadzadeh et al. [208] proposed a simple form of HSDT using Hamilton’s principle for a modal study of FG plates. Kulikov et al. [209] analyzed the nonlinear dynamics of an FG sandwich plate using the Runge–Kutta method. Altenbech et al. [210] employed a hybrid mixed four-node finite element to analyze FG plates. Vasiliev [64] published a detailed presentation of a sixth-order plate theory. Altenbech et al. [211] and Zhavoronok [212] modified the theories of plates and shells incorporating surface stresses into them. Piskunov [213] used the 3-D reduction technique and developed a shell model using the Lagrangian density and other boundary conditions to formulate a Vekua-type shell model. Neves et al. [214] developed a higher-order theory to obtain a stress–strain relationship for shearing and compressive loads. Piskunov and Rasskazov [66] implemented the FE method and approximated nonclassical 3-D theories by a 2-D model.

2. Formulation of Displacement Fields

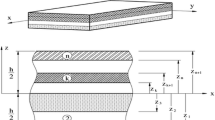
Kirchhoff [1] formulated his theory of plates in 1850. He considered the displacements of a plate as functions of two coordinates, neglected the transverse one, and assumed that the 3-D displacement field can be expressed as a 2-D one. Later Reissner [15] and Mindlin [30] abandoned the Kirchhoff’s assumption and assumed that the normal to the midsurface of plates remains during their deformation unchanged, but not necessarily perpendicular to the midsurface of thick plates. Mindlin assumed that the displacement in the thickness direction is linear and the thickness of plates is unchanged, whereas Reissner reasoned that the stress in the thickness direction varies quadrically in nature. Later, various researchers modified the theories by introducing various assumptions. The displacement fields of existing plate theories can be summarized as follows (see Fig. 1):

Fig. 1
figure 1

Displacement of the midsurface of a thin plate in the CLPT and FSDT [77].

Full size image

CLPT

$$ u={u}_0-z\frac{\partial {w}_0}{\partial x},v={v}_0-z\frac{\partial {w}_0}{\partial y},w={w}_0; $$
(1)

FSDT

$$ u={u}_0+z{\phi}_x,v={v}_0+z{\phi}_y,w={w}_0; $$
(2)

SSDT

$$ u={u}_0+z{\phi}_x+{z}^2{\psi}_x,v={v}_0+z{\phi}_y+{z}^2{\psi}_y,w={w}_0+z{\phi}_z; $$
(3)

TSDT

$$ {\displaystyle \begin{array}{c}u={u}_0+z{\phi}_x+{z}^2{\psi}_x+{z}^3{\theta}_x,\\ {}v={v}_0+z{\phi}_y+{z}^2\psi y+{z}^3{\theta}_y,\\ {}w={w}_0+z{\phi}_z+{z}^2{\psi}_z;\end{array}} $$
(4)

Nth order shear deformation theory

$$ {\displaystyle \begin{array}{c}u-{u}_0+z{\phi}_{1x}+{z}^2{\phi}_{2x}+{z}^3{\phi}_{3x}+\dots +{z}^n{\phi}_{nx},\\ {}v-{v}_0+z{\phi}_{1y}+{z}^2{\phi}_{2y}+{z}^3{\phi}_{3y}+\dots +{z}^n{\phi}_{ny},\\ {}w-{w}_0+z{\phi}_{1z}+{z}^2{\phi}_{2z}+{z}^3{\phi}_{3z}+\dots +{z}^{n-1}{\phi}_{\left(n-1\right)y}.\end{array}} $$
(5)

The displacement fields stated by Eqs. (4) and (5) have a polynomial form, but they can be modified to other forms depending upon the assumptions made and can be reformulated in parabolic, hyperbolic, trigonometric, and other ones. Examples of displacement fields adopted by different researchers are presented in Table 1.

Table 1 Displacement Functions Adopted by Various Researchers
Full size table

3. Constitutive Relations

According to Reddy’s theory, the generalized displacement field for an orthotropic laminate having k layers can be written as

$$ u=\sum_{i=1}^k{U}_i{\phi}^i(z),v=\sum_{i=1}^k{V}_i{\phi}^i(z),w=\sum_{i=1}^k{W}_i{\phi}^i(z). $$
(6)

For linear variations of displacements across the plate thickness, the functions for ϕ are given by

$$ {\phi}^1(z)={\psi}_1^1(z),{z}_1\le z\le {z}_2, $$
$$ {\displaystyle \begin{array}{c}{\phi}^i(z)=\Big\{\begin{array}{c}{\psi}_2^{i-1}(z),{z}_{i-1}\le z\le {z}_i,\\ {}{\psi}_1^i(z),{z}_i\le z\le {z}_{i+1},\end{array}\\ {}{\phi}^n(z)={\psi}_2^{K_e}(z),{z}_{k-1}\le z\le {z}_k,\end{array}} $$
(7)

where \( {\psi}_1^n=1-\frac{\overline{z}}{h_k},\mathsf{and}\;{\psi}_2^n=\frac{\overline{z}}{h_k},o\le \overline{z}\le {h}_n. \)

In some cases, displacement fields are assumed quadratic, namely,

$$ {\displaystyle \begin{array}{c}{\phi}^i(z)={\psi}_1^1(z),{z}_1\le z\le {z}_3,\\ {}{\phi}^{2i}(z)={\psi}_2^i(z),{z}_{2i-1}\le z\le {z}_{2i+1},\\ {}{\phi}^{2i+1}(z)=\Big\{\begin{array}{c}{\psi}_3^i(z),{z}_{2i-1}\le z\le {z}_{2i+1},\\ {}{\psi}_1^i(z),{z}_{2i+1}\le z\le {z}_{2i+3},\end{array}\\ {}{\phi}^n(z)={\psi}_3^{K_e}(z),{z}_{k-2}\le z\le {z}_k,\end{array}} $$
(8)

where

$$ {\displaystyle \begin{array}{c}{\psi}_1^n=\left(1-\frac{\overline{z}}{h_n}\right)\left(1-\frac{2\overline{z}}{h_n}\right),\\ {}{\psi}_2^n=4\frac{\overline{z}}{h_n}\left(1-\frac{\overline{z}}{h_n}\right),\\ {}{\psi}_2^n=-\frac{\overline{z}}{h_n}\left(1-\frac{\overline{z}}{h_n}\right),o\le \overline{z}\le {h}_n.\end{array}} $$
(9)

The normal strains associated with the displacement field for an n th-order displacement are

$$ {\displaystyle \begin{array}{c}{\varepsilon}_{xx}=\sum_{i=1}^k\frac{\partial {U}_i}{\partial x}{\phi}^i,{\varepsilon}_{yy}=\sum_{i=1}^k\frac{\partial {V}_i}{\partial y}{\phi}^i,{\varepsilon}_{zz}=\sum_{i=1}^{n-1}\frac{\partial {W}_i}{\partial z}\frac{d{\psi}^i}{dz},\\ {}{\gamma}_{xy}=\sum_{i=1}^n\left(\frac{\partial {U}_i}{\partial y}+\frac{\partial {V}_i}{\partial x}\right){\phi}^i,{\gamma}_{yz}=\sum_{i=1}^n{V}_i\frac{\partial {\phi}_i}{\partial z}+\sum_{i=1}^{n-1}\frac{d{W}_i}{dy}{\psi}^i,\\ {}{\gamma}_{xy}=\sum_{i=1}^n{U}_i\frac{\partial {\phi}_i}{\partial z}+\sum_{i=1}^{n-1}\frac{d{W}_i}{dx}{\psi}^i,i,j=1,2,3.\end{array}} $$
(10)

For a composite plate with k layers, the assembled stress–strain equation is written as

$$ {\sigma}_i^k=\sum_{i=1}^6{Q}_{ij}^k{\varepsilon}_j^k,\kern0.5em i,j=1,2,\dots, 6. $$
(11)

Equation (11) in the matrix form is

$$ \left\{\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\sigma}_{zz}\\ {}{\tau}_{xy}\\ {}{\tau}_{yz}\\ {}{\tau}_{zx}\end{array}\right\}={\left[\begin{array}{cccccc}{Q}_{11}& {Q}_{12}& {Q}_{13}& 0& 0& 0\\ {}{Q}_{12}& {Q}_{22}& {Q}_{23}& 0& 0& 0\\ {}{Q}_{13}& {Q}_{23}& {Q}_{33}& 0& 0& 0\\ {}0& 0& 0& {Q}_{44}& {Q}_{45}& 0\\ {}0& 0& 0& {Q}_{45}& {Q}_{55}& 0\\ {}0& 0& 0& 0& 0& {Q}_{66}\end{array}\right]}^K\cdot \left\{\begin{array}{c}{\varepsilon}_{xx}-{\alpha}_{xx}\varDelta T\\ {}{\varepsilon}_{yy}-{\alpha}_{yy}\varDelta T\\ {}{\varepsilon}_{zz}-{\alpha}_{zz}\varDelta T\\ {}{\gamma}_{yz}\\ {}{\gamma}_{xz}\\ {}{\gamma}_{xz}-2{\alpha}_{xy}\varDelta T\end{array}\right\}, $$
(12)

whereQij are the stiffness coefficients of laminate layers.

For thin plates, neglecting the stresses and strains across its thickness, Eq. (12) can be reduced to a 2D form, namely,

$$ {\displaystyle \begin{array}{c}\left\{\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{yy}\\ {}{\sigma}_{zz}\end{array}\right\}=\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {}{Q}_{12}& {Q}_{22}& 0\\ {}0& 0& {Q}_{33}\end{array}\right]\cdot \left\{\begin{array}{c}{\varepsilon}_{xx}\\ {}{\varepsilon}_{yy}\\ {}{\gamma}_{xy}\end{array}\right\},\\ {}{Q}_{11}=\frac{E_{11}}{1-{v}_{12}{v}_{21}},{Q}_{12}=\frac{v_{12}{E}_{11}}{1-{v}_{12}{v}_{21}},{Q}_{22}=\frac{E_{22}}{1-{v}_{12}{v}_{21}},{Q}_{33}={G}_{13}.\end{array}} $$

The normal and shear strains in the x, y, and z directions are

$$ {\varepsilon}_{xx}=\frac{\partial u}{\partial x},{\varepsilon}_{yy}=\frac{\partial v}{\partial y},{\gamma}_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}. $$
(13)

Assuming bending and shearing of the plate, the matrix strains can be expressed in terms of displacement as

$$ {\displaystyle \begin{array}{c}\left\{\begin{array}{c}{\varepsilon}_x\\ {}{\varepsilon}_y\\ {}{\gamma}_{xy}\end{array}\right\}=\left\{\begin{array}{c}{\varepsilon}_x^0\\ {}{\varepsilon}_y^0\\ {}{\gamma}_{xy}^0\end{array}\right\}+z\left\{\begin{array}{c}{k}_x^b\\ {}{k}_y^b\\ {}{k}_{xy}^b\end{array}\right\}+f(z)\left\{\begin{array}{c}{k}_x^s\\ {}{k}_y^s\\ {}{k}_{xy}^s\end{array}\right\},\\ {}\left\{\begin{array}{c}{\gamma}_{yz}\\ {}{\gamma}_{xz}\end{array}\right\}=g(z)\left\{\begin{array}{c}{\gamma}_{yz}^s\\ {}{\gamma}_{xz}^s\end{array}\right\},\\ {}\left\{\begin{array}{c}{\varepsilon}_x^0\\ {}{\varepsilon}_y^0\\ {}{\gamma}_{xy}^0\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial {u}_0}{\partial x}\\ {}\frac{\partial {v}_0}{\partial x}\\ {}\frac{\partial {u}_0}{\partial y}+\frac{\partial {v}_0}{\partial x}\end{array}\right\},\left\{\begin{array}{c}{\varepsilon}_x^b\\ {}{\varepsilon}_y^b\\ {}{k}_{xy}^b\end{array}\right\}=\left\{\begin{array}{c}\frac{-{\partial}^2{w}_b}{\partial {x}^2}\\ {}\frac{-{\partial}^2{w}_b}{\partial {y}^2}\\ {}\frac{-2{\partial}^2{w}_b}{\partial x\partial y}\end{array}\right\},\end{array}} $$
(14)
$$ \left\{\begin{array}{c}{k}_x^s\\ {}{k}_y^s\\ {}{k}_{xy}^s\end{array}\right\}=\left\{\begin{array}{c}\frac{-{\partial}^2{w}_s}{\partial {x}^2}\\ {}\frac{-{\partial}^2{w}_s}{\partial {y}^2}\\ {}\frac{-2{\partial}^2{w}_s}{\partial x\partial y}\end{array}\right\},\left\{\begin{array}{c}{\gamma}_{yz}^s\\ {}{\gamma}_{xz}^s\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial {w}_s}{\partial y}\\ {}\frac{\partial {w}_s}{\partial x}\end{array}\right\}, $$
(15)

where g(z) = 1− f′ (z) and f (z) is a shape function.

3.2 Kinematics equations

According to the principle of virtual work, the normalized strain energy in the plate is given by

$$ U=\frac{1}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}\underset{-h/2}{\overset{h/2}{\int }}{\sigma}_{ij}{\varepsilon}_{ij} dxdydz, $$
(16)
$$ U=\frac{1}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}\underset{-h/2}{\overset{h/2}{\int }}\left(\begin{array}{c}{\sigma}_x\delta {\varepsilon}_x+{\sigma}_y\delta {\varepsilon}_y+{\sigma}_z\delta {\varepsilon}_z\\ {}+{\tau}_{xy}\delta {\gamma}_{xy}+{\tau}_{xz}\delta {\gamma}_{xz}\end{array}\right) dxdydz. $$
(17)

In term of stress resultants, the normalized strain energy is expressed as

$$ {\displaystyle \begin{array}{c}U=\frac{1}{2}\underset{0}{\overset{a}{\int }}\underset{0}{\overset{b}{\int }}\underset{-h/2}{\overset{h/2}{\int }}{N}_x\delta {\varepsilon}_x^0+{N}_y\delta {\varepsilon}_y^0+{N}_z\delta {\varepsilon}_z^0+{N}_{xy}\delta {\gamma}_{xy}^0+{M}_x^b\delta {k}_x^b+{M}_y^b\delta {k}_y^0+{M}_{xy}^b\delta {k}_{xy}^b\\ {}+{M}_x^s\delta {k}_x^s+{M}_y^s\delta {k}_y^s+{S}_{yz}^s\delta {\gamma}_{yz}^0+{S}_{yz}^s\delta {\gamma}_{yz}^0\Big) dxdydz\end{array}} $$
(18)

For an orthotropic plate, the stress resultants are shown in Fig. 2, and they are determined as

$$ \left[\begin{array}{ccc}{N}_x& {N}_y& {N}_{xy}\\ {}{M}_x^b& {M}_y^b& {M}_{xy}^b\\ {}{M}_x^s& {M}_y^s& {M}_{xy}^s\end{array}\right]=\underset{-h/2}{\overset{h/2}{\int }}\left({\sigma}_x,{\sigma}_y,{\tau}_{xy}\right)\left\{\begin{array}{c}1\\ {}z\\ {}f(z)\end{array}\right\} dz, $$
(19)
$$ {N}_z=\underset{-h/2}{\overset{h/2}{\int }}{\sigma}_zg^{\prime }(z) dz, $$
(20)
$$ \left({S}_{xz}^s,{S}_{yz}^s\right)=\underset{-h/2}{\overset{h/2}{\int }}\left({\tau}_{xz},{\tau}_{yz}\right)g(z) dz. $$
(21)
Fig. 2
figure 2

Stress resultants in beam cross section.

Full size image

For a laminated orthotropic plate, the stress resultants in terms of total strain are expressed as

$$ {\displaystyle \begin{array}{c}\left\{\begin{array}{c}N\\ {}{M}^b\\ {}{M}^S\end{array}\right\}=\left[\begin{array}{ccc}A& B& {B}^S\\ {}B& D& {D}^S\\ {}{B}^S& {D}^S& {H}^s\end{array}\right]\left\{\begin{array}{c}\varepsilon \\ {}{k}^b\\ {}{k}^S\end{array}\right\}+\left\{\begin{array}{c}L\\ {}{L}^a\\ {}R\end{array}\right\}{\varepsilon}_z^0,\\ {}S={A}^s\gamma, \\ {}N=\left\{\begin{array}{ccc}{N}_x& {N}_y& {N}_{xy}\end{array}\right\},{M}^b=\left\{\begin{array}{ccc}{M}_x^b& {M}_y^b& {M}_{xy}^b\end{array}\right\},{M}^b=\left\{\begin{array}{ccc}{M}_x^s& {M}_y^s& {M}_{xy}^s\end{array}\right\},\end{array}} $$
(22)
$$ \varepsilon =\left\{\begin{array}{ccc}{\varepsilon}_x^0& {\varepsilon}_y^0& {\gamma}_{xy}^0\end{array}\right\},{k}^b=\left\{\begin{array}{ccc}{k}_x^b& {k}_y^b& {k}_{xy}^b\end{array}\right\},{k}^s=\left\{\begin{array}{ccc}{k}_x^s& {k}_y^s& {k}_{xy}^s\end{array}\right\},i,j=x,y,z, $$
(23)
$$ {\displaystyle \begin{array}{c}A=\left[\begin{array}{ccc}{A}_{11}& {A}_{12}& {A}_{16}\\ {}{A}_{12}& {A}_{22}& {A}_{26}\\ {}{A}_{16}& {A}_{26}& {A}_{66}\end{array}\right],B=\left[\begin{array}{ccc}{B}_{11}& {B}_{12}& {B}_{16}\\ {}{B}_{12}& {B}_{22}& {B}_{26}\\ {}{B}_{16}& {B}_{26}& {B}_{66}\end{array}\right],D=\left[\begin{array}{ccc}{D}_{11}& {D}_{12}& {D}_{16}\\ {}{D}_{12}& {D}_{22}& {D}_{26}\\ {}{D}_{16}& {D}_{26}& {D}_{66}\end{array}\right],\\ {}{B}^S=\left[\begin{array}{ccc}{B}_{11}^s& {B}_{12}^s& {B}_{16}^s\\ {}{B}_{12}^s& {B}_{22}^s& {B}_{21}^s\\ {}{B}_{16}^s& {B}_{26}^s& {B}_{66}^s\end{array}\right],{D}^S=\left[\begin{array}{ccc}{D}_{11}^s& {D}_{12}^s& {D}_{16}^s\\ {}{D}_{12}^s& {D}_{22}^s& {D}_{21}^s\\ {}{D}_{16}^s& {D}_{26}^s& {D}_{66}^s\end{array}\right],\\ {}{A}^S=\left[\begin{array}{cc}{A}_{44}^s& {A}_{45}^s\\ {}{A}_{45}^s& {A}_{66}^s\end{array}\right],\gamma ={\left\{{\gamma}_{xz},{\gamma}_{yz}\right\}}^T,\end{array}} $$
(24)
$$ \left({A}_{ij},{B}_{ij},{D}_{ij},{B}_{ij}^s,{D}_{ij}^s,{H}_{ij}^s\right)=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}\left(1,z,{z}^2,f(z), zf(z),\left[f{(z)}^2\right]\right) dz, $$
(25)
$$ {A}_{ij}^s=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}{\left[g(z)\right]}^2 dz,i,j=4,5. $$
(26)

According to Hamilton’s principle, the equations of motions based on the first variation of Langragian can be obtained as follows:

$$ L=\varPi -P, $$
(27)
$$ \varPi =\frac{1}{2}\underset{-h/2}{\overset{h/2}{\int }}\int \rho \left({u}^2+{v}^2+{w}^2\right) dAdz, $$
(28)
$$ P=U+U^{\prime } $$
(29)

Using appropriate boundary conditions, the displacements are given by

$$ \left\{\begin{array}{c}{u}_0\\ {}{v}_0\\ {}{w}_0\end{array}\right\}=\sum_{m=\mathrm{l}}^{\infty}\sum_{n=\mathrm{l}}^{\infty}\left\{\begin{array}{c}{U}_{mn}S\left(\lambda x\right)C\left(\varsigma y\right){e}^{iwt}\\ {}{V}_{mn}S\left(\lambda x\right)S\left(\varsigma y\right){e}^{iwt}\\ {}{W}_{mn}S\left(\lambda x\right)S\left(\varsigma y\right){e}^{iwt}\end{array}\right\}. $$
(30)

Inserting them into the Langragian equation, the folowing equation for vibration characteristics is obtained:

$$ \left(\left[K\right]-{\omega}^2\left[M^{\prime}\right]\right)\left\{\varDelta \right\}=\left\{0\right\} $$
(31)

4. Comparative Results of Plate Theories

4.1 Shape functions

In this review, all models of LCPs are categorized. The current work is intended to clear up the ability of different plate theories to predict the influence of transverse shear. To get effective results, the HSDT can be used. The variations of displacement field and shear strains in the CLPT, FSDT, and HSDT are illustrated in Fig. 3. Computation of shear strains and stresses in thethe 3-D elasticity formulation (Eqs. (11)-(22)) is difficult and time-consuming due to the great number of parameters. Therefore, the shear and wrapping effects are included in the general formulations of HSDT. The transverse displacements of plates are described using a shape function. The shape functions adopted by different researchers are presented and compared in Table 1. The variations of displacement fields across the plate thickness in different plate theories with various shape functions are shown (Fig. 4).

Fig. 3
figure 3

Variation of transverse displacements of plates in different plate theories.

Full size image
Fig. 4
figure 4

Variation of shape function f(z) across the thickness z/h of plates in different plate theories.

Full size image

4.2 Static analysis

A static analysis of results for LCPs found by different shear deformation theories were based on literature data. Square LCPs with material property E1 = 174.6 GPa, E2 = 7 GPa, G = 3.5 GPa and ν =0.25 [188] and different aspect ratios are subjected to uniform loads. The central deflections and stresses are taken in the nondimensional form

$$ {\displaystyle \begin{array}{c}\overline{w}=w\left(\frac{a}{2},\frac{b}{2},0\right),{\overline{\sigma}}_{xx}=\frac{h}{a{q}_0}{\sigma}_{xx}\left(\frac{a}{2},\frac{b}{2},z\right),\\ {}{\overline{\sigma}}_{yy}=\frac{h}{a{q}_0}{\sigma}_{yy}\left(\frac{a}{2},\frac{b}{2},z\right),{\overline{\tau}}_{xz}=\frac{h}{a{q}_0}{\tau}_{xz}\left(0,\frac{b}{2},0\right).\end{array}} $$
(32)

Figure 5 a shows the nondimensional central deflections \( \overline{w} \) of plates subjected to a uniform load q vs. aspect ratio a/h based on different plate theories. The normal \( {\overline{\sigma}}_{xx} \) and shear \( {\overline{\tau}}_{xz} \) stresses as functions of a/h are presented in Fig. 5 b, c.

Fig. 5
figure 5

(a) Nondimensional central deflection \( \overline{w} \) of the plate vs. aspect ratio a/h. (b) Normal stress \( {\overline{\sigma}}_{xx} \) vs. aspect ratio a/h. (c) Shear stress \( {\overline{\tau}}_{xz} \) vs. aspect ratio a/h. (d) Nondimensional central deflection w under a uniform load q. (e) Normal stress \( {\overline{\sigma}}_{xx} \) vs. load q. (f): Shear stress \( {\overline{\tau}}_{xz} \) vs. load q.

Full size image

Fig. 5 d, f shows the nondimensional central \( \overline{w} \) and the normal \( {\overline{\sigma}}_{xx} \) and shear \( {\overline{\tau}}_{xz} \) stresses as functions of the uniform load q according to different theories.

4.3 Dynamic analysis

The natural dimensionless frequencies of plates with various aspect ratios given by different shear deformation theories are presented in Table 2. The ratio of elastic moduli E1/E2 was kept fixed at 20. The nondimensional fundamental frequency \( \overline{\omega} \) was calculated by a simplified Eq. (31), namely,

$$ \overline{\omega}={\omega}_{mn} ah\sqrt{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{${E}_2$}\right.} $$
(33)
Table 2 Comparison of Nondimensional Natural Frequencies of Square Antisymmetric LCPs with Different Aspect Ratios a/h.
Full size table

Figure 6 shows the nondimensional natural frequency \( \overline{\omega} \) as a function of aspect ratio a/h. It is seen that the natural frequencies of thin to moderately thick plates with a high aspect ratio do not depend on plate theory assumptions. The decrease in the natural frequency with increasing aspect ratio is a usual phenomenon caused by significant losses in the plate stiffness. This is illustrated in Fig. 6.

Fig. 6
figure 6

Nondimensional natural frequency \( \overline{\omega} \) vs. aspect ratio a/h.

Full size image

5. Conclusions

In this investigation, different plate theories used for static and dynamic analyses of LCPs have been reviewed and analyzed.

For thin to moderately thick plates, the CLPT and FSDT are used to simplify the equation of motions and to find exact solutions. In these theories, shear correction factors are neglected, and the distribution of shear strain is assumed linear. CLT and FSDT are efficient and economical in predicting the total response of laminates rather than the local responses due to the presence of such local defects as notches, holes, grooves, and steppings. However, it is reported that the values of stresses components derived from the plate theories are not so accurate than those given by exact elasticity theory solutions. It is found that the mean square error depends on plate thickness [71, 72].

In some cases, to minimize the variation of results, shear correction factors are introduced into the FSDT.

It the plate thickness is great enough to cause rotational deformations, the shear strain is included in the displacement equation and the displacement field is formed as in the HSDT, where the distribution of shear stress and strain is assumed parabolic, hyperbolic, or trigonometric. But the unknown parameters in the displacement functions are reliant on the plate thickness. HSDTs with a greater number of unknown variables are more effective.

Plate theories rarely take into account the distributions of transverse stresses and strains distribution across the plate thickness; therefore, it is also important to address the exact static and dynamic behavior of LCPs.

• New theories have to be developed for LCPs based on old fundamental solution methods, which can result in a united approach to the analysis of LCPs.

• The HSDTs using trigonometric functions for shear deformations need further investigations.

• The FEA is the most widely used method, as reported in the literature.

• The meshless method is a reliable alternative to the FEA, irrespective of plate thickness. Computations in it are based on 3-D equilibrium equations and give rather accurate results. However, they are very laborious due to the involvement of many variables, depending on the number of layers in a LCP.

• To minimize this difficulty, the shear (ws) and warping (wb) are included directly in formulations.

• Linear analyses of free vibrations of LCPs are more common than nonlinear ones.

• From the comparison of numerical models for static and dynamic analyses, the following conclusions can be drawn.

• The central deflections of plates calculated by the CLPT are smaller than those given by the FSDT and other forms of HSDT.

• The distribution of normal stresses is linear in the CLPT, irrespective of aspect ratios.

• The nondimensional normal stress increases with growing load, but the shear stress decreases.

• The natural frequency of LCPS with high aspect ratios (of thin plates) is constant irrespective of the theory used for computation.

Advantages of HSDT

• The results obtained for the natural frequencies, deflections, stresses, and strains are more real due to the use of higherorder polynomials.

• The inclusion of shear stress and strain is feasible.

• The geometrical nonlinearity in the structures can be considered.

• A reduced integration is not required to obtain acceptable results.

• The distribution of shear in beam profile can be designed and modeled according to the assumptions accepted, i.e., it can be parabolic, hyperbolic, or trigonometric.

• It is useful for determining the local stress-strain state in plates.

• The use of shear correction factors is unnecessary.

• The theories are easy to formulate and they require less computation time.

• In the static analysis, the HSDT yields more accurate and consistent result for the displacement field

Disadvantages of HSDT

• The complexity of computation is rather high due to the inclusion of higher-order polynomial terms to accurately predict result.

• HSDTs with more than five unknown variables are cumbersome and highly demanding.

• For layered solids, the constitutive parameters are specific for each layer, and they have to be incorporated in computations when approximating the constitutive relations and equations of motions.

• The consistency of property variations when using HSDT has not been explored.

• In a dynamic analysis, at high vibrations, the use of HSDT gives a poor approximation for the true shear stress.

• The true shear is maximized at the outer surfaces, which may not be correct in reality.