Experimental Study of a Disk Diaphragm Thickness Influence on a Planar Shock Wave Formation and Position During its Propagation in a Gas Shock Tube

Abstract

A Shock tube is a piece of equipment in which, by creating a pressure difference between the driver and the driven section via the bursting membrane, it has the ability to generate shock waves with very short rise time. One of the important parameters in the shock tube is the planar shock wave and the distance of its formation along the driven section. In this study, the shock wave pressure was measured at different sections along the shock tube as well as at different radial distances, using three piezoresistive pressure sensors. Experiments were repeated with three different thicknesses of diaphragms 0.1, 0.2, and 0.3 mm. Diaphragms were made of Mylar. The results of the tests were extracted using TRAww software, which is a software for signal processing of the pressure sensors, and the distance of the planar shock wave for different diaphragms was obtained. The results show that by increasing the diaphragm thickness and thus increasing the explosion pressure (pressure of the driver area), the shock wave pressure increased, and the planar shock wave propagates further away in the driven section. The uniform duration of the shock wave using a diaphragm with a thickness of 0.1 mm is smaller than the other two diaphragms, and the planar shock wave is not stable until the end of the shock tube. Also, the pressure drop in the driven section after the failure of the diaphragm increases with increasing diaphragm thickness.

Introduction

Investigation and measurement of shock wave properties have received much attention in recent years due to their influence on unconventional applications such as blast or impact structure loadings analysis and rapid, severe or explosions metal forming processes. A shock tube has been one of the most important instruments to identify the shock wave properties. The shock wave has beneficial uses in the forming, formability evaluation, and impact testing, so shock wave properties have been investigated through dynamic transducers such as piezoresistive and piezoelectric transducers. However, it has been found that studies in the field of planar shock wave generation and its parameters in a gas shock tube are weak. One way for measuring the dynamic pressure of the shock wave is to use piezoelectric and optic transducers to detect waves in shock tube[1]. The scope of the shock tube application is extensive, including gas flow evaluation [2], modeling and investigation of the boundary layer in physical specimens [3], combustion pattern of gaseous combinations and solid fuel [4], and medical and military applications, including assessment of brain damage due to explosion [5] and the manufacture of armor and protective equipment to mitigate these effects. For example, Gong et al., by using transducers in measuring, showed that the pressure in the storage does not decrease immediately after the release of high-pressure hydrogen, and the rate of pressure discharge in the storage increases initially and then decreases [1]. Nguyen et al. (2014) used a shock tube for developing a system to investigate biological specimens. Experiments were carried out with Mylar and Aluminum diaphragms of various thicknesses to control output pressure. Results showed the dual-diaphragm system could control pressure more accurately and diaphragm failure pressure linearly increases as thickness increased [6]. Glass (2012) presented a comprehensive report about shock tubes and demonstrated that the expansion waveform is fixed by preliminary conditions of the driver and expansion of the shock wave depends on diaphragm pressure ratio [7]. Diao et al. (2019) investigated the influence of vibration on the dynamic calibration of pressure sensors based on the shock tube system. The experimental results showed that the impact of vibration from the failure of the diaphragm on dynamic calibration could be avoided suitably by using the mount with high damping material or a shock tube with a long driven section [8]. Liang et al. (2015) investigated the performance of PZT thick-film pressure sensors. Blastwave pressure test was conducted using a shock tube setup to test its sensing ability in response to air pressure loading. Different sized sensors were tested and showed a nearly linear relationship to blast pressure in the experimental conditions [9]. Hosseinzadeh (2014) investigated the design and fabrication of a diaphragm shock tube for the calibration of pressure sensors. A dynamic pressure sensor calibrator was designed, and finally, a device capable of producing accurate shock waves and high repeatability was developed.

However, although some parameters of shock wave such as velocity and pressure were evaluated recently, little attention has been paid to the pressure distribution along the shock tube and the planar shock wave location in gas shock tubes. The present paper presents pressure changes along the driven area of the shock tube through experiments on a gas shock tube, which has been designed and established in the K.N.Toosi University of Technology, Tehran, IRAN. Piezoresistive transducers are used for pressure measurement in the shock tube. Eventually, the pressure changes along the driven area of the shock tube are measured and a formula obtained to predict the distance of the formation of a planar shock wave from the diaphragm.

Methodology

One of the critical issues in the design of the shock tube is the planar shock wave formation. Possible sources of a non-planar shock wave in a shock tube are generally divided into static and dynamic sources. The static effects are stable at constant shock coordinates and include the boundary layer effect followed by the surface finishing. In equilibrium pressures, the boundary layer is thin in comparison with the tube radius, and the theory of the flat plate is correct. In lower pressures, the shock wave shape is complicated due to the multiple interactions of the viscous area in the shock amplitude and wall deviations.

The purpose of this study was to investigate the effect of uniform shock wave formation and the impact of burst pressure and diaphragm thickness on the distance of planar shock wave forming location in the driven area of the shock tube using the KNTU1 shock tube at the KNTU Laboratory of Explosion Mechanics.

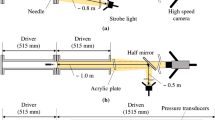
Shock Tube and Diaphragm

This shock tube is a 3-inch close-ended cold gas actuator, with nitrogen gas being injected into the chamber. For this purpose, a high-pressure capsule is used, which adjusts the output pressure by the regulator and directs it into the driven by the control valve. This cold shock tube works with a pressure rate in the range of 100 bar at a thermal scale of 0-100 at high-pressure ratios and is capable of producing shock waves with high pressure ranging from a few hundred KPa to a few MPa and with velocity from two to five Mach.

The diaphragm in the KNTU1 shock tube gets failure only by the pressure difference between the driver and the driven. For this reason, if the diaphragms had not been the same, it would lead to significant differences in explosion pressures.

Diaphragms of different materials have different burst pressures. For these experiments, in the low-pressure difference, the Mylar sheets were used. When more considerable differences are needed to achieve a higher Mach number, stainless steel diaphragms are used in different thicknesses. However, due to inconsistency in the production process, finishing on all sheets is not the same. As a result, it will be difficult to predict the burst pressure.

In this study, three types of Mylar sheets with thicknesses of 0.1 mm, 0.2 mm, and 0.3 mm were used. Since the nature of diaphragm failure had a significant effect on the formation of the ideal shock wave and reaching the planar shock wave, the experiments in which the diaphragm was torn apart in petal shape were included in the investigation. An example of the diaphragm and its ideal failure is shown in Fig. 1.

Fig. 1

A case of the diaphragm and its ideal failure

Transducer

A piezoresistive pressure transducer is a transducer in which its electrical output is proportional to the pressure on its sensitive surface. Although its usage is similar to a strain gauge transducer, the piezoresistive transducer has the advantages of lighter weight, smaller size, higher output, and higher frequency response than other types of transducers. Unlike a piezoelectric transducer, a piezoresistive transducer is also useful for measuring static pressure as much as dynamic pressures. A zero frequency response is essential for long-term and transient precision measurements.

In this study, three Endevco Model 8530B piezoresistive transducers were used (Fig. 2). In addition to their high quality and performance, these transducers are very miniature. The active part of the pressure-sensitive surface made of silicon is only 2 mm in diameter. The key to the performance and power of the transducer is its unique sensor design, featuring a Wheatstone bridge mounted on a silicon chip. Instead of a simple flat diaphragm, Endevco has developed a particular form of silicon chip that creates tension in the place of resistive elements. The silicon chip gives higher sensitivity to a given resonant frequency and also substantially increases the instability.

Fig. 2

A sample of the piezoresistive transducer used in the experiments

In many applications, the output signal from a piezoresistive pressure transducer is large enough that it does not need amplification. However, the use of amplifiers is sometimes necessary to achieve matching impedance or galvanometer incitement. The amplifier used in this study is Endevco's Model 136, a three-channel DC amplifier programmable manually or automatically.

This amplifier model is designed for use with piezoresistive accelerometers, variable capacity accelerometers, and pressure transducers. The device has an AC output voltage proportional to the input voltage and is designed for 90–240 VDC power.

Fundamentals of Shock Wave Theory

It is useful to understand the Rankine-Hugoniot (R-H) relations in understanding the relationship between the fluid state before and after the passage shock front. The overpressure, which is related to the initial shock leap, can be determined using R-H leap conditions and by knowing the initial conditions and velocity of the shock wave. After defining the pressure theory, it can be used to express the relationship with the voltage output of the sensor under the influence of the shock pressure after the justifications made. Mass, momentum, and energy conservation laws are used to express the gas state before and after the shock front passes. This section assumes that the one-dimensional planar shock wave is propagating in an unlimited gas environment. The velocity of sound which defined by α depends on the physical properties and mode of transmission environment [10].

Assuming that a specific gas is used in the shock tube, by placing the shock wave velocities and the contact surface in the Rankine-Hugoniot relation and considering $p=\rho RT$and $h=\frac{\gamma RT}{\gamma -1}$ the temperature and density ratio can be calculated [7]:

$$ \frac{{T}_{2}}{{T}_{1}}= \frac{{P}_{2}}{{P}_{1}}\left(\frac{\frac{\gamma +1}{\gamma -1}+\frac{{P}_{2}}{{P}_{1}}}{1+\frac{\gamma +1}{\gamma -1}\frac{{P}_{2}}{{P}_{1}}}\right)$$

(1)

$$ \frac{{\rho }_{2}}{{\rho }_{1}}= \frac{1+\frac{\gamma +1}{\gamma -1}\left(\frac{{P}_{2}}{{P}_{1}}\right)}{\frac{\gamma +1}{\gamma -1}+\frac{{P}_{2}}{{P}_{1}}}$$

(2)

Where T denotes the fluid temperature, P, $\rho ,$ and $\gamma$ denote the pressure, density, and the ratio of specific heat, respectively. The notation by number 1 denotes characteristics of the driven area before the failure of the diaphragm, and number 2 denotes characteristics of the area affected by the shock wave.

When the air velocity exceeds the velocity of sound due to mechanical disturbance, a shock wave is generated. Depending on the strength of the disturbance, the initial fluid state immediately after the shock front can be determined. This condition is measured using gas law, unit area, and adiabatic density. As can be seen from these relations that the change in gas properties depends on the pressure ratio. If the Mach of shock wave is defined as the ratio of the wave velocity to the velocity of sound, the vertical shock wave relation can be used to obtain the Mach number, which is a function of the pressure ratio at the tube length:

$$ \sqrt{\frac{{\upgamma }+1}{2{\upgamma }}\left(\frac{{P}_{2}}{{P}_{1}}-1\right)+1}$$

(3)

Where Ms denotes the Mach of shock front.

The following equation is used to obtain the speed of the contact surface:

$$ \frac{{a}_{1}}{\gamma }(\frac{{p}_{2}}{{p}_{1}}-1)\sqrt{\left[\frac{\frac{2\gamma }{\gamma +1}}{\frac{{p}_{2}}{{p}_{1}}+\frac{\gamma -1}{\gamma +1}}\right]}$$

(4)

Where UP denotes the velocity of the contact surface, and $a$ denotes the speed of sound in the fluid.

Dividing equation (4) by the speed of sound in the driver gives the following equation:

$$ \frac{{U}_{P}}{{a}_{2}}= \frac{1}{\gamma }\left(\frac{{P}_{2}}{{P}_{1}}-1\right){\left[\frac{\frac{2\gamma }{\gamma +1}}{\frac{{P}_{2}}{{P}_{1}}+\frac{\gamma -1}{\gamma +1}}\right]}^{\frac{1}{2}}{\left[\frac{1+\frac{\gamma +1}{\gamma -1}\left(\frac{{P}_{2}}{{P}_{1}}\right)}{\frac{\gamma +1}{\gamma -1}\left(\frac{{P}_{2}}{{P}_{1}}\right)+{\left(\frac{{P}_{2}}{{P}_{1}}\right)}^{2}}\right]}^{\frac{1}{2}}$$

(5)

If the pressure ratio $\frac{{P}_{2}}{{P}_{1}}$ tends to infinity, or in other words, the shock wave be infinitely strong, then:

$$ \frac{{U}_{P}}{{a}_{2}}=\sqrt{\frac{2}{\gamma (\gamma -1)}}$$

(6)

And for air with $\gamma =1.4$, when a very strong shock wave is desirable, $\frac{{U}_{P}}{{a}_{2}}$ reaches to 1.89.

According to the above relations, the properties of the flow produced after the diaphragm's failure or the valve opening in the shock tube can be investigated. Equations (7) to (9) can be used to obtain the properties of any point in the area of expansion waves.

$$ \frac{P}{{P}_{4}}= {\left[1-\left(\frac{\gamma -1}{2}\right)\left(\frac{u}{{a}_{4}}\right)\right]}^{\frac{2\gamma }{\gamma -1}}$$

(7)

$$ \frac{T}{{T}_{4}}= {\left[1-\left(\frac{\gamma -1}{2}\right)\left(\frac{u}{{a}_{4}}\right)\right]}^{2}$$

(8)

$$ \frac{\rho }{{\rho }_{4}}= {\left[1-\left(\frac{\gamma -1}{2}\right)\left(\frac{u}{{a}_{4}}\right)\right]}^{\frac{2}{\gamma -1}}$$

(9)

Where the notation by number 4 denotes characteristics of the driver area before the failure of the diaphragm, and u denotes the fluid velocity. The following equation holds for the beginning and end of the expansion waves:

$$ \frac{{P}_{3}}{{P}_{4}}=1-\left(\frac{{\gamma }_{4}-1}{2}\right){\left(\frac{{u}_{3}}{{a}_{4}}\right)}^{\frac{2{\gamma }_{4}}{{\gamma }_{4}-1}}$$

(10)

Where the notation by number 3 denotes characteristics of the area affected by the expansion wave.

According to equations (4) and (10), and knowing ${u}_{3}={u}_{2}$ the following relation is obtained [11]:

$$ {u}_{3}= \frac{{2a}_{4}}{{\gamma }_{4}-1}\left[1-\left(\frac{{P}_{2}}{{P}_{4}}\right)\frac{{\gamma }_{4}-1}{{2\gamma }_{4}}\right]$$

(11)

The power of the shock wave depends on the ratio of $\frac{{P}_{2}}{{P}_{1}}$ which can be calculated using the mass, momentum, and energy conservations law for a normal shock wave:

$$ \frac{{P}_{4}}{{P}_{1}}= \frac{{P}_{2}}{{P}_{1}}{\left\{1-\frac{({\gamma }_{4}-1)\left(\frac{{a}_{1}}{{a}_{4}}\right)(\frac{{p}_{2}}{{p}_{1}}-1)}{\sqrt{2{\gamma }_{1}\left[2{\gamma }_{1}+({\gamma }_{1}+1)(\frac{{p}_{2}}{{p}_{1}}-1)\right]}}\right\}}^{\frac{-2{\gamma }_{4}}{{\gamma }_{4}-1}}$$

(12)

Where α1 is the velocity of sound in the driver gas, which is calculated from the equation for the ideal gas. Also, index 1 means upstream conditions, and index 2 indicates downstream conditions. Now with the ratio of $\frac{{P}_{2}}{{P}_{1}}$, the velocity can be calculated:

$$ {V}_{s}={\alpha }_{1}\sqrt{\frac{\gamma +1}{2\gamma }\left(\frac{{P}_{2}}{{P}_{1}}-1\right)+1}$$

(13)

Where Vs denote the velocity of the shock front. Therefore the Mach number of the shock wave will be equal to:

$$ {M}_{s}=\frac{{V}_{s}}{{\alpha }_{1}}$$

(14)

By calculating the shock wave's Mach number and placed it in the following equation, the peak overpressure of the shock wavefront can be calculated.

$$ \frac{{P}_{2}}{{P}_{1}}=\frac{2\gamma {M}^{2}-(\gamma -1)}{(\gamma +1)}$$

(15)

This value is compared with the overpressure peak obtained from the piezoresistive sensor. Also, considering $\gamma =1.4$ for air, equation (15) will be as follow:

$$ \frac{{P}_{2}}{{P}_{1}}=1.16{M}^{2}-0.16$$

(16)

Experiments

The purpose of this study was to investigate the uniform shock wave formation and the effect of burst pressure and diaphragm thickness on the location of planar shock wave formation in the driven area of shock tube using the shock tube designed and fabricated in the Explosion Mechanics Laboratory of the K.N.Toosi University of Technology, Iran. The experiments were designed to accommodate piezoresistive transducers at different intervals along the driven to achieve the uniformity distance of the shock wave.

Since it is necessary to measure the pressure at various points of the wave cross-section to detect the planar wave formation, a fixture was designed to allow transducers to be mounted at different radial distances. The installation was made of a 7 cm diameter aluminum piece equal to the inside diameter of the shock tube. The thickness of this piece was selected according to the dimensions obtained from the transducer catalog provided by the manufacturer (Fig. 3).

Fig. 3

Transducer schematic and its components and Wheatstone bridge circuit of sensing element [12]

For mounting transducers, holes were created at different radial distances, with a diameter of 0.5 mm based on the transducer catalog. The fixture is shown in Fig. 4.

Fig. 4

Transducers positioning

Three samples of the installation were made and mounted on a rod with a length of 1.2 m at different distances to constrain the fixture inside the shock tube.

Once the transducers were mounted on this fixture, the assembly inside the shock tube must also be restrained in the direction of the tube axis so as not to be affected by the impact resulting from the shock. Otherwise, the transducers will not be able to measure the correct value of shock wave pressure. For fastening the fixture in the tube axis direction, the aluminum rod retained at the end of the driven section by attaching it to a steel plate using three bolts and two flanges.

Three transducers are positioned on the fixture in different radius and connected to the amplifier. Finally, connecting the amplifier to the signal processing unit, the results of the pressure measurement within the tube are displayed by the individual transducers as voltage output. The sensors used in this study have a conversion factor of 0.8, which means that by multiplying the output voltage obtained by the measurement in this number, the pressure value can be obtained in “bar.”

The design of the experiments was in such a way that the transducers were mounted on the fixture in three different radiuses at 205, 220, 240, 250, 260, 275, 280, 295, and 300 cm from the diaphragm in the shock tube. Each of these intervals was repeated for all three Mylar sheets with 0.1 mm, 0.2 mm, and 0.3 mm thickness. Figure 5 illustrates how transducers are arranged on the fixture.

Fig. 5

The positioning of transducers on the fixture

To test the repeatability of the device and to ensure the accuracy of the results, some experiments were repeated, and several tests were excluded from the analysis process due to human errors or problems such as unreliable diaphragm failure. Finally, 27 correct tests were selected from the results of the experiments and analyzed.

Results

Ideal Shock Wave Generation

After the experiments, the results were extracted from the software in the form of voltage-time diagrams. After measuring the peak overpressure, the maximum voltage value was calculated in each experiment and multiplying this value by the transducer conversion number, i.e., 1.379, the overpressure value was obtained in the "bar" unit (Fig. 6).

Fig. 6

An example of ideal shock wave generation (Shock wave peak pressure-time-distance diagram)

Planar Shock Wave Formation Distance

Pressure values at different distances and diaphragms of different thicknesses are collected in Tables 1, 2, and 3, which were measured by three transducers.

Table 1 Test results for 0.1 mm thick diaphragm

Table 2 Test results for 0.2 mm thick diaphragm

Table 3 Test results for 0.3 mm thick diaphragm

The pressures measured by all three transducers were compared to discover the location of planar shock wave formation. The interval of which pressure values differences were less than 10% (acceptable error value of the test) was considered as the planar wave formation distance.

Also, the shock wave diagrams can be used to identify the location of the planar wave, so that the shock wave diagrams of three transducers were plotted simultaneously for each interval and diaphragm, then comparing their peak pressure will show the overlap time of the graphs (Fig. 7).

Fig. 7

Shock wave peak pressure-time diagram of three transducers in equal distance from diaphragm A) before planar shock wave formation B) after planar shock wave formation

The analytical solution of the shock tube problem is complex and cannot be solved manually, so previous research results were used to compare the empirical and analytical results. An analytical program using MATLAB software has been developed to determine driver and driven length. Program input variables include time after diaphragm failure, primary pressure of high-pressure section, primary pressure of low-pressure section, primary temperature, the primary temperature of the low-pressure section, and adequate length of the driver and driven section. The equation constants for air include a specific heat ratio of 1.4, and the universal gas constant for an ideal gas is 287.05 J⋅kg − 1⋅K − 1. Program outputs also include variations in sound velocity in the fluid at a specific time, fluid-particle velocity and pressure, density, and temperature variations at different points in the shock tube. In this program, after determining the initial conditions (before the diaphragm failure), the shock wave peak pressure was determined using equation (12) by the inverse quadratic interpolation method. Figure 8 illustrates the diagram of the shock wave peak pressure, according to the initial pressure of the high-pressure section (P4-P2) using analytical equations.

Fig. 8

P₂-P₄ (Shock wave peak pressure-Burst pressure) diagram from analytical results

Using the results obtained for the P2 to P4 pressure ratio analysis, and by using MATLAB software, the equation for the relationship between these two values of pressure was obtained as follows:

$$ {P}_{2} = 0.02796\text{*}{P}_{4}^2 -0.1441\text{*}{P}_{4} + 1.251$$

(17)

The results of empirical experiments and theory in terms of identical burst pressures are presented in Table 4.

Table 4 The pressure obtained from the experimental and analytical results

Using the results obtained from the tests and the shock wave peak pressure (P2) in experiments with different diaphragms and with the instantaneous diaphragm failure pressure (P4) using the pressure gauge, the P2 graph can be plotted for the experimental results. Figure 9 shows the graph along with the graph of the theoretical results and the theoretical and experimental results are compared.

Fig. 9

Comparison of experimental and analytical results. (Shock wave peak pressure-Burst pressure)

The trend of pressure changes resulting from analytical solutions and experiments were almost similar. The differences between the two solutions were due to assumptions in the analytical solution, including the ideal gas assumption and other boundary conditions, and in empirical experiments, these differences are due to the experimental errors. The error between the experimental results and the analysis was calculated using the mean square error method, which was 19%.

According to the results of the pressure-time diagrams, it was observed that at the beginning of the driven section, the pressure difference in the transducers (pressure difference at different points of the tube cross-section) was high, indicating that the shock wave was non-planar. In these regions, the flow is quite turbulent. As the distance increases, it was observed that the pressure of the two transducers in similar radial position approaches each other, indicating a spherical shock wave. However, the shock wave has not yet become planar.

Figures 10, 11, and 12 illustrate the pressure-distance diagrams of the transducers for diaphragms with a thickness of 0.1 mm, 0.2 mm, and 0.3 mm.

Fig. 10

Shock wave peak pressure (P₂)-distance diagram for 0.1 mm diaphragm

Fig. 11

Shock wave peak pressure (P₂)-distance diagram for 0.2 mm diaphragm

Fig. 12

Shock wave peak pressure (P₂)-distance diagram for 0.3 mm diaphragm

The pressure-distance diagram plotted in Fig. 10 shows the peak values of the pressure measured by three transducers at different distances from the diaphragm. The initially measured pressures are very different, then they get closer to each other as distance increases, and within a range of about 245 to 264 cm for this aperture (0.1 mm), the planar wave state remains stable. As can be seen, this planar wave disappears at the end of the shock tube, and it becomes turbulent due to the weak shock created by this diaphragm and its collision with the embedded spots of the transducers in the shock tube.

Figures 11 and 12, respectively, refer to the pressure variations along the shock tube for the thickness diaphragms of 0.2 mm and 0.3 mm, in which the uniform wave section for these two series of tests is longer in comparison with the diaphragm with 0.1 mm thickness, and it extends to the end of the shock tube. For experiments with a 0.2 mm diaphragm, the uniform wave and planar wave formation start in 278 cm from the diaphragm, and for the experiments with a 0.3 mm diaphragm, it begins at a distance of 283 cm. A comparison of these figures shows that with increasing the diaphragm thickness and consequently the diaphragm burst pressure, the planar wave is formed farther away, and the length of its uniform area is increased.

Peak Overpressure Prediction

Since the procedure of pressure change for the different diaphragms is almost the same, all three sets of peak pressure and burst pressure data for the diaphragm types are plotted in Fig. 13. This graph shows the trend of maximum peak pressure changes relative to the burst pressure in three different distances from the diaphragm. The best curve fitted to the process is a quadratic polynomial curve. The equation of each curve is written alongside the correlation coefficient (R2), which is the coefficient of confidence of the equation. These curves are handy tools for the design of gas shock tubes. Using these curves, and having an explosion pressure, one can predict the maximum peak pressure with a good approximation.

Fig. 13

Peak overpressure (P₂) relative to burst pressure (P₄)

Conclusion

Prior work has documented the effectiveness of diaphragm thickness in diaphragm failure pressure and investigated the expansion waveform according to the preliminary conditions of the driver. However, these studies have either been investigations on double-diaphragm shock tubes or have not focused on the trend of shock wave peak pressure after diaphragm failure or its relation with diaphragm thickness and burst pressure. In this study, 27 experiments were carried out on a gas shock tube, and three different diaphragms were used. So, the effectiveness of diaphragm thickness on a planar shock wave formation and its position during propagation were investigated.

Based on the graphs extracted from the transducers, it is found that the shock wave pressure decreases steadily along with the driven section. First, the shock wave theory relations were extracted, and a relation was obtained for the ratio of shock wave pressure to burst pressure. The values of shock wave pressure at different burst pressures were calculated through this relation, and a graph was drawn using MATLAB software. Then, the best fitting curve to the results was plotted, which was a quadratic polynomial curve, according to Fig. 8, and the corresponding regression equation was given in equation (17).

In the next step, the shock wave pressure using 27 experiments was measured at different distances within the driven and with three different diaphragms using three piezoresistive sensors. According to the results of these experiments, the location of the planar shock wave formation inside the shock tube was calculated, which can be seen in Figs. 10, 11, and 12 that presents the pressure change along with the driven. According to the figures, the distance of the planar wave location was obtained, and it was observed that this distance varies for different diaphragms, and as the diaphragm thickness increases, the shock wave uniformity distance from the beginning of the driven section increases. When the 0.1 mm diaphragm was used, the planar shock wave formation was in the range of 245 to 264 centimeters, the 0.2 mm thickness diaphragm in the range of 278–300 cm, and the 3 mm thickness diaphragm, the distance was 283 cm to the end of the shock tube.

Also, the results of the experiments were compared with the results of theoretical relations, and the error was calculated using the mean square error equation, which was approximately 19%. Figure 9 shows a graph of shock wave pressure to burst pressure for both theoretical and experimental results, and these graphs were compared with each other. As shown in Fig. 9, the process of pressure changes resulting from the experiments was similar to the theoretical state, which confirms the correctness of the experiments.

Finally, three equations were derived to predict peak pressure values for all diaphragms. Three regression equations with a correlation coefficient of 0.9 were obtained by using the three graphs drawn in Fig. 13 and the fitting curves. Through these equations, the shock wave peak pressure can be estimated with high accuracy according to the burst pressure and at different distances from the diaphragm.