Introduction

Tube hydroforming (THF) is a specialized metal-forming technique. Using this process, thin-walled metal tubes are formed into die cavities with the desired cross-sectional shapes by high-pressure liquids. The manufactured components have low weight, high stiffness and strength, and good crash performance. Even though THF offers immense advantages over conventional tube stamping through the reduction of manufacturing steps and variations in workpieces, it still requires expensive pressurization equipment such as pumps and intensifiers. As an alternative, liquid impact forming (LIF), proposed by American Greenville Tool & Die Company, combines the use of a stamping press and a liquid medium to form the desired shape on a workpiece [1]. As illustrated in Fig. 1, a metal tube, initially filled with liquid at approximately atmospheric pressure, is rapidly formed into a die cavity by the liquid (hydraulic pressure P), which is rapidly pressurized during the stamping process by impact loading (Fa) from a pusher, driven by the faster descending ram of a stamping equipment. This technique is a synthesis of two metalworking processes, conventional stamping (metalworking) and hydroforming, and utilizes the increase in the internal pressure of the liquid inside the tube during the stamping process. It is characterized by high forming speed, high production efficiency, and low production cost, eliminating the need to pressurize the tube prior or subsequent to stamping and the use of the abovementioned equipment [2]. It is especially suited for the cold forming of the tubular structural parts in automotive, railroad, and aerospace industries.

Fig. 1
figure 1

Schematic diagram of liquid impact forming (LIF) of a tube

Full size image

In LIF, the tubular material is deformed at a very high speed due to the fast liquid impact loading (Fa), and the deformation behaviour may conceivably differ from that in the moderate-speed conventional THF. Therefore, the deformation behaviour of tubular materials in LIF is currently the biggest concern. A material structural model or an equivalent stress-strain relationship is generally used to describe the deformation behaviour of metals. A precision structural model is essential for the effective analysis of forming processes, reliable assessment of the formability of materials, and the finite element (FE) simulation of the forming process. Most materials for industry and society are essentially geometrical randomness and material randomness, and these randomness are intrinsically stochastic that affect the deformation behaviours of the materials. Identifying the material randomness is an experimentally demanding task [3]. Bayesian inference (BI) can be applied for the stochastic identification of material parameters and the parameter identification of nonlinear constitutive models but only requires a limited number of testing or experiments [4]. Subsequently, BI is a relatively new and rather different to understand and use but a promising approach to quantify the constitutive equation [5].

Uniaxial tensile tests (UTTs) are usually applied to quantify the constitutive equations or determine the model coefficients in existing constitutive equations. Hydro-bulging tests are also appropriate methods of establishing biaxial stress-strain relationships [6]. A major advantage of the hydro-bulging tests over the conventional UTT is that extended stress-strain curves can be achieved under the biaxial state of stress. Many researchers use the Ludwik-Hollomon model σ = K·εn to model the deformation behaviour of tubular materials in conventional forming processes and determine the model coefficients using hydro-bulging tests combined with analytical or FE simulation approaches [7,8,9,10,11]. Those studies demonstrated that the hydro-bulging test is more suitable than the UTT for THF. However, considering the high-speed deformation feature in LIF, it is appropriate to apply a material structural model in which the strain rate variable is used to model the deformation behaviour of tubes in LIF.

Apart from the basic quasi-static hydro-bulging test, dynamic hydro-bulging tests have been increasingly utilized to perform biaxial tests on metals at high strain rates. Grolleau et al. [12] used a split Hopkinson pressure bar apparatus with viscoelastic nylon bars to perform dynamic hydro-bulging tests on aluminium sheets at plastic strain rates up to 500 s−1. Huang et al. [13] developed a simple experimental tool, including a stamping device and THF apparatus, and conducted conventional THF and LIF experiments on SS304 stainless steel tubes in rectangular cross-sectional die cavities. The results showed that the forming speed has an influence on the formability of the tubes. Farshid et al. [14] modelled and investigated impulsive hydroforming processes of aluminium 6061-T6 tubes at high strain rates using FE simulation and the ABAQUS finite element commercial code and found that the high strain rate of impulsive hydroforming enabled the material to undergo higher stress.

Previous studies quantified the Ludwik-Hollomon model, σ = K·εn, using hydro-bulging tests based on the total strain theory and showed that the hydro-bulging test is more feasible for THF. However, considering the high-speed deformation feature in LIF, it is appropriate to apply a material structural model in which the strain rate is used to model the deformation behaviour of the tubes in the LIF process. To date, the determination of the constitutive relationship of tubular materials in the LIF process has never been reported. The purpose of this work is to model the material deformation behaviour of the tubes in LIF using the Johnson-Cook(JC) structural model and obtain the model coefficients A, B, C, and n for SS304 stainless steel tubular materials at various impact velocities (v) using hydro-bulging experiments and analytical approaches, to reveal the response of the material to the various impact velocities (v).

Methodology

The material structural model includes mathematical equations that relate the induced strain parameters such as strain, strain rate, strain hardening, and temperature. The JC model is commonly used to describe the constitutive relationship for metals, which are sensitive to the strain rate. The primary objective of this work is to determine the model coefficients A, B, C, and n for SS304 stainless steel tubular materials at various impact velocities using hydro-bulging experiments along with an analytical approach.

In the absence of a temperature parameter, the JC model is given as

$$ {\sigma}_{\mathrm{e}}=\left(A+B{\varepsilon}_e^n\right)\left(1+C\ln \frac{\dot{\varepsilon}}{\varepsilon_0}\right) $$
(1)

where σe and εe are the equivalent stress and strain, respectively. The first term in equation (1) stands for the work hardening response at the reference strain rate (\( \dot{\varepsilon_0} \)=1) and the second term is related to the effects of the strain rate on the stress in the material.

Model coefficients A, B, n, and C are obtained through experiments by fitting the obtained stress-strain curve to the overall shape of the model to calculate the JC coefficients. The procedure can be summarized as follows.

  1. (1)

    The relationship between the stress and the strain components is analytically established in the equations. Strain components (εθ, εx) used to calculate the equivalent strain (εe) can be directly measured, while the stress components (σθ, σx) used to calculate equivalent stress (σe) cannot be technically measured in hydro-bulging experiments. Consequently, the equations for calculating stress components were derived using the force equilibrium condition and the plastic theory.

  2. (2)

    Quasi-static (\( \dot{\varepsilon_0} \) ≈0.04 s−1) hydro-bulging experiments on SS304 stainless steel tubular materials were carried out on a customized hydro-bulging system and deformation data were gathered by a digital image correlation (DIC) system. The strain components and equivalent strains were calculated using the experimental deformation data and the derived stress components and equivalent stresses were calculated using the relationship between the stress and strain components. The strain rate in the quasi-static hydro-bulging process was defined as the reference strain rate (\( \dot{\varepsilon_0} \)) and model coefficients A, B, and n of the first term in the JC model were calculated through the experiments by fitting the obtained stress-strain curve to the first term of the model. The same method is also described in Yang et al. [15].

  3. (3)

    Impact (dynamic, \( \dot{\varepsilon} \)=0.11–5.13 s−1) hydro-bulging experiments on SS304 stainless steel tubular materials at various impact velocities (v) were carried out on the hydro-bulging system. The deformation data including the strain components (εθ, εx) at each given impact velocity were gathered by the DIC system. The equivalent strain (εe) and equivalent strain rates at each given impact velocity were calculated. The model coefficient C of the second term in the JC model at each given impact velocity was calculated by fitting the obtained stress-strain curve to the overall shape of the JC model. Because the influence of strain rate on the resultant stress is represented by log strain rate term in the JC model, in most of the previous studies, the deformation behavior of strain-rate sensitive materials were represented by the JC model with one parameter set (constants A, B, C, and n). However, the coefficient C of the log strain rate term may actually be different (non-constant) within a wide range of strain rates, for example, 1~150 mm/s. Therefore, we fit the coefficient C in JC model independently to each experiment to investigate the strain rates on the coefficient C.

  4. (4)

    FE simulations of hydro-bulging processes of the tubes at various velocities were conducted with the resultant JC models as input material models. The bulged profiles and heights were compared between the FE simulations and the experimental results to validate the JC models.

Analytical Approaches

Geometrical Representation

The first step for deriving the relationship between the stress and strain components in the hydro-bulging process is the proper geometrical representation of the bulged tubes.

The model for hydro-bulging is illustrated in Fig. 2, where a tube is subjected to a high-speed liquid impact loading (hydraulic pressure P) in the die cavity. At the peak b of the axial bulged profiles, the meridian direction is only coincident with the longitudinal direction or the x-axis.

Fig. 2
figure 2

Schematic of the geometrical representation of hydro-bulging under hydraulic pressure P: (a) axial bulged profile, and (b) stress components at the peak b

Full size image

The circumferential radius ρθ at the peak can be evaluated by

$$ {\rho}_{\theta }={r}_0+h $$
(2)

where r0 is the initial outer radius of the tube and h is the bulging height of the bulged tube.

Stress Calculation

The tube is assumed to be thin enough for the plane stress hypothesis to be valid, i.e., thickness stress σr = 0, in Fig. 2. For the element at the peak, the longitudinal and circumferential stress components at peak b can be derived using the membrane theory and the force equilibrium in two directions, respectively [16].

$$ {\sigma}_x=\frac{P{\left({\rho}_{\theta }-{r}_0\right)}^2}{2t\left({\rho}_{\theta }-t/2\right)} $$
(3)
$$ {\sigma}_{\theta }=\frac{P\left({\rho}_{\theta }-t/2\right)}{t}\times \left\{\left[1-\frac{t}{2\left({\rho}_{\theta }-t/2\right)}\right]\left[1-\frac{t}{2\left({\rho}_x-t/2\right)}\right]-\frac{{\left({\rho}_{\theta }-t\right)}^2}{2\left({\rho}_x-t/2\right)\left({\rho}_{\theta }-t/2\right)}\right\} $$
(4)

where t is the instantaneous wall thickness of the bulged tube.

The effective stress based on the Von-Mises yield function for the plane stress condition can be expressed as

$$ {\sigma}_{\mathrm{e}}=\sqrt{\sigma_{\theta}^2-{\sigma}_{\theta }{\sigma}_x+{\sigma}_x^2} $$
(5)

Strain Calculation

The radial thickness strain at the peak b is expressed by

$$ {\varepsilon}_t=\ln \frac{t}{t_0} $$
(6)

If the longitudinal and circumferential strain values are determined, the radial strain can also be evaluated based on the incompressibility condition of the material

$$ {\varepsilon}_t=-{\varepsilon}_{\theta }-{\varepsilon}_x $$
(7)

Combining equation (5) with equation (6), the instantaneous wall thickness (t) for the implementation of Eqs. (3), (4), and (6) can be calculated as follows:

$$ t={t}_0\exp \left(-{\varepsilon}_{\theta }-{\varepsilon}_x\right) $$
(8)

The effective strain using the circumferential strain and the longitudinal strain for the plane stress condition can be derived in equation (9) using the equivalent plastic work definition (total strain theory), incompressibility, and the normality condition [17].

$$ {\varepsilon}_{\mathrm{e}}=\frac{2}{\sqrt{3}}\sqrt{\left({\varepsilon}_{\theta}^2+{\varepsilon}_{\theta }{\varepsilon}_x+{\varepsilon}_x^2\right)} $$
(9)

Strain Rate Calculation

Because the strain components εθ and εx can be continuously measured at each time step by the DIC system in the hydro-bulging experiments, the equivalent strains (εe) at each time step can be calculated using equation (9). Then, the equivalent strain rates in the hydro-bulging process of each given impact velocity can be calculated as follows:

$$ {\dot{\varepsilon}}_{\mathrm{e}}=\frac{d{\varepsilon}_{\mathrm{e}}}{dt} $$
(10)

Experiments and Simulations

The instantaneous variables including the hydraulic pressure (P), strain components (εθ and εx), circumferential curvature radii (ρθ), and axial curvature radii (ρx) must be determined to calculate the longitudinal and circumferential stress components (σθ, σx) as expressed by Eqs. (3) and (4). The former four variables can be measured directly during the hydro-bulging experiments; however, the axial curvature radii (ρx), which cannot be measured directly, can be determined using the curve fitting method described in subsection ‘Determination of the axial curvature radii’.

Tube and Material

SUS304 stainless steel tubes were adopted in this investigation. The geometric dimensions and material properties determined by UTT are given in Table 1. The test tubes were sprayed with two types of paints to form irregular black speckles on a white background prior to the hydro-bulging experiments. This is shown in Fig. 3.

Table 1 Geometric dimensions and material properties of the test SUS304 stainless steel tubes obtained by uniaxial tensile tests
Full size table
Fig. 3
figure 3

A test tube prior to and deformed by hydro-bulging experiments: (a) Initial state, (b) sprayed with paints, and (c) after hydro-bulging deformation

Full size image

Experimental Setup

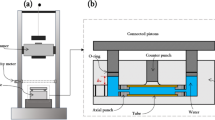
A simple and practical hydro-bulging system was developed to conduct the experiments (Fig. 4). The experimental system comprises five sections [18, 19]:

  1. (1)

    Impact loading providers. A YB98-220A hydro-press (with rated working speed of 1~10 mm / s, maximum fluid pressure of 100 MPa and clamping force of 1200 kN) and a punch press (with rated working speed of 150 mm / s) work independently as impact loading providers that provide the impact loading (Fa) of diversified impact velocities (v) (Fig. 1). For present experiments, the former produced impact velocities of 1, 5, and 10 mm/s, while the latter produced an impact velocity of 150 mm/s.

  2. (2)

    A liquid pressurization device. It consists of a hydraulic chamber and a piston. The liquid pressurization device was installed on the workbenches of the hydro-press and the punch press, respectively. The liquid (regular engine oil) in the chamber was stamped by the piston and pressurized when the piston was driven down by one of the impact loading providers.

  3. (3)

    A hydraulic pressure detection and recording system. It is composed of a MIK-P300 pressure transmitter and a USB-2610 digital recorder with a precision ±0.2% full scale (FS) and a measurement range of 0–100 MPa. The system was adopted to measure in real time the hydraulic pressure P produced in the hydraulic chamber. The measured data were displayed and stored in the digital recorder with a precision of ±0.02% FS and highest acquisition frequency of 650 kHz.

  4. (4)

    A customized hydro-bulging device. This is where a test tube is hydro-bulged. The test tube was positioned between the locating rings and filled with the liquid; then, it was pre-locked and pre-sealed at each end by urethane plugs, the binding bolt, and locked nuts. A free bulge zone lb (the unsupported section) was formed between the two locating rings. The test tube was hydro-bulged gradually within the bulge zone by the hydraulic liquid from the liquid pressurization device via the binding bolt.

  5. (5)

    A digital image correlation (DIC) system. This system mainly consists of two charge coupled device (CCD) cameras, two light emitting diode lights (LED), a tripod, a control box, and a computer. The main technical parameters of the system are listed in Table 2. It was used to capture the plastic deformation field data (speckled images) in real-time during the hydro-bulging experiments including the strain components (εθ and εx), and the three-dimensional (3D) coordinate values of all the points on the bulged profiles at each time step.

Fig. 4
figure 4

Customized hydro-bulging system adopted in the experiments

Full size image
Table 2 Main technical parameters of the three-dimensional DIC system
Full size table

Determination of the Axial Curvature Radii (ρx)

After the plastic deformation data during the hydro-bulging experiments were captured by the DIC system, the 3Dcoordinate values of all points on the bulged profiles at each time step could be obtained using the DIC software. Spline function were used to fit these coordinate points and then the axial bulged profiles at each time step could be achieved (Fig. 5). Then, the axial curvature radii (ρx) at the peak point at each time step could be determined by calculating the derivative of the spline functions with time.

Fig. 5
figure 5

Axial bulged profiles at time steps measured in the hydro-bulging experiments

Full size image

Finite Element Simulations

FE simulations were carried out using commercial code ABAQUS/Explicit 6.10 on the hydro-bulging process of SS304 stainless steel tubes to obtain the deformation data required for the calculation of the equivalent stress and strain values. The geometric and mechanical parameters used in the FE simulation are reported in Table 1. The model coefficients A, B, n, and C (Table 3), obtained in the hydro-bulging experiments for the JC model, were taken as the input material models for the FE simulation.

Table 3 Johnson-Cook structural model coefficients for SS304 stainless steel tubes
Full size table

The FE model for hydro-bulging is displayed in Fig. 6. The tubular material, under the isotropic and homogeneous assumption, was modelled as the deformed shell and meshed using 48,400 QUAD4-type elements (Quadrilateral plate element) in sweep method. The result of the mesh convergence is generally believed to be impacted by element size. In view of this, initially three initial element sizes including coarse (0.3 mm), medium (0.2 mm) and fine (0.1 mm), were tried in the simulation to check the convergence and maximum deviation of 3.7% in term of bulging heights were observed between the results if an automatic adaptive remeshing and refinement technique was utilised to optimise the initial element size. In consideration of result accuracy and computational efficiency, the initial element size of 0.20 mm was adopted for the present simulation with an automatic adaptive remeshing and refinement technique being adopted. The locating rings and urethane plugs were modelled as in deformable rigid solids to simplify the analysis and reduce the analysis time. The contact interfaces between the tubular material and the tool were modelled using the Coulomb friction model with a coefficient of friction of 0.12.

Fig. 6
figure 6

Geometrical FE model for hydro-bulging

Full size image

The loading curves, i.e., the variation in the hydraulic pressure versus the bulging time, were purposely designed to be consistent with those measured in the hydro-bulging experiments. The loading curves that are used to fit the measured points were adopted as the loading curves for the FE simulations (Fig. 7).

Fig. 7
figure 7

Loading curves for the simulations

Full size image

After the simulations, bulging heights (h) at the peak points at the middle cross-section of the axial bulged profiles at all time steps were extracted directly from the FE simulation results and compared to those from the hydro-bulging experiments to validate the obtained JC models.

Results and Discussion

The equivalent stress-strain curves at various impact velocities were compared to probe the effect of strain rates on the flow stress of the SS304 stainless steel tubes. The bulging heights at the peak points at the middle cross-section of the axial bulged profiles were compared to those from the hydro-bulging experiments to validate the resultant JC models for the hydro-bulging process of the tube.

Relationship between the Strain Rates and Impact Velocities

A higher impact velocity (v) usually leads to a shorter total hydro-bulging time between the start of the plastic deformation and the onset of bursting in the test tubes. The total hydro-bulging times for all impact velocities are normalized for comparison (Fig. 8). Figure 8 shows that a higher impact velocity leads to a higher strain rate (\( \dot{\varepsilon} \)) in a bulged tube; the strain rates at the peak points at the middle cross-section of the axial bulged profiles increased linearly in hydro-bulging processes and increased faster at higher impact velocities. The strain rates at the velocity of 150 mm/s increased much faster (from 1.81 to 5.13 s−1) than those at the velocities of 1, 5, and 10 mm/s (from 0.11 to 1.64 s−1).

Fig. 8
figure 8

Variations in the strain rates at the peak points at the middle cross-section of the axial bulged profiles versus the impact velocity (experimental data)

Full size image

Comparison of Equivalent Stress–Strain Curves at Different Impact Velocities

Figure 9 shows that the impact velocity has a great influence on the equivalent stress-strain curves. The equivalent stress-strain curves move to a higher position as the impact velocity increases, i.e., the flow stress is increased with the increase in the impact velocity.

Fig. 9
figure 9

Equivalent stress–strain curves at various impact velocities in LIF

Full size image

Specifically, for SS304 stainless steel tubular materials, the influence of the impact velocity on the yield stress and coefficient C in the JC model is evident. The yield stress and model coefficient C increased as the impact velocity increased; e.g., the yield stresses were 385, 405, 413, and 493 MPa and the C values were 0.029, 0.030, 0.032, and 0.081 at the impact velocities of 1, 5, 10, and 150 mm/s, respectively. However, the values of the model coefficient C at lower impact velocities were almost equal (0.029, 0.030, 0.032), in contrast to the value (0.081) at the highest impact velocity of 150 mm/s (Table 3).

Comparison of Bulging Heights between the FE Simulations and Experimental Results

In all impact velocities, the bulge heights at the peak points at the middle cross-section of the axial bulged profiles increased with the increase in the hydraulic pressure (Fig. 10). However, the bulge heights at lower impact velocities increased faster than at the high impact velocity of 150 mm/s, because the slopes of the former are all larger than that of the latter under a specific hydraulic pressure. This implies that the test tube deformed faster under the same hydraulic pressure at lower impact velocities.

Fig. 10
figure 10

Variations in the bulge heights at the peak points at the middle cross-section of the axial bulged profiles versus hydraulic pressure

Full size image

Figure 10 shows that the experimental points fall on the FE simulation curves of the bulge heights versus the hydraulic pressure, with maximum deviation rates of 7.2% between the FE simulation curves and the experimental points listed in Table 4. Therefore, the hydro-bulging process of SS304 stainless steel tubes can be accurately predicted using the JC model determined by the proposed approach.

Table 4 Deviation rates (%) of bulging heights obtained from the FE simulations relative to those obtained from the experiments
Full size table

Conclusion

In this study, the deformation behaviour of SS304 stainless steel tubes in LIF were modelled using the Johnson-Cook model. The model coefficients A, B, C, and n in the equation were determined using the hydro-bulging experiments along with the analytical approach. The relationship between the strain rates and the impact velocities was investigated, the bulging heights between the equivalent stress-strain curves at different impact velocities were analysed, and the bulging heights between the FE simulative and experimental results were compared. The results can be summarized as follows:

  1. 1.

    The LIF of SS304 stainless steel tubes can be accurately predicted using the JC model determined by of the hydro-bulging experiments combined with the analytical approach, with a maximum deviation rate of 7.2% in terms of bulging heights between the FE simulations and the experimental results.

  2. 2.

    A higher impact velocity leads to a higher strain rate in the bulged tube; the strain rate increases in the hydro-bulging process and get faster at a higher impact velocity.

  3. 3.

    The impact velocity has a significant influence on the equivalent stress-strain curves; the flow stress including the yield stress of the test tube increases with the increase in the impact velocity. The coefficient C in the JC model for SS304 stainless steel tubes can be regarded as a coefficient (0.029~0.032) at lower impact velocities (<10 mm/s), which is much smaller than that (0.081) at the highest impact velocity of 150 mm/s (Table 3). This indicate the coefficient C in the JC model for the material can be constant at a certain range of impact velocity

  4. 4.

    The bulge heights increase with the increase in hydraulic pressure and the test tube deforms faster at lower impact velocities.