Introduction

Due to its excellent stiffness-to-weight and strength-to-weight ratios, metallic foams with a cellular structure are used in a wide range of applications, such as structural sandwich panels, energy absorption devices and acoustical damping panels [1]. Among of metallic foams, aluminum foams have much low density and are attractive materials for constructional purpose used as the cores of sandwich panels, shells, and tubes. To better understand its mechanical behaviors, a large amount of research had been conducted on aluminum closed-cell or open-cell foams experimentally by means of optical techniques. For example, Bastawros et al. [2] investigated the evolution of plastic deformation of aluminum alloy upon axial compression through a digital image correlation procedure. In the work presented in [3, 4], X-ray micro-tomography was employed to collect three-dimensional images of aluminum closed-cell foam in compressive deformation experiment and to characterize the internal structure in three dimensions. Regarding to dynamic experiment, several researchers employed digital image correlation (DIC) together with high-speed photography to study strain-rate effects of the aluminum foam in the Split-Hopkinson Pressure Bar test [5, 6]. Other mechanical data is either needed for the evaluation of specific applications or more generally to build databases which are needed for computer aided modelling of cellular materials. For example, Young’s modulus is an essential parameter for modelling of aluminum foam in Finite Element Method (FEM). The challenges for aluminum Foam and its sandwich structure used in aerospace or automotive environment include the long exposure time to flutter. Due to its cellular structure and inhomogeneous with an unknown mass distribution, it is difficult to obtain the effective (average) Young’s modulus and resonant mode shapes by finite element method. Hence it is very important to call for an effective and faster investigation method for evaluating dynamic behavior without damage.

As we know, the vibration analysis is one of the simply methods to determine Young’s modulus. Optical techniques like holography and laser Doppler vibrometry (LDV) are well suited for measuring vibrations. Time-averaged interferometric holography is a non-destructive and full-field method for vibration analysis with a sensitivity of vibration amplitude of 0.1 μm. It is a popular technique for inspection of defects in bonded structures, turbine blades, etc. [7, 8]. LDV can also characterize the dynamic response of an entire surface, however, it needs 2-D fast-scan mirrors and it is time-consuming. With the advent of speckle interferometry, time-averaged holographic interferometry was taken over by electronic speckle pattern interferometry (ESPI), also called TV holography [9]. When time-averaged ESPI method is applied to vibration analysis, because of DC signal component in the interference terms, the fringe visibility is very poor. Therefore, Creath and Slettermoen [10] proposed digital subtraction method for DC removal and fringes’ visibility enhancement. In the subtraction method, one speckle pattern is first recorded as the reference image before vibration and continuously subtracted from the incoming speckle pattern after vibration. To increase the visibility of the fringe pattern and reduce environmental noise, Wang et al. [11] introduced an amplitude-fluctuation ESPI method (AF-ESPI) for measuring resonant vibration. In AF-ESPI method, two speckle patterns corresponding to the object in vibrating state are captured and the fringe pattern is generated by digital subtraction and can be observed in quasi real time. As presented in [11], the intensity of fringe pattern from AF-ESPI method is a first-order Bessel function. On the other hand, Ma and Huang [12] used a zero-order Bessel function to describe intensity of fringe pattern reproduced by AF-ESPI method. One may mind that there is a little discrepancy between these two functions representing the contour of vibration amplitude reconstructed in AF-ESPI technique.

In this paper, the terminology of laser phase noise is used to explain the fringe pattern reproduced in so-call AF-ESPI method. Subsequently, ESPI and real-time subtraction with self-refreshed image method is employed for mode shape determination of closed-cell aluminum foam cantilever beam under out-of-plane and in-plane vibration, respectively. Based on the model of Euler-Bernoulli beam, Young’s modulus of the aluminum foam beam is obtained using vibration analysis accordingly.

Theory

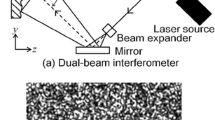
The schematic of out-of-plane and in-plane vibrating study using ESPI method is shown in Fig. 1(a) and (b), respectively. The surface of vibrating object, illuminated by laser light from different directions, is recorded by a CCD camera as a speckle interference pattern. Vibrating surfaces may be studied using either time-averaged or real time digital subtraction speckle interferometry. The intensity of speckle pattern formed by interference between object and reference light waves describes as follows. For the simplicity of illustration, we only introduce the theory of ESPI for out-of-pane vibration measurement as presented in Fig. 1(a).

Fig. 1
figure 1

Schematic of optical setup for (a) out-of-plane; and (b) in-plane vibrating measurement

Full size image

Time-Averaged ESPI

As shown in Fig. 1(a), the laser beam was diverged by a beam-splitter as two beams as reference and object beams for illuminating the reference object and the vibrating object, respectively. If the vibrating object at rest, the interference pattern is formed by the addition of wave-fronts from the surface of the reference object and from the surface of the vibration object at rest. The intensity recorded by CCD camera is given by

$$ I\left(x,y\right)={I}_{\mathrm{o}}+{I}_r+2\sqrt{I_o{I}_r}\cos \left[\phi \left(x,y\right)\right] $$
(1)

where I o is the object beam intensity, I r is the reference beam intensity, ϕ(x, y) is the phase difference between object and reference beams and is time-independent [10].

Assuming the object is excited with sinusoidal vibration at a circular frequency ω, the vibrating object presents a continuum of surface deformations. A unique interferometric pattern is associated with each state of the surface for any particular point in time during the vibrating cycle. Hence, the image of the vibrating object observed is visual time average of this continuum set of interference patterns. Because the refresh time of CCD sensor is usually multiple vibration periods, the image obtained by CCD camera shown in Fig. 1 may be thought of as a continuum set of exposures. The end result is represented as

$$ I\left(x,y,t\right)=\frac{1}{\tau }{\int}_0^{\tau}\left[{I}_o+{I}_r+2\sqrt{I_o{I}_r}\cos \left(\phi \left(x,y\right)+\varphi \left(x,y,t\right)\right)\right] dt $$
(2)

Where τ is the CCD refreshing time, φ(x, y, t) is the phase related to out-of-plane displacement of the specimen at point (x, y). From the optical setup shown in Fig. 1(a), the phase φ(x, y, t) for normal illumination is given as

$$ \varphi \left(x,y,t\right)=\frac{4\pi A\left(x,y\right)\cos \left(\omega t\right)}{\lambda } $$
(3)

Here, A(x, y) is the amplitude of vibration and λ is wavelength of laser light. In time-averaged ESPI method, CCD sensor is exposed for a period of time τ much greater than the period of vibration, the intensity of speckle pattern can be reproduced as [13]

$$ I\left(x,y,\mathrm{t}\right)={I}_o+{I}_r+2\sqrt{I_o{I}_r}{J}_0\left(\frac{4\pi A\left(x,y\right)}{\lambda}\right)\cos \phi \left(x,y\right) $$
(4)

where J 0 is a zero-order Bessel function of the first kind as illustrated in Fig. 2A. It can be seen from (equation (4)) and Fig. 2A that the result from time-average ESPI method is a speckle fringe pattern related to the surface vibration, in which the fringe lines represent contours of constant vibration amplitude. The nodes of the vibrating object (for regions at rest) yield the maximum possible value for zero-order Bessel function, and therefore appear brighter than any other feature in the speckle pattern, while regions in motion (antinodes) will appear dark. In time-averaged ESPI method, due to DC signal component, the fringe visibility is very poor. Hence, Creath and Slettermoen [10] proposed digital subtraction method for DC removal and fringes’ visibility enhancement.

Fig. 2
figure 2

Curves of Bessel functions. A, J 0(m), B, 1-J 0(m), and C, J1(m)

Full size image

Subtraction Method

In the traditionally time-averaged ESPI method for vibration analysis, a single frame of the speckle pattern is recorded. In this case, in order to improve visibility of the fringe pattern, the I r and I o terms in (equation (4)) will be cancelled by DC filtering, and the fringe pattern is rectified, and then squared.

Since I r and I o are time independent, it can be assumed that they will not change between the two recorded speckle patterns. They can be cancelled by continuously subtracting a reference frame from the time-averaged data frames of the vibrating object. The subtraction ESPI method generally employs the frame captured the vibrating object at rest as the reference and subtracts from incoming frames of the vibrating object. It yields the fringe pattern expression for out-of-plane vibration as

$$ I\left(x,y\right)=2\sqrt{I_o{I}_r}\mid \cos \phi \left(x,y\right)\left[{J}_0\left(\frac{4\pi A\left(x,y\right)}{\lambda}\right)-1\right]\mid $$
(5)

If the object is vibrating sinusoidally, the intensity of speckle fringe pattern by subtraction method is proportional to a function of 1-J 0(m) as shown in Fig. 2B. Thus vibration nodes will appear to be dark, and subsequent fringe orders will have a minimum greater than 0 and modulate about a value of 1.

Real-Time Subtraction with Self-Refreshed Frame Method

In the time-averaged and subtraction methods, the dynamic range of the ESPI does not reach that of holographic films so that only about 5–10 fringes can be seen, depending on the gamma correction, level of digitization and noise performance of the system. To produce good fringe contrast, the slowly varying intensity must be removed by high-pass filtering. This will significantly enhance the fringe contrast. However, there is residual noise owing to the self-interference of both the object and the reference beams with themselves that is left after filtering.

In order to enhance the contrast of the speckle fringe pattern and reduce the environmental noise, Wang et al. [11] proposed an amplitude-fluctuation ESPI (AF-ESPI) method for vibration measurement. In the AF-ESPI method, the reference frame is recorded in a vibrating state and then repeatedly subtracted from other time-averaged speckle patterns of the vibrating object. In the viewpoint of AF-ESPI method, owing to the environmental or electronic noises of the vibration system, the vibration amplitude would be varied slightly during each cycle even for a periodic vibrating motion. According to literature [11], the brightness distribution B(x, y) of AF-ESPI method is expressed as

$$ B\left(x,y\right)\propto 2\sqrt{I_{\mathrm{o}}{I}_r}\mid {J}_1\left[\Big(\frac{4\pi A\left(x,y\right)}{\lambda}\right]\cos \phi \left(x,y\right)\mid $$
(6)

where J 1 is a first-order Bessel function of the first kind as illustrated in Fig. 2C. Based on (equation (6)), nodal area of vibrating surface will appear dark. However, experimental outcomes shown in [11] is in conflict with the prediction. Therefore, Ma and Huang [12] carried out a modification of the expression for AF-ESPI method as

$$ B\left(x,y\right)=\frac{\sqrt{I_o{I}_r}}{2}\mid \cos \phi \left(x,y\right){\left(\frac{4\pi \varDelta A}{\lambda}\right)}^2{J}_0\left[\Big(\frac{4\pi A\left(x,y\right)}{\lambda}\right]\mid $$
(7)

where ΔA stands for the drift of amplitude in out-of-plane vibration. The function of fringe intensity is modulated by a zero-order Bessel function. However, the amplitude of nodal regions is null and ΔA should be equal to zero too. It will affect the brightness of the nodal area. Hence, this analysis still failed to agree with the experimental results.

As we know that the output of well-stabilized laser is affected in two ways owing to quantum noise. One is the amplitude of the laser output is caused to fluctuate about its stabilized value, and another is the phase of laser output to change with time in a random fashion. This random phase fluctuation determines the theoretical minimum linewidth of well-stabilized laser. In two-beam interferometers, such as Michelson interferometers, coherent interference is the basic mechanism of the nonlinear conversion process of phase to intensity modulation. Due to the laser phase noise, the interferometric phase changes randomly with time. Consequently, the intensity exhibits some random fluctuations.

In practice, as shown in Fig. 1, it is difficult to ensure the length of the two arms to balance perfectly. According to the analysis of Armstrong [14] and Petermann et al. [15], when the delay between the two arms of the interferometer is far less than linewidth of laser source, the influence of laser intensity noise can be neglected. Phase noise of laser is dominant and it is the time-varying random phase of the light [16].

Owing to laser phase noise, the phase ϕ(x, y) shown in (equations (1), (2) and (4)) is not time-independent. It will slightly fluctuate with time. For the sake of simplicity, the intensity of the reference frame from time-averaged method is still represented by (equation (4)), and those of the incoming frames of the vibrating object is given by

$$ G\left(x,y,\mathrm{t}\right)={I}_o+{I}_r+2\sqrt{I_o{I}_r}{J}_0\left(\frac{4\pi A\left(x,y\right)}{\lambda}\right)\cos \left[\phi \left(x,y\right)+\delta (t)\right] $$
(8)

Where δ(t) stands for laser phase noise, it is small in amount and time-varying randomly. Hereby, it will yield the fringe pattern expression for out-of-plane vibration by subtraction (equations (8)) from (equation (4)),

$$ {\displaystyle \begin{array}{l}I\left(x,y\right)=\mid G\left(\left(x,y,t\right)\right)-I\left(x,y,t\right)\mid \\ {}\kern2.5em =4\sqrt{I_o{I}_r}\mid \sin \left[\right(\phi \left(x,y\right)+\frac{\delta (t)}{2}\Big]\sin \frac{\delta (t)}{2}\mid \cdot \mid {J}_0\left(\frac{4\pi A\left(x,y\right)}{\lambda}\right)\mid \end{array}} $$
(9)

Here, laser phase noise in the reference represented as (equation (4)) is set to zero for simplification. Hence, the speckle fringe pattern represents the contour of vibration amplitude related through the absolute of the Bessel function of zero order. The nodes of the vibrating object yield the maximum possible value for the absolute zero-order Bessel function, and therefore appear brighter than any other feature in the speckle pattern. The dark fringes, at which the intensity drops to zero, correspond to the zeros of the function |J 0(m)|.

Young’s Modulus Determination by Vibration Analysis

Measurements of aluminum foam properties are difficult when compared to pure aluminum. One method for finding the modulus of elasticity of metal foam is from frequency analysis of a cantilever beam. If the cantilever beam studied is long and thin, the Euler-Bernoulli theory can be used to describe its vibrating response [17]. For a long slender cantilever beam with a uniform symmetric cross-section, when it vibrates transversely as illustrated in Fig. 3, the natural frequencies of the vibrating beam are computed from the Euler-Bernoulli theory as

$$ {\omega}_n=\frac{\beta_n^2}{l^2}\sqrt{\frac{EI}{\rho A}}\kern2.75em \left(n=1,2,3,\cdots \right) $$
(10)
Fig. 3
figure 3

A cantilever beam under transverse vibration

Full size image

Where β 1 = 1.875, β 2 = 4.694, β 3 = 7.855, β 4 = 10.996, et al. l is the beam length, E is the Young’s modulus of the material, I is the moment of inertia of the beam cross section about the y axis (I = bt 3/12, b the width and t the thickness of the beam), ρ is the mass density and A is the cross-sectional area of the beam. The natural frequencies of the vibrating beam may be measured experimentally, thus the Young’s modulus of the material can be determined based on (equation (10)).

Experimental and Numerical Analog Comparison

Specimen Preparation

The optical system for vibration measurement is illuminated in Fig. 1. As shown in Fig. 4, the tested specimen used in this paper is a closed-cell aluminum foam cantilever beam with a porosity of 87.6% and a size of 180×40×20mm3. In order to keep an ideal clamped boundary without damaging the cellular structure during vibration, two pure aluminum plates with a size of 30×40×1 mm3 are attached to the top and bottom faces at one end of the beam using expoy. When the specimen is clamped as a cantilever beam, the size of its free part is 150×40×20 mm3. That is to say, the beam used in this study, is l = 150 mm long, b = 40 mm wide, and t = 20 mm thick. Generally speaking, if the length l is much larger than the thickness t, for example the ratio of them is larger than 5, the beam can be assumed as very slender. This assumption leads to a good approximation by using the Euler-Bernoulli theory.

Fig. 4
figure 4

Closed-cell aluminum foam cantilever beam (a) top, (b) bottom, and (c) side views respectively

Full size image

As illustrated in Fig. 3, when the beam bends along x-direction in the plane x-z plane, it will deflect into a curve. The deflection deformation can be measured by using the optical setup shown in Fig. 1(a). If the beam vibrates along x-direction or y-direction in x-y plane, the deformation is in the form of in-plane displacement, it can be determined using the optical setup shown in Fig. 1(b). In this case, the laser beam passes through the beam splitter and is divided into two parts, this two beams of light are expanded and symmetrically illuminated on the surface of the object with irradiation angle θ, then two beams of light produced by diffuse reflection interference on the target surface of CCD camera. The phase φ(x, y, t) appeared in (equation (2)) is given by

$$ \varphi \left(x,y,t\right)=\frac{4\pi A\left(x,y\right)\cos \left(\omega t\right)\sin \theta }{\lambda } $$
(11)

In this study, the harmonic out-of-plane displacement generated by a small PZT actuator attached to the bottom face of the beam as shown in Fig. 4(b). The in-plane deformation is generated by another PZT actuator attached to one side face of the beam as shown in Fig. 4(c). Thanks to the repetition of the PZT excitation, harmonic wave-field is formed in the beam. The out-of-plane and in-plane vibration modes of the top surface of the tested beam can be obtained by the ESPI experimental systems as illustrated in Fig. 5(a) and (b), respectively.

Fig. 5
figure 5

The experimental systems for (a) out-of-plane; and (b) in-plane vibrating measurement, respectively

Full size image

Numerical Analogy

Because of its complex cellular structures, it is difficult to establish closed-cell aluminum foam beam’s model and perform vibration analysis by the finite element method (FEM). Hence, as an analogy for a certain degree, the FEM is employed to yield the first 7 orders out-of-plane vibration mode shapes and the first 4 orders in-plane vibration mode shapes of one pure aluminum beam with the same size as the tested aluminum foam specimen. The physical parameters of the finite element model of the pure aluminum cantilever beam are Young’s Modulus E = 70Gpa, Poisson’s ratio ν = 0.33, mass density ρ = 2700 kg/m3.

All the numerical results of resonant mode shapes are calculated by the commercial code ANSYS package in which solid element 186 is selected. Fig. 6 shows the first 7 order out-of-plane resonant mode shapes of the pure aluminum cantilever beam obtained by the FE method. The first 4 order in-plane vibration mode shapes results of the FEM simulation analysis present in Fig. 7.

Fig. 6
figure 6

First 7 order out-of-plane vibration mode shapes obtained by the FEM simulation

Full size image
Fig. 7
figure 7

First 4 order in-plane mode shapes of aluminum beam vibrating components in x- and y-directions result from the FEM analysis, respectively

Full size image

Experimental Results and Analysis

  1. (1).

    Out-of-plane vibration measurement

The aluminum foam beam is clamped at the left end for a length of 30 mm and is excited through forced vibration at the bottom using a PZT attached to the beam with adhesive as shown in Fig. 4(b). Tests for deflection vibrating were conducted using a MSL-FN-671 nm laser and with a 1280×1024 pixel monochrome CCD camera manufactured by IDS Inc. The reference image of the vibrating beam was acquired and real-time subtracted incoming frames, and yielded speckle fringe pattern directly shown on the PC screen.

Figure 8 shows the specimen’s first seven modes of vibration obtained by the ESPI method. The speckle fringe pattern shown in Fig. 8(a) represents the first flap, the beam oscillates back and forth of its free end relative to the root. Figure 8(b), (d) and (f) are second, third and fourth flap, respectively. The first torsion, where each corner of the beam tip oscillates in opposite directions, twisting the beam along its central axis, is shown in Fig. 8(c). Comparing with the mode shapes shown Fig. 6, it can be seen that, except for the second flap, there is no significant demarcation between the fringe patterns in the case of experimental and FEM results. It is obvious that the fringe contrast obtained by real-time subtraction with self-refreshed frame method improves greatly. For example, the total number of fringes can reach about 45 presenting in Fig. 8(d). Figure 9 provides a quantitative comparison of vibration amplitude obtained by experimental measurement and theoretical prediction, respectively. According to (equation (9)), the brightest fringes are the nodes of the vibrating object and the dark fringes, at which the intensity drops to zero, correspond to the zeros of the function |J 0(m)|. The digit indicating dark fringes order is labelled on the image of the second flap as shown in Fig. 9(a). Base on the theoretical prediction, numerical simulation and experimental measurement, the vibration amplitude distribution along the central line is depicted in Fig. 9(b), with well agreement between the two results.

Fig. 8
figure 8

Out-of-plane vibrating responses at frequencies (a) 346 Hz, (b) 2062 Hz, (c) 2122 Hz, (d) 5289 Hz, (e) 6280 Hz, (f) 9321 Hz and (g) 10,728 Hz

Full size image
Fig. 9
figure 9

Comparison of the second out-of-plane mode, (a) Mode shape from FEM and experiment; (b) the displacement distribution along the central line of the beam obtained by experiment and theory

Full size image
  1. (2).

    In-plane vibration measurement

Figures 1(b) and 5(b), respectively, present the optical setup and experimental system for real-time subtraction ESPI system used to measure in-plane vibration. The aluminum foam beam is still clamped at the left end for a length of 30 mm and is excited through forced vibration at the side using a PZT attached to the beam with adhesive as shown in Fig. 4(c). Tests for in-plane vibrating were conducted using a green light laser with a wavelength of 532 nm. The laser light illuminated the specimen at a symmetrical angle of 30 degree. The reference image of the vibrating beam was acquired by a monochrome CCD camera with resolution of 1280×1024 pixels and real-time subtracted from incoming frames, and yielded speckle fringe pattern.

Figure 10(a)-(d) show the first 4 order mode shapes of the test beam vibrating along x-direction, and Fig. 10(e)-(h) present the first 4 order mode shapes of the beam vibrating along y-direction, respectively. Because the moment of inertia I of the test beam cross section about the z axis (I z  = tb 3/12) is larger than that about the y axis (I y  = bt 3/12), the exciting frequency of in-plane vibration is higher than that of out-of-plane vibration response. Based on (equation (10)), for the test beam studied in this paper, the fundamental frequency of in-plane flap is double that of out-of-plane. It is obvious that the experimental result is well agreed with the theory prediction from 647 Hz/346 Hz = 1.870. Due to its higher bending stiffness, the response amplitude of in-plane vibration is smaller than that of out-of-plane under the same exciting force. Hence the number of fringes shown in Fig. 10 is less than that in Fig. 8. In contrast to the mode shapes shown in Fig. 7, the experimental results presented in Fig. 10 are in excellent agreement with the theory prediction.

Fig. 10
figure 10

In-plane vibrating responses at frequencies (a) 647 Hz, (b) 3337 Hz, (c) 7880 Hz, (d) 12,942 Hz, (e) 647 Hz, (f) 3337 Hz (g) 7880 Hz and (h) 12,942 Hz

Full size image

It needs to point out that each resonant mode of in-plane vibration has one mode shape with the U and V configurations. Owing to the limitation of testing system shown in Fig. 1(b), it can only measure one modal component at a time. Therefore, the specimen needs to rotate 90 degree about z-axis and measure another component under the same controlled condition after one configuration is acquired.

  1. (3).

    Measurement of Young’s modulus

Owing to its cellular structure and inhomogeneous with an unknown mass distribution, it is difficult to obtain the effective Young’s modulus of aluminum foam by conventional experimental methods, such as stress-strain analysis of uniaxial compression or tension testing. Therefore, alternative measurement methods need to develop. Vibration of cantilever beams is a simple and effective method. If the following assumptions of a slender cantilever beam is fulfilled: small deflections, linearly elastic and uniform cross-section, the Euler-Bernoulli theory can be employed to determine the resonant frequencies of flap as given by (equation (10)). From the previous experimental results, the maximum amplitude of the tested specimen deflection is about several micrometers as presented in Fig. 9(b), here it is reasonable to calculate the Young’s modulus of aluminum foam using (equation (10)).

Equation (10) is used to measure modulus of elasticity of the aluminum foam from the fundamental frequency as given by

$$ E=\frac{\rho A{\omega}_1^2{l}^4}{\beta_1^4I} $$
(12)

Here, ρ = (1–0.876)×2700kg/m3 = 334.8 kg/m3, A = 0.02×0.04 = 8×10−4 m2, ω 1 = 346×2π = 2174/s, l = 0.15 m, β 1 = 1.875, and I the moment of inertia of the beam cross section about the y axis is 2.667×10−8m4. It yields E value of 1.944GPa.

Ashby and Evans et al. introduced extensive analytical, numerical and experimental works on metal foams for the Young’s modulus E and compressive strength in [18], and their analytical solution for E is given as

$$ \frac{E}{E_m}=0.3163\left(\frac{\rho }{\rho_m}\right) $$
(13)

where E m and ρ m are the elastic modulus and mass density of the parent material, respectively. It is need to note that (equation (13)) predicts the upper bound elastic moduli of closed-cell foams whose relative density is less than 20%. For pure aluminum E m  = 69 GPa and ρ m  = 2700 kg/m3, and the relative density is 12.4% of the close-cell aluminum foam used in this research. Equation (13) gives an E of 2.704 GPa. This value is 28% higher than that of the present study. Considering the microstructural defects and local density fluctuation will attenuate the E, the result of vibration analysis for Young’s modulus measurement is well agreed with the prediction in a certain degree.

Conclusion

Based on the laser phase noise, a reasonable representation of speckle fringe pattern generated by real-time subtraction ESPI method for vibration measuring is proposed. The vibration response of closed-cell aluminum foam cantilever beam is investigated by speckle interferometry. The first seven order deflection vibrating mode shapes and two components of the first four order in-plane vibration mode shapes are obtained. Comparing with mode shapes of the pure aluminum beam from the FEM simulation, it can be found that the irregular shape of cells and its random distribution in space does not influence the cantilever beam’s vibration mode shapes at all. This paper also demonstrates the capability of vibration analysis for metal foams Young’s modulus measurement using the ESPI method. Owing to the nature of noncontact, full-field, and results visualization, vibration of cantilever beams cannot be used to determine the modulus of material elasticity only, but also be employed to measure damping properties [19].