Bayesian Inference in a Structural Model of Family Home Prices

Abstract

We review the implications of an intertemporal representative consumer model for the analysis of housing prices, describing the choice between non-housing and housing consumption, and provide an explanation for the excess return of housing over the riskless rate based on weakly separable preferences. Further considerations are presented regarding the role of liquidity constraints. A Bayesian structural vector autoregression predicts relations between real rent growth, interest rates and housing prices consistently with the representative consumer model. The orthogonalized impulse response functions show, that housing prices are relatively unresponsive to shocks to fundamental value. The logarithmic rent/price ratio increases or does not significantly change following shocks to the real rent growth and relative bill rates. The dynamics of housing prices over the business cycle is mainly determined by financial factors. A shock to the natural logarithm of the rent/price ratio does not have significant predictive properties for subsequent real rent growth and relative bill rates. Moreover, the logarithmic rent/price ratio is a highly persistent variable displaying momentum and long term reversal.

1 Introduction

Housing is an important component of household wealth. Estimates released by the Italian National Institute of Statistics (Istat) and the Bank of Italy imply, that in the 2005–2021 period dwellings on average represented a fraction of 53.9 per cent of net household wealth. In the same period the average ratio between net household wealth and gross disposable income was equal to 8.6.

In the field of the consumption function studies have traditionally described the role of disposable income and household wealth as conditioning variables. Further, for the purposes of the analysis of the business cycle, gross disposable income can be modelled as a function of aggregate consumption. As shown in contributions by Campbell and Cocco (2007) and Case et al. (2013), the modelling of aggregate consumption can be improved distinguishing between financial and housing wealth.

Housing price dynamics is an important factor for the determination of housing wealth. Moreover, it may have an impact on the business cycle also through its effects on residential investment. Further, housing wealth may be deployed as collateral in lending operations. Therefore, housing price changes over the business cycle entail corresponding variations in the collateral value of dwellings and in this way contribute to the definition of the borrowing constraints faced by households in the real estate lending market. Some important features of the real estate market, as those relating to mortgage choice, are described in Campbell and Cocco (2003), Fabozzi et al. (2008) and Shiller et al. (2019) among other works.

In the present work we analyse the implications of an intertemporal representative consumer model. We follow an approach that has formerly been applied in Lustig and Van Nieuwerburgh (2005) and Piazzesi et al. (2007) for the study of asset prices, who consider the consequences of the assumptions regarding the separability of preferences and collateral constraints. We model the representative consumer choice between non-housing and housing consumption and provide an explicit formulation of the cross-equation restriction that must hold in the housing market, due to the no arbitrage condition, when rentals and owner occupied housing services are not perfect substitutes.

Our approach is also related to the long tradition of research in consumer behaviour reviewed in Muellbauer (2012, 2022), where housing prices are viewed as the result of market equilibrium, relating the user cost of housing to consumption through an inverted demand function. The user cost of housing is the cost incurred by economic agents for the consumption of housing services in each time period. In turn, the cost of housing services may be defined as proportional to the housing price and accounts for the opportunity cost of equity, mortgage interest, maintenance and repair of the dwelling and the capital gains due to housing price changes over time.

In the econometric application quarterly housing prices data for the 1996Q1-2019Q3 period support an explanation of housing risk premia based on weakly separable preferences, because of the relatively low variance of consumption. We provide some further discussion on the additional effects that may result from financial market imperfections.

The main propositions holding in the representative consumer economy allow us to identify a Bayesian structural vector autoregression (BVAR) model of the relation between real rent growth, interest rates and housing prices. Following recent research in Baumeister and Hamilton (2015, 2018) we estimate the model from the structural form. Prior assumptions are made with regard to the contemporaneous relations between the endogenous variables, according to the predictions of the representative consumer model. The posterior distributions compiled on the basis of the 1996Q1-2019Q3 sample imply, that our priors are relatively informative for some parameters, while for the remaining ones more information is provided by the available observations.

The orthogonalized impulse response functions deliver robust evidence with regard to the informational content of housing prices for the patterns of future real rent growth and interest rates. Housing prices are a persistent variable, relatively unresponsive to real rent growth and interest rate shocks. Moreover, there is excess sensitivity to the news regarding fundamental value conveyed by shocks to the logarithmic rent/price ratio.

The results overall suggest that financial factors have a significant role for the business cycle, through their effects on housing price dynamics. This consideration acquires even more relevance with reference to the sample period of the present study, which features several periods of economic expansion followed by crises and contractions.

The remainder of the work is structured as follows. Section 2 describes the representative consumer model. Section 3 presents the data. Section 4 reviews the relations between excess returns in housing markets and the volatility of the stochastic discount factor. Section 5 analyses the consequences of assumptions regarding separability of preferences and collateral constraints. Section 6 defines the Bayesian structural vector autoregression model. Section 7 illustrates the estimation results. Some conclusions are drawn in Sect. 8.

2 A Representative Agent Economy

We review the intertemporal model that was introduced in Lustig and Van Nieuwerburgh (2005) and Piazzesi et al. (2007) for the analysis of asset prices. In the representative agent endowment economy, consumer preferences are defined as a function of non-housing and housing consumption: $X_{ct}$ and $X_{ht}$. Agents optimize consumption subject to a dynamic budget constraint. The assumptions regarding the separability of preferences between non-housing and housing consumption imply a multiplicative form for the stochastic discount factor and have consequences for the relation between real gross asset returns and riskless rates. An explanation for the excess return of assets over the riskless rate can be provided for values of the intertemporal elasticity of substitution consistent with the estimates resulting from econometric studies of the consumption function. Further, in the presence of financial market imperfections and collateral constraints the stochastic discount factor compounds the effects of an additional multiplicative term, which entails lower riskless rates.

Denoting with $u\left( X_{ct},X_{ht}\right)$ the single period utility function, we assume it is increasing and quasiconcave: $u_{X_{c}}\left( X_{ct},X_{ht}\right) \ge 0$ and $u_{X_{h}}\left( X_{ct},X_{ht}\right) \ge 0$. In each time period housing consumption is a function of rentals and services from the housing stock: $X_{nt}$ and $X_{st}$. We assume an homothetic housing aggregator function $X_{ht} =h\left( X_{nt},X_{st}\right)$ increasing and quasiconcave in its arguments: $h_{X_{n}}\left( X_{nt},X_{st}\right) \ge 0$ and $h_{X_{s}}\left( X_{nt},X_{st}\right) \ge 0$.¹

The analysis of the intertemporal optimization problem proceeds first under the assumption of perfect financial markets, describing the relation between the dynamic equations of the optimization model and the no arbitrage conditions in the housing market.

In each period the representative agent maximizes expected utility over an infinite horizon, we assume the utility function is additively separable in the time dimension:

$$\begin{aligned} U =E_{t}\sum \limits _{\tau =0}^{ +\infty }\rho ^{\tau }u\left( X_{ct +\tau } ,X_{ht +\tau }\right) \end{aligned}$$

(2.1)

where $0<\rho <1$ is the intertemporal rate of time preference and $E_{t}$ defines expectations conditional on period t information.

We denote with $Y_{t}$ the representative consumer income and suppose the economy has N financial assets to be used for savings, whose traded quantities in period t are $X_{it}$ for $i =1,\ldots ,N$. The consumer budget constraint is:

$$\begin{aligned} X_{ct}= & {} Y_{t} +\sum \limits _{i =1}^{N}\left( P_{it} +D_{it}\right) X_{it -1} \nonumber \\{} & {} +P_{st}X_{st -1}\left( 1 -\delta \right) -P_{nt}X_{nt} \nonumber \\{} & {} -P_{st}X_{st} -\sum \limits _{i =1}^{N}P_{it}X_{it} \end{aligned}$$

(2.2)

where $0<\delta <1$ is the constant housing depreciation rate, $P_{nt}$ and $P_{st}$ are the housing rental and stock prices, $P_{it}$ and $D_{it}$ are the price and dividend of asset i in period t. Representative consumer income, housing rental and stock prices, asset prices and dividends are measured in non-housing consumption units.

In each period of time consumer wealth is composed of income, the sum of the value and dividends of financial assets carried forward from the previous period and the value of housing stock holdings. Representative agent wealth is allocated between consumption and savings. The role played by housing as an asset and a consumption good introduces an important form of temporal dependence in the economy, which can be described analysing the solution to the optimization model.

The first order conditions include the equality of the marginal utility of consumption in periods t and $t +1$:

$$\begin{aligned} u_{X_{c}}\left( X_{ct} ,X_{ht}\right) P_{it} =\rho E_{t}\left[ u_{X_{c}}\left( X_{ct +1} ,X_{ht +1}\right) \left( P_{it +1} +D_{it +1}\right) \right] \end{aligned}$$

(2.3)

Equation (2.3) holds for $i =1,\ldots ,N$, as each asset i can be used to discount utility between time periods.

Moreover, a condition equating the marginal rate of substitution between non-housing and housing rental consumption and the relative price of housing rents applies:

$$\begin{aligned} u_{X_{c}}\left( X_{ct} ,X_{ht}\right) P_{nt} =u_{X_{h}}\left( X_{ct} ,X_{ht}\right) h_{X_{n}}\left( X_{nt} ,X_{st}\right) \end{aligned}$$

(2.4)

In addition, an equality between the marginal utility of non-housing consumption in period t and the sum of the marginal utility of owner occupied housing and of non-housing consumption in period $t +1$ is satisfied:

$$\begin{aligned} u_{X_{c}}\left( X_{ct},X_{ht}\right) P_{st}= & {} u_{X_{h}}\left( X_{ct},X_{ht}\right) h_{X_{s}}\left( X_{nt},X_{st}\right) \nonumber \\{} & {} +\rho E_{t}\left[ u_{X_{c}}\left( X_{ct +1},X_{ht +1}\right) P_{st +1}\left( 1 -\delta \right) \right] \end{aligned}$$

(2.5)

Following the analysis of the consumption function in Deaton (1992) we note, that the system of dynamic equations (2.3)–(2.5) with the optimization model transversality conditions admits two interpretations. Conditional on the representative agent income and non-housing consumption, housing and asset prices (2.3)–(2.5) represent a system of stochastic non-linear first order difference equations, which can be used to study the dynamics of the real consumption variables $X_{ct}$, $X_{nt}$ and $X_{st}$. Conversely, conditioning on the stochastic processes for the real variables the system describes the dynamic motion of the non-housing consumption, housing and asset price variables.²

In the present work we take the second perspective and analyse the system of equations (2.3)–(2.5) as a pricing model. The N equations in (2.3) correspond to the ones that usually feature in the consumption based capital asset pricing model (CCAPM). Dividing both sides of (2.3) with the term on its left-hand side, defining the real gross return of asset i as $1 +R_{it +1} =\left( P_{it +1} +D_{it +1}\right) /P_{it}$, the stochastic discount factor as $M_{t +1} =\rho u_{X_{c}}\left( X_{ct +1},X_{ht +1}\right) /u_{X_{c}}\left( X_{ct},X_{ht}\right)$ and rearranging yields:

$$\begin{aligned} E_{t}\left[ M_{t +1}\left( 1 +R_{it +1}\right) \right] =1 \end{aligned}$$

(2.6)

for $i =1,\ldots ,N$.

Equation (2.6) is essentially a no arbitrage condition. From a fundamental result for the analysis of asset markets reviewed in Hansen and Richard (1987) it follows, that no arbitrage implies the existence of a stochastic discount factor $M_{t +1}$ and of a system of equations equivalent to (2.6). The stochastic discount factor is a process positive with probability one in each time period and it is defined almost everywhere in its domain of definition.

Assuming asset N is riskless, from (2.6) we obtain:

$$\begin{aligned} 1 +R_{Nt +1} =1/E_{t}\left( M_{t +1}\right) \end{aligned}$$

(2.7)

Equation (2.7) states that the conditional expected value of the stochastic discount factor is equal to the inverse of the riskless real gross return between periods t and $t +1$.

Further, due to the timing convention for housing and assets, we may define the real gross housing return as: $1 +R_{ht +1} =P_{st +1}/\left( P_{st} -P_{nt}\right)$. The assumption that the no arbitrage condition holds in the housing market, results in a pricing equation analogous to (2.6):

$$\begin{aligned} E_{t}\left[ M_{ht +1}\left( 1 +R_{ht +1}\right) \right] =1 \end{aligned}$$

(2.8)

In Eq. (2.8) the housing stochastic discount factor accounts for depreciation: $M_{ht +1} =M_{t +1}\left( 1 -\delta \right)$.³

In the representative agent economy the stochastic discount factor is equal to the ratio between non-housing consumption marginal utility in periods $t +1$ and t. Equations (2.4), (2.5) and (2.8) therefore imply the following cross-equation restriction between rentals and services from the housing stock:

$$\begin{aligned} h_{X_{n}}\left( X_{nt} ,X_{st}\right) =h_{X_{s}}\left( X_{nt} ,X_{st}\right) \end{aligned}$$

(2.9)

From Eq. (2.9) and the assumption of homotheticity of the housing aggregator function it follows, that in equilibrium the ratio between rentals and services from the housing stock $X_{nt}/X_{st}$ must be constant.

In order to interpret this result notice, that no arbitrage implies that the consumer does not make utility gains by trading rentals for owner occupied services in any time period. When the cross-equation restriction (2.9) holds, Eq. (2.5) defines an equivalence in each time period between rents and the user cost of owner occupied housing: $P_{nt} =P_{st} -E_{t}\left( M_{ht +1}P_{st +1}\right)$.

3 Descriptive Statistics

The econometric application employs the residential property price index series for Italy released on a quarterly basis by the Bank of Italy, which is based on transaction values for both new and existing dwellings. Rents are measured with the actual rentals for housing component of the harmonised index of consumer prices (HICP) released by the Italian National Institute of Statistics (Istat). We use the overall HICP series as a deflator for both the housing price and rent indices. The HICP series have a monthly frequency, comparable quarterly series are compiled as simple arithmetic means of the monthly indices for each quarter in the sample period. The sample period for the analysis runs from 1996Q1 to 2019Q3.

We employ the quarterly estimates of non-durable and services consumption and of actual and imputed rentals for housing in the national accounts series of final consumption expenditure of households, to produce measures of real non-housing consumption, the ratio between non-housing and housing consumption and the corresponding non-housing expenditure share.

Finally, we use Treasury bill and bond rates taken from the Bank of Italy Statistical database (BDS) as indicators of riskless rates. The Treasury bill rate is measured with the monthly gross yield at issue of 12 month BOTs (Buoni ordinari del Tesoro). For the Treasury bond rate we use the gross yield to maturity of 10 year BTPs (Buoni del Tesoro poliennali). The Treasury bill and bond rate series are aggregated at quarterly frequency taking simple arithmetic averages of the monthly figures.⁴

We adopt continuous compounding throughout and, denoting natural logarithms of variables with lower case letters, let $p_{nt} =\log \left( P_{nt}\right)$, $p_{st} =\log \left( P_{st}\right)$ and $x_{ct} =\log \left( X_{ct}\right)$. In addition, defining the expenditure ratio between non-housing and housing consumption as $X_{zt} =X_{ct}/\left[ P_{nt}\left( X_{nt} +X_{st}\right) \right]$ and the non-housing expenditure share $X_{wt} =X_{zt}/\left( 1 +X_{zt}\right)$, we let $x_{zt} =\log \left( X_{zt}\right)$ and $x_{wt} =\log \left( X_{wt}\right)$. Moreover, we denote with $r_{ht +1} =\log \left( 1 +R_{ht +1}\right)$ the real continuously compounded gross housing return rate, with $r_{bt +1}$ and $r_{10yt +1}$ the real continuously compounded Treasury bill and bond rates. We define the real continuously compounded excess return of housing over the Treasury bill and bond rates as $er_{bt +1} =r_{ht +1} -r_{bt +1}$ and $er_{10yt +1} =r_{ht +1} -r_{10yt +1}$ and the term spread as $sr_{t +1} =r_{10yt +1} -r_{bt +1}$. Finally, we denote with $rel_{t +1}$ the relative bill rate, defined as the difference between the Treasury bill rate and its four quarter moving average, and with $p_{nt} -p_{st}$ the logarithmic transformation of the housing rent/price ratio.

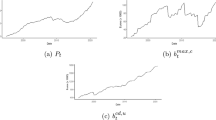
Table 1 and Figs. 1, 2, 3 provide descriptive statistics for the main variables of interest. While real housing prices and rents have remained relatively stable on average, as shown in Fig. 1 there have been significant cyclical movements of the logarithmic transformation of the rent/price ratio. The log rent/price ratio increased in the years leading to the adoption of the Euro currency. Subsequently, the ratio decreased in the economic growth years lasting until the first half of 2007. Following the crisis in the USA subprime mortgage market in the second quarter of 2007, which later led to the worldwide great recession, the log rent/price ratio reversed its course. The increase in the log rent/price ratio continued after the sovereign debt crisis in the second quarter of 2011. In the last few years of the sample period the ratio has remained relatively stable.

Table 1 Descriptive statistics on price and return variables

Fig. 1

Logarithmic rent/price ratio. Note: Natural logarithm of the real housing rent/price ratio. Sample period 1996Q1-2019Q3

Fig. 2

Real gross housing excess return rate. Note: The bold and dashed lines depict the real gross housing excess return rate with respect to the Treasury bill and bond rates. Sample period 1996Q1-2019Q3

Fig. 3

Term spread. Note: Spread between Treasury bond and bill rates. Sample period 1996Q1-2019Q3

In the 1996Q1-2019Q3 period real non-housing consumption expenditure has grown at an average quarterly pace of 0.2 per cent. The real quarterly housing rate of return has been on average equal to 2.7 percentage points, respectively about 10 and 5 times greater than the average Treasury bill and bond rates.

Figure 2 reveals, that the excess returns of housing over the Treasury bill and bond rates have been greater than average in the economic growth years until the first half of 2007 and lower than average in the great recession period and in the sovereign debt crisis years. In the last years of the sample period excess returns have turned above average. Figure 3 depicts an increase of the term spread in the sample period following the USA subprime mortgage crisis.

4 Risk Premia

In order to analyse the relation between real gross housing returns and Treasury bill and bond rates, we find it convenient to use log-linear transformations of (2.6)–(2.8). For this purpose assume, that the stochastic discount factor $M_{t +1}$ and the real gross return $1 +R_{it +1}$ of asset $i =1,\ldots ,N$ have a joint conditional log-normal distribution. Equation (2.6) then implies:

$$\begin{aligned} E_{t}\left( r_{it +1}\right) = -E_{t}\left( m_{t +1}\right) -\frac{1}{2}\left( \sigma _{i}^{2} +\sigma _{m}^{2} +2\sigma _{im}\right) \end{aligned}$$

(4.1)

for $i =1,\ldots ,N -1$.

In (4.1) we denote with $r_{it +1} =\log \left( 1 +R_{it +1}\right)$ and $m_{t +1} =\log \left( M_{t +1}\right)$ the real rate of return of asset i and the logarithmic transformation of the stochastic discount factor and with $\sigma _{i}^{2} =VAR_{t}\left( r_{it +1}\right)$, $\sigma _{m}^{2} =VAR_{t}\left( m_{t +1}\right)$ and $\sigma _{im} =COV_{t}\left( r_{it +1},m_{t +1}\right)$ their conditional variances and covariances, for $i =1,\ldots ,N -1$.

In addition, Eq. (2.7) implies the riskless rate relation:

$$\begin{aligned} r_{Nt +1} = -E_{t}\left( m_{t +1}\right) -\frac{\sigma _{m}^{2}}{2} \end{aligned}$$

(4.2)

Moreover, assuming the housing stochastic discount factor and the real gross housing return have a joint conditional log-normal distribution, Eq. (2.8) implies:

$$\begin{aligned} E_{t}\left( r_{ht +1}\right) -\delta = -E_{t}\left( m_{t +1}\right) -\frac{1}{2}\left( \sigma _{h}^{2} +\sigma _{m}^{2} +2\sigma _{hm}\right) \end{aligned}$$

(4.3)

where $r_{ht +1} =\log \left( 1 +R_{ht +1}\right) ,$ $\sigma _{h}^{2} =VAR_{t}\left( r_{ht +1}\right)$ and $\sigma _{hm} =COV_{t}\left( r_{ht +1},m_{t +1}\right)$ denote the real gross housing return rate, its conditional variance and covariance with the stochastic discount factor and we use the first order approximation $\log \left( 1 -\delta \right) = -\delta$.

Subtracting (4.2) from (4.1) we obtain the real excess return relation for assets:

$$\begin{aligned} E_{t}\left( r_{it +1} -r_{Nt +1}\right) +\frac{\sigma _{i}^{2}}{2} = -\sigma _{im} \end{aligned}$$

(4.4)

for $i =1,\ldots ,N -1$.

According to Eq. (4.4), the excess return of stock $i =1,\ldots ,N -1$ adjusted for the effect of Jensen’s inequality should be equal to the opposite of its covariance with the stochastic discount factor.

Similarly, subtracting (4.2) from (4.3) we obtain the housing real excess return relation:

$$\begin{aligned} E_{t}\left( r_{ht +1} -r_{Nt +1} -\delta \right) +\frac{\sigma _{h}^{2}}{2} = -\sigma _{hm} \end{aligned}$$

(4.5)

Equation (4.5) predicts, that the excess return of housing, adjusted for both depreciation and Jensen’s inequality, should be equal to the opposite of its covariance with the stochastic discount factor.

The Cauchy–Schwarz’s inequality implies that $\left| \sigma _{im}\right| \le \sigma _{i}\sigma _{m}$ and $\left| \sigma _{hm}\right| \le \sigma _{h}\sigma _{m}$. Substituting in (4.4) and (4.5) we obtain the following bounds on the standard deviation of the stochastic discount factor:

$$\begin{aligned} \sigma _{m} \ge \frac{E_{t}\left( r_{it +1} -r_{Nt +1}\right) +\frac{\sigma _{i}^{2}}{2}}{\sigma _{i}} \end{aligned}$$

(4.6)

for $i =1,\ldots ,N -1$ and:

$$\begin{aligned} \sigma _{m} \ge \frac{E_{t}\left( r_{ht +1} -r_{Nt +1} -\delta \right) +\frac{\sigma _{h}^{2}}{2}}{\sigma _{h}} \end{aligned}$$

(4.7)

which hold provided real gross excess returns in both asset and housing markets are positive.

Volatility bounds of this type were advanced in Shiller (1982) and further analysed in Hansen and Jagannathan (1991). Following Eqs. (4.6) and (4.7) the standard deviation of the stochastic discount factor should be greater than or equal to the logarithmic Sharpe ratio, defined as the ratio between the real gross excess return with respect to the riskless rate corrected for Jensen’s inequality and the standard deviation, of each asset $i =1,\ldots ,N -1$ and of housing. For housing the excess return accounts for depreciation.

Table 2 reports estimates of the housing logarithmic Sharpe ratio, compiled using either the Treasury bill or the bond rate as measures of the riskless rate. For this calculation we assume, that government bills and bonds trade in the asset market with constant term premia of the same order of magnitude as the depreciation rate. The table also displays the Sharpe ratio calculated using the term spread as a measure of the excess return of bonds over bills. The reported bounds imply, that the stochastic discount factor should have a very high volatility to be consistent with the predictions of the asset pricing model.

Table 2 Sharpe ratios

5 Separability and Collateral Constraints

In the representative agent economy real gross excess returns in asset and housing markets may be explained from characteristics of consumer preferences and other aspects of the intertemporal optimization problem. We describe the consequences of separability between non-housing and housing consumption and liquidity constraints.

5.1 Constant Elasticity of Substitution Specification

Piazzesi et al. (2007) analyse the constant elasticity of substitution (CES) single period utility function:

$$\begin{aligned} u\left( {\widetilde{X}}_{t}\right) =\frac{{\widetilde{X}}_{t}^{1 -\frac{1}{\sigma }} -1}{1 -\frac{1}{\sigma }} \end{aligned}$$

(5.1)

with the consumption aggregator:

$$\begin{aligned} {\widetilde{X}}_{t} =\left[ \alpha X_{ct}^{\frac{\epsilon -1}{\epsilon }} +\left( 1 -\alpha \right) X_{ht}^{\frac{\epsilon -1}{\epsilon }}\right] ^{\frac{\epsilon }{\epsilon -1}} \end{aligned}$$

(5.2)

where $\sigma >0$ and $\epsilon >0$ represent the intertemporal and intratemporal elasticities of substitution and $0<\alpha <1$ is a consumption weight parameter.⁵

In Eqs. (5.1) and (5.2) non-housing and housing consumption are weakly separable, the utility function is additively separable when $\sigma =\epsilon$. The stochastic discount factor is equal to the ratio between non-housing consumption marginal utility in periods $t +1$ and t. The CES specification implies:

$$\begin{aligned} M_{t +1} =\rho \left[ \frac{\alpha +\left( 1 -\alpha \right) \genfrac(){}{}{X_{ht +1}}{X_{ct +1}}^{\frac{\epsilon -1}{\epsilon }}}{\alpha +\left( 1 -\alpha \right) \genfrac(){}{}{X_{ht}}{X_{ct}}^{\frac{\epsilon -1}{\epsilon }}}\right] ^{\frac{\sigma -\epsilon }{\sigma \left( \epsilon -1\right) }}\genfrac(){}{}{X_{ct +1}}{X_{ct}}^{ -\frac{1}{\sigma }} \end{aligned}$$

(5.3)

Moreover, provided the housing aggregator function is linearly homogeneous, the first order conditions of the representative consumer optimization problem yield the following expression for the expenditure ratio between non-housing and housing consumption:

$$\begin{aligned} X_{zt} =\frac{\alpha }{1 -\alpha }\genfrac(){}{}{X_{ct}}{X_{ht}}^{\frac{\epsilon -1}{\epsilon }} \end{aligned}$$

(5.4)

Equation (5.4) may be derived from the expenditure ratio definition, using the first order condition (2.4) and the cross-equation restriction (2.9), and noticing that Euler’s theorem implies $h\left( X_{nt},X_{st}\right) =h_{X_{nt}}\left( X_{nt},X_{st}\right) X_{nt} +h_{X_{st}}\left( X_{nt},X_{st}\right) X_{st}$, due to the linear homogeneity of the housing aggregator function. Substituting (5.4) in (5.3) simple algebra shows, that the stochastic discount factor takes the following multiplicative form:

$$\begin{aligned} M_{t +1} =M_{ct +1}M_{wt +1} \end{aligned}$$

(5.5)

where $M_{ct +1} =\rho \left( X_{ct +1}/X_{ct}\right) ^{ -1/\sigma }$ and $M_{wt +1} =\left( X_{wt +1}/X_{wt}\right) ^{\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right] }$.

The first term on the right hand side of (5.5) will be recognized as the stochastic discount factor usually featuring in the CCAPM, a function of the growth rate of non-housing consumption. The second term is a consequence of weak separability between non-housing and housing consumption and is defined as a function of the ratio between the non-housing consumption expenditure shares in periods $t +1$ and t. When preferences over non-housing and housing consumption are additively separable $M_{t +1} =M_{ct +1}$, because $M_{wt +1} =1$.

Defining $m_{ct +1} =\log \left( M_{ct +1}\right)$ and $m_{wt +1} =\log \left( M_{wt +1}\right)$ and taking the natural logarithm of both sides of Eq. (5.5), we can show that the conditional variance of the logarithmic transformation of the stochastic discount factor is equal to the sum of the variances of $m_{ct +1}$ and $m_{wt +1}$ and of twice their covariance: $VAR_{t}\left( m_{t +1}\right) =VAR_{t}\left( m_{ct +1}\right) +VAR_{t}\left( m_{wt +1}\right) +2COV_{t}(m_{ct +1},m_{wt +1})$. As the elasticity term $\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right]$ and its square are multiplicative factors in the definition of $COV_{t}(m_{ct +1},m_{wt +1})$ and $VAR_{t}\left( m_{wt +1}\right)$, their asymptotic properties allow to replicate any required volatility for the natural logarithm of the stochastic discount factor $m_{t +1}$. The conditions $\lim _{\epsilon \rightarrow 1^{ +}}\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right] = +\infty$ and $\lim _{\epsilon \rightarrow 1^{ -}}\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right] = -\infty$ hold for $\sigma <1$, or $\lim _{\epsilon \rightarrow 1^{ +}}\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right] = -\infty$ and $\lim _{\epsilon \rightarrow 1^{ -}}\left( \epsilon -\sigma \right) /\left[ \sigma \left( \epsilon -1\right) \right] = +\infty$ are fullfilled for $\sigma >1$.

In order to further asses the properties of this model it is useful to provide a description for the case of additively separable preferences. The natural logarithm of the stochastic discount factor reduces to $m_{t +1} =\log \rho -\gamma \varDelta x_{ct +1}$ when $\sigma =\epsilon$, where $\gamma =1/\sigma$ denotes the coefficient of relative risk aversion. This in turn implies, that the covariance of the excess real gross housing return rate with the stochastic discount factor is equal to the opposite of the product between the coefficient of relative risk aversion and the covariance of the excess real gross housing return with the growth rate of non-housing consumption: $\sigma _{hm} = -\gamma \sigma _{hc}$, where $\sigma _{hc} =COV_{t}\left( r_{ht +1},\varDelta x_{ct +1}\right)$. Table 1 shows that the excess real gross housing returns, compiled using either Treasury bills or bonds as riskless assets, are positively correlated with the growth rate of non-housing consumption. We can therefore substitute in Eq. (4.5) and estimate the coefficient of relative risk aversion as the ratio between the real excess gross housing return rate, corrected for the effect of Jensen’s inequality, and its covariance with the non-housing consumption growth rate: $\gamma =\left[ E_{t}\left( r_{ht +1} -r_{Nt +1} -\delta \right) +\frac{\sigma _{h}^{2}}{2}\right] /\sigma _{hc}$. This criterion results in estimates of the coefficient of relative risk aversion of the order of 200. Similar results are obtained using the corresponding computations for the term spread.

Moreover, we can use the riskless rate relation (4.2) to derive an estimator of the intertemporal rate of time preference. When $\sigma =\epsilon$ substituting the logarithmic transformation of the stochastic discount factor in (4.2) yields: $\log \rho = -r_{Nt +1} +\gamma E_{t}\left( \varDelta x_{ct +1}\right) -\left( \gamma \sigma _{c}\right) ^{2}/2$, where $\sigma _{c}^{2}$ denotes the conditional variance of the non-housing consumption growth rate: $\sigma _{c}^{2} =VAR_{t}\left( \varDelta x_{ct +1}\right)$. With additive separable preferences $\sigma _{m}^{2} =\left( \gamma \sigma _{c}\right) ^{2}$. Taking either the Treasury bill or bond rates as measures of the riskless rate yields estimates of the natural logarithm of the intertemporal rate of time preference of the order of -30.

Since in our sample the growth rates of non-housing consumption and of the non-housing expenditure share are positively correlated, the implausibly high estimates for the coefficient of relative risk aversion obtained with additive separable preferences could be corrected assuming non-separable preferences, with either $\epsilon \rightarrow 1^{ +}$ and $\sigma >1$ or $\epsilon \rightarrow 1^{ -}$ and $\sigma <1$. We finally note that with non-separable preferences the estimates of the natural logarithm of the intertemporal rate of time preference remain in the range observed in the case of additive separability, when using either Treasury bills or bonds as riskless assets.⁶

5.2 Liquidity Constraints

A possible solution is to introduce additional features in the model. Market imperfections as the presence of liquidity constraints could be of relevance, because the estimated Sharpe ratios suggest financial and housing markets are incomplete in our sample.

The role of liquidity constraints for the determination of household savings is described in Deaton (1991). More recently, Lustig and Van Nieuwerburgh (2005) have analysed the relation between consumption and risk premia in the asset market, in a model featuring both non-housing and housing consumption and collateral constraints.

In the present framework collateral constraints may be introduced with two types of restrictions. The first one rules out short sales in the asset market:

$$\begin{aligned} P_{it}X_{it} \ge 0 \end{aligned}$$

(5.6)

and holds for each risky asset $i =1,\ldots ,N -1$.

The second limits the amount of borrowing on the riskless asset:

$$\begin{aligned} -P_{Nt}X_{Nt} \le \theta P_{st}X_{st} \end{aligned}$$

(5.7)

where the parameter $0<\theta <1$ represents the maximum allowable loan to value ratio.

With these constraints the stochastic discount factor takes the multiplicative form:

$$\begin{aligned} M_{t +1} =M_{ct +1}M_{wt +1}M_{\lambda t +1} \end{aligned}$$

(5.8)

In Eq. (5.8) $M_{\lambda t +1} =u_{X_{c}}\left( X_{ct},X_{ht}\right) /\left[ u_{X_{c}}\left( X_{ct},X_{ht}\right) -\lambda _{it}\right]$ and $\lambda _{it} \ge 0$ denotes the Lagrange multiplier for constraint $i =1,\ldots ,N$.

Moreover, the housing stochastic discount factor has the form:

$$\begin{aligned} M_{ht +1} =M_{t +1}M_{\theta t +1}\left( 1 -\delta \right) \end{aligned}$$

(5.9)

where $M_{\theta t +1} =\left[ u_{X_{c}}\left( X_{ct},X_{ht}\right) -\lambda _{Nt}\right] /\left[ u_{X_{c}}\left( X_{ct},X_{ht}\right) -\lambda _{Nt}\theta \right]$.

The collateral constraints and the no arbitrage condition in the real estate market in addition imply the following cross-equation restriction:

$$\begin{aligned} h_{X_{n}}\left( X_{nt} ,X_{st}\right) =h_{X_{s}}\left( X_{nt} ,X_{st}\right) M_{\lambda t +1}M_{\theta t +1} \end{aligned}$$

(5.10)

which generalizes the one holding without liquidity constraints.⁷

In order to interpret the above results note, that in equilibrium each Lagrange multiplier $\lambda _{it}$ represents the marginal increase in consumer utility resulting from a reduction of the i-th constraint by an amount equivalent to one non-housing consumption unit. When the collateral constraints are non binding, $\lambda _{it} =0$ for $i =1,\ldots ,N$ and hence $M_{\lambda t +1} =M_{\theta t +1} =1$. The stochastic discount factor with non binding constraints is equivalent to the one holding in the model without liquidity restrictions.

Since the stochastic process for $M_{t +1}$ is defined up to a set of probability measure equal to zero in its domain, the no arbitrage condition in the asset market and Eq. (5.8) moreover imply, that either all collateral constraints are binding and $\lambda _{it} =\lambda \ge 0$ for all $i =1,\ldots ,N$, or the constraints are non binding.

Although the terms $M_{\lambda t +1}$ and $M_{\theta t +1}$ contribute to the volatility the stochastic discount factors defined in (5.8) and (5.9), they perform a different and more important function. As $M_{\lambda t +1} \ge 1$ with equality when (5.6) and (5.7) are non binding, the presence of collateral constraints determines an increase of the equilibrium financial asset prices $P_{it}$, for $i =1,\ldots ,N$, and of the housing stock price $P_{st}$, other conditions being held constant. The term $M_{\theta t +1}$ has a similar additional role for the housing stock price, since $M_{\theta t +1} \ge 1$ with equality when (5.6) and (5.7) are non binding. When the collateral constraints are binding financial and real assets are more valuable, because they can be deployed to ease the restrictions.

6 Bayesian Vector Autoregression

The predictive ability of the asset pricing equations and the stochastic properties of the housing price and return series can be further studied in a multivariate statistical framework. We analyse a structural vector autoregression model with the following form:

$$\begin{aligned} Ay_{t} =Bx_{t -1} +u_{t} \end{aligned}$$

(6.1)

where $y_{t}$ is an $n \times 1$ vector of endogenous variables, $x_{t -1} =\left( y_{t -1}^{ \prime },\ldots ,y_{t -m}^{ \prime },d_{t}^{ \prime }\right) ^{ \prime }$ is a $k \times 1$ vector, $k =mn +l$, defined by m lagged values of the endogenous variables and an $l \times 1$ vector of deterministic terms $d_{t}$.

In Eq. (6.1) A is an $n \times n$ structural matrix, representing the contemporaneous relations between the endogenous variables, B is an $n \times k$ parameter matrix and $u_{t}$ is an $n \times 1$ vector disturbance term, independent and identically distributed over time: $E_{t -1}\left( u_{t}\right) =0$ and $E_{t -1}\left( u_{t}u_{t}^{ \prime }\right) =\Omega$. We assume the elements of $u_{t}$ are contemporaneously uncorrelated and hence that $\Omega$ is an $n \times n$ diagonal matrix.

We define the vector of endogenous variables as to include the real rent growth rate, the relative bill rate and the logarithmic transformation of the housing rent/price ratio: $y_{t} =\left( \varDelta p_{nt},rel_{t},p_{nt} -p_{st}\right) ^{ \prime }$. Moreover, we include in $d_{t}$ an intercept and three seasonal indicator variables, one for each of the quarters from second to fourth.

The reduced form corresponding to the structural model (6.1) is the following:

$$\begin{aligned} y_{t} =\Phi x_{t -1} +\varepsilon _{t} \end{aligned}$$

(6.2)

where $\Phi =A^{ -1}B$ and $\varepsilon _{t} =A^{ -1}u_{t}$.

The structural matrix A has full rank equal to n by assumption and is therefore invertible. The reduced form disturbance vector in Eq. (6.2) is independent and identically distributed over time: $E_{t -1}\left( \varepsilon _{t}\right) =0$ and $E_{t -1}\left( \varepsilon _{t}\varepsilon _{t}^{ \prime }\right) =\Sigma$ where $\Sigma =A^{ -1}\Omega \left( A^{ -1}\right) ^{ \prime }$. We estimate the model with an order of three lags.⁸

We adopt a Bayesian approach to identification and estimation of the econometric model in (6.1) and (6.2). For this purpose two issues need to be addressed, regarding the prior restrictions on the matrix A following from economic theory and the methods of estimation of the structural and reduced form parameters.

Following Sims and Zha (1998), when the structural matrix A is identified, estimation can in principle proceed from either the structural or the reduced form. Bayesian algorithms of estimation based on the reduced form are proposed in Rubio-Ramírez et al. (2010) and Arias et al. (2018). Reduced form methods are based on the classical identification problem in structural models. The structural and reduced forms have respectively $n\left( n +1\right) +nk$ and $n\left( n +1\right) /2 +nk$ parameters. Therefore, for any value of the reduced form matrices $\Phi$ and $\Sigma$, $n\left( n +1\right) /2$ restrictions are required in order to identify the structural matrices. The unit normalization of the structural variance matrix $\Omega =I_{n}$ yields n restrictions. The remaining $n\left( n -1\right) /2$ restrictions could be provided by the Cholesky decomposition of the variance matrix $\Sigma$. Since by definition $\Sigma$ is symmetric positive definite, there exists a unique lower triangular matrix H that makes $\Sigma =HH^{ \prime }$. Identification may therefore be obtained imposing a recursive form on the n structural equations describing the relations between the endogenous variables, letting $A =H^{ -1}$ and $\varepsilon _{t} =Hu_{t}$. More generally, defining $\varepsilon _{t} =HQu_{t}$ and $A =Q^{ \prime }H^{ -1}$ where Q is any $n \times n$ orthogonal matrix results in an exactly identified model, because $E_{t -1}\left( \varepsilon _{t}\varepsilon _{t}^{ \prime }\right) =HH^{ \prime }$ as $QQ^{ \prime } =Q^{ \prime }Q =I_{n}$.⁹

In Bayesian estimation it is usually assumed that the reduced form disturbance has a normal distribution, with zero mean and variance $\Sigma$: $\varepsilon _{t} \mid \Phi ,\Sigma \sim N\left( 0,\Sigma \right)$. The vector of endogenous variables conditional on its own lags, deterministic terms and the parameters is therefore normally distributed with mean $\Phi x_{t -1}$ and variance $\Sigma$: $y_{t} \mid x_{t -1},\Phi ,\Sigma \sim N\left( \Phi x_{t -1},\Sigma \right)$. In a natural conjugate inference framework a choice for the prior distribution for $\Phi$ and $\Sigma$ is the normal-inverse Wishart, defined as the product of a normal distribution for the coefficient matrix $\Phi$ conditional on $\Sigma$ and an inverse Wishart distribution for the variance $\Sigma$: $\Phi \mid \Sigma \sim N\left( {\overline{\Phi }},\Sigma \otimes V\right)$ and $\Sigma \sim IW\left( {\overline{\Sigma }},\nu \right)$ with mean and scaling parameters ${\overline{\Phi }}$, V and ${\overline{\Sigma }}$ of order $n \times k$, $k \times k$ and $n \times n$ and $\nu >n -1$. These assumptions entail a normal-inverse Wishart posterior distribution for the parameters, which can be simulated to yield estimates for the statistics of interest. The computation of structural statistics proceeds through random sampling from the space of orthogonal matrices Q. Identification of the structural form in each simulation is usually obtained combining sign and zero restrictions on the matrix A.

In the present work we apply the methods advanced in Baumeister and Hamilton (2015, 2018) and estimate the BVAR model from the structural form. In order to specify the restrictions on the structural matrix $A =\left[ a_{ij}\right] _{i,j =1}^{n}$, we use the normalization conditions $a_{ii} =1$ for $i =1,\ldots ,n$ and consider the following equation, relating the logarithmic housing rent/price ratio to expectations on forthcoming changes in real rent growth and housing return rates:

$$\begin{aligned} p_{nt} -p_{st} = -\frac{\iota }{1 -\eta } -E_{t}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }\varDelta p_{nt +\tau } +E_{t}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }r_{ht +\tau } \end{aligned}$$

(6.3)

where $\eta =1 -\exp \left( p_{n} -p_{s}\right)$, $p_{n} -p_{s}$ is the mean value of the logarithmic rent/price ratio and $\iota = -\eta \log \eta -\left( 1 -\eta \right) \log \left( 1 -\eta \right)$. We assume $0<\eta <1$, the mean values of the real rent growth and relative bill rates to be lower than its reciprocal and rule out housing rational speculative bubbles imposing the limiting condition $\lim _{\tau \rightarrow +\infty }\eta ^{\tau }E_{t}\left( p_{nt +\tau } -p_{st +\tau }\right) =0$.¹⁰

Equation (6.3) implies, that the natural logarithm of the real housing/rent price ratio is respectively negatively and positively related to expected forthcoming real rent growth and housing return rates in each time period. Moreover, from (4.5) it follows that the real gross housing return rate is equal to the riskless rate plus a constant risk premium. Assuming that the Treasury bill rate is equal to the riskless rate plus a constant term premium, the asset pricing framework rules out contemporaneous relations between the real rent growth and relative bill rates and the logarithmic transformation of the rent/price ratio. We therefore set $a_{13} =a_{23} =0$.

In addition, we assume that the real rent growth rate is contemporaneously negatively related to the relative bill rate, the relative bill rate conversely responds positively to the real rent growth rate and the logarithmic transformation of the housing rent/price ratio is positively related to both variables. We therefore impose the following sign restrictions on the structural matrix elements: $a_{12} \ge 0$, $a_{21} \le 0$, $a_{31} \le 0$ and $a_{32} \le 0$.

The sign restrictions may be supported with the representative consumer model. We use the relative bill rate as a measure of the long term movements of the riskless rate. The effect of the riskless rate on the real rent growth rate follows from Eqs. (2.4) and (2.7), the single period utility function in (5.1)–(5.2) and the stochastic discount factor in (5.5). From Eqs. (2.7) and (5.5) an increase of the riskless rate, implies a decrease of period t non-housing consumption. In turn, from Eqs. (2.4) and (5.1)–(5.2) the reduction in non-housing consumption determines a decrease of housing consumption and of the real rent price and growth rate. Moreover, we assume interest rates perform a stabilization role and the relative bill rate increases after a positive real rent growth shock. Finally, the impacts of the real rent growth and relative bill rates on the logarithmic rent/price ratio follow from previous assumptions and Eq. (6.3). The effect of the real rent growth rate is due to the definition of the logarithmic rent/price ratio. We might suppose in addition, that an increase of the relative bill rate determines expectations of forthcoming reductions in real rent growth rates.¹¹

For the purposes of Bayesian estimation we assume, that the structural disturbance term has a normal distribution with zero mean and variance $\Omega$: $u_{t} \mid B,\Omega ,A \sim N\left( 0,\Omega \right)$. The endogenous variables vector $Ay_{t}$ conditional on the explanatory variables $x_{t -1}$ and the parameters is therefore normally distributed with mean $Bx_{t -1}$ and variance $\Omega$: $Ay_{t} \mid x_{t -1},B,\Omega ,A \sim N\left( Bx_{t -1},\Omega \right)$. These assumptions are equivalent to the ones made above for the reduced form.

A natural conjugate framework is employed to define the prior distributions for the parameters conditional on the structural matrix A. Following Baumeister and Hamilton (2015, 2018) we assume, that the prior distribution for the matrices B and $\Omega$ conditional on A has the normal-inverse Gamma form, defined as the product of independent normal distributions for each row of B conditional on $\Omega$ and A and of independent inverse Gamma distributions for each diagonal element of $\Omega$ conditional on A. Denoting with $b_{i}^{ \prime }$ the i-th row of B we suppose $b_{i} \mid \Omega ,A \sim N\left( m_{i},\omega _{ii}V_{i}\right)$, where $m_{i}$ is a $k \times 1$ vector, $V_{i}$ is a $k \times k$ matrix and $\omega _{ii}$ is the i-th diagonal element of $\Omega$, for $i =1,\ldots ,n$. Moreover, we assume: $\omega _{ii}^{ -1} \mid A \sim \Gamma \left( \kappa _{i},\varphi _{i}\right)$ for $i =1,\ldots ,n$. The mean vector $m_{i}$, the variance matrix $V_{i}$ and the Gamma distribution parameters $\kappa _{i}$ and $\varphi _{i}$ are functions of A. These assumptions ensure that the posterior distribution of B and $\Omega$ conditional on A has the normal-inverse Gamma form.

Finally, since the posterior distribution of the structural matrix A has a non-standard form for any choice of the prior, it is simulated using Markov chain Monte Carlo methods. The compilation of the statistics of interest is then performed in a multi-stage approach: a draw is taken from the normal-inverse Gamma posterior distribution of the parameter matrices B and $\Omega$ conditional on each of the retained draws for the structural matrix A.¹²

7 Estimation and Model Simulation

For the purposes of Bayesian estimation we assume that the elements of the structural matrix A are distributed as independent truncated Student’s t variables, with location and scale parameters $\mu _{ij}$ and $\sigma _{ij}$ for $i,j =1,\ldots ,n$ and $\nu =3$ degrees of freedom: $a_{ij} \sim t^{ +}\left( \mu _{ij},\sigma _{ij},\nu \right)$ if $a_{ij} \ge 0$ and $a_{ij} \sim t^{ -}\left( \mu _{ij},\sigma _{ij},\nu \right)$ if $a_{ij} \le 0$. Table 3 summarizes our assumptions about the location and scale parameters of the elements of A for which a prior is formed and the sign restrictions.¹³

Table 3 Prior distribution parameters for contemporaneous structural coefficients

We use a version of the Minnesota prior of Litterman (1986) and Doan et al. (1984) for the structural matrix B. With reference to the reduced form we assume each endogenous variable could be modelled as a first order autoregression. Defining the $n \times k$ vector autoregression matrix ${\overline{\Phi }} =\left[ I_{n},0\right]$, where $I_{n}$ is the $n \times n$ identity matrix and 0 is the $n \times \left( k -n\right)$ zero matrix, we suppose that the prior mean for the i-th row of B is equal to $0.75a_{i}^{ \prime }{\overline{\Phi }}$, where $a_{i}^{ \prime }$ denotes the i-th row of A: $m_{i} =0.75{\overline{\Phi }}^{ \prime }a_{i}$. We set the prior mean of each autoregressive parameter equal to 0.75, assuming that the endogenous variables are most likely to be stationary. The variance matrix $V_{i}$ is assumed to assign greater confidence to the prior assumptions made for higher lags in the BVAR model and to normalize for the variance of the dependent variables. To this end we estimated an autoregression of order three for each endogenous variable, including an intercept and seasonal indicator variables. Denoting with $s_{ii}$ the error sample variance for the i-th variable and defining the $m \times 1$ and $n \times 1$ vectors $v_{1} =\left( 1/1^{2\gamma _{1}},1/2^{2\gamma _{1}},\ldots ,1/m^{2\gamma _{1}}\right) ^{ \prime }$ and $v_{2} =\left( s_{11}^{ -1},s_{22}^{ -1},\ldots ,s_{nn}^{ -1}\right) ^{ \prime }$, we assume $V_{i}$ is a diagonal matrix with main diagonal equal to the $k \times 1$ vector $v_{3} =\gamma _{0}^{2}\left[ \left( v_{1} \otimes v_{2}\right) ^{ \prime },v_{3}^{ \prime }\right] ^{ \prime }$, where $v_{3} =(\gamma _{3}^{2},\ldots ,\gamma _{3}^{2})^{ \prime }$ is an $l \times 1$ vector representing the confidence in the prior for the deterministic terms in the BVAR model and $\gamma _{0}$ is a constant summarizing the overall confidence. In estimation we remain relatively non informative on the deterministic terms, assume $\gamma _{1} =1$ and $\gamma _{3} =100$. We scale the overall confidence with $\gamma _{0} =0.1$.¹⁴

The Minnesota prior is a parsimonious model, as it assumes the process for each endogenous variable takes the form of an autoregression. Furthermore, in order to account for differences in volatility between variables, the variance of each element in the parameter matrix is rescaled with the ratio between the corresponding dependent and independent variable variances in the structural form. The increasing degree of confidence for parameters at higher lags in the BVAR model improves the precision of the estimates, because in the posterior distribution a greater weight is given to the sample information at lower lags and to the prior assumptions at higher ones. The first and third lag of each endogenous variable in the BVAR model are weighted in proportions of five to fifteen observations.

With regard to the prior for the structural variance matrix $\Omega$, each Gamma distribution has mean $k_{i}\varphi _{i}$ and variance $k_{i}\varphi _{i}^{2}$, we set $k_{i} =2$ for all $i =1,\ldots ,n$. Letting S denote the sample variance matrix of the residuals from the estimated autoregressions for the endogenous variables, we define each parameter $\varphi _{i}$ in order to let the mean of $\omega _{i}^{ -1}$ equal to the reciprocal of the structural variance of the i-th equation: $\varphi _{i} =\left( k_{i}a_{i}^{ \prime }Sa_{i}\right) ^{ -1}$. These assumptions assign a weight equivalent to four observations to the prior distribution for the variance $\Omega$.

As the posterior distribution of the structural matrix A is non-standard, it is simulated using a random walk Metropolis-Hastings algorithm. In order to describe our application, let $a =\left( a_{12},a_{21},a_{31},a_{32}\right) ^{ \prime }$ denote the vector of the elements of A whose distribution is to be simulated. The algorithm runs in the following steps: (i) for an initial draw of a generate a new candidate $a^{ \prime } =a +\psi P\upsilon$, where $\upsilon$, $\psi >0$ and P are a vector of independent standard Student’s t variables with 2 degrees of freedom of the same size as a, a scaling parameter and a square matrix of order equal to the size of a; (ii) compute the acceptance ratio $\pi \left( a,a^{ \prime }\right) =\min \left\{ p\left( a^{ \prime }\right) /p\left( a\right) ,1\right\}$, where $p( \cdot )$ denotes the posterior density of A evaluated at a and $a^{ \prime }$; (iii) accept the candidate draw or retain the initial one with probability $\pi \left( a,a^{ \prime }\right)$ or $1 -\pi \left( a,a^{ \prime }\right)$. The scaling parameter and matrix are defined as to optimize the draws and ensure an acceptance rate equal to 30 per cent, we run the algorithm with 1,000,000 pre-simulation and 500,000 simulation draws.¹⁵

Fig. 4

a Prior and posterior distributions for contemporaneous structural coefficients. Note: The top-left, -right, bottom-left, -right charts represent the densities of the structural parameters $a_{12}$, $a_{21}$, $a_{31}$ and $a_{32}$ respectively. The bold lines depict the prior truncated Student’s t distributions, the histogram plots reproduce the posterior distributions. The prior and posterior densities are measured in the right and left axes. The posterior distributions are compiled using a random walk Metropolis-Hastings algorithm with 1,000,000 pre-simulation and 500,000 simulation draws and a 30 per cent acceptance rate. b Posterior distributions for contemporaneous structural coefficients. Note: The top-left, -right, bottom-left, -right charts represent the densities of the structural parameters $a_{12}$, $a_{21}$, $a_{31}$ and $a_{32}$ respectively. The posterior distributions are compiled using a random walk Metropolis-Hastings algorithm with 1,000,000 pre-simulation and 500,000 simulation draws and a 30 per cent acceptance rate

Fig. 5

Impulse responses to unit structural shocks. Note: Rows reproduce the responses of the real rent growth rate, the relative bill rate and the logarithmic rent/price ratio. Columns display the responses to the real rent growth rate, relative bill rate and logarithmic rent/price ratio shocks. The bold lines depict median four quarter moving averages of the orthogonalized impulse responses, the shaded areas and dashed lines delimit 68 and 95 per cent credibility sets

For each simulation draw for the matrix A, draws are then computed from the posterior Gamma distributions of the structural variance $\Omega$. Finally, simulation draws are compiled from the posterior normal distributions of each row of the parameter matrix B.

Figure 4 presents a graphical depiction of the prior and posterior distributions of the structural matrix A. In panel (a) the bold lines draw the prior distributions for each element of A, the histogram plots represent the posteriors. Panel (b) reproduces the histogram plots of the posterior distributions. The model simulations show that the prior and posterior distributions for the response of the real rent growth rate to the relative bill rate are roughly equal. Conversely, the posterior distributions for the remaining contemporaneous coefficients are much more concentrated around the mode. The posteriors for the response of the the logarithmic transformation of the rent/price ratio to the real rent growth and relative bill rates are distributed near zero.

The simulation draws for the parameter posterior distribution may be used to compile the impulse response functions of the BVAR model. The orthogonalized impulse response function describes the response of each endogenous variable to each structural shock for variable time horizon:

$$\begin{aligned} \frac{ \partial y_{t +\tau }}{ \partial u_{t}^{ \prime }} =\Psi _{\tau }A^{ -1} \end{aligned}$$

(7.1)

where $\Psi _{\tau }$ is the non orthogonalized impulse response function matrix for $\tau \ge 0$: $\partial y_{t +\tau }/ \partial \varepsilon _{t}^{ \prime } =\Psi _{\tau }$.¹⁶

Figure 5 reproduces four quarter moving averages of the orthogonalized impulse response functions compiled according to (7.1). Each panel displays the median response and the 68 and 95 per cent credibility sets. A shock to the real rent growth rate raises it initially, the response remains positive in the subsequent periods decreasing to zero in an horizon of five years. Conversely, a shock to the relative bill rate entails a contemporaneous significant decrease of the real rent growth rate, the response returns subsequently gradually towards zero. A shock to the logarithmic transformation of the rent/price ratio does not have a significant effect on the real rent growth rate over the simulation horizon. The median impact response of the real rent growth rate is greater than 0.15 per cent for an own 1 per cent shock and lower than $-$0.40 per cent for a relative bill rate shock of the same order.

The contemporaneous response of the relative bill rate to a real rent growth rate shock is positive and significant. The relative bill rate shows negative autocorrelation at higher lags, the response returns to zero in an horizon of five years. A shock to the relative bill rate raises it initially, the response declines gradually to zero in the following periods. Conversely, a shock to the logarithmic transformation of the rent/price ratio does not have significant effects on the relative bill rate. The median response of the relative bill rate is on impact greater than 0.05 per cent for a 1 per cent real rent growth rate shock and greater than 0.3 per cent for an own shock of the same size.

A shock to the real rent growth rate is followed by an increase of the logarithmic transformation of the rent/price ratio over the simulation horizon, while a shock to the relative bill rate does not have significant effects. The logarithmic transformation of the rent/price ratio increases significantly and persistently following an own shock.

The impulse response functions allow us to assess the rational expectations constraint in Eq. (6.3). Subtracting from both sides of (6.3) the expectation of each term conditional on information available in period $t -1$ we obtain:

$$\begin{aligned}{} & {} \left( p_{nt} -p_{st}\right) -E_{t -1}\left( p_{nt} -p_{st}\right) \nonumber \\{} & {} \quad =-\left[ E_{t}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }\varDelta p_{nt +\tau } -E_{t -1}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }\varDelta p_{nt +\tau }\right] \nonumber \\{} & {} \quad \quad +\left[ E_{t}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }r_{ht +\tau } -E_{t -1}\sum \limits _{\tau =1}^{ +\infty }\eta ^{\tau }r_{ht +\tau }\right] \end{aligned}$$

(7.2)

Following Eq. (7.2) a shock to the natural logarithm of the rent/price ratio in period t should be related to a change in expectations between periods $t -1$ and t, concerning forthcoming real rent growth and housing return rates. An increase of the log rent/price ratio, relative to its expected value conditional on period $t -1$ information, should be followed by either a decrease of real rent growth rates or an increase of forthcoming real housing return rates.

Figure 6 reports four quarter moving averages of the cumulative impulse response functions for the real rent growth and relative bill rates, compiled with the estimated BVAR model from the first two rows of the sum: $\sum _{\tau =1}^{T}\eta ^{\tau }\Psi _{\tau }A^{ -1}$. We let the time horizon run from 1 to 40 quarters. Each panel reproduces the median cumulative impulse response and the 68 and 95 per cent credibility sets. The cumulative response of the real rent growth rate is positive following an own shock and negative as a consequence of a relative bill rate shock. Conversely, the cumulative response of the relative bill rate is negative following a real rent growth rate shock and positive after an own shock. For both the real rent growth and the relative bill rate the cumulative response to a logarithmic rent/price ratio shock is not significantly different from zero.

Fig. 6

Cumulative impulse responses to unit structural shocks. Note: Rows reproduce the cumulative responses of the real rent growth rate and the relative bill rate. Columns display the cumulative responses to the real rent growh rate, relative bill rate and logarithmic rent/price ratio shocks. Cumulative responses are calculated discounting with the factor $\eta =0.9737$ estimated at the sample mean value of the natural logarithm of the rent/price ratio. The bold lines depict median four quarter moving averages of the cumulative orthogonalized impulse responses, the shaded areas and dashed lines delimit 68 and 95 per cent credibility sets

The cumulative impulse response functions deliver further evidence regarding the persistence of the logarithmic rent/price ratio. The increase of the logarithmic rent/price ratio following a real rent growth rate shock is consistent with our prior assumptions and shows that real housing prices are relatively unresponsive to changes in fundamental value. The cumulative responses of the real rent growth and relative bill rates imply at the same time, that the logarithmic rent/price ratio should decrease following a real rent growth rate shock. Similarly, the logarithmic rent/price ratio does not react to the relative bill rate, although consistently with our assumptions it should increase following a relative bill rate shock. Furthermore, there is evidence of overshooting of the logarithmic rent/price ratio to own shocks, which do not seem to be related to subsequent real rent growth and relative bill rate changes. In addition, the logarithmic rent/price ratio displays momentum and long term reversal, as the initial response following an own shock increases in subsequent quarters and return to equilibrium occurs in a long period of time.

These results are consistent with a large amount of evidence on the behaviour of asset and housing markets. For the purposes of the present study they can be taken as evidence, that the dynamics of housing prices has been determined mostly by financial factors in Italy over our sample period. This in turn implies, that financial factors have played a relevant broader role for the business cycle.

8 Concluding Remarks

Excess returns of housing relatively to the riskless rate have been substantial in Italy in the 1996Q1-2019Q3 sample period. The quarterly figures imply annualized excess returns of the order of eight to ten per cent, when the riskless rate is measured by either the Treasury bill or the bond rate. In an asset pricing perspective no arbitrage in the residential property market entails a relation between the excess return of housing over the riskless rate and the volatility of the logarithmic transformation of the stochastic discount factor. The observed excess real housing returns imply a very high volatility of the logarithmic transformation of the stochastic discount factor.

With an intertemporal representative consumer framework a weakly separable structure of preferences provides an explanation for the observed excess real housing returns. Weakly separable preferences between non-housing and housing consumption imply, that the stochastic discount factor is equal in each time period to the product of the term usually appearing in the CCAPM, defined as a function of the real non-housing consumption growth rate, and a term in the ratio between the non-housing consumption expenditure shares in periods $t +1$ and t. The volatility of the logarithmic transformation of the stochastic discount factor is therefore a function of the variance of the logarithmic transformations of both terms and of their covariance. The required volatility can in general be obtained for values of the elasticities of intertemporal and intratemporal substitution in the neighbourhood of one. We have argued at the same time, that these assumptions do not provide a solution for the riskless rate puzzle, since estimates of the intertemporal rate of time preference are in a very low range.

With the representative consumer framework we identify a structural vector autoregression model of the relation between real rent growth, interest rates and housing prices. The results of Bayesian estimation allow us to assess the consistency of the relations between the endogenous variables with the predictions of economic theory. Most importantly, our prior assumptions have been based on the evidence from many past econometric studies, that investor expectations in stock and housing markets are often not related to fundamental value.

In an interesting review of the properties of survey based expectations of stock market returns Greenwood and Shleifer (2014) for instance show that expectations of stock market returns are respectively positively and negatively correlated to past and future returns. In the present study the impulse response functions reveal that real housing prices are relatively unresponsive to real rent growth and interest rate shocks. Moreover, there is overshooting to financial shocks and the logarithmic rent/price ratio is a persistent variable displaying momentum and long term reversal.

We have argued, that the above results show that the dynamics of housing prices in Italy in the sample period is mainly explained by financial factors. This in turn implies that asset and housing prices have a most relevant role as conditioning variables for the modelling of aggregate consumption, disposable income and the business cycle.

Finally, alternative explanations for excess real returns in financial markets have in the past been provided from different perspectives. The results obtained in the present work for the case of weakly separable preferences and our analysis of the consequences of collateral constraints for the form of the stochastic discount factor imply, that complementarity between the explanatory mechanisms resulting from different assumptions should be sought in further research.