1 Introduction

In the big data era, high-dimensional data are increasingly more common in many fields. Real-world examples include genomics, healthcare, audio signal, digital photograph, and financial datasets, among others. Dimensionality reduction refers to the transformation of high-dimensional data into a meaningful representation of reduced dimensionality. Such a reduced representation aims to preserve the intrinsic dimensionality of the data. Dimensionality reduction methods include linear and nonlinear approaches. Linear-based methods are mostly incapable to appropriately capture intricate nonlinear data patterns. Recently, many related nonlinear methods have been introduced, including methodological frameworks inspired in metric learning [1,2,3,4,5,6].

Dimensionality reduction-based metric learning replaces widely adopted distance measures (e.g. Euclidean distance) through an adaptive manner. The resulting intrinsic distance function aims to be a more suitable, condensed, and insightful representation of the dataset. Among other machine learning tasks, this is particularly convenient to address classification problems [7,8,9]. The isometric feature mapping (ISOMAP) is one of the pioneering algorithms for dimensionality reduction metric learning [10]. It consists of a global method that adopts the multidimensional scaling (MDS) [11] technique to find an embedding of a pairwise distance matrix onto an Euclidean space.

In the last decade, many extensions to the ISOMAP have been proposed to overcome limitations of the original algorithm. The robust kernel ISOMAP method intends to address two relevant caveats, namely the generalization property and topological stability [12]. Another methodological extension refers to the landmark-ISOMAP (L-ISOMAP), which improves the scalability of the ISOMAP. This is achieved by performing most of its computations on a subset of points, called landmarks [13]. It searches to a minimum set cover of the neighbourhoods along the k-nearest neighbours (KNN) graph, removing observations that belong to neighbour sets of other points. The self-organizing incremental neural network L-ISOMAP extension addresses the problem of automatically selecting an appropriate number and position of landmarks, reducing short-circuit errors [14]. In addition, in the path-based ISOMAP, a low-dimensional embedding is computed through a path-mapping algorithm instead of preserving pairwise geodesic distances, which decreases time and memory complexity [15].

A recent work [16] introduces a method for nonlinear dimensionality reduction, in which a manifold is built considering smooth geodesics. It aims to address problems where manifold measurements are either sparse or noise corrupted. This methodological innovation indicates an improved performance with embedding of face images and handwritten digits compared to the ISOMAP algorithm. In addition, the parallel transport unfolding (PTU) refers to a geometrical approach to evaluate geodesic distances of discrete paths, which may be adopted to devise faster variants of the ISOMAP—e.g. the L-ISOMAP [17]. As the MDS algorithm is a crucial step within the ISOMAP, more efficient variations have been proposed to decrease its computational complexity, from quadratic to quasi-linear [18]. Further recent studies report that the ISOMAP may be applied to embed subsets of data within one dimension. It details the conditions under which high density clusters in the original space are guaranteed to be separable onto the 1-D embedding [19].

The approximate representation of the manifold by an KNN graph is one of the limitations of the ISOMAP. The edges of the KNN network are commonly weighted, adopting the pointwise Euclidean distance. This is particularly sensitive to noisy data and outliers. While manifold learning methods provide reasonable results for a variety of datasets, their computational complexity increase concurrently with their adaptability to nonlinearity or noise in the data [20]. Thus, replacing the Euclidean distance with a more suitable measure should provide a more robust data classification, without significantly increasing computational costs.

In the present paper, it is introduced a new patch-based method that explores symmetrized Kullback–Leibler divergences between one-dimensional local densities, namely the kernel density estimation-based ISOMAP or KDE–ISOMAP method. It is computed in a nonparametric fashion for each local patch of the \(\epsilon \)-neighbourhood graph, replacing the pointwise Euclidean distance. A pivotal contribution of this method refers to an increase in the robustness to noise within the ISOMAP. This is achieved as a consequence of replacing a pointwise similarity measure with a patch-based one. Computational experiments indicate that the KDE–ISOMAP yields superior clustering results in terms of the silhouette coefficient (SC) compared to state-of-the-art manifold learning algorithms, such as the ISOMAP, unified manifold approximation and projection (UMAP) [21], and t-distributed stochastic neighbour embedding (t-SNE) [22]. Moreover, the proposed method outperforms several competing established algorithms in terms of classification accuracy, suggesting its effective applicability on real-world data.

This paper is organized as follows. The ISOMAP method is detailed in Sect. 2. The kernel density estimation (KDE) approach is presented in Sect. 3. The new KDE–ISOMAP is described in Sect. 4. Tests and results are reported in Sect. 5. Lastly, Sect. 6 summarizes the main findings of the present work and future research possibilities.

2 Isometric Feature Mapping

The fundamental principle of the ISOMAP is to build a graph to approximate the underlying manifold by connecting the KNN within the input space. The ISOMAP may be broken down into three primary phases. Firstly, it is created an undirected proximity graph from the input data \(\vec {x}_1,\ldots , \vec {x}_n \in R^m\) with the KNN or \(\epsilon \)-neighbourhood rule, where the cost of the edge \((v_i, v_j)\) is the Euclidean distance between the vectors \(\vec {x}_i\) and \(\vec {x}_j\). Subsequently, it is calculated the pairwise distance matrix D through n executions of either the Dijkstra algorithm or a single execution of the Floyd–Warshall algorithm. Lastly, the new coordinates of the points in an Euclidean subspace of \(R^d\) are determined by adopting the MDS technique, while preserving their distances.

Thus, the ISOMAP computes the shortest paths between each pair of vertices to find a mapping onto an Euclidean subspace of \(R^d\), while preserving the geodesic distances between data points. The shortest paths in the KNN graph should consist of reliable estimates of the actual geodesic distances in the manifold.

2.1 Multidimensional Scaling

The coordinates of the n points \(\vec {x}_r \in R^d\) for \(r=1,\ldots ,n\) in an Euclidean subspace are recovered through the MDS from a square matrix \(n \times n\) of pairwise distances, where the dimensionality output d consists of a user defined parameter [11, 23]. It is worth noticing that the elements of the pairwise distance matrix \(D = \{ d_{rs}^2 \}\) are:

$$\begin{aligned} d_{rs}^2 = \left\Vert \vec {x}_r - \vec {x}_s \right\Vert ^2 = \left( \vec {x}_r - \vec {x}_s\right) ^T \left( \vec {x}_r - \vec {x}_s\right) \end{aligned}$$
(1)

The Gram matrix of inner products is represented by the term B, where \(B = \{b_{rs}\}\) and \(b_{rs} = \vec {x_r}^T \vec {x_s}\). In order to determine the embedding, the MDS must obtain the matrix B from D. Considering that a translation of the samples retain their pairwise distances, it is crucial to assume that the data has zero mean. Otherwise, there would exist an infinite number of possible solutions. Manipulating the previous equation leads to the following:

$$\begin{aligned} d_{rs}^2 = \vec {x}_r^T \vec {x}_r + \vec {x}_s^T \vec {x}_s - 2\vec {x}_r^T \vec {x}_s \end{aligned}$$
(2)

The average of an arbitrary column s of the matrix D is:

$$\begin{aligned} \frac{1}{n}\sum _{r=1}^{n} d_{rs}^2 = \frac{1}{n}\sum _{r=1}^{n} \vec {x}_r^T \vec {x}_r + \vec {x}_s^T \vec {x}_s \end{aligned}$$
(3)

While the average of an arbitrary row r is:

$$\begin{aligned} \frac{1}{n}\sum _{s=1}^{n} d_{rs}^2 = \vec {x}_r^T \vec {x}_r + \frac{1}{n}\sum _{s=1}^{n} \vec {x}_s^T \vec {x}_s \end{aligned}$$
(4)

It is worth noticing that the average of all the elements in D is:

$$\begin{aligned} \frac{1}{n^2}\sum _{r=1}^{n}\sum _{s=1}^{n} d_{rs}^2 = \frac{2}{n}\sum _{r=1}^{n} \vec {x}_r^T \vec {x}_r \end{aligned}$$
(5)

From (2), the term \(b_{rs}\) may be expressed as:

$$\begin{aligned} b_{rs} = \vec {x}_r^T \vec {x}_s = -\frac{1}{2}(d_{rs}^2 - \vec {x}_r^T \vec {x}_r - \vec {x}_s^T \vec {x}_s) \end{aligned}$$
(6)

Combining Eqs. (3)–(5) yields the following:

$$\begin{aligned} b_{rs} = -\frac{1}{2}\left( d_{rs}^2 -\frac{1}{n}\sum _{r=1}^{n} d_{rs}^2 - \frac{1}{n}\sum _{s=1}^{n} d_{rs}^2 + \frac{1}{n^2}\sum _{r=1}^{n}\sum _{s=1}^{n} d_{rs}^2 \right) \end{aligned}$$
(7)

Defining \(a_{rs} = -\frac{1}{2}d_{rs}\), one may formulate the following equation:

$$\begin{aligned} a_{r.} = \frac{1}{n}\sum _{s=1}^{n} a_{rs} \quad a_{.s} = \frac{1}{n}\sum _{r=1}^{n} a_{rs} \quad a_{..} = \frac{1}{n}\sum _{r=1}^{n}\sum _{s=1}^{n} a_{rs} \end{aligned}$$
(8)

Which leads to:

$$\begin{aligned} b_{rs} = a_{rs} - a_{r.} - a_{.s} + a_{..} \end{aligned}$$
(9)

In matrix notation, it is expressed as \(B = { HAH}\), where:

$$\begin{aligned} H = I - \frac{1}{n}\vec {1}\vec {1}^T \end{aligned}$$
(10)

The term H is the centring matrix. An eigendecomposition of the matrix B must be performed to find the coordinates of the points in \(R^d\), which is:

$$\begin{aligned} B = V \Lambda V^T \end{aligned}$$
(11)

where V is the matrix which columns are the eigenvectors of B, and \(\Lambda = {{\,\textrm{diag}\,}}(\lambda _1,\ldots , \lambda _n)\) is the diagonal matrix with the eigenvalues of B. Considering that \(X^T X = V \Lambda V^T\), the intrinsic coordinates are expressed as follows:

$$\begin{aligned} B = \Lambda ^{1/2} V^T \end{aligned}$$
(12)

The computational complexity of ISOMAP is \(O(n^3)\).

3 Kernel Density Estimation

The KDE is a nonparametric statistical technique to estimate the probability density function of a random variable [24, 25]. Let \(\{ x_1,\ldots , x_n \}\) be an i.i.d. sample from an 1-D random variable x, with unknown density function f(x). The KDE of f(x) is given by:

$$\begin{aligned} \hat{f_h}(x) = \frac{1}{n}\sum _{i=1}^{n} K_h(x - x_i) = \frac{1}{nh}\sum _{i=1}^{n} K\left( \frac{x - x_i}{h} \right) \end{aligned}$$
(13)

where K(x) is the kernel function and h is the bandwidth—i.e., a parameter that controls the degree of smoothing of the density estimate. Several kernel functions have been proposed and successfully applied in many problems. The Gaussian, Epanechnikov, uniform, and triangular are among the most relevant cases. In the present work, Gaussian kernels are adopted. This is due to the fact that they are capable of providing a reasonable approximation for many distributions in the datasets included in the analysis. Moreover, Gaussian kernels should preserve properties that allow for some simplification of otherwise costly calculations [26].

3.1 Bandwidth Estimation Methods

The choice of the bandwidth h is pivotal for an appropriate estimation of the unknown density function. Large values of h result in over-smoothing, where \(\hat{f_h}(x)\) becomes unimodal and with a large variance. Conversely, small values of h commonly lead to noisy data, yielding large variations in \(\hat{f_h}(x)\) for points in the neighbourhood of x. The optimal bandwidth value is a trade-off between a smooth constraint and data fidelity.

In the case that both the kernel function and the unknown density are Gaussian, then the optimal bandwidth in terms of a minimum (IMSE) may be computed through the Silverman’s rule of thumb [27]:

$$\begin{aligned} h_{SIL} = 0.9\,\min \left( \hat{\sigma }, \frac{{ IQR}}{1.34} \right) n^{-1/5} \end{aligned}$$
(14)

where \(\hat{\sigma }\) is the standard deviation of the samples, \({ IQR} = Q_3 - Q_1\) is the interquartile range, and n is the sample size. In addition, still under the Gaussian assumption, the Scott’s rule for bandwidth estimation rule is also optimal in terms of the IMSE [28], as follows:

$$\begin{aligned} h_{SC} = 3.49 \hat{\sigma } n^{-1/3} \end{aligned}$$
(15)

where \(\hat{\sigma }\) is the standard deviation of the samples, and n is the sample size.

4 KDE-Based Entropic Isometric Feature Mapping

The parametric principal component analysis (PCA) metric learning algorithm is the main inspiration to devise the KDE–ISOMAP. The former computes the entropic covariance matrix of the data, adopting information-theoretic divergences between densities estimated in local patches along the neighbourhood graph [29]. The primary distinction between the existing ISOMAP and the proposed KDE–ISOMAP lies in the first phase of the algorithm.

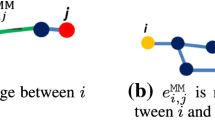
The data matrix is denoted by \(X = \{\vec {x}_1,\ldots , \vec {x}_n \}\), where each column \(\vec {x}_i \in R^m\) represents an observation. The \(G = (V, E)\) refers to the \(\epsilon \)-neighbourhood graph induced from X by creating an edge between each pair of samples \(\vec {x}_i\) and \(\vec {x}_j\) if \(d_E(\vec {x}_i, \vec {x}_j) < \epsilon \), where \(d_E(.,.)\) is the regular Euclidean distance. Consequently, a patch \(P_i\) may be defined as the set formed by a sample \(\vec {x}_i\) and its neighbourhood. For a sufficiently high sample density, it belongs to a single Euclidean subspace [30].

Let \(k_i\) be the number of \(\vec {x}_i\) neighbours in G, then the patch \(P_i\) is the following \((k+1) \times m\) matrix:

$$\begin{aligned} P_i = \begin{bmatrix} \vec {x}_i \\ \vec {x}_{i1} \\ \vec {x}_{i2} \\ \vdots \\ \vec {x}_{ik_i} \end{bmatrix} = \begin{bmatrix} \vec {x}_i(1) &{}\quad \vec {x}_i(2) &{}\quad \cdots &{}\quad \vec {x}_i(m) \\ \vec {x}_{i1}(1) &{}\quad \vec {x}_{i1}(2) &{}\quad \cdots &{}\quad \vec {x}_{i1}(m) \\ \vec {x}_{i2}(1) &{}\quad \vec {x}_{i2}(2) &{}\quad \cdots &{}\quad \vec {x}_{i2}(m) \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \vec {x}_{ik_i}(1) &{}\quad \vec {x}_{ik_i}(2) &{}\quad \cdots &{}\quad \vec {x}_{ik_i}(m) \end{bmatrix} \end{aligned}$$

The \(k_i\) neighbours of \(\vec {x}_i\) in the \(\epsilon \)-neighbourhood network are denoted by \(\{ \vec {x}_{i1}, \ldots , \vec {x}_{ik_i} \}\). Consider each column of the matrix \(P_i\) being a sample of an 1-D random variable \(x_k\), with a probability density function \(f(x_k)\). These probability density functions \(f(x_k)\) are estimated for \(k = 1, \ldots , m\) for each patch of the \(\epsilon \)-neighbourhood graph using the KDE—which is a nonparametric approach. Because each patch includes m 1-D densities and the graph contains n patches, the total number of nonparametric densities is nm, resulting in a computational cost of \(O(n^3 m)\) to run the KDE–ISOMAP.

The relative entropies (KL-divergences) between the densities predicted for each pair of nearby patches \(P_i\) and \(P_j\) are used to replace the pointwise Euclidean distances in the edges \((\vec {x}_i, \vec {x}_j) \in E\). This is known as the entropic \(\epsilon \)-neighbourhood graph. Having precisely m pairings of 1-D densities, there are m KL-divergences to compute for each pair of patches \(P_i\) and \(P_j\). The KL-divergence of distributions \(\vec {p} = [p_1, \ldots , p_L]\) and \(\vec {q} = [q_1, \ldots , q_L]\), where L is the number of points (bins) employed in the KDE, may be calculated as follows:

$$\begin{aligned} D_{KL}\left( \vec {p}, \vec {q}\right) = \frac{1}{L}\sum _{i=1}^{L} p_i\, \log \left( \frac{p_i}{q_i} \right) \end{aligned}$$
(16)

Moreover, the symmetrized KL-divergence may be found as detailed below:

$$\begin{aligned} D_{s}\left( \vec {p}, \vec {q}\right)= & {} \frac{1}{2} \left( D_{KL}\left( \vec {p}, \vec {q}\right) + D_{KL}\left( \vec {q}, \vec {p}\right) \right) \nonumber \\= & {} \frac{1}{2} \left( H\left( \vec {p}, \vec {q}\right) - H\left( \vec {p}\right) + H\left( \vec {q}, \vec {p}\right) - H\left( \vec {q}\right) \right) \nonumber \\= & {} \frac{1}{2}\left( H\left( \vec {p}, \vec {q}\right) + H\left( \vec {q}, \vec {p}\right) \right) - \frac{1}{2} \left( H\left( \vec {p}\right) + H\left( \vec {q}\right) \right) \end{aligned}$$
(17)

This reflects the average of the cross-entropies minus the average of the individual entropies. A vector of relative entropies \(\vec {\Psi }_{ij}\) is built after computing the KL-divergences between the m pairings of 1-D densities in \(P_i\) and \(P_j\):

$$\begin{aligned} \vec {\Psi }_{ij} = \left[ D_{s}\left( \vec {p}_1, \vec {q}_1\right) , \ldots , D_{s}\left( \vec {p}_m, \vec {q}_m\right) \right] \end{aligned}$$
(18)

Lastly, the weight of the edge \((\vec {x}_i, \vec {x}_j) \in E\) is replaced by:

$$\begin{aligned} w_{ij} = \vec {\Psi }_{ij}^T \vec {\Psi }_{ij} = \Vert \vec {\Psi }_{ij} \Vert ^2 \end{aligned}$$
(19)

This leads to the entropic neighbourhood graph. The second and third phases of the KDE–ISOMAP are the same ones adopted in the regular ISOMAP algorithm.

5 Results

Two sets of computational experiments are conducted to evaluate the performance of the proposed KDE–ISOMAP for dimensionality reduction-based metric learning. Firstly, a comparison of the clusters obtained after mapping the data onto a two-dimensional subspace, adopting the SC to measure the difference in terms of clustering fit. Secondly, after the same feature extraction process, a comparison is performed between the average classification accuracy of the following widely adopted supervised classifiers: KNN, support vector machines (SVM), and Bayesian classifier under the Gaussian hypothesis.

In the case that the underlying metrics are successfully learnt, this should be reflected through a substantial increase in the SC and clustering fit measures while examining many multivariate datasets. The proposed KDE–ISOMAP is directly evaluated with the following seven competing methods: PCA, kernel PCA (KPCA), ISOMAP, locally linear embedding (LLE), Laplacian eigenmaps (LAP), t-SNE, and UMAP. In addition, the KDE–ISOMAP is modelled considering three different variations: the KDE–ISOMAP with fixed bandwidth h \(=\) 0.1 for all probability density functions (K-ISO-F), the KDE–ISOMAP with Silverman’s rule for bandwidth estimation (K-ISO-SIL), and the KDE–ISOMAP with Scott’s rule for bandwidth estimation (K-ISO-SC). In the experiments, the number of density points (bins) used in the KDE is set to \(L = 256\).

All datasets included in the analysis are publicly available at openML.org/url, along with details on their respective number of instances, features, and classes. The results of the first set of experiments are reported in Table 1. It is worth noticing that in 28 out of 30 datasets, one of the KDE–ISOMAP versions yields the best SC value, corresponding to almost 93% of the cases. The averages and medians resulted from the proposed method outperform the existing methodological alternatives.

Fig. 1
figure 1

Scatterplots for the AIDS dataset after dimensionality reduction. From left to right and top to bottom, these refer to the ISOMAP, t-SNE, UMAP, and KDE–ISOMAP. In cases where the number of samples is limited, the t-SNE and UMAP tend to perform below the expectations due to numerical optimization

Full size image

A nonparametric Friedman test is performed to check whether the superior results of the KDE–ISOMAP are statistically significant. The null hypothesis that all groups are identical is rejected (\(p = 1.11 \times 10^{-16}\)), considering a significance level of \(\alpha = 0.05\). Moreover, a post-hoc Nemenyi test is applied to determine if groups are statistically different between themselves. At a significance level of \(\alpha = 0.05\), this test indicates a considerably higher SC of the K-ISO-F, K-ISO-SIL, and K-ISO-SC compared to the PCA, KPCA, ISOMAP, LLE, LAP, t-SNE, and UMAP. The p values of these tests are reported in Table 2. There is no evidence that the K-ISO-F and K-ISO-SC vary in terms of the SC (\(p = 0.965\)). Similar results are reported for the K-ISO-F and K-ISO-SIL (\(p = 0.982\)) as well as the K-ISO-SIL and K-ISO-SC (\(p = 0.949\)).

Table 1 Silhouette coefficients (SC) for clusters generated by the algorithms PCA, KPCA, ISOMAP, LLE, LAP, KDE–ISOMAP (K-ISO-F, K-ISO-SIL, K-ISO-SC), t-SNE, and UMAP for 30 openML.org datasets (2-D case)
Full size table

Subsequently to the dimensionality reduction-based metric learning, in the second set of experiments 50% of the samples of each of the datasets are used to train three different classifiers. Those refer to the Bayesian classifier under the Gaussian hypothesis with different covariance matrices for each class (i.e., parametric and quadratic classifier), the SVM with no kernel (i.e., nonparametric and linear classifier), and the KNN with \(K = 7\) (i.e., nonparametric and nonlinear classifier). The 50% remaining samples from the test set are classified using those three classifiers, being selected the classifier with the highest accuracy to assess how each metric learning method affects supervised classification. The findings of this analysis are reported in Table 3. Remarkably, one of the three variations of the proposed KDE–ISOMAP yields the largest classification accuracy in 26 out of 30 datasets, corresponding to 86% of the cases.

A nonparametric Friedman test is performed to determine whether the prevailing results in terms of classification accuracy achieved by the KDE–ISOMAP are statistically significant. There is strong evidence against the null hypothesis that all groups are identical, considering a significance level of \(\alpha = 0.05\). A post-hoc Nemenyi test is also applied to determine whether the groups are equivalent. The test finds that the K-ISO-F, K-ISO-SIL, and K-ISO-SC provide a significantly higher classification accuracy compared to the PCA, KPCA, ISOMAP, LLE, LAP, t-SNE, and UMAP. The p values for the tests performed are reported in Table 4. There is no evidence that the K-ISO-F and K-ISO-SC vary in terms of classification accuracy (\(p = 0.550\)). Similar results hold true regarding the K-ISO-F and K-ISO-SIL (\(p = 0.508\)) as well as the K-ISO-SIL and K-ISO-SC (\(p = 0.949\)).

Table 2 Results of the post-hoc Nemenyi tests for the silhouette coefficient (SC)
Full size table

A convenient attribute of the proposed KDE–ISOMAP refers to its strategy to address the out-of-sample problem in manifold learning. Most unsupervised metric learning algorithms are not capable of appropriately handling new samples that are not part of the training set. A natural choice is to include such new samples to the dataset and perform another full training round, which may be time consuming. It is worth noticing that the ISOMAP is directly related to the KPCA. In fact, the KPCA becomes the ISOMAP when the kernel matrix \(K(\vec {x}_i, \vec {x}_j)\) is defined as minus one-half of the geodesic distance matrix [31]. Thus, it is possible to tackle out-of-sample instances thorugh the KDE–ISOMAP while adopting the same projection strategy of the KPCA.

A caveat of the KDE–ISOMAP method refers the specification of the parameter \(\epsilon \) (radius), which determines the patch size—i.e., number of neighbours of a particular sample in the \(\epsilon \)-neighbourhood graph. Tests report that the classification accuracy and SC are substantially affected by changes in this parameter. In the present work, the following strategy is employed: For each dataset, the complete graph is built by linking a sample to every other sample. Then, for each sample \(\vec {x}_i\), the approximate distribution of the distances from \(\vec {x}_i\) to any other sample \(\vec {x}_j\) is computed. In addition, for each dataset the whole network is constructed by connecting each sample to every other sample. Subsequently, for each sample \(\vec {x}_i\) the estimated distribution of the distances between any other sample \(\vec {x}_j\) and itself is computed.

Previous works report that the percentiles p of distributions that fall within the range \(P = [1, 20]\) provide the most suitable values of \(\epsilon \) (radius). Thus, in the best model selection process, several percentiles of this distribution are tested as the radius that maximizes the classification accuracy among all values of \(p \in P\). Differently from an KNN graph, this graph is not regular due to the fact that the degree of the vertices may be considerably different. It is worth mentioning that, besides using the class labels to perform a model selection, the feature extraction stage is fully unsupervised—i.e., the KDE–ISOMAP performs unsupervised metric learning.

To illustrate how the KDE-ISOMAP may improve clustering and classification accuracy by learning a suitable metric, Fig. 1 depicts scatterplots exploring the AIDS dataset—after reducing the number of features into two. In comparison with the original ISOMAP, t-SNE, and UMAP, the proposed KDE–ISOMAP provides less overlapping samples in terms of data discrimination. The two classes (male and female—represented as circles and crosses, respectively) are more clearly identified in the KDE-ISOMAP compared to popular competing methods.

Table 3 Maximum accuracy between the KNN, SVM, and Bayesian classifiers after dimensionality reduction with the PCA, KPCA, ISOMAP, LLE, LAP, KDE-ISOMAP (K-ISO-F, K-ISO-SIL, K-ISO-SC), t-SNE and UMAP for 30 openML.org datasets (2-D case)
Full size table
Table 4 Results of the post-hoc Nemenyi tests for classification accuracy
Full size table

6 Conclusion

It is highly desirable to overcome limitations of the Euclidean distance while extracting nonlinear characteristics from data. Manifold learning and unsupervised metric learning are commonly used interchangeably due to the fact that both aim to find intrinsic geometric structures of data. In the present work, the relative entropy between distributions estimated from patches along the \(\epsilon \)-neighbourhood graph is introduced. This consists of an alternative to the Euclidean distance through an entropic ISOMAP based on the KDE method.

Computational analyses confirm two key points to consider the proposed KDE–ISOMAP as a competing alternative regarding widely adopted learning algorithms. Firstly, the nonlinear features of the KDE–ISOMAP may be more discriminative in supervised classification than features produced using state-of-the-art manifold learning algorithms. Secondly, the KDE–ISOMAP provides superior quality clustering compared to the same competing algorithms. In particular, the superiority of the proposed KDE–ISOMAP compared to the t-SNE and UMAP becomes clearer while exploring datasets with limited number of samples. This is due to the fact that these two existing algorithms require numerical optimization methods that are overly dependent upon the sample size.

The main contribution of the proposed KDE–ISOMAP framework refers to its robustness to the presence of noisy date and outliers. This is contrast to the pointwise Euclidean distance because of the fact that the KDE–ISOMAP adopts a patch-based distance function to measure similarity between samples. Furthermore, considering that a projection matrix may be created, tackling out-of-sample data becomes simpler due to the relationship between the KPCA and ISOMAP. In addition, it is worth mentioning the fact that the KDE–ISOMAP is suitable for small sample sizes, thus not requiring a large amount of data for convergence purposes. This is an advantage compared to autoencoders and other deep-learning-based algorithms.

Suggestions of future work include the adoption of further information-theoretic divergences and families of entropies, such as the Hellinger, Bhattacharyya, Cauchy–Schwarz, total variation divergences, Renyi, and Sharma–Mittal entropies. Moreover, a supervised version of the KDE–ISOMAP may be devised by combining the relative entropy and Euclidean distance. Such a framework would adopt a single similarity measure to weight the edge for neighbouring samples of a same class, whereas the sum of the distances may discourage the shortest paths from crossing that edge for neighbouring samples belonging to different classes.