1 Introduction

In research analysis, consequential occurrences may not be necessary to obtain data for decision making, where we have access to antecedent outcomes. So, data science, data analysis and data modeling help us to gain meaningful insights in an attempt to obtain viable information. Data science is an interdisciplinary field that intertwines statistical applications, computational and machine learning methods to extrapolate usable information from big data for predictive modeling. In this area, lucrative advances have been made in big data analytics, business and optimization based data mining, internet of things, real-time decision making and artificial Intelligence [1,2,3,4]. These data that go through statistical, algorithmic or scientific processes is usually unstructured involving tasks such as data preprocessing and feature engineering; unlike data analysis which deals with data cleaning and visualization for structured data. However, data modeling as a primary objective of probability distribution is the analysis of data by projecting the likelihood of different outcomes using relevant models.

The development of new probability distributions does not entail a lack of appreciation for the existent; rather, it is an attempt to achieve greater effectiveness in data modeling. There are many methodologies for the modification of an existing distribution, as studied by Lai [5]. Among many methods are the transformation method, compounding, convolution, mixture model, skewing, parameterization and the avalanched generalization methods. More emphatically, the generalization method has been used more frequently in recent decades to increase the number of parameters of classical distributions. This approach is conventionally aimed at improving model flexibility by primarily reconstructing for robustness. Moreover, these modifications also have a great impact on the nature of hazard functions of distributions, featuring various real-life representations.

Tahir et al. [6] described a methodology for the development of some of these generalized distributions, given in cumulative distribution function (CDF) order:

$$ {\text{F}}\left( {x, \omega } \right) = \mathop \int \limits_{{R_{l} }}^{\beth \left( x \right)} m\left( t \right)dt\;or\;\mathop \int \limits_{\beth \left( x \right)}^{{R_{u} }} m\left( t \right)dt. $$
(1)

where \(\beth \left( x \right)\) is the link function, which is derived from the quantile function of a random variable \(X\); \(m\left( t \right)\) is the probability density function (PDF) of a dummy random variable T; and \(R\) is the (lower or upper) boundary support. Tahir tabulated the various link functions for the continuous distribution category. Some of the generators or distributions developed in this order are logistic X, Gompertz inverse exponential, Sin G, the Marshal–Olkin transformation with TX, the Gull Alpha Power, the Normal-Power-Logistic, the Exponentiated Odd Log-Logistic Weibull, and several others [6,7,8,9,10,11,12].

The addition of parameter(s) is a great economic process harnessed by different methods of probability model development. The motivation of this research stems from the challenge posed by the parameter inclusion strategy of some existing distributions, which allows the incorporation of (extra) parameters by inserting PDF and/or CDF structures to form higher parametric compound models. However, a more direct procedure can be adopted to efficiently achieve the same result. Hence, our interest in this study is to develop a new approach for increasing the number of parameters in an existing distribution without allowing for model insertions, as found with the generalization method. Second, we propose a probability distribution to exemplify the relevance of the approach. Of course, the proposed model is flexible and can model outcomes that mirror monotonically decreasing and increasing, right-skewed and modified unimodal trends.

The remaining parts of this work are arranged as follows: Sect. 2 of this paper features a direct strategy for parameter inclusion. In Sect. 3, a proposal is made for a new probability model using the insights in the previous section. Section 4 details the study on some of the properties of the proposed distribution. Section 5 describes the applicability of the proposed model through data analysis and/or performance comparison.

2 Omega Type Probability Models

In this development, extra parameters are premeditatedly implanted as a function of a variable, directly into an extracted variable component from a root model. After the application of a mathematical technique, the derivation of a new PDF is suitable. The procedure composes of the “integration method” and the concept of the “normalizing constant”, as detailed in [13].

To achieve this, we capture the variable components, say \( \theta \left( {x,\omega } \right)\), of an existing distribution and treat it as an arbitrary function, where \( x and \omega\) are the variable and vector of parameters, respectively. The extracted components, however, can be modified by primitively adding some parameters to form new probability distribution(s). This is constructed such that the root distribution \(f\left(x,\omega \right)\) is obtained as a special case of the new development, as in the generalization method. Now, the choice of the number of parameters to possibly add depends on the structure of the variable in a density function. For example, the variable \(x\) in the variable component \(\theta \left( {x,\omega } \right) = e^{ - ax}\) from the exponential distribution can discretely be changed to \( x^{b}\). Hence, we obtain \(\theta_{r} \left( {x,\omega } \right) = e^{{ - ax^{b} }}\) as a new arbitrary function, so long as it retains the propensity to return the initial component \( e^{ - ax}\) at a given value of \( b\).

Moreover, if we define

$$ \theta \left( {x,\omega } \right) = \left( {1 + x} \right)e^{ - ax} , $$
(2)

from the Lindley distribution, for example; thus, we have increased options for parametric inclusion. In this case, the new possible arbitrary functions become

$$ \theta_{r} \left( {x,\omega } \right) = \left( {1 + x} \right)e^{{ - ax^{b} }} or $$
(3)
$$ \theta_{r} \left( {x,\omega } \right) = \left( {1 + x^{b} } \right)e^{{ - ax^{c} }} , $$
(4)

which are composites of two or three parameters, respectively. Another approach to this inclusion is to replace a replicated parameter in the root variable component \(\theta \left( {x,\omega } \right)\) with a new parameter. Recall the Kumaraswamy distribution, which has a variable component given by,

$$ \theta \left( {x,\omega } \right) = x^{ - 1 + a} \left( {1 - x^{a} } \right)^{ - 1 + b} . $$
(5)

The parameter “a” is replicated twice. However, the variable \(x^{a}\) in the second component \(\left( {1 - x^{a} } \right)\) can be replaced with \( x^{c}\) which gives us a new three-parameter arbitrary function.

$$ \theta_{r} \left( {x,\omega } \right) = x^{ - 1 + a} \left( {1 - x^{c} } \right)^{ - 1 + b} $$
(6)

Consequently, by integrating the new arbitrary functions \(\theta_{r} \left( {x,\omega } \right)\) and applying the concept of a normalizing constant, a new probability density function can be realized. Currently, this development is not limited to cases of superscripts, as in \( x^{*}\), but seems more consistent in mathematical structures expressed in chain format. This suggests that we could also integrate parameters in components of this sort:

$$ \sin \left( x \right) \to {\text{sin}}\left( {ax} \right), Log\left( x \right) \to Log\left( {bx} \right), \Gamma \left( x \right) \to \Gamma \left( {cx} \right), erf\left( x \right) \to erf\left( {ax} \right) $$

and several others. Now, let X and \(\omega\) be a random variable and a vector of parameters, respectively; then, a probability distribution can be constructed:

$$ u\left( {x, \omega } \right) = \theta_{r} \left( {x,\omega } \right)\left[ { \mathop \int \limits_{ - \infty }^{\infty } \theta_{r} \left( {x,\omega } \right)dx } \right]^{ - 1} $$
(7)

for the probability density function, and the cumulative distribution function is

$$ U\left( {x, \omega } \right) = \mathop \int \limits_{ - \infty }^{x} \left\{ {\theta_{r} \left( {t,\omega } \right)\left[ { \mathop \int \limits_{ - \infty }^{\infty } \theta_{r} \left( {t,\omega } \right)dt } \right]^{ - 1} } \right\}dt $$
(8)

where \(\theta_{r} \left( {x,\omega } \right)\) is the new variable component modified from an existing distribution as already defined. Of course, the result obtained from \(\left[ { \mathop \int \limits_{ - \infty }^{\infty } \theta_{r} \left( {x,\omega } \right)dx } \right]^{ - 1}\) is a constant-parameter function that serves as the normalizing constant. This implies that the product of \(\theta_{r} \left( {x,\omega } \right)\) and the normalizing constant yields a new PDF. In this approach, it should be noted that, consistently, the root distribution is returned as a special case of new development.

For the purposes of nomenclature, we term this construction Omega \(\omega\)-Type Probability Models, where omega \(\omega\) represents the primitive parametric substitution and Type denotes the root model from which the arbitrary function was taken.

3 Omega Lindley Distribution

Originally, the Lindley distribution was introduced by Lindley [14], and its properties were studied by Ghitany Atieh and Nadarajah [15]. However, to compensate for the monotonic property of the Lindley distribution, several authors, including [16,17,18,19] among others, have proposed at least a generalization of the Lindley distribution. These developments have increased the flexibility of the baseline distribution in different ways, ranging from monotone increasing trends, symmetric trends, left- and right-skewed trends, bathtubs, etc., in terms of density and hazard considerations. However, a real-life observation characterized by a modified unimodal (bathtub + inverted bathtub) trend in both density and hazard function considerations is not yet a feature of the Lindley family of distributions. Hence, we introduce a probability model, which will capture that essence. Considering the exemplified function in (4), we give a construction, and by recalling (7), we obtain the new PDF as

$$ u\left( {x,~\omega } \right) = \left\{ {\left( {1 + x^{b} } \right){\text{e}}^{{ - ax^{c} }} } \right\}\left[ {~\mathop \smallint \limits_{{ - \infty }}^{\infty } \left( {1 + x^{b} } \right){\text{e}}^{{ - ax^{c} }} dx~} \right]^{{ - 1}} , = \frac{{c~~~a^{{1 + b/c}} }}{{N_{^\circ } }}\left( {1 + x^{b} } \right)~{\text{e}}^{{ - ax^{c} }} , \quad x > 0, \quad a > 0, \quad b > 0, \quad c > 0. $$
(9)

where \(N_{^\circ } = a^{b/c} { }\Gamma \left[ \frac{1}{c} \right] + \Gamma \left[ {\frac{1 + b}{c}} \right]\).

and the corresponding cumulative distribution function is given by

$$ U\left( {x, \omega } \right) = \frac{{\left( {ax^{c} } \right)a^{{\frac{1 + b}{c}}} x^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}, $$
(10)

where \(\varphi_{abc} = \left\{ {\left[ {\left( {ax^{c} } \right)^{b/c} \left( {\Gamma \left[ \frac{1}{c} \right] - \Gamma \left[ {\frac{1}{c}, ax^{c} } \right]} \right) } \right] + \left[ {x^{b} \Gamma \left( {\frac{1 + b}{c}} \right)} \right] - \left[ {\Gamma \left( {\frac{1 + b}{c}, ax^{c} } \right)} \right]} \right\}\).

However, by evaluating \( b = c = 1\), (9) and (10) reduce to the Lindley distribution, which is the root model.

4 Mathematical Properties of the Omega Lindley Distribution

In this section, we derive several possible mathematical properties, such as series representation, shape of the density, hazard and survival functions, moments and related measures, order statistics, quantile function and parameter estimation. Notably, algorithms from Wolfram Mathematica aided the derivations and numerical analyses in this work.

4.1 Series Representation

The following forms of mathematical (and special) functions can be represented as series:

$$ {\text{e}}^{{ - ax^{c} }} = \mathop \sum \limits_{i = 0}^{\infty } \frac{{\left( { - ax^{c} } \right)^{i} }}{i!}. $$
(11)
$$ \left( {1 + x^{b} } \right) = \mathop \sum \limits_{j = 0}^{\infty } \left( {\begin{array}{*{20}c} 1 \\ j \\ \end{array} } \right)x^{bj} $$
(12)
$$ \Gamma \left( {\theta , x} \right) = \Gamma \left( \theta \right) - \mathop \sum \limits_{p = 0}^{\infty } \frac{{\left( { - 1} \right)^{p} x^{\theta + p} }}{{p! \left( {\theta + p} \right)}} $$
(13)
$$ \to \Gamma \left[ {\frac{1}{c}, ax^{c} } \right] = \Gamma \left( \frac{1}{c} \right) - \mathop \sum \limits_{p = 0}^{\infty } \frac{{\left( { - 1} \right)^{p} \left( {ax^{c} } \right)^{{\frac{1}{c} + p}} }}{{p! \left( {\frac{1}{c} + p} \right)}}. $$
(14)
$$ \Gamma \left( {\frac{1 + b}{c}, ax^{c} } \right) = \Gamma \left( {\frac{1 + b}{c}} \right) - \mathop \sum \limits_{p = 0}^{\infty } \frac{{\left( { - 1} \right)^{p} \left( {ax^{c} } \right)^{{\frac{1 + b}{c} + p}} }}{{p!\left( {\frac{1 + b}{c} + p} \right)}} $$
(15)

By implication generally, Eqs. (9) and (10) are represented as.

$$ u\left( {x, \omega } \right) = \frac{{c a^{b/c} }}{{N_{^\circ } }} \mathop \sum \limits_{j = 0}^{\infty } \mathop \sum \limits_{i = 0}^{\infty } \left( {\begin{array}{*{20}c} 1 \\ j \\ \end{array} } \right) \frac{{\left( { - ax^{c} } \right)^{i} }}{i!} x^{bj} . $$
(16)
$$ U\left( {x, \omega } \right) = \frac{{\left( {ax^{c} } \right)a^{{\frac{1 + b}{c}}} x^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}, $$
(17)

where \( \begin{aligned} \varphi_{abc} &= \left[ {\left( {ax^{c} } \right)^{b/c} \left( {\Gamma \left[ \frac{1}{c} \right] - \left[ {\Gamma \left( \frac{1}{c} \right) - \mathop \sum \limits_{p = 0}^{\infty } \frac{{\left( { - 1} \right)^{p} \left( {ax^{c} } \right)^{{\frac{1}{c} + p}} }}{{p! \left( {\frac{1}{c} + p} \right)}}} \right]} \right) } \right] \\ &\quad + \left[ {x^{b} \Gamma \left( {\frac{1 + b}{c}} \right)} \right] - \left[ {\Gamma \left( {\frac{1 + b}{c}} \right) - \mathop \sum \limits_{p = 0}^{\infty } \frac{{\left( { - 1} \right)^{p} \left( {ax^{c} } \right)^{{\frac{1 + b}{c} + p}} }}{{p! \left( {\frac{1 + b}{c} + p} \right)}}} \right] \end{aligned}\).

These, in essence, simply reduce the computational complexities that come with having a variable in special functions such as the incomplete gamma function.

4.2 The Shape of the Density, Hazard and Survival Functions of the Omega Lindley Distribution

Here, we examine the various possible shapes of the density function obtained in (9), where the hazard rate function and survival model of the \(\omega - Lindley\) distribution are derived as

$$ H\left( {x,\omega } \right) = \frac{{u\left( {x, \omega } \right)}}{{1 - U\left( {x, \omega } \right)}}; S\left( {x,\omega } \right) = 1 - U\left( {x, \omega } \right). $$
(18)

The different plots are intended to X-ray the modeling potentials of the proposed distribution.

The graphical plot in Fig. 1 indicates that the density function of the \(\omega - Lindley\) distribution exhibits a monotonic increasing and decreasing trend and a right skewed, approximately symmetric and modified unimodal trend (bathtub and inverted bathtub). This is a more robust improvement to the exponential and Lindley distribution, which is characterized by a monotonic decreasing trend only. The respective parameter combinations for each of the density shapes are given thus:

  • a = 1.28, b = 6.48, c = 1 || a = 0.21, b = 3.4, c = 1.2;

  • a = 1, b = 1.15, c = 1 || a = 1, b = 1, c = 1;

  • a = 0.01, b = 2.11, c = 0.29;

  • a = 0.1, b = 0.51, c = 0.57.

Fig. 1
figure 1

Density shapes of the \( \omega - Lindley\) distribution

Full size image

The respective parameter combinations for each of the hazard shapes are given thus:

  • a = 2.43, b = 1, c = 0.25

  • a = 1, b = 2, c = 0.27

  • a = 2.26, b = 1, c = 0.24

  • a = 4.17, b = 2.56, c = 0.49

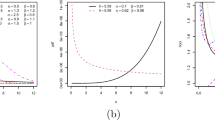
The graphical plots in Fig. 2 show that the hazard rate function of the \(\omega -\) Lindley distribution exhibits both decreasing and increasing trends: bathtub and modified unimodal shaped properties. In addition, Fig. 3 shows the survival trend, which is conventionally marked by its decreasing characteristics; however, a constant trend is also obtained. By implication, the proposed distribution would not only model systems or components that will definitely terminate but also one such system that can be sustained over a given time.

Fig. 2
figure 2

Hazard plots for the \( \omega - Lindley\) distribution

Full size image
Fig. 3
figure 3

Survival plots for \( \omega - Lindley\) distribution

Full size image

4.3 Moments and Related Measures

If X is a random variable from a continuous distribution and \(g\left( x \right)\) is the density function, then the \(rth\) moment about the origin of X is defined by

$$ E\left( {X^{r} } \right) = \mathop \int \limits_{0}^{\infty } x^{r} g\left( x \right)dx = \mu_{^{\prime}}^{r} . $$
(19)

Now, for the \(\omega -\) Lindley distribution, we recall (9) and obtain

$$ E\left( {X^{r} } \right) = \frac{{c a^{1+b/c} }}{{N_{^\circ } }} \mathop \int \limits_{0}^{\infty } x^{r} \left( {1 + x^{b} } \right) {\text{e}}^{{ - ax^{c} }} , $$
(20)
$$ = \frac{{a^{{\frac{1 + b}{c} - \frac{1 + b + r}{c}}} \left( {a^{b/c} \Gamma \left[ {\frac{1 + r}{c}} \right] + \Gamma \left[ {\frac{1 + b + r}{c}} \right]} \right)}}{{N_{^\circ } }}. $$
(21)

Of course, the first four \(r^{th}\) moments of the \(\omega -\) Lindley distribution are further obtained at \(r = 1,\;2,\;3\; \text{and}\; 4\)

$$ \mu_{1}^{\prime} = \frac{{a^{{\frac{1 + b}{c} - \frac{2 + b}{c}}} \left( {a^{b/c} \;\Gamma \left[ \frac{2}{c} \right] + \Gamma \left[ {\frac{2 + b}{c}} \right]} \right)}}{{N_{^\circ } }} = \mu \mu_{2}^{\prime} = \frac{{a^{{\frac{1 + b}{c} - \frac{3 + b}{c}}} \left( {a^{b/c} { }\Gamma \left[ \frac{3}{c} \right] + \Gamma \left[ {\frac{3 + b}{c}} \right]} \right)}}{{N_{^\circ } }} , $$
(22)
$$ \mu_{3}^{\prime} = \frac{{a^{{\frac{1 + b}{c} - \frac{4 + b}{c}}} \left( {a^{b/c} { }\Gamma \left[ \frac{4}{c} \right] + { }\Gamma \left[ {\frac{4 + b}{c}} \right]} \right)}}{{N_{^\circ } }} \;\mu_{4}^{\prime} = \frac{{a^{{\frac{1 + b}{c} - \frac{5 + b}{c}}} \left( {a^{b/c} { }\Gamma \left[ \frac{5}{c} \right] + \Gamma \left[ {\frac{5 + b}{c}} \right]} \right)}}{{N_{^\circ } }} $$
(23)

Therefore, the variance, skewness and kurtosis of the \(\omega -\) Lindley distribution can be obtained

$$Variance(\mu _{2} ) = \mu _{2}^{{\prime }} - \mu ^{2} = \sigma ^{2} \;Skewness\left( {S_{k} } \right) = \frac{{\mu _{3} }}{{\left( {\mu _{2} } \right)^{{3/2}} }} = \frac{{\mu _{3}^{{\prime }} - 3\mu _{2}^{{\prime }} \mu + 2\mu ^{3} }}{{\left( {\mu _{2}^{,} - \mu ^{2} } \right)^{{3/2}} }}$$
(24)
$$ Kurtosis \left( {K_{s} } \right) = \frac{{\mu_{4} }}{{\left( {\mu_{2} } \right)^{2} }} = \frac{{\mu_{4}^{\prime} - 4\mu_{3}^{\prime} \mu + 6\mu_{2}^{\prime} \mu^{2} - 3\mu^{4} }}{{\left( {\mu_{2}^{\prime} - \mu^{2} } \right)^{2} }} . $$
(25)

Numerical analysis of the theoretical moments of the \(\omega -\) Lindley distribution for the selected parameter values is shown in Tables 1, 2 and 3.

Table 1 Moments of \(\upomega -\text{Lindley}\) distribution at \(\text{c}=1\)
Full size table
Table 2 Moments of \(\upomega -\text{Lindley}\) distribution at \(\text{c}=1.5\)
Full size table
Table 3 Moments of \(\upomega -\text{Lindley}\) distribution at \(\text{c}=5\)
Full size table

By carefully observing Tables 1, 2 and 3, we see that the \(\omega -Lindley\) distribution is right skewed \((S_{k} > 0)\), approximately symmetric \( (S_{k} \approx 0)\), leptokurtic \( (K_{s} > 3)\), platykurtic \((K_{s} < 3)\) and mesokurtic \( \left( {K_{s} \approx 3} \right)\). These numerical characteristics are backup points that support the graphical illustration of the density function, as shown in Fig. 1.

4.4 Order Statistics

Let \(X_{1} , X_{2} , \ldots ,X_{n}\) be a random sample of size n from the \(\omega - Lindley\) distribution. Let \(X_{1} < X_{2} < , \ldots , < X_{n}\) denote the corresponding order statistics. The density and distribution functions of the kth-order statistics \(Y = X_{k} \) are given by:

$$ f_{Y} \left( {\text{y}} \right) = { }\frac{{{\text{n}}!}}{{\left( { k - 1} \right)!\left( { n - k} \right)!}} f\left( y \right) F^{k - 1} \left( y \right) \left\{ {1 - F\left( y \right)} \right\}^{n - k} , $$
(26)

However, \( \left\{ {1 - F\left( y \right)} \right\}^{n - k} = \mathop \sum \limits_{l = 0}^{\infty } \left( {\begin{array}{*{20}c} {n - k} \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l} \left[ {F\left( y \right)} \right]^{l}\)

$$ \therefore f_{Y} \left( {\text{y}} \right) = { }\frac{{{\text{n}}!{ }c a^{1+b/c} }}{{\left( { k - 1} \right)!\left( { n - k} \right)!}} \left\{ { \left( {1 + y^{b} } \right) {\text{e}}^{{ - ay^{c} }} } \right\}N_{^\circ }^{ - 2} \left\{ {\left( {ay^{c} } \right) a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} } \right\}^{k - 1} $$
$$ \left\{ {\mathop \sum \limits_{l = 0}^{\infty } \left( {\begin{array}{*{20}c} {n - k} \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l} \left[ {\frac{{\left( {ay^{c} } \right)a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}} \right]^{l} } \right\}. $$
(27)
$$ {\text{and}}\;F_{Y} \left( {\text{y}} \right) = \mathop \sum \limits_{j = k}^{n} \left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right) F^{j} \left( y \right) \left\{ {1 - F\left( y \right)} \right\}^{n - j} $$
(28)
$$ = F_{Y} \left( {\text{y}} \right) = \mathop \sum \limits_{j = k}^{n} \mathop \sum \limits_{l = 0}^{n - j} \left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n - j} \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l } F^{j + l} \left( y \right), $$
(29)
$$ = \mathop \sum \limits_{j = k}^{n} \mathop \sum \limits_{l = 0}^{\infty } \left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n - j} \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l} \left[ {\frac{{\left( {ay^{c} } \right) a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}} \right]^{j + l} . $$
(30)

By implication, the PDF of minimum order statistics is obtained by evaluating \( j = k = 1\) in (27) to obtain:

$$ f_{1:n} = { }c a^{1+b/c} \left\{ { \left( {1 + y^{b} } \right) {\text{e}}^{{ - ay^{c} }} } \right\} N_{^\circ }^{ - 2} \left\{ {\mathop \sum \limits_{l = 0}^{\infty } \left( {\begin{array}{*{20}c} {n - 1} \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l} \left[ {\frac{{\left( {ay^{c} } \right) a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}} \right]^{l} } \right\}. $$
(31)

where the corresponding PDF of the maximum order statistics is obtained at \( j = k = n\) in (27):

$$ f_{n:n} = { }c a^{1+b/c} \left\{ { \left( {1 + y^{b} } \right) {\text{e}}^{{ - ay^{c} }} } \right\}N_{^\circ }^{ - 2} \left\{ {\left( {ay^{c} } \right) a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} } \right\}^{n - 1} $$
$$ \left\{ {\mathop \sum \limits_{l = 0}^{\infty } \left( {\begin{array}{*{20}c} 0 \\ l \\ \end{array} } \right)\left( { - 1} \right)^{l} \left[ {\frac{{\left( {ay^{c} } \right)a^{{\frac{1 + b}{c}}} y^{{ - \frac{1 + b}{c}}} \varphi_{abc} }}{{N_{^\circ } }}} \right]^{l} } \right\}. $$
(32)

4.5 The Quantile Function of the Omega Lindley Distribution

The expression \(Q_{x} \left( p \right) = U^{ - 1} \left( p \right)\) gives the quantile function of the \(\omega - Lindley\) distribution, where \(0 < p < 1\) and the function \(U\) is the cumulative distribution function. Now, recalling (10), the \(p^{th}\) quantile function is obtained by solving

$$ U\left( {x, \omega } \right) = p. $$
(33)

Structurally, it may not be feasible to obtain the inverse of \(x\) as in \(Q_{x} \left( p \right) = U^{ - 1} \left( p \right)\) due to the gamma components in the CDF; hence, we leave the expression as a nonlinear equation; thus,

$$ U\left( {x, \omega } \right) - p = 0. $$
(34)

Moreover, the median of the \(\omega - Lindley\) distribution can be obtained by evaluating \(p = 0.5\) in (34). The derivation of the quantile function of the proposed distribution is intentionally skipped due to the special functions in the CDF. Hence, we use algorithms in Wolfram Mathematica to generate random numbers.

4.6 Parameter Estimation

In this section, we present methods for estimating the parameters of the \(\omega - Lindley\) distribution, which include the Cramer–von Mises estimator, the maximum product of spacing estimators and the maximum likelihood estimator.

4.6.1 Cramer–Von Mises (CVM) Estimator

Macdonald [20] proposed CVM as an estimation method with the objective of minimizing the following function:

$$ V_{c} = \left( {12n} \right)^{ - 1} + \mathop \sum \limits_{i = 1}^{n} \left[ {F\left( {x_{\left( i \right)} } \right) - \frac{2i - 1}{{2n}}} \right]^{2} . $$
(35)

Now, by substituting the CDF of the \(\omega - Lindley\) distribution \(U\left( {x, \omega } \right)\) as in (10) into (35), we obtain

$$ V_{c} \left( {a,b,c} \right) = \left( {12n} \right)^{ - 1} + \mathop \sum \limits_{i = 1}^{n} \left[ {A\left( {a x_{\left( i \right)}^{c} x_{\left( i \right)}^{{ - \frac{1 + b}{c}}} \varphi_{abc}^{{x_{\left( i \right)} }} } \right) - \frac{2i - 1}{{2n}}} \right]^{2} , $$
(36)

where \(A = \frac{{ a^{{\frac{1 + b}{c}}} }}{{N_{^\circ } }}\).

Using a software algorithm, (36) can be minimized to obtain the estimates of the CVM, or we can maximize it by solving

$$ \frac{{\partial V_{c} \left( {a,b,c} \right)}}{\partial a} = 0; \frac{{\partial V_{c} \left( {a,b,c} \right)}}{\partial b} = 0; \frac{{\partial V_{c} \left( {a,b,c} \right)}}{\partial c} = 0. $$
(37)

4.6.2 Maximum Product of Spacing (MPS) Estimators

This method was originally used by Cheng and Amin [21] to estimate the parameters of lognormal distributions and is given as

$$ M_{p} = \frac{1}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \log R_{i} , $$
(38)

where \(R_{i} = F\left( {x_{\left( i \right)} } \right) - F\left( {x_{{\left( {i - 1} \right)}} } \right)\) and \(F\left( {x_{\left( 0 \right)} } \right) = 0\); \(F\left( {x_{{\left( {n + 1} \right)}} } \right) = 1\).

To obtain the function in (38) for the \(\omega - Lindley\) distribution, we substitute the CDF \(U\left( {x, \omega } \right)\) in \(F\left( {x_{\left( * \right)} } \right)\)

$$ M_{p} \left( {a,b,c} \right) = \frac{1}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \log \left[ {U\left( {x_{\left( i \right)} } \right) - U\left( {x_{{\left( {i - 1} \right)}} } \right)} \right], $$
(39)
$$ = \frac{A}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \log \left[ {\left( {\left( {ax_{\left( i \right)}^{c} } \right) x_{\left( i \right)}^{{ - \frac{1 + b}{c}}} \varphi_{abc}^{{x_{\left( i \right)} }} } \right) - \left( {\left( {ax_{{\left( {i - 1} \right)}}^{c} } \right) x_{{\left( {i - 1} \right)}}^{{ - \frac{1 + b}{c}}} \varphi_{abc}^{{x_{{\left( {i - 1} \right)}} }} } \right)} \right] $$
(40)

The MPS can be estimated by maximizing (40) at \( \frac{{\partial M_{p} \left( {a,b,c} \right)}}{\partial \omega } = 0\), where

$$ \frac{{\partial M_{p} \left( {a,b,c} \right)}}{\partial a} = \frac{1}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \frac{\partial }{\partial a}\left\{ {\log \left[ {U\left( {x_{\left( i \right)} } \right) - U\left( {x_{{\left( {i - 1} \right)}} } \right)} \right]} \right\} . $$
(41)
$$ \frac{{\partial M_{p} \left( {a,b,c} \right)}}{\partial b} = \frac{1}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \frac{\partial }{\partial b}\left\{ {\log \left[ {U\left( {x_{\left( i \right)} } \right) - U\left( {x_{{\left( {i - 1} \right)}} } \right)} \right]} \right\}. $$
(42)
$$ \frac{{\partial M_{p} \left( {a,b,c} \right)}}{\partial c} = \frac{1}{n + 1} \mathop \sum \limits_{i = 1}^{n + 1} \frac{\partial }{\partial c}\left\{ {\log \left[ {U\left( {x_{\left( i \right)} } \right) - U\left( {x_{{\left( {i - 1} \right)}} } \right)} \right]} \right\}. $$
(43)

4.6.3 Maximum Likelihood Estimator (MLE)

Myung [22] highlighted the objective of MLE, which is to obtain the parameter values of a model that maximizes the likelihood function over the spatial dimension of the parameters.

Let \(x_{i} , i = 1,2, \ldots ,n\) be a vector of observations from the \(\omega - Lindley\) distribution; then, the log-likelihood function is defined by

$$ lnL = \mathop \sum \limits_{i = 1}^{n} \log f\left( {x_{i} ;\omega } \right) = \mathop \sum \limits_{i = 1}^{n} \log \left[ {\frac{{c a^{1+b/c} \left( {1 + x^{b} } \right) {\text{e}}^{{ - ax^{c} }} }}{{a^{b/c} { }\Gamma \left[ \frac{1}{c} \right] + \Gamma \left[ {\frac{1 + b}{c}} \right]}}} \right], $$
(44)
$$ = log\left[ {\frac{{c a^{1+b/c} }}{{a^{b/c} { }\Gamma \left[ \frac{1}{c} \right] + \Gamma \left[ {\frac{1 + b}{c}} \right]}}} \right]^{n} + \mathop \sum \limits_{i = 1}^{n} log\left( {1 + x^{b} } \right) - a\mathop \sum \limits_{i = 1}^{n} x_{i}^{c} , $$
(45)
$$ = nlog c + n\left( {1 + \frac{b}{c}} \right)\log a - n\left( \frac{b}{c} \right)\log a - \log \Gamma \left( \frac{1}{c} \right) $$
$$ - \log \Gamma \left( {\frac{1 + b}{c}} \right) + \mathop \sum \limits_{i = 1}^{n} log\left( {1 + x^{b} } \right) - a\mathop \sum \limits_{i = 1}^{n} x_{i}^{c} . $$
(46)

The score function for (46) is defined by

$$ \frac{\partial lnL}{{\partial a}} = n\left( {1 + \frac{b}{c}} \right)\left( \frac{1}{a} \right) - n\left( \frac{b}{c} \right)\left( \frac{1}{a} \right) - \mathop \sum \limits_{i = 1}^{n} x_{i}^{c} , $$
(47)

\(\frac{n}{a} - \mathop \sum \limits_{i = 1}^{n} x_{i}^{c} = 0\).

$$ \frac{\partial lnL}{{\partial b}} = n\left( \frac{1}{c} \right)\log a - n\left( \frac{1}{c} \right)\log a - \frac{{P_{g} \left( {0, \frac{1 + b}{c}} \right)}}{c} + \mathop \sum \limits_{i = 1}^{n} \frac{{x^{b} logx}}{{\left( {1 + x^{b} } \right)}} , $$
(48)
$$ \mathop \sum \limits_{i = 1}^{n} \frac{{x_{i}^{b} logx}}{{\left( {1 + x_{i}^{b} } \right)}} - \frac{{P_{g} \left( {0, \frac{1 + b}{c}} \right)}}{c} = 0. $$
$$\begin{aligned} \frac{\partial lnL}{{\partial c}} &= \frac{n}{c} - n\left( {\frac{b}{{c^{2} }}} \right)\log a + n\left( {\frac{b}{{c^{2} }}} \right)\log a + \frac{{P_{g} \left( {0, \frac{1}{c}} \right)}}{{c^{2} }}\\ &\quad + \frac{{\left( {1 + b} \right){ }P_{g} \left( {0, \frac{1 + b}{c}} \right)}}{{c^{2} }} - a\mathop \sum \limits_{i = 1}^{n} x_{i}^{c} \log (x_{i} ), \end{aligned}$$
(49)

\(\frac{n}{c} + \frac{{P_{g} \left( {0, \frac{1}{c}} \right)}}{{c^{2} }} + \frac{{\left( {1 + b} \right){ }P_{g} \left( {0, \frac{1 + b}{c}} \right)}}{{c^{2} }} - a\mathop \sum \limits_{i = 1}^{n} x_{i}^{c} \log (x_{i} ) = 0\).

where \(P_{g} \left( {*,*} \right)\) is poly-gamma.

It can be clearly seen that (47, 48 and 49) is in close form. Therefore, a numerical analysis such as the Newton–Raphson iterative method, which is a root finding algorithm, can be used to obtain the MLEs of \( \hat{a},\hat{b} \;and \;\hat{c}\). This scheme is given by

$$ \hat{\omega } = \omega - H^{ - 1} \left( \omega \right) S\left( \omega \right). $$
(50)

where \(S\left( \omega \right)\) is the score function and \(H^{ - 1} \left( \omega \right)\) is the second derivative of the log-likelihood function termed the Hessian matrix. Refer to [23, 24] for a detailed study.

4.7 Interval Estimation

Furthermore, we present the asymptotic confidence intervals for the parameters of the \(\omega - Lindley\) distribution. In this attempt, the Fisher information matrix is adopted with the goal of measuring the amount of information that a random vector of variables carries about unknown parameters of a probability model that forecasts for \( X_{i} , i = 1,2,3, \ldots n\). The information matrix is given by

$$ I\left( {\omega_{k} } \right) = - E\left[ {H\left( {\omega_{k} } \right)} \right] = - E\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} l}}{{\partial a^{2} }}} & {\frac{{\partial^{2} l}}{\partial a\partial b}} & {\frac{{\partial^{2} l}}{\partial a\partial c}} \\ {\frac{{\partial^{2} l}}{\partial a\partial b}} & {\frac{{\partial^{2} l}}{{\partial b^{2} }}} & {\frac{{\partial^{2} l}}{\partial b\partial c}} \\ {\frac{{\partial^{2} l}}{\partial a\partial c}} & {\frac{{\partial^{2} l}}{\partial b\partial c}} & {\frac{{\partial^{2} l}}{{\partial c^{2} }}} \\ \end{array} } \right], \omega = \left( {a,b,c} \right)^{T} . $$
(51)

Under the normality condition \( \hat{\omega } \sim N\left( {\omega , I^{ - 1} \left( \omega \right)} \right)\), is obtained by inverting (51). Consequently, the interval estimate is obtained by the approximation of \(\left( {1 - \alpha } \right)100\) confidence intervals constructed for the parameters \( a, b and c\):

\(\hat{a} \pm Z_{\alpha /2} \sqrt {var\left( {\hat{a}} \right)}\); \(\hat{b} \pm Z_{\alpha /2} \sqrt {var\left( {\hat{b}} \right)}\); \(\hat{c} \pm Z_{\alpha /2} \sqrt {var\left( {\hat{c}} \right)}\). where \(var\left( \omega \right)\) are the variances of the parameters, which are given by the respective diagonal elements of the variance‒covariance matrix \(I^{ - 1} \left( {\omega_{k} } \right)\), and \(Z_{\alpha /2}\) is the upper percentile of the standard normal distribution.

5 Real Data Analysis

The analyses of two real-life datasets are detailed in this section to demonstrate the applicability of the proposed distribution. Ghitany [15] presented a dataset that measures the waiting time (in minutes) of 100 bank customers, whereas the second dataset represents the remission time of 128 bladder cancer patients, as reported in [25]. The omega \(\omega - Lindley\) distribution is fitted to these data alongside other Lindley families of distributions:

  • The three-parameter generalized Lindley distribution (TPGLD) was described in [18]:

    $$ g\left( x \right) = \frac{{ac^{2} {\text{e}}^{{ - cx^{a} }} x^{ - 1 + a} \left( {b + x^{a} } \right) }}{1 + bc}, x > 0, a,b,c > 0. $$
    (52)

  • The new generalized two parameter Lindley distribution (NG2PLD) was described in [17]:

    $$ g\left( x \right) = \frac{{a^{2} {\text{e}}^{ - ax} \left( {1 + \frac{{a^{ - 2 + b} x^{ - 1 + b} }}{\Gamma \left[ b \right]}} \right)}}{1 + a}, x > 0, a,b > 0. $$
    (53)

The power Lindley distribution (PLD) was described in [16]:

$$ g\left( x \right) = \frac{{a b^{2} {\text{e}}^{{ - b x^{a} }} \left( {1 + x^{a} } \right) x^{a - 1} }}{1 + b}, x > 0, a,b > 0. $$
(54)

The Lindley distribution (LD) was described in [14]:

$$ g\left( x \right) = \frac{{a^{2} {\text{e}}^{ - ax} \left( {1 + x} \right)}}{1 + a}, x > 0, a > 0. $$
(55)

The measurement criteria used for performance comparison in this work were the Cramer–von Mises (\(C_{{{\varvec{v}}{\mathbf{\mathcal{M}}}}}\)), Anderson Darling , and Pearson chi-square (\(\chi^{2}\)) test statistics and their corresponding P values. These automatically selected statistics are based on the following:

$$C_{{{\varvec{v}}{\mathbf{\mathcal{M}}}}} { }\sim {\text{ Expectation}} \left\{ {\left[ {\hat{F}\left( x \right) - F\left( x \right)} \right]^{2} } \right\}$$

where \( F\left( x \right)\) and \(\hat{F}\left( x \right)\) are the CDFs of the distributions and the empirical CDFs of the data, respectively, and \(o_{i}\) and \(e_{i}\) are the observed and expected frequencies, respectively. The parameter estimates and analytical results are summarized in Tables 4, 5, 6 and 7, and Figs. 4, 5, 6 and 7 are the supporting diagrammatical analogy of the empirical inference.

Table 4 Parameters for the comparative analysis of dataset 1
Full size table
Table 5 Inferential results of the proposed model and selected Lindley families of distribution (data 1)
Full size table
Table 6 Parameters for the comparative analysis of data 2
Full size table
Table 7 Inferential results of the proposed model and selected Lindley families of distribution (data 2)
Full size table
Fig. 4
figure 4

Density fit plots for dataset 1

Full size image
Fig. 5
figure 5

Fitted quantile (q-q) plot [left] and probability (p-p) plot [right] for data 1

Full size image
Fig. 6
figure 6

Density fit plots for dataset 2

Full size image
Fig. 7
figure 7

Fitted quantile (q-q) plot [left] and probability (p-p) plot [right] for dataset 2

Full size image

Judging from the inferential measures, which project comparative goodness based on the least empirical status of the three automatically selected test criteria, it can clearly be observed from Tables 5 and 7 that the proposed distribution is a better fit for the datasets. This is also proven diagrammatically according to Figs. 4 and 6, which represent the density fit plots. Further support for the results can be found in Figs. 5 and 7, which include quantile and probability (q-q and p-p) plots.

6 Concluding Remarks

In this research, a more efficient approach to increasing the number of parameters in an existing distribution apart from the generalization method is presented, and by applying this concept, a new distribution is proposed. Some mathematical properties of the proposed distribution, including series representations of the PDF and CDF, density, hazard and survival shapes, moments and related measures, quantile functions, parameter estimations, interval estimates and order statistics, are derived and/or realized. Due to the special functions in the CDF, both the hazard and survival functions are rendered in a closed-form structure. As a result, they yield both monotonic and nonmonotonic trends, which is a great economy in data modeling. The survival function uniquely features a uniform trend, which implies that the proposed distribution can model systems or components whose lifespan is sustained over a given range of time. The parameter estimation is theoretically studied under three different methods, including the Cramer Von Mise, maximum product of spacing and maximum likelihood approaches. Finally, the proposed model is fitted to two real-life datasets to assess its flexibility. Based on the obtained empirical and diagrammatical results, the proposed distribution can better forecast the datasets than several other rival lifetime models. The proposed parameter inclusion strategy is expected to be adopted in the field of mathematical statistics, and the proposed model has wider applications in areas consistent with survival data analysis.