Quantile Generated Nadarajah–Haghighi Family of Distributions

Abstract

The T-NH{Y} family is developed and study in this paper. Various statistical properties such as the mode, quantile, moments and Shannon entropy were derived. Two special distributions namely, exponential-NH{log-logistic}and Gumbel-NH{logistic} were developed. Plots of the failure rate functions for these distributions for some given parameter values indicated that the hazard rate functions can exhibit different types of non-monotonic failure rates. Two applications using real datasets on failure times revealed that the exponential-NH{log-logistic} distribution provides better fits to the datasets than the other fitted models.

1 Introduction

Arriving at a sound statistical inference for any given dataset heavily depends on the use of appropriate statistical model. Thus, selecting an appropriate model for analyzing this barrage of datasets generated from different fields of study often pose a challenge to researchers. This is because when an inadequate model is selected for a particular dataset, it will reduce the power and efficiency of the statistical test associated with that dataset. To improve the precision when fitting the data, statistical data analysts are therefore interested in using a model that leads to no or less loss of information. Among these models often used, probability distributions play an integral role. However, identifying an appropriate distribution that best describes the traits of a given dataset is often a challenge despite the existence of several probability distributions. This can be ascribed to the fact that no single distribution can be identified as best for all kinds of datasets.

To fill this lacuna, researchers are proposing techniques for generalizing existing distributions. These techniques seek to improve the performance of the distributions or make them more flexible in modeling datasets with traits such as skewness, kurtosis, monotonic and non-monotonic (bathtub, modified bathtub, upside-down bathtub and modified upside-down bathtub) failure rates. One of the techniques used in literature in recent time by researchers is the quantile based approach of Aljarrah et al. [3] which is often referred to as the $T - R\{ Y\}$ family. This method is an extension of Alzaatreh et al. [7] transformed-transformer (T-X) family of distributions.

Suppose $F_{T} (x) = P(T \le x),F_{R} (x) = P(R \le x)$ and $F_{Y} (x) = P(Y \le x)$ are the cumulative distribution functions of the random variables $T,R$ and $Y$ respectively. Let the inverse distributions (quantile functions) of the random variables be given by $Q_{T} (u),Q_{R} (u)$ and $Q_{Y} (u)$, where $Q_{z} (u) = Inf\{ z:F_{Z} (z) \ge u\}$, $0 \le u \le 1$. Also, if the density functions of $T,R$ and $Y$ exists, and are represented by $f_{T} (x),f_{R} (x)$ and $f_{Y} (x)$ respectively. If we assume that $T,Y \in (\varphi_{1} ,\varphi_{2} )$ for $- \infty \le \varphi_{1} < \varphi_{2} \le \infty$, then the cumulative distribution function (CDF) of the random variable $X$ in the $T - R\{ Y\}$ family of Aljarrah et al. [3] is given by:

$$ F_{X} (x) = \int\limits_{{\varphi_{1} }}^{{Q_{Y} (F_{R} (x))}} {f_{T} (t)dt} = F_{T} \left[ {Q_{Y} (F_{R} (x))} \right] . { } $$

(1)

The corresponding probability density function (PDF) and hazard rate function are

$$ \begin{aligned} f_{X} (x) & = f_{R} (x)Q_{Y}^{'} (F_{R} (x))f_{T} \left[ {Q_{Y} (F_{R} (x))} \right] \\ & { = }f_{R} (x)\frac{{f_{T} \left[ {Q_{Y} (F_{R} (x))} \right]}}{{f_{Y} \left[ {Q_{Y} (F_{R} (x))} \right]}} \\ \end{aligned} $$

(2)

and

$$ \tau_{X} (x) = \tau_{R} (x)\frac{{\tau_{T} \left[ {Q_{Y} (F_{R} (x))} \right]}}{{\tau_{Y} \left[ {Q_{Y} (F_{R} (x))} \right]}}, $$

(3)

respectively. $\tau ( \cdot )$ denotes the hazard rate function of the random variables.The $T - R\{ Y\}$ method have been adopted by number of researchers to develop new families of distributions and these include: extended generalized Burr III family [11]; T-exponential{Y} class [22]; generalized Burr family [16]; T-normal family [6]; T-Pareto family [10]; T-gamma{Y} family [5]; Lomax-R {Y} family [14]; Weibull-R{Y} family [9] and T-Weibull family [4].

In this study, we assume that the random variable $R$ follows that Nadarajah-Haghighi (NH) distribution [15] and proposed the T-NH{Y} family of distributions.

Our motivation for developing this family of distributions are: to produce distributions capable of modeling data sets that exhibit monotonic and non-monotonic failure rates; to produce heavy-tailed distributions; to make kurtosis more flexible as compared to the baseline distribution; to generate distributions with left-skewed, right-skewed, symmetric and reversed-J shapes; and to provide better parametric fit to given data sets than other existing distributions. The remaining parts of the article are presented as follow: the T-NH{Y} family is presented in Sect. 2, the statistical properties of the proposed family are given in Sect. 3, the special distributions are proposed in Sect. 4, the estimation of the parameters are presented in Sect. 5, Sect. 6 presents the Monte Carlo simulations, the empirical applications are given in Sect. 7 and the conclusions of the study are given in Sect. 8.

2 T-NH {Y} Family of Distributions

Given that the underlying distribution of the random variable $R$ is NH with CDF and PDF given by; $F_{R} (x) = 1 - \exp (1 - (1 + \gamma x)^{\alpha } ),x > 0,\gamma > 0,\alpha > 0$ and $f_{R} (x) = \alpha \gamma (1 + \gamma x)^{\alpha - 1} \exp (1 - (1 + \gamma x)^{\alpha } )$ respectively. Then, the CDF of the T-NH{Y} family is:

$$ F_{X} (x) = \int\limits_{{\varphi_{1} }}^{{Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } )}} {f_{T} (t)dt} = F_{T} \left[ {Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } )} \right]. $$

(4)

The PDF and hazard function of the family are respectively given by:

$$ \begin{aligned} f_{X} (x) & = \alpha \gamma (1 + \gamma x)^{\alpha - 1} \exp (1 - (1 + \gamma x)^{\alpha } )Q_{Y}^{'} (1 - \exp (1 - (1 + \gamma x)^{\alpha } )) \\ & \quad \times \, f_{T} \left[ {Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } ))} \right] \\ \end{aligned} $$

(5)

and

$$ \tau_{X} (x) = \alpha \gamma (1 + \gamma x)^{\alpha - 1} \frac{{\tau_{T} \left[ {Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } ))} \right]}}{{\tau_{Y} \left[ {Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } ))} \right]}}. $$

(6)

Remark 1

If $X$ follows the T-NH{Y} family of distributions, then the following holds:

• (i) If $\alpha = 1$, then the T-NH{Y} family becomes the T-exponential{Y} family.

• (ii) $X{ = }\frac{1}{\gamma }\left\{ {\left[ {1 - \log (1 - F_{Y} (T))} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}$.

• (iii) $Q_{X} (u) = \frac{1}{\gamma }\left\{ {\left[ {1 - \log (1 - F_{Y} (Q_{T} (u)))} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\},u \in [0,1]$

• (iv) If $Y = {\text{ NH}}(\alpha ,\gamma )$, then $X = \, T$.

• (v) If $T = \, Y$, then $X = \, NH(\alpha ,\gamma )$.

2.1 Some Sub-families of T-NH{Y}

In this sub-section, two sub-families of the T-NH{Y} family are discussed. These are: the T-NH{log-logistic} and T-NH{logistic} families.

2.1.1 T-NH{log-logistic} Family

If the random variable $T$ is defined on the support $(0,\infty )$ and $Y$ follows the log-logistic (LL) distribution with quantile function $Q_{Y} (u) = \lambda [(1 - u)^{ - 1} - 1]^{{\tfrac{1}{\beta }}}$. The CDF and PDF of the T-NH{LL} family are respectively given by:

$$ F_{X} (x) = F_{T} \left[ {\lambda \left( {\exp ((1 + \gamma x)^{\alpha } - 1) - 1} \right)^{{\tfrac{1}{\beta }}} } \right] $$

(7)

and

$$ f_{X} (x) = \frac{{\alpha \gamma (1 + \gamma x)^{\alpha - 1} \left( {\exp ((1 + \gamma x)^{\alpha } - 1) - 1} \right)^{{\tfrac{1}{\beta } - 1}} }}{{\beta \exp (1 - (1 + \gamma x)^{\alpha } )}}f_{T} \left[ {\lambda \left( {\exp ((1 + \gamma x)^{\alpha } - 1) - 1} \right)^{{\tfrac{1}{\beta }}} } \right]. \, $$

(8)

The T-NH{LL} family reduces to the T-exponential{LL} family when the parameter $\alpha = 1$.

2.1.2 T-NH{logistic} Family

If the support of the random variable $T$ is defined on the interval $( - \infty ,\infty )$ and the distribution of the random variable $Y$ is logistic (L) with quantile function $Q_{Y} (u) = - \frac{1}{\lambda }\log (u^{ - 1} - 1)$. Then, the CDF and PDF of the T-NH{L} family are respectively given by;

$$ F_{X} (x) = F_{T} \left[ {\frac{ - 1}{\lambda }\log \left[ {(1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1} \right]} \right] $$

(9)

and

$$ \begin{aligned} f_{X} (x) & = \frac{{\alpha \gamma (1 + \gamma x)^{\alpha - 1} \exp (1 - (1 + \gamma x)^{\alpha } )}}{{\lambda \left( {1 - \exp (1 - (1 + \gamma x)^{\alpha } )} \right)^{2} \left[ {\left( {1 - \exp (1 - (1 + \gamma x)^{\alpha } )} \right)^{ - 1} - 1} \right]}} \\ & \quad \times f_{T} \left[ {\frac{ - 1}{\lambda }\log \left[ {\left( {1 - \exp (1 - (1 + \gamma x)^{\alpha } )} \right)^{ - 1} - 1} \right]} \right] .\\ \end{aligned} $$

(10)

When $\alpha = 1$, the T-NH{L} family becomes the T-exponential{L} family.

3 Statistical Properties of T-NH{Y} Family

This section presents some statistical properties of the T-NH{Y} family of distributions.

3.1 Mode

The mode of the T-NH{Y} family is presented in this sub-section.

Proposition 1

The mode of the T-NH{Y} family of distributions can be obtained from the solution of the equation:

$$ \begin{aligned} & \Psi \left[ {Q_{Y}^{'} (1 - \exp (1 - (1 + \gamma x)^{\alpha } ))} \right] + \Psi \left[ {f_{T} \left( {Q_{Y} (1 - \exp (1 - (1 + \gamma x)^{\alpha } ))} \right)} \right] \\ & \quad + \frac{\gamma (\alpha - 1)}{1 + \gamma x} - \alpha \gamma (1 + \gamma x)^{\alpha - 1} = 0, \\ \end{aligned} $$

(11)

where ${\Psi (f)} = {{f^{\prime}}/f}$.

Proof

Finding the first derivative of the logarithm of Eq. (5) with respect $x$ and equating it to zero completes the proof.□

3.2 Transformation

Lemma 1

Given that the random variable $T$ has CDF $F_{T} (x)$, then the random variable:

• (i) $X = \frac{1}{\gamma }\left\{ {\left[ {1 + \log \left( {1 + (T/\lambda )^{\beta } } \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}$ has the T-NH{LL} distribution.

• (ii) $X = \frac{1}{\gamma }\left\{ {\left[ {1 + \left( {\lambda T + \log (1 + \exp ( - \lambda T))} \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}$ has the T-NH{L} distribution.

Proof

The proof easily follows from Remark 1 (ii).□

3.3 Quantile Function

Quantile functions are useful in statistical analysis. For instance, they can be used to compute measures of shapes of a distribution and generate random observations during simulation experiments.

Lemma 2

The quantile functions of the T-NH{LL} and T-NH{L} are respectively given by:

• (i) $Q_{X} (u) = \frac{1}{\gamma }\left\{ {\left[ {1 + \log \left( {1 + (Q_{T} (u)/\lambda )^{\beta } } \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\},u \in [0,1]$.

• (ii) $Q_{X} (u) = \frac{1}{\gamma }\left\{ {\left[ {1 + \left( {\lambda Q_{T} (u) + \log (1 + \exp ( - \lambda Q_{T} (u)))} \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\},u \in [0,1]$.

Proof

The proof of this Lemma can easily be derived from Remark 1 (iii).□

3.4 Moments

Moments are used to estimate measures of central tendencies, shapes and dispersions. This subsection presents the moments of the T-NH{Y} family and its sub-families.

Proposition 2

The kth non-central moment of the T-NH{Y} family is given by:

$$ E(X^{k} ) = E\left[ {\frac{1}{{\gamma^{k} }}\left\{ {\left[ {1 - \log (1 - F_{Y} (T))} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}^{k} } \right],\quad k = 1,2, \ldots $$

(12)

Proof

The proof follows from Remark 1 (ii).□

Corollary 1

The kth non-central moments of T-NH{LL} and T-NH{L} are respectively given by:

• (i) $E(X^{k} ) = E\left[ {\frac{1}{{\gamma^{k} }}\left\{ {\left[ {1 + \log (1 + (T/\lambda )^{\beta } )} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}^{k} } \right],\quad k = 1,2, \ldots$.

• (ii) $E(X^{k} ) = E\left[ {\frac{1}{{\gamma^{k} }}\left\{ {\left[ {1 + \left( {\lambda T + \log (1 + \exp ( - \lambda T))} \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\}^{k} } \right],\quad k = 1,2, \ldots$.

Proof

The proof of Corollary 1 follows from Lemma 1.□

Proposition 3

The upper bound for the moment of the T-NH{Y} family is given by:

$$ E(X^{k} ) \le \alpha \gamma \exp (1){\text{I}}(k,0,1)E[(1 - F_{Y} (T))^{ - 1} ], $$

(13)

where

$$ {\text{I}}(k,0,1) = \frac{1}{{\alpha \gamma^{k + 1} }}\sum\limits_{i = 0}^{k} {( - 1)^{k - i} \left( {\begin{array}{*{20}c} k \\ i \\ \end{array} } \right)\varGamma (\tfrac{i}{\alpha } + 1,1)} . $$

Proof

From Theorem 1 of Aljarrah et al. [3], if $R$ is a non-negative random variable and $E[(1 - F_{Y} (T))^{ - 1} ] < \infty$, then $E(X^{k} ) \le E(R^{k} )E[(1 - F_{Y} (T))^{ - 1} ]$. From Nadarajah and Haghighi [15], the $k{\text{th}}$ non-central moment of the NH distribution is $\alpha \gamma \exp (1){\text{I}}(k,0,1)$. Substituting and simplifying yields the proof of Proposition 3.□

Corollary 2

The upper bound for the moments of T-NH{LL} and T-NH{L} are respectively given by:

• (i) $E(X^{k} ) \le \alpha \gamma \exp (1){\text{I}}(k,0,1)[1 + E((T/\lambda )^{\beta } )]$.

• (ii) $E(X^{k} ) \le \alpha \gamma \exp (1){\text{I}}(k,0,1)E[(1 - (1 + \exp ( - \lambda T))^{ - 1} )^{ - 1} ]$.

Proof

Substituting the CDFs of the LL and L distributions into Proposition 3 and simplifying gives the results obtained in Corollary 2.□

3.5 Entropy

Entropies are useful measures of uncertainty. Although different types of entropies exist in literature, in this sub-section, we derived the Shannon entropy of the T-NH{Y} family and its sub-families. The Shannon entropy of a random variable $X$ with PDF $f_{X} (x)$ is defined as $\eta_{X} = - E[\log (f_{X} (X))]$ [19].

Proposition 4

The Shannon entropy of the T-NH{Y} family is given by:

$$ \eta_{X} = \eta_{T} - \log (\alpha \gamma ) - 1 + E[\log f_{Y} (T)] + (1 - \alpha )E[\log (1 + \gamma X)] + E[(1 + \gamma X)^{\alpha } ], $$

(14)

where $\eta_{T}$ is the Shannon entropy of the random variable $T$.

Proof

Since $X = Q_{R} (F_{Y} (T))$, it implies that $T = Q_{Y} (F_{R} (X))$. Thus,

$$ f_{X} (x) = f_{R} (x) \times \frac{{f_{T} (t)}}{{f_{Y} (t)}}. $$

This implies that

$$ \eta_{X} = \eta_{T} + E[\log f_{Y} (T)] - E[\log f_{R} (X)]. $$

Substituting the PDF of the random variable $R$ and simplifying completes the proof.□

Corollary 3

The Shannon entropies of the T-NH{LL} and T-NH{L} are respectively given by:

• (i) $\begin{aligned} \eta_{X} & = \eta_{T} - \log (\alpha \gamma ) - 1 + \log (\beta \lambda^{ - \beta } ) + (\beta - 1)E(T) - 2E[\log (1 + (T/\lambda )^{\beta } )] \\ & \quad + (1 - \alpha )E[\log (1 + \gamma X)] + E[(1 + \gamma X)^{\alpha } ] \\ \end{aligned}$.

• (ii) $\begin{aligned} \eta_{X} & = \eta_{T} - \log (\alpha \gamma ) - 1 + \log (\lambda ) - \lambda E(T) - 2E[\log (1 + \exp ( - \lambda T))] \\ & \quad + (1 - \alpha )E[\log (1 + \gamma X)] + E[(1 + \gamma X)^{\alpha } ] \\ \end{aligned}$.

Proof

The Proof of Corollary 3 follows by substituting the PDFs of LL and L distributions in Proposition 4.□

4 Special Distributions

This section presents some new probability distributions arising from the T-NH{LL} and T-NH{L} families using different distributions of the random variable $T$.

4.1 Exponential-NH{LL} Distribution

Suppose the random variable $T$ follows the standard exponential distribution, that is $T - {\text{exponential}}(1)$. The CDF and PDF of the Exponential-NH{LL} (ENHLL) distribution are respectively given by:

$$ F_{X} (x) = 1 - \exp [ - \lambda (\exp ((1 + \gamma x)^{\alpha } - 1) - 1)^{{\tfrac{1}{\beta }}} ],\quad x > 0,\alpha > 0,\beta > 0,\gamma > 0,\lambda > 0, $$

(15)

and

$$ f_{X} (x) = \frac{{\alpha \gamma \lambda (1 + \gamma x)^{\alpha - 1} \exp ((1 + \gamma x)^{\alpha } - 1)}}{{\beta (\exp ((1 + \gamma x)^{\alpha } - 1) - 1)^{{1 - \tfrac{1}{\beta }}} }}\exp [ - \lambda (\exp ((1 + \gamma x)^{\alpha } - 1) - 1)^{{\tfrac{1}{\beta }}} ],\quad x > 0. \, $$

(16)

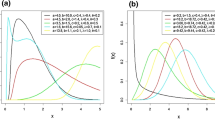
Figure 1 shows the plot of the density function of the ENHLL distribution for some given parameter values. The density function exhibits right skewed, decreasing and approximately symmetric shapes for the chosen parameter values.

Fig. 1

Plots of the density function of the ENHLL distribution

The hazard rate function of the ENHLL distribution is given by:

$$ \tau_{X} (x) = \frac{{\alpha \gamma \lambda (1 + \gamma x)^{\alpha - 1} \exp ((1 + \gamma x)^{\alpha } - 1)}}{{\beta (\exp ((1 + \gamma x)^{\alpha } - 1) - 1)^{{1 - \tfrac{1}{\beta }}} }},\quad x > 0. $$

(17)

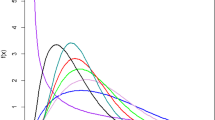
The hazard rate function plot for some selected parameter values are presented in Fig. 2. The hazard rate function exhibit different kinds of shapes such as decreasing, bathtub and upside-down bathtub.

Fig. 2

Hazard rate function plot of the ENHLL distribution

To generate random observations from the ENHLL distribution, the quantile function is need. Hence, the quantile function of the ENHLL distribution is given by:

$$ Q_{X} (u) = \frac{1}{\gamma }\left\{ {\left[ {\log \left( {1 + \left( { - \lambda^{ - 1} \log (1 - u)} \right)^{\beta } } \right)} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\},\quad u \in [0,1]. $$

(18)

Substituting $u = 0.25,0.5$ and 0.75 yields the first quartile, median and third quartile of the ENHLL distribution respectively.

4.2 Gumbel-NH{L} Distribution

This section presents the Gumbel-NH{L} (GNHL) distribution. Given that $T \sim {\text{Gumbel}}(0,1)$ with CDF $F_{T} (x) = \exp ( - \exp ( - x))$ and PDF$f_{T} (x) = \exp ( - x - \exp ( - x))$. The CDF and PDF of the GNHL distribution are respectively given by:

$$ F_{X} (x) = \exp [ - ((1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1)^{{\tfrac{1}{\lambda }}} ],x > 0,\alpha > 0,\gamma > 0,\lambda > 0, $$

(19)

and

$$ f_{X} (x) = \frac{{\alpha \gamma (1 + \gamma x)^{\alpha - 1} \exp (1 - (1 + \gamma x)^{\alpha } )\exp [ - ((1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1)^{{\tfrac{1}{\lambda }}} ]}}{{\lambda [1 - \exp (1 - (1 + \gamma x)^{\alpha } )]^{2} [(1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1]^{{1 - \tfrac{1}{\lambda }}} }},\quad x > 0. \, $$

(20)

The plot of the density function of the GNHL distribution for some selected parameter values is shown in Fig. 3. The density function exhibit reversed-J and right skewed shapes for the chosen parameter values.

Fig. 3

Density function plot of the GNHL distribution

The hazard rate function of the GNHL distribution is given by:

$$ \begin{aligned} & \tau_{X} (x) = \\ & \quad \frac{{\alpha \gamma \exp (1 - (1 + \gamma x)^{\alpha } )[1 - \exp (1 - (1 + \gamma x)^{\alpha } )]^{ - 2} \exp [ - ((1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1)^{{\tfrac{1}{\lambda }}} ]}}{{\lambda (1 + \gamma x)^{1 - \alpha } \{ 1 - \exp [ - ((1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1)^{{\tfrac{1}{\lambda }}} ]\} [(1 - \exp (1 - (1 + \gamma x)^{\alpha } ))^{ - 1} - 1]^{{1 - \tfrac{1}{\lambda }}} }},\quad x > 0. \, \\ \end{aligned} $$

(21)

The hazard rate function plot of the GNHL distribution for some chosen parameter values is presented in Fig. 4. The hazard rate function of the GNHL distribution exhibit decreasing, bathtub and upside-down bathtub shapes for the given parameter values.

Fig. 4

Hazard rate function plot for the GNHL distribution

The quantile function of the GNHL distribution is given by:

$$ Q_{X} (u) = \frac{1}{\gamma }\left\{ {\left[ {1 - \log \left[ {1 - (1 + ( - \log (u))^{\lambda } )^{ - 1} } \right]} \right]^{{\tfrac{1}{\alpha }}} - 1} \right\},\quad u \in [0,1]. $$

(22)

Putting $u = 0.25,0.5$ and 0.75 gives the first quartile, median and upper quartile of the GNHL distribution respectively.

5 Parameter Estimation

The section presents three procedures for estimating the parameters of the ENHLL distribution.

5.1 Maximum Likelihood Method

The maximum likelihood method is the most common parameter estimation technique used in literature. Given that $X \sim {\text{ENHLL}}(\alpha ,\beta ,\gamma ,\lambda )$, $\varvec{\vartheta}= (\alpha ,\beta ,\gamma ,\lambda )^{T}$, $z = \exp ((1 + \gamma x)^{\alpha } - 1) - 1$ and $\overline{z} = \exp ((1 + \gamma x)^{\alpha } - 1)$. For a single observation $x$ of $X$ from the ENHLL distribution, the log-likelihood function $\ell = \ell (\varvec{\vartheta})$ is given by:

$$ \ell = \log ({{\alpha \gamma \lambda } \mathord{\left/ {\vphantom {{\alpha \gamma \lambda } \beta }} \right. \kern-0pt} \beta }) + (\alpha - 1)\log (1 + \gamma x) + ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta } - 1)\log (z) + [(1 + \gamma x)^{\alpha } - 1] - \lambda z^{{\tfrac{1}{\beta }}} . $$

(23)

The first partial derivatives of the log-likelihood function with respect to $\varvec{\vartheta}= (\alpha ,\beta ,\gamma ,\lambda )^{T}$ are:

$$ \begin{aligned} \frac{\partial \ell }{\partial \alpha } = \frac{1}{\alpha } + \log (1 + \gamma x) + (1 + \gamma x)^{\alpha } \log (1 + \gamma x) + \frac{{\overline{z} ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta } - 1)(1 + \gamma x)^{\alpha } \log (1 + \gamma x)}}{z} - \hfill \\ \, \frac{{\overline{z} z^{{\tfrac{1}{\beta } - 1}} \lambda (1 + \gamma x)^{\alpha } \log (1 + \gamma x)}}{\beta }, \hfill \\ \end{aligned} $$

$$ \frac{\partial \ell }{\partial \beta } = - \frac{1}{\beta } - \frac{\log (z)}{{\beta^{2} }} + \frac{{z^{{\tfrac{1}{\beta }}} \lambda \log (z)}}{{\beta^{2} }}, $$

$$ \frac{\partial \ell }{\partial \gamma } = \frac{1}{\gamma } + \frac{(\alpha - 1)x}{1 + \gamma x} + \alpha x(1 + \gamma x)^{\alpha - 1} + \frac{{\overline{z} \alpha ({1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta } - 1)x(1 + \gamma x)^{\alpha - 1} }}{z} - \frac{{\overline{z} z^{{\tfrac{1}{\beta } - 1}} \alpha \lambda x(1 + \gamma x)^{\alpha - 1} }}{\beta }, $$

and

$$ \frac{\partial \ell }{\partial \lambda } = \frac{1}{\lambda } - z^{{\tfrac{1}{\beta }}} . $$

For a random sample of $m$ observations $x_{1} ,x_{2} , \ldots ,x_{m}$ from the ENHLL distribution, the total log-likelihood function is given by $\ell_{m}^{*} = \sum\nolimits_{j = 1}^{m} {\ell_{j} (\varvec{\vartheta})}$, where $\ell_{j} (\varvec{\vartheta}),j = 1,2, \ldots ,m$ is defined in Eq. (23). To obtain the estimates of the parameters, the first partial derivatives with respect to the parameters are equated to zero and the resulting system of equations solved simultaneously. However, apart from the equation for the parameter $\lambda$, the rest of the resulting system of equations are not tractable and have to be solved numerically to obtain the estimates of the parameters. Thus, the estimates are obtained by solving the nonlinear system of equation $({{\partial \ell_{m}^{*} } \mathord{\left/ {\vphantom {{\partial \ell_{m}^{*} } {\partial \alpha }}} \right. \kern-0pt} {\partial \alpha }},{{\partial \ell_{m}^{*} } \mathord{\left/ {\vphantom {{\partial \ell_{m}^{*} } {\partial \beta }}} \right. \kern-0pt} {\partial \beta }},{{\partial \ell_{m}^{*} } \mathord{\left/ {\vphantom {{\partial \ell_{m}^{*} } {\partial \gamma }}} \right. \kern-0pt} {\partial \gamma }},{{\partial \ell_{m}^{*} } \mathord{\left/ {\vphantom {{\partial \ell_{m}^{*} } {\partial \lambda }}} \right. \kern-0pt} {\partial \lambda }})^{T} = 0$. Solving the system of equation using numerical methods can sometimes be time consuming. Hence, we can efficiently find the maximum likelihood estimates of the parameters by maximizing the total likelihood equation directly using MATLAB, MATHEMATICA and R software. In this study, the mle2 function in the bbmle package of the R software is used [8].

To find confidence interval for the parameters of the ENHLL distribution, a $4 \times 4$ observed information matrix $I(\varvec{\vartheta}) = \{ I_{pq} \}$ for $p,q = \alpha ,\beta ,\gamma ,\lambda$ is needed. The multivariate normal $N_{4} ({\mathbf{0}},I(\widehat{\varvec{\vartheta}}))$ distribution can be employed to construct approximate confidence interval for the parameters under the usual regularity conditions. $I(\widehat{\varvec{\vartheta}})$ is the total observed information matrix evaluated at $\widehat{\varvec{\vartheta}}$. A $100(1 - \rho )\%$ asymptotic confidence interval (ACI) for each parameter $\vartheta_{p}$ is given by:

$$ ACI_{p} = (\widehat{\vartheta }_{p} - z_{{{\raise0.5ex\hbox{$\scriptstyle \rho $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} \times se(\widehat{\vartheta }_{p} ),\widehat{\vartheta }_{p} + z_{{{\raise0.5ex\hbox{$\scriptstyle \rho $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} \times se(\widehat{\vartheta }_{p} )), $$

where $se(\widehat{\vartheta }_{p} )$ is the standard error of the estimated parameter and is obtained as $se(\widehat{\vartheta }_{p} ) = \sqrt {I_{pp} (\widehat{\vartheta })} ,p = \alpha ,\beta ,\gamma ,\lambda$, and $z_{{{\raise0.5ex\hbox{$\scriptstyle \rho $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}$ is the upper $({\rho \mathord{\left/ {\vphantom {\rho 2}} \right. \kern-0pt} 2})$th quantile of the standard normal distribution.

5.2 Ordinary and Weighted Least Squares

The methods of ordinary least squares (OLS) and weighted least squares (WLS) were proposed by Swain et al. [20]. Given that $x_{(1)} ,x_{(2)} , \ldots ,x_{(m)}$ are order statistics of a random sample of size $m$ from the ENHLL distribution. The OLS estimates $\widehat{\alpha }_{LSE} ,\widehat{\beta }_{LSE} ,\widehat{\gamma }_{LSE} ,\widehat{\lambda }_{LSE}$ for the parameters of the ENHLL distribution can be obtained by minimizing function:

$$ L(\alpha ,\beta ,\gamma ,\lambda ) = \sum\limits_{j = 1}^{m} {\left[ {F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) - \frac{j}{m + 1}} \right]}^{2} , $$

(23)

with respect to $\alpha ,\beta ,\gamma$ and $\lambda$. Alternatively, the following nonlinear equations can be solved numerically to obtain the OLS estimates. That is

$$ \sum\limits_{j = 1}^{m} {\left[ {F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) - \frac{j}{m + 1}} \right]} \varOmega_{q} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) = 0,\quad q = 1,2,3,4, $$

where$\varOmega_{1} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) = \frac{\partial }{\partial \alpha }F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ), \, \varOmega_{2} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) = \frac{\partial }{\partial \beta }F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ),$ $\varOmega_{3} (x_{(j)} |\alpha ,\beta ,\lambda ,\gamma ) = \frac{\partial }{\partial \gamma }F_{X} (x_{(j)} |\alpha ,\beta ,\lambda ,\gamma )$ and $\varOmega_{4} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) = \frac{\partial }{\partial \lambda }F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda )$.The WLS estimates $\widehat{\alpha }_{WLS} ,\widehat{\beta }_{WLS} ,\widehat{\gamma }_{WLS} ,\widehat{\lambda }_{WLS}$ of the ENHLL distribution parameters are obtained by minimizing the function:

$$ W(\alpha ,\beta ,\gamma ,\lambda ) = \sum\limits_{j = 1}^{m} {\frac{{(m + 1)^{2} (m + 2)}}{j(m - j + 1)}} \left[ {F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) - \frac{j}{m + 1}} \right]^{2} , $$

(24)

with respect to the parameters. Also, the WLS estimates of the parameters can be obtained by solving the following nonlinear equation numerically. That is

$$ \sum\limits_{j = 1}^{m} {\frac{{(m + 1)^{2} (m + 2)}}{j(m - j + 1)}} \left[ {F_{X} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) - \frac{j}{m + 1}} \right]\varOmega_{q} (x_{(j)} |\alpha ,\beta ,\gamma ,\lambda ) = 0,\quad q = 1,2,3,4, $$

where $\varOmega_{1} ( \cdot |\alpha ,\beta ,\gamma ,\lambda ), \, \varOmega_{2} ( \cdot |\alpha ,\beta ,\gamma ,\lambda ), \, \varOmega_{3} ( \cdot |\alpha ,\beta ,\gamma ,\lambda )$ and $\varOmega_{4} ( \cdot |\alpha ,\beta ,\gamma ,\lambda )$ are the same as defined above.

6 Monte Carlo Simulation

This section presents Monte Carlo simulation results for the estimators of the parameters of the ENHLL distribution. The average absolute bias (AB) and mean square error (MSE) of the maximum likelihood estimator (MLE), OLS and WLS estimators for the parameters are presented in Tables 1 and 2 for some parameters values. The simulations results revealed that the ABs and MSEs of the estimators’ decreases as the sample size increases. This means that the MLE, OLS and WLS estimators are consistent. However, it was also evident that in most cases the MLE had the least values of the AB and MSE for the different parameter values employed for the simulation exercise.

Table 1 Simulation results for $\varvec{\vartheta}= (\alpha = 0.8,\beta = 0.9,\gamma = 0.3,\lambda = 0.5)^{T}$

Table 2 Simulation results for $\varvec{\vartheta}= (\alpha = 0.3,\beta = 0.2,\gamma = 0.3,\lambda = 0.5)^{T}$

7 Empirical Applications

The section presents empirical applications of the ENHLL distribution using two real datasets. The first dataset comprises the failure time of 36 appliances subjected to automatic life test. The data can be found in Lawless [12] and are given by: 11, 35, 49, 170, 329, 381, 708, 958, 1062, 1167, 1594, 1925, 400, 2451, 2471, 2551, 2565, 2568, 2694, 2702, 2761, 2831, 3034, 3059, 3112, 3214, 3478, 3504, 4329, 6367, 6976, 7846, 13,403. The second dataset which comprises the failure times of 100 cm polyster/viscose yarn subjected to 2.3% strain level in textile experiment in order to examine the tensile fatigue characteristics of the yarn. The dataset can be found in Quesenberry and Kent [18] and are: 86, 146, 251, 653, 98, 249, 400, 292, 131, 169, 175, 176, 76, 264, 15, 364, 195, 262, 88, 264, 157, 220, 42, 321, 180, 198, 38, 20, 61, 121, 282, 224, 149, 180, 325, 250, 196, 90, 229, 166, 38, 337, 65, 151, 341, 40, 40, 135, 597, 246, 211, 180, 93, 315, 353, 571, 124, 279, 81, 186, 497, 182, 423, 185, 229, 400, 338, 290, 398, 71, 246, 185, 188, 568, 55, 55, 61, 244, 20, 284, 393, 396, 203, 829, 239, 236, 286, 194, 277, 143, 198, 264, 105, 203, 124, 137, 135, 350, 193, 188. The performance of the ENHLL distribution is compared with the Weibull NH (NH) [17], Topp-Leone NH (TLNH) [21], Kumaraswamy NH (KNH) [13] and Exponentiated NH (ENH) [2] using the Akaike information criterion (AIC), consistent Akaike information criterion (CAIC), Bayesian information criterion (BIC), $- 2\ell$, Cramér-von Mises (W^*) and Anderson–Darling (AD) test statistics. The smaller the values of the model selection criteria and the goodness-of-fit statistics, the better the model. The PDFs of the WNH, TLNH, KNH and ENH distributions are respectively given by:

$$ F(x) = 1 - \exp \left[ { - a[\exp ((1 + \lambda x)^{\alpha } - 1) - 1]^{b} } \right],\quad a > 0,b > 0,\alpha > 0,\lambda > 0,x > 0, $$

$$ F(x) = \left[ {1 - \exp (2(1 - (1 + \lambda x)^{\alpha } ))} \right]^{\beta } ,\quad \alpha > 0,\beta > 0,\lambda > 0,x > 0, $$

$$ F(x) = 1 - \left[ {1 - [1 - \exp (1 - (1 + \lambda x)^{\alpha } )]^{a} } \right]^{b} ,\quad a > 0,b > 0,\alpha > 0,\lambda > 0,x > 0, $$

and

$$ F(x) = \left[ {1 - \exp (1 - (1 + \lambda x)^{\alpha } )} \right]^{a} ,\quad a > 0,\alpha > 0,\lambda > 0,x > 0. $$

Often the choice of statistical distributions for modeling a given dataset can easily be made if the nature of the failure rate of the dataset is known. To establish the nature of the failure rate of a given dataset, the total time on test (TTT) plot developed by Aarset [1] can be used. Plotting

$$ T(i/n) = {{\left[ {\left( {\sum\limits_{j = 1}^{i} {x_{(j)} } } \right) + (n - i)x_{(i)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\sum\limits_{j = 1}^{i} {x_{(j)} } } \right) + (n - i)x_{(i)} } \right]} {\sum\limits_{j = 1}^{n} {x_{(j)} } }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {x_{(j)} } }}, $$

where $i = 1, \ldots ,n$ and $x_{(j)} (j = 1, \ldots ,m)$ are the order statistics obtained from the sample of size $n$, against $i/n$ gives the TTT plot. Figure 5 shows the TTT plots for the datasets. From the TTT plots, the appliances dataset exhibit modified bathtub failure rate since the curve first display convex shape, followed by concave shape and then convex shape again. The yarn data has increasing failure rate since the curve exhibit concave shape.

Fig. 5

TTT plots for a appliances and b yarn datasets

Tables 3 and 4 shows the maximum likelihood estimates for the parameters, their corresponding standard errors and confidence intervals (CI) for the appliances and yarn datasets respectively.

Table 3 Parameter estimates, standard error and CI for appliances dataset

Table 4 Parameter estimates, standard error and CI for yarn dataset

Tables 5 and 6 shows the model selection criteria and goodness-of-fit statistics for the appliances and yarn datasets. The results revealed that the ENHLL distribution provides better fit to the datasets compared to the other fitted distributions since for all the model selection criteria and goodness-of-fit statistics it has the least values.

Table 5 Model selection criteria and goodness-of-fit statistics for appliances dataset

Table 6 Model selection criteria and goodness-of-fit statistics for yarn dataset

Figures 6 and 7 displays the histograms, fitted densities, empirical CDFs and fitted CDFs of the distributions for the appliances and yarn datasets respectively. From both plots, the ENHLL distribution mimics the shapes of the datasets well than the other fitted distributions.

Fig. 6

Fitted densities and CDFs for the appliances dataset

Fig. 7

Fitted densities and CDFs for the yarn dataset

8 Conclusion

This study presents a new class of distributions called the T-NH{Y} family using the T-R{Y} framework. Statistical properties such as mode, quantile function, moments and Shannon entropy of the family are derived. Two special distributions, that is the ENHLL and GNHL distributions are proposed and the shapes of their densities and hazard rate functions for some given parameter values studies. The plots of the hazard rate functions revealed that the ENHLL and GNHL can exhibit different types of non-monotonic failure rates. This makes the ENHLL and GNHL distributions suitable for modeling datasets that exhibit these kinds of failure rates. Three estimations techniques; maximum likelihood, ordinary least squares and weighted least squares are employed in estimating the parameters of the ENHLL distribution and Monte Carlo simulations performed to examine how this methods perform. The findings revealed that the three techniques are all consistent as the sample size increases but in most cases the maximum likelihood tends to have smaller values of the average absolute bias and mean square error. Empirical illustrations with two failure time datasets revealed that the ENHLL distribution provides better fit to the datasets than other generalizations of the NH distribution in literature.