1 Introduction

The modeling and analysis of lifetime phenomenon play a prominent role in a wide variety of scientific and technological fields. Recently, several new lifetime distributions have been proposed. Mudholkar and Srivastava [35] and Mudholkar et al. [36] introduced a generalization of the Weibull distribution called generalized Weibull (GW) distribution. The generalized exponential (GE) distribution presented by [19]. Nadarajah and Kotz [37] introduced four generalized (exponentiated) type distributions: the exponentiated gamma, exponentiated Weibull, exponentiated Gumbel and the exponentiated Frechet distributions. Sarhan and Kundu [48] proposed the generalized linear failure rate (GLFR) distribution and they explained that this distribution can have increasing, decreasing, and bathtub-shaped hazard rate functions which are quite desirable for data analysis purposes. Recently, Sarhan [47] proposed the generalized quadratic hazard rate (GQHR) distribution. This distribution is more general than several well-known distributions such as GE, GLFR, and generalized Rayliegh (GR) distributions. In addition, the GQHR distribution has an increasing, bathtub-shaped, unimodal and inverted bathtub-shaped hazard rate functions.

A new generalization of quadratic hazard rate distribution called the Kumuraswamy quadratic hazard rate (KQHR) distribution was introduced by [15]. Another distribution which is called the beta QHR distribution is investigated by [33]. Okasha et al. [40] introduced the QHR-geometric distribution.

Several distributions have been proposed in the literature to model lifetime data by compounding some useful lifetime distributions. Adamidis and Loukas [1] introduced a two parameter distribution known as exponential-geometric (EG) distribution by compounding an exponential distribution with a geometric distribution. Kundu and Raqab [27] introduced the generalized Rayleigh distribution. Ku [29] and Tahmasbi and Rezaei [51] introduced the exponential-Poisson (EP) and exponential-logarithmic (EL) distributions, respectively. Recently, Chahkandi and Ganjali [12] proposed the exponential power series (EPS) class of distributions, which contains as special cases these distributions. Some other recent works are: exponentiated exponential-Poisson (EEP) by [7]; Weibull-geometric (WG) by [8]; Weibull-power series (WPS) by [34]; complementary exponential power series by [16]; extended Weibull-power series (EWPS) distribution by [49]; double bounded Kumaraswamy power series distribution by [9]; the Burr-XII power series distribution by [50]; the complementary Weibull geometric distribution by [52]; the Birinbaum-Sanders power series distribution by [11]; the complementary extended Weibull power series distribution by [14]; the Burr-XII negative binomial distribution by [42]; the generalized linear failure rate-power series (GLFRPS) distribution by [20]; the bivariate exponentiated extended Weibull family of distributions by [43]; the quadratic hazard rate power series distribution by [45]; the generalized modified Weibull power series distribution by [4]; and the power series skew normal class of distributions by [44]; For compounding continuous distributions with a discrete distribution, Nadarajah et al. [38] introduced a package Compounding in R software (R Development Core Team, 2014). We are motivated to introduce our new distribution for (i) the wide usage of the general class of quadratic hazard rate distribution, (ii) the proposed model has some interesting physical interpretations as well. Hence, it may be more flexible than the existing models and it will give the practitioner one more option to choose a model among the possible class of models for analyzing data., (iii) the stochastic representation \(Y=\min {(X_1, \ldots , X_n)}\), which can arises in series systems with identical components in many industrial applications and biological organisms.

The main purpose of this paper is to introduce GQHRPS distribution and study some of its properties. This new model has the following distributions as special cases: (i) the QHR, (ii) the generalized linear failure rate power series (GLFRPS), (iii) the generalized Rayleigh power series and (iv) the generalized exponential power series (GEPS) distributions.

First we derive the GQHRPS by compounding the GQHR distribution with the power series class of distributions. We like to mention that the GQHR distribution has several interesting properties. We obtain these properties and also provide the marginal and conditional distributions of the GQHRPS distribution. The proposed class has five unknown parameters. The maximum likelihood estimators (MLEs) cannot be obtained in closed form. The MLEs can be obtained by solving five non-linear equations simultaneously. The standard Newton–Raphson algorithm may be used for this purpose, but it requires a very good choice of the initial guesses of the five parameters. Otherwise, it has the standard problem of converging to a local maximum rather the global maximum. It is observed that the implementation of the proposed EM algorithm is very simple in practice. We have analyzed one data set for illustrative purposes. The performance is quite satisfactory.

The rest of the paper is organized as follows. In Sect. 2 we introduce the new class of generalized quadratic hazard rate power series distributions. The density, survival, failure rate, and moment generating functions as well as the moments, mean residual life, mean past lifetime, quantiles, the stress–strength parameter and order statistics are given in Sect. 3. In Sect. 4, we have discussed some of the cases and study some of their distributional properties in details. Certain characterizations of GQHRPS distribution are presented in Sect. 5. Estimation of the parameters is discussed in Sect. 6. The Standard errors of the estimates and simulations are obtained in Sects. 7 and 8, respectively. The application is considered in Sect. 9 to show the flexibility and potentiality of the new distribution. Finally, some concluding remarks are presented in Sect. 10.

2 The GQHRPS Distribution

The four-parameter distribution known as generalized quadratic hazard rate (GQHR) distribution, was introduced by [47]. The cumulative distribution function (cdf) of the GQHR distribution is given by

$$\begin{aligned} G(x; \alpha , \lambda , \beta , \gamma )=\left( 1-\exp {(-v_{x})} \right) ^{\gamma } \ \ \ x>0, \end{aligned}$$
(1)

where \(\alpha \), \(\beta \) non-negative, \(\gamma \) positive, \(\lambda \ge -2\sqrt{\alpha \beta }\) are parameters and \(v_{x}=\alpha x+ (\lambda /2 )x^2 + (\beta /3) x^3\).

Given N, let \({X_1, \ldots , X_N}\) be independent and identically distributed (i.i.d.) random variables following a GQHR distribution with cdf (1). Here N is independent of \(X_{i}^{'}\)s and it is a member of the family of power series distribution, truncated at zero, with the probability mass function (pmf)

$$\begin{aligned} P(N=n)=\dfrac{a_{n}{\theta }^n}{A(\theta )},\quad n=1,2,\ldots , \end{aligned}$$
(2)

where \(a_{n} \ge 0\) depends only on n, \(A(\theta )=\sum _{n=1}^{\infty }a_{n}{\theta }^n\), \({\theta }\in (0,s)\) (s can be \(+\infty \)) is such that \(A(\theta )\) is finite and its first, second and third derivatives exist and are denoted by \(A^{\prime }(.), A^{\prime \prime }(.)\) and \(A^{\prime \prime \prime }(.)\). Table 1 shows some power series distributions (truncated at zero) such as Poisson, geometric, logarithmic, binomial and negative binomial (with m being the number of replicates) distributions.

It is noticeable that the probability distributions of the form (2) have been considered in [10, 41]. For more properties of this class of distributions, see [39].

Table 1 Useful quantities for some power series distributions
Full size table

Now, let \(X_{(1)}=\min \{ X_1, X_2, \ldots , X_N\}\). The conditional cdf of \(X_{(1)}|N=n\) is given by

$$\begin{aligned} F_{X_{(1)}|N=n}(x)= 1-\left[ 1- G(x; \alpha , \lambda , \beta , \gamma ) \right] ^n = 1-\left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] ^n, \ \ x> 0. \end{aligned}$$

Observe that \(X_{(1)}|N=n\) follows a KQHR distribution with parameters \(\alpha , \lambda , \beta , \gamma \), and n, which was defined by [15] and it is denoted by \(KQHR(\alpha , \lambda , \beta , \gamma , n)\). The marginal cdf of \(X_{(1)}\)

$$\begin{aligned} F(x)=F(x; \alpha , \lambda , \beta , \gamma , \theta )= & {} \sum _{n=1}^{\infty } \dfrac{a_n \theta ^n}{A(\theta )} \left( 1-\left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] ^n \right) \end{aligned}$$
(3)
$$\begin{aligned}= & {} 1-\dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }{A(\theta )}; \ \ x\ge 0, \end{aligned}$$
(4)

defines the cdf of GQHRPS distribution. We denote a random variable X following the GQHRPS distribution with parameters \(\alpha , \lambda , \beta , \gamma \), and \(\theta \) by \( X \sim GQHRPS(\alpha , \lambda , \beta , \gamma , \theta )\).

This proposed class of distributions include lifetime distributions presented by [47] (generalized quadratic hazard rate distribution), [31] (generalized exponential power series distribution), Flores et al. [16] (complementary exponential power series distribution), Harandi and Alamatsaz [20] (generalized linear failure rate power series distribution), and Okasha et al. [40] (quadratic hazard rate-geometric distribution) among others.

3 Statistical and Reliability Properties

In this section we derive the probability density function (pdf), survival function, hazard rate function, reversed hazard rate function, mean residual life (MRL) and mean past lifetime (MPL) functions. The pdf of a random variable \(X \sim GQHRPS(\alpha , \lambda , \beta , \gamma , \theta )\) is given by

$$\begin{aligned} f(x)= & {} f(x; \alpha , \lambda , \beta , \gamma , \theta )\nonumber \\= & {} \dfrac{1}{A(\theta )}\nonumber \\&\times \, \theta \gamma v^{\prime }(x) \exp {(-v_{x})} \left( 1-\exp {(-v_{x})} \right) ^{\gamma -1} \nonumber \\&\times \, A^{\prime }\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) . \end{aligned}$$
(5)

Proposition 3.1

The KQHR distribution with parameters \(\alpha , \lambda , \beta , \gamma \), and c is a limiting distribution of the GQHRPS distribution when \( \theta \rightarrow 0^{+}\), where \(c=\min \{ n \in \mathbf{N }: a_n \succ 0 \}\).

Proof

$$\begin{aligned} \lim _{\theta \rightarrow 0^{+}} F(x)= & {} \lim _{\theta \rightarrow 0^{+}} \left\{ 1-\dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }{A(\theta )} \right\} \\= & {} 1-\lim _{\theta \rightarrow 0^{+}} \dfrac{\sum _{n=c}^{\infty } a_n \left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) ^n}{\sum _{n=c}^{\infty } a_n \theta ^n } \\= & {} 1-\lim _{\theta \rightarrow 0^{+}} \dfrac{\left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] ^c }{1+a_c^{-1} \sum _{n=c+1}^{\infty } a_n \theta ^{n-c} }\\&+\,\dfrac{a_c^{-1} \sum _{n=c+1}^{\infty } a_n \theta ^{n-c} \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] ^n}{1+a_c^{-1} \sum _{n=c+1}^{\infty } a_n \theta ^{n-c} }\\= & {} 1- \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] ^c. \end{aligned}$$

\(\square \)

Proposition 3.2

The pdf of GQHRPS distribution can be written as a mixture of the density function of KQHR distribution with parameters \(\alpha , \lambda , \beta , \gamma \), and n.

Proof

We know that \(A^{\prime }(\theta )=\sum _{n=1}^{\infty } n a_n \theta ^{n-1}\). Therefore by Eq. (5), we have

$$\begin{aligned} f(x)= & {} \sum _{n=1}^{\infty }\dfrac{1}{A(\theta )} \\&\times \, n a_n \theta ^{n} \gamma v^{\prime }(x) \exp {(-v_{x})} \left( 1-\exp {(-v_{x})} \right) ^{\gamma -1} \\&\times \, \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] ^{n-1}\\= & {} \sum _{n=1}^{\infty } P(N=n) g(x;\alpha , \lambda , \beta , \gamma , n), \end{aligned}$$

where \(g(x;\alpha , \lambda , \beta , \gamma , n)\) is the density function of \(KQHR(\alpha , \lambda , \beta , \gamma , n)\) distribution. \(\square \)

It is well-known that an important measure of aging is the hazard rate function, defined as

$$\begin{aligned} h(x)=\lim _{\triangle x\rightarrow 0} \dfrac{P(X<x+\triangle x|X>x)}{\triangle x}=\dfrac{f(x)}{{\overline{F}}(x)}. \end{aligned}$$

The survival and hazard rate functions of GQHRPS distribution are given by

$$\begin{aligned} {\overline{F}}(x)={\overline{F}}(x;\alpha , \lambda , \beta , \gamma , \theta )= \dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }{A(\theta )} \end{aligned}$$

and

$$\begin{aligned} h(x)= & {} h(x;\alpha , \lambda , \beta , \gamma , \theta )\\= & {} \dfrac{1}{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }\\&\times \, \theta \gamma v^{\prime }(x) \exp {(-v_{x})} \left( 1-\exp {(-v_{x})} \right) ^{\gamma -1}\\&\times \, A^{\prime }\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) , \end{aligned}$$

respectively.

Similarly, the reversed hazard rate function of GQHRPS distribution is given by

$$\begin{aligned} r(x)= & {} r(x;\alpha , \lambda , \beta , \gamma , \theta )\\= & {} \dfrac{1}{A(\theta )- A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) } \\&\times \, \theta \gamma v^{\prime }(x) \exp {(-v_{x})} \left( 1-\exp {(-v_{x})} \right) ^{\gamma -1}\\&\times \, A^{\prime }\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) . \end{aligned}$$

An alternative aging measure, widely used in applications, is the mean residual life (MRL) function, defined as

$$\begin{aligned} \mu (x)=E(X-x|X>x)=\dfrac{1}{{\overline{F}}(x)} \int _{x}^{+ \infty } {\overline{F}}(t) dt, \end{aligned}$$

where E is the expectation operator.

Proposition 3.3

The MRL function of GQHRPS distribution is given by

$$\begin{aligned} \mu (x)= & {} \dfrac{T_{l,s,k,m,n}}{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }\\&\times \,\left[ \dfrac{\varGamma (2k+3m+1, \alpha sx)}{(\alpha s)^{2k+3m+1}} \right] . \end{aligned}$$

where \(\varGamma (a,x)=\int _{x}^{\infty } e^{-t} t^{a-1} dt\) and

$$\begin{aligned} T_{l,s,k,m,n}= & {} \sum _{n=1}^{\infty } \sum _{l=0}^{\infty } \sum _{s=0}^{\infty } \sum _{k=0}^{\infty } \sum _{m=0}^{\infty } \dfrac{a_n \theta ^n \varGamma (n+l) \varGamma (\gamma l+s)}{\varGamma (n) l! \varGamma (\gamma l) s!} \\&\times \, \dfrac{(-1)^{k+m} s^{k+m} \lambda ^k \beta ^m }{k! m! 2^k 3^m}. \end{aligned}$$

Proof

See the “Appendix”. \(\square \)

The MPL function or mean waiting time function is a well-known reliability measure that has applications in many disciplines such as reliability theory and actuarial studies. The MPL function of a random variable X is defined by

$$\begin{aligned} M(x)=\dfrac{1}{F(x)} \int _{0}^{x} F(t) dt, \ \ x>0. \end{aligned}$$

As mentioned in [40], the MPL is a dual property of the MRL. The MPL function could be of ineterest for describing different maintenance strategies. Chandra and Roy [13] showed that the MPL function cannot decrease on (0, 1). Other interpretation, properties and applications of the MPL function can be found in [2, 3, 22, 25, 26] and the references therein. The next proposition provides the MPL of GQHRPS distribution.

Proposition 3.4

The MPL of GQHRPS distribution is given by

$$\begin{aligned} M (x)= & {} \dfrac{A(\theta )}{A(\theta )-A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] \right) }\\&\times \, \left[ x- \dfrac{T_{l,s,k,m,n}}{A(\theta )}\dfrac{\gamma (2k+3m+1, s \alpha x)}{(s \alpha )^{2k+3m+1}} \right] , \end{aligned}$$

where \(\gamma (a,x)=\int _{0}^{x} e^{-t} t^{a-1} dt\).

Proof

See the “Appendix”. \(\square \)

3.1 Moments and Moment Generating Function

Let Y be a random variable following the KQHR distribution with parameters \(\alpha , \lambda , \beta , \gamma \) and n. Elbatal and Butt [15] obtained the moment generating function (mgf) of the random variable Y as follows

$$\begin{aligned} \kappa _{Y}(t)= & {} W_{i,j,k,m}\left[ \dfrac{\alpha \varGamma (2k+3m+1)}{[\alpha (j+1)-t]^{2k+3m+1}}\right. \nonumber \\&+\, \lambda \dfrac{\varGamma (2k+3m+2)}{[\alpha (j+1)-t]^{2k+3m+2}}\nonumber \\&\left. +\,\beta \dfrac{\varGamma (2k+3m+3)}{[\alpha (j+1)-t]^{2k+3m+3}}\right] , \end{aligned}$$

where

$$\begin{aligned} W_{i,j,k,m}= & {} \sum _{i=j=k=m=0}^{\infty } (-1)^{i+j+k+m} \left( {\begin{array}{c}n-1\\ i\end{array}}\right) \\&\times \, \left( {\begin{array}{c}\gamma (i+1)-1\\ j\end{array}}\right) \dfrac{\lambda ^k \beta ^m (j+1)^{k+m}}{2^k m^m k! m!}. \end{aligned}$$

Combining Eq. (6) and Proposition (3.2) yields the mgf of the GQHRPS distribution

$$\begin{aligned} \kappa _{X}(t)= & {} \sum _{n=1}^{\infty } \dfrac{a_n \theta ^n}{A(\theta )} \nonumber \\&\times \, W_{i,j,k,m} \left[ \dfrac{\alpha \varGamma (2k+3m+1)}{[\alpha (j+1)-t]^{2k+3m+1}}\right. \nonumber \\&+\, \lambda \dfrac{\varGamma (2k+3m+2)}{[\alpha (j+1)-t]^{2k+3m+2}} \nonumber \\&\left. +\,\beta \dfrac{\varGamma (2k+3m+3)}{[\alpha (j+1)-t]^{2k+3m+3}}\right] . \end{aligned}$$
(6)

The r-th moment of the KQHR distribution with parameters \(\alpha , \lambda , \beta , \gamma \) and n is given by

$$\begin{aligned} E(X^r)= & {} W_{i,j,k,m} \left[ \dfrac{\alpha \varGamma (r+2k+3m+1)}{[\alpha (j+1)]^{r+2k+3m+1}}\right. \\&+\, \lambda \dfrac{\varGamma (r+2k+3m+2)}{[\alpha (j+1)]^{r+2k+3m+2}}\\&\left. +\beta \dfrac{\varGamma (r+2k+3m+3)}{[\alpha (j+1)]^{r+2k+3m+3}}\right] , \end{aligned}$$

(see [15]). Thus, the r-th moment of the GQHRPS distribution is given by

$$\begin{aligned} \mu _{r}= & {} \sum _{n=1}^{\infty } \dfrac{a_n \theta ^n}{A(\theta )} \nonumber \\&\times W_{i,j,k,m}\left[ \dfrac{\alpha \varGamma (r+2k+3m+1)}{[\alpha (j+1)]^{r+2k+3m+1}}\right. \nonumber \\&+\, \lambda \dfrac{\varGamma (r+2k+3m+2)}{[\alpha (j+1)]^{r+2k+3m+2}} \nonumber \\&\left. +\,\beta \dfrac{\varGamma (r+2k+3m+3)}{[\alpha (j+1)]^{r+2k+3m+3}}\right] . \end{aligned}$$
(7)

Based on Eq. (7), the measures of variation, skewness and kurtosis of GQHRPS distribution can be obtained via the following relations:

$$\begin{aligned} CV_{GQHRPS}= & {} \sqrt{\dfrac{\mu _{2}}{\mu _{1}}-1},\\ SK_{GQHRPS}= & {} \dfrac{\mu _3 -3\mu _1 \mu _2 +2\mu _1^3}{[\mu _2 - \mu _1^2]^{3/2}},\\ K_{GQHRPS}= & {} \dfrac{\mu _4 -4\mu _1 \mu _3+6\mu _1^2 \mu _2 -3\mu _1^4}{[\mu _2-\mu _1^2]^{2}}. \end{aligned}$$

3.2 Order Statistics

Let \(X_1, \ldots , X_n\) be a random sample from a GQHRPS distribution and \(X_{i:n}\), \(i=1,2,\ldots , n\), denote its i-th order statistics. The pdf of \(X_{i:n}\) is given by

$$\begin{aligned} f_{i:n}(x)=\dfrac{1}{B(i,n-i+1)} f(x) [F(x)]^{i-1} [{\overline{F}}(x)]^{n-i}, \end{aligned}$$
(8)

where f, F, and \({\overline{F}}\) are the pdf, cdf, and survival function of GQHRPS distribution, respectively. Equation (8) can be written in the following forms

$$\begin{aligned} f_{i:n}(x)=\dfrac{1}{B(i,n-i+1)} \sum _{k=0}^{n-i} \left( {\begin{array}{c}n-i\\ k\end{array}}\right) (-1)^k f(x) [{F}(x)]^{k+i-1} \end{aligned}$$
(9)

or

$$\begin{aligned} f_{i:n}(x)=\dfrac{1}{B(i,n-i+1)} \sum _{k=0}^{i-1} \left( {\begin{array}{c}i-1\\ k\end{array}}\right) (-1)^k f(x) [{\overline{F}}(x)]^{k+n-i}. \end{aligned}$$
(10)

In view of the fact that

$$\begin{aligned} f(x) [{F}(x)]^{k+i-1}=\dfrac{1}{k+i} \dfrac{d}{dx}[{F}(x)]^{k+i}, \end{aligned}$$

the cdf of \(f_{i:n}(x)\) denoted by \(F_{i:n}(x)\), becomes

$$\begin{aligned} F_{i:n}(x)= & {} 1-\dfrac{1}{B(i,n-i+1)}\sum _{k=0}^{n-i} \dfrac{\left( {\begin{array}{c}n-i\\ k\end{array}}\right) (-1)^k}{k+i} [{F}(x)]^{k+i}\\= & {} 1-\dfrac{1}{B(i,n-i+1)}\sum _{k=0}^{n-i} \dfrac{\left( {\begin{array}{c}n-i\\ k\end{array}}\right) (-1)^k}{k+i}\\&\left[ 1- \dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] \right) }{A(\theta )} \right] ^{k+i}. \end{aligned}$$

An alternative expression for \(F_{i:n}(x)\), using Equation (10), is

$$\begin{aligned} F_{i:n}(x)= & {} 1-\dfrac{1}{B(i,n-i+1)}\\&\times \, \sum _{k=0}^{i-1} \dfrac{\left( {\begin{array}{c}i-1\\ k\end{array}}\right) (-1)^k}{k+n-i+1} [{\overline{F}}(x)]^{k+n-i+1}\\= & {} 1-\dfrac{1}{B(i,n-i+1)}\sum _{k=0}^{i-1} \dfrac{\left( {\begin{array}{c}i-1\\ k\end{array}}\right) (-1)^k}{k+n-i+1} \\&\times \, \left[ \dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] \right) }{A(\theta )} \right] ^{k+n-i+1} \end{aligned}$$

The Gauss hypergeometric function \(_2F_1(a,b:c;z)\) is the particular case of generalized hypergeometric function and is defined by

$$\begin{aligned} _2F_1(a,b:c;z)=\sum _{k=0}^{\infty } \dfrac{(a)_k (b)_k}{(c)_k} \dfrac{z^k}{k!}, \end{aligned}$$

where \((a)_m=\dfrac{\varGamma (a+m)}{\varGamma (a)}\) is the Pochhammer symbol with the convention that \((0)_0=1\). The next proposition states \(F_{i:n}(x)\) in terms of Gauss hypergeometric function.

Proposition 3.5

For all \(1\le i \le n\) and \(x \ge 0\),

$$\begin{aligned} F_{i:n}(x)=\left( {\begin{array}{c}n\\ i\end{array}}\right) B^{i} \ _2F_1(-n+i,i:i+1;B) \end{aligned}$$

is a polynomial in B, where

$$\begin{aligned} B=1- \dfrac{A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] \right) }{A(\theta )}. \end{aligned}$$

Moreover, \(F_{n:n}(x)=B^n\)

Proof

See the “Appendix”. \(\square \)

Expressions for moments of the ith order statistics \(X_{i:n}\), \(i=1,2,\ldots , n\), with cdf \(F_{i:n}(x)\) can be obtained using a result of [6] as follows:

$$\begin{aligned} E(X_{i:n}^r)= & {} r \sum _{k=n-i+1}^{n} (-1)^{k-n+i-1} \left( {\begin{array}{c}k-1\\ n-i\end{array}}\right) \left( {\begin{array}{c}n\\ k\end{array}}\right) \\&\int _{0}^{\infty } x^{r-1} [{\overline{F}}(x)]^k dx, \\= & {} r \sum _{k=n-i+1}^{n} \dfrac{(-1)^{k-n+i-1}}{A^k(\theta )} \left( {\begin{array}{c}k-1\\ n-i\end{array}}\right) \left( {\begin{array}{c}n\\ k\end{array}}\right) \\&\int _{0}^{\infty } x^{r-1} \left[ A\left( \theta \left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma }\right] \right) \right] ^k dx, \end{aligned}$$

for \(r=1,2, \ldots \) and \(i=1,2, \ldots , n\). An application of the first moment of order statistics can be considered in calculating the L-moments which are in fact the linear combination of the expected order statistics, See [21] for details.

By inserting the pdf and cdf of GQHRG distribution into Eq. (10), we obtain the pdf of the i-th order statistics of GQHRG distribution as follows:

$$\begin{aligned} f_{i:n}(x)= & {} \dfrac{1}{B(i,n-i+1)} \sum _{j=0}^{\infty } \sum _{k=0}^{i-1} \left( {\begin{array}{c}i-1\\ k\end{array}}\right) \\&\times \, (-1)^k \dfrac{\varGamma (k+n-i+j+2)}{\varGamma (k+n-i+2) j!}\\&\times \, \ B \ (1-\theta ) ^{k+n-i+1} \theta ^j A^{k+n-i+j}, \end{aligned}$$

where B and A are defined as above. By definition of density function of KQHR distribution in [15], the pdf of the i-th order statistics of GQHRG distribution can be written as

$$\begin{aligned} f_{i:n}(x)= & {} \dfrac{1}{B(i,n-i+1)} \sum _{j=0}^{\infty } \sum _{k=0}^{i-1} \left( {\begin{array}{c}i-1\\ k\end{array}}\right) \\&\times \, (-1)^k \dfrac{\left( {\begin{array}{c}k+n-i+j\\ j\end{array}}\right) }{k+n-i+1} (1-\theta ) ^{k+n-i+1} \theta ^j\\&\times \, f_{KQHR} (x; \alpha , \lambda , \beta , \gamma , k+n-i+j+1), \end{aligned}$$

where \(f_{KQHR}\) is the density function of KQHR distribution. As we see, the pdf of order statistics of GQHRG distribution can be expressed as a linear combination of the pdf of KQHR distribution. Therefore, some properties of the i-th order statistic, such as the mgf and moments, can be obtained directly from those of KQHR distribution. Foe example, the moments of the i-th order statistic of GQHRG distribution are given by

$$\begin{aligned} E(X_{i:n}^r)= & {} \dfrac{1}{B(i,n-i+1)}\\&\times \, \sum _{j=0}^{\infty } \sum _{k=0}^{i-1} (-1)^{k} \left( {\begin{array}{c}i-1\\ k\end{array}}\right) \\&\times \, \dfrac{\left( {\begin{array}{c}k+n-i+j\\ j\end{array}}\right) }{k+n-i+1} (1-\theta ) ^{k+n-i+1} \theta ^j \\&\times \, W_{i,j,k,m}^{*} \left[ \dfrac{\alpha \varGamma (r+2k+3m+1)}{[\alpha (j+1)]^{r+2k+3m+1}}\right. \\&+\, \lambda \dfrac{\varGamma (r+2k+3m+2)}{[\alpha (j+1)]^{r+2k+3m+2}} \\&\left. +\,\beta \dfrac{\varGamma (r+2k+3m+3)}{[\alpha (j+1)]^{r+2k+3m+3}}\right] , \end{aligned}$$

for \(r=1,2,\ldots \), where

$$\begin{aligned} W_{i,j,k,m}^{*}= & {} \sum _{i=j=k=m=0}^{\infty } (-1)^{i+j+k+m} \left( {\begin{array}{c}k+n-i+j\\ i\end{array}}\right) \\&\left( {\begin{array}{c}\gamma (i+1)-1\\ j\end{array}}\right) \dfrac{\lambda ^k \beta ^m (j+1)^{k+m}}{2^k m^m k! m!}. \end{aligned}$$

3.3 Stress–Strength Parameter of the QHRG Distribution

The stress–strength parameter \(R = P(X >Y)\) is a measure of component reliability and its estimation problem when X and Y are independent and follow a specified distribution has been discussed widely in the literature. Let X be the random variable of the strength of a component which is subjected to a random stress Y. The component fails whenever \(X <Y\) and there is no failure when \(X >Y\). Here, we obtain an expression for the stress–strength parameter of the QHRG distribution.

Let \(X\sim QHRG(\alpha , \lambda , \beta , \theta _1)\) and \(Y \sim QHRG(\alpha , \lambda , \beta , \theta _2)\) be independent random variables. The stress–strength parameter is defined as

$$\begin{aligned} R=P(Y<X)= & {} \int _{0}^{\infty } f_{X}(x) f_{Y}(x) dx \\= & {} \int _{0}^{\infty } \dfrac{(1-\theta _1) v^{\prime }_x \exp (- v_x)}{[1-\theta _1 \exp (- v_x) ]^2}\\&\times \dfrac{1- \exp (- v_x)}{1-\theta _2 \exp (- v_x)} dx, \end{aligned}$$

Changing the variable \(u=\exp (- v_x) \), we obtain

$$\begin{aligned} R= & {} \int _{0}^{\infty } \dfrac{(1-\theta _1) (1-u)}{[1-\theta _1 u ]^2 [1-\theta _2 u]} du \\= & {} (1-\theta _1) \left[ \dfrac{E}{\theta _1^2} \ln |1-\theta _1|- \dfrac{G}{\theta _2} \ln |1-\theta _2|+\dfrac{F \theta _1+E}{\theta _1-\theta _1^2}\right] , \end{aligned}$$

where \(E=\dfrac{\theta _2^2 (\theta _2-1)}{\theta _2^2-2\theta _1^2+\theta _1}\), \(F=\dfrac{\theta _2^2-2\theta _1^2- \theta _1\theta _2+2\theta _1}{\theta _2^2-2\theta _1^2+\theta _1}\), and \(G=\dfrac{\theta _1\theta _2-\theta _1}{\theta _2^2-2\theta _1^2+\theta _1}\).

Fig. 1
figure 1

Probability density function of the generalized quadratic hazard rate Poisson (first), generalized quadratic hazard rate geometric (second), generalized quadratic hazard rate logarithmic (third) and generalized quadratic hazard rate negative binomial (forth) distributions

Full size image
Fig. 2
figure 2

Hazard rate function of the generalized quadratic hazard rate Poisson (first), generalized quadratic hazard rate geometric (second), generalized quadratic hazard rate logarithmic (third) and generalized quadratic hazard rate negative binomial (forth) distributions

Full size image

4 Special Cases of the GQHRPS Distribution

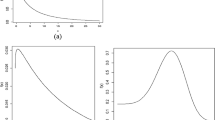
In this section, we study basic distributional properties of the generalized quadratic hazard rate-geometric (GQHRG), generalized quadratic hazard rate-Poisson (GQHRP), generalized quadratic hazard rate-logarithmic (GQHRL), generalized quadratic hazard rate-binomial (GQHRB) and generalized quadratic hazard rate-negative binomial (GQHRNB) distributions as special cases of GQHRPS distribution. In addition, expressions for the pdf and moments of order statistics as well as the stress–strength parameter of the QHRG distribution are obtained. First, to illustrate the flexibility of the distributions, plots of the density and hazard rate functions are presented in Figs. 1 and 2 for some selected values of parameters.

Using Table 1 and some equations in Sect. 2, basic distributional properties of the five special distributions of GQHRPS model are immediately obtained. Table 2 contains the survival function, pdf, hazard rate, MRL, and MPL functions of the GQHRG, GQHRP, GQHRL, GQHRB, and GQHRNB distributions.

Table 2 Survival, pdf, hazard rate, MRL, and MPL functions of special distributions of GQHRPS model
Full size table

where \(A=\left[ 1- \left( 1-\exp {(-v_{x})} \right) ^{\gamma } \right] ,\)\(B=\gamma v^{\prime }(x) \exp {(-v_{x})} \left( 1-\exp {(-v_{x})} \right) ^{\gamma -1},\)

$$\begin{aligned} B(x)= & {} \dfrac{\varGamma (2k+3q+1, \alpha s x)}{(\alpha s)^{2k+3q+1}},\\ T(x)= & {} \dfrac{\gamma (2k+3q+1, s \alpha x)}{(s \alpha )^{2k+3q+1}}, \end{aligned}$$

and

$$\begin{aligned} V_{l,s,k,q,n}= \sum _{n=1}^{\infty } \sum _{l=0}^{\infty } \sum _{s=0}^{\infty } \sum _{k=0}^{\infty } \sum _{q=0}^{\infty } \dfrac{ \theta ^n \varGamma (n+l) \varGamma (\gamma l+s)}{\varGamma (n) l! \varGamma (\gamma l) s!} \dfrac{(-1)^{k+q} s^{k+q} \lambda ^k \beta ^q }{k! q! 2^k 3^q}. \end{aligned}$$

5 Characterizations

This section is devoted to certain characterizations of GQHRPS distribution. These characterizations are based on: (i) a simple relation between two truncated moments and (ii) the hazard function. One of the advantages of the characterization (i) is that the cdf is not required to have a closed form.

We present our characterizations (i)–(ii) in two subsections.

5.1 Characterizations in Terms of the Ratio of Two Truncated Moments

In this subsection we present characterizations of GQHRPS distribution in terms of a simple relationship between two truncated moments. This characterization result employs a theorem due to [17], see Theorem 1 of “Appendix A”. Note that the result holds also when the interval H is not closed. Moreover, as mentioned above, it could also be applied when the cdf F does not have a closed form. As shown in [18], this characterization is stable in the sense of weak convergence.

Proposition 5.1

Let \(X:\varOmega \rightarrow \left( 0,\infty \right) \) be a continuous random variable and let \(q_{1}\left( x\right) =\left\{ A^{\prime }\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) \right\} ^{-1}\) and \(q_{2}\left( x\right) =q_{1}\left( x\right) \left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\) for \(x>0.\) The random variable X has pdf \(\left( 2.5\right) \) if and only if the function \(\eta \) defined in Theorem 1 has the form

$$\begin{aligned} \eta \left( x\right) =\frac{1}{2}\left\{ 1+\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right\} ,\quad x>0. \end{aligned}$$

Proof

Let X be a random variable with pdf \(\left( 2.5\right) \), then

$$\begin{aligned} \left( 1-F\left( x\right) \right) E\left[ q_{1}\left( x\right) \text { }|\text { }X\ge x\right] =\frac{\theta }{A\left( \theta \right) }\left\{ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right\} ,\quad x>0, \end{aligned}$$

and

$$\begin{aligned} \left( 1-F\left( x\right) \right) E\left[ q_{2}\left( x\right) \text { }|\text { }X\ge x\right] =\frac{\theta }{2A\left( \theta \right) }\left\{ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{2\gamma }\right\} , \quad x>0, \end{aligned}$$

and finally

$$\begin{aligned} \eta \left( x\right) q_{1}\left( x\right) -q_{2}\left( x\right) =\frac{1}{2}q_{1}\left( x\right) \left\{ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right\}>0,\quad for\, x>0. \end{aligned}$$

Conversely, if \(\eta \) is given as above, then

$$\begin{aligned} s^{\prime }\left( x\right) =\frac{\eta ^{\prime }\left( x\right) q_{1}\left( x\right) }{\eta \left( x\right) q_{1}\left( x\right) -q_{2}\left( x\right) }=\frac{\gamma \upsilon _{x}^{\prime }\exp \left( -\upsilon _{x}\right) \left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}}{1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }}\quad x>0, \end{aligned}$$

and hence

$$\begin{aligned} s\left( x\right) =-\log \left\{ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right\} ,\quad x>0. \end{aligned}$$

Now, in view of Theorem 1, X has density \(\left( 2.5\right) .\)\(\square \)

Corollary 5.1

Let \(X:\varOmega \rightarrow \left( 0,\infty \right) \) be a continuous random variable and let \(q_{1}\left( x\right) \) be as in Proposition 5.1. The pdf of X is \(\left( 2.5\right) \) if and only if there exist functions \(q_{2}\) and \(\eta \) defined in Theorem 1 satisfying the differential equation

$$\begin{aligned} \frac{\eta ^{\prime }\left( x\right) q_{1}\left( x\right) }{\eta \left( x\right) q_{1}\left( x\right) -q_{2}\left( x\right) }=\frac{\gamma \upsilon _{x}^{\prime }\exp \left( -\upsilon _{x}\right) \left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}}{1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }},\quad x>0. \end{aligned}$$

The general solution of the differential equation in 5.1 is

$$\begin{aligned} \eta \left( x\right) =\left\{ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right\} ^{-1}\left[ \begin{array} [c]{c} -\int \gamma \upsilon _{x}^{\prime }\exp \left( -\upsilon _{x}\right) \left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}\times \\ \left( q_{1}\left( x\right) \right) ^{-1}q_{2}\left( x\right) +D \end{array} \right] , \end{aligned}$$

where D is a constant. Note that a set of functions satisfying the above differential equation is given in 5.1 with \(D=\frac{1}{2}.\) However, it should be also noted that there are other triplets \(( q_{1},q_{2},\eta ) \) satisfying the conditions of Theorem 1.

5.2 Characterization Based on Hazard Function

It is known that the hazard function, \(h_{F}\), of a twice differentiable distribution function, F, satisfies the first order differential equation

$$\begin{aligned} \frac{f\text { }^{\prime }(x)}{f\text { }(x)}=\frac{h_{F}^{\prime }(x)}{h_{F} (x)}-h_{F}(x). \end{aligned}$$

For many univariate continuous distributions, this is the only characterization available in terms of the hazard function. The following characterization establish a non-trivial characterization of GQHRPS distribution which is not of the above trivial form.

Proposition 5.2

Let \(X:\varOmega \rightarrow \left( 0,\infty \right) \) be a continuous random variable. The pdf of X is \(\left( 2.5\right) \) if and only if its hazard function \(h_{F}\left( x\right) \) satisfies the differential equation

$$\begin{aligned} h_{F}^{\prime }\left( x\right) +\upsilon _{x}^{\prime }h_{F}\left( x\right)&=\theta \gamma \exp \left( -\upsilon _{x}\right) \\&\quad \times \frac{d}{dx}\left\{ \frac{\upsilon _{x}^{\prime }\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}A^{\prime }\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) }{A\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) }\right\} , \end{aligned}$$

\(x>0.\)

Proof

If X has pdf \(\left( 3.3\right) \), then clearly the above differential equation holds. Now, this differential equation holds, then

$$\begin{aligned}&\frac{d}{dx}\left\{ \exp \left( \upsilon _{x}\right) h_{F}\left( x\right) \right\} \\&\quad =\theta \gamma \frac{d}{dx}\left\{ \frac{\upsilon _{x}^{\prime }\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}A^{\prime }\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) }{A\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) }\right\} , \end{aligned}$$

\(x>0\) , from which, we obtain

$$\begin{aligned} h_{F}\left( x\right) =\frac{\upsilon _{x}^{\prime }\exp \left( -\upsilon _{x}\right) \left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma -1}A^{\prime }\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) }{A\left( \theta \left[ 1-\left( 1-\exp \left( -\upsilon _{x}\right) \right) ^{\gamma }\right] \right) },\quad x>0, \end{aligned}$$

which is the hazard function of GQHRPS distribution. \(\square \)

Remark 5.1

For \(\gamma =1\) , we have a simpler differential equation in terms of the hazard function

$$\begin{aligned} h_{F}^{\prime }\left( x\right) +\upsilon _{x}^{\prime }h_{F}\left( x\right) =\theta \exp \left( -\upsilon _{x}\right) \frac{d}{dx}\left\{ \frac{\upsilon _{x}^{\prime }A^{\prime }\left( \theta \exp \left( -\upsilon _{x}\right) \right) }{A\left( \theta \exp \left( -\upsilon _{x}\right) \right) }\right\} , \quad x>0. \end{aligned}$$

6 Parameters Estimation via the EM Algorithm and Simulation Studies

In this section, we compute maximum likelihood estimates (MLE) of the parameters via the EM algorithm. The EM algorithm is a method for computing MLE when some of the variables have missing values. The EM algorithm is an iterative procedure which consists of two steps. In the E step, we compute expectation of the log-likelihood of complete data, which contains observed and unobserved data, given observed data. In the M step, MLEs values updates by maximizing the obtained function in the E step. This iteration process is repeated until convergence.

In this paper, we assume that N is a missing variable and denote it by Z and we define a hypothetical complete data distribution with a joint probability density function in the form

$$\begin{aligned} g(x,z;\varTheta )= & {} \frac{a_z\theta ^z}{A(\theta )}\times z\gamma \nu '_x \exp {(-\nu _x)}(1-\exp {(-\nu _x)})^{\gamma -1}[1-(1-\exp {(-\nu _x)})^{\gamma }]^{z-1}, \end{aligned}$$

where \(\varTheta =(\alpha ,\lambda ,\beta ,\gamma ,\theta )\) denotes the set of parameters. In the \((t+1)\)th iteration of the EM algorithm, \(E(Z|X,\varTheta )\) is evaluated at \(\varTheta ^{(t)}\) where \(\varTheta ^{(t)}\) denotes the value of \(\varTheta \) obtained in the t-th iteration of the EM algorithm. So, we need to obtain the conditional distribution of Z given X. We have

$$\begin{aligned} g(z|x)= & {} \frac{a_z\theta ^{z-1} z [1-(1-\exp {(-\nu _x)})^{\gamma }]^{z-1}}{A'(\theta [1-(1-\exp {(-\nu _x)})^{\gamma }])}. \end{aligned}$$

So,

$$\begin{aligned} a= & {} E(Z|X,\varTheta )\\= & {} \frac{1}{A'(\theta [1-(1-\exp {(-\nu _x)})^{\gamma }])}\sum _{z=1}^{\infty } a_z z^2 (\theta [1-(1-\exp {(-\nu _x)})^{\gamma }])^{z-1}\\= & {} 1+\frac{\theta [1-(1-\exp {(-\nu _x)})^{\gamma }] A''(\theta [1-(1-\exp {(-\nu _x)})^{\gamma }])}{A'(\theta [1-(1-\exp {(-\nu _x)})^{\gamma }])} \end{aligned}$$

since \(A'(\theta )+\theta A''(\theta )=\sum _{z=1}^{\infty } z^2 a_z\theta ^{z-1}\).

The conditional expectation of the complete data log-likelihood given observed data is

$$\begin{aligned} E(\ln L(\varTheta ;x,z|x))\propto & {} \sum _{i=1}^{n} a_{i}\ln (\theta )-n\ln (A(\theta ))+n\ln (\gamma )+\sum _{i=1}^{n}\ln (\nu '_{x_i})-\sum _{i=1}^{n}\nu _{x_i}\\&+\,\sum _{i=1}^{n}(\gamma -1)\ln (1-\exp {(-\nu _{x_{i}})})\\&+\,\sum _{i=1}^n (a_i-1)\ln [1-(1-\exp {(-\nu _{x_i})})^{\gamma }]. \end{aligned}$$

In the M step, by differentiation \(E(\ln L(\varTheta ;x,z|x))\) with respect to \(\theta \), we obtain the following recursive equation

$$\begin{aligned} {\hat{\theta }}^{(t+1)}=\frac{ A({\hat{\theta }}^{(t+1)})}{n A'({\hat{\theta }}^{(t+1)})}\sum _{i=1}^{n} a_{i}^{(t)} \end{aligned}$$

By taking differentiation with respect to the \(\gamma \), we have \({\gamma }=h(\gamma )\) where

$$\begin{aligned} h(\gamma )= & {} n\left[ \sum _{i=1}^n (a_i-1) \frac{(1-\exp {(-\nu _{x_{i}})})^{\gamma } \ln (1-\exp {(-\nu _{x_{i}})})}{1-(1-\exp {(-\nu _{x_{i}})})^{\gamma }}\right. \\&\left. -\,\sum _{i=1}^{n} \ln (1-\exp {(-\nu _{x_{i}})})\right] ^{-1} \end{aligned}$$

We solve this equation with a simple iteration method as Kundu and Gupta [28]. Starting with an initial guess \(\gamma ^{(0)}\), then \(\gamma ^{(1)}=h(\gamma ^{(0)})\), similarly, \(\gamma ^{(2)}=h(\gamma ^{(1)})\) and so on. Continue the process until the convergence is obtained.

\(\alpha \) is the solution of the following equation

$$\begin{aligned}&\frac{\partial }{\partial \alpha }E(\ln L(\varTheta ;x,z|x))\\&\quad = \sum _{i=1}^{n}\frac{1}{\nu _{x_{i}}^\prime }+\sum _{i=1}^{n}\frac{(\gamma -1) x_i\exp (-\nu _{x_{i}})}{1-\exp (-\nu _{x_{i}})}-\,\sum _{i=1}^{n}x_i-\sum _{i=1}^n x_i A_i^{(1)}=0, \end{aligned}$$

where \(A_i^{(1)}=(a_i-1)\gamma \exp (-\nu _{x_{i}})\times \frac{(1-\exp (-\nu _{x_{i}}))^{\gamma -1}}{1-(1-\exp (-\nu _{x_{i}}))^{\gamma }}\).

Unfortunately, there is no closed form solution. We have employed the Newton–Raphson method to compute the solution. Using this method, the following recursive equation can be found

$$\begin{aligned} \alpha ^{(t+1)}=\alpha ^{(t)}-\frac{\frac{\partial }{\partial \alpha }E(\ln L(\varTheta ;x,z|x))}{\frac{\partial ^2}{\partial \alpha ^2}E(\ln L(\varTheta ;x,z|x))}, \end{aligned}$$

where

$$\begin{aligned} \frac{\partial ^2}{\partial \alpha ^2}E(\ln L(\varTheta ;x,z|x))= & {} -\sum _{i=1}^{n}\frac{1}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}\frac{(\gamma -1) x_i^2 \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2}-\sum _{i=1}^n x_i^2A_i^{(2)} \end{aligned}$$

where \(A_i^{(2)}=(a_i-1)\gamma \exp (-\nu _{x_{i}})(1-\exp (-\nu _{x_{i}}))^{\gamma -2} \frac{\Big [(1-\exp (-\nu _{x_{i}}))^{\gamma }+\gamma \exp (-\nu _{x_{i}})-1\Big ]}{(1-(1-\exp (-\nu _{x_{i}}))^{\gamma })^2}\).

Similarly, the \(\lambda ^{(t+1)}\) is obtained by the following equations

$$\begin{aligned}&\frac{\partial }{\partial \lambda }E(\ln L(\varTheta ;x,z|x))\\&\quad = \sum _{i=1}^{n}\frac{x_{i}}{\nu _{x_{i}}^\prime }+\sum _{i=1}^{n}(\gamma -1) \frac{x_i^2}{2}\times \frac{\exp (-\nu _{x_{i}})}{1-\exp (-\nu _{x_{i}})}-\sum _{i=1}^{n}\frac{x_i^2}{2}-\sum _{i=1}^n \frac{x_i^2}{2}A_i^{(1)} \end{aligned}$$

and

$$\begin{aligned}&\frac{\partial ^2}{\partial \lambda ^2}E(\ln L(\varTheta ;x,z|x))\\&\quad = -\sum _{i=1}^{n}\frac{x_i^2}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1)\left( \frac{x_i^2}{2}\right) ^2 \times \,\frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2} -\sum _{i=1}^n \left( \frac{x_i^2}{2}\right) ^2 A_i^{(2)} \end{aligned}$$

Analogously to the previous paragraph, the following relationships can be obtained for computing \(\beta ^{(t+1)}\)

$$\begin{aligned} \frac{\partial }{\partial \beta }E(\ln L(\varTheta ;x,z|x))= & {} \sum _{i=1}^{n}\frac{x_{i}^2}{\nu _{x_{i}}^\prime }+\sum _{i=1}^{n}(\gamma -1) \frac{x_i^3}{3}\\&\times \,\frac{\exp (-\nu _{x_{i}})}{1-\exp (-\nu _{x_{i}})}-\sum _{i=1}^{n}\frac{x_i^3}{3}-\sum _{i=1}^n \frac{x_i^3}{3}A_i^{(1)} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2}{\partial \beta ^2}E(\ln L(\varTheta ;x,z|x))= & {} -\sum _{i=1}^{n}\frac{(x_i^2)^2}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1)\left( \frac{x_i^3}{3}\right) ^2\\&\times \,\frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2} -\sum _{i=1}^n \left( \frac{x_i^3}{3}\right) ^2 A_i^{(2)} \end{aligned}$$

It worth be noted that, in all of above equalities, in the \((t+1)\)-th iteration of the EM algorithm, except the parameter that is being estimated, for other parameters we used their estimated values from the t-th iteration of the EM algorithm.

7 Standard Errors of the Estimates

The inverse of the observed information matrix \(\text {I}({\hat{\varTheta }};{\mathbf{x}})\) can be used for approximating the asymptotic covariance matrix of the ML estimator. A few methods for computing \(\text {I}({\hat{\varTheta }};x)\) when the EM algorithm is carried out are proposed in some researches. Among these, some methods are provided by Louis [30], Meng and Rubin [32], Baker [5] and Jamshidian and Jennrich [23, 24]. In here, we used Supplemented EM (SEM) algorithm that introduced by Meng and Rubin [32]. The most important feature of the SEM method is that related calculation can be readily done by using only the EM code. Meng and Rubin [32] show that

$$\begin{aligned} \text {I}({\hat{\varTheta }};x)^{-1}=\text {I}^{-1}_{com}({\hat{\varTheta }};x)+\varDelta \mathbf{V}, \end{aligned}$$

where \(\varDelta \mathbf{V}=(\text {I}_d-\hbox {J}({\hat{\varTheta }}))^{-1} \hbox {J}({\hat{\varTheta }})\text {I}^{-1}_{com}({\hat{\varTheta }};x)\), \(\text {I}_{com}({\hat{\varTheta }};x)=-E(\frac{\partial ^2}{\partial {\varTheta }\partial {\varTheta '}} \log L({\varTheta };x, z)|x)\), \(\text {I}_d\) denotes the \(d\times d\) identity matrix and \(\hbox {J}({\hat{\varTheta }})=\frac{\partial }{\partial \varTheta } \hbox {M}({\hat{\varTheta }})\) where \(\hbox {M}({\varTheta })\) is the EM map defined as \({\varTheta }^{(t+1)}=\hbox {M}({\varTheta }^{(t)})\) and \(\hbox {J}({\hat{\varTheta }})\) is referred as the matrix rate of convergence. They showed that \(\hbox {J}({\hat{\varTheta }})\) can be approximated by using the EM code.

In our model, the (i, j)th element of the symmetric matrix \(\text {I}_{com}({\hat{\varTheta }};x)\), \(i,j=1,2 \), is denoted by \(\text {I}_{com}({\hat{\theta }}_i;{\hat{\theta }}_j)\) and can be obtained as follows

$$\begin{aligned} \text {I}_{com}({\alpha },{\alpha })= & {} -\sum _{i=1}^{n}\frac{1}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1) x_i^2\times \frac{\exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2}-\sum _{i=1}^n x_i^2A_i^{(2)}\\ \text {I}_{com}({\lambda },{\lambda })= & {} -\sum _{i=1}^{n}\frac{x_i^2}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1)\left( \frac{x_i^2}{2}\right) ^2\\&\times \,\frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2}-\sum _{i=1}^n \left( \frac{x_i^2}{2}\right) ^2 A_i^{(2)}\\ \text {I}_{com}({\beta },{\beta })= & {} -\sum _{i=1}^{n}\frac{(x_i^2)^2}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1)\left( \frac{x_i^3}{3}\right) ^2\\&\times \,\frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2}-\sum _{i=1}^n \left( \frac{x_i^3}{3}\right) ^2 A_i^{(2)}\\ \text {I}_{com}({\gamma },{\gamma })= & {} \frac{-n}{\gamma ^2}-\sum _{i=1}^n (a_i-1) (1-\exp {(-\nu _{x_{i}})})^{\gamma } \Big (\frac{ \ln (1-\exp {(-\nu _{x_{i}})})}{1-(1-\exp {(-\nu _{x_{i}})})^{\gamma }}\Big )^2\\ \text {I}_{com}({\theta },{\theta })= & {} \frac{-\sum _{i=1}^n a_i}{\theta ^2}-n\frac{A''(\theta )}{A(\theta )}+n\frac{A'(\theta )^2}{A(\theta )^2}\\ \text {I}_{com}({\theta },{\alpha })= & {} \text {I}_{com}({\theta },{\lambda })=\text {I}_{com}({\theta },{\beta })=\text {I}_{com}({\theta },{\gamma })=0\\ \text {I}_{com}({\gamma },{\alpha })= & {} \sum _{i=1}^{n}x_i\Bigg \{\frac{\exp {(-\nu _{x_{i}})}}{1-\exp {(-\nu _{x_{i}})}}-(a_i-1)A_i^{(3)}\Bigg \}\\ \text {I}_{com}({\gamma },{\lambda })= & {} \sum _{i=1}^{n}\frac{x_i^2}{2}\Bigg \{\frac{\exp {(-\nu _{x_{i}})}}{1-\exp {(-\nu _{x_{i}})}}-(a_i-1)A_i^{(3)}\Bigg \}\\ \text {I}_{com}({\gamma },{\beta })= & {} \sum _{i=1}^{n}\frac{x_i^3}{3}\Bigg \{\frac{\exp {(-\nu _{x_{i}})}}{1-\exp {(-\nu _{x_{i}})}}-(a_i-1)A_i^{(3)}\Bigg \}\\ \text {I}_{com}({\alpha },{\lambda })= & {} -\sum _{i=1}^{n}\frac{x_i}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1) \frac{x_i^3}{2}\times \frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2}-\sum _{i=1}^n \frac{x_i^3}{2} A_i^{(2)}\\ \text {I}_{com}({\alpha },{\beta })= & {} -\sum _{i=1}^{n}\frac{x_i^2}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1) \frac{x_i^4}{3}\times \frac{\exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2} -\sum _{i=1}^n \frac{x_i^4}{3} A_i^{(2)}\\ \text {I}_{com}({\lambda },{\beta })= & {} -\sum _{i=1}^{n}\frac{x_i^3}{(\nu _{x_{i}}^\prime )^2}-\sum _{i=1}^{n}(\gamma -1) \frac{x_i^5}{6}\times \frac{ \exp (-\nu _{x_{i}})}{(1-\exp (-\nu _{x_{i}}))^2} -\sum _{i=1}^n \frac{x_i^5}{6} A_i^{(2)} \end{aligned}$$

where \(A_i^{(3)}=\frac{\exp {(-\nu _{x_{i}})} (1-\exp {(-\nu _{x_{i}})})^{\gamma -1}}{\Big (1-(1-\exp {(-\nu _{x_{i}})})^{\gamma }\Big )^2}\Big [ \ln (1-\exp {(-\nu _{x_{i}})})^\gamma +1-(1-\exp {(-\nu _{x_{i}})})^\gamma \Big ]\).

\(A_i^{(2)}\), \(A_i^{(3)}\) and all of the parameters in the above equalities are computed in \({\hat{\varTheta }}\).

Table 3 True value of parameters along with means (Est.) and standard deviations (SD) for the estimated parameters obtain from simulation
Full size table

8 Simulation Study

To illustrate the performance and the accuracy of the EM algorithm in estimating the model parameters we performed a simulation study. To investigate the effect of the sample size we consider \(n=35, 50\) and 100. In each replication, a random sample of size n is drawn from the GQHRP, GQHRL and GQHRG distributions. The true values of the parameters, that we use in the simulation, are given in Table 3 For each n, we simulate 500 random data sets from the proposed model. For each data set, the model parameters are estimated via the EM algorithm. We calculate means and standard deviations of the obtained estimates from 500 replications and these are given in Table 3 The results given in this table are shown that the differences between the average estimates and the true values are almost small and also we can see that by increasing the sample size, standard deviations of parameters are reduced. So, overall, the obtained results are satisfactory.

Table 4 Time between failures (thousands of hours) of secondary reactor pumps data presented
Full size table
Table 5 Descriptive statistics for the times between successive failures (in thousands of hours) of secondary reactor pumps
Full size table
Table 6 MLEs (SE), AIC, BIC, AICc statistics for data
Full size table

9 Real Data Analysis

The data set given by [46] on the represent the times between successive failures (in thousands of hours) in events of secondary reactor pumps. The data are presented in Table 4. Table 5 gives some statistic measures for these data, which indicate that the empirical distribution is skewed to the left and platykurtic. The MLEs of the parameters along with the standard errors (SE) of the estimates, AIC (Akaike Information Criterion), BIC (Bayesian information criterion), and AICc are displayed in Table 6 for this data set and the following distributions (BGG and TGG). The Beta Generalized Gamma distribution (BGG) is given by the PDF

$$\begin{aligned} f(x)=\dfrac{1}{B(\alpha ,\lambda )} g_{a,\nu ,p} G_{a,\nu ,p}^{\alpha -1}(1-G)^{\lambda -1} \end{aligned}$$
(11)

where

$$\begin{aligned} G_{a,\nu ,p}(x)=\dfrac{\gamma (\nu ,[x/a]^{p})}{\varGamma (\nu )} \end{aligned}$$

and

$$\begin{aligned} g_{a,\nu ,p}(x)=\dfrac{\mid p\mid }{a\varGamma (\nu )}\left( \frac{x}{a}\right) ^{\nu p-1} \exp \left[ -\left( \frac{x}{a}\right) ^{p}\right] . \end{aligned}$$

Here p is not zero and the other parameters are positive. The Transmuted Generalized Gamma (TGG) distribution is given by the PDF

$$\begin{aligned} f(x)=p x^{p\nu -1} \dfrac{\exp \{-(x/a)^p\}}{a^{p\nu }\varGamma (\nu )}\left[ 1+\lambda -2\lambda \dfrac{\gamma [\nu ,(x/a)^{p}}{\varGamma (\nu )}\right] \end{aligned}$$
(12)

for \( p>0 \), \( \mid \lambda \mid \le 1 \), \( a>0 \) and \( \nu >0 \). The \( MLE_{s} \), the value of the Akaike information criterion (AIC), the value of the Bayesian information criterion (BIC) and the second-order AIC (AICc) for goodness of fit are reported in Table 5 for each of the fitted distributions.

Based on the AIC and BIC and AICc statistics, we see that four of the fitted generalized quadratic hazard rate power series distribution perform better than the generalized quadratic hazard rate binomial distribution. The generalized quadratic hazard rate logarithmic distribution gives the best fit with the smallest values for AIC, BIC and AICc and p value = 0.9989. The generalized quadratic hazard rate geometric with p value = 1 gives the second smallest values for AIC , BIC and AICc . The generalized quadratic hazard rate Poisson with p value = 1 gives the third smallest values for AIC, BIC and AICc. The generalized quadratic hazard rate negative binomial distribution with p value = 0.9985, \(m=3\) gives the forth smallest values for AIC, BIC and AICc. The Transmuted Generalized Gamma distribution gives the worst fit with the largest values for AIC, BIC and AICc. The Beta Generalized Gamma distribution gives the second worst fit with the second largest values for AIC, BIC and AICc.

10 Concluding Remarks

In this paper we have introduced the new class of lifetime distributions. It contains a number of known special submodels such as generalized exponential power series, generalized linear failure rate power series, quadratic hazard rate geometric distributions, among others. We think the formulas derived are manageable by using modern computer resources with analytic and numerical capabilities. The proposed model has enough flexibility that can be used quite effectively for modelling lifetime data. The generation of random samples from proposed distribution is very simple, and therefore Monte Carlo simulation can be performed very easily for different statistical inference purpose. Maximum likelihood estimates of the new model are discussed. Analyses of one real data set indicate the good performance and usefulness of the new model.