1 Introduction

The idea of developing new distributions remains an important topic in the recent literatures. It provides more flexible distributions that can model complex data structure. Lee et al. [12] in their review paper provided an overview of most methods used to generate family of continuous distributions. They pointed out that prior to 1980, methods of generating distributions can be categorized into three categories; method of differential equation, method of transformation and method of quantile function. For more details about these methods, one is referred to Pearson [20], Johnson [10] and Tukey [23]. Since 1980, several methods of generating distributions proposed in the literature. Lee et al. [12] categorized these methods as “method of combination”. These methods focused mainly on adding parameters to an existing distribution or combining existing distributions. For more details about the recent developments in generalizing distributions, we refer the reader to Johnson et al. [11], Eugene et al. [7], Jones [9], Alzaatreh et al. [1,2,3] and Tahir et al. [22].

Recently, Mahdavi and Kundu [16] proposed the so called alpha power transformation (APT) family. The parameter \(\alpha \) is introduced to incorporate skewness to the base distribution. The APT family is defined as follows: Let F(x) be the cumulative density function (CDF) of any continuous random variable X,  then the CDF of the APT family is given by

$$\begin{aligned} F_{\mathrm{APT}} (x;\alpha )=\left\{ {\begin{array}{ll} \frac{\alpha ^{F(x)}-1}{\alpha -1} &{} \mathrm{if}\, \alpha >0,\alpha \ne 1 \\ F(x) &{}\mathrm{if}\, \alpha =1. \\ \end{array}} \right. \end{aligned}$$
(1)

The corresponding probability density function (PDF) is

$$\begin{aligned} f_{\mathrm{APT}} (x;\alpha )=\left\{ {\begin{array}{ll} \frac{\log \alpha }{\alpha -1}f(x)\alpha ^{F(x)} &{}\mathrm{if}\, \alpha >0,\alpha \ne 1 \\ f(x) &{}\mathrm{if}\, \alpha =1. \\ \end{array}} \right. \end{aligned}$$

Mahdavi and Kundu [16] applied the proposed method to the exponential distribution and proposed the alpha power exponential distribution. They studied various properties of the proposed distribution such as explicit expressions for the moments, quantiles and moment generating function.

This paper is organized in the following way: In Sect. 2, we propose a new method for generating continuous distributions based on the family of distributions in (1). The proposed family of distributions has a connection with weighted distributions. In Sect. 3, a member of the proposed family namely, Alpha Power within Weibull Quantile Distribution (APWQ), is proposed. General properties of the APWQ are studied in Sect. 4 including, quantile, moments, moment generating function, Shannon entropy, mean residual life and mean waiting time functions. The maximum likelihood estimation and Applications to complete and censored cancer data sets are studied in Sect. 5. Section 6 offers some concluding remarks.

2 General Properties of the New Method

Let g(x) and G(x) be, respectively, the PDF and CDF of any random variable X . Then the CDF, F(x), of the new proposed method for generating distributions can be obtained by inverting the following equation

$$\begin{aligned} \frac{\alpha ^{F(x)}-1}{\alpha -1}=G(x), \alpha \ne 1. \end{aligned}$$
(2)

Therefore,

$$\begin{aligned} F(x)=\frac{\log (1+(\alpha -1)G(x))}{\log (\alpha )} , x\in {\mathbb {R}},\quad \alpha >0,\alpha \ne 1. \end{aligned}$$
(3)

The corresponding PDF is

$$\begin{aligned} f(x)=\frac{(\alpha -1)g(x)}{\log (\alpha )(1+(\alpha -1)G(x))} \end{aligned}$$
(4)

Note that when \(\alpha \rightarrow 1\), f(x) reduces to g(x). Equation (4) can be written in the following form

$$\begin{aligned} f(x)=\frac{g(x)\omega (x)}{c}. \end{aligned}$$
(5)

From (5), it is clear that f(x) is a weighted version of g(x), where the weight function is

$$\begin{aligned} \omega (x)=(1+(\alpha -1)G(x))^{-1} \end{aligned}$$

and the normalizing constant \(c=\log (\alpha )/(\alpha -1)\). A useful expansion for the CDF and PDF in (3) and (4) for \(0\le \alpha \le 2, \alpha \ne 1\) are given by

$$\begin{aligned} F(x)=\frac{1}{\log (\alpha )}\sum _{k=1}^\infty {\frac{(-1)^{k}(\alpha -1)^{k}}{k}} G(x)^{k}. \end{aligned}$$

and

$$\begin{aligned} f(x)=\frac{g(x)}{\log (\alpha )}\sum _{k=0}^\infty {(-1)^{k}(\alpha -1)^{k+1}G(x)^{k}} \end{aligned}$$
(6)

From (3) and (4), the hazard rate function, h(x), is given by

$$\begin{aligned} h(x)=\frac{(\alpha -1)g(x)}{(1+(\alpha -1)G(x))\left[ {\log (\alpha )-\log (1+(\alpha -1)G(x))} \right] } . \end{aligned}$$

Remark 1

If X follows the distribution in (3), then the quantile function is given by

$$\begin{aligned} x_q =G^{-1}\left( {\frac{\alpha ^{q}-1}{\alpha -1}} \right) , 0\le q\le 1. \end{aligned}$$

Note that Remark 1 can be used to simulate random sample from F(x) distribution by first simulating random sample \(U_i \sim \hbox {Uniform}(0,1), i=1,\ldots ,n\). Then the random sample \(X_i =G^{-1}\left( {\frac{\alpha ^{U_i }-1}{\alpha -1}} \right) , i=1,\ldots ,n\) follow F(x) distribution.

Theorem 1

If a random variable X follows the family of distributions in (4), then the Shannon entropy defined as \(\eta _X =E\left[ {-\log f(x)} \right] \) is given by

$$\begin{aligned} \eta _X =\log \left( {\frac{\sqrt{\alpha }\log (\alpha )}{\alpha -1}} \right) -E\left\{ {\log g(X)} \right\} . \end{aligned}$$
(7)

3 Alpha Power within Weibull Quantile Distribution

The Weibull distribution is a popular life time distribution in reliability theory. Numerous articles have been written demonstrating the applications of the Weibull distribution in biology, medicine, engineering and meteorology. In the last few years, several researchers have developed various extensions and generalizations of the Weibull distribution to model various types of data. Among these, Mudholkar et al. [18, 19] introduced and studied the exponentiated Weibull distribution to analyze bathtub failure data by adding an extra shape parameter to the Weibull distribution. Xie and Lai [24] introduced the additive Weibull distribution, Jalmar et al. [8] introduced the generalized modified Weibull distribution and Cordeiro et al. [5] studied the exponential-Weibull distribution. Next, Eq. (3) is used to introduce the APWQ distribution.

Let X be a random variable follows the Weibull distribution with CDF \(G(x)=1-e^{-\lambda x^{\beta }}, x>0\). From (3), the CDF of the APWQ distribution is defined as

$$\begin{aligned} F(x)=\frac{\log (1+(\alpha -1)(1-e^{-\lambda x^{\beta }}))}{\log (\alpha )}, x>0. \end{aligned}$$
(8)

The corresponding PDF is

$$\begin{aligned} f(x)=\frac{(\alpha -1)\lambda \beta x^{\beta -1}e^{-\lambda x^{\beta }}}{\log (\alpha )(1+(\alpha -1)(1-e^{-\lambda x^{\beta }}))}, \end{aligned}$$
(9)

where \(\alpha ,\beta >0\) are shape parameters and \(\lambda >0\) is a scale parameter. Table 1 lists various special models of the APWQ distribution.

Table 1 Sub-models of the APWQ distribution
Full size table

Remark 2

Using the result in (6), the PDF in (9) for \(0\le \alpha \le 2, \alpha \ne 1\), can be expressed in a generalized mixture form of the Weibull distributions as

$$\begin{aligned} f(x)=\frac{1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}(\alpha -1)^{k+1}g_{WD} (x;\lambda (j+1),\beta )} \end{aligned}$$
(10)

where \(g_{WD} (x;\lambda (j+1),\beta )\) is the PDF of the Weibull distribution with scale parameter \(\lambda (j+1)\) and shape parameter \(\beta \).

On the other hand, if \(\alpha >2\), and using the expansion

$$\begin{aligned} \left[ {1+(\alpha -1)(1-e^{-\lambda x^{\beta }})} \right] ^{-1}=\alpha ^{-1}\sum _{k=0}^\infty {\left( {1-1/\alpha } \right) ^{k}} e^{-\lambda kx^{\beta }} \end{aligned}$$

the PDF in (9) can be written as

$$\begin{aligned} f(x)=\frac{1}{\log (\alpha )}\sum _{k=0}^\infty {\left( {1-1/\alpha } \right) ^{k+1}} g_{WD} (x;\lambda (k+1),\beta ) \end{aligned}$$
(11)

The survival function and hazard rate function for APWQ are, respectively, given by

$$\begin{aligned} S(x)=\frac{\log (\alpha )-\log (1+(\alpha -1)(1-e^{-\lambda x^{\beta }}))}{\log (\alpha )}, \end{aligned}$$

and

$$\begin{aligned} h(x)=\frac{(\alpha -1)\lambda \beta x^{\beta -1}e^{-\lambda x^{\beta }}}{(1+(\alpha -1)(1-e^{-\lambda x^{\beta }}))\left[ {\log (\alpha )-\log (1+(\alpha -1)(1-e^{-\lambda x^{\beta }}))} \right] } , x>0. \end{aligned}$$

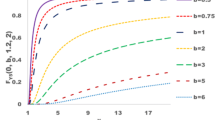
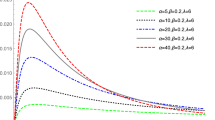
Figures 1 and 2 display some plots of the APWQ density and hazard rate functions respectively for various parameter values of \(\alpha \) and \(\beta \) where the scale parameter \(\lambda =1\). These plots show that the APWQ is flexible in terms of shapes. The APWQ distribution can be left-skewed or right-skewed. Also, the hazard rate function can be very flexible. It can be increasing (IFR), decreasing (DFR), bathtub (BT), upside down bathtub (UBT) or bimodal failure rate shapes.

Fig. 1
figure 1

Density plots of APWQ density for various values of \(\alpha \) and \(\beta \)

Full size image
Fig. 2
figure 2

Hazard rate plots of APWQ distribution for various values of \(\alpha \) and \(\beta \)

Full size image

4 Properties of the APWQ Distribution

In this section, we provide some general properties of the APWQ distribution including quantile function, mode, moments, entropy, order statistics and mean residual life and mean waiting time.

Remark 3

The q-th quantile function of APWQ distribution is given by

$$\begin{aligned} x_q =\left( {\frac{-1}{\lambda }\log \left[ {\frac{\alpha -\alpha ^{q}}{\alpha -1}} \right] } \right) ^{1/\beta }, 0\le q\le 1. \end{aligned}$$

Theorem 2

The APWQ is unimodal. When \(\beta \le 1\), the mode is at \(x=0\). And when \(\beta >1\), the mode is at \(x=x_0\) where \(k(x_0 )=0\) and

$$\begin{aligned} k(x)=1-\beta +\alpha \left\{ {\beta -1+\hbox {e}^{x^{\beta }\lambda }(1-\beta +x^{\beta }\beta \lambda )} \right\} . \end{aligned}$$

Proof

Since \(\lambda \) is a scale parameter, without loss of generality assume \(\lambda =1\). From (9), \({f}'(x)=0\Leftrightarrow x^{\beta -2}[(\beta -1-\lambda \beta x^{\beta })(\alpha +(1-\alpha )e^{-\lambda x^{\beta }})+\lambda \beta (1-\alpha )x^{\beta }e^{-\lambda x^{\beta }}]=0\). Therefore the critical values of f(x) are \(x=0\) or the solution of the equation \((\beta -1-\lambda \beta x^{\beta })(\alpha +(1-\alpha )e^{-\lambda x^{\beta }})+\lambda \beta (1-\alpha )x^{\beta }e^{-\lambda x^{\beta }}=0\). This implies that \((\beta -1-\lambda \beta x^{\beta })(\alpha e^{\lambda x^{\beta }}+1-\alpha )+\lambda \beta (1-\alpha )x^{\beta }=0\). This simplifies to \(\alpha (\beta -1-\lambda \beta x^{\beta })e^{\lambda x^{\beta }}+(1-\alpha )(\beta -1)=0\). Hence, the critical values of f(x) are \(x=0\) or \(x=x_0 \) where \(k(x_0 )=0\). Consider the derivative of k(x) as \({k}'(x)=\alpha \beta \hbox {e}^{x^{\beta }}x^{\beta -1}(1+x^{\beta }\beta )\). Clearly \({k}'(x)>0\) for all \(x>0\). Therefore, k(x) is strictly increasing. Now assume \(\beta \le 1.\) Since \(k(0)=1-\beta \ge 0\), this implies that \(x=0\) is the only critical values of f(x). Also, \(\lim \limits _{x\rightarrow 0} f(x)=\infty \) if \(\beta <1\) and \((\alpha -1)\log \alpha \) if \(\beta =1\). Hence, the mode is at \(x=0\). Now assume \(\beta >1\). The fact that \(k(0)=1-\beta <0\) and k(x) is strictly increasing, implies that k(x) has a unique solution at \(x=x_0\). Furthermore, when \(\beta >1\), \(\lim \limits _{x\rightarrow 0} f(x)=0\) and therefore, \(x=0\) is not a modal point. This completes the proof. \(\square \)

4.1 Moment and Moment Generating Function

In this subsection, we will derive the r-th moments and the moment generating function for the APWQ distribution.

If \(0\le \alpha \le 2, \alpha \ne 1\) and From (10), it is easy to obtain the \(r-\hbox {th}\) moment of APWQ as

$$\begin{aligned} E(X^{r})=\frac{\Gamma (1+r/\beta )}{\lambda ^{r/\beta }\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) \frac{(-1)^{k+j}(\alpha -1)^{k+1}}{(j+1)^{1+r/\beta }}} } . \end{aligned}$$
(12)

Similarly, if \(\alpha >2\), the \(r-\hbox {th}\) moment of APWQ can be obtained from (11) as

$$\begin{aligned} E(X^{r})=\frac{\Gamma (1+r/\beta )}{\lambda ^{r/\beta }\log (\alpha )}\sum _{k=0}^\infty {\frac{\left( {1-1/\alpha } \right) ^{k+1}}{(k+1)^{1+r/\beta }}} \end{aligned}$$
(13)

Also, the moment generating function for \(0\le \alpha \le 2, \alpha \ne 1\), can be written as

$$\begin{aligned} M_x (t)=\frac{1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\sum _{m=0}^\infty {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } \frac{(-1)^{k+j}(\alpha -1)^{k+1}t^{m}}{m! (j+1)^{1+m/\beta }\lambda ^{m/\beta }}\Gamma (1+m/\beta )} } . \end{aligned}$$

Similarly, the moment generating function for \(\alpha >2\), takes the form

$$\begin{aligned} M_x (t)=\frac{1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{m=0}^\infty {\frac{\left( {1-1/\alpha } \right) ^{k+1}t^{m}\Gamma (1+m/\beta )}{m!(k+1)^{1+m/\beta }\lambda ^{m/\beta }}} } \end{aligned}$$

Remark 3, Theorem 2 and Eqs. (12) and (13) are used to obtain the mean, median, mode, variance, skewness and kurtosis for the APWQ distribution. The median is obtained by setting \(q=0.5\) in Remark 3. The mean \(\mu \) is obtained by setting \(r=1\) in Eqs. 12 or 13 based on the value of \(\alpha \). The variance \(\sigma ^{2}\), skewness \(\gamma _1 \) and kurtosis \(\gamma _2 \) are obtained using the formulas \(\sigma ^{2}=E(X^{2})-\mu ^{2}\), \(\gamma _1 =E[(X-\mu )/\sigma ]^{3}\) and \(\gamma _2 =E[(X-\mu )/\sigma ]^{4}\). These values are reported in Table 2 for various values of \(\alpha \) and \(\beta \) where the scale parameter \(\lambda =1\). From Table 2, it is noted that for fixed \(\beta \) and \(\lambda \), the mean, median and mode of APWQ are decreasing function of \(\alpha \), and the skewness is increasing function of \(\alpha \). Also, for fixed \(\alpha \) and \(\lambda \), the median is an increasing function of \(\beta \), the mode is an increasing function of \(\beta >1\), while the variance and skewness are decreasing function of \(\beta \). Also, Table 2 shows that the APWQ is a flexible distribution. It can be left skewed, right skewed or approximately symmetric. Furthermore, it can be platykurtic (kurtosis \(<3\)) or leptokurtic (kurtosis \(>3\)).

Table 2 Mean, median, mode, variance, skewness, and kurtosis of APWQ for \(\lambda =1\) and various values of \(\alpha \) and \(\beta \)
Full size table

4.2 Shannon Entropy

Using (7) and (9), the Shannon entropy, \(\eta _X \), for \(0\le \alpha \le 2, \alpha \ne 1\) is given by

$$\begin{aligned} \eta _X =\log \left( {\frac{\sqrt{\alpha }\log (\alpha )}{(\alpha -1)\lambda \beta }} \right) -\int _0^\infty {\left\{ {I_1 -I_2 } \right\} f(x)dx} \end{aligned}$$
(14)

where \(I_1 =(\beta -1)\log (x)\) and \(I_2 =\lambda x^{\beta }\). Now

$$\begin{aligned} \int _0^\infty {I_1 f(x)} dx= & {} \frac{\lambda \beta (\beta -1)}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}(\alpha -1)^{k+1}}\nonumber \\&\times \int _0^\infty {x^{\beta -1}e^{-\lambda (j+1)x^{\beta }}\log (x)dx} . \end{aligned}$$
(15)

On using the \(\int _0^\infty {e^{-ax}\log xdx} =-\frac{1}{a}(C+\log a)\), where C is the Euler constant, (15) can be written as

$$\begin{aligned} \int _0^\infty {I_1 f(x)} dx=\frac{\beta -1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } \frac{(-1)^{k+j-1}}{\beta (j+1)}(\alpha -1)^{k+1}} \left[ {C+\log (\lambda (j+1))} \right] . \end{aligned}$$
(16)

Similarly,

$$\begin{aligned} \int _0^\infty {I_2 f(x)} dx=\frac{1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}\frac{(\alpha -1)^{k+1}}{(j+1)^{2}}} . \end{aligned}$$
(17)

From (14), (16) and (17), \(\eta _X \) reduces to

$$\begin{aligned} \eta _X= & {} \log \left( {\frac{\sqrt{\alpha }\log (\alpha )}{(\alpha -1)\lambda \beta }} \right) -\frac{\beta -1}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } \frac{(-1)^{k+j+1}(\alpha -1)^{k+1}}{j+1}} \\&\times \left[ {\frac{C+\log (\lambda (j+1))}{\beta }+\frac{1}{(\beta -1)(j+1)}} \right] . \end{aligned}$$

Using similar approach, the Shannon entropy, for \(\alpha >2\) is given by

$$\begin{aligned} \begin{array}{l} \eta _X =\log \left( {\frac{\sqrt{\alpha }\log (\alpha )}{(\alpha -1)\lambda \beta }} \right) +\frac{\beta -1}{\log (\alpha )}\sum _{k=0}^\infty {\frac{(1-1/\alpha )^{k+1}}{k+1}\left[ {\frac{C+\log (\lambda (k+1))}{\beta }+\frac{1}{(\beta -1)(k+1)}} \right] } . \\ \\ \end{array} \end{aligned}$$

4.3 Mean Residual Life and Mean Waiting Time

Let X be a continuous random variable. The mean residual life is the expected additional lifetime that a component has survived after a fixed time point t. The mean residual life function, say \(\mu (t)\), is given by

$$\begin{aligned} \mu (t)=E(T-t|T>t)=\frac{1}{S(t)}\int _t^\infty {x f(x)dx} -t, \end{aligned}$$

where

$$\begin{aligned} \int _t^\infty {x f(x)dx} =\frac{\lambda ^{-1/\beta }}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}(\alpha -1)^{k+1}\frac{\Gamma (\lambda (j+1)t^{\beta },1+1/\beta )}{(j+1) ^{1+1/\beta }}} , \end{aligned}$$

where \(\Gamma (a,b)\) is the upper incomplete gamma function and \(0\le \alpha \le 2, \alpha \ne 1\). When \(\alpha >2\) we have

$$\begin{aligned} \int _t^\infty {x f(x)dx} =\frac{\lambda ^{-1/\beta }}{\log (\alpha )}\sum _{k=0}^\infty {(1-1/\alpha )^{k+1}\frac{\Gamma (\lambda (k+1)t^{\beta },1+1/\beta )}{(k+1) ^{1+1/\beta }}} \end{aligned}$$

The mean waiting time represents the waiting time elapsed since the failure of an object on condition that this failure had occurred in the interval [0, t]. The mean waiting time of X, say \(\bar{{\mu }}(t)\), is defined by

$$\begin{aligned} \bar{{\mu }}(t)=t-\frac{m(t)}{F(t)} \end{aligned}$$
(18)

where F(t) is the CDF given by (8) and m(t) is the first incomplete moment given by

$$\begin{aligned} m(t)= & {} \int _0^t {xf(x)dx}\nonumber \\= & {} \frac{\lambda ^{-1/\beta }}{\log (\alpha )}\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}(\alpha -1)^{k+1}\frac{\gamma \left\{ {\lambda (j+1)t^{\beta },1+1/\beta } \right\} }{(j+1) ^{1+1/\beta }}}\nonumber \\ \end{aligned}$$
(19)

where \(\gamma (a,b)\) is the lower incomplete gamma function and \(0\le \alpha \le 2, \alpha \ne 1\). Substituting (8) and (19) in (18), \(\bar{{\mu }}(t)\) can be written as

$$\begin{aligned} \bar{{\mu }}(t)=t-\lambda ^{-1/\beta }\sum _{k=0}^\infty {\sum _{j=0}^k {\left( {{\begin{array}{l} k \\ j \\ \end{array} }} \right) } (-1)^{k+j}(\alpha -1)^{k+1}\frac{\gamma \left\{ {\lambda (j+1)t^{\beta },1+1/\beta } \right\} }{(j+1) ^{1+1/\beta }\log (\alpha +(1-\alpha )e^{-\lambda t^{\beta }})}} . \end{aligned}$$

Similarly, \(\bar{{\mu }}(t)\) in the case of \(\alpha >2\) can be written as

$$\begin{aligned} \bar{{\mu }}(t)=t-\lambda ^{-1/\beta }\sum _{k=0}^\infty {(1-1/\alpha )^{k+1}\frac{\gamma \left\{ {\lambda (k+1)t^{\beta },1+1/\beta } \right\} }{(k+1) ^{1+1/\beta }\log (\alpha +(1-\alpha )e^{-\lambda t^{\beta }})}} . \end{aligned}$$

5 Estimation and Applications

Let \(x_1 ,x_2 ,\ldots , x_n \) be a random sample from APWQ. The log-likelihood function is given by

$$\begin{aligned} \ell (\alpha ,\lambda ,\beta )= & {} n\log (\alpha -1)-n\log (\log (\alpha ))+n\log (\lambda \beta )+(\beta -1)\sum _{i=1}^n {\log (x_i } )\nonumber \\&-\lambda \sum _{i=1}^n {x_i^\beta }-\sum _{i=1}^n {\log \left[ {1+(\alpha -1)\varphi _i } \right] } , \end{aligned}$$
(20)

where \(\varphi _i =1-e^{-\lambda x_i^\beta }\).

Therefore, the MLE’s of \(\alpha , \lambda \) and \(\beta \) can be computed by maximizing the log-likelihood function in (20). We used the routine OPTIM which is available in the R software. Next, the APWQ distribution is used to model different types of cancer data sets including complete and censored data.

Table 3 The MLEs (standard errors in parentheses), and the goodness of fit statistics for the breast cancer data
Full size table

5.1 Complete Data

The data set represents the survival times of 121 patients with breast cancer obtained from a large hospital in a period from 1929 to 1938 [14]. This data set has recently been studied by [21]. The data are:

0.3, 0.3, 4.0, 5.0, 5.6, 6.2, 6.3, 6.6, 6.8, 7.4, 7.5, 8.4, 8.4, 10.3,11.0, 11.8, 12.2, 12.3, 13.5, 14.4, 14.4, 14.8, 15.5, 15.7, 16.2, 16.3, 16.5, 16.8, 17.2, 17.3, 17.5,17.9, 19.8, 20.4, 20.9, 21.0, 21.0, 21.1, 23.0, 23.4, 23.6, 24.0, 24.0, 27.9, 28.2, 29.1, 30.0, 31.0,31.0, 32.0, 35.0, 35.0, 37.0, 37.0, 37.0, 38.0, 38.0, 38.0, 39.0, 39.0, 40.0, 40.0, 40.0, 41.0, 41.0,41.0, 42.0, 43.0, 43.0, 43.0, 44.0, 45.0, 45.0, 46.0, 46.0, 47.0, 48.0, 49.0, 51.0, 51.0, 51.0, 52.0,54.0, 55.0, 56.0, 57.0, 58.0, 59.0, 60.0, 60.0, 60.0, 61.0, 62.0, 65.0, 65.0, 67.0, 67.0, 68.0, 69.0,78.0, 80.0,83.0, 88.0, 89.0, 90.0, 93.0, 96.0, 103.0, 105.0, 109.0, 109.0, 111.0, 115.0, 117.0, 125.0,126.0, 127.0, 129.0, 129.0, 139.0, 154.0.

The APWQ distribution is fitted to the data set and compared with several other competitive models namely: McDonald Weibull (Mc-W) [6], Beta Weibull (BW) [13], Modified Weibull (MW) [4], Marshall-Olkin Weibull (MOW) [17] and Zografos-Balakrishnan log-logistic (ZBLL) [25].

Table 3 lists the MLEs (and the corresponding standard errors in parentheses) of the parameters, negative likelihood values \([-\,\ell (\hat{{\theta }})]\), Kolmogorov–Smirnov (K–S) test and the p value for the K–S statistics for all fitted models. From Table 3, it is observed that the APWQ distribution has the lowest values of \([-\,\ell (\hat{{\theta }})]\) and K–S and the largest p value for the K–S statistics, which implies that the APWQ distribution provides the best fit among all fitted distributions followed by MOW distribution. Figures 3a displays the histogram and the fitted APWQ density for the data set. Also, the plots of the fitted APWQ survival and the empirical survival functions for the data set are displayed in Fig. 3b. It is clear that these plots show that APWQ provides good fit to the data set and this supports the results in Table 3.

Fig. 3
figure 3

a Histogram and the fitted APWQ distribution. b Fitted APWQ survival and empirical survival functions for the first data set

Full size image

5.2 Censored Data

Censored data are very common in lifetime applications. Some mechanisms of censoring are identified in literature such as type I and II censoring. The fact that APWQ has closed form survival function advantages the distribution to be used in analyzing lifetime data in the presence of censoring. Consider a data set \(D=(x;\,r)\), where \(x=(x_1 ,x_2 ,x_3 ,\ldots ,x_n )\) are the observed failure times and \(r_i =(r_1 ,\ldots ,r_n )\) are the censored failure times where \(r_i \) is equal to 1 if a failure is observed and 0 otherwise. Suppose that the data are independently and identically distributed follows a distribution with probability density and survival functions \(f(x,\theta )\) and \(S(x,\theta )\) respectively. Then the likelihood function for parameters \(\theta =(\alpha ,\lambda , \beta )^{T}\) can be written as

$$\begin{aligned} L(D;\theta )=\prod _{i=1}^n {[f(x_i ,\theta )]^{r_i }[S(x_i ,\theta )]^{1-r_i }} . \end{aligned}$$

For the APWQ distribution, the log-likelihood function is given by

$$\begin{aligned} \ell= & {} r\log \left( {\frac{(\alpha -1)\lambda \beta }{\log (\alpha )}} \right) +\sum _{i=1}^n {r_i } \left( {(\beta -1)\log x_i -\lambda x_i^{\beta } -\log (1+(\alpha -1)\varphi _i )} \right) \nonumber \\&+\sum _{i=1}^n {(1-r_i )\left\{ {\log \left[ {\log (\alpha )-\log (1+(\alpha -1)\varphi _i )} \right] -\log (\log (\alpha ))} \right\} } \end{aligned}$$
(21)

where \(r=\sum \limits _{i=1}^n {r_i } \) and \(\varphi _i\) is defined in (20). The log likelihood function in (21) can be maximized numerically in order to obtain the ML estimates. The routine OPTIM which is available in the R software can be used.

We consider a censored data set that contains remission times for bladder cancer patients. The data set has 137 observations with 9 censored. More details about the data can be found in Lee and Wang [15]. The TTT plot in Fig. 4a is concave then convex which gives an indication of upside down bathtub failure rate. The distribution fits are given in Table 4. From the table, we can see that APWQ distribution has the lowest Akaike information criterion (AIC) and Bayesian information criterion (BIC) values as compared to other fitted models.

Table 4 The MLEs (standard errors in parentheses), and the corresponding AIC and BIC values for second censored data set
Full size table

The survival curve of the fitted APWQ distribution given in Fig. 4b fits the Kaplan Meier curve well.

Fig. 4
figure 4

a TTT plot b fitted survival curve of APWQ distribution

Full size image

6 Conclusions

In this paper, a method for generating family of distributions is proposed based on the APT family proposed recently by Mahdavi and Kundu [16]. The proposed method can produce a flexible hazard rate functions. Some general properties of the proposed family are studied. A member of the proposed family, APWQ distribution is studied in details. The APWQ distribution is the generalization of the Weibull distribution with attractive shape flexibilities for both the density and the hazard rate functions. In fact, the density function can be left-skewed, right-skewed or about symmetric. The hazard rate function possesses an IFR, DFR, BT or UBT shapes. Real data sets are used to show the applicability of the APWQ distribution to complete as well as censored data sets. The fact that APWQ has only three parameters with closed form CDF and at the same time possesses several types of hazard rate shapes; make this distribution an attractive choice to be used in various filed of studies including cancer research.