On a Weibull-Inverse Exponential Distribution

Abstract

In this paper we study various reliability properties of a Weibull inverse exponential distribution. The maximum likelihood and Bayes estimates of unknown parameters and reliability characteristics are obtained. Bayes estimates are obtained with respect to the squared error loss function under proper and improper prior situations. We use the Lindley method and the Metropolis–Hastings algorithm to compute the Bayes estimates. Interval estimation is also considered. Asymptotic and highest posterior density intervals of unknown parameters are constructed in this respect. We perform a numerical study to compare the performance of all methods and obtain comments based on this study. We also analyze two real data sets for illustration purposes. Finally a conclusion is presented.

1 Introduction

In the past a number of probability distributions have been proposed in literature that provide a comprehensive coverage for the reliability data analysis. Such studies have increasingly become very common in various research areas including, among others, industrial and engineering applications, agricultural and bio-medical experiments, weather predictions etc. Probability distributions like generalized exponential, Weibull, lognormal, gamma etc. have found widespread applications in reliability theory because of their applicability to model various failure time data indicating a broad range of hazard rate behavior such as unimodal and monotonic pattern. Still these models can be inadequate in situations where hazard rates indicate bathtub shaped behavior. Several attempts have been made to extend family of distributions by utilizing a number of techniques, the most commonly used of which is introduction of additional parameter in corresponding survival functions. Mudholkar and Srivastava [6] studied properties of an exponentiated Weibull distribution which is quite a flexible extension of the Weibull distribution due to its monotonic, unimodal or bathtub shaped hazard rate behavior. In a subsequent paper Mudholkar and Hutson [7] further studied reliability properties of this family of distribution. One may also refer to Alzaatreh [1], Lin et. al.[4] and Tahir [12] for some more interesting results on this topic. In this paper we study properties of a Weibull inverse exponential distribution and obtain inference for unknown parameters, reliability and hazard rate functions. Note that the density function of an inverted exponential distribution is given by

$$\begin{aligned} \displaystyle g(x) = \frac{\lambda }{x^2}e^{-\frac{\lambda }{x}};\quad x>0,\lambda >0, \end{aligned}$$

(1.1)

and the cumulative distribution function is

$$\begin{aligned} \displaystyle G(x) = e^{-\frac{\lambda }{x}};\quad x>0,\lambda >0. \end{aligned}$$

(1.2)

The corresponding hazard rate function is given by

$$\begin{aligned} \displaystyle h(x) = \frac{\frac{\lambda }{x^2}e^{-\frac{\lambda }{x}}}{1 - e^{-\frac{\lambda }{x}}};\quad x>0,\lambda >0. \end{aligned}$$

(1.3)

where $\lambda$ is the rate parameter.

Weibull distribution is one of the most widely used distribution in reliability analysis, particularly in situations where data indicate monotonic hazard rates. However as mentioned it may not be an adequate model for reliability data with bathtub shaped or unimodal hazard rates. Examples of such nature often abound in reliability theory. In this connection we mention that a number of modifications have been proposed to the Weibull distribution in literature. Bourguignon et al. [2] studied various reliability properties of a new wider Weibull-G family of distributions. They derived some new special distributions from this family by assuming Weibull model as a base distribution. They further showed that mathematical properties developed for the original model are equally applicable to special cases also. In particular properties of quantile function, moments, generating function and order statistics are established. To proceed further with the notations suppose that $g(x;\varLambda )$ and $G(x;\varLambda )$ denote the density and distribution functions of a base model with $\varLambda$ being a vector of parameters. Also note that distribution function of a two-parameter Weibull distribution is of the form $F(x;\alpha ,\beta ) = 1 - e^{-\alpha x^{\beta }},~x>0,$ where $\alpha >0$ and $\beta >0$ are unknown parameters. Based on such an assumption, Bourguignon et al. [2] established a new generalization of Weibull distribution, namely $Weibull-G$ family of distributions. They replaced the variable x with the term $\frac{G(x; \varLambda )}{1-G(x; \varLambda )}$ and obtained the distribution function of new Weibull generalized distribution as

$$\begin{aligned} \begin{aligned} \displaystyle F(x;\alpha , \beta , \varLambda )&= \int _{0}^{\frac{G(x;\varLambda )}{1-G(x;\varLambda )}} \alpha \beta t^{\beta -1}e^{-\alpha t^{\beta }}dt \\&= 1 - e^{-\alpha \left[ \frac{G(x;\varLambda )}{1-G(x;\varLambda )}\right] ^{\beta }};\quad x\in R,\alpha>0,\beta >0, \end{aligned} \end{aligned}$$

(1.4)

where $G(x;\varLambda )$ denotes distribution function of the base model. Thus the corresponding density function turns out to be

$$\begin{aligned} \displaystyle f(x;\alpha , \beta , \varLambda ) = \alpha \beta g(x; \varLambda )\frac{\left[ G(x; \varLambda )\right] ^{\beta -1}}{\left[ 1-G(x; \varLambda )\right] ^{\beta +1}}e^{-\alpha \left[ \frac{G(x;\varLambda )}{1-G(x;\varLambda )}\right] ^{\beta }};\quad x\in R,\alpha>0,\beta >0. \end{aligned}$$

(1.5)

We denote this density function using the notation $Weibull-G(\alpha , \beta , \varLambda )$. Observe that for $\beta = 1$ the corresponding Weibull generator reduces to an exponential generator. We further note that the odds ratio that a component having lifetime Z with distribution function G(.) would fail at a time point x is $\frac{G(x)}{1-G(x)}$. Now if the randomness of this odds ratio of failure is modeled using the random variable X where X follows a Weibull distribution then it is seen that

$$\begin{aligned} \displaystyle P(Z \le x) = P\left( Z \le \frac{G(x)}{1-G(x)}\right) = F(x;\alpha , \beta , \varLambda ) \end{aligned}$$

(1.6)

corresponds to the original expression as given in Eq. (1.4). The survival function of $Weibull-G$ distribution is

$$\begin{aligned} \displaystyle S(x; \alpha , \beta , \varLambda )= 1 - F(x;\alpha , \beta , \varLambda ) = e^{-\alpha \left[ \frac{G(x;\varLambda )}{1-G(x;\varLambda )}\right] ^{\beta }};\quad x\in R,\alpha>0,\beta >0\nonumber \\ \end{aligned}$$

(1.7)

and the hazard rate function is given by

$$\begin{aligned} \begin{aligned} \displaystyle h(x; \alpha , \beta , \varLambda )&= \frac{f(x; \alpha , \beta , \varLambda )}{S(x; \alpha , \beta , \varLambda )} = \alpha \beta g(x; \varLambda )\frac{\left[ G(x; \varLambda )\right] ^{\beta -1}}{\left[ 1-G(x; \varLambda )\right] ^{\beta +1}} \\&= \alpha \beta h(x; \varLambda )\frac{\left[ G(x; \varLambda )\right] ^{\beta -1}}{\left[ 1-G(x; \varLambda )\right] ^{\beta }};\quad x\in R,\alpha>0,\beta >0, \end{aligned} \end{aligned}$$

(1.8)

where $h(x;\varLambda )$ denotes the hazard rate function of the base model. Furthermore, Bourguignon et al. [2] estimated unknown model parameters using maximum likelihood method and analyzed real data sets for illustration purpose. Tahir et al. [13] further proposed another Weibull-G family of distributions and studied its various probabilistic and statistical properties in a manner similar to Bourguignon et al. [2].

The rest of the paper is organized as follows. In Sect. refs2, we introduce the model and discuss some of its mathematical properties. The maximum likelihood estimates (MLEs) of unknown model parameters and reliability characteristic are obtained in Sect. 3. Bayes estimators are derived with respect to the squared error loss function in Sect. 4. The Lindley method and the Metropolis–Hastings algorithm have been used for this purpose. In Sect. 5, a numerical study is performed to compare suggested estimates in terms of their mean square error and bias values. We analyze two real data sets in Sect. 6. Finally a conclusion is presented in Sect. 7.

2 The Weibull-Inverted Exponential Distribution

In this section we propose a three parameter Wiebull-inverted exponential (WIE) distribution. Assume G(x) and g(x) are as in Eqs. (1.1) and (1.2). Then using Eq. (1.4), the corresponding distribution function of WIE distribution is given by

$$\begin{aligned} \displaystyle F(x; \alpha , \beta , \lambda ) = 1 - e^{-\alpha \left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta }};\quad x > 0. \end{aligned}$$

(2.1)

The associated density function is given by

$$\begin{aligned} \displaystyle f(x; \alpha , \beta , \lambda ) = \frac{\alpha \beta \lambda }{x^2}e^{\frac{\lambda }{x}}\left( e^{\frac{\lambda }{x}} -1\right) ^{-\beta -1}e^{-\alpha \left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta }};\quad x>0 \end{aligned}$$

(2.2)

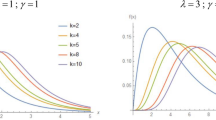
for $\alpha>0,~\beta>0,~\lambda >0$. We denote this distribution as $WIE(\alpha , \beta , \lambda )$. The inverse exponential distribution with parameter $\lambda$ corresponds to the case when $\alpha = 1, \beta = 1$. Figures 1 and 2 depict plots of density and distribution functions of $WIE(\alpha , \beta , \lambda )$ distribution, respectively, for different choices of values of parameters $\alpha ,\beta$ and $\lambda$. Visual analysis of Fig. 1 suggests that the proposed distribution is quite flexible in nature and can acquire a variety of shapes such as positively skewed, J-reversed and symmetric as well. We further observe that the corresponding distribution function is an increasing function in x (Fig. 2).

Fig. 1

Plots of the pdf for different values of $\alpha , \beta$ and $\lambda$

Fig. 2

Plots of the cdf for different values of $\alpha , \beta$ and $\lambda$

The survival function $S(x; \alpha , \beta , \lambda )$, the hazard rate function $h(x; \alpha , \beta , \lambda )$ and the reverse hazard rate function $r(x; \alpha , \beta , \lambda )$ of this distribution are respectively given by

$$\begin{aligned} \displaystyle S(x; \alpha , \beta , \lambda ) = e^{-\alpha \left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta }};\quad x > 0, \end{aligned}$$

(2.3)

$$\begin{aligned} \displaystyle h(x; \alpha , \beta , \lambda ) = \frac{\alpha \beta \lambda }{x^2}e^{\frac{\lambda }{x}}\left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta -1};\quad x > 0 \end{aligned}$$

(2.4)

and

$$\begin{aligned} \displaystyle r(x; \alpha , \beta , \lambda ) = \frac{\frac{\alpha \beta \lambda }{x^2}e^{\frac{\lambda }{x}}\left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta -1}e^{-\alpha \left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta }}}{1-e^{-\alpha \left( e^{\frac{\lambda }{x}}-1\right) ^{-\beta }}};\quad x > 0 \end{aligned}$$

(2.5)

for $\alpha>0,~\beta >0$ and $\lambda >0$.

Fig. 3

Plots of the hrf for different values of $\alpha , \beta$ and $\lambda$

Fig. 4

Plots of the reverse hrf for different values of $\alpha , \beta$ and $\lambda$.

In Figs. 3 and 4 we have plotted hazard rate function and reverse hazard rate function for arbitrarily chosen values of parameters $\alpha , \beta$ and $\lambda$. Figure 3 indicates the flexibility of the proposed distribution in terms of hazard rate function as it can acquire different shapes such as constant, decreasing, increasing, unimodal, j-shaped or bathtub shaped over the parameter space. The reverse hazard rate function is decreasing function as can be seen in Fig. 4. These features suggest that prescribed model can be used to fit different reliability data.

2.1 Mixture Representation

In this section we derive some mathematical properties of the prescribed model. We first observe that analysis related to a $WIE(\alpha , \beta , \lambda )$ distribution can also be performed using the following representation. By expanding the exponential term in Eq. (1.5), we have

$$\begin{aligned} \displaystyle f(x;\alpha , \beta , \varLambda )= & {} \alpha \beta g(x; \varLambda )\frac{\left[ G(x; \varLambda )\right] ^{\beta -1}}{\left[ 1-G(x; \varLambda )\right] ^{\beta +1}}\sum _{r=0}^{\infty }\frac{(-1)^{r} \alpha ^{r}}{r!}\left( \frac{G(x,\varLambda )}{1-G(x,\varLambda )} \right) ^{\beta r} \nonumber \\= & {} \alpha \beta g(x; \varLambda )\sum _{r=0}^{\infty }\frac{(-1)^{r} \alpha ^{r}}{r!} \frac{\left( G(x,\varLambda )\right) ^{\beta (r+1)-1}}{\left( 1-G(x,\varLambda )\right) ^{\beta (r+1)+1}}. \end{aligned}$$

(2.6)

Also from generalized binomial theorem, we have

$$\begin{aligned} \displaystyle \left( 1-G(x,\varLambda )\right) ^{-(\beta (r+1)+1)} = \sum _{j=0}^{\infty }\frac{\varGamma (\beta (r+1)+j+1)}{j!\varGamma (\beta (r+1)+1)}\left( G(x;\varLambda )\right) ^{j}. \end{aligned}$$

(2.7)

Substituting Eq. (2.7) in (2.6), we find that we have

$$\begin{aligned} \displaystyle f(x;\alpha , \beta , \varLambda ) = \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1}\beta \varGamma (\beta (r+1)+j+1)}{r!j!\varGamma (\beta (r+1) +1)}g(x; \varLambda )(G(x;\varLambda ))^{\beta (r+1)+j-1}.\nonumber \\ \end{aligned}$$

(2.8)

Now combining Eqs. (1.1), (1.2) and (2.8), an alternative form of $WIE(\alpha , \beta , \lambda )$ distribution turns out as

$$\begin{aligned} \displaystyle f(x;\alpha , \beta , \lambda )= & {} \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1}\beta \varGamma (\beta (r+1)+j+1)}{r!j!\varGamma (\beta (r+1) +1)}\frac{\lambda }{x^2}e^{-\frac{\lambda }{x}}\left( e^{-\frac{\lambda }{x}}\right) ^{\beta (r+1)+j-1}\nonumber \\= & {} \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1} \beta \varGamma (\beta (r+1)+j+1)}{r!j!\varGamma (\beta (r+1) +1)}\frac{\lambda }{x^2}\left( e^{-\frac{\lambda }{x}}\right) ^{\beta (r+1)+j} \nonumber \\= & {} \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1} \beta \varGamma (\beta (r+1)+j)}{r!j!\varGamma (\beta (r+1) +1)}\frac{\lambda (\beta (r+1)+j)}{x^2}e^{-\frac{\lambda (\beta (r+1)+j)}{x}} \nonumber \\= & {} \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1} \beta \varGamma (\beta (r+1)+j)}{r!j! \varGamma (\beta (r+1) +1)}g(x;\lambda (\beta (r+1)+j)), \end{aligned}$$

(2.9)

where $g(x;\varLambda )$ denotes the density function of an inverted exponential distribution with $\varLambda = \lambda (\beta (r+1)+j)$. The corresponding alternative form of the distribution function can be obtained as

$$\begin{aligned} \displaystyle F(x;\alpha , \beta , \lambda ) = \sum _{r=0}^{\infty }\sum _{j=0}^{\infty } \frac{(-1)^{r}\alpha ^{r+1} \beta \varGamma (\beta (r+1)+j)}{r!j! \varGamma (\beta (r+1) +1)}G(x;\lambda (\beta (r+1)+j)), \end{aligned}$$

(2.10)

where $G(x;\varLambda )$ denotes the distribution function of an inverted exponential distribution with $\varLambda = \lambda (\beta (r+1)+j)$. These above two representations are quite useful for inferential applications.

2.2 Quantile, Median and Random Number Generation

Suppose that X represents a continuous random variable with distribution function F(x). The pth quantile $x_{p}$, $0<p<1$ is then given by $F(x_{p}) = p$. Accordingly using the equation

$$\begin{aligned} \displaystyle 1 - e^{-\alpha \left( e^{\frac{\lambda }{x_{p}}}-1\right) ^{-\beta }} = p, \end{aligned}$$

(2.11)

we obtain the pth quantile of the considered model as

$$\begin{aligned} \displaystyle x_{p} =\frac{\lambda }{\log \left[ 1+((-\alpha ^{-1})\log (1-p))^{\frac{-1}{\beta }}\right] }. \end{aligned}$$

(2.12)

The corresponding median is

$$\begin{aligned} \displaystyle x_{0.5} = \frac{\lambda }{\log \left[ 1+\left( \frac{1}{\alpha } \log (2)\right) ^{\frac{-1}{\beta }}\right] }. \end{aligned}$$

(2.13)

Monte Carlo simulations for a WIE distribution can be done using the probability integral transformation technique.

2.3 Moments

We now discuss the kth noncentral moment of the $WIE(\alpha , \beta , \lambda )$ distribution. These moments can be used to make inference about other characteristics of this model such as measures of spread, skewness, kurtosis etc. The desired moment is given by

$$\begin{aligned} \begin{aligned} \displaystyle \mu _{k}^{\prime } = E[X^k]&= \int _{0}^{\infty } x^k \,f(x; \alpha , \beta , \lambda )dx \\&= \int _{0}^{\infty } x^k \, \sum _{r=0}^{\infty }\sum _{j=0}^{\infty } \frac{(-1)^{r}\alpha ^{r+1} \beta \varGamma (\beta (r+1)+j)}{r!j! \varGamma (\beta (r+1)+1)}g(x;\lambda (\beta (r+1) +j)) dx \\&= \sum _{r=0}^{\infty }\sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1}\beta \varGamma (\beta (r+1)+j)}{r!j! \varGamma (\beta (r+1) +1)}\int _{0}^{\infty } x^k \frac{\lambda (\beta (r+1)+j)}{x^2} e^{-\frac{\lambda (\beta (r+1)+j)}{x}} dx. \end{aligned} \end{aligned}$$

(2.14)

Assume $z = \frac{\lambda (\beta (r+1)+j)}{x}$ then after some simplifications, we have

$$\begin{aligned} \displaystyle \mu _{k}^{\prime } = E[X^k] = \sum _{r=0}^{\infty } \sum _{j=0}^{\infty }\frac{(-1)^{r}\alpha ^{r+1}\beta \varGamma (\beta (r+1)+j)}{r!j! \varGamma (\beta (r+1) +1)} \frac{\varGamma (1-k)}{(\lambda (\beta (r+1) +j))^{(1-k)}},\quad \forall ~~ k < 1. \end{aligned}$$

(2.15)

Note that the above series does not exist for $k > 1$. Therefore, the kth moment of $WIE(\alpha , \beta , \lambda )$ distribution does not exist since the expression in Eq. (2.15) only exist for $k < 1$.

2.4 Moment Generating Function

The moment generating function (mgf), $M_X(t)$, provides an alternative way for making inference related to certain probabilistic features. The desired mgf can be obtained as

$$\begin{aligned} M_X(t) = E(e^{tX}) = \int _{0}^{\infty }e^{tx}f (x; \alpha , \beta , \lambda ) dx . \end{aligned}$$

This can be further rewritten as

$$\begin{aligned} \begin{aligned} \displaystyle M_X(t) = E(e^{tX})&= \sum _{k = 0}^{\infty } \frac{t^k}{k!}\int _{0}^{\infty }x^{k} f(x; \alpha , \beta , \lambda ) dx \\&= \sum _{k = 0}^{\infty }\frac{t^k}{k!}\mu _{k}^{\prime }. \end{aligned} \end{aligned}$$

(2.16)

Thus the moment generating function of $WIE(\alpha , \beta , \lambda )$ distribution does not exist since kth moment of X exists only for $k < 1$.

2.5 Order Statistics

In this section we study properties of order statistics of the WIE distribution. Here we discuss some useful properties related to the $WIE(x; \alpha , \beta , \lambda )$ distribution. Let $X_1, X_2, \ldots , X_n$ denotes observations from this distribution and that $X_{(1)}, X_{(2)}, \ldots , X_{\left( n\right) }$ be the corresponding order statistics. Then density function of the ith order statistic $X_{\left( i\right) }$ is given by

$$\begin{aligned} \displaystyle f_{i}(x; \alpha , \beta , \lambda )= & {} \frac{1}{B(i,n-i+1)}f(x; \alpha , \beta , \lambda )[F(x; \alpha , \beta , \lambda )]^{(i-1)}\nonumber \\&[1-F(x; \alpha , \beta , \lambda )]^{(n-i)}, \end{aligned}$$

(2.17)

where B(., .) is the beta function. Since $0< F(x; \alpha , \beta , \lambda ) < 1$ for $x>0$, therefore the term $[1-F(x; \alpha , \beta , \lambda )]^{(n-i)}$ can be expanded as

$$\begin{aligned} \displaystyle [1-F(x; \alpha , \beta , \lambda )]^{(n-i)} = \sum _{j=0}^{n-i}(-1)^{j}\genfrac(){0.0pt}0{n-i}{j}[F(x; \alpha , \beta , \lambda )]^{j}. \end{aligned}$$

(2.18)

Substituting this in Eq. (2.17), we have

$$\begin{aligned} \displaystyle f_{i}(x; \alpha , \beta , \lambda ) = \frac{f(x; \alpha , \beta , \lambda )}{B(i,n-i+1)}\sum _{j=0}^{\infty }(-1)^{j} \genfrac(){0.0pt}0{n-i}{j}[F(x; \alpha , \beta , \lambda )]^{i+j-1}. \end{aligned}$$

(2.19)

Further, note that

$$\begin{aligned} \displaystyle [F(x; \alpha , \beta , \lambda )]^{i+j-1} = \sum _{k=0}^{\infty } (-1)^{k}\genfrac(){0.0pt}0{i+j-1}{k} e^{-\alpha k \left( e^{\frac{\lambda }{x}} -1\right) ^{-\beta }} \end{aligned}$$

(2.20)

and then by substituting Eq. (2.1) in (2.20), we get

$$\begin{aligned} \displaystyle f_{i}(x; \alpha , \beta , \lambda )= & {} \sum _{j=0}^{n-i} \sum _{k=0}^{\infty } \frac{(-1)^{(j+k)}}{(k+1)B(i,n-i+1)} \genfrac(){0.0pt}0{n-i}{j}\genfrac(){0.0pt}0{i+j-1}{k}\nonumber \\&f(x; \alpha (k+1), \beta , \lambda ), \end{aligned}$$

(2.21)

where $f(x; \varSigma )$ denotes the density function of the model with $\varSigma = (\alpha (k+1), \beta , \lambda )$. Thus the corresponding density function is a mixture of WIE densities.

In the next section we derive the maximum likelihood estimators of unknown parameters $\alpha , \beta , \lambda$ along with reliability and hazard rate functions.

3 Maximum Likelihood Estimation

Let $X_{1}, X_{2}, \ldots , X_{n}$ be a random sample of size n taken from a $WIE(\alpha , \beta , \lambda )$ with observed values being $x_{1}, x_{2}, \ldots , x_{n}$. Then the likelihood function of $\alpha , \beta$ and $\lambda$ is given by

$$\begin{aligned} \displaystyle L(\alpha ,\beta ,\lambda )=\displaystyle \prod _{i=1}^{n} f(x_{i}; \alpha , \beta , \lambda ). \end{aligned}$$

(3.1)

Now using Eq. (2.1), we have

$$\begin{aligned} \displaystyle L(\alpha ,\beta ,\lambda )= & {} \displaystyle \prod _{i=1}^{n} \frac{\alpha \,\beta \,\lambda }{x_i^2} ~e^{\frac{\lambda }{x_i}} \left( e^{\frac{\lambda }{x_{i}}}-1\right) ^{-\beta -1} \, e^{-\alpha \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta }} \nonumber \\= & {} \displaystyle \alpha ^n \, \beta ^n \, \lambda ^n \prod _{i=1}^{n} x_{i}^{-2} e^{\left( \sum _{i=1}^{n} \frac{\lambda }{x_i}\right) } \, e^{-\alpha \sum _{i=1}^{n} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta }}\prod _{i=1}^{n} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\nonumber \\ \end{aligned}$$

(3.2)

and corresponding log likelihood function is given by

$$\begin{aligned}&\displaystyle l \propto \displaystyle n\log \alpha +n\log \beta +n\log \lambda + \sum _{i=1}^{n}\frac{\lambda }{x_i} -\alpha \sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } \nonumber \\&\quad -(\beta + 1)\sum _{i=1}^{n} \log \left( e^{\frac{\lambda }{x_i}}-1\right) , \end{aligned}$$

(3.3)

where $l = l(\alpha , \beta , \lambda )$. The associated likelihood equations are obtained as

$$\begin{aligned} \displaystyle \frac{\partial l}{\partial \alpha }= & {} \displaystyle \frac{n}{\alpha } - \sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta } = 0, \end{aligned}$$

(3.4)

$$\begin{aligned} \displaystyle \frac{\partial l}{\partial \beta }= & {} \displaystyle \frac{n}{\beta }+ \alpha \sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } \log \left( e^{\frac{\lambda }{x_i}}-1\right) - \sum _{i=1}^{n}\log \left( e^{\frac{\lambda }{x_i}}-1\right) =0, \end{aligned}$$

(3.5)

$$\begin{aligned} \displaystyle \frac{\partial l}{\partial \lambda }= & {} \displaystyle \frac{n}{\lambda }- \sum _{i=1}^{n}\frac{1}{x_i} + \alpha \beta \sum _{i=1}^{n} \frac{e^{\frac{\lambda }{x_i}}}{x_i}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, -\left( \beta +1\right) \sum _{i=0}^{n}\frac{x_i^{-1}\frac{\lambda }{x_i}}{\left( e^{\frac{\lambda }{x_i}}-1\right) }=0.\nonumber \\ \end{aligned}$$

(3.6)

The maximum likelihood estimates $\hat{\alpha } ~$, $\hat{\beta } ~$ and $\hat{\lambda }$, of $\alpha$, $\beta ~$ and $\lambda$, respectively, are simultaneous solutions of the Eqs. (3.4), (3.5) and (3.6). Observe that $\hat{\alpha }$, $\hat{\beta }$ and $\hat{\lambda }$ can not be obtained in closed forms and so we have employed a numerical technique to compute these estimates.

In the next section Bayes estimators of unknown parameters and reliability characteristics are obtained.

4 Bayes Estimation

This section deals with deriving Bayes estimators of unknown parameters $\alpha , \beta , \lambda$ and reliability characteristics R(t) and h(t) with respect to the squared error loss function defined as,

$$\begin{aligned} L_{S}(\hat{\mu }(\theta ),\mu (\theta )) = (\hat{\mu }(\theta )-\mu (\theta ))^{2}, \end{aligned}$$

where $\hat{\mu }(\theta )$ denotes an estimate of $\mu (\theta )$. The corresponding Bayes estimate $\hat{\mu }_{BS}$ is obtained as the posterior mean of $\mu (\theta )$. Suppose that ${X_{1}}, {X_{2}},\ldots ,{X_{n}}$ is a random sample taken from a $WIE(\alpha , \beta , \lambda )$ distribution. Based on this sample we derive corresponding estimates of all unknowns. We assume that $\alpha$, $\beta$ and $\lambda$ are statistically independent and are a priori distributed as Gamma$(p_1,q_1)$, Gamma$(p_2,q_2)$ and Gamma$(p_3,q_3)$ distributions respectively. Thus the joint prior distribution of $\alpha$, $\beta$ and $\lambda$ turns out to be

$$\begin{aligned} \displaystyle \pi (\alpha , \beta , \lambda )\propto \alpha ^{p_1-1}\,e^{-\alpha \,q_1}~\beta ^{p_2-1}\,e^{-\beta \,q_2}~\lambda ^{p_3-1}\,e^{-\lambda \, q_3}, \end{aligned}$$

(4.1)

for $\alpha>0, ~p_1>0,\,q_1>0, ~\beta>0, \,p_2>0,\,q_2>0~\lambda>0,\,p_3>0,\,q_3>0$. Accordingly the posterior distribution is given by

$$\begin{aligned} \begin{aligned} \displaystyle \pi (\alpha ,\,\beta , \,\lambda |\,{\underline{x}})&= \displaystyle \frac{1}{k}\, \alpha ^{n+p_1 - 1}\, \beta ^{n+p_2 - 1}\, \lambda ^{n+p_3-1}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } + q_1\right) }\,\\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}, \end{aligned} \end{aligned}$$

(4.2)

where ${\underline{x}}=(x_{1},x_{2},\ldots ,x_{n})$ and

$$\begin{aligned} k= & {} \displaystyle \int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }\displaystyle \alpha ^{n+p_1 - 1}\, \beta ^{n+p_2 - 1}\, \lambda ^{n+p_3-1}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta } + q_1\right) }\,\\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1} \, d\alpha \, d\beta \, d\lambda . \end{aligned}$$

Now respective Bayes estimates of $\alpha , \beta$ and $\lambda$ under the squared error loss are obtained as

$$\begin{aligned} \displaystyle \tilde{\alpha }_{BS}= & {} \displaystyle \frac{1}{k}\int _{0}^{\infty }\int _{0}^{\infty } \int _{0}^{\infty }\displaystyle \alpha ^{n+p_1}\, \beta ^{n+p_2 - 1}\, \lambda ^{n+p_3-1}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } + q_1\right) }\,\\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, d\alpha \, d\beta \, d\lambda ,\\ \displaystyle \tilde{\beta }_{BS}= & {} \displaystyle \frac{1}{k}\int _{0}^{\infty }\int _{0}^{\infty } \int _{0}^{\infty }\displaystyle \alpha ^{n+p_1-1}\, \beta ^{n+p_2}\, \lambda ^{n+p_3-1}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } + q_1\right) }\,\\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, d\alpha \, d\beta \, d\lambda \end{aligned}$$

and

$$\begin{aligned} \displaystyle \tilde{\lambda }_{BS}= & {} \displaystyle \frac{1}{k}\int _{0}^{\infty } \int _{0}^{\infty }\int _{0}^{\infty }\displaystyle \alpha ^{n+p_1-1}\, \beta ^{n+p_2 - 1}\, \lambda ^{n+p_3}\,e^{-\alpha \left( \sum _{i=0}^{n} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } + q_1\right) }\,\\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, d\alpha \, d\beta \, d\lambda . \end{aligned}$$

Similarly Bayes estimates of R(t) and h(t) are obtained as

$$\begin{aligned} \displaystyle \tilde{R}(t)_{BS}= & {} \displaystyle \frac{1}{k}\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } \displaystyle \alpha ^{n+p_1 - 1}\, \beta ^{n+p_2 - 1}\, \lambda ^{n+p_3-1}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta } + q_1\right) }\, \\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times e^{-\alpha \left( e^{\frac{\lambda }{t}}-1\right) ^{-\beta }} \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, d\alpha \, d\beta \, d\lambda \end{aligned}$$

and

$$\begin{aligned} \displaystyle \tilde{h}(t)_{BS}= & {} \displaystyle \frac{1}{k}\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } \displaystyle \alpha ^{n+p_1 }\, \beta ^{n+p_2 }\, \lambda ^{n+p_3}\,e^{-\alpha \left( \sum _{i=0}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta } + q_1\right) }\, \\&\quad e^{\lambda \left( \sum _{i=0}^{n}x_i^{-1}-q_3\right) } \times \frac{1}{t^2}e^{\frac{\lambda }{t}}\left( e^{\frac{\lambda }{t}}-1\right) ^{-\beta -1} \prod _{i=0}^{n}x_i^{-2}\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\, d\alpha \, d\beta \, d\lambda \end{aligned}$$

respectively. We observe that all the Bayes estimates are in the form of ratio of two integrals and it is quite difficult to solve them analytically. So in the next section we propose the Lindley approximation method which is very useful in such situation.

4.1 Lindley Approximation

In this section we use the Lindley [5] method to obtain Bayes estimates of unknown quantities. Consider the posterior expectation I(X) given by

$$\begin{aligned} \displaystyle I(X)=\frac{\int _{(\delta _{1},\delta _{2}, \delta _{3})}u(\delta _{1},\delta _{2},\delta _{3})e^{l(\delta _{1}, \delta _{2},\delta _{3})+\rho (\delta _{1},\delta _{2},\delta _{3})} d(\delta _{1},\delta _{2},\delta _{3})}{\int _{(\delta _{1},\delta _{2}, \delta _{3})}e^{l(\delta _{1},\delta _{2},\delta _{3}) +\rho (\delta _{1} ,\delta _{2},\delta _{3})}d(\delta _{1},\delta _{2},\delta _{3})}, \end{aligned}$$

(4.3)

where $\displaystyle u(\delta _{1} ,\,\delta _{2},\,\delta _{3})$ is function of $\delta _{1}$, $\delta _{2}$ and $\delta _{3}$, $l(\delta _{1},\delta _{2},\delta _{3})$ is the log-likelihood and $\rho (\delta _{1}, \delta _{2},\delta _{3})$ is the logarithm of joint prior distribution of $\delta _{1}, \delta _{2}$ and $\delta _{3}$. Suppose that $(\hat{\delta _{1}}, \hat{\delta _{2}}, \hat{\delta _{3}})$ denotes the MLE of $(\delta _{1}, \delta _{2},\delta _{3})$. Using the Lindley method the function I(X) can be written as

$$\begin{aligned} \displaystyle I(X)= & {} \displaystyle u\left( \hat{\delta _{1}},\hat{\delta _{2}},\hat{\delta _{3}}\right) +(u_{1} \upsilon _{1}+u_{2}\upsilon _{2}+u_{3}\upsilon _{3}+\upsilon _{4}+\upsilon _{5})\\&+\,0.5[A(u_{1}\sigma _{11}+u_{2}\sigma _{12}+u_{3}\sigma _{13}) \\&+\,B(u_{1}\sigma _{21}+u_{2}\sigma _{22}+u_{3}\sigma _{23}) + C(u_{1}\sigma _{31}+u_{2}\sigma _{32}+u_{3}\sigma _{33})], \end{aligned}$$

where $\hat{\delta _{1}},\hat{\delta _{2}}$ and $\hat{\delta _{3}}$ denote MLEs of $\delta _{1},\delta _{2}$ and $\delta _{3}$ respectively. Also

$$\begin{aligned} \upsilon _{i}= & {} \rho _{1}\sigma _{i1} +\rho _{2}\sigma _{i2}+\rho _{3}\sigma _{i3},\quad i=1, 2, 3, \quad \upsilon _{4}=u_{12}\sigma _{12}+u_{13}\sigma _{13}+u_{23}\sigma _{23},\nonumber \\ \upsilon _{5}= & {} 0.5(u_{11}\sigma _{11}+u_{22}\sigma _{22}+u_{33} \sigma _{33}),\\ A= & {} \sigma _{11}l_{111}+2\sigma _{12}l_{121}+2\sigma _{13}l_{131}+2\sigma _{23}l_{231} +\sigma _{22}l_{221}+\sigma _{33}l_{331}, \\ B= & {} \sigma _{11}l_{112}+2\sigma _{12}l_{122}+2\sigma _{13}l_{132}+2\sigma _{23}l_{232} +\sigma _{22}l_{222}+\sigma _{33}l_{332}, \\ C= & {} \sigma _{11}l_{113}+2\sigma _{12}l_{123}+2\sigma _{13}l_{133}+2\sigma _{23}l_{233} +\sigma _{22}l_{223}+\sigma _{33}l_{333} \end{aligned}$$

with subscripts 1,2,3 on the right-hand sides referring to $\delta _{1},\delta _{2},\delta _{3}$ respectively and

$$\begin{aligned} \rho _{i}= & {} \frac{\partial \rho }{\partial \delta _{i}},\quad u_{i}=\frac{\partial u(\delta _{1} ,\,\delta _{2},\,\delta _{3})}{\partial \delta _{i}},\quad u_{ij}=\frac{\partial ^{2} u(\delta _{1} ,\,\delta _{2},\,\delta _{3})}{\partial \delta _{i}\partial \delta _{j}},\quad l_{ij}=\frac{\partial ^{2}l}{\partial {\delta _{i}} \partial {\delta _{j}}},\\ l_{ijk}= & {} \frac{\partial ^{3}l}{\partial \delta _{i}\partial \delta _{j}\partial \delta _{k}}, \end{aligned}$$

$i,j,k=1,2,3$. Furthermore $\sigma _{i,j}$ denotes (i, j)th element of inverse of the matrix $\left[ -\frac{\partial ^2 l(\alpha ,\beta , \lambda \mid {\underline{x}})}{\partial \alpha \partial \beta \partial \lambda }\right] ^{-1}$ evaluated at $(\hat{\alpha }, \hat{\beta }, \hat{\lambda })$. Other expressions are,

$$\begin{aligned} l_{11}= & {} -\frac{n}{\alpha ^{2}},\quad \ l_{12}=l_{21}= \sum _{i=1}^{n} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta }\left( \log \left( e^{\frac{\lambda }{x_i}}-1\right) \right) ,\quad l_{13}=l_{31}\\= & {} \beta \sum _{i=1}^{n}x_i^{-1}e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1},\\ l_{22}= & {} \frac{-n}{\beta ^{2}}-\alpha \sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta }\,\left( \log {\left( e^{\frac{\lambda }{x_i}}-1\right) }\right) ^2,\quad l_{111}=\frac{2n}{\alpha ^3},\\ l_{112}= & {} l_{113} = l_{121} = l_{131} = l_{211} = l_{311} = 0 , \\ l_{23}= & {} l_{32}=\alpha \sum _{i=1}^{n}x_i^{-1}e^{\frac{\lambda }{x_i}} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\left[ 1-\beta \log \left( e^{\frac{\lambda }{x_i}}-1\right) \right] - \sum _{i=1}^{n} \frac{x_i^{-1}e^{\frac{\lambda }{x_i}}}{\left( e^{\frac{\lambda }{x_i}}-1\right) }, \\ l_{33}= & {} -\frac{n}{\lambda ^2} + \alpha \beta (\beta +1)\sum _{i=1}^{n} x_i^{-2}\left( e^{\frac{\lambda }{x_i}}\right) ^2\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -2} + \alpha \beta \sum _{i=1}^{n}x_i^{-2} \left( e^{\frac{\lambda }{x_i}}\right) \left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta -1}\nonumber \\&- \left( \beta +1\right) \sum _{i=1}^{n} \frac{x_i^{-2}\left( e^{\frac{\lambda }{x_i}} - \frac{\lambda }{x_i} e^{\frac{\lambda }{x_i}}-1\right) }{\left( e^{\frac{\lambda }{x_i}}-1\right) ^2},\quad l_{222} = \frac{2n}{\beta ^2} - \alpha \sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta }\left( \log \left( e^{\frac{\lambda }{x_i}}-1\right) \right) ^3, \\ l_{122}= & {} l_{212} = l_{221} = -\sum _{i=1}^{n}\left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta }\,\left( \log {\left( e^{\frac{\lambda }{x_i}}-1\right) }\right) ^2, \\ l_{123}= & {} l_{132}=l_{213}=l_{231}=l_{312}=l_{321}=\sum _{i=1}^{n} x_i^{-1}\, e^{\frac{\lambda }{x_i}}\,\left( e^{\frac{\lambda }{x_i}}-1\right) ^{\left( -\beta -1\right) }\, \left( 1-\beta \,\log {\left( e^{\frac{\lambda }{x_i}}-1\right) }\right) , \\ l_{133}= & {} l_{131}=l_{331}=\beta \sum _{i=1}^{n}x_i^{-2}e^{\frac{\lambda }{x_i}} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}-\beta \left( \beta +1\right) \sum _{i=1}^{n}x_i^{-2}\left( e^{\frac{\lambda }{x_i}}\right) ^2\, \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -2},\\ l_{223 }= & {} l_{232}=l_{322}=\alpha \sum _{i=1}^{n}x_i^{-1}e^{\frac{\lambda }{x_i}} \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}\log \left( e^{\frac{\lambda }{x_i}} -1\right) \left( \beta \log \left( e^{\frac{\lambda }{x_i}}-1\right) - 2\right) , \\ l_{233}= & {} l_{323}=l_{332}=\sum _{i=1}^{n}\frac{x_i^{-2}e^{\frac{\lambda }{x_i}}}{\left( e^{\frac{\lambda }{x_i}}-1\right) ^2}+\alpha \sum _{i=1}^{n}x_i^{-2} e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1} \left( 1-\beta \log \left( e^{\frac{\lambda }{x_i}}-1\right) \right) \\&-\,\alpha \sum _{i=1}^{n}x_i^{-2}\left( e^{\frac{\lambda }{x_i}}\right) ^2 \left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -2}\left( \beta +\left( \beta +1\right) \left( 1-\beta \log \left( e^{\frac{\lambda }{x_i}}-1\right) \right) \right) ,\\ l_{333}= & {} \frac{2n}{\lambda ^3}+\alpha \beta \sum _{i=1}^{n}x_i^{-3}e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -1}-3\alpha \beta (\beta +1) \sum _{i=1}^{n}x_i^{-3}e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) ^{-\beta -2}\\&\quad +\,\alpha \beta (\beta +1)(\beta +2) \sum _{i=1}^{n}x_i^{-3}e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}} -1\right) ^{-\beta -3}\\&\quad +\,(\beta +1)\sum _{i=1}^{n}x_i^{-3} \left( \frac{\frac{\lambda }{x_i}e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) ^2 + 2e^{\frac{\lambda }{x_i}}\left( e^{\frac{\lambda }{x_i}}-1\right) \left( e^{\frac{\lambda }{x_i}}-\frac{\lambda }{x_i}e^{\frac{\lambda }{x_i}}-1\right) }{\left( e^{\frac{\lambda }{x_i}}-1\right) ^4}\right) , \\ \rho _{1}= & {} \left( \frac{p_1-1}{\alpha }-q_1\right) ,\quad \ \rho _{2}=\left( \frac{p_2-1}{\beta }-q_2 \right) ,\quad \ \rho _{3}=\left( \frac{p_3-1}{\lambda }-q_3 \right) . \end{aligned}$$

The desired Bayes estimates of $\alpha , \beta$ and $\lambda$ can respectively be obtained as follows.

• (1) If $u(\alpha , \beta , \lambda ) = \alpha$ then we get the Bayes estimate of $\alpha$ as

  $$\begin{aligned} \tilde{\alpha }_{BS}=\hat{\alpha }+\rho _{1}\,\sigma _{11}+\rho _{2}\,\sigma _{12} +\rho _{3}\,\sigma _{13}+0.5(\sigma _{11}A+\sigma _{21}B+\sigma _{31}C). \end{aligned}$$

• (2) Similarly setting $u(\alpha , \beta , \lambda ) = \beta$ we get Bayes estimate of $\beta$ as

  $$\begin{aligned} \tilde{\beta }_{BS}=\hat{\beta }+\rho _{1}\,\sigma _{21}+\rho _{2}\,\sigma _{22} +\rho _{3}\,\sigma _{23}+0.5(\sigma _{12}A+\sigma _{22}B+\sigma _{32}C). \end{aligned}$$

• (3) Finally Bayes estimate of $\lambda$ is obtained as

  $$\begin{aligned} \tilde{\lambda }_{BS}=\hat{\lambda }+\rho _{1}\,\sigma _{31}+\rho _{2}\,\sigma _{32} +\rho _{3}\,\sigma _{33}+0.5(\sigma _{13}A+\sigma _{23}B+\sigma _{33}C). \end{aligned}$$

Proceeding similarly the desired estimates for the reliability and the hazard rate functions can be obtained. We next propose a Metropolis–Hastings (MH) algorithm and derive some more Bayes estimates of unknown quantities. One may refer to Metropolis et al. [8] and Hastings [3] for several other applications of this method.

4.2 MH Algorithm

In this section we discuss the Metropolis–Hastings algorithm which is useful in situations when a posterior distribution is analytically intractable. This procedure can be used to compute Bayes estimates of unknown parameters as well as to construct credible intervals. The corresponding posterior samples can be obtained using following steps.

Step 1: :

Choose an initial guess of $(\alpha , \beta , \lambda )$, say $(\alpha _0,\beta _0, \lambda _0)$.

Step 2: :

Generate $\alpha ^{\prime }$ using the normal $N\left( \alpha _{n-1}, \sigma ^{2}\right)$ proposal distribution and $\lambda ^{\prime }$ using the normal $N\left( \lambda _{n-1}, \sigma ^{2}\right)$ proposal distribution. Then generate $\beta ^{\prime }$ from $G_{\beta |(\alpha ,\lambda )}\left( n+p_2, q_2+\sum _{i=1}^{n}\log {\left( -1+e^{\lambda _{n-1}\,x_i^{-1}}\right) }\right)$.

Step 3: :

Compute $h = \frac{\pi \left( \alpha ^{\prime },\beta ^{\prime },\lambda ^{\prime }\vert x\right) }{\pi \left( \alpha _{n-1},\beta _{n-1},\lambda _{n-1}\vert x\right) }$.

Step 4: :

Then generate a sample u from the uniform U(0, 1) distribution.

Step 5: :

If $u \le h$ then set $\alpha _{n}\leftarrow \alpha ^{\prime } ;$  $\alpha _{n}\leftarrow \alpha _{n-1} ;$ $\beta _{n}\leftarrow \beta ^{\prime } ;$   otherwise   $\beta _{n}\leftarrow \beta _{n-1} ;$ $\lambda _{n}\leftarrow \lambda ^{\prime };$  $\lambda _{n}\leftarrow \lambda _{n-1} ;$

Step 6: :

Repeat steps (2–5) Q times and collect adequate number of replicates.

Finally, the associated Bayes estimates of $\alpha , \beta$ and $\lambda$ are respectively given by

$$\begin{aligned} \tilde{\alpha }_{{mh}} = \frac{1}{Q - Q_0} \sum _{i = Q_0 + 1}^{Q} \alpha _{i},\quad \tilde{\beta }_{{mh}} = \frac{1}{Q - Q_0} \sum _{i = Q_0 + 1}^{Q} \beta _{i},\quad \tilde{\lambda }_{{mh}} = \frac{1}{Q - Q_0} \sum _{i = Q_0 + 1}^{Q} \lambda _{i}, \end{aligned}$$

where Q denotes the total number of generated samples and $Q_0$ denotes the initial burn-in period. Similarly Bayes estimates of R(t) and h(t) can be computed. The highest posterior density intervals of unknown parameters can easily be obtained using these MH samples. In the next section performance of all estimates is discussed using Monte Carlo simulations.

5 Numerical Comparisons

In Sects. 3 and 4 we obtained different estimates of $\alpha ,~\beta ,~\lambda$, R(t) and h(t) of a $WIE(\alpha , \beta ,\lambda )$ distribution. In this section performance of all estimates is compared numerically in terms of mean square errors (MSEs) and bias values. We compute these estimates based on 5000 replications from a $WIE(\alpha , \beta ,\lambda )$ distribution using different sample sizes such as $n = 40, 60, 80, 100$ and 120. The true value of $(\alpha , \beta , \lambda )$ is arbitrarily taken as (0.2, 0.4, 0.5). We have performed all computations on R statistical software. The corresponding Bayes estimates are obtained under informative and non-informative prior situations. Informative estimates are computed when hyper-parameters are assigned values as $p_1 = 1, q_1 = 5, p_2 = 2, q_2 = 5, p_3 = 4, q_3 = 8$ and for non-informative case, all hyper-parameters approach the zero value. The corresponding MSEs and average estimates of R(t) and h(t) are computed for two distinct choices of t. In Tables 1–4, we have tabulated MSEs and bias values of different estimators of $\alpha , \beta ,\lambda , R(t), H(t)$ and confidence intervals for various sample sizes. We draw the following conclusions from the tabulated values.

Table 1 Average values and MSEs of all estimators of $\alpha$, $\beta$ and $\lambda$ for different choices of n

Table 2 Average values and MSEs of all estimators of R(t) for different values of n and T

Table 3 Average values and MSEs of all estimators of h(t) for different values of n and T

Table 4 Interval estimates of $\alpha$, $\beta$ and $\lambda$ for different values of n

(1) In Table 1, we have tabulated MSEs and estimated values of estimators $\hat{\alpha }, \tilde{\alpha }_{LI}, \tilde{\alpha }_{MH}, \hat{\beta }, \tilde{\beta }_{LI}, \tilde{\beta }_{MH}$ and $\hat{\lambda }, \tilde{\lambda }_{LI}, \tilde{\lambda }_{MH}$. In this table the first column represents the sample size n and corresponding to each n, next three columns represent ML, lindley and MH estimates of $\alpha$ and then next three columns represent ML, lindley and MH estimators of $\beta$ and the last three columns represent analogous estimates of $\lambda$. In case of Bayes estimates each cell contains four values. The first value denotes the noninformative estimate, the second value denotes the corresponding MSE, the third value denotes the informative estimates and fourth value denotes the corresponding MSE value. From this table we observe that the respective maximum likelihood estimates of unknown parameters $\alpha , \beta$ and $\lambda$ compete good with corresponding noninformative Bayes estimates in terms of bias and MSE values. However proper Bayes estimates show superior performance compared to these two estimates. In particular estimates obtained using the MH procedure perform quite good compared to the corresponding Lindley estimates. Performance of different Lindley estimates improve with an increase in sample size. This holds for all the three parameters and different sample sizes. In general suggested estimation procedures provide better estimates for unknown model parameters when sample size increases.

(2) In Table 2, we have tabulated MSEs and estimated values of different reliability estimators $\hat{R}(t)$, $\tilde{R}_{LI}(t)$ and $\tilde{R}_{MH}(t)$ for two different choices of t such as 1 and 8. Lindley and MH estimates of R(t) are computed using the informative prior (IP) and the noninformative prior (NIP) distributions. Here also the MLE of R(t) show good performance compared to noninformative Bayes estimates. We again observe that proper Bayes estimators have an advantage over the MLE in terms of MSE and bias values. Performance of MH estimates is quite good compared to the corresponding Lindley estimates. This holds true for different values of t. Also as sample size increases we obtain better estimates of reliability.

Table 5 Goodness of fit tests for all four distributions for Example 1

(3) The MSEs and average values of estimates $\hat{h}(t)$, $\tilde{h}_{LI}(t)$ and $\tilde{h}_{MH}(t)$ of the hazard rate function h(t) are presented in Table 3 for different sample sizes. These estimates are computed against two arbitrarily selected values of t, namely 0.1 and 0.75. We again observed that performance of Bayes estimators is quite good compared to the MLE of h(t). Particularly performance of MH estimates is highly appreciated. In general mean squared error values of all estimates tend to decrease as n increases.

Table 6 Estimates of $\alpha , \beta , \lambda$ and R(t), h(t) for Example 1

Table 7 Goodness of fit tests for all four distributions for Example 2

Table 8 Estimates of $\alpha , \beta , \lambda$ and R(t), h(t) for Example 2

(4) Finally in Table 4 we have presented asymptotic confidence intervals and HPD intervals of unknown parameters $\alpha , \beta$ and $\lambda$ for different values of n. In this table we have computed both informative and noninformative HPD intervals for all unknown parameters. It is seen that asymptotic intervals compete well with noninformative HPD intervals in terms of average length obtained. However proper prior HPD intervals perform really good compared to the other two intervals as far as average interval length is concerned. We also observed that when the sample size increases the average length of proposed confidence intervals tend to decrease.

6 Data Analysis

In this section two real data sets are analyzed for the purpose of illustration.

Example 1

In this example we consider a data set originally discussed in Nichols and Padgett [10] and it consists of 100 observations on breaking stress of carbon fibres (in Gba). The data are as follows

Mead and Abd-Eltawab [9] fitted this real data set to Kumaraswamy Fréchet distribution and obtained useful inference for the prescribed model. We first check whether the WIE distribution is suitable for analyzing this data set. Three different distributions are fitted and compared with WIE distribution. These are the Kumaraswamy inverse exponential distribution (KIED), Weibull inverse Rayleigh Distribution (WIRD) and inverse exponential distribution (IED). The MLEs of unknown parameters of competing models and the values of the negative log-likelihood criterion (NLC), Akaike’s information criterion (AIC), the corresponding second order information criterion (AICc), Bayesian information criterion (BIC) are reported to judge the goodness of fit. A lower value of these criteria indicate a better fit to the data. The parameter estimates and goodness-of-fit statistics are given in Table 5. These results indicate that a WIE distribution fits the data set quite well compared to other competing models. Therefore we analyze the given data set using this distribution and obtain inference on unknown parameters and reliability characteristics. The maximum likelihood and Bayes estimates of unknown parameters and reliability characteristic are tabulated in Table 6. We mention that Bayes estimates are obtained using a noninformative prior distribution where each hyperparameters approach the zero value. Estimates for reliability and hazard rate functions are obtained for arbitrarily selected values $t=1.5$ and $t=3$. The asymptotic and noninformative highest posterior density intervals of unknown parameters are also given in this table.

Example 2

Here we analyze a data set which is discussed in Smith and Naylor [11]. The data are about the strengths of 1.5 cm glass fibres, measured at the National Physical Laboratory, England. The observed data are as follows:

The goodness of fit estimates for this data are given in Table 7 for different competing models. The tabulated values suggest that a WIE distribution provides the best fit for this data also. In Table 8, MLEs and Bayes estimates of unknown parameters and reliability characteristic are presented. The reliability function are obtained at $t=50$ and $t=100$ and hazard rate function are calculated at $t=30$ and $t=60$. Interval estimates are also given in the table.

7 Conclusion

In this paper we have studied a Weibull inverse exponential distribution under the complete sampling situation. Several statistical properties of this distribution are obtained which are quite useful in reliability analysis. We observed that corresponding hazard rate function can acquire various shapes depending upon the parameters values. In fact the WIE distribution can be used to model a variety of data indicating monotone, bathtub or unimodal hazard rate behavior. We estimated unknown parameters and reliability characteristic of this distribution using the maximum likelihood and Bayesian methods. We found through a simulation study that if some proper prior information is available on unknown parameters then Bayes estimates provide better estimates than corresponding maximum likelihood estimates. We analyzed two real data sets and observed that proposed methods work well in these situations.