Brittle–Ductile Transitions of Rubber Toughened Polypropylene Blends: A Review

Wee, Jung-Wook; Chudnovsky, Alexander; Choi, Byoung-Ho

doi:10.1007/s40684-023-00581-w

645 Accesses
2 Citations
Explore all metrics

Abstract

Polypropylene (PP) blended with rubber particles has been recognized for significantly increasing impact resistance, which is increasingly demanded in industries such as electric vehicles and consumer electronics. However, a comprehensive understanding of the toughening mechanisms underlying these lightweight impact-resistant materials is imperative for future research. This article provides a detailed review of the ductile-to-brittle (DB) transition behavior and the improvements in impact resistance observed in rubber-toughened PP blends. Firstly, the fracture behavior of homogeneous PP is summarized across different strain rates and temperatures, including the DB transition and yielding and crazing criteria. Furthermore, the influence of notches and defects on the DB transition is discussed extensively. Subsequently, the article examines the theoretical and practical aspects of the toughening mechanisms facilitated by the rubber phase in PP-rubber blends. The percolation model is used to investigate the inter-distance criterion between neighboring rubber particles and the impact of particle size and content on toughening behavior. The primary objective of this article is to enhance the understanding of the toughening behavior exhibited by PP and rubber blends. Additionally, this study aims to provide valuable insights for developing advanced lightweight materials using PP-based blends for various industrial applications.

Polypropylene/polyolefin elastomer composites with enhanced impact strength: the effect of rubber domain size on toughness

Article 23 May 2023

Specimen Geometry Effect on the Deformation Mechanisms of Polypropylene-Based Composites Under Impact Loading at Different Temperatures

Article 25 January 2016

Brittle-ductile transition of impact PP blends: effect of modulus ratio of PP matrix to impact modifier

Article 26 May 2022

Discover the latest articles, news and stories from top researchers in related subjects.

Polymers

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

1 Introduction

The application of polymer materials in various industries that traditionally use metals or ceramics is rapidly increasing with the development of polymer materials. In the case of consumer industries such as automobiles and home appliances, the application and market of polymers are rapidly expanding due to the need for weight reduction of the products. Polypropylene is a low-cost commodity polymer with appropriate mechanical properties, which is used in many modern industries. However, it is often processed in the form of filled composites mixed with functional fillers rather than in the form of neat polymers to satisfy various physical and mechanical properties. In particular, depending on the temperature range and loading conditions, polypropylene often has insufficient impact energy absorption characteristics. Therefore, rubber has been commonly added as a functional filler in polypropylene to improve toughness.

Polypropylene is a semi-crystalline thermoplastic that exhibits ductile behavior and fracture at room temperature. The mechanical properties of polypropylene are strongly influenced by test conditions such as temperature and strain rate. Moreover, Young's modulus and yield stress decrease with increasing temperature and decreasing strain rate. For example, if the strain rate is approximately 0.007 s⁻¹, Young’s modulus and yield stress of polypropylene P700 are approximately 2000 and 45 MPa at 0 °C, and 700 and 20 MPa at 50 °C, respectively. The fracture stress exhibits similar behavior but changes slowly with temperature and strain rate. Therefore, for a particular strain rate, a certain temperature exists below which the material becomes brittle. Moreover, at a constant temperature, the transition from ductile to brittle mode occurs when the strain rate becomes high enough.

The toughness of polypropylene, particularly its notched toughness, is insufficient to be used as an engineering plastic. Notched specimens remain brittle with low toughness under impact conditions up to approximately 100 °C, whereas un-notched specimens are brittle only below 10–20 °C. However, adding a rubbery polymer dispersed over the polypropylene matrix can significantly improve the notched impact toughness. The brittle–ductile transition of polypropylene-rubber blends is commonly attributed to the competition of two deformation mechanisms: crazing and shear banding. Crazing and brittle fracture with low energy absorption occur in the failure mode when the craze initiation stress is less than the shear initiation stress. Otherwise, shear banding and tough fracture with high energy absorption are the primary deformation mechanisms. The rubber phase is assumed to reduce the shear initiation stress and lower the brittle–ductile transition temperature.

Many aspects of mechanical behaviors common to all polymers, notably the brittle–ductile transition, have been studied for a long time, dating back to the 1950s. However, these studies were mostly for polystyrene, polymethyl methacrylate, and polycarbonate, which are quite different from polypropylene. The present study is equally concerned with observations and hypotheses directly related to polypropylene and those that began with investigations of other polymers and were later found to be applicable to polypropylene also.

2 Mechanisms of Fracture Behavior

2.1 Engineering Stress–Strain Curves

The mechanical properties of polypropylene (PP), similar to those of many other thermoplastics, are greatly influenced by temperature and strain rate. Generally, the load-elongation curve at a constant strain rate will change with increasing temperature, exhibiting at least four different types of material behavior and fracture. First, at low temperatures, the load increases approximately linearly with increasing elongation up to a breaking point where the material fractures at small strains in a brittle manner, similar to glass. Second, at higher temperatures, the yield point is observed and the load falls before failure, revealing a certain extent of crazing. Although no yielding appears and strain at the failure point is still quite low, this is commonly referred to as ductile failure. Third, the yield point appears at even higher temperatures as in the previous case. However, the material can go beyond it, experiencing crazing followed by yielding and sometimes necking and cold drawing. Here, the peak of the applied stress is also called the yield point, and it originates from crazing, not from yielding. Finally, yielding governs the deformation in the fourth type, which occurs at high temperatures. The maximum applied stress is reached due to shear banding and is referred to as the real yield point. After this point, the stress decreases and the deformation is primarily caused by necking and subsequent cold drawing, with generally significant extension.

Jang et al. [1, 2] conducted tensile experiments on PP and PP-rubber blends over a wide range of temperatures and strain rates. The typical dependence of the engineering stress–strain $(\sigma -\varepsilon )$ curve on temperature and strain rate for rubber-modified PPs is presented in Fig. 1 (the specimens are 3 inches long).

Curve 10 represents an extreme of the tensile behavior, which can be observed at low temperatures or at high strain rates and is loosely described as brittle. Samples here exhibit first initial elastic strain and then break rapidly. Visual investigation using transmission light and scanning electron microscopy reveals many crazes developed as planes perpendicular to the stress direction. These crazes possess all the morphological characteristics of crazes in amorphous polymers. The gauge sections of the specimens show little to no necking. The material tested under these conditions appears quite stiff, as reflected by the relatively high tensile modulus of elasticity.

The other extreme is represented by curves 1–3. The initiation of shear banding accompanies the onset of non-linearity on these curves. The material here is soft, and the deformation extends far beyond the maximum of the $\sigma -\varepsilon$ curves. Molecular orientation causes a significant stress drop, followed by strain-hardening and cold drawing. Shear band-like features are almost always identified near the boundary between drawn and indrawn materials, and no craze-like features are identified in the gauge section. This is known as shear-type yielding, and it occurs when samples are deformed at high temperatures or low strain rates.

Curves 4–9 represent an intermediate case of fracture behavior. These are examples of the phenomenon known as plasticity governed by crazing (Jang [1, 2]). In this case, the elastic deformation is interrupted by the formation of crazes at a certain stress level (or possibly strain). Therefore, the stress–strain curve deviates from the straight line corresponding to the elastic strain regime. Providing that the rate of craze growth satisfies a certain condition, the $\sigma -\varepsilon$ curve goes through the maximum point and experiences a stress drop (a more detailed analysis will be given in a later section). The presence of pronounced stress whitening in the deformed samples indicates the formation of crazes. The samples deformed beyond the maximum point of the $\sigma -\varepsilon$ curve sometimes exhibit some extent of shear yielding, and sometimes the shear yielding is followed by necking and cold drawing.

2.2 Fracture Mechanisms and Energy Dissipation

The previous description reveals at least four transitions in the pattern of fracture of PP and rubber modified PP: (1) brittle-to-crazing; (2) crazing-to-shear yielding; (3) shear yielding-to-necking; (4) necking-to-cold drawing. It is evident that each subsequent fracture type is associated with a deformation mechanism that requires greater mobility of polymer molecules than the previous one. Figure 2 shows force–deflection diagrams of various polymers at different temperatures obtained from Charpy impact tests by Ramsteiner [3] as an example of the evolution in mechanism mobility with temperature. These polymers are highly deformable near room temperature (right column RT) and consequently ductile. At liquid nitrogen temperatures (left column) the same materials are brittle and can only store elastic energy. The force–deflection diagrams in the middle column are given at temperatures where the molecules are starting to become mobile enough to allow the onset of plastic deformation processes but not mobile enough to avoid the crack formation and fracture.

It was also demonstrated that the transition of the deformation process during the tensile test is clearly dependent on the strain rate for PP and HDPE [4]. The fibrillation at a low strain rate is transformed into craze-tearing at a high strain rate for HDPE. However, the craze was observed in PP even in the low strain rate cases. The yield stress is also monotonically increased with the strain rate for these materials (see Fig. 3). Dasari et al. [5] carefully investigated the microstructure evolution of PP during the tensile deformation and constructed the deformation mechanism map based on the strain and strain rate. Figure 4 shows the deformation mechanism map of long-chain and short-chain low crystallinity PP, where the melt flow rate of the long-chain and short-chain samples are 6 and 23 g/10min, respectively. The fracture surface with distinguished fracture mechanisms of long-chain high crystallinity PP is shown in Fig. 5 [5].

Therefore, among all polymer deformation and fracture mechanisms available at a given temperature and strain rate, the process with the maximum energy dissipation is the operative one. From this perspective, the main mechanisms governing material behavior can be arranged in the following order of increasing dissipated energy: (1) elastic-brittle, (2) crazing, (3) shear yielding, (4) necking, and (5) cold drawing.

According to Ramsteiner [3], the impact test does not allow one to precisely locate the temperature for the elastic–plastic transition because the onset of plastic deformation is not very sharp. Moreover, its detection depends not only on temperature but also on some factors, such as molecular weight and orientation of the molecules. However, the temperature dependence of the internal friction proves to be instructive for finding the temperature region for the beginning of the mobility of molecules and plastic deformation on a large scale.

3 Brittle Stress and Yield Stress

3.1 Definition and Measurements

Over the last half-century, scientists have debated how to define the brittle stress ${\sigma }_{B}$, and yield stress ${\sigma }_{Y}$, and adequate method of measuring these properties. Vincent [6, 7] proposed the following definitions:

1.
The tensile yield stress ${\sigma }_{Y}$ is defined as the stress, at which the specimen continues to extend in a tensile test without increase in load.
2.
Brittle fracture is defined as fracture, which occurs at low extensions, before the applied stress reaches the yield stress.
3.
The brittle stress ${\sigma }_{B}$ is defined as the stress, at which brittle fracture occurs.

Vincent writes further: “The yield stress can easily be measured in a tensile test; if the specimen is brittle in tension, an estimate of the yield stress can be obtained from a uniaxial compression test. It is not so simple to decide on a satisfactory technique for measuring the brittle stress.”

Currently, the stress–strain curve provides all the information needed to calculate brittle stress and yield stress (Ward [8]). Brittle behavior is defined as the failure of a specimen at its maximum load at relatively low strains (say, less than 10%). Pure brittle fracture is presented by curve 10 of Fig. 1; the brittle stress, ${\sigma }_{B}$, is evaluated as the maximum stress of this curve.

The distinction between brittle and ductile failures is manifested in two ways: (1) the energy dissipated in fracture, and (2) the nature of the fracture surface and the presence of whitening in the vicinity of fracture. The energy dissipated is an important consideration for practical applications and forms the basis of the Charpy and Izod impact tests [9]. The impact strengths measured during these tests and typically quoted in terms of the fracture energy are not material characteristics and must be associated with a standard specimen. Therefore, in terms of energy dissipation due to fracture, the boundary separating the brittle mode of fracture from the ductile mode may not be perfectly definite. A more reliable approach, at least as a practical way, to distinguish the brittle failure from the ductile one is the analysis of fracture surface and the detection of whitening caused by fracture. However, the latter is an indication that fracture is accompanied by crazing.

The yield stress measurement, ${\sigma }_{Y}$, is also based on the stress–strain curve. ${\sigma }_{Y}$ is determined as the stress corresponding to the maximum of the $\sigma -\varepsilon$ curve. This means that, unlike the yielding in metals, this phenomenon in PP and other thermoplastics can be associated with various deformation mechanisms, particularly with crazing (for example, curve 7 of Fig. 1) and shear banding (curves 1 ~ 3 of Fig. 1). It should also be noted that the brittle–ductile transition observed in tensile tests and quoted in terms of stresses do not necessarily coincide with the transition determined based on impact tests and expressed in terms of energy consumption. Moreover, the definition and measurement of the brittle stress and yield stress are a matter of engineering practice, not an academic issue. Both approaches can be considered satisfactory because they consistently characterize the material fracture within the spectrum of behaviors ranging from pure brittle to pure ductile.

3.2 Brittle Stress and Yield Stress as Function of Temperature and Strain Rate

The simplest way to describe the competition between the brittle and ductile modes of failure in terms of ${\sigma }_{B}$ and ${\sigma }_{Y}$ under variable strain rates and temperatures is based on the Ludwik-Davidenkov-Orowan (LDO) hypothesis [10,11,12], which is illustrated by Fig. 6. It can be thought that the fracture occurs at the intersection between the flow and fracture stress (see Fig. 6a). This approach was first proposed for metals, and Vincent [6] was the first to obtain evidence to support its application for thermoplastics. Brittle fracture and plastic flow are assumed to be independent processes, yielding separate characteristic curves for brittle stress and yield stress as functions of strain rate at constant temperature or functions of temperature at a certain strain rate (Fig. 6b). It is then argued that whichever process can occur at lower stress will be the operative one. This can be either fracture or yield. The intersection of the ${\sigma }_{B}/{\sigma }_{Y}$ curves define the brittle–ductile transition. If the strain rate remains constant as the temperature increases, the material is brittle at all temperatures below the transition point and ductile at all temperatures above this point. The influence of chemical and physical structure on the brittle–ductile transition can be analyzed from this starting point by considering how these factors affect the brittle stress and yield stress curves. Thus, the LDO concept of considering yield and fracture as competitive processes provide a useful starting point.

According to Vincent [6], the brittle stress, ${\sigma }_{B}$, is affected by strain rate and temperature only by a factor of two in the temperature range of − 180 to + 20 °C. However, the yield stress, ${\sigma }_{Y}$, is greatly affected by strain rate and temperature, increasing with increasing strain rate and decreasing with increasing temperature. For example, a typical figure would be a factor of 10 over the temperature range of − 180 to + 20 °C. In the absence of experimental data for PP, the LDO concept is illustrated by the polymethyl methacrylate results in Fig. 7 (Vincent [13]).

The material behavior regarding the effect of strain rate variations on ${\sigma }_{B}$ and ${\sigma }_{Y}$ is quite complicated (Vincent [6, 7]). Cold drawing is typically observed at low strain rates within a certain temperature range. However, the specimen may fail in a ductile manner within the same temperature range, even if the strain rate is high. This is because heat is not rapidly conducted away at high strain rates, preventing strain hardening and brittle fracture. This does not affect the yield stress and therefore does not affect the brittle–ductile transition. However, even if the material behavior remains ductile and brittle fracture does not occur, it can cause a significant reduction in the energy to break with increasing strain rate. This phenomenon is known as the isothermal–adiabatic transition. Therefore, it is assumed that there are two critical points at which the fracture energy decreases sharply as the strain rate increases: the ductile–brittle transition and the isothermal–adiabatic transition. It is reasonable to expect that changes in ambient temperature have minimal effect on the position of the isothermal–adiabatic transition but a significant effect on the brittle–ductile transition.

Figure 8 (Vincent [6]) shows the combined effect of temperature and strain rate on the behavior of rigid polyvinyl chloride in tensile tests. Here the curve represents the brittle–ductile transition, the vertical line segment represents the isothermal–adiabatic transition, and the oblique line represents the transition from hard to soft ductile behavior. The figure indicates that: (1) the temperature of the ductile–brittle transition rapidly increases with strain rate, (2) the strain rate of isothermal–adiabatic transition is temperature independent, and (3) if the strain rate is increased at a certain temperature, say, at RT, the isothermal–adiabatic transition occurs first.

3.3 Crazing-to-Yielding Transition

The LDO hypothesis applied to polymers suffers from a lack of specificity because, as previously stated, the transition of ${\sigma }_{B}-to-{\sigma }_{Y}$, or vice versa, is not associated with a specific transition of fracture mechanisms (Jang et al. [2]). Therefore, no microstructural features, such as crazing and shear banding, which are known to be the most responsible for the fracture process in glassy polymers, are considered at the level of the LDO concept. Henceforth, to clarify the concept of brittle–ductile transition, the considerations in this Section will be limited to only one type of brittle–ductile transition, namely the phenomenon associated with the transition from crazing to shear banding. In other words, in terms of the $\sigma -\varepsilon$ curves of Fig. 1, this is the transition from, say, curve 7 to curves 1–3.

According to Vincent [6], the origin of the crazing-to-yielding transition may be understood as follows: any stress system can be regarded as the superposition of a shear stress, which tends to change the specimen shape (deviatoric component), and a triaxial (hydrostatic) stress, which tends to change its volume (dilatational component). As the stress increases, the specimen fails either in shear if the deviatoric component exceeds the shear-yield strength or in craze if the mean stress exceeds the triaxial tension required for craze formation. Shear yielding is responsible for the ductile failure and may be characterized by the yield stress in tension. The brittle–ductile transition represents a change from triaxial tensile to shear failure. Matsushige et al. [14] reported quantitative studies of how the superposition of hydrostatic pressure induces the brittle–ductile transition in amorphous polymers, polystyrene, and polymethyl methacrylate, at room temperature. The detailed stress–strain analysis resulted in a conclusion that confirms the above description of the origin of the craze-yielding transition. It was convincingly demonstrated that applying hydrostatic pressure suppresses craze formation and thus promotes yielding, causing the $\sigma -\varepsilon$ curve to shift from the craze-yielding type to the pure-yielding type. According to the experimental results of Robertson [15], Roetling [16, 17] and others, the shear-yield strength, which is dependent on deviatoric stress, increases considerably with decreasing test temperature or/and increasing strain rate. In contrast to this high sensitivity to strain rate and temperature of the shear-yield strength, the craze-yield strength, which is dependent on triaxial tension, appears to be relatively unaffected by these variables (Lazurkin [18]). This is in good agreement with Vincent’s prediction [6] about the dependencies of ${\sigma }_{B}$ and ${\sigma }_{Y}$ on strain rate and temperature.

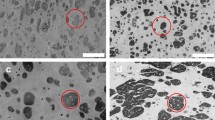
The microstructure of polymers can also influence this type of damage mode. Wu et al. [19] discovered the effect of the spherulitic structure of PP on tensile damage behavior. The quenched and annealed samples reveal the smallest spherulites and weak intra-spherulitic strength (Fig. 9a, b). Therefore, the microstructure can be easily fragmented into small lamellae and leads to the global necking with fibrillation (Fig. 11a, b), i.e., shear band (Fig. 10a, b). On the contrary, the isothermally cooled sample has large and rigid spherulites as shown in Fig. 9c, resulting in several inter-spherulitic crazings with the brittle fracture behavior (Figs. 10c, 11c, d). These two mechanisms, inter- and intra-spherulitic deformation, can occur simultaneously, as evidenced by the double yielding behavior of PP. Similar results were reported by Ding et al. [20], revealing the clearer difference between the shear band and craze-dominated yield with different microstructures of PP (Fig. 12). Nevertheless, the following section will be dedicated to the transition behavior with the strain rate and temperature.

3.4 Diagrams of Yield Stress Versus Strain Rate at Various Temperatures

The results of extensive tensile tests covering a wide range of temperatures and strain rates obtained by Jang et al. [1, 2] are presented in Fig. 13. The normalized yield stress is defined as the maximum stress in the $\sigma -\varepsilon$ curve divided by the test temperature, ${\sigma }_{Y}/T$, is plotted as a function of $log\dot{\varepsilon }$ where $\dot{\varepsilon }$ is the strain rate. Moreover, each curve represents the behavior at a specific temperature, and the higher temperature, the lower the curve. Furthermore, a high strain rate and low test temperature favor crazing, while a low strain rate and high temperature promote shear yielding. A transition zone is observed in the spectrum of rates and temperatures where crazes and shear bands coexist. The samples exhibit crazing after the initial elastic (possibly along with viscoelastic) regime, followed by general yielding and a small extent of cold drawing. As temperature further decreases or the strain rate increases, the extent of cold drawing is reduced, and the shear yielding gradually gives way to crazing. In Fig. 13, changes in the slope of the ${\sigma }_{Y}/T - log\dot{\varepsilon }$ curves reflect the transition from shear yielding to crazing. For a given test temperature, a strain rate exists above which deformation is dominated by crazing. For a given test rate, there exists a temperature that limits crazing from yielding. The solid line is based on the Eyring’s theory [21].

Meanwhile, van Breemen et al. [22] described such transition by the $\alpha$ and $\beta$ transition on the chain motion (see Fig. 14). Moreover, they estimated the variation of compressive yield stress on the strain rate and temperature, using the multi-process constitutive mode, based on the EGP-model [23, 24]. As shown in Fig. 15, the multi-process model accurately predicted experimental compressive test data of PP (symbols). It is worth noting that this multi-process model can estimate the s–s curve of various polymers, including PMMA, PLLA, and PS [22].

4 Crazing and Yield Governed by Crazing: Shear Bands of Crazed Material

4.1 Crazing of Thermoplastics

The earlier descriptions of crazing in thermoplastics belong to Merz et al. [25], Hsiao and Sauer [26] and Sauer et al. [27]. The work [26] reads: “By ‘crazing’ of thermoplastics is meant the development of a state, in which the normal optical transparency of the material is reduced. For such thermoplastics as polystyrene or polymethyl methacrylate, crazing may be described in terms of the development of mechanical cracks, ‘crazing cracks’, visible to the naked eye or as a blushing of the material produced by the scattering and reflection of light. However, crazing is not necessarily actual cracks, but may be some sort of infinitesimal openings, which are either still within the field of molecular attraction or are physically prevented by other neighboring molecules from developing into cracks. The most basic fact about the development of crazing in specimens is that the observed crazing cracks are always found to be at right angles to the direction of maximum tensile stress. If the specimen is subject to pure compression rather than tension, no crazing will occur”. The above two facts are illustrated by Figs. 16 and 17. Figure 16 from Ward [8] shows the craze formation in polystyrene; the direction of all crazes is perpendicular to the load line. Both facts are simultaneously observable when a specimen is subject to pure bending, as shown in Fig. 17 [26]. From the mechanical point of view, the distinction between cracks and crazes is evident only from the fact [26] that a crazed specimen is capable of bearing considerable loads even after crazes extend over its entire cross-section (see Fig. 17). The crazing behavior of PP during the tensile deformation is shown in Figs. 18 and 19 [28, 29]. As previously stated, an increase in strain rate causes an increase in craze density on the spherulitic structure in the perpendicular direction to the load line [28, 29]. According to Bucknall [30], rates of craze formation are highly dependent upon stress and temperature. Crazing is accompanied by small but measurable elongation of the specimen. Under steady stress and temperature conditions, new crazes are formed, existing crazes grow, and after an initial settling-down period, the rate of crazing becomes constant. However, no new crazes are formed under constant strain conditions, and the rate of crazing decreases with time. In case of PS, the crazes decrease the stiffness of the material and increase the elongation at break (see Fig. 20) [26]. The results of Kambour [31] show that crazes can elongate greater than 40%, apparently in an elastic manner. Crazing considerably lowers the material stiffness: Young’s modulus of crazed material is estimated as 10–20 times less than that of the original material [31]. Choi et al. [32] applied Hashin-Strikman’s equations to predict Young’s modulus and proposed an analytical model to predict the softening of PP with the formation of crazes from rubbers.

Although the structure and behavior of crazes in various plastics have been studied for at least four decades, many aspects of this subject remain unexplored. Nevertheless, it is established that craze formation can occur equally in amorphous and semi-crystalline polymers, particularly in PP and its rubber blends. Jang et al. [2] investigated the craze morphology in PP in detail. The structure of crazed materials is characterized by a collection of fibrils and membranes separated by voids, which are responsible for the craze's overall low density (according to Kambour [33] estimation, the void fraction in crazed materials can attain 50%).

4.2 Conditions of craze formation

As described in Sect. 4.1, crazes initiate from the spherulitic structure and grow in a direction perpendicular to the load line. Given the significance of craze formation, it is essential to formulate a criterion for craze formation based on micromechanical concepts. The criterion for craze formation analogous to the von Mises criterion for plasticity was proposed by Sternstein et al. [34]. Examining the craze formation under biaxial stress conditions, it was found that both principal stresses ${\sigma }_{1}$ and ${\sigma }_{2}$ $({\sigma }_{1}>{\sigma }_{2})$ affect material crazing. The criterion for craze formation is formulated as:

$${\sigma }_{1}-{\sigma }_{2}=A+\frac{B}{{\sigma }_{1}+{\sigma }_{2}}$$

(1)

where A and B are constants, which depend on temperature. Oxborough and Bowden [35] introduced a different criterion, to a certain degree similar to the previous one:

$${\sigma }_{1}-\nu {\sigma }_{2}=A+\frac{B}{{\sigma }_{1}+{\sigma }_{2}}$$

(2)

where the ν denotes the Poisson’s ratio. The wide circle of questions concerning the craze formation and growth was considered by Argon [36, 37]. The critical analysis of the abovementioned criteria can be found in Ward [8]. Bucknall also suggested the new criterion for craze initiation, based on linear elastic fracture mechanics (LEFM) to consider the small defects by inclusions or imperfections [38]. The nascent craze initiation criterion can be formulated as:

$${\sigma }_{1}\left(\mathrm{nasc}\right)\ge {\left[\frac{E{G}_{1}\left(\mathrm{nasc}\right)}{{Y}^{2}\left(1-{\nu }^{2}\right)\pi {a}_{0}}\right]}^{1/2}$$

(3)

where the E is the elastic modulus, G₁(nasc) denotes the critical energy release rate for nascent craze, Y is the geometric factor, ν is the Poisson’s ratio, and a₀ is the estimated craze length.

4.3 Yield Governed by Crazing

As stated in Sect. 4.1, formation and propagation of crazes are responsible for the phenomenon known as the plasticity governed by crazing by Jang et al. [1, 2] (see, for example, curve 7 of Fig. 1). In this type of behavior, the onset of non-linearity on the stress–strain curve is accounted for the initiation of craze growth followed by the maximum point on this curve. The stress corresponding to this point is called yield stress, although it is associated with crazing, not yielding. Qualitatively, this phenomenon is clear, and its simple quantitative description can be given as follows.

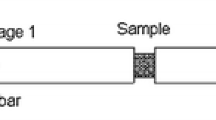
The elongation of the bar shown in Fig. 21 is written as

$$\Delta L=\frac{F\left(1-\eta \right)L}{{E}_{0}A}+\frac{F\eta L}{{E}_{c}A}$$

(4)

where ${E}_{0}$ and ${E}_{c}$ $({E}_{0}>{E}_{c})$ are Young’s moduli of original and crazed materials, respectively, $\eta$ is fraction of the crazed length, and A is the cross-sectional area of the bar. Introducing notations $\varepsilon =\Delta L/L$ and $\sigma =F/A$, Eq. (4) becomes

$$\varepsilon =\left(\frac{1-\eta }{{E}_{0}}+\frac{\eta }{{E}_{c}}\right)\sigma$$

(5)

Hence

$$\dot{\varepsilon }=\left(\frac{1-\eta }{{E}_{0}}+\frac{\eta }{{E}_{c}}\right)\dot{\sigma }+\left(\frac{1}{{E}_{c}}-\frac{1}{{E}_{0}}\right)\dot{\eta }\sigma$$

(6)

where the strain rate $\dot{\varepsilon }$ is a constant. The last equation is reduced to the form

$$\dot{\sigma }+\frac{1}{t+a}\sigma =\frac{\dot{\varepsilon }{E}_{0}a}{t+a}$$

(7)

with

$$a=\frac{1}{\left(\frac{{E}_{0}}{{E}_{c}}-1\right)\dot{\eta }}$$

(8)

The t in Eq. (7) indicates the elapsed time. Let craze formation start at the point $\sigma ={\sigma }_{c}$. While $\sigma <{\sigma }_{c}$, deformation of the bar is linearly elastic, $\dot{\varepsilon }=\dot{\sigma }/{E}_{0}$. Beginning with the point, at which craze extends over all length $L$, i.e., at $\eta =1$, the bar is deformed elastically with Young’s modulus ${E}_{c}$, $\dot{\varepsilon }=\dot{\sigma }/{E}_{c}$. However, in the further analysis it is supposed that the craze encompasses only a small fraction of $L$.

First, assume that the speed of craze propagation is constant, $\dot{\eta }=const$. The solution of Eq. (7) going through the point $({\sigma }_{c},{t}_{c})$, where the t_c stands for the time to craze formation, can be written by

$$\sigma =\frac{{t}_{c}+a}{t+a}\left[{\sigma }_{c}+\frac{\dot{\varepsilon }{E}_{0}a}{{t}_{c}+a}\left(t-{t}_{c}\right)\right] (t\ge {t}_{c})$$

(9)

or if ${t}_{c}=0$,

$$\sigma =\frac{a}{t+a}\left({\sigma }_{c}+\dot{\varepsilon }{E}_{0}t\right) (t\ge 0)$$

(10)

Normalizing the stress, $s=\sigma /{\sigma }_{c}$, and designating ${\varepsilon }_{c}={\sigma }_{c}/{E}_{0}$, one has

$$s=\frac{a}{t+a}\left(1+\frac{\dot{\varepsilon }}{{\varepsilon }_{c}}t\right) (t\ge 0)$$

(11)

Three types of function Eq. (11) behaviors are possible. First, if $\dot{\varepsilon }a/{\varepsilon }_{c}>1$ (high strain rate), Eq. (11) is an increasing function; second, if $\dot{\varepsilon }a/{\varepsilon }_{c}<1$ (low strain rate), Eq. (11) is a decreasing function; function Eq. (11) is constant if $\dot{\varepsilon }a/{\varepsilon }_{c}=1$. The curves corresponding to the types of stress behavior indicated are presented in Fig. 22. Here $\varepsilon ={\varepsilon }_{c}+\dot{\varepsilon }t$, $a=0.1$ and $\dot{\varepsilon }/{\varepsilon }_{c}=15$ (high strain rate, s increases), $\dot{\varepsilon }/{\varepsilon }_{c}=5$ (low strain rate, s decreases) and $\dot{\varepsilon }/{\varepsilon }_{c}=10$ ($s\equiv 1$). None of these curves describes the behavior of the material subject to the yield governed by crazing (see, for example, curve 7 of Fig. 1).

Now assume that the speed of craze growth changes in the course of the process, for example, it depends on stress as $\dot{\eta }={\eta }_{0}{s}^{\alpha } (\alpha >0)$. In this case Eq. (7) can be solved numerically based on the solution of Eq. (11) and using the following step-by-step procedure:

$${s}_{i+1}=\frac{{a}_{i}}{t+{a}_{i}}\left(1+\frac{\dot{\varepsilon }}{{\varepsilon }_{c}}t\right) (t\ge 0)$$

(12)

where ${a}_{i}=a/{s}_{i}^{\alpha }$. The stress–strain curve shown in Fig. 23 is constructed for the speed of craze growth proportional to the stress, $\dot{\eta }={\dot{\eta }}_{0}s (\alpha =1)$, and thus according to Eq. (8) ${a}_{i}=a/{s}_{i}$. It is accepted that $a=0.1$ and $\dot{\varepsilon }/{\varepsilon }_{c}=15$. Craze formation begins when the normalized stress attains the value of unity, $s=1 (\sigma ={\sigma }_{c})$, and the yield point corresponds to the maximum of the stress–strain curve.

The criteria for craze formation could be written by the equations, such as Eqs. (4)–(12). However, the numerical simulations to investigate the crazing phenomena are also required to analyze the arbitrary configurations. The simulations of the craze formation and growth can be performed by molecular dynamics (MD) [39,40,41]. The MD simulation was applied to the glassy polymers, and the s–s curves with the craze morphology can be accurately simulated. The entire failure procedure of glassy polymers, i.e., craze initiation, growth, and failure, can be seen (Figs. 24, 25) [39, 40].

4.4 Shear Banding of Crazed Material

After the material goes through the stress peak on the stress–strain curve, it may experience shear banding followed sometimes by necking and cold drawing. In the existing literature, observations of the formation of shear bands within the crazed material are sparingly described. A possible explanation of this transition is presented below.

Let the craze be considered as a crack, which is opened by applied load and closed by the stresses of craze fibrils and membranes. The stress intensity factor at the craze tip is designated as K. Let, a plastic zone be developed in the vicinity of the craze tip with the shape depicted in Fig. 26a and the size in the direction perpendicular to the craze plane being of the order of,

$$r=0.5\frac{{K}^{2}}{{E}_{0}{\sigma }_{Y}}$$

(13)

(see Rice and Johnson [42]). Assuming that the craze fraction of specimen length is small $(\eta \ll 1)$ and the number of crazes is $n$, the distance between two neighboring crazes can be evaluated as $h=L/n$. The probability of the appearance of massive shielding sharply increases if the plastic zones of neighboring crazes overlap, or in other words, if $r$ becomes equal to or greater than $h/2$. The shear band percolating the specimen cross-section is shown in Fig. 26b.

5 Notch Sensitivity

The presence of a sharp notch can change the fracture of a metal from ductile to brittle, and similar considerations apply to the behavior of polymers, particularly PP. For this reason, a standard impact test for a polymer is the Charpy or Izod test with a notched bar. Under impact conditions, an un-notched PP specimen features a clear brittle–ductile transition between 0 and 20 °C, whereas a notched PP specimen is characterized by a transition temperature of approximately 100 °C (Van der Wal et al. [43]).

Orowan [12] introduced a simple explanation of the effect of notching. He considered an ideally deep and sharp notch in an infinite solid, for which the plastic constraint increases the yield stress to 3 according to the von Mises criterion for plane strain conditions. (consider that the plane strain does not exist at the specimen surface. Irwin used a value of approximately 1.7). This leads to the following classification for brittle–ductile behavior:

1.
If ${\sigma }_{B}<{\sigma }_{Y}$, the material is brittle.
2.
If ${\sigma }_{Y}<{\sigma }_{B}<3{\sigma }_{Y}$, the material is ductile in un-notched tensile tests but brittle when a sharp notch is introduced.
3.
If ${\sigma }_{B}>3{\sigma }_{Y}$, the material is fully ductile, i.e., ductile in all tests, including those in notched specimens.

This classification explicitly states that the brittle fracture remains unaltered by the notch presence and that only the yield behavior is affected.

Vincent [7] proposed another approach to the problem in question. He writes: “In order to construct a ${\sigma }_{B}-{\sigma }_{Y}$ diagram (Fig. 27), ${\sigma }_{Y}$ has been taken as the yield stress in a tensile test; for the materials which were brittle in tension, ${\sigma }_{Y}$ was assessed from a uniaxial compression test. The value of ${\sigma }_{B}$ has been taken as the flexural strength. The line A divides the brittle materials on the right from the tough materials on the left. It is the line ${\sigma }_{B}/{\sigma }_{Y}=2.25$, but this can only be an approximation. The number 2.25 may well be in error by up to 30% either way for different materials. (Note that, although a material may become brittle when ${\sigma }_{B}={\sigma }_{Y}$, the dividing line A is not ${\sigma }_{B}/{\sigma }_{Y}=1$. The difference is because ${\sigma }_{B}$ is measured in flexure, not tension.) The line B divides the materials, which are brittle when notched, on the right, from the materials, which are tough even when notched, on the left. This line is necessarily even more approximate because the effect of a notch is so dependent on precise dimensions of the notch. By means of these simple tests, the characteristic points of other samples of these polymers and of samples of other polymers may be determined and plotted in this ${\sigma }_{B}-{\sigma }_{Y}$ diagram; this gives a useful preliminary guide to their behavior. It can be seen where the characteristic points lie relative to the lines A and B and so the materials may be classified as brittle, tough or notch-brittle. It can also be seen whether they lie near to well-known polymers and then it can be taken that their behavior will be somewhat similar. It cannot be claimed that this diagram gives a complete representation of material behavior, but it is claimed that it is substantially better than using the results of a single test to assess toughness. In particular, it assists in understanding results. If it is desired to explain a change in toughness, it is an essential first step to decide whether this change is related to a change in ${\sigma }_{B}$ or ${\sigma }_{Y}$ or both. When this step is omitted, quite inappropriate explanations of behavior may be suggested. Use of the ${\sigma }_{B}-{\sigma }_{Y}$ diagram encourages this distinction and thus guides explanations into more appropriate directions”.

Neither Orowan’s approach nor Vincent’s gives any convincing explanation of the effect of the notch presence on the shift in the brittle–ductile transition temperature. Perhaps a more plausible explanation of this effect can be given as follows.

Let the notch length be $l$ and the radius of the notch curvature at its tip be $r$, with the ratio of $l/r$ being much greater than unity. Under such a condition, the coefficient of stress concentration α_c at the notch tip can approximately be evaluated as:

$${\alpha }_{c}\approx 2\sqrt{\frac{l}{r}} (>1)$$

(14)

The condition for brittle fracture is written in the form,

$${\alpha }_{c}{p}_{B}={\sigma }_{B}$$

(15)

where ${p}_{B}$ is the applied stress required to break the specimen. Equation (15) means that the brittle stress of the notched specimen decreases to the value of

$${p}_{B}=\frac{{\sigma }_{B}}{{\alpha }_{c}}$$

(16)

At the same time, as stated before, the notch introduction increases the stress required to initiate yielding (p_Y) up to a value of

$${p}_{Y}=3{\sigma }_{Y}$$

(17)

As it follows from Eqs. (16) and (17), the notch presence promotes brittle fracture and suppresses yielding. Hence the following classification can be proposed:

1.
If ${\sigma }_{B}<{\sigma }_{Y}$, the material is brittle.
2.
If ${\sigma }_{B}>{\sigma }_{Y}$, but ${p}_{B}<{p}_{Y}$, the material is ductile in un-notched tensile tests but brittle when a sharp notch is introduced.
3.
If ${p}_{B}>{p}_{Y}$, the material is fully ductile, i.e., ductile in all tests, including those in notched specimens.

Figure 28 illustrates the increase in the temperature of brittle–ductile transition due to the presence of a notch.

Similarly, like PP, other thermoplastic materials such as polycarbonate (PC) and polyvinyl chloride (PVC) may exhibit notch sensitivity. PC, known for its excellent mechanical properties, is widely utilized in engineering applications such as electronic housing and automotive components. Despite its remarkable toughness, PC can also experience embrittlement due to notches. The notch sensitivity of polycarbonate (PC) was also implemented by a theoretical large-deformation model [44, 45]. In this study, the competition between the ductile and brittle fracture was modeled to determine the brittle and ductile fracture criterion, based on the local elastic volumetric strain ${\epsilon }^{e}$ and effective plastic stretch ${\lambda }^{p}$ [44]. The brittle fracture will occur when ${\epsilon }^{e}$ increases up to its critical value ${\epsilon }_{f}^{e}$, while the specimen will fail in ductile manner when ${\lambda }^{p}$ reaches its critical value, ${\lambda }_{f}^{p}$. Further, the mean normal stress $\sigma$ and ${\lambda }^{p}$ during the bending test with blunt and sharp notches were simulated by finite element method, i.e., the ductile fracture at blunt notch and brittle at sharp notch (Figs. 29, 30). The simulated load–displacement curves were also in agreement with the experimental results [44].

6 Rubber Modified Polymers: Criteria of Brittle–Ductile Transition

6.1 Toughness by Rubber Phase

The toughness of some ductile polymers, particularly nylons and PP, is insufficient for their use as engineering plastics. One of the most often used methods to overcome this drawback is blending such polymers with other polymers, especially with different types of rubber-like materials. Adding a rubber phase increases impact strength, sometimes very significantly [46,47,48,49]. Examples of growth in impact strength of nylon and PP with rubber content are shown in Figs. 31 and 32. The former from Borggrave et al. [50] presents the results of notched Izod tests conducted on nylon-rubber blends at − 40 °C. When the rubber phase is only 2%, the increase in impact energy is already approximately a factor of 2. A further remarkable gain in impact strength occurs when the rubber content increases. At this temperature, − 40 °C, all blends fracture in a brittle manner, even the blends with the maximum of notched impact strength, approximately 24 kJ m⁻². Muratoglu et al. [51] also studied the toughening behavior of rubber-modified polyamides. The Izod strength of PA66-EPDR (ethylene propylene diene rubber) blends is increased from 75 to 966 J/m when the composition of EPDR is changed from 6 to 12 wt% under the constant rubber particle size. Bagheri and Pearson [52] investigated the fracture toughness of rubber-toughened epoxies using the SENB (single edge notched bending) test, and the fracture toughness was increased from 0.85 to 1.45 MPa·m^0.5 when only 1%vol of rubber phase is introduced. Figure 32 (Pukanszky et al. [53] and Chiang et al. [54] depicts the data obtained from notched Izod tests on PP modified by EPDM (ethylene-propylene-diene) and BDS (butadiene-styrene). It shows a clear increase of the impact strength with rubber phase concentration if the modifier is EPDM (filled and empty squares) and no growth if the modifier is BDS (filled and empty circles). According to [53, 54], this difference results from the level of adhesion of PP to these two modifiers—high to EPDM and low to BDS. A rubber phase added to a polymer relieves the mechanisms with greater energy dissipation, i.e., to improve polymer ductility as shown in Fig. 33 [55]. In terms of the competition between fracture strength and yield stress (see Fig. 6), the rubber phase lowers the yield stress. Therefore, the yield stress drops below the fracture strength, and the fracture mode changes from brittle to ductile [51, 52, 55].

6.2 Polymer Phase

There are two types of polymer matrices: brittle and pseudo-ductile. This classification is not rigorous since time–temperature-geometry effects are ignored. However, it gives a convenient basis for further discussion. Brittle polymers tend to craze, have low crack initiation energy, and low crack propagation energy. Therefore, both un-notched and notched impact strengths are low. Examples are polystyrene and polymethyl methacrylate. Matrix crazing is the main energy dissipation mechanism in such polymer rubber blends. However, as evidenced by some observations, matrix yielding occurs after crazing. The blend will be tough only when a crazed matrix exhibits yielding.

Pseudo-ductile polymers tend to shear yield and have high crack initiation energy but low crack propagation energy. Therefore, their un-notched impact strength is high, but the notched impact strength is low. Examples are nylons and polypropylene. The main energy dissipation mechanism in such polymer rubber blends is matrix yielding. Thus, the toughening behavior could depend on the matrix properties [56, 57], and the selection of polypropylene phase in rubber toughened polypropylene blends is quite important.

The boundary between brittle behavior and ductile behavior may be determined in terms of the competition between the fracture strength and yield stress and is, to a great extent, fuzzy. As the temperature increases, the yield stress falls below the fracture strength and the fracture type shifts from brittle to ductile. Adding a rubber phase enhances the ductility, i.e., the ${\sigma }_{Y}-T$ curve of Fig. 6 is lowered, and the brittle–ductile transition temperature is shifted towards lower temperatures. Thus, an effect of the introduction of a rubber phase was observed in many polymers.

6.3 Brittle-to-Crazing Transition

There are at least two hypotheses that were proposed for the action of rubbers in improving the impact strength. The earlier one belongs to Bucknall [30, 58] and was called by him as the Craze Theory of Toughening. Summarizing his observations on polystyrene, polymethyl methacrylate, and polycarbonate, Bucknall [30] writes: “The sequence of events following the application of a load is the same in a rubber modified polymer as it is in the corresponding pure polymer: the material deforms elastically until the craze initiation stress is reached, and crazing then proceeds until the stress is released by the fracture of the specimen; in both cases fracture involves the rupture of a craze”. Bucknall presents Fig. 34, redrawn from Kato [59], as an example of craze appearance in the regions surrounding rubber particles. It is worth noting here that there is at least one more scenario of craze development in which shear banding follows the crazing. “The effect of introducing rubber particles into the polymer is to lower the craze initiation stress relative to the fracture stress, thereby prolonging the crazing stage of deformation. It is not difficult to explain why rubber particles lower the craze initiation stress: in most rubber modified thermoplastics the Young’s modulus of the rubber is about 1000 times lower than that of the surrounding resin, and the applied stress is therefore concentrated in the resin. The problem is rather to explain why the rubber particles do not lower the fracture stress to the same extent, by concentrating the applied stress in the neighboring regions of crazed polymer; the material would be no tougher than a pure polymer if this were to happen”. Bucknall [30] attempted to explain the situation by analyzing the interaction of the rubber particles with the surrounding resin: “At the first sight it is difficult to reconcile the load-bearing function of the rubber with its low Young’s modulus, but on closer inspection of the problem it becomes clear that the relevant property of the rubber is not Young’s modulus, but the very much higher bulk modulus: the forces acting on the rubber particles after crazing has been initiated are triaxial rather than uniaxial. Crazing involves an extension along the axis of the applied stress without a significant contraction in the normal directions, and the rubber particle is therefore subject to dilatant forces as long as it remains bonded to the surrounding resin”. The idea that the rubber phase can influence the matrix's stress state during craze formation and propagation is difficult to justify, largely because it contradicts experimental data, which shows that rubber particles particularly break due to material crazing. Numerous observations indicate that the maximum effect of the rubber phase can be obtained only if the resin is chemically well-grafted to the rubber (for example, Turley [60], Lundstedt and Beviliacqua [61], Pukanszky et al. [53] and Chiang et al. [54]).

Yang et al. [62] investigated the effect of elastomer modulus in the HDPE matrix. It was confirmed that the HDPE could be toughened when the modulus ratio of elastomer and matrix is above 10 (see Fig. 35). The same conclusion was also derived theoretically by Jiang et al. [63]. As shown in Fig. 36, the transition temperature is rapidly decreased with the modulus ratio of matrix to elastomer, but it slowly decreases when the ratio is larger than 10. These studies support the abovementioned toughening mechanisms.

Rabinovitch et al. [64] studied the fracture morphology of the rubber-modified PP after the Izod impact test. The interface between the rubber and PP delaminates due to the impact load. Thus the cavitation and voids are formed at the interface (Fig. 37b, c). Then the extensive crazes are generated with the fiber pull-out (Fig. 37d, e). Under the static condition, the rubbery phase increases the ductility in a similar mechanism [55]. Figure 38 shows the voids and dilatational bands at the tensile test of rubber-modified PP. Thus, the crazes are more densified by the micro-damage mechanisms in the case of the rubber-modified PP (see Fig. 39). Therefore, it can be explained in the way that the main role of rubbers is to absorb the energy due to their voiding and stretching preceding and leading to craze formation.

The Bucknall question [30] of why the rubber particles added to a brittle polymer strongly affect the craze initiation and are indifferent regarding the brittle fracture has no easy answer because both fracture modes are governed primarily by the same factor—the hydrostatic component of the stress state. However, since the criteria of brittle fracture are noticeably different in formulations from Eqs. (1) and (2) for craze initiation, the comparative analysis of the fracture and crazing criteria can offer a clue to solving the problem. However, of the two mechanisms, elastic-brittle and crazing, the latter absorbs significant energy, which may explain why materials typically exhibit superior resistance to brittle fracture under impact conditions.

In a notched impact test, fracture occurs in two stages: the stresses at the base of the notch build up to a critical level during the first stage; a crack is then initiated and propagates across the specimen during the second stage. In a rubber-modified polymer, it is possible to obtain information about the pattern of energy absorption not only from the force–time curve but also from examining the fracture surface and the inspection where stress whitening takes place. As it follows from observations on rubber-modified polystyrene by Bucknall [58], there exist three manners of fracture behavior, which are explained as follows:

1.
Low temperatures: The rubber cannot relax at any fracture stage. There is no craze formation, and brittle fracture occurs.
2.
Intermediate temperatures: The rubber cannot relax during the relatively slow build-up of stress at the base of the notch but not during the fast crack propagation stage. Stress whitening occurs only in the first (pre-crack) fracture stage and is therefore confined to the region near the notch.
3.
High temperatures: The rubber can relax even in the rapidly forming stress field ahead of the traveling crack. Stress whitening occurs over the whole of the fracture surface.

Bucknall and Smith [65] report similar impact test results for other rubber-modified polymers. The above manners of fracture behavior are illustrated in Fig. 40, which shows fracture surfaces and force–time curves at three different temperatures. The increased absorption of energy due to stress whitening, i.e., crazing, is reflected in the impact strength-temperature curve, as shown in Fig. 41.

Bucknall [30, 58] concludes: “Detailed studies of mechanical properties are now required in order to put the Craze Theory of Toughening on a quantitative basis. There can be little doubt that considerable advances will be made in this interesting and important field of polymer rheology during the next few years”.

Similar observations have been reported by Grein et al. [66], revealing the Charpy impact energy of rubber-modified PP with different viscosity against the wide range of temperatures (Fig. 42). The amount of stress-whitening is also correlated with the D-B transition of these blends (Fig. 43). The rubber-toughened PVC reveals similar behavior under the falling weight impact test (Fig. 44) [67].

6.4 Brittle-to-Yield Transition

The second hypothesis regarding the toughening effect of rubber particles embedded in a brittle polymer was stated in Borggrave et al. [50, 68] for nylon-rubber blends and in Van der Wal et al. [69, 70] for PP-rubber blends. According to these works, the rubber particles increase polymer toughness not by acting to nucleate crazing or local plastic deformation but rather by acting to relieve the volume strain, i.e., decrease the hydrostatic component of the stresses by delamination and internal cavitations, which leads to decreasing the von Mises yield stress. The internal voiding of the rubber particles eliminates triaxial stresses, allowing for yielding in the matrix similar to that of a homogeneous solid under uniaxial tension. It may be interesting to note that these reasons based on observations of blends with pseudo-ductile matrices are just the opposite of those given by Bucknall, who mostly experimented on blends with brittle matrices. In agreement with this, Borggrave et al. [50, 68] and Van der Wal et al. [69, 70] explain stress whitening by voiding of the rubber particles, whereas Bucknall [30, 58] explain it by crazing.

The following fact can be indicated in favor of the second hypothesis. As shown by Piggotti and Leidner [71], Kunori and Geil [72], and discussed by Nielsen [73], Sahu and Broutman [74], Gupta and Purwar [75], among others, the yield stress of a rubber-modified polymer is well determined using either the equation

$${\sigma }_{Y}={\sigma }_{Y}^{0}\left(1-\phi \right)$$

(18)

or the equation

$${\sigma }_{Y}={\sigma }_{Y}^{0}\left(1-{\phi }^{2/3}\right)$$

(19)

where ${\sigma }_{Y}$ and ${\sigma }_{Y}^{0}$ are the yield stresses of the blend and the parental material, respectively, and $\phi$ is the volume fraction of a dispersed rubber phase. Equations (18) and (19) result from the consideration that the yield stress of the blend comes out as a result of averaging the matrix stress over all its volume and over the weakest cross-section, respectively. In both cases, the material is considered uniaxially tensile. Equation (19) can be somewhat altered if the area of the weakest cross-section is estimated assuming that particles are packed in the simple cubic lattice:

$${\sigma }_{Y}={\sigma }_{Y}^{0}\left[1-\frac{\pi }{4}{\left(\frac{6\phi }{\pi }\right)}^{2/3}\right]$$

(20)

The yield stress of a PP-rubber blend as a function of inclusion concentration at room temperature and strain rate 8.3 × 10⁻⁴ s⁻¹ is given by Van der Wal et al. [69]. The linear approximation of this function is depicted in Fig. 45 along with Eqs. (18) and (20). As seen, these equations provide reasonable upper and lower bounds for the yield stress. This fact can be treated as the evidence that the stress state of the blend is really uniaxial.

However, the Borggrave et al. [50, 68] and Van der Wal et al. [69, 70] explanation of the rubber particles effect, which makes the emphasis on relieving the hydrostatic stress and promoting the uniaxial yield, can hardly be accepted as completely convincing. If the rubber phase really acted only in this way, it would not be necessary to introduce this phase—a tensile specimen of the parental material experiences just the uniaxial stress and yielding. It is more productive to consider thermoplastic rubber modification as a method of switching fracture behavior from the elastic-brittle mode that consumes energy inefficiently to a different mode that dissipates far more energy. Under such consideration, the above two hypotheses can be characterized based on common ground: according to the first of them, the rubber phase shifts the elastic-brittle behavior towards craze formation and growth, while according to the second one, towards shear yielding. Regarding the fracture behavior described by the curves of Fig. 1, the first hypothesis states that adding a rubber phase leads to the transition from curve 10 to, say, curve 7, and the second hypothesis from curve 10 to curves 1–3. Which of the two above transitions occurs depends primarily on matrix properties: the former is more likely to occur if the matrix is brittle, while the latter is more likely to occur if the matrix is pseudo-ductile.

6.5 Criterion of Center-to-Center Interparticle Distance

In the fundamental understanding of the mechanism of brittle-to-shear yielding transition, the important role belongs to the work by Hobbs et al. [76]. Here, the transition was numerically modeled based on the hypothesis that interacting shear stress fields between neighboring particles were the dominant force in promoting shear band formation leading to enhanced plastic flow. In this respect, the results of this work have general applicability to all blends with pseudo-ductile matrices, i.e., to the thermoplastic blends, in which shear flow occurs in preference to other deformation modes. High impact strengths are expected in practical tests such as the Izod when the brittle–ductile transition is shifted to a rate comparable to that of the experiment.

The maximum shear stress contours for an isolated hole in a two-dimensional solid were plotted by Sternstein et al. [34]. Inspection of these plots shows that stress field overlap becomes significant for two particles lying on a line running at 45° to the applied tensile force when the interparticle separation is less than two particle diameters. This interaction is shown in Fig. 46. The three-dimensional solid was also considered by using a certain approximation of the results obtained for the two-dimensional solid. In the three-dimensional case, for the particles packed in the simple cubic lattice, there is the following connection between the particle diameter, $d$, and the cell size, $L:$ $L={\left(\pi /6\phi \right)}^{1/3}d$ with $\phi$ being the particle volume concentration. The above condition of stress field overlap, $L\le 2d$, simply means that $\phi \ge \pi /48\approx 0.065$. A series of computer-generated images showing typical three-dimensional packing densities at various particle volume concentrations is presented in Fig. 47. The corresponding two-dimensional cross sections are presented in Fig. 48. It is important to note the rapid increase in the number of particles required for a given increase in their concentration when the concentration becomes high. It is surprising to see how rapidly the space fills and how early potential interactions are established. Figure 49 shows the number of particles interacting with 1, 2, and 3 other particles and the integrated total of all interactions as a function of the particle volume concentration. The interactions are observed to increase with the particle concentration rapidly. At a concentration of 5%, more than half of the particles satisfy the requirements for shear stress field overlap with at least one other particle. At higher levels of concentration, the increase is much less rapid. Based on this analysis, the shear band density is expected to increase rapidly with particle concentration and then stop growing at high concentrations. It is assumed that the probability of brittle–ductile transition changes similarly.

Experimental verification of the above hypothesis was provided by measuring the rate dependence of the brittle–ductile transition as a function of impact modifier concentration. The tests were conducted on nylon-PEgMA blends and PP-EPDM blends, both exhibiting extensive shear banding. The results are plotted in Fig. 49, along with the calculated interactions. In both cases, the shifts at each concentration are normalized by dividing by the maximum shift observed at the modifier concentration of 30%. The shift in the brittle–ductile transition justifies this normalization method asymptotes rapidly at higher modifier levels and is almost constant above 30%. For both systems, the theoretical results predicted from shear stress field overlap considerations are in good agreement with the experimental data. This allows the authors to conclude that the model provides a realistic means of predicting the improvement in ductility by an impact modifier when the matrix is pseudo-ductile.

According to Hobbs et al. [76], the transition from the elastic-brittle mode of fracture to the shear banding mode occurs when the center-to-center interparticle distances become small enough to allow a given particle to interact with other neighboring particles in thermoplastics where shear flow dominates deformation, particularly in PP. The shear band in a polymer modified by rubber particles is schematically depicted in Fig. 50.

It is worth repeating that, as hypothesis [76] states, the only parameter responsible for brittle–ductile transition is the rubber phase concentration (see above), which is not confirmed by any one of the tens of experiments in this field, except for the experiments conducted by the authors themselves. The importance of the Hobbs et al. approach is not that it offers the complete and justified solution to the problem in question but that it draws attention to a new aspect of the problem, namely to the connection of the phenomenon of brittle–ductile transition with the ideology of the percolation theory.

It would be logical to believe that the surface-to-surface interparticle distance criterion for brittle–ductile transition introduced by Wu [77, 78] and the modeling of this transition in terms of the percolation theory proposed by Margolina and Wu [79] are immediate and natural developments of the idea of Hobbs et al. [76].

6.6 Criterion of Surface-to-Surface Interparticle Distance (Or Matrix Ligament Thickness)

When studying a pseudo-ductile polymer, nylon-66, modified by rubber particles, Wu [77, 78] found that the brittle–ductile transition closely correlates with the average surface-to-surface interparticle distance and occurs if this distance becomes smaller than a certain critical value. Figure 51 shows schematics of two rubber particles in a matrix, where $d$ is the particle diameter, $L$ the center-to-center interparticle distance and $\tau$ the surface-to-surface interparticle distance, i.e., the matrix ligament thickness. The notched Izod impact strength versus the number-average particle diameter at constant rubber fraction (10, 15 and 25% by weight) for nylon-66 modified with a carboxylated ethylene-propylene rubber is presented in Fig. 52. The brittle–ductile transition occurs at critical particle diameters, which vary with the rubber volume fraction. However, when plotted versus the average surface-to-surface interparticle distance (τ), shown in Fig. 53, the onset of brittle–ductile transition is found to occur at a single critical value ${\tau }_{c}$. Therefore, the condition for rubber toughening for blends with the nylon matrix is simply,

$$\tau <{\tau }_{c}$$

(21)

The value of ${\tau }_{c}$ is independent of rubber volume fraction and particle size, and is characteristic of the matrix properties, temperature and rate of deformation. For blends with spherical particles packing in a regular lattice, the thickness of matrix ligament τ is determined as

$$\tau =d\left[k{\left(\pi /6\phi \right)}^\frac{1}{3}-1\right]$$

(22)

where $\phi$ is the volume rubber fraction as before, and $k$ is a geometric parameter: $k=1$ for simple cubic lattice, $k={\left(2\right)}^{1/3}$ for body-centered lattice and $k={\left(4\right)}^{1/3}$ for face-centered lattice. The d denotes the particle diameter. It is shown that condition in Eq. (21) is in good agreement with observations only if the spatial packing of rubber particles is the simple cubic lattice, i.e., $k=1$. Experiments with other pseudo-ductile matrices lead to the conclusion that the above criterion is general for blends of this type. To shift the focus from rubber particles to the matrix ligament, the author refers to the condition in Eq. (21) as the matrix ligament thickness criterion rather than the surface-to-surface interparticle distance one. This reinterpretation makes the criterion in Eq. (21) more appropriate to explain the effects of phase morphology, size polydispersity, and particle flocculation. It allows the assumption that the criterion can be extended to blends with brittle matrices. Moreover, this new interpretation allows the following understanding of Borggrave et al. [50, 68] and Van der Wal et al. [69, 70] observations. Particle voiding and stretching relieve the triaxial dilative stress and create the uniaxial stress state in matrix ligaments. This, in turn, leads to the shear yielding of those matrix ligaments whose thickness is equal to or smaller than the critical value. Cavitation is not always required because the dispersed rubber phase needs only to have a lower modulus than that of the matrix for the dilative stress to be relieved and the yielding of thin ligaments to occur.

The extension of criterion Eq. (21) to blend with brittle matrices allows the interpretation of matrix yielding after crazing observed by Gilbert and Donald [80]. This phenomenon was explained by overlapping the plastic zones around neighboring crazes (see Fig. 26). The detailed study has been performed to consider the probabilistic distribution of rubber particles [81,82,83,84]. Liu et al. [84] studied the DB transition with the NBR contents with different wt% of AN (see Fig. 54). The critical rubber volume fractions at the DB transition are different from one another, but a master curve can be established when the matrix ligament thickness is formulated by,

$$\tau =d\left[k{\left(\pi /6\phi \right)}^\frac{1}{3}\mathrm{exp}(1.5\;{\mathrm{ln}}^{2}\sigma )-\mathrm{exp}(0.5\;{\mathrm{ln}}^{2}\sigma )\right]$$

(23)

where the $\sigma$ is the parameter for the dispersity of rubber particle size, i.e., $\sigma =1$ indicates the mono-dispersity, whereas the polydispersity for $\sigma >1$ [81]. As shown in Fig. 55, experimental data for same wt% AN collapses into each master curve and reveals same critical ligament thickness [84].

A similar analysis of the above phenomenon is given in Wu [78]. Figure 56 shows a stage during the fracture of a polystyrene-rubber blend after the scanning of electron photomicrograph [80]. Large rubber particles, $d>{d}_{z}$ where ${d}_{z}$ is the minimum particle diameter for craze formation, first initiate crazes, which start to break down on continued deformation. If the matrix ligament is thicker than a critical value ${\tau }_{c}$, secondary crazes are found to form at the bases of the ligament, where the tensile stresses are the greatest. The secondary crazes continue to grow, and the ligament fails catastrophically in a brittle fashion. When this occurs, the blend is only marginally tough. However, if the matrix ligament is thinner than ${\tau }_{c}$, secondary crazes are not formed; rather the ligament is found to yield. Only when this occurs, the blend can be considered as really tough. Thus the conditions for toughening of blends with brittle matrices are,

$$\tau <{\tau }_{c}\quad and \quad d>{d}_{z}$$

(24)

At constant rubber content, the matrix ligaments are thinner with smaller particles. However, larger particles are more efficient for craze initiation. Therefore, there is an optimum rubber particle size at which the toughness is the greatest. If one approximates the matrix ligament thickness by Eq. (22) with $k=1$, then the optimum rubber particle size, ${d}_{0}$, can be estimated as:

$${d}_{0}={\tau }_{c}{\left[{\left(\pi /6\phi \right)}^\frac{1}{3}-1\right]}^{-1}$$

(25)

Equation (25) is reported to be in good agreement with the experimental data of Gilbert and Donald [80].

Hobbs et al. [76] argue that the matrix ligament experiences yielding if the elastic stress fields around neighboring particles overlap (see Fig. 46). But both criteria, [76,77,78], are based on the hypothesis that in order for the inter-particle shear band to occur, either the distance between particle centers [76] or the matrix ligament thickness [77, 78] must be smaller than a certain critical value. This leads Wu to the idea [78] that “the onset of brittle–ductile transition may be formulated as a problem of the connectivity of thin ligaments.” Therefore, the analysis of elastic stress fields overlap (Dijkstra and Ten Bolscher [85]) has only indirect relation to ligament yielding. However, “the validity” of the Hobbs et al. and Wu hypotheses is “disputable” (any hypothesis is disputable), but not because “the physical explanation” of ligament yielding “in terms of stress field overlap must be questioned” (see Borggrave et al. [50]). Despite the above critical remark, the last work confirms the Wu criterion for nylon-rubber blends and Van der Wal et al. [86] for PP-rubber blends. The Wu criterion is at least recognized as a starting point for the analysis of brittle–ductile transition in rubber modified thermoplastics.

At the same time, the brittle–ductile transition cannot be explained exclusively by geometric parameters. The rubber particle concentration and size, similar to the Hobbs et al. and Wu criteria can be used to formulate, since there are numerous experiments showing that other factors can greatly affect the transition, particularly, the adhesion of rubber particles to a paternal polymer (see, for example, Pukanszky et al. [53] and Chiang et al. [54]).

6.7 Percolation Model

The percolation model of the brittle–ductile transition was proposed by Margolina and Wu [79] to implement the Wu idea that this transition is a connectivity problem [78]. This also allows expressing the criterion [77, 78] in rigorous terms of the theory of percolation. The work [79] reads: “There is a distribution of thick $(\tau >{\tau }_{c})$ and thin $(\tau <{\tau }_{c})$ matrix ligaments. During fracture, thin ligaments may yield, while thick ones may not. However, if a thick ligament is surrounded by thin ligaments, the yielding of thin ligaments could also relieve the dilative stress and cause the thick ligament to yield. When yielding propagates and pervades over the entire deformation zone, a tough behavior is obtained. Thus, we may formulate the propagation of yielding process as the percolation, i.e., connectivity, of thin ligaments. At the percolation threshold (i.e., the formation of first percolation path), many thick ligaments may not be surrounded by sufficient numbers of thin ligaments, and so cannot yield. In this case, crazing will be favored over yielding, and brittle behavior will be observed. For tough behavior to occur, therefore, a certain level of connectivity of thin ligaments must be attained. This is an important feature of the toughness problem. The exact level of connectivity required is not known at this time. However, the connectivity is known to increase rapidly beyond the percolation threshold. Thus, the onset of tough behavior will be only slightly different from the first-path percolation threshold. In other words, the onset of observed tough behavior may not exactly coincide with the first-path percolation threshold. There is a small difference between the two, which arises from the mechanical nature of the fracture process. Thus, we propose that the onset of brittle–ductile transition occurs near the percolation threshold of thin ligaments. If, on the other hand, the percolation of thin ligaments cannot occur, fracture will proceed mainly by crazing, resulting in brittle behavior”.

It is considered the equal-sized rubber particles occupying a random lattice. The lattice sites can be linked with bonds to form tetrahedrons such that each tetrahedron contains no other sites and all percolation model tetrahedrons fill the space without overlap. Each bonds have length $L=d+\tau$ (see Fig. 51). The matrix ligaments fill the whole matrix space, and each matrix ligament is associated with one and only one lattice bond. The thickness of a matrix ligament $\tau$ is a part of the bond length between the surfaces of two neighboring rubber particles.

Tough behavior occurs when thin ligaments are interconnected, allowing the yielding to propagate and pervade over the entire matrix in the deformation zone. This corresponds to the phenomenon of bond percolation in the random lattice, which is shown to be equivalent to the continuum percolation of spheres. As in customary use, the percolation threshold refers to as the onset of the first-path connectivity, which is slightly below the actual onset of tough behavior.

Further, the notion of the effective spherical particle in the random lattice is introduced (the authors refer to the effective particle as the spherical “stress volumes”). Each effective particle centers at the corresponding rubber particle and has the diameter of $S=d+{\tau }_{c}$ (Fig. 57). Two neighboring effective particles are considered connected if they overlap, i.e., $L<S$. The overlap of rubber (physical) particles is not allowed, $L>d$. Continuum percolation of the effective particles will occur when their concentration, $\varphi =\left(\pi /6\right){\left(S/L\right)}^{3}$, reaches its critical value, $\varphi ={\varphi }_{c}$. This condition can be written in the form

$$\varphi =\phi {\left(S/d\right)}^{3}>{\varphi }_{c}$$

(26)

where the $\phi$ is the rubber phase concentration as before. At higher rubber concentrations, the effective particles tend to overlap. The percolation threshold ${\varphi }_{c}$ was found as a function of the ratio of $S/d$ by means of numerical simulations at a given value of the critical ligament thickness ${\tau }_{c}$.

The percolation model was applied to analyze the impact strength of nylon-66-rubber blends. The curve of brittle–ductile threshold ${\varphi }_{c}$ as a function of $S/d$ for the considered system proves to be similar to the theoretical percolation threshold curve for the equal-sized spheres.

To make sure that the brittle–ductile transition is a percolation phenomenon, the scaling law above the percolation threshold ${\varphi }_{c}$ was confirmed:

$$G={G}_{0}{\left(\varphi -{\varphi }_{c}\right)}^{g}$$

(27)

where $G$ is the toughness, ${G}_{0}$ a constant, and $g$ the critical exponent. It was proved that the considered data indeed obey the scaling law with $g=0.45\pm 0.06$. This value of the critical exponent is for the brittle–ductile transition, and it may be termed as critical “mechanical” exponent. This value is practically equal to the critical “geometric” exponent, $g\approx 0.44$, found for the classical percolation in three-dimensional case.

The publication [79] provoked a polemic letter by Gaymans and Dijkstra [87] followed by an explanatory reply of the authors [88]. To our knowledge, during the past years, the percolation model of brittle–ductile transition in polymers has been discussed only by Jiang et al. [89,90,91]. However, these works are lacking in any new ideas and are full of groundless speculations. Meanwhile, the incorporation of the percolation ideology into the theory of brittle–ductile transition appears to be a promising and productive way for further investigations.

7 Effect of Rubber Particle Content and Size of Brittle–Ductile Transition

7.1 Impact Strength-Temperature Curves

In terms of the competition between the brittle stress and yield stress, there is a temperature or rather a narrow temperature interval where the brittle mode of fracture behavior is transformed into the ductile one (Fig. 58). This transition is manifested itself as a sharp increase in the notched impact strength with temperature. Since rubber particles produce a shift in fracture behavior towards ductility, the transition temperature is expected to decrease with rubber content. It is more difficult to predict the dependence of transition temperature on particle size. Figure 59 shows the effect of rubber particles on the notched Izod impact strength of modified nylon-6 (Borggrave et al. [50]). This figure shows that smaller particles shift the brittle–ductile transition to lower temperatures. Moreover, the impact energy in the brittle region is higher when the particle diameter is smaller. Figure 60 exhibits the effect of an average diameter of rubber particles on the transition temperature of nylon-6 and rubber blends [92]. Accordingly, the transition temperature increases with the average particle size. Comprehensive data about the notched Izod impact strength of rubber-modified PPs as a function of temperature are reported in Van der Wal et al. [69, 70, 86, 93, 94]. As Fig. 61 [86] represents, the impact strength-temperature curve is strongly affected by both the rubber particle concentration and size. The curves have an S-shape, and with increasing rubber content and decreasing particle size, the curves shift to lower temperatures. The sharp increase in the impact strength is typical for the impact behavior of these blends. At the onset of this increase, the fracture changes from brittle to ductile during crack propagation [94, 95]. In the brittle region, hardly any deformation can be observed, while ductile fractured samples exhibit massive stress whitening and deformation of the material next to the fracture plane.

7.2 Dependent of Transition Temperature on Particle Content and Size

Owing to a significant scatter of impact strength measurements, data processing may affect the results obtained from observations. The treatment and interpretation of the experimental data [86] and, consequently, some conclusions proposed further in this, and next Sections differ to a certain extent from those by Van der Wal et al. [86].

The data about PP-EPR blends shown in Fig. 61 can be presented in the form of ${T}_{bd}-d$ curves at constant rubber contents, $\phi$=0.05, 0.10, and 0.20, as Fig. 62 depicts. Here ${T}_{bd}$ is the temperature of brittle–ductile transition, and $d$ the weight average particle diameter. The dependence of transition temperature ${T}_{bd}$ on rubber content $\phi$ is obtained as cross-sections of the ${T}_{bd}-d$ curves at constant particle sizes (Fig. 63). The link between the critical values of rubber content, ${\phi }_{c}$, and particle diameter, ${d}_{c}$, i.e., between those values of $\phi$ and $d$, at which the brittle–ductile transition occurs at a particular temperature, is found as a cross-section of the ${T}_{bd}-d$ curves at a constant temperature (Fig. 64).

Using Fig. 63 and Eq. (22) rewritten in the form

$${\tau }_{c}={d}_{c}\left[k{\left(\pi /6{\phi }_{c}\right)}^\frac{1}{3}-1\right]$$

(28)

the ${\tau }_{c}-{\phi }_{c}$ curves are constructed at temperatures 30, 40, 50, and 60 °C for various lattices, $k=1$, $k={2}^{1/3}$, and $k={4}^{1/3}$ (Fig. 65). From this figures it is clearly seen that the ${\tau }_{c}$ behavior at $k=1$ qualitatively differs from those at $k={2}^{1/3}$, and $k={4}^{1/3}$: in the first case, the critical ligament thickness, ${\tau }_{c}$, can be considered as a random function of rubber content, ${\phi }_{c}$, with a constant mean value, whereas in two other cases ${\tau }_{c}$ tends to grow with ${\phi }_{c}$. This confirms the Wu conclusion [78] that the thickness of matrix ligament entering his criterion should be evaluated for the simple cubic particle packing. Figure 65a also allows the assumption that the point $({d}_{c},{\phi }_{c})$, which characterizes the rubber phase geometry at the brittle–ductile transition, correlates with a certain constant, ${\tau }_{c}$, connected with coordinates ${d}_{c}$ and ${\phi }_{c}$ by Eq. (28). Such a correlation can just be considered as the confirmation of the validity of the Wu criterion [77, 78]. The results of Borggrave et al. [50] for nylon blends also support this criterion.

Cross sections of the ${\tau }_{c}-{\phi }_{c}$ curves of Fig. 65a at constant rubber contents, ${\phi }_{c}$=0.05, 0.10, and 0.20, are shown in Fig. 66. If the brittle–ductile transition had exactly obeyed the Wu criterion, then at a particular temperature, the value of ${\tau }_{c}$ would have been a constant, i.e., independent of ${\phi }_{c}$. Considering the fact that condition ${\tau }_{c}$=const. at a particular temperature is merely an approximation and there is a great scatter of experimental data, it would be unrealistic to expect the ${T}_{bd}-{\tau }_{c}$ curves of Fig. 66 to merge into one curve. Therefore, the discrepancies between the ${T}_{bd}-{\tau }_{c}$ curves for different temperatures are not sufficient reasons to disprove the Wu criterion. Meanwhile, Van der Wal et al. [86] write with reference to the figure similar to Fig. 66: “If all data points fall on one line one can say that ${T}_{bd}$ and ID (i.e., ${\tau }_{c}$) correlate. The 5% and 20% rubber data do not fall on one line and the 10% data are in-between. Thus the ${T}_{bd}$ as measured by the notched Izod for these blends cannot be described with an ID parameter”.

As was predicted in [77], the critical value of ligament thickness, being independent of rubber content and particle size, changes with material properties and experiment conditions, i.e., with temperature and strain rate. The dependence of ${\tau }_{c}$, determined as an averaged value over the range of rubber content from 0.05 to 0.20, on temperature is given by Fig. 67. For comparison, similar dependence for nylon blends is shown in Fig. 68 (Borggrave et al. [50]).

The matrix ligament thickness criterion, as stated above, focuses attention on two parameters of rubber-modified polymers, particle content and size, in a way that accurately reflects the geometric aspect of the brittle–ductile transition in ductile thermoplastics such as nylon and PP blends. However, it bypasses all other factors affecting the phenomenon, and for this reason, cannot provide—and is not intended to—any complete solution to the problem as a whole [96].

Recently, Lendvai [97] has also demonstrated that the smaller rubber particles show improved ductility of the rubber-toughened PP. He used the fast evaporation mixing technique based on the water-assisted melt mixing (WA) methods to improve the dispersion of particles, where the additives are introduced as an aqueous suspension, not the dry particles, and blow-up of water evaporation thereafter [98, 99]. Figure 69 shows morphologies of natural rubber (NR) particles of 10 wt% NR samples. The low molecular weight (LMW) and high molecular weight (HMW) PP was used for the matrix. The number-average and weight-average particle diameters are denoted by D_n and D_w, respectively. The interparticle distance (IPD) was determined by Eq. (22) where k = 1, and the interfacial area per unit volume (A_i) was determined based on [100]. It can be clearly seen that the fast evaporation mixing (-L) shows a smaller particle size and IPT and larger A_i than the conventional dry method (-D). The larger strain arises at the break on the tensile test (Fig. 70), and impact strength (Fig. 71) for the evaporation mixing samples. The evaporation mixing method was also shown to be more efficient for lower molecular weight PP [97]. Deblieck et al. [101] investigated the impact behavior at the low temperature range of the rubber-toughened PP with the various strain rate based on the Van der Sanden, Meijer, and Tervoort (VMT) model. The critical IPD could be estimated even in the low temperature range. Chang et al. suggested that the nano-fibrillated EPDM inclusions could dramatically enhance the toughening performance, through the additional energy dissipation mechanism [102]. Also, to improve the toughness of the PP-rubber blend at the low temperature further, the tertiary blend with the ethylene-co-octene (EOC) was suggested [103]. It was also revealed that the impact resistance could be significantly improved for tertiary blend (PP/PA6/EPDM), due to the reduced particle size [104]. The core–shell structures for generated in this ternary blend results in the increased toughness [105]. The compatibilizers between the rubbery phase and PP matrix also could enhance the performance of such blends [106]. It was also showed that the small amount of carbon nanotube (CNT), e.g., 2 wt%, could increase the impact strength even at the lower rubber content [107].

8 Conclusions

This article aims to provide a comprehensive understanding of the toughening mechanism in rubber-modified PP. The extensive utilization of polypropylene-rubber blends in various industries is primarily attributed to their improved impact resistance and expanded application range compared to neat PP. Consequently, the DB transition behavior in PP-rubber blends has been extensively investigated for several decades. This article provides a summary of the fracture mechanisms observed in homogeneous PP and explores the impact modifications achieved by incorporating rubber particles, along with their associated toughening mechanisms. It is firmly believed that this review will offer valuable insights for developing advanced lightweight materials based on PP-like thermoplastics. Here is the summary of what is covered in this article.

The overview of the criteria distinguishing between ductile and brittle fractures in homogeneous PP demonstrates that the transition between deformation modes, specifically crazing and yielding, is influenced by temperature and strain rate. Brittle fractures tend to occur at high strain rates and low temperatures, whereas ductile fractures are predominant at low strain rates and high temperatures. Additionally, this article comprehensively addresses the transition in damage morphology from yielding to crazing.

The discussion then delves into the phenomenon of crazing in thermoplastics and the conditions necessary for craze formation. The constitutive equation for craze formation is introduced, and recent molecular dynamic (MD) simulations pertaining to craze formation are reviewed, offering insights into the process of craze formation, growth, and final fracture. Furthermore, the effect of notches on the DB transition is considered.

Subsequently, the article focuses on the influence of rubber modification on the DB transition of PP. The addition of rubber particles to PP generally reduces its yield stress while significantly enhancing ductility and impact resistance. The energy release mechanism resulting from delamination, cavitation, and micro-damages in the rubbery phase, coupled with altering the stress state near rubber particles, contributes to additional energy dissipation and, consequently, the toughening of PP-based materials. Therefore, the modulus of the rubbery phase must be significantly lower than that of the matrix phase, with a modulus ratio of matrix to rubber greater than 10 for effective toughening.

Finally, the article provides a detailed discussion of the effect of rubber particle size and content on the DB transition. Experimental results demonstrate that increasing rubber content reduces the DB transition temperature, thereby enhancing material ductility. Additionally, smaller particle sizes improve material ductility and lower the transition temperature. In other words, both rubber content and size exert an influence on the DB transition behavior. The critical matrix ligament thickness criterion is utilized to analyze this combined effect, and master curves for the DB transition temperature are developed for PP-based and nylon-based blends. The article also reviews a recent method capable of directly controlling rubber morphology, encompassing size and interparticle distance.

Data availability

Data will be made available on request.

References

Jang, B. Z., Uhlmann, D. R., & Sande, J. B. V. (1984). Ductile–brittle transition in polymers. Journal of Applied Polymer Science, 29, 3409–3420.
Google Scholar
Jang, B. Z., Uhlmann, D. R., & Sande, J. B. V. (1985). The rubber particle size dependence of crazing in polypropylene. Polymer Engineering and Science, 25, 643–651.
Google Scholar
Ramsteiner, F. (1979). Structural changes during the deformation of thermoplastics in relation to impact resistance. Polymer, 20, 839–842.
Google Scholar
Dasari, A., & Misra, R. D. K. (2003). On the strain rate sensitivity of high density polyethylene and polypropylenes. Materials Science and Engineering: A, 358, 356–371.
Google Scholar
Dasari, A., Rohrmann, J., & Misra, R. D. K. (2003). Microstructural evolution during tensile deformation of polypropylenes. Materials Science and Engineering: A, 351, 200–213.
Google Scholar
Vincent, P. I. (1960). The tough-brittle transition in thermoplastics. Polymer, 1, 425–444.
Google Scholar
Vincent, P. I. (1964). Yield stress and brittle strength. Plastics, 29, 79.
Google Scholar
Ward, I. M., & Sweeney, J. (2012). Mechanical properties of solid polymers (3rd ed.). London: Wiley.
Google Scholar
An, J., Kim, C., Choi, B.-H., & Lee, J.-M. (2014). Characterization of acrylonitrile–butadiene–styrene (ABS) copolymer blends with foreign polymers using fracture mechanism maps. Polymer Engineering and Science, 54, 2791–2798.
Google Scholar
Ludwik, P. (1927). Die Bedeutung des Gleit- und Reißwiderstandes für die Werkstoffprüfung. Z. des Verein. deutscher Ingenieure, 71, 1532–1538.
Davidenkov, N. N., & Wittman, F. (1937). Physical Technical Institute (USSR), 4, 300.
Google Scholar
Orowan, E. (1949). Fracture and strength of solids. Reports on Progress in Physics, 12, 185–232.
Google Scholar
Vincent, P. I. (1961). The effect of temperature. Plastics, 26, 141–143.
Google Scholar
Matsushige, K., Radcliffe, S. V., & Baer, E. (1976). The pressure and temperature effects on brittle-to-ductile transition in PS and PMMA. Journal of Applied Polymer Science, 20, 1853–1866.
Google Scholar
Robertson, R. E. (1963). On the cold-drawing of plastics. Journal of Applied Polymer Science, 7, 443–450.
Google Scholar
Roetling, J. A. (1965). Yield stress behaviour of poly(ethyl methacrylate) in the glass transition region. Polymer, 6, 615–619.
Google Scholar
Roetling, J. A. (1966). Yield stress behaviour of isotactic polypropylene. Polymer, 7, 303–306.
Google Scholar
Lazurkin, J. S. (1958). Cold-drawing of glass-like and crystalline polymers. Journal of Polymer Science, 30, 595–604.
Google Scholar
Wu, T., Cao, Y., Yang, F., & Xiang, M. (2014). Investigation on double yielding behavior under tensile loading in isotactic polypropylene. Materials and Design, 60, 153–163.
Google Scholar
Ding, L., Wu, T., Yang, F., & Xiang, M. (2017). Deformation and pore formation mechanism under tensile loading in isotactic polypropylene. Polymer International, 66, 1129–1140.
Google Scholar
Ree, T., & Eyring, H. (1955). Theory of Non-Newtonian flow. I. Solid plastic system. Journal of Applied Physics, 26, 793–800.
Google Scholar
van Breemen, L. C. A., Engels, T. A. P., Klompen, E. T. J., Senden, D. J. A., & Govaert, L. E. (2012). Rate- and temperature-dependent strain softening in solid polymers. Journal of Polymer Science Part B: Polymer Physics, 50, 1757–1771.
Google Scholar
Klompen, E. T. J., Engels, T. A. P., Govaert, L. E., & Meijer, H. E. H. (2005). Modeling of the postyield response of glassy polymers: Influence of thermomechanical history. Macromolecules, 38, 6997–7008.
Google Scholar
van Breemen, L. C. A., Klompen, E. T. J., Govaert, L. E., & Meijer, H. E. H. (2011). Extending the EGP constitutive model for polymer glasses to multiple relaxation times. Journal of the Mechanics and Physics of Solids, 59, 2191–2207.
Google Scholar
Merz, E. H., Claver, G. C., & Baer, M. (1956). Studies on heterogeneous polymeric systems. Journal of Polymer Science, 22, 325–341.
Google Scholar
Hsiao, C. C., & Sauer, J. A. (1950). On crazing of linear high polymers. Journal of Applied Physics, 21, 1071–1083.
Google Scholar
Sauer, J. A., Marin, J., & Hsiao, C. C. (1949). Creep and damping properties of polystyrene. Journal of Applied Physics, 20, 507–517.
Google Scholar
Dijkstra, P. T. S., Van Dijk, D. J., & Huétink, J. (2002). A microscopy study of the transition from yielding to crazing in polypropylene. Polymer Engineering and Science, 42, 152–160.
Google Scholar
Pawlak, A., & Galeski, A. (2008). Cavitation during tensile deformation of polypropylene. Macromolecules, 41, 2839–2851.
Google Scholar
Bucknall, C. (1967). The relationship between the structure and mechanical properties of rubber-modified thermoplastics. British Plastics, 40, 118–122.
Google Scholar
Kambour, R. P. (1965). Report no. 65RL 3982C.
Choi, B. H., Chudnovsky, A., & Pham, H. (2011). Observation and modeling of the tensile behavior of rubber toughened polypropylene. In 69th annual technical conference of the society of plastics engineers 2011, ANTEC 2011 (pp. 1077–82). Boston, MA, USA.
Kambour, R. P. (1964). Structure and properties of crazes in polycarbonate and other glassy polymers. Polymer, 5, 143–155.
Google Scholar
Sternstein, S. S., Ongchin, L., & Silverman, A. (1968). Inhomogeneous deformation and yielding of glasslike high polymers. Applied Polymer Symposia, 7, 175.
Google Scholar
Oxborough, R. J., & Bowden, P. B. (1973). A general critical-strain criterion for crazing in amorphous glassy polymers. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 28, 547–559.
Google Scholar
Argon, A. S., & Hannoosh, J. G. (1977). Initiation of crazes in polystyrene. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 36, 1195–1216.
Google Scholar
Argon, A. S., & Salama, M. M. (1977). Growth of crazes in glassy polymers. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 36, 1217–1234.
Google Scholar
Bucknall, C. B. (2007). New criterion for craze initiation. Polymer, 48, 1030–1041.
Google Scholar
Venkatesan, S., & Basu, S. (2015). Investigations into crazing in glassy amorphous polymers through molecular dynamics simulations. Journal of the Mechanics and Physics of Solids, 77, 123–145.
MathSciNet Google Scholar
Rottler, J., & Robbins, M. O. (2003). Growth, microstructure, and failure of crazes in glassy polymers. Physical Review E, 68, 011801.
Google Scholar
Mahajan, D. K., Singh, B., & Basu, S. (2010). Void nucleation and disentanglement in glassy amorphous polymers. Physical Review E, 82, 011803.
Google Scholar
Rice, J. R., & Johnson, M. A. (1970). The role of large crack tip geometry changes in plane strain fracture. Inelastic Behaviour of Solids, 1970, 641–672.
Google Scholar
van der Wal, A., Mulder, J. J., Thijs, H. A., & Gaymans, R. J. (1998). Fracture of polypropylene: 1. The effect of molecular weight and temperature at low and high test speed. Polymer, 39, 5467–5475.
Google Scholar
Gearing, B. P., & Anand, L. (2004). Notch-sensitive fracture of polycarbonate. International Journal of Solids and Structures, 41, 827–845.
Google Scholar
Anand, L., & Gurtin, M. E. (2003). A theory of amorphous solids undergoing large deformations, with application to polymeric glasses. International Journal of Solids and Structures, 40, 1465–1487.
Google Scholar
Praveen, K. M., Taleb, K., Pillin, I., Kervoelen, A., Grohens, Y., Thomas, S., et al. (2022). Comparative mechanical, morphological, rheological, and thermal properties of polypropylene/ethylene-propylene-diene rubber blends. Polymers for Advanced Technologies, 33, 3296–3311.
Google Scholar
Mohamad, N., Zainol, N. S., Rahim, F. F., Maulod, H. E. A., Rahim, T. A., Shamsuri, S. R., et al. (2013). Mechanical and morphological properties of polypropylene/epoxidized natural rubber blends at various mixing ratio. Procedia Engineering, 68, 439–445.
Google Scholar
Du, H., Zhang, Y., Liu, H., Liu, K., Jin, M., Li, X., et al. (2014). Influence of phase morphology and crystalline structure on the toughness of rubber-toughened isotatic polypropylene blends. Polymer, 55, 5001–5012.
Google Scholar
Fasihi, M., & Mansouri, H. (2016). Effect of rubber interparticle distance distribution on toughening behavior of thermoplastic polyolefin elastomer toughened polypropylene. Journal of Applied Polymer Science, 133, 1.
Google Scholar
Borggreve, R. J. M., Gaymans, R. J., Schuijer, J., & Housz, J. F. I. (1987). Brittle-tough transition in nylon-rubber blends: Effect of rubber concentration and particle size. Polymer, 28, 1489–1496.
Google Scholar
Muratoglu, O. K., Argon, A. S., Cohen, R. E., & Weinberg, M. (1995). Toughening mechanism of rubber-modified polyamides. Polymer, 36, 921–930.
Google Scholar
Bagheri, R., & Pearson, R. A. (1996). Role of particle cavitation in rubber-toughened epoxies: 1. Microvoid toughening. Polymer, 37, 4529–4538.
Google Scholar
Pukánszky, B., Tüdös, F., Kalló, A., & Bodor, G. (1989). Multiple morphology in polypropylene/ethylene-propylene-diene terpolymer blends. Polymer, 30, 1399–1406.
Google Scholar
Chiang, W.-Y., Yang, W.-D., & Pukánszky, B. (1992). Polypropylene composites. II: Structure–property relationships in two- and three-component polypropylene composites. Polymer Engineering and Science, 32, 641–648.
Google Scholar
Zebarjad, S. M., Bagheri, R., Reihani, S. M. S., & Lazzeri, A. (2003). Deformation, yield and fracture of elastomer-modified polypropylene. Journal of Applied Polymer Science, 90, 3767–3779.
Google Scholar
Bagheri, R., & Pearson, R. A. (2000). Role of particle cavitation in rubber-toughened epoxies: II. Inter-particle distance. Polymer, 41, 269–276.
Google Scholar
Wang, D., Li, F., Xu, X., Zhong, L., Guan, C., Gao, Y., et al. (2022). Brittle ductile transition of POE toughened HDPE and its lowest rigidity loss: Effect of HDPE molecular weight. Journal of Polymer Research, 29, 38.
Google Scholar
Bucknall, C. (1967). British Plastics, 40, 84.
Google Scholar
Kato, K. (1965). Electron microscopy of ABS plastics. Journal of Electron Microscopy, 14, 220–221.
Google Scholar
Turley, S. G. (1963). A dynamic mechanical study of rubber-modified polystyrenes. Journal of Polymer Science Part C: Polymer Symposia, 1, 101–116.
Google Scholar
Lundstedt, O. W., & Bevilacqua, E. M. (1957). Polystyrene-rubber blends. Journal of Polymer Science, 24, 297.
Google Scholar
Yang, J., Li, F., Guan, C., Xu, X., Zhong, L., Gao, Y., et al. (2022). Brittle–ductile transition of elastomer toughened HDPE: Effect of elastomer modulus. Journal of Polymer Research, 29, 173.
Google Scholar
Jiang, W., An, L., & Jiang, B. (2001). Brittle–tough transition in elastomer toughening thermoplastics: Effects of the elastomer stiffness. Polymer, 42, 4777–4780.
Google Scholar
Rabinovitch, E. B., Summers, J. W., & Smith, G. (2003). Impact modification of polypropylene. Journal of Vinyl and Additive Technology, 9, 90–95.
Google Scholar
Bucknall, C. B., & Smith, R. R. (1965). Stress-whitening in high-impact polystyrenes. Polymer, 6, 437–446.
Google Scholar
Grein, C., Bernreitner, K., Hauer, A., Gahleitner, M., & Neißl, W. (2003). Impact modified isotatic polypropylene with controlled rubber intrinsic viscosities: Some new aspects about morphology and fracture. Journal of Applied Polymer Science, 87, 1702–1712.
Google Scholar
Hassan, A., & Haworth, B. (2006). Impact properties of acrylate rubber-modified PVC: Influence of temperature. Journal of Materials Processing Technology, 172, 341–345.
Google Scholar
Borggreve, R. J. M., Gaymans, R. J., & Eichenwald, H. M. (1989). Impact behaviour of nylon-rubber blends: 6. Influence of structure on voiding processes; toughening mechanism. Polymer, 30, 78–83.
Google Scholar
van der Wal, A., Mulder, J. J., Oderkerk, J., & Gaymans, R. J. (1998). Polypropylene–rubber blends: 1. The effect of the matrix properties on the impact behaviour. Polymer, 39, 6781–6787.
Google Scholar
van der Wal, A., Nijhof, R., & Gaymans, R. J. (1999). Polypropylene–rubber blends: 2. The effect of the rubber content on the deformation and impact behaviour. Polymer, 40, 6031–6044.
Google Scholar
Piggott, M. R., & Leidner, J. (1974). Misconceptions about filled polymers. Journal of Applied Polymer Science, 18, 1619–1623.
Google Scholar
Kunori, T., & Geil, P. H. (1980). Morphology-property relationships in polycarbonate-based blends. II. Tensile and impact strength. Journal of Macromolecular Science, Part B, 18, 135–175.
Google Scholar
Nielsen, L. E. (1966). Simple theory of stress–strain properties of filled polymers. Journal of Applied Polymer Science, 10, 97–103.
Google Scholar
Sahu, S., & Broutman, L. J. (1972). Mechanical properties of particulate composites. Polymer Engineering and Science, 12, 91–100.
Google Scholar
Gupta, A. K., & Purwar, S. N. (1984). Tensile yield behavior of PP/SEBS blends. Journal of Applied Polymer Science, 29, 3513–3531.
Google Scholar
Hobbs, S. Y., Bopp, R. C., & Watkins, V. H. (1983). Toughened nylon resins. Polymer Engineering and Science, 23, 380–389.
Google Scholar
Wu, S. (1985). Phase structure and adhesion in polymer blends: A criterion for rubber toughening. Polymer, 26, 1855–1863.
Google Scholar
Wu, S. (1988). A generalized criterion for rubber toughening: The critical matrix ligament thickness. Journal of Applied Polymer Science, 35, 549–561.
Google Scholar
Margolina, A., & Wu, S. (1988). Percolation model for brittle-tough transition in nylon/rubber blends. Polymer, 29, 2170–2173.
Google Scholar
Gilbert, D. G., & Donald, A. M. (1986). Toughening mechanisms in high impact polystyrene. Journal of Materials Science, 21, 1819–1823.
Google Scholar
Liu, Z. H., Zhang, X. D., Zhu, X. G., Qi, Z. N., & Wang, F. S. (1997). Effect of morphology on the brittle ductile transition of polymer blends: 1. A new equation for correlating morphological parameters. Polymer, 38, 5267–5273.
Google Scholar
Liu, Z. H., Li, R. K. Y., Tjong, S. C., Qi, Z. N., Wang, F. S., & Choy, C. L. (1998). Influence of particle dispersion on the matrix ligament thickness of polymer blends. 1. The configuration of well-dispersed particles versus simple cubic lattice. Polymer, 39, 4433–4436.
Google Scholar
Liu, Z. H., Li, R. K. Y., Tjong, S. C., Choy, C. L., Zhu, X. G., Qi, Z. N., et al. (1999). Influence of particle dispersion on the matrix ligament thickness of polymer blends: 2. A generalized equation and particle spatial distributions for different morphologies. Polymer, 40, 2903–2915.
Google Scholar
Liu, Z., Zhu, X., Wu, L., Li, Y., Qi, Z., Choy, C., et al. (2001). Effects of interfacial adhesion on the rubber toughening of poly(vinyl chloride) Part 1. Impact tests. Polymer, 42, 737–746.
Google Scholar
Dijkstra, K., & Ten Bolscher, G. H. (1994). Nylon-6/rubber blends. Journal of Materials Science, 29, 4286–4293.
Google Scholar
van der Wal, A., Verheul, A. J. J., & Gaymans, R. J. (1999). Polypropylene–rubber blends: 4. The effect of the rubber particle size on the fracture behaviour at low and high test speed. Polymer, 40, 6057–6065.
Google Scholar
Gaymans, R. J., & Dijkstra, K. (1990). Comments on ‘Percolation model for brittle-tough transition in nylon/rubber blends.’ Polymer, 31, 971.
Google Scholar
Wu, S., & Margolina, A. (1990). Reply to comments on percolation model for brittle-tough transition in nylon/rubber blends. Polymer, 31, 972–974.
Google Scholar
Jiang, W., Liang, H., & Jiang, B. (1998). Interparticle distance-temperature-strain rate equivalence for the brittle-tough transition in polymer blends. Polymer, 39, 4437–4442.
Google Scholar
Jiang, W., Tjong, S. C., & Li, R. K. Y. (2000). Brittle–tough transition in PP/EPDM blends: Effects of interparticle distance and tensile deformation speed. Polymer, 41, 3479–3482.
Google Scholar
Jiang, W., An, L.-J., & Jiang, B.-Z. (2003). Brittle–ductile transition of polymers and its percolation model. Chinese Journal of Polymer Science, 21, 129–133.
Google Scholar
Okada, O., Keskkula, H., & Paul, D. R. (2000). Fracture toughness of nylon 6 blends with maleated ethylene/propylene rubbers. Polymer, 41, 8061–8074.
Google Scholar
van der Wal, A., & Gaymans, R. J. (1999). Polypropylene–rubber blends: 3. The effect of the test speed on the fracture behaviour. Polymer, 40, 6045–6055.
Google Scholar
van der Wal, A., & Gaymans, R. J. (1999). Polypropylene–rubber blends: 5. Deformation mechanism during fracture. Polymer, 40, 6067–6075.
Google Scholar
Kotter, I., Grellmann, W., Koch, T., & Seidler, S. (2006). Morphology–toughness correlation of polypropylene/ethylene–propylene rubber blends. Journal of Applied Polymer Science, 100, 3364–3371.
Google Scholar
Zhao, C., Wu, G., Zhou, C., Yang, H., & Zhang, H. (2006). Independence of the brittle–ductile transition from the rubber particle size for impact-modified poly(vinyl chloride). Journal of Polymer Science Part B: Polymer Physics, 44, 696–702.
Google Scholar
Lendvai, L. (2021). A novel preparation method of polypropylene/natural rubber blends with improved toughness. Polymer International, 70, 298–307.
Google Scholar
Karger-Kocsis, J., Kmetty, Á., Lendvai, L., Drakopoulos, S. X., & Bárány, T. (2015). Water-assisted production of thermoplastic nanocomposites: A review. Materials, 2015, 72–95.
Google Scholar
Gao, W., & Guo, J. (2017). A novel processing method namely fast evaporation mixing to prepare fluoroelastomer/montmorillonite composites. Composites Science and Technology, 139, 26–35.
Google Scholar
Francis, B., Thomas, S., Asari, G. V., Ramaswamy, R., Jose, S., & Rao, V. L. (2006). Synthesis of hydroxyl-terminated poly(ether ether ketone) with pendent tert-butyl groups and its use as a toughener for epoxy resins. Journal of Polymer Science Part B: Polymer Physics, 44, 541–556.
Google Scholar
Deblieck, R., Remerie, K., Van den Fonteyne, W., & Boerakker, M. (2021). A morphology-based model to describe the low-temperature impact behaviour of rubber-toughened polypropylene. Polymers, 13, 1.
Google Scholar
Chang, E., Zhao, J., Zhao, C., Li, G., Lee, P. C., & Park, C. B. (2022). Scalable production of crosslinked rubber nanofibre networks as highly efficient toughening agent for isotactic polypropylene: Toughening mechanism of non-traditional anisotropic rubber inclusion. Chemical Engineering Journal, 438, 134060.
Google Scholar
Kim, D.-K., Lee, S. H., Hong, S.-K., Han, S. W., Lee, D. H., & Yu, S. (2022). Low-temperature-toughened polypropylene blends with highly packed elastomeric domains. ACS Applied Polymer Materials, 4, 7834–7840.
Google Scholar
Hasanpour, M., Mazidi, M. M., & Aghjeh, M. K. R. (2019). The effect of rubber functionality on the phase morphology, mechanical performance and toughening mechanisms of highly toughened PP/PA6/EPDM ternary blends. Polymer Testing, 79, 106018.
Google Scholar
Mazidi, M. M., Razavi Aghjeh, M. K., Khonakdar, H. A., & Reuter, U. (2016). Structure–property relationships in super-toughened polypropylene-based ternary blends of core–shell morphology. RSC Advances, 6, 1508–1526.
Google Scholar
Mahendra, I. P., Wirjosentono, B., Tamrin, Ismail, H., Mendez, J. A., & Causin, V. (2019). The influence of maleic anhydride-grafted polymers as compatibilizer on the properties of polypropylene and cyclic natural rubber blends. Journal of Polymer Research, 26, 215.
Google Scholar
Yang, C.-J., Huang, T., Yang, J.-H., Zhang, N., Wang, Y., & Zhou, Z.-W. (2017). Carbon nanotubes induced brittle–ductile transition behavior of the polypropylene/ethylene-propylene-diene terpolymer blends. Composites Science and Technology, 139, 109–116.
Google Scholar

Download references

Acknowledgements

This research was supported by the Ministry of Trade, Industry and Energy (MOTIE), Korea Institute for Advancement of Technology (KIAT) through the Virtual Engineering Platform Program (P0022334). It was also supported by a Korea University fund. The authors would like to extend their special thanks to the late Dr. Yuri Shulkin.

Author information

Authors and Affiliations

Department of Mechanical System Engineering, Kumoh National Institute of Technology, 61 Daehak-ro, Gumi, Gyeongbuk, 39177, Republic of Korea
Jung-Wook Wee
Department of Civil and Materials Engineering, University of Illinois at Chicago, 842W. Taylor St., Chicago, IL, 60607, USA
Alexander Chudnovsky
School of Mechanical Engineering, College of Engineering, Korea University, 145 Anam-ro, Seongbuk-gu, Seoul, 02841, Republic of Korea
Byoung-Ho Choi

Authors

Jung-Wook Wee
View author publications
You can also search for this author in PubMed Google Scholar
Alexander Chudnovsky
View author publications
You can also search for this author in PubMed Google Scholar
Byoung-Ho Choi
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

J-WW: Conceptualization, methodology, formal analysis, investigation, data curation, writing—original draft preparation, visualization. AC: Conceptualization, resources, methodology. B-HC: Conceptualization, methodology, investigation, resources, writing—review and editing, investigation, supervision, project administration.

Corresponding author

Correspondence to Byoung-Ho Choi.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This paper is an invited paper (Invited Review).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Cite this article

Wee, JW., Chudnovsky, A. & Choi, BH. Brittle–Ductile Transitions of Rubber Toughened Polypropylene Blends: A Review. Int. J. of Precis. Eng. and Manuf.-Green Tech. 11, 1361–1402 (2024). https://doi.org/10.1007/s40684-023-00581-w

Download citation

Received: 27 June 2023
Revised: 22 October 2023
Accepted: 24 October 2023
Published: 19 November 2023
Issue Date: July 2024
DOI: https://doi.org/10.1007/s40684-023-00581-w

Keywords

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Brittle–Ductile Transitions of Rubber Toughened Polypropylene Blends: A Review

Abstract

Similar content being viewed by others

Polypropylene/polyolefin elastomer composites with enhanced impact strength: the effect of rubber domain size on toughness

Specimen Geometry Effect on the Deformation Mechanisms of Polypropylene-Based Composites Under Impact Loading at Different Temperatures

Brittle-ductile transition of impact PP blends: effect of modulus ratio of PP matrix to impact modifier

Explore related subjects

1 Introduction

2 Mechanisms of Fracture Behavior

2.1 Engineering Stress–Strain Curves

2.2 Fracture Mechanisms and Energy Dissipation

3 Brittle Stress and Yield Stress

3.1 Definition and Measurements

3.2 Brittle Stress and Yield Stress as Function of Temperature and Strain Rate

3.3 Crazing-to-Yielding Transition

3.4 Diagrams of Yield Stress Versus Strain Rate at Various Temperatures

4 Crazing and Yield Governed by Crazing: Shear Bands of Crazed Material

4.1 Crazing of Thermoplastics

4.2 Conditions of craze formation

4.3 Yield Governed by Crazing

4.4 Shear Banding of Crazed Material

5 Notch Sensitivity

6 Rubber Modified Polymers: Criteria of Brittle–Ductile Transition

6.1 Toughness by Rubber Phase

6.2 Polymer Phase

6.3 Brittle-to-Crazing Transition

6.4 Brittle-to-Yield Transition

6.5 Criterion of Center-to-Center Interparticle Distance

6.6 Criterion of Surface-to-Surface Interparticle Distance (Or Matrix Ligament Thickness)

6.7 Percolation Model

7 Effect of Rubber Particle Content and Size of Brittle–Ductile Transition

7.1 Impact Strength-Temperature Curves

7.2 Dependent of Transition Temperature on Particle Content and Size

8 Conclusions

Data availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Conflict of interest

Additional information

Publisher's Note

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation