1 Introduction

Contact manifolds arise naturally as convex boundaries of symplectic manifolds, it was known by Gromov [15] and Eliashberg [10] in the late 1980s that not all contact manifolds can be realized in such a way. Therefore understanding symplectic fillings of contact manifolds is a fundamental question in contact topology. Such questions were extensively studied by many researchers starting from the case of no fillings [7,8,9, 11, 12, 14, 24, 31], the case of unique (only for the topological type in many cases) fillings [5, 9, 13, 15, 25, 30, 32], and at the end of this spectrum, the case of infinitely many filings [2,3,4, 6, 27, 28]. As one can always blow up a symplectic filling to change the topology, we need to restrict to Liouville or Weinstein fillings for the question of infinite fillings. Unlike the no-filling and unique-filling situations, which typically depend on some rigidity arguments using pseudo-holomorphic curves, the construction of contact manifolds with infinitely many fillings usually uses the topological or flexible side of symplectic topology. The first contact manifold (beyond the trivial case of \(S^1\)) with infinitely many different Weinstein fillings was constructed by Ozbagci and Stipsicz [28] in dimension 3. Nowadays, there are many constructions with various constraints on the topology of fillings in dimension 3, see [2,3,4, 6]. Oba [27] generalized Ozbagci and Stipsicz’s result to dimension \(4n-1.\) Their constructions were based on the open book construction of contact manifolds and finding infinitely many different factorizations by positive Dehn–Seidel twists of the monodromy in the symplectic mapping class group. Such an approach is most efficient in dimension 3, as the symplectic mapping class group agrees with the classical mapping class group in the case of surfaces. In higher dimensions, the symplectic mapping class group is different from the classical mapping class group in general, and much less is known. It is worth pointing out that Lazarev [19] constructed contact manifolds with many different Weinstein fillings in dimension \(\ge 5,\) where the number of fillings can be arbitrarily large, from a surgical perspective.

In this note, we give a new construction of contact manifolds with infinitely many different Weinstein fillings in any dimension. The construction is based on spinal open books—a generalization of contact open books, introduced by Lisi et al. [20]. The spinal open book was used by Baykur et al. [6] to construct contact 3-manifolds which admit infinitely many Weinstein fillings with arbitrarily big Euler characteristics and arbitrarily small signatures. Heuristically speaking, spinal open books arise as the contact boundary of a Lefschetz fibration over a general surface with boundary. Such contact manifolds, especially in dimension 4, were studied systematically in [20, 21, 23]. Moreover, there are notions of spinal open books, which fiber over Liouville domains of dimension higher than 2, see e.g. [22, 26]. In this note, we restrict to the case of the surface base.

Theorem 1.1

Let V be the plumbing of two \(T^*S^n\) along three points. Then the contact boundary \(\partial (\Sigma _{1,1} \times V)\) has infinitely many different Weinstein fillings, where \(\Sigma _{1,1}\) is a genus one Riemann surface with one boundary component,  viewed as a Weinstein filling of \(S^1.\)

We point out that our construction is local in nature, i.e. if V contains the domain in Theorem 1.1 as a symplectic subdomain and the homology computation in the proof works, then the conclusion can be drawn for \(\partial (\Sigma _{1,1} \times V).\) For example, it holds for V in Theorem 1.1 taking boundary connected sum with any Weinstein domain. Moreover, similar phenomena hold for more general plumbings of spheres. When n is odd, i.e. when the contact manifold is of dimension \(4k-1,\) we can take V to be two \(T^*S^n\) plumbed at one point.

Our strategy is similar to [27, 28]: the contact boundary \(\partial (\Sigma _{1.1} \times V)\) is the trivial spinal open book over \(\Sigma _{1,1},\) and any representation \(\rho :\pi _1(\Sigma _{1,1})\rightarrow \pi _0({\textrm{Symp}}_c(V))\) such that \(\rho (\partial \Sigma _{1,1}) = {{\,\textrm{id}\,}}\) gives rise to a Weinstein filling by a V-fiber bundle over \(\Sigma _{1,1}.\) Sending a generator of \(\pi _1(\Sigma _{1,1})\) to the identity always yields one such representation, hence every element \(\phi \) of \(\pi _0({\textrm{Symp}}_c(V)),\) i.e. the image of the other generator under \(\rho ,\) induces a filling. Then by understanding the effect of \(\phi \) on the homology of V,  we can get infinite many fillings. In particular, we do not need to consider factorizations in the symplectic mapping class group.

Theorem 1.1 still uses classical topological invariants to differ symplectic fillings, a natural question is whether the phenomena of infinite fillings can be purely symplectic, that is:

Question 1.2

Are there contact manifolds with infinitely many different Weinstein/Liouville fillings with the same formal data,  i.e. as the same differential/almost complex/almost Weinstein manifold (relative to the boundary)?

We expect the answer to the question to be yes, at least for dimensions high enough. However, to the best of the author’s knowledge, we do not even know examples of contact manifolds with more than one smoothly same, but symplectically different fillings. Unlike Theorem 1.1, rigidity techniques, e.g. holomorphic curves or sheaves, must enter the picture to solve the above question. Using spinal open books, we have candidates for Question 1.2 at least for in dimension \(4n+1.\)

Question 1.3

Let \(\phi \in \pi _0({\textrm{Symp}}_c(V))\) be generated by the eighth powers of the Dehn–Seidel twist along any Lagrangian sphere in V,  where \(\dim V = 4n.\) Is the symplectic fiber bundle induced from \(\pi _1(\Sigma _{1,1})\rightarrow \pi _0{\textrm{Symp}}_c(V)\) by sending one generator to \(\phi \) and the other to \({{\,\textrm{id}\,}}\) symplectomorphic to \(\Sigma _{1,1}\times V?\)

Clearly, the motivation behind such a question is the fact that eighth powers of the Dehn–Seidel twist are smoothly isotopic to identity in dimension 4n [17], yet not symplectically isotopic to identity [5, 29]. In dimensions 4 and 12, one can replace the eighth power with a square.

2 Proof

Let V be a Liouville domain and \(\phi \in \pi _0({\textrm{Symp}}_c(V)).\) We can endow

$$\begin{aligned} \Sigma _{g,1}\times \partial V \cup _{S^1\times \partial V} V_{\phi } \end{aligned}$$

a contact structure by a generalization of the Thurston–Winkelnkemper construction, see [20, §2.3], where \(\Sigma _{g,1}\) is a genus g surface with one boundary component and \(V_{\phi }\) is the mapping torus \(V\times [0,1]/ (x,0)\sim (\phi (x),1).\) This is a very special case of the spinal open book considered in [20], where the vertebrae (\(\Sigma _{g,1}\) here) can have more boundary components and be disconnected. In this paper, we only consider the case of \(g=1\) and \(\phi ={{\,\textrm{id}\,}}.\) Then the contact manifold is the contact boundary \(\partial (\Sigma _{1,1}\times V).\)

Lemma 2.1

[6, 20] Let \(\Sigma \) be a connected Riemann surface with boundary and V be a Weinstein domain. Any representation \(\pi _1(\Sigma ) \rightarrow \pi _0({\textrm{Symp}}_c(V))\) mapping the boundary to \({{\,\textrm{id}\,}}\) gives rise to a Weinstein filling of \(\partial (\Sigma \times V),\) which is diffeomorphic to the V-bundle over \(\Sigma \) from \(\pi _1(\Sigma ) \rightarrow \pi _0({\textrm{Symp}}_c(V)).\)

More generally, if the monodromy of the spinal open book is \(\phi \) and there exist \(\phi _1,\psi _1,\ldots , \phi _{g}, \psi _{g}\in {\textrm{Symp}}_c(V)\) and \(\tau _1,\ldots ,\tau _k\) are Dehn–Seidel twists along some exact Lagrangian spheres in V,  such that

$$\begin{aligned} \phi = \prod \tau _i \prod [\phi _{i},\psi _{i}]. \end{aligned}$$

Then the spinal open book given by \((\Sigma _{g,1},V,\phi )\) is the contact boundary of a symplectic Lefschetz fibration over \(\Sigma _{g,1}\) with k singular fibers. When V is Weinstein, the total space of the Lefschetz fibration is a Weinstein filling of the spinal open book.

Lemma 2.2

Let \(V_{\phi }\) be the mapping torus,  then we have short exact sequences

$$\begin{aligned} 0\rightarrow \ker ( \phi _*-{{\,\textrm{id}\,}}) \rightarrow H_*(V_{\phi }) \rightarrow {{\,\textrm{coker}\,}}(\phi _*-{{\,\textrm{id}\,}})[-1] \rightarrow 0. \end{aligned}$$

Proof

The homology of \(V_{\phi }\) can be computed from the cone of \(C_*(V){\mathop {\longrightarrow }\limits ^{\phi _*-{{\,\textrm{id}\,}}}} C_*(V).\) We have an induced long exact sequence

$$\begin{aligned} \ldots \longrightarrow H_*(V)\longrightarrow H_*(V_{\phi }) \longrightarrow H_{*-1}(V){\mathop {\longrightarrow }\limits ^{\phi _*-{{\,\textrm{id}\,}}}} H_{*-1}(V)\longrightarrow \ldots \end{aligned}$$

see [16, Example 2.48] for details. Then the claimed short exact sequence follows from the exactness of the above sequence. \(\square \)

More generally, let \(V_{\phi \vee {{\,\textrm{id}\,}}}\) be the V-fiber bundle over \(S^1\vee S^1\) (or homotopically equivalently over \(\Sigma _{1,1}\)), such that the monodromy over one \(S^1\) is \(\phi \) and is \({{\,\textrm{id}\,}}\) over the other \(S^1.\) Then we have a short exact sequence

$$\begin{aligned} 0\rightarrow & {} \ker (\phi _*-{{\,\textrm{id}\,}})|_{H_k(V;{{\mathbb {Z}}})} \rightarrow H_k(V_{\phi \vee {{\,\textrm{id}\,}}};{{\mathbb {Z}}}) \\\rightarrow & {} H_{k-1}(V;{{\mathbb {Z}}}) \oplus {{\,\textrm{coker}\,}}( \phi _*-{{\,\textrm{id}\,}})|_{H_{k-1}(V;{{\mathbb {Z}}})}\rightarrow 0 \end{aligned}$$

for \(k\ge 1.\) In particular, when V is a Weinstein domain of dimension 2n,  then the cardinality of the torsion of \(H_{n+1}(V_{\phi \vee {{\,\textrm{id}\,}}})\) will be at least that of \({{\,\textrm{coker}\,}}( \phi _*-{{\,\textrm{id}\,}})|_{H_{n}(V;{{\mathbb {Z}}})}.\)

Lemma 2.3

(Picard–Lefschetz formula, [18, (6.3.3)]) Let L be an oriented Lagrangian n-sphere in an exact domain W and \(\tau _L\) the Dehn–Seidel twist along L, Footnote 1 then \((\tau _L)_*:H_*(W;{{\mathbb {Z}}})\rightarrow H_*(W;{{\mathbb {Z}}})\) is given by

$$\begin{aligned} (\tau _L)_*(c) = \left\{ \begin{array}{ll} c+(-1)^{\frac{(n+1)(n+2)}{2}}\langle \,c,[L] \,\rangle [L], &{}\quad c\in H_n(W;{{\mathbb {Z}}}); \\ c, &{}\quad c\in H_j(W;{{\mathbb {Z}}}), j\ne n. \end{array}\right. \end{aligned}$$

where \(\langle \,\cdot , \cdot \,\rangle :H_n(W;{{\mathbb {Z}}})\otimes H_n(W;{{\mathbb {Z}}})\rightarrow {{\mathbb {Z}}}\) is the intersection product.

Recall the plumbing of two cotangent bundles \(T^*Q_1\) and \(T^*Q_2\) at one point is given by choosing balls \(B_i\) around the plumbing point in \(Q_i,\) and identifying their disc cotangent bundles \(D^*B_i \subset D^*Q_i\) by a symplectomorphism which interchanges the zero-section and fiber directions. We refer readers to [1, §2.3] for details of the plumbing construction. Let \(V^{2n}\) be plumbing of two \(T^*S^n\) along three points. We use \(L_1, L_2\) to denote the two Lagrangian spheres, oriented such that \(\langle \,[L_1],[L_2] \,\rangle = (-1)^{\frac{n(n+1)}{2}}3.\) More precisely, we first choose an orientation of \(L_1,\) then we orient \(L_2\) by the induced orientation of the fiber \(T^*_qL_1,\) where q is an intersection point, since the fiber is identified with a neighborhood of q in \(L_2\) in the plumbing construction. Then the intersection number of \(L_1,L_2\) using the orientation on \(T^*L_1\) induced from the orientation of \(L_1\) is 3. The extra sign comes from the fact that the symplectic orientation (using \(-\textrm{d}\sum p_i\textrm{d}q_i,\) i.e. the standard symplectic orientation on \({\mathbb {R}}^{2n}=T^*{\mathbb {R}}^n\)) is different from the induced orientation on \(T^*L_1\) from that of \(L_1\) by \((-1)^{\frac{n(n+1)}{2}}.\) Note that \(\langle \,[L_1],[L_1] \,\rangle = \langle \,[L_2],[L_2] \,\rangle =0\) when n is odd and \(\langle \,[L_1],[L_1] \,\rangle = \langle \,[L_2],[L_2] \,\rangle =(-1)^{\frac{n(n+1)}{2}}2\) when n is even. When \(n>1,\) under the free basis \([L_1], [L_2]\) of \(H_{n}(V^{2n};{{\mathbb {Z}}}),\) by the Picard–Lefschetz formula, the effect of the Dehn–Seidel twists \(\tau _{L_1},\tau _{L_2}\) on \(H_n(V^{2n};{{\mathbb {Z}}})\) is given by

$$\begin{aligned} \left[ \begin{array}{cc} 1 &{} -3 \\ 0 &{} 1 \end{array}\right] , \left[ \begin{array}{cc} 1 &{} 0\\ 3 &{} 1 \end{array}\right] \end{aligned}$$

for n odd respectively, and

$$\begin{aligned} \left[ \begin{array}{cc} -1 &{} -3 \\ 0 &{} 1 \end{array}\right] , \left[ \begin{array}{cc} 1 &{} 0 \\ -3 &{} -1 \end{array}\right] \end{aligned}$$

for n even respectively.

When \(n=1,\) \(H_{1}(V;{{\mathbb {Z}}})={{\mathbb {Z}}}^4\) and \((\tau _{L_1})_*,\) using the basis \([L_1],[L_2]\) and two other cycles (with suitable orientation) glued from two arcs from \(L_1,L_2,\) is given by

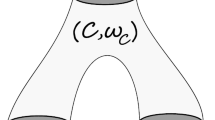
$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} -3 &{} -1 &{} -1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$
(2.1)

To see this, the Lagrangian skeleton of the plumbing is sketched below, where the dashed blue line is the part of \(L_2\) that goes under \(L_1.\) The extra middle crossing of the projection is necessary as the intersection points between \(L_1,L_2\) have the same orientation (Fig. 1).

Fig. 1
figure 1

The Lagrangian skeleton and homology basis

Full size image

The two green loops are the other two free generators of \(H_1(V;{{\mathbb {Z}}}),\) whose intersection numbers with \(L_1\) are \(\pm 1\) from the middle intersection point of the green solid line with \(L_1.\) It is clear that we can choose orientations of those two green loops to form a basis of \(H_1(V;{{\mathbb {Z}}})\) such that \((\tau _{L_1})_*\) on \(H_1(V;{{\mathbb {Z}}})\) is (2.1).

Proof of Theorem 1.1

Let \(\gamma _1,\gamma _2\) be two loops in \(\Sigma _{1,1},\) representing the bases of the fundamental group in the torus. We consider the representation \(\rho :\pi _1(\Sigma _{1,1})\rightarrow \pi _0({\textrm{Symp}}_c(V)), \gamma _1\mapsto \phi , \gamma _2\mapsto {{\,\textrm{id}\,}}.\) By Lemma 2.1, it gives rise to a filling of \(\partial (\Sigma _{1,1}\times V),\) which is homotopically equivalent to \(V_{\phi \vee {{\,\textrm{id}\,}}}.\)

When \(n>1\) is odd, we take \(\phi \) to be \(\tau _{L_1}.\) Since \(\phi _*^k\) on \(H_n(V;{{\mathbb {Z}}})\) is given by

$$\begin{aligned} \left[ \begin{array}{cc} 1 &{} -3k \\ 0 &{} 1 \end{array}\right] . \end{aligned}$$

Then by the discussion after Lemma 2.2, we know that \(H_{n+1}(V_{\phi ^k\vee {{\,\textrm{id}\,}}};{{\mathbb {Z}}})\) has a torsion of \({{\mathbb {Z}}}/3k.\) As a consequence, each k yields a different Weinstein filling.

When \(n=1,\) we take \(\phi \) to be \(\tau _{L_1}.\) Then \(\phi _*^k\) on \(H_n(V;{{\mathbb {Z}}})\) is given by

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} -3k &{} -k &{} -k\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

We know that \(H_{2}(V_{\phi ^k\vee {{\,\textrm{id}\,}}};{{\mathbb {Z}}})\) has a torsion of \({{\mathbb {Z}}}/k.\) As a consequence, each k yields a different Weinstein filling.

When n is even, we take \(\phi \) to be \(\tau _{L_1}\circ \tau _{L_2}.\) Then \(\phi _*\) on \(H_n(V;{{\mathbb {Z}}})\) is given by

$$\begin{aligned} \left[ \begin{array}{cc} 8 &{} 3 \\ -3 &{} -1 \end{array}\right] . \end{aligned}$$

This matrix has positive eigenvalues \(\lambda _1 = \frac{7+3\sqrt{5}}{2}>1, \lambda _2=\frac{7-3\sqrt{5}}{2}<1.\) As a consequence, we have

$$\begin{aligned} |\det ((\phi _*)^k-{{\,\textrm{id}\,}})|=|2-\lambda _1^k-\lambda _2^k|, \end{aligned}$$

which grows exponentially. The torsion of \(H_{n+1}(V_{\phi ^k\vee {{\,\textrm{id}\,}}})\) is of size \(|2-\lambda _1^k-\lambda _2^k|,\) which yields infinitely many different fillings as before. \(\square \)

When n is odd, we can simply take V to be the plumbing of two \(T^*S^n\) at one point. Then \(\tau ^k_{L_1}\) acts on \(H_n(V;{{\mathbb {Z}}})\) by

$$\begin{aligned} \left[ \begin{array}{cc} 1 &{} -k \\ 0 &{} 1 \end{array}\right] \end{aligned}$$

which yields infinitely many fillings.