Geodesic complexity of a cube

Abstract

The topological (resp. geodesic) complexity of a topological (resp. metric) space is roughly the smallest number of continuous rules required to choose paths (resp. shortest paths) between any points of the space. We prove that the geodesic complexity of a 3-dimensional cube exceeds its topological complexity by exactly 2. The proof involves a careful analysis of cut loci of the cube.

1 Introduction

In [6], Farber introduced the concept of the topological complexity, ${\text {TC}}(X)$, of a topological space X, which is the minimal number k, such that there is a partition

$$\begin{aligned} X\times X=E_1\sqcup \cdots \sqcup E_k \end{aligned}$$

with each $E_i$ being locally compact and admitting a continuous function $\phi _i:E_i\rightarrow P(X)$, such that $\phi _i(x_0,x_1)$ is a path from $x_0$ to $x_1$. Here, P(X) is the space of paths in X with the compact-open topology, and each $\phi _i$ is called a motion-planning rule. If X is the space of configurations of one or more robots, this models the number of continuous rules required to program the robots to move between any two configurations.

Recio-Mitter [8] suggested that if X is a metric space, then we require that the paths $\phi _i(x_0,x_1)$ be minimal geodesics (shortest paths) from $x_0$ to $x_1$, and defined the geodesic complexity, ${\text {GC}}(X)$, to be the smallest number k, such that there is a partition

$$\begin{aligned} X\times X= E_1\sqcup \cdots \sqcup E_k \end{aligned}$$

with each $E_i$ being locally compact and admitting a continuous function $\phi _i:E_i\rightarrow P(X)$, such that $\phi _i(x_0,x_1)$ is a minimal geodesic from $x_0$ to $x_1$.¹ Each function $\phi _i$ is called a geodesic motion-planning rule (GMPR).

One example discussed by Recio-Mitter [8] was when X is (the surface of) a cube. It is well known that here ${\text {TC}}(X)={\text {TC}}(S^2)=3$, and he showed that ${\text {GC}}(X)\ge 4$. In this paper, we prove that in this case, ${\text {GC}}(X)=5$.

Theorem 1.1

If X is a cube, then ${\text {GC}}(X)=5$.

For comparison, in [3], the author proved that for a regular tetrahedron T, ${\text {GC}}(T)=4$ or 5, but was not able to establish the precise value. Here again, ${\text {TC}}(T)={\text {TC}}(S^2)=3$.

Our work relies heavily on the work of the author and Guo [4], where they analyzed the isomorphism classes of cut loci on the cube as labeled graphs. In Sect. 2, we review the relevant parts of that work. In Sect. 3, we prove that ${\text {GC}}(X)\le 5$ by constructing five explicit geodesic motion-planning rules. In Sect. 4, we prove ${\text {GC}}(X)\ge 5$, using methods similar to those used in [3, 8].

2 Background on cut loci of a cube

In this section, we present background material, mostly from [4], regarding cut loci for a cube. The distance, d(P, Q), between points on the cube is the Euclidean distance for points on the same face, while for any points, it is $\min (\sum _{i=0}^{n-1} d(P_i,P_{i+1}))$, over all sequences with $P_0=P$, $P_n=Q$, and $P_i$ and $P_{i+1}$ in the same face.

The cut locus of a point P on a polyhedron, denoted $L_P$, is the closure of the set of points Q, such that there is more than one shortest path (minimal geodesic) from P to Q. The cut locus is a labeled graph with corner points of the polyhedron labeling the leaves ([9, Corollary of Lemma 4.4]). It is possible that a degree-2 vertex of the graph might also be labeled by a corner point. Two labeled graphs are isomorphic if there is a graph bijection between them preserving labels. We let $\textbf{L}$ denote the isomorphism class of a cut locus.

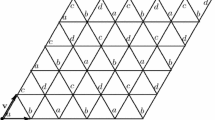
Figure 1, from [4], shows the partition of a face of a cube into 193 connected subsets with constant $\textbf{L}$. Figure 2, also from [4], is a reparametrized version of the regions in the left quadrant of Fig. 1.

Fig. 1

Decomposition of a face into subsets on which ${\textbf {L}}$ is constant

Fig. 2

Regions in left quadrant of Fig. 1

In [4], we listed, in stylized form, the $\textbf{L}$ for the various regions, but here, as we are interested in continuity of motion-planning rules, we are concerned about other aspects, such as the placement of edges of the cut locus with respect to one another.

The cut loci are found by the method of star unfolding and Voronoi diagrams, as developed in [1, 7]. We will use the same numbering of the corner points of the cube as was used in [4] and appears in Fig. 3, also taken from [4], which, for future reference, includes an example of the cut locus of the midpoint of edge 5–8.

Fig. 3

A cube with labeled corner points, and the cut locus for the middle point of an edge highlighted

In [4], we explain how the diagram on the right side of Fig. 4 is obtained, depicting in bold red the cut locus of the point P in the left side of Fig. 4. The numbers at half of the vertices of the polygon correspond to the corner points in Fig. 3, and the labels $P_1,\ldots ,P_8$ at the other vertices are different positions of the point P in an unfolding of the cube. Every point of the cube occurs exactly once inside or on the 16-gon in Fig. 4, except that some occur on two boundary segments, and P occurs eight times. Note that the boundary segments of the polygon in Fig. 4 are straight line segments from P to corner points of the cube.

Fig. 4

Voronoi cells and cut locus of P

For example, the region in the right side of the 16-gon in Fig. 4 bounded above and below by the segments coming in from the vertices labeled 6 and 7, on the right by $P_5$, and on the left by the short vertical segment I is all the points that are closer to the $P_5$ version of point P than to the others. This is called the Voronoi cell of $P_5$. The segment I is equally close to versions $P_1$ and $P_5$. There are two equal minimal geodesics from P to points on I; one crosses the segment connecting corner points 1 and 4, while the other crosses the segment connecting 6 and 7.

It is proved in [5] that the top and bottom halves of cut loci of the cube can be considered separately. Although all the regions in Fig. 2 have distinct $\textbf{L}$, some have isomorphic top halves. For example, as can be seen in [4, Figure 2.2], regions F, E, I, C, and H all have isomorphic top halves. We combine these here into a single region, which we will call F. Note the different font. Similarly, regions D, B, and I$'$ in Fig. 2 have the same top half of $\textbf{L}$ and are combined into a single region, D. Also, D$'$ and E$'$ combine to form $D'$, F$'$ and G$'$ combine to $F'$, and A, G, and H$'$ combine into A. This simplifies Fig. 2 into our schematic Fig. 5, which only concerns top halves of $\textbf{L}$. We will discuss bottom halves later in this section.

Fig. 5

Regions with same top half of $\textbf{L}$

There are also curves DF, FA, $DD'$, $D'F'$, and $F'A$ bounding these combined regions. There is also $*$, the intersection point of five curves, and the left edge $\mathcal {E}$, connecting corner points 8 and 5. In Fig. 6, we depict the top half of the cut loci for these regions, with arrows indicating convergence of points in a region to points in its boundary, in each of which an edge of the graph is collapsed.

Fig. 6

Top halves of cut loci

The bottom half of the cut locus of a point (x, y) in a region R in Fig. 2 is obtained from the top half of the cut locus of the vertical reflection $(x,-y)$ of the point, which is in reflected region R$'$, by inverting it and applying the permutation $(1\ 4)(2\ 3)(5\ 8)(6\ 7)$ to the labels. The collecting of several regions of Fig. 2 into a single region with the same bottom half of $\textbf{L}$ is essentially a vertical reflection of what was done in forming Fig. 5 for top halves. For example, the vertical reflection of the region $D'$ of Fig. 5 contains regions D and E of Fig. 2, and its cut locus bottom is as in Fig. 7, which is obtained by inverting the upper left diagram in Fig. 6 and applying the above permutation.

Fig. 7

Cut-locus bottom of reflection of region $D'$ of Fig. 5

Each region in the top quadrant of Fig. 1 is obtained from the corresponding region in the left quadrant by a clockwise rotation of $\pi /2$ around the center of the square. The cut locus of the new region is obtained from that of the old one by applying the permutation $(1\ 4\ 3\ 2)(5\ 8\ 7\ 6)$ to the labels and then rotating the resulting figure $\pi /2$ counter-clockwise. In Fig. 8, we show the cut locus of points in region A, in the rotated region A$_R$, and in the half-diagonal separating them.

Fig. 8

Cut locus of rotation of region

In [4], we were only concerned about isomorphism type as a graph, but here we care about the relative positions of the labeled arms.

3 Geodesic motion-planning rules

In this section, we construct five geodesic motion-planning rules for the cube. The remainder of this section is devoted to the proof of the following result.

Theorem 3.1

If X is the cube, then $X\times X$ can be partitioned into five locally compact subsets $E_i$ with a GMPR $\phi _i$ on each.

3.1 The set $E_1$

We define $E_1$ to be the set of pairs (P, Q), such that there is a unique minimal geodesic from P to Q, and let $\phi _1(P,Q)$ be that path. It is well known ([2, Chapter 1, 3.12 Lemma]) that such a function is continuous. Note that a corner point V at a leaf of the cut-locus graph of a point P is not in the cut locus, so these (P, V) are in $E_1$.

3.2 The set $E_2$

We define the multiplicity of (P, Q) (or of just Q if P is implicit) to be the number of distinct minimal geodesics from P to Q. If Q is in the interior of an edge (resp. is a vertex) of the cut-locus graph of P, then the multiplicity of (P, Q) equals 2 (resp. the degree of the vertex).

We define $E_2$ to be the set of all (P, Q) of multiplicity 2. The points Q will be interiors of edges of the cut-locus graph or occasionally a degree-2 vertex, such as vertex 2 in the cut locus of $\mathcal {E}$ in Fig. 6. The function $\phi _2$ is defined below using an orientation of the cube, i.e., a continuous choice of direction of rotation around each point.

The cut loci of points in a quadrant are a tree consisting of two parts connected by a segment parallel to the edge of the quadrant. See, for example, the cut loci of points in regions A and A$_R$ pictured in Fig. 8. For a three-dimensional example, see Fig. 3. See Sections 5 and 6 of [5], which contains more detail than [4], for a proof. For points P on the diagonals separating quadrants, the connecting “segment” in $L_P$ consists of a single point. See the middle diagram in Fig. 8.

Think of rotating the cut locus around the center of the connecting segment in the direction given by the orientation. If Q is not on the connecting segment, we define $\phi _2(P,Q)$ to be the geodesic from P to Q which approaches Q in the direction of the rotation. We will deal with the connecting segments shortly.

In Figs. 9 and 10, we add to Figs. 8 and 6 red dots on the edges of several cut loci indicating the side from which Q should be approached if the orientation is clockwise.

Fig. 9

Direction for $\phi _2$ for some cut loci

Fig. 10

Direction for $\phi _2$ in some top halves

Regarding the connecting segments, note that each edge of the cube bounds two quadrants, and all $L_P$ for P in those two quadrants have parallel connecting segments. For each quadrant pair, arbitrarily make a uniform choice of a side of these segments. Let $\phi _2(P,Q)$ for Q in those connecting segments be the minimal geodesic from P to Q which approaches Q from the selected side. Because the quadrants are bounded by diagonals in which the connecting points of cut loci halves are vertices of degree 4 and so are not part of $E_2$, compatibility of the GMPRs for connecting segments in distinct quadrant-pairs is not an issue.

We now discuss the continuity of $\phi _2$. For P within a region of constant $\textbf{L}$, the vertices $v_i$ of its cut locus $L_P$ vary continuously with P, as they are intersections of perpendicular bisectors of corresponding segments $P_\alpha P_\beta$, where $P_\alpha$ and $P_\beta$ vary linearly with P (see [4, (3.3)]). The edges in the cut-locus graph are segments connecting two of these vertices $v_i$ and $v_j$, and hence, if $Q_t$ denotes a point $tv_i+(1-t)v_j$ for $0<t<1$, then $Q_t$ varies continuously with P. The orientation of the cube determines the same side of the segment for all P in the region, and then, $\phi _2(P,Q_t)$ will be linear paths between continuously varying points in continuously varying Voronoi cells. For example, in Fig. 4, which corresponds to a point in region A of Fig. 2, let $Q_t$ be the point a fraction t along the edge extending to the left from the point labeled 6, which is corner point 6 of the cube. Then, if the orientation of the cube is clockwise around the midpoint of segment I, $\phi _2(P,Q_t)$ would be the linear path from $P_4$ to $Q_t$, while if it is counter-clockwise, it would be from $P_5$ to $Q_t$. (Recall that all the $P_\alpha$ are different versions of the point P.) Since $Q_t$ varies continuously with P, $\phi _2$ is continuous on each subset of $E_2$ of the form

$$\begin{aligned} \{(P,Q): P\text { lies in a region of constant }\textbf{L},\ Q\text { on an open edge of }L_P\}. \end{aligned}$$

For Q in the interior of a connecting edge of $L_P$, $\phi _2(P,Q)$, defined in the preceding paragraph, did not involve the orientation, but its continuity is clear from the ideas in this paragraph.

Suppose points P in an open region of constant $\textbf{L}$ approach a curve bounding the region, such as points in region A in Fig. 8 approaching a point $P_0$ in the half-diagonal in that figure. The Voronoi diagram, such as Fig. 4, of points P will approach the Voronoi diagram of $P_0$. For example, the segment I in Fig. 4 collapses to a point, and the segment to the left of point 6 approaches the horizontal segment connecting 6 and 2. The paths $\phi _2(P,Q_t)$, for $Q_t$ on this limiting segment, will still be linear paths from $P_4$ or $P_5$, depending on the selected orientation of the cube. Thus, the continuity of $\phi _2$ extends from the open regions to their closures.

The cut locus of a corner point consists of the three edges and three diagonals emanating from the opposite corner point. Although continuous variation of $L_P$ with P is not quite true when P is a corner point, we show that our defining $\phi _2$ on $E_2$ using rotation around a central point is still continuous at the corner point. In Fig. 11, we depict the cut loci of corner point $V_8$ and of points P close to $V_8$ along the 5–8 edge, along the curve DE in Fig. 2, and along the diagonal, adorned with red dots indicating the direction from which the side should be approached using $\phi _2$. As we will explain, DE is supposed to be illustrative of all points between the edge and diagonal near $V_8$.

Fig. 11

Cut locus of a corner point and of points near it

The points $(V_8,Q)$ which are in $E_2$ are those for which Q lies in the interior of the six segments in the $V_8$ diagram in Fig. 11. Continuity of $\phi _2$ at these points follows similarly to that at other points as discussed earlier in this subsection. Limits of points (P, Q) in $E_2$ with P approaching $V_8$ and Q on the edge of $L_P$ emanating from vertex 8 will not have $(V_8,Q)$ in $E_2$, and hence, continuity at the limit point is not an issue.

For all points P on the 5–8 edge, excluding its endpoints, points Q on the edge from vertex 8 to vertex 3 are part of $L_P$. However, these points Q are not in $L_{V_8}$, and so, $(V_8,Q)$ is in $E_1$. A similar situation holds for P in the diagonal of face 5678, where $L_P$ is pictured on the right side of Fig. 11, and the edge from vertex 8 to vertex 4 is not in $L_{V_8}$.

As P moves from the 5–8 edge toward the diagonal, the end point of the cut-locus edge from vertex 8 moves along the cut-locus segment emanating from vertex 3 until it meets the end point of the cut locus segment emanating from vertex 4. In the DE diagram, it is just shy of this meeting. Then, it moves along the cut-locus segment emanating from vertex 4 until it reaches vertex 4 when P is on the diagonal.

As these P approach $V_8$, the limit of this portion of $L_P$ is on a segment from $V_8$ to a point on edge 3–4 followed by a segment down to $V_2$. All such limiting points $(V_8,Q)$ are in $E_1$.

3.3 The set $E_3$

The set $E_3$ consists of 56 points (P, Q), such that Q is a vertex of the cut locus of P of degree 5 or 6. Since this is a discrete set, the function $\phi _3$ can be defined arbitrarily. Eight of these points have P a corner point of the cube and Q the opposite corner point. The cut locus of a corner point was depicted in the left side of Fig. 11.

Another point in $E_3$ has P equal to the point $*$, which was introduced in Fig. 5. The top half of its cut locus is shown in Fig. 6; we show its entire cut locus in Fig. 12.

Fig. 12

Cut locus of $*$

For $P=*$ and Q the indicated degree-5 vertex, we place (P, Q) in $E_3$. The vertical reflection $*'$ of $*$ has cut locus a reindexed vertical reflection of Fig. 12, and we place $(*',Q')$, where $Q'$ is its degree-5 vertex, in $E_3$. Each quadrant has two analogous points in $E_3$. There are 24 quadrants, so 48 such points altogether.

3.4 The sets $E_4$ and $E_5$

Two more sets, $E_4$ and $E_5$, are required for (P, Q) with Q a vertex of degree 3 or 4 of the cut locus of P. In Fig. 13, we depict this for Q in the top half of cut loci of points P in the left quadrant of the 5678 face. Because the degree-5 vertex in the cut locus of $*$ has been placed in $E_3$, we need not worry about continuity as $*$ is approached.

Fig. 13

Approach to vertices of cut loci

We place in $E_4$ all (P, Q) in which Q can be approached from the 2–5 region, and depict them by solid disks. For example, comparing the diagram labeled A in Fig. 13 with Fig. 4 shows how our schematic $\textbf{L}$ correspond to actual cut loci. The three degree-3 vertices in A in Fig. 13 correspond to three vertices in Fig. 4 which are very close together. The segments coming from vertices 1 and 5 meet at a point just to the left of the top of segment I. The paths $\phi _4(P,Q)$ for Q any of these three vertices are the segments from $P_3$ in Fig. 4. The “2–5 region” means the region between the segments of either of these diagrams emanating from vertices 2 and 5. The black dots in Fig. 13 indicate that for these vertices Q of the cut locus, $\phi _4(P,Q)$ is the path from $P_3$ in Fig. 4, the path passing between vertices 2 and 5. In Sect. 3.2, we showed that the points Q vary continuously with P, implying continuity of $\phi _4$.

In $E_5$, we place those (P, Q) not in $E_4$ which can be approached from the 2–6 region, and depict them by open circles. In Diagram A in Fig. 13, the rightmost degree-3 vertex can be approached from the 2–6 region, but has already been placed in $E_4$. In Diagram $F'$ in Fig. 13, the intersection points have changed and now, the end of the segment from 6 can no longer be approached from $P_3$ in the analogue of Fig. 4, so we choose to approach it from $P_4$, the 2–6 region.

The cases, in D, F, and DF, where certain Q cannot be approached from the 2–5 or 2–6 regions are placed in $E_4$ or $E_5$ as indicated by $\bullet$ or $\circ$. For example, the point (P, Q) with Q the vertex at the end of the edge from vertex 1 in Diagram D could not have been placed in $E_5$, because they approach a $DD'$ diagram in $E_5$ whose $\phi _5$ path is impossible for them to approach. Note that the degree-2 vertex when P is on the edge $\mathcal {E}$ is in $E_2$, which was already considered. The GMPRs $\phi _4$ and $\phi _5$ choose the minimal geodesic from P to Q which approach Q from region 2–5, 2–6, or 1–5.

Each arrow in Fig. 13 represents points P in a region approaching points in its boundary. A segment in a cut locus shrinks to a point. Continuity of $\phi _4$ and $\phi _5$ follows similarly to that of $\phi _2$.

All quadrants of all faces are handled similarly, using permutations of corner-point numbers. In particular, if P is in the analogue of the large region A in any quadrant, and Q is a vertex of the top half of the cut locus of P, then (P, Q) is placed in $E_4$. For the degree-3 and degree-4 vertices Q of the cut locus of points P in the diagonals of a face (see Fig. 8), we place (P, Q) in $E_5$. Then, since A is the only region abutting the diagonal, then there is no worry about continuity of $\phi$ functions at these points, as long as we make consistent choices. The cut locus of the center of a face has four arms emanating from a central vertex, with a degree-2 vertex on each arm. In the 5678 face, it is obtained from the cut locus of the diagonal pictured in Fig. 8 by collapsing the arms from 1 and 3 to a point. We make an arbitrary choice of $\phi _5(P,Q)$ when Q is the degree-4 vertex of the cut locus of the center P of a face, and then choose $\phi _5(P,Q)$ compatibly when Q is the degree-4 vertex of the cut loci of points P on the diagonals of the face.

In the paragraph following Fig. 6, we described how bottom halves of cut loci are determined from top halves of cut loci. We put these (P, Q) with Q a vertex of degree 3 or 4 in the bottom half of the cut locus of P in sets $E_i$ with GMPRs $\phi _i$, $4\le i\le 5$, analogously to what was done for the top halves.

The cube is composed of 12 regions such as that in Fig. 14, each bounded by half-diagonals of faces, and symmetrical about an edge of the cube. For cut-locus vertices of degree 3 or 4, the GMPRs on the diagonals are in separate sets ($E_5$) from those ($E_4$) on the A-regions abutting them, and so the 12 regions can be considered separately. Once we have defined the GMPRs for P in the region containing the 5–8 edge, GMPRs on the other regions can be defined similarly, using permutations of corner-point numbers.

Fig. 14

A subset of the cube

The cut locus of a point $\widetilde{P}$ on the left half of Fig. 14 is obtained from that of its horizontal reflection by applying the permutation $(1\ 6)(4\ 7)$ and reflecting horizontally. In Fig. 15, we show top halves of cut loci for points in the reflection of the edge $\mathcal {E}$ and of the regions abutting it, together with their GMPRs for vertices of degree $\ge 3$. Note that $\mathcal {E}=\widetilde{\mathcal {E}}$, so they have the same cut loci, but the depictions of them from the star unfolding are different depending on whether they are the left or right edge.

Fig. 15

Horizontal reflection

The sets $E_i$ and functions $\phi _i$, $4\le i\le 5$, for the left side of Fig. 14 are defined like those on the primed (or unprimed) version on the right side, with 2 and 5 interchanged. Compare $\widetilde{D'}$ (resp. $\widetilde{D}$) in Fig. 15 with D (resp. $D'$) in Fig. 13. This completes the proof of Theorem 3.1.

4 Lower bound

In this section, we prove the following result, which is the lower bound in Theorem 1.1. The method is similar to that developed by Recio-Mitter [8] and applied by the author in [3].

Theorem 4.1

If X is a cube, it is impossible to partition $X\times X$ into sets $E_i$, $1\le i\le 4$, with a GMPR $\phi _i$ on $E_i$.

The proof involves many subsequences and uses the following elementary lemma.

Lemma 4.2

If a sequence $x_n$ approaches V, and for all n, there are sequences $x_{n,m}$ approaching $x_n$, then, there exist increasing sequences $n_k$ and $m_k$, such that $\lim _{k}x_{n_k,m_k}=V$, and we have $\lim _{\ell }x_{n_k,m_\ell }=x_{n_k}$.

Remark 4.3

We will abuse notation and say that in the situation of this lemma, there is a diagonal subsequence with $x_{n,n}\rightarrow V$. In cases of multiple subscripts, the limit is taken over the final subscript.

We will apply this to situations where each x is a pair (P, Q).

Proof of Theorem 4.1

Assume such a decomposition exists. Note that the specific $E_i$ of the previous section are not relevant here. Let $V_i$ be the corner point numbered i in our treatment of the cube. The cut locus of $V_8$ is as in the left side of Fig. 11. It consists of edges of the cube from $V_2$ to $V_1$, $V_3$, and $V_6$, and diagonals of a face from $V_2$ to $V_4$, $V_5$, and $V_7$.

Let $E_1$ be the set containing $(V_8,V_2)$, and suppose $\phi _1(V_8,V_2)$ is the geodesic passing between $V_3$ and $V_4$. Other cases can be handled in the same way, using a permutation of corner points.

Points P on the curve DE of Fig. 2 have top half of cut loci as in Fig. 16. (This is part of the curve DF in Fig. 5.)

Fig. 16

Top half of cut locus of points on curve DE

Let Q be the vertex of degree 4 in $L_P$, and $\alpha$, $\beta$,$\gamma$, and $\delta$ the four regions of approach to Q, as indicated in the figure. As P approaches $V_8$ along DE, Fig. 16 approaches the top half of the cut locus of $V_8$ (Fig. 11); the segment from Q to $V_2$ shrinks to the point $V_2$, and the other vertical segment collapses, too. Suppose there were a sequence of points $P_n$ on DE approaching $V_8$ with $Q_n$ the degree-4 vertex in $L_{P_n}$, as illustrated by the point Q in Fig. 16, and $(P_n,Q_n)\in E_1$. Then, $\phi _1(P_n,Q_n)$ would approach $\phi _1(V_8,V_2)$, but this is impossible, since they pass through different regions. Therefore, there must be a sequence $P_n$ on DE approaching $V_8$ for which $(P_n,Q_n)$ is in a different set, $E_2$, and restricting further, we may assume that $\phi _2(P_n,Q_n)$ all pass through the same region, $\alpha$, $\beta$, $\gamma$, or $\delta$.

Points in region D have top half of cut locus as in Fig. 17. See Fig. 6.

Fig. 17

Top half of cut locus of points P in region D

Let $Q_\alpha$ and $Q_\gamma$ be the indicated vertices in Fig. 17; i.e., $Q_\alpha$ is the point in $L_P$ where edges from $V_5$ and $V_2$ intersect, and similarly for $Q_\gamma$. If $\phi _2(P_n,Q_n)$ passes through region $\alpha$ (resp. $\gamma$) in Fig. 16, consider a sequence of points $P_{n,m}$ in region D approaching $P_n$, and let the associated cut-locus points $Q_{n,m}$ be the $Q_\alpha$ (resp. $Q_\gamma$) just defined. Such a sequence $(P_{n,m},Q_{n,m})$ cannot have a convergent subsequence in $E_2$, since, if it did, reindexing to include just the points in the subsequence, $\phi _2(P_{n,m},Q_{n,m})\rightarrow \phi _2(P_n,Q_n)$, but paths going to $Q_\alpha$ (resp. $Q_\gamma$) cannot approach a path passing through region $\alpha$ (resp. $\gamma$) in Fig. 16. Therefore, we may restrict to points $(P_{n,m},Q_{n,m})$ not in $E_2$, and restricting further, we may assume that they are in the same $E_i$ for all n and m. If $i=1$, then by Lemma 4.2 and Remark 4.3, a subsequence $(P_{n,n},Q_{n,n})$ would approach $(V_8,V_2)$ and would have $\phi _1(P_{n,n},Q_{n,n})\rightarrow \phi _1(V_8,V_2)$, which is impossible, since these paths pass through different regions. Thus, all $(P_{n,m},Q_{n,m})$ must be in either $E_3$ or $E_4$, and we may assume that they are all in $E_3$.

A similar argument works if all $\phi _2(P_n,Q_n)$ pass through region $\beta$ or $\delta$ in Fig. 16, using points $P_{n,m}$ in region E of Fig. 2 approaching $P_n$, and $Q_{n,m}$ the intersection points in $L_{P_n,m}$ illustrated by $Q_\beta$ or $Q_\delta$ in Fig. 18, which depicts the top half of the cut locus of points in region E of Fig. 2. (Region E of Fig. 2 is part of region F of Fig. 5.) Thus, we conclude that all $(P_{n,m},Q_{n,m})$ are in $E_3$, regardless of whether $\phi _2(P_n,Q_n)$ passed through $\alpha$, $\beta$, $\gamma$, or $\delta$.

Fig. 18

Top half of cut locus of points in region E

Suppose all $\phi _2(P_n,Q_n)$ pass through region $\alpha$ in Fig. 16, and $Q_{n,m}$ are the intersection points in $L_{P_{n,m}}$ corresponding to $Q_\alpha$ in Fig. 17. An argument similar to the one that we will provide works if $\alpha$ is replaced by $\beta$, $\gamma$, or $\delta$. All that matters is that the vertex $Q_\alpha$ (or its analogue) has degree 3. In Fig. 19, we isolate the relevant portion of Fig. 17, with $Q_{n,m}$ at the indicated vertex.

Fig. 19

A portion of Fig. 17, the cut locus of $P_{n,m}$

We may assume, after restricting, that all $\phi _3(P_{n,m},Q_{n,m})$ pass through the same one of the three regions in Fig. 19, which we call region R. For a sequence $Q_{n,m,\ell }$ approaching $Q_{n,m}$ on the edge not bounding R, $(P_{n,m},Q_{n,m,\ell })$ cannot have a convergent subsequence in $E_3$, since $\phi _i(P_{n,m},Q_{n,m,\ell })$ cannot pass through R. Restricting more, we may assume that all $(P_{n,m},Q_{n,m,\ell })$ are in the same $E_i$, with $i\ne 3$. If $i=2$, then, using Lemma 4.2 and Remark 4.3, a subsequence $\phi _2(P_{n,m},Q_{n,m,m})$ approaches $\phi _2(P_n,Q_n)$. Recall that as $P_{n,m}$ approaches $P_n$, the cut locus of $P_{n,m}$ depicted in Fig. 17 approaches that of $P_n$ illustrated in Fig. 16. The limit of a sequence of linear paths approaching vertex $Q_\alpha$ ($=Q_{n,m}$) in Fig. 17 cannot pass through region $\alpha$ in Fig. 16, as the former lie above the cut-locus edge emanating from $V_6$, while the latter lie below it. Therefore, $i\ne 2$. Also, i cannot equal 1, because if so, applying Lemma 4.2 and Remark 4.3 twice, $\phi _1(P_{n,n},Q_{n,n,n})\rightarrow \phi _1(V_8,V_2)$, but $\phi _1(V_8,V_2)$ passes between $V_3$ and $V_4$ in the lower half of the cut locus. Therefore, $i=4$.

We may assume, after restricting, that all the $\phi _4(P_{n,m},Q_{n,m,\ell })$ come from the same side of the edge going out from $Q_{n,m}$ in $L_{P_{n,m}}$ which contains the points $Q_{n,m,\ell }$. Choose points $Q_{n,m,\ell ,k}$ in the complement of the cut locus of $P_{n,m}$ on the opposite side of the edge converging to $Q_{n,m,\ell }$. Restricting, we may assume that all $(P_{n,m},Q_{n,m,\ell ,k})$ are in the same $E_i$. Note that $\phi _i(P_{n,m},Q_{n,m,\ell ,k})$ is the unique geodesic between these points. This i cannot equal 4, since $\phi _i(P_{n,m},Q_{n,m,\ell ,k})$ and $\phi _4(P_{n,m},Q_{n,m,\ell })$ approach the edge from opposite sides. It cannot equal 3, since $\phi _i(P_{n,m},Q_{n,m,\ell ,\ell })$ and $\phi _3(P_{n,m},Q_{n,m})$ approach the vertex in Fig. 19 from different regions. It cannot equal 2, since, applying Lemma 4.2 twice, subsequences $(P_{n,m},Q_{n,m,m,m})\rightarrow (P_n,Q_n)$, but $\phi _i(P_{n,m},Q_{n,m,m,m})$ and $\phi _2(P_{n},Q_{n})$ approach the vertex in Fig. 16 from different regions. And, it cannot equal 1, since $\phi _i(P_{n,n},Q_{n,n,n,n})$ and $\phi _1(V_8,V_2)$ approach $V_2$ from different regions. Therefore, a fifth $E_i$ is required. $\square$