Duality in convex optimization for the hyperbolic augmented Lagrangian

Abstract

We guarantee the strong duality and the existence of a saddle point of the hyperbolic augmented Lagrangian function (HALF) in convex optimization. To guarantee these results, we assume a set of convexity hypothesis and the Slater condition. Finally, we computationally illustrate our theoretical results obtained in this work.

1 Introduction

Throughout this work, we are interested in studying the following optimization problem:

$$\begin{aligned} (P) \;\;\;\;\;\;\; x^* \in X^*= argmin\{f(x)\;\vert \; x\in S \}, \end{aligned}$$

where

$$\begin{aligned} S=\{x \in {\mathbb {R}}^n \;\vert \; g_i(x) \ge 0,\;\; i=1,\ldots ,m \} \end{aligned}$$

is the convex feasible set of the problem (P), the function $f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ is convex, $g_i: {\mathbb {R}}^n \rightarrow {\mathbb {R}},\;i=1,\ldots ,m,$ is concave and we also assume that f and $g_i$ are continuously differentiable.

The augmented Lagrangian algorithms solve convex problem (P), see [11] and [12]. Recently, it was guaranteed that the hyperbolic augmented Lagrangian algorithm (HALA) also solves problem (P), see [9]. In [9], it is guaranteed that a subsequence generated by HALA converges toward a Karush–Kuhn–Tucker (KKT) point. The HALA minimizes the HALF (this minimization problem is known as the subproblem generated by the augmented Lagrangian algorithm). With the solution found in the subproblem, the Lagrange multipliers will be updated through an update formula. The theory of duality is a current topic and this theory is studied in more general spaces, see [20]. In this work, we are interested in developing the duality theory for HALF in the Euclidean space.

The main result of our work is: we guarantee the strong duality for the HALF for the convex case. In this way, we assure a solution to the primal and dual problems. With these results, we can also note that HALF has similar properties to Log-Sigmoid Lagrangian function (LSLF), see [12], modified Frisch function (MFF), and modified Carroll function (MCF), these last two functions are studied in [11].

The work is organized as follows: in Sect. 2, we present some basic results, the hyperbolic penalty function, and some of its properties; in Sect. 3, we present the HALF; in Sect. 4, we develop the duality theory for HALF, and in Sect. 5, we present a set of computational illustrations to verify our theoretical results.

Notation

Throughout this work, ${\mathbb {R}}$ is the Euclidean space, ${\mathbb {R}}_{+} = \{ a \in {\mathbb {R}} \; : \; a \ge 0\},$ ${\mathbb {R}}_{++} = \{ a \in {\mathbb {R}} \; : \; a > 0\}$ and $\left\| \cdot \right\|$ is the Euclidean norm.

2 Preliminaries

Henceforth, we consider the following assumption:

A. Slater constraint qualification holds, i.e., there exists $\hat{x}\in S$ which satisfies $g_{i}(\hat{x})>0,\; i=1,\ldots ,m.$

The Lagrangian function associated with the problem (P) is $\; L:{\mathbb {R}}^n \times {\mathbb {R}}_+^m \rightarrow {\mathbb {R}}^n ,\;$ defined as

$$\begin{aligned} L(x,\lambda )=f(x)-\sum _{i=1}^{m}\lambda _{i} g_i(x), \end{aligned}$$

where $\lambda _i \ge 0, i=1,\ldots ,m,$ are called Lagrange multipliers. The dual function $\Phi : {\mathbb {R}}_{+}^m \rightarrow {\mathbb {R}},$ is defined as

$$\begin{aligned} \Phi (\lambda )=\inf _{x \in {\mathbb {R}}^n } L(x,\lambda ), \end{aligned}$$

(2.1)

and the dual problem consists of finding (D):

$$\begin{aligned} \lambda ^* \in \Lambda ^*= \text {argmax}\{\Phi (\lambda ) \;\vert \; \lambda \in {\mathbb {R}}^{m}_{+} \}. \end{aligned}$$

2.1 Hyperbolic penalty

The hyperbolic penalty method, introduced in [16], is meant to solve the problem (P). The penalty method adopts the hyperbolic penalty function (HPF) as follows:

$$\begin{aligned} P(y,\lambda ,\tau )= -\lambda y+ \sqrt{ \left( \lambda y \right) ^2+ \tau ^2 }, \end{aligned}$$

(2.2)

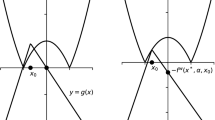
where $P: {\mathbb {R}} \times {\mathbb {R}}_+ \times {\mathbb {R}}_{++} \rightarrow {\mathbb {R}}.$ The graphic representation of $P(y,\lambda ,\tau )$ is as shown in Fig. 1. Now, in the present work, we consider $\tau >0$ fixed.

Fig. 1

Hyperbolic penalty function

Remark 2.1

The HPF is originally proposed in [16] and also studied in [17]. In these works, the following properties are important for HPF:

• (a) $P(y, \lambda , \tau )$ is asymptotically tangent to the straight lines $r_1(y)= -2 \lambda y$ and $r_2(y)=0$ for $\tau >0.$

• (b) $P(y, \lambda , 0)=0,$ for $y \ge 0$ and $P(y, \lambda , 0)=-2 \lambda y,$ for $y < 0.$

  Due to the properties (a) and (b),  the HPF perform a smoothing of the penalty studied by Zangwill, see [19].

For more details of the HPF, see [16] and [17]. In particular, we use the following properties of the function P:

• (P0) $P(y,\lambda ,\tau )$ is $k-$times continuously differentiable for any positive integer k for $\tau >0.$

• (P1) $P(0,\lambda ,\tau )=\tau ,$ for $\tau > 0$ and $\lambda \ge 0.$

• (P2) $P(y,\lambda ,\tau )$ is strictly a decreasing function of y,  i.e.,

  $$\begin{aligned} \nabla _{y} P(y, \lambda , \tau )= -\lambda \left( 1- \frac{\lambda y}{ \sqrt{ (\lambda y)^2 + \tau ^2}} \right) <0,\;\; \text {for},\;\; \tau>0 , \; \lambda >0. \end{aligned}$$

Remark 2.2

For any $\lambda \ge 0,$ $y \ge 0$ and $\tau >0.$ We have

$$\begin{aligned} - \lambda y- \sqrt{( \lambda y)^2 + \tau ^2}<0 <-\lambda y + \sqrt{( \lambda y)^2 + \tau ^2}. \end{aligned}$$

(2.3)

Considering the definition of the function P in (2.3), we have $P(y, \lambda , \tau )>0.$

3 Hyperbolic augmented Lagrangian function

We define the HALF of problem (P) by $\;L_H: {\mathbb {R}}^n \times {\mathbb {R}}_{++}^m \times {\mathbb {R}}_{++} \rightarrow {\mathbb {R}},\;$

$$\begin{aligned} L_H(x, \lambda , \tau )= f(x)+\sum _{i=1}^{m} P(g_i(x),\lambda _i,\tau ), \end{aligned}$$

which can be written as

$$\begin{aligned} L_H(x, \lambda ,\tau )=f(x)+\sum _{i=1}^{m}\left( -\lambda _i g_i(x)+\sqrt{ \left( \lambda _i g_i(x)\right) ^2 +\tau ^2} \right) , \end{aligned}$$

(3.1)

where $\tau$ is the penalty parameter and a fixed value. Note that this function belongs to class $C^{\infty }$ if the involved functions f(x) and $g_i(x),\; i=1,\ldots ,m,$ are too.

Proposition 3.1

Let us assume that if f(x) and all $g_i(x) \in C^{2},$ and that f(x) is strictly convex, then $L_H(x, \lambda , \tau )$ is strictly convex in ${\mathbb {R}}^n$ for any fixed $\lambda >0$ and $\tau >0.$

Proof

We only need to prove that the Hessiana of $L_H$ is defined positive. Let $\lambda =(\lambda _1,\ldots , \lambda _m)>0$ and $\tau >0$ be fixed. The Hessian of $L_H(x,\lambda ,\tau )$ is

$$\begin{aligned} \nabla ^2_{xx} L_H(x,\lambda ,\tau )= & {} \nabla _{xx}^2 f(x)-\sum _{i=1}^{m} \lambda _i \nabla _{xx}^2 g_i(x)\nonumber \\{} & {} +\sum _{i=1}^{m} \left( \frac{(\lambda _i)^2}{\sqrt{(\lambda _i g_i(x))^2+\tau ^2}} -\frac{(\lambda _i)^4 g_i^2(x) }{((\lambda _i g_i(x))^2+ \tau ^2)^{\frac{3}{2}}} \right) \nabla _{x} g_i(x) \nabla ^{T}_{x} g_i(x)\nonumber \\{} & {} +\sum _{i=1}^{m}\frac{(\lambda _i)^2 g_i(x) }{\sqrt{(\lambda _i g_i(x))^2+ \tau ^2}} \nabla _{xx}^2 g_i(x). \end{aligned}$$

(3.2)

In (3.2), the $\nabla _{xx}^2 g_i(x)$ is factored, so we can rewrite (3.2) as follows:

$$\begin{aligned} \nabla ^2_{xx} L_H(x,\lambda ,\tau )= & {} \nabla _{xx}^2 f(x) -\sum _{i=1}^{m} \lambda _i \left( 1-\frac{\lambda _i g_i(x) }{\sqrt{(\lambda _i g_i(x))^2+ \tau ^2}} \right) \nabla _{xx}^2 g_i(x) \nonumber \\{} & {} +\sum _{i=1}^{m} \left( \frac{(\lambda _i)^2}{\sqrt{(\lambda _i g_i(x))^2+\tau ^2}} -\frac{(\lambda _i)^4 g_i^2(x) }{((\lambda _i g_i(x))^2+ \tau ^2)^{\frac{3}{2}}} \right) \nabla _{x} g_i(x) \nabla ^{T}_{x} g_i(x). \nonumber \\ \end{aligned}$$

(3.3)

On the other hand, we know that we have

$$\begin{aligned} \left( \left( \lambda _i g_i(x) \right) ^2 + \tau ^2 \right) \lambda _i^2 > \lambda _i^2 (\lambda _i g_i(x))^2. \end{aligned}$$

The above inequality can be written as

$$\begin{aligned} \frac{\lambda _i^2}{ \left( \left( \lambda _i g_i(x) \right) ^2 + \tau ^2 \right) ^{\frac{1}{2}}} - \frac{\lambda _i^4 g_i^2(x)}{\left( \left( \lambda _i g_i(x) \right) ^2 + \tau ^2 \right) ^{\frac{3}{2}}} >0. \end{aligned}$$

(3.4)

Replacing (3.4) in (3.3) and since $-\lambda _i \left( 1- \frac{\lambda _i g_i(x)}{ \sqrt{ (\lambda _i g_i(x))^2 + \tau ^2}} \right) <0,$ in (3.3), we get that, $\nabla _{xx}^2 L_H(x, \lambda , \tau )>0,$ for $\lambda >0$ and $\tau >0$ fixed. $\square$

Remark 3.1

Henceforth, we are going to assume that there is a solution for the subproblem generated by HALA. Now, considering this assumption of existence of a solution and considering the Proposition 3.1 for any $\lambda >0$ and $\tau >0,$ then there exists a unique minimizer for problem (P). This minimizer is defined as

$$\begin{aligned} \check{x}= \check{x}(\lambda , \tau )=argmin \left\{ L_H(x, \lambda , \tau )\;\vert \; x \in {\mathbb {R}}^n \right\} . \end{aligned}$$

4 Duality

In this section, we adapt the classic results already existing in the literature (Chapter 9 of [10] and Section 7 of [11]) for our HALF. The following result is also verified by MFF and MCF, see [11].

Proposition 4.1

Consider the convex problem (P). Assume the assumption A holds. Then, $x^* \in S$ is a solution of problem (P) for any $\tau >0$ if and only if:

• (i) There exists a vector $\lambda ^* \ge 0$ such that

  $$\begin{aligned} \lambda _i^* g_i(x^*)=0,\; i=1,\ldots ,m \;\;\;\;and \;\;\;\; L_H(x, \lambda ^*, \tau )\ge L_H(x^*, \lambda ^*, \tau ),\;\; \forall x\in {\mathbb {R}}^n. \nonumber \\ \end{aligned}$$

  (4.1)

• (ii) The pair $(x^*, \lambda ^*)$ is a saddle point of $L_H,$ that is,

  $$\begin{aligned} L_H(x, \lambda ^*, \tau ) \ge L_H(x^*, \lambda ^*, \tau ) \ge L_H(x^*, \lambda , \tau ), \;\; \; \; \forall x\in {\mathbb {R}}^n, \; \; \forall \lambda \in {\mathbb {R}}_{+}^m.\nonumber \\ \end{aligned}$$

  (4.2)

Proof

$(\Rightarrow )$ Let any $\tau >0$ be fixed. Assume $x^*$ is a solution for convex problem (P) satisfying the assumption A. Then the system

$$\begin{aligned}{} & {} f(x)-f(x^*)<0,\\{} & {} -g_i(x)<0,\; i=1,\ldots ,m, \end{aligned}$$

has no solution in ${\mathbb {R}}^n.$ Hence, by the Proper Separation Theorem (see, Theorem 2.26 (iv) of Dhara and Dutta [3]), there exists a vector $(\tilde{\lambda }, \hat{\lambda }) \ne (0,0) \in {\mathbb {R}} \times {\mathbb {R}}^m$ such that

$$\begin{aligned} \tilde{\lambda } \left( f(x)-f(x^*) \right) - \sum _{i=1}^{m} \hat{\lambda }_i g_i(x)\ge 0, \end{aligned}$$

for all $x \in {\mathbb {R}}^n.$ We can rewrite the inequality above as

$$\begin{aligned} \tilde{\lambda } \left( f(x)-f(x^*) \right) \ge \sum _{i=1}^m \hat{\lambda }_i g_i(x), \end{aligned}$$

(4.3)

for all $x \in {\mathbb {R}}^n.$ Now, we follow an analysis similar to Theorem 4.2 of [3], so by A, we have that there exists $\lambda _i^*= \frac{\hat{\lambda }_i}{\tilde{\lambda }},\; i=1,\ldots ,m,$ with $\tilde{\lambda }>0.$ Then, by (4.3) we have

$$\begin{aligned} f(x)-f(x^*) \ge \sum _{i=1}^m \lambda _i^* g_i(x), \end{aligned}$$

(4.4)

for all $x \in {\mathbb {R}}^n.$ In particular, (4.4) holds for $x=x^*.$ So, we have

$$\begin{aligned} 0 \ge \sum _{i=1}^m \lambda _i^* g_i(x^*). \end{aligned}$$

(4.5)

On the other hand, since $g_i(x^*) \ge 0$ and $\lambda _i^* \ge 0$ for $i=1,\ldots ,m,$ then by (4.5), we obtain

$$\begin{aligned} \lambda _i^*g_i(x^*)=0,\;\; i=1,\ldots ,m, \end{aligned}$$

(4.6)

which holds, thus, we have the first part of (4.1).

Now, we are interested in proving the second part of (4.1). From (4.6) and (4.4), we have

$$\begin{aligned} f(x^*)- \sum _{i=1}^m \lambda _i^* g_i(x^*)= f(x^*) \le f(x)- \sum _{i=1}^m \lambda _i^* g_i(x), \end{aligned}$$

(4.7)

for all $x \in {\mathbb {R}}^n.$ Now, since we have (4.6), we can obtain

$$\begin{aligned} \sum _{i=1}^m \sqrt{ ( \lambda _i^* g_i(x^*) )^2 + \tau ^2} \le \sum _{i=1}^m \sqrt{( \lambda _i^* g_i(x) )^2 + \tau ^2}. \end{aligned}$$

(4.8)

Considering (4.7) and (4.8), we have

$$\begin{aligned} L_H(x,\lambda ^*,\tau ) \ge L_H(x^*, \lambda ^*,\tau ), \;\; \forall x \in {\mathbb {R}}^n, \end{aligned}$$

(4.9)

which concludes the proof of (4.1).

Now, we are interested in verifying item (ii),  first we will prove that $L_H(x^*, \lambda ^*, \tau ) =f(x^*)+ m \tau .$ Indeed, we consider (4.6) in the definition of function $L_H$ (see (3.1)), so we have

$$\begin{aligned} L_H(x^*, \lambda ^*, \tau )=f(x^*)+m \tau . \end{aligned}$$

(4.10)

On the other hand, $x^*$ is feasible, i.e.,

$$\begin{aligned} g_i(x^*)\ge 0,\;\; i=1,\ldots ,m. \end{aligned}$$

(4.11)

By applying the property P2 of the HPF in (4.11), we obtain

$$\begin{aligned} P(g_i(x^*),\lambda _i,\tau ) \le P(0,\lambda _i,\tau ),\;\; i=1,\ldots ,m. \end{aligned}$$

(4.12)

By applying property P1 on the right side of expression (4.12) and by performing the sum of 1 to m in the inequality, it follows

$$\begin{aligned} \sum _{i=1}^m P(g_i(x^*),\lambda _i, \tau ) \le \sum _{i=1}^{m} \tau =m \tau . \end{aligned}$$

Adding $f(x^*)$ to both sides of the expression, we obtain

$$\begin{aligned} f(x^*)+\sum _{i=1}^m P(g_i(x^*),\lambda _i, \tau ) \le f(x^*)+m \tau . \end{aligned}$$

(4.13)

By definition of $L_H,$ (4.13) becomes

$$\begin{aligned} L_H(x^*, \lambda , \tau ) \le f(x^*)+m \tau . \end{aligned}$$

(4.14)

Now, by (4.14) and (4.10), we have

$$\begin{aligned} L_H(x^*,\lambda , \tau )\le f(x^*)+m \tau =L_H(x^*,\lambda ^*,\tau ). \end{aligned}$$

(4.15)

Finally, from (4.9) and (4.15), there exists $\lambda ^* \ge 0$ such that the primal-dual solution $(x^*, \lambda ^*)$ is a saddle point of $L_H,$ $\forall x \in {\mathbb {R}}^n$ and $\tau >0.$

($\Leftarrow$) We assume that $(x^*,\lambda ^*)$ is a saddle point of $L_H,$ so (4.2) holds. Then, for all $x \in {\mathbb {R}}^n,$ $\lambda \in {\mathbb {R}}_{+}^{m}$ and for any $\tau >0$ fixed, we have

$$\begin{aligned}{} & {} f(x^*)-\sum _{i=1}^{m} \lambda _i g_i(x^*)+\sum _{i=1}^m\sqrt{\left( \lambda _i g_i(x^*) \right) ^2 +\tau ^2}=L_H(x^*,\lambda ,\tau )\nonumber \\{} & {} \quad \le L_H(x^*,\lambda ^*,\tau )=f(x^*)- \sum _{i=1}^m \lambda ^*_i g_i(x^*)+\sum _{i=1}^m \sqrt{\left( \lambda _i^* g_i(x^*) \right) ^2 +\tau ^2}. \nonumber \\ \end{aligned}$$

(4.16)

This relation (4.16) is possible only if $g_i(x^*)\ge 0.$ If this relation is violated $(i.e.,\; g_i(x^*)<0)$ for some index i,  we can choose $\lambda _i$ sufficiently large so that (4.16) becomes false. So, $x^*$ is feasible for problem (P).

We will prove the complementarity condition of (4.1). So again, by (4.16), since that $\lambda _i\ge 0,\;i=1,\ldots ,m,$ and in particular taking $\lambda _i=0,\;i=1,\ldots ,m,$ in (4.16), we obtain

$$\begin{aligned} \sum _{i=1}^m \left( \left( \lambda _i^* g_i(x^*) \right) ^2 + \tau ^2+2 \tau \lambda _i^* g_i(x^*) \right) \le \sum _{i=1}^m \left( (\lambda _i^* g_i(x^*))^2 + \tau ^2 \right) . \end{aligned}$$

Thus, $\sum _{i=1}^m \lambda _i^* g_i(x^*)\le 0,$ and since $\lambda ^*_i \ge 0$ and $g_i(x^*) \ge 0,\;i=1,\ldots ,m,$ it must be true that

$$\begin{aligned} \lambda _i^* g_i(x^*)=0,\; i=1,\ldots ,m. \end{aligned}$$

(4.17)

By (4.17) and the definition of $L_H,$ we obtain

$$\begin{aligned} L_H(x^*, \lambda ^*, \tau )= f(x^*)+ m \tau . \end{aligned}$$

(4.18)

From the definition of saddle point, we know that $L_H(x, \lambda ^*, \tau ) \ge L_H(x^*, \lambda ^*, \tau ).$ By (4.18) and by the definition of $L_H,$ we can write

$$\begin{aligned} f(x^*)+ m\tau= & {} L_H(x^*,\lambda ^*,\tau )\le L_H(x,\lambda ^*,\tau )\nonumber \\= & {} f(x)+\sum _{i=1}^{m}P(g_i(x),\lambda ^*_i,\tau ). \end{aligned}$$

(4.19)

On the other hand, once again considering the property P2 of HPF, for any feasible point x,  i.e., $g_i(x)\ge 0,\; i=1,\ldots ,m,$ we will carry out a similar approach as was done on equation (4.11)-(4.13), thus, obtaining

$$\begin{aligned} f(x)+\sum _{i=1}^{m}P(g_i(x),\lambda _i^*,\tau )\le f(x)+ m \tau . \end{aligned}$$

(4.20)

Now, we replace (4.20) in (4.19), so it follows $f(x^*) \le f(x)$ whenever x is feasible. Therefore, $x^*$ is a global optimal solution of (P). $\square$

Let us consider the following definitions. Let

$$\begin{aligned} F_{\tau }(x)=\sup _{\lambda \ge 0}L_H(x, \lambda , \tau ). \end{aligned}$$

Then, $F_{\tau }(x)=f(x)+m \tau$ if $g_i(x) \ge 0,\; i=1,\ldots ,m$ and $F_{\tau }(x)= \infty ,$ otherwise. Therefore, we can consider the following problem:

$$\begin{aligned} x^*=argmin \left\{ F_{\tau }(x)\; \vert \; x \in {\mathbb {R}}^n \right\} , \end{aligned}$$

(4.21)

that is the problem (P) reduces to solving (4.21).

Let

$$\begin{aligned} \phi _{\tau }(\lambda )= \inf _{x \in {\mathbb {R}}^n} L_H(x, \lambda , \tau ) \end{aligned}$$

(possibly $\phi _{\tau }(\lambda )= -\infty$ for some $\lambda$) and consider the following dual problem of (P) that consists of finding

$$\begin{aligned} \lambda ^*=\text {argmax} \left\{ \phi _{\tau }(\lambda )\; \vert \; \lambda \ge 0 \right\} . \end{aligned}$$

(4.22)

In the following result, we are going to verify the weak duality.

Proposition 4.2

Let x be a feasible solution to problem (P) and let $\lambda$ be a feasible solution to problem (4.22). Then,

$$\begin{aligned} \phi _{\tau }(\lambda )\le F_{\tau }(x)=f(x)+m \tau , \;\;\;\; \forall x \in S, \; \forall \; \lambda \in {\mathbb {R}}^m_{+}. \end{aligned}$$

Proof

For any feasible x and $\lambda ,$ we have the weak duality. Indeed, by the definition of $\phi _{\tau },$ we have

$$\begin{aligned} \phi _{\tau }(\lambda )= & {} \inf _{w \in {\mathbb {R}}^n} L_H(w,\lambda ,\tau )=\inf _{w \in {\mathbb {R}}^n} \left\{ f(w) +\sum _{i=1}^{m}P(g_i(w),\lambda _i,\tau ) \right\} \nonumber \\\le & {} \inf _{w \in S} \left\{ f(w) +\sum _{i=1}^{m}P(g_i(w),\lambda _i,\tau ) \right\} \nonumber \\= & {} f(x)+\sum _{i=1}^{m} P(g_i(x),\lambda _i,\tau ). \end{aligned}$$

(4.23)

Since we know that x is feasible, we immediately have $g_i(x)\ge 0, \; i=1,\ldots ,m.$ Then, from the property P2 of the HPF, we have the following expressions

$$\begin{aligned} \sum _{i=1}^{m} P(g_i(x),\lambda _i,\tau )\le \sum _{i=1}^{m} P(0,\lambda _i,\tau ). \end{aligned}$$

Now, applying property P1 on the right side of the previous inequality, and adding f(x),  to both sides of the inequality above, we have

$$\begin{aligned} f(x)+\sum _{i=1}^{m} P(g_i(x),\lambda _i,\tau )\le f(x)+ m \tau . \end{aligned}$$

(4.24)

Replacing (4.24) in (4.23), we finally obtain

$$\begin{aligned} \phi _{\tau }(\lambda ) \le f(x)+m\tau ,\;\;\;\; \forall x\in S,\;\; \forall \lambda \in {\mathbb {R}}_{+}^{m}. \end{aligned}$$

(4.25)

$\square$

If $\hat{x}$ and $\hat{\lambda }$ are feasible solutions of the primal and dual problems and $F_{\tau }(\hat{x})= \phi _{\tau }(\hat{\lambda }),$ then $\hat{x}= x^*$ and $\hat{\lambda }= \lambda ^*.$ From Remark 3.1, with the smoothness of f(x) and $g_i(x),\; i=1,\ldots ,m,$ we ensure the smoothness for the dual function $\phi _{\tau }(\lambda ).$

Theorem 4.1

The problem (P) is considered. The assumption A is verified. Then, the existence of a solution of problem (P) implies that the problem (4.22) has a solution and

$$\begin{aligned} \phi _{\tau }(\lambda ^*)= f(x^*)+ m \tau ,\;\; for\; any\;\; \tau >0. \end{aligned}$$

(4.26)

Proof

Let $x^*$ be a solution of problem (P). From A, we get $\lambda ^* \ge 0,$ so that (4.1) is verified. So, we have

$$\begin{aligned} \phi _{\tau }(\lambda ^*)= & {} \min _{x \in {\mathbb {R}}^n} L_H(x, \lambda ^*, \tau )= L_H(x^*, \lambda ^*, \tau )\\\ge & {} L_H(x^*, \lambda ,\tau ) \ge \min _{x \in {\mathbb {R}}^n} L_H(x, \lambda , \tau )= \phi _{\tau }(\lambda ),\;\; \forall \lambda \ge 0. \end{aligned}$$

Therefore, $\phi _{\tau }(\lambda ^*)= \max \left\{ \phi _{\tau }(\lambda ) \; \vert \; \lambda \in {\mathbb {R}}_{+}^{m} \right\} .$ In this way, $\lambda ^* \in {\mathbb {R}}^m_{+}$ is a solution of the dual problem and since we have $L_H(x^*, \lambda ^*, \tau )= f(x^*)+m \tau ,$ (4.26) holds. $\square$

Proposition 4.3

Suppose that (4.26) holds, for the viable points $x^*$ and $\lambda ^*.$ Then, $x^*$ is a solution of the problem (P) and $\lambda ^*$ is a solution of the dual problem (4.22).

Proof

Let $g_i(x^*) \ge 0,\; i=1,\ldots ,m,$ with $x^* \in S,$ $\lambda _i^* \ge 0, \; i=1,\ldots ,m$ and (4.26) with $\tau >0$ be fixed. Then from (4.25), where x and $\lambda$ are viable, we can obtain the following

$$\begin{aligned} f(x) + m \tau \ge \phi _{\tau }(\lambda ^*)=f(x^*) + m \tau \ge \phi _{\tau }(\lambda ), \end{aligned}$$

i.e., $x^*$ is solution of the problem (P) and $\lambda ^*$ is solution of (4.22), which corresponds to the validity of the strong duality. $\square$

5 Computational illustration

We are going to use HALA (see [9]) to guarantee the theory proposed in this work. The program was compiled by the GNU Fortran compiler version 4:7.4.0-1ubuntu2.3. The numerical experiments were conducted on a notebook with the operating system Ubuntu 18.04.5, CPU i7-3632QM and 8GB RAM. The unconstrained minimization tasks were carried out by means of a Quasi-Newton algorithm employing the BFGS updating formula, with the function VA13 from HSL library [6]. The algorithm stopped when the solution was viable (feasible) and the absolute value of the difference of the two consecutive solutions $\Vert x^k-x^{k-1} \Vert$ was less than $10^{-5}$

We are going to take advantage of this section to make some comparisons of our algorithm HALA (see Table 18) with respect to the following algorithms:

• Alg1 = [4], a truncated Newton method;

• Alg2 = [5], a primal–dual interior-point method;

• Alg3 = [14], an interior-point algorithm;

• Alg4 = [13], a QP-free method;

• Alg5 = [2], a primal–dual feasible interior-point method;

• Alg6 = [18], a feasible sequential linear equation algorithm;

• Alg7 = [15], an inexact first-order method

• Alg8 = [7], a feasible direction interior-point technique;

• Alg9 = [1], an interior-point algorithm.

For completeness reasons, we are going to present HALA:

Algorithm 1

Hyperbolic Augmented Lagrangian Algorithm

With the following examples proposed in the book [8], we are going to verify the strong duality. In each example, the value of m means the total number of restrictions. Also, in all the examples starting points are considered so that assumption A is verified.

Example 5.1

Problem 1 (HS1).

$$\begin{aligned}{} & {} \min _{x \in {\mathbb {R}}^2} f(x)=100(x_2- x_1^2)^2 + (1-x_1)^2\\{} & {} \quad s.t.\;\;g_1(x)=x_2+1.5 \ge 0. \end{aligned}$$

Starting with $x^0=(-2,1)$ (feasible), $f(x^0)=909$ and $m=1.$ The minimum value is $f(x^*)=0$ at the optimal solution $x^*=(1, 1).$

Example 5.2

Problem 30 (HS30).

$$\begin{aligned} \min _{x \in {\mathbb {R}}^3} f(x)= & {} x_1^2+ x_2^2+x_3^2 \\ s.t.\;\;g_1(x)= & {} x_1^2 + x_2^2-1 \ge 0,\\ g_2(x)= & {} x_1-1 \ge 0,\\ g_3(x)= & {} 10 -x_1 \ge 0,\\ g_4(x)= & {} x_2 +10 \ge 0,\\ g_5(x)= & {} 10 - x_2 \ge 0,\\ g_6(x)= & {} x_3+10 \ge 0,\\ g_7(x)= & {} 10 - x_3 \ge 0. \end{aligned}$$

Starting with $x^0=(1, 1, 1)$ (feasible), $f(x^0)=3$ and $m=7.$ The minimum value is $f(x^*)=1$ at the optimal solution $x^*=(1, 0, 0).$

Example 5.3

Problem 66 (HS66).

$$\begin{aligned} \min _{x \in {\mathbb {R}}^3} f(x)= & {} 0.2 x_3 - 0.8 x_1 \\ s.t.\;\;g_1(x)= & {} x_2 - e^{x_1} \ge 0,\\ g_2(x)= & {} x_3 - e^{x_2} \ge 0,\\ g_3(x)= & {} x_1 \ge 0,\\ g_4(x)= & {} x_2 \ge 0,\\ g_5(x)= & {} x_3 \ge 0,\\ g_6(x)= & {} 100- x_1 \ge 0,\\ g_7(x)= & {} 100 -x_2 \ge 0,\\ g_8(x)= & {} 10 -x_3 \ge 0. \end{aligned}$$

Starting with $x^0=(0, 1.05, 2.9)$ (feasible), $f(x^0)=0.58$ and $m=8.$ The minimum value is $f(x^*)=0.5181632741$ at the optimal solution $x^*=(0.1841264879, 1.202167873, 3.327322322).$

Example 5.4

Problem 76 (HS76).

$$\begin{aligned} \min _{x \in {\mathbb {R}}^4} f(x)= & {} x_1^2+0.5 x_2^2+ x_3^2 + 0.5 x_4^2 - x_1 x_3+ x_3 x_4- x_1 - 3 x_2+x_3-x_4 \;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\\ s.t.\;\;g_1(x)= & {} 5-x_1- 2 x_2 - x_3 - x_4 \ge 0,\\ g_2(x)= & {} 4- 3x_1- x_2 - 2 x_3 + x_4 \ge 0,\\ g_3(x)= & {} x_2 + 4 x_3 - 1.5 \ge 0,\\ g_4(x)= & {} x_1 \ge 0,\\ g_5(x)= & {} x_2 \ge 0,\\ g_6(x)= & {} x_3 \ge 0,\\ g_7(x)= & {} x_4 \ge 0.\\ \end{aligned}$$

Starting with $x^0=(0.5, 0.5, 0.5, 0.5)$ (feasible), $f(x^0)=-1.25$ and $m=7.$ The minimum value is $f(x^*)=-4.681818181$ at the optimal solution $x^*=(0.2727273, 2.090909, -0.26E{-}10, 0.5454545).$

Example 5.5

Problem 100 (HS100).

$$\begin{aligned} \min _{x \in {\mathbb {R}}^7} f(x)= & {} (x_1 -10)^2+ 5 (x_2 -12)^2+ x_3^4 + 3(x_4 -11)^2 + 10 x_5^6\\{} & {} + 7 x_6^2 + x_7^4 - 4 x_6 x_7 - 10 x_6 - 8 x_7\\ s.t.\;\;g_1(x)= & {} 127- 2 x_1^2 -3 x_2^4 - x_3 -4x_4^2 -5 x_5 \ge 0,\\ g_2(x)= & {} 282-7 x_1 - 3 x_2 -10 x_3^2 - x_4 + x_5 \ge 0,\\ g_3(x)= & {} 196 -23 x_1 - x_2^2 - 6 x_6^2 + 8 x_7 \ge 0,\\ g_4(x)= & {} -4 x_1^2 - x_2^2 +3 x_1 x_2- 2 x_3^2 -5 x_6 + 11 x_7 \ge 0. \end{aligned}$$

Starting with $x^0=(1, 2, 0, 4, 0, 1, 1)$ (feasible), $f(x^0)=714$ and $m=4.$ The minimum value is $f(x^*)=680.6300573$ at the optimal solution $x^*=(2.330499, 1.951372, -0.4775414, 4.365726, -0.6244870, 1.038131, 1.594227).$

Example 5.6

Problem 11 (HS11).

$$\begin{aligned} \min _{x \in {\mathbb {R}}^2} f(x)= & {} (x_1 -5)^2 + x_2^2 -25\;\;\;\;\;\\ s.t.\;\;g_1(x)= & {} -x_1^2 + x_2 \ge 0,\;\;\;\;\;\;\;\;\;\\ \end{aligned}$$

Starting with $x^0=(4.9, 0.1)$ (not feasible), $f(x^0)=-24.98$ and $m=1.$ The minimum value is $f(x^*)=-8.498464223.$

Table 1 Example 5.1

Table 2 Example 5.1

Table 3 Example 5.2

Table 4 Example 5.2

Table 5 Continuation of Table 4

Table 6 Example 5.3

5.1 Results

For each table, the letter N indicates the name of the problem, $\lambda$ is the multiplier Lagrange, x is the primal variable, f(x) is the value of the objective function, $g_i(x)$ are the constraints of each problem, $L_H(\cdot , \cdot , \cdot )$ is the value of the HALF and via = viable = feasible where, in each iteration, the obtained point can be viable, then its value is $``0 = yes$” or the point can be inviable, then the value is $``1 = not$” and $\tau$ is the penalty parameter. In all the examples, we will use $\tau =0.10E{-}04.$ Let us analyze the examples.

Table 7 Example 5.3

Table 8 Continuation of Table 7

Table 9 Example 5.4

Table 10 Example 5.4

Table 11 Continuation of Table 10

Table 12 Example 5.5

Table 13 Example 5.5

Table 14 Example 5.6 with $\tau ^0=0.01$

Table 15 Example 5.6 with $\tau ^0=0.01$

Table 16 Example 5.6 with $\tau ^0=0.01$

Table 17 Example 5.6 with $\tau ^0=0.01$

Table 18 Iterations

• Example 5.1: The HALA solves this example even though function f is non-convex, see Tables 1 and 2. The time used is 0.000250 s.

• Example 5.2: the function f is strictly convex. From Table 3, we can see that in iteration 2, the Theorem 4.1 can be verified, i.e., we have the following:

  $$\begin{aligned} f(x^*)+m \tau = 1.00000000 + (7) (0.00001)= 1.00007 \end{aligned}$$

  and

  $$\begin{aligned} \phi _{\tau }(\lambda ^*)=L_H(x^*, \lambda ^*, \tau )=1.00007, \end{aligned}$$

  then, $\phi _{\tau }(\lambda ^*)= f(x^*)+ m \tau .$ So, $x^*=(0.100000000E+01, 0.100000000E+01)$ is the solution of the primal problem and from Tables 4 and 5, we can see the $\lambda ^*$ is the solution of the dual problem in the iteration 2. The time used is 0.000434 s.

• Example 5.3: the function f is linear. From Table 6, we can see that in iteration 3 the Theorem 4.1 can be verified, i.e., we have the following:

  $$\begin{aligned} f(x^*)+m \tau = 0.518163274 + (8) (0.00001)= 0.518243274 \end{aligned}$$

  and

  $$\begin{aligned} \phi _{\tau }(\lambda ^*)=L_H(x^*, \lambda ^*, \tau )=0.518243274, \end{aligned}$$

  then, $\phi _{\tau }(\lambda ^*)= f(x^*)+ m \tau .$ So, $x^*$ is the solution of the primal problem and from Tables 7 and 8, we can see the $\lambda ^*$ is the solution of the dual problem in the iteration 3. The time used is 0.000804 s.

• Example 5.4: the function f is strictly convex. From Table 9, we can see that in iteration 2, the Theorem 4.1 can be verified, i.e., we have the following:

  $$\begin{aligned} f(x^*)+m \tau = -4.68181818 + (7) (0.00001)= -4.68174818 \end{aligned}$$

  and

  $$\begin{aligned} \phi _{\tau }(\lambda ^*)=L_H(x^*, \lambda ^*, \tau )=-4.68174818, \end{aligned}$$

  then, $\phi _{\tau }(\lambda ^*)= f(x^*)+ m \tau .$ So, $x^*$ is the solution of the primal problem and from Tables 10 and 11, we can see the $\lambda ^*$ is the solution of the dual problem in the iteration 2. The time used is 0.000652 s.

• Example 5.5: the function f is convex. From Table 12, we can see that in iteration 2, the Theorem 4.1 can be verified, i.e., we have the following:

  $$\begin{aligned} f(x^*)+m \tau = 680.630057+ (4) (0.00001)= 680.630097 \end{aligned}$$

  and

  $$\begin{aligned} \phi _{\tau }(\lambda ^*)=L_H(x^*, \lambda ^*, \tau )=680.630097, \end{aligned}$$

  then, $\phi _{\tau }(\lambda ^*)= f(x^*)+ m \tau .$ The optimal value $x^*$ is reported in the Table 12 and the optimal value $\lambda ^*$ is reported in the Table 13. The time used is 0.002140 s.

In Table 18, we can see that HALA is more efficient in the sense that it uses fewer iterations with respect to the other algorithms. We can observe in the computational results that the HALA remains in the viable region in all the examples. On the other hand, despite being the theory developed in this work on convexity hypothesis, our algorithm shows in the Example 5.1 that it can also solve non-convex problems.

A computational experiment with update of parameter “$\tau$”

We show a computational experiment, considering a condition to update parameter $\tau .$ So, we present our Algorithm 2. In this algorithm we will additionally assume that the sequence $\{\tau ^k \}$ is bounded.

Algorithm 2

Hyperbolic Augmented Lagrangian Algorithm

• Example 5.6.

  This example is solved with Algorithm 1 and Algorithm 2.

  For both algorithms, we are considering the same initial values: $x^0=(4.9, 0.1),$ $\lambda ^0= 10,$ $\tau ^0=0.01$ and $\alpha = 0.2$ (for the case of Algorithm 2). The algorithm stopped when the solution was viable (feasible) and the absolute value of the difference of the two consecutive solutions $\Vert x^k-x^{k-1} \Vert$ was less than $10^{-3}.$ Thus, we have the following observations:

  • (a) Algorithm 1 (with $\tau$ fixed).

    The results can be seen on the Tables 14 and 15. We can observe that this algorithm uses 12 iterations to solve the problem.

  • (b) Algorithm 2 (with a rule to update $\tau$).

    The results can be seen on the Tables 16 and 17. We can observe that this algorithm uses 2 iterations to solve the problem.

  After seeing (a) and (b), we can decide that Algorithm 2 solves Example 5.6, using fewer iterations compared to Algorithm 1. This motivates us to investigate new rules to update parameter $\tau .$