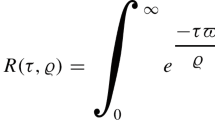1 Introduction

Researchers are actively involved in the overall transformation of theme development because it is suitable for describing and analyzing physical systems [1, 5, 6, 10, 16, 22, 25]. Jackson [17] introduced q-calculus. Now, the q-calculus has become very important in various fields of science and technology. The concept of q-calculus can be used in fractions and control problems [18]. Some integral transformations have different q analogs. The research is carried out on the q-calculus [4, 7, 8, 11, 15]. The new integral transform called ARA transform, which is established by [25], generalizes some variants of the Laplace transform, Sumudu transform, Elzaki transform, natural transform, Yang transform and Shehu transform. So we motivate to introduce the concept q-ARA transform to get the advantages in q-calculus.

We start from the definition of the ARA-transform [25] of the function \( f (\xi ) \) is defined by

We introduce the concept of ARA transform in q-calculus namely q-ARA transform and establish some properties. Furthermore, several propositions concerned with the properties of q-ARA transform are explored. We also give some applications of q-ARA transform for solving some ordinary and partial differential equations with initial and boundary values problems.

2 Preliminaries

In this section, we give some remarkable notes and mathematical symbols used in literature [7, 13, 19, 20, 23, 24].

The q-shifted factorials for \(q\in (0,1)\) and \(\kappa \in \mathbb {C}\) are defined as

$$\begin{aligned} (\kappa , q) = 1,(\kappa , q)_{n} = \prod ^{n-1}_{k=0} (1-\kappa q^{k}), n= 1,2,\ldots ,&\end{aligned}$$
$$\begin{aligned} (\kappa ;q)_{\infty }= \lim _{n \rightarrow \infty } (\kappa ;q)_{n}= \prod ^{\infty }_{k=0} (1-\kappa q^{k}).&\end{aligned}$$

Also we write \([\kappa ]_{q}\) = \(\dfrac{1-q^{\kappa }}{1-q}\), \([\kappa ]_{q}!\) = \(\dfrac{(q;q)_{n}}{(1-q)^{n}},~ n\in \mathbb {N}\).

The q-derivatives \(D_{q}f\) and \(D_{q}^{+}\) of a function f, given by Kac and Cheung [18] \((D_{q}f) (\alpha ) = \dfrac{f(\alpha )-f(q\alpha )}{(1-q)\alpha } \), if \((\alpha \ne 0)\) \((D_{q}f) (0) = f^{\prime } ( 0)\) exists.

If f is differentiable, then \((D_{q} f) (\alpha ) \), tend to \(f^{\prime }(\alpha )\) as q tend to 1. For \(n\in \mathbb {N}\), we have \(D^{1}_{q}\) = \(D_{q}\),     \((D_{q}^{+})^{1}= D^{+}_{q}.\)

The q-derivative of the product \(D_{q} (f.g) (\alpha ) \) \(= g(\alpha ) D_{q}f(\alpha )+f(q\alpha ) D_{q} g(\alpha ).\)

The q-Jackson integral from 0 to k and from 0 to \(\infty \) given by Jackson [17]

$$\begin{aligned} \int _{0}^{\kappa } f(\alpha ) d_{q}\alpha = (1-q)\alpha \sum _{n=0}^{\infty } f(\alpha q^{n}) q^{n},&\end{aligned}$$
$$\begin{aligned} \int _{0}^{\infty } f(\alpha ) d_{q}\alpha = (1-q) \sum _{n=-\infty }^{\infty } f( q^{n}) q^{n},&\end{aligned}$$

provided these sums converge absolutely. A q-analogue of integration by parts formulae is given by the following relation

Gasper and Rahamen [14], Kac and Cheung [18] have given the following relation

$$\begin{aligned}&E_{q}^{\rho } = \sum _{n=0}^{\infty } q^{\dfrac{n(n-1)}{2}} \dfrac{\rho ^{n}}{[n]!}= (-(1-q)z;q)_{\infty }, \end{aligned}$$
(1)
$$\begin{aligned}&e^{\rho }_{q} = \sum _{n=0}^{\infty } \dfrac{\rho ^{n}}{[n]!} = \dfrac{1}{((1-q)\rho ;q)_{\infty }},~ ~|z| < \dfrac{1}{1-q}. \end{aligned}$$
(2)

The above Eqs. (1) and (2) satisfy the following equations

\(D_{q}e^{\rho }_{q}= e^{\rho }_{q}\),   \(D_{q} E^{\rho }_{q}\) = \(E^{q\rho }_{q}\), and

\(e^{\rho }_{q}E^{-\rho }_{q}\) = \(E^{-\rho }_{q} e^{\rho }_{q} =1.\)

Jackson [17] has given the concept of q-analogue of gamma function and many more results have been given [7, 13, 21, 26]

by

$$\begin{aligned} \Gamma _{q}(\vartheta ) = \dfrac{(q;q)_{\infty }}{(q^{\vartheta };q)_{\infty }}(1-q)^{\vartheta -1}, \quad \vartheta \ne 0,-1,-2, \ldots ~. \end{aligned}$$

If satisfies the following conditions

\(\Gamma _{q}(\vartheta +1)= [\vartheta ]_{q} \Gamma (\vartheta ) \), \(\Gamma _{q} (1)= 1\), and

$$\begin{aligned} \lim _{q\rightarrow 1^{-}} \Gamma _{q} (\vartheta ) = \Gamma (\vartheta ),~~ Re (\vartheta ) >0.&\end{aligned}$$

The function \(\Gamma _{q}\) has the following q -integral representations

The q-integral representation \(\Gamma _{q}\) is defined in [13, 18, 27] as follows: For all \(\gamma ,\vartheta > 0\), we have

and

where,

$$\begin{aligned} K_{q} (\vartheta ) = \dfrac{(-q,-1;q)_{\infty }}{(-q^{\vartheta },-q^{1-\vartheta };q)_{\infty }}. \end{aligned}$$

If \(\dfrac{\log (1-q)}{\log (q)}\in \mathbb {Z}, \) we obtain

3 Main results

Definition 3.1

The q-ARA transform of a function \(f(\xi )\) is defined by

$$\begin{aligned} R_{n} [f(\xi )] (\kappa ) = F (n, \kappa ) = \dfrac{\kappa }{(1-q)} \int _{0}^{\infty } \xi ^{n-1}~ e_{q}^{-\kappa \xi }~ f(\xi )~ d_{q} \xi . \end{aligned}$$
(3)

Property 3.2

(Linearity property) Let \( \omega (\xi ) \) and \( \Lambda (\xi )\) be two functions in which q-ARA transform exists, then

$$\begin{aligned} R_{n} [ A \omega (\xi )+ B \Lambda (\xi )] (\kappa ) = A R_{n} [\omega (\xi )] (\kappa ) + B R_{n} [\Lambda (\xi )] (\kappa ) \end{aligned}$$

where A and B are nonzero constants.

Proof

\(\square \)

Property 3.3

(Change of the scale property)

$$\begin{aligned} R_{n} [f(\chi \xi )] (\kappa ) = \dfrac{1}{\chi ^{n-1}} F \left( n, \dfrac{\kappa }{\chi }\right) . \end{aligned}$$

Proof

Using the concept (3), we obtain

     Let us put \( M = \chi \xi \) \( \Rightarrow \xi = \dfrac{M}{\chi } \)

\(\square \)

Property 3.4

Shifting in \(\kappa \)-Domain

$$\begin{aligned} R_{n} [e_{q}^{-\Lambda \xi } f(\xi )] (\kappa ) = \dfrac{\kappa }{\kappa +\Lambda } F (n, \kappa +\Lambda ). \end{aligned}$$

Proof

\(\square \)

Property 3.5

Shifting in n-Domain

\( R_{n} [\xi ^{m} f(\xi ) ] (\kappa ) = F_{n+m} [f(\xi )] = F(n+m, \kappa ). \)

Proof

\(\square \)

Property 3.6

Shifting on \( \xi \)-Domain

$$\begin{aligned} F_{n} [\omega _{\Lambda } (\xi ) f(\xi -\Lambda ) ] (\kappa ) = e_{q}^{-\kappa \Lambda } F_{1} \Big [f(\lambda ) (\Lambda +\lambda )^{n-1} \Big ] . \end{aligned}$$

Proof

letting \( \xi - \Lambda = \lambda \) and substituting in the above equation we get

\(\square \)

Property 3.7

We introduce some practicals examples for finding q-ARA

transform for some functions:

  1. (1)
  2. (2)
  3. (3)
  4. (4)
  5. (5)
  6. (6)
    $$\begin{aligned} R_{n} [\sin _{q} (\chi \xi ) ] (\kappa )= & {} R_{n} \Big [ \dfrac{e_{q}^{i\chi \xi } - e_{q}^{-i\chi \xi } }{2i} \Big ] \\= & {} \dfrac{1}{2i} \Big ( R_{n} [e_{q}^{i\chi \xi }] - R_{n} [-e_{q}^{-i\chi \xi }] \Big )\\= & {} \dfrac{\kappa }{2i} \Gamma _{q} (n) \Big ( \dfrac{1}{(\kappa -\chi )^{n}} - \dfrac{1}{(\kappa -\chi )^{n}} \Big ) \\= & {} \dfrac{\kappa }{2i} \Gamma _{q} (n) \Bigg ( \dfrac{2i}{(\kappa ^{2}+\chi ^{2})^{\dfrac{n}{2}}} \sin (n \tan ^{-1} \Big (\dfrac{\kappa }{\chi }\Big )\Big ) \Bigg ) \\= & {} \Big (1+ \dfrac{\chi ^{2}}{\kappa ^{2}} \Big )^{-\dfrac{n}{2}} ~ \kappa ^{1-n}~ \Gamma _{q} (n)~\Bigg ( \sin (n~ \tan ^{-1} \Big (\dfrac{\kappa }{\chi }\Big ) \Bigg ) . \end{aligned}$$
  7. (7)
    $$\begin{aligned} R_{n} [\sinh _{q} (\chi \xi ) ] (\kappa )= & {} R_{n} \Big [ \dfrac{e_{q}^{i\chi \xi } - e_{q}^{-i\chi \xi } }{2} \Big ] \\= & {} \dfrac{1}{2} \Big ( R_{n} [e_{q}^{i\chi \xi }] - R_{n} [-e_{q}^{-i\chi \xi }] \Big ) \\= & {} \dfrac{\kappa }{2} \Gamma _{q} (n) \Big ( \dfrac{1}{(\kappa -\chi )^{n}} - \dfrac{1}{(\kappa -\chi )^{n}} \Big ) \\= & {} \dfrac{\kappa }{2} \Gamma _{q} (n) \dfrac{1}{\kappa ^{n}} \Bigg ( \dfrac{1}{(1-\dfrac{\chi }{\kappa })^{n}} - \dfrac{1}{(1+\dfrac{\chi }{\kappa })^{n}} \Bigg ). \end{aligned}$$
  8. (8)
    $$\begin{aligned} R_{n} [\cosh _{q} (\chi \xi ) ] (\kappa )= & {} R_{n} \Big [ \dfrac{e_{q}^{i\chi \xi } + e_{q}^{-i\chi \xi } }{2} \Big ] \\= & {} \dfrac{1}{2} \Big ( R_{n} [e_{q}^{i\chi \xi }] + R_{n} [-e_{q}^{-i\chi \xi }] \Big )\\= & {} \dfrac{\kappa }{2} \Gamma _{q} (n) \Big ( \dfrac{1}{(\kappa -\chi )^{n}} + \dfrac{1}{(\kappa -\chi )^{n}} \Big ) \\= & {} \dfrac{\kappa }{2} \Gamma _{q} (n) \dfrac{1}{\kappa ^{n}} \Bigg ( \dfrac{1}{(1-\dfrac{\chi }{\kappa })^{n}} + \dfrac{1}{(1+\dfrac{\chi }{\kappa })^{n}} \Bigg ). \end{aligned}$$

Theorem 3.8

If the q-ARA transform of a function \( f(\xi ) \) exists, then

$$\begin{aligned} ARA_{q} \bigg [ f(\xi -M)~ h(\xi -M) \Bigg ] = e_{q}^{-\kappa M} ARA_{q} [f(\xi -M)] \end{aligned}$$

     where \( h (\xi ) \) is heaviside unit step function defined on \( h(\xi -M) = 1, \)

     where \( \eta > M \) and \(h(\xi -M) = 0, \) \( \eta < M\).

Proof

We have by definition

               Putting, \( A= \xi -M \)

\(\square \)

Theorem 3.9

If the ARA transform of the \(f(\xi )\) exists where \( f(\xi ) \) is a

periodic function of periods A (That is \(f(\xi +A)\) = \( f(\xi ), \forall \xi ),\) then

Proof

Setting \( \xi = A+M \) in the second integral, we have

\(\square \)

Theorem 3.10

q-ARA convolution product

The convolution of \( f(\omega ) \) and \( g(\omega ) \) is defined by

4 Convolution theorem

4.1 Statement

Let \( ARA_{q} (f(\xi )) = F(n; \kappa ) \) and \( ARA_{q} (g(\xi )) = G(n; \kappa ) \) be

     such that \( f(\xi ) \) and \( g(\xi ) \) are picewise continuous functions on \([0, \infty )\).

     Then convolution \((f*g)\) is defined by

     \( ARA_{q} (f*g) (\xi ) = F(n: \kappa )~ G(n, \kappa ). \)

Proof

        Putting \( \xi - \omega = \rho \Rightarrow d_{q} \xi = d_{q} \rho \) and write

\(\square \)

5 Applications

Application 4.1

Consider the initial value problem

$$\begin{aligned} y^{/}(\xi ) + y(\xi ) = 0, ~ y(0) = 1. \end{aligned}$$
(4)

Applying q-ARA transform \(F_{1}\) on both side of equation (4)

\( F_{1} [y^{/}(\xi )] (\kappa ) + F_{1} [y(\xi )] (\kappa ) = 0 \)

or, \( \kappa F_{1} [y(\xi )] (\kappa ) - \kappa ~ ARA_{q}~ y(0) + F_{1} [y(\xi )] (\kappa ) = 0 \)

or, \(F_{1} [y(\xi )] (\kappa )\) = \(\dfrac{\kappa }{(1-q)~ (\kappa +1)}\)

or, \(y(\xi )\) = \( _q{}F_{1}^{-1} \Big \{ \dfrac{\kappa }{(1-q)~ (\kappa +1)} \Big \} \)

  or, \(y(\xi )\) = \( e_{q}^{\xi }. \)

Application 4.2

Consider the initial value problem

$$\begin{aligned} y^{/} (\xi ) - y(\xi ) = e_{q}^{2\xi }, ~ ~ y(0) = 1. \end{aligned}$$
(5)

Applying q-ARA-transform \( F_{1} \) on both side of equation (5)

$$\begin{aligned} F_{1} [y^{/}(\xi )] (\kappa ) + F_{1} [y(\xi )] (\kappa ) = F_{1} [e_{q}^{2 \xi }] (\kappa ) \end{aligned}$$

or,

$$\begin{aligned} \kappa F_{1} [y(\xi )] (\kappa ) - \kappa ~ ARA_{q} \{y(0)\} -F_{1}[y(\xi )] (\kappa ) = \dfrac{\kappa }{(1-q) (\kappa -2) } \end{aligned}$$

or,

$$\begin{aligned} F_{1} [y(\xi )] (\kappa ) = \dfrac{1}{\kappa -1} \Big ( \dfrac{\kappa }{(\kappa -2) (1-q)} + \kappa \Big ) \end{aligned}$$

or,

$$\begin{aligned} F_{1} [y(\xi )] (\kappa )= \dfrac{\kappa }{(\kappa -2) (\kappa -1) (1-q) } + \dfrac{\kappa }{\kappa -1} \end{aligned}$$

or,

$$\begin{aligned} y(\xi ) = q_{}F_{1}^{-1} \left\{ \dfrac{\kappa }{(\kappa -2) (\kappa -1) (1-q) } + \dfrac{\kappa }{\kappa -1} \right\} \end{aligned}$$

or, \( y(\xi ) = e_{q}^{-2\xi }\).

Application 4.3

Consider the initial value problem

$$\begin{aligned} y^{//} (\xi ) + y (\xi ) = 0, ~ ~ y(0)= 1, ~ y^{/}(0)= 1. \end{aligned}$$
(6)

Applying q-ARA-transform \( F_{1} \) on both side of equation (6)

\( F_{1} [y^{//}(\xi )] (\kappa ) + F_{1} [y(\xi )] (\kappa ) =0 \)

or,

$$\begin{aligned} \kappa ^{2} F_{1} [ y(\xi ) ](\kappa ) -\kappa ^{2} ~ ARA_{q} \{ y(0)\}- \kappa ~ ARA_{q} \{ y^{/}(0)\} + F_{1} [ y(\xi ) ](\kappa ) =0 \end{aligned}$$

or,

$$\begin{aligned} \kappa ^{2} F_{1} [ y(\xi ) ](\kappa ) - \dfrac{\kappa ^{2}}{(1-q)} - \dfrac{\kappa }{(1-q)} + F_{1} [ y(\xi ) ](\kappa ) = 0 \end{aligned}$$

or,

$$\begin{aligned} ( \kappa ^{2} +1) F_{1} [ y(\xi ) ](\kappa ) = \dfrac{\kappa ^{2}}{(1-q)} + \dfrac{\kappa }{(1-q)} \end{aligned}$$

or,

$$\begin{aligned} F_{1} [ y(\xi ) ](\kappa ) = \dfrac{\kappa ^{2}}{ (1-q)~ ( \kappa ^{2} +1) } + \dfrac{\kappa }{ (1-q)~ ( \kappa ^{2} +1) } \end{aligned}$$

or,

$$\begin{aligned} y(\xi ) = _q{}F_{1}^{-1} \Big \{ \dfrac{\kappa ^{2}}{ (1-q)~ ( \kappa ^{2} +1) } + \dfrac{\kappa }{(1-q)~ ( \kappa ^{2} +1) } \Big \}. \end{aligned}$$

Application 4.4

Consider the initial value problem

$$\begin{aligned} y^{//} -y^{/} + 6y = 8 e_{q}^{2\xi },~ y(0) = 0, ~ y^{/}(0)=0 \end{aligned}$$
(7)

Applying q-ARA-transform \( F_{1} \) on both side of equation (7)

$$\begin{aligned}&\Big [\kappa ^{2}F_{1}[y(\xi )](\kappa )- \kappa ^{2}~ ARA_{q} \{ y(0)\} - \kappa ~ ARA_{q} \{ y^{/}(0)\} \Big ] - \Big [\kappa F_{1} [y(\xi )] (\kappa ) \\&\quad -\kappa ~ ARA_{q} \{ y(0)\} \Big ] + 6 F_{1} [ y(\xi )] (\kappa ) = \dfrac{8 \kappa }{(1-q) (\kappa -2) } \end{aligned}$$

or,

$$\begin{aligned} (\kappa ^{2} -\kappa + 6) F_{1} [ y(\xi )] (\kappa ) = 3 \kappa + \dfrac{8 \kappa }{(1-q) (\kappa -2) } \end{aligned}$$

or,

$$\begin{aligned} F_{1} [ y(\xi )] (\kappa ) = \dfrac{3 \kappa }{\kappa ^{2} -\kappa + 6} + \dfrac{8 \kappa }{(1-q) (\kappa -2) (\kappa ^{2} -\kappa + 6) } \end{aligned}$$

or,

$$\begin{aligned} y(\xi ) (\kappa ) = _q{}F_{1}^{-1} \Big \{ \dfrac{3 \kappa }{\kappa ^{2} -\kappa + 6} + \dfrac{8 \kappa }{(1-q) (\kappa -2) (\kappa ^{2} -\kappa + 6) } \Big \}. \end{aligned}$$

Application 4.5

Find the solution of the equation

$$\begin{aligned} \dfrac{\partial _{q} \omega }{\partial _{q} \xi } = K \dfrac{\partial ^{2}_{q} \omega }{\partial _{q} \eta ^{2} } \end{aligned}$$
(8)

which tends to zeros as \( \eta \rightarrow 0 \) and which satisfies the conditions \( \omega = f(\xi ) \)

     when \( \eta = 0, \)   \( \xi > 0 \) and \( \omega = 0 \) when \( \eta > 0\), \( \xi = 0. \)

Taking the \( q-ARA \) transform of both sides of the given equation(8), we

     have

$$\begin{aligned} ARA_{q} \left\{ \dfrac{\partial _{q} \omega }{\partial _{q} \xi } \right\} = K~ ARA_{q} \left\{ \dfrac{\partial ^{2}_{q} \omega }{ \partial _{q} \eta ^{2} }\right\} \end{aligned}$$

or,

$$\begin{aligned} \kappa ~ \overline{\omega } (\xi , \kappa ) - \kappa ~ ARA_{q}~ \{ \omega (0)\} = K \dfrac{d^{2}_{q}\omega }{d_{q} \eta ^{2}} \end{aligned}$$

or,

$$\begin{aligned} \dfrac{d^{2}_{q}\omega }{d_{q} \eta ^{2}} - \dfrac{\kappa }{K} \overline{\omega } = 0 \end{aligned}$$

       whose solution is

$$\begin{aligned} \overline{\omega } = A~ e_{q}^{\sqrt{\dfrac{\kappa }{K }}\eta } + B~ e_{q}^{-\sqrt{\dfrac{\kappa }{K }}\eta }&\end{aligned}$$

        Since \(\omega \rightarrow 0 \) as \( \eta \rightarrow \infty . \)

     From which it follows that A=0.

$$\begin{aligned} \therefore \overline{\omega } = B~ e_{q}^{-\sqrt{\dfrac{\kappa }{K }}\eta }&\end{aligned}$$
(9)

Again, when

Again from (9), we get that,

        \(B = \overline{G} (\kappa )\).

Hence \( \overline{\omega } = \overline{G} (\kappa )~ e_{q}^{-\sqrt{\dfrac{\kappa }{K }}\eta } \).

$$\begin{aligned} \therefore \omega (\eta , \xi ) = ARA_{q}^{-1} \left\{ \overline{G} (\kappa )~ e_{q}^{-\sqrt{\dfrac{\kappa }{K }}\eta } \right\} . \end{aligned}$$

Application 4.6

A semi-infinite solid \( \eta > 0 \) is initially at temperature zero. At time \( \xi > 0, \) a constant temperature \( \lambda _{0} > 0 \) is applied and maintained at the face \( \eta =0. \) Find the temperature at any point of the solid at any time \(\eta > 0\).

Here the temperature \( \omega (\eta , \xi ) \) at any point of the solid at any time \( \xi > 0 \) is governed by one dimensional heat equation

$$\begin{aligned} \dfrac{\partial _{q} \omega }{ \partial _{q} \xi } = C^{2} \dfrac{\partial _{q}^{2} \omega }{ \partial _{q} \eta ^{2}} \end{aligned}$$
(10)

with the boundary and initial conditions \( \omega (0, \xi ) = \lambda _{0}\),  \( \omega (\eta , 0) = 0. \)

Taking the q-ARA transform of both the sides of equation (10), we have

$$\begin{aligned} ARA_{q}\left\{ \dfrac{\partial _{q} \omega }{\partial _{q} \xi }\right\} = C^{2}~ ARA_{q} \left\{ \dfrac{\partial ^{2}_{q} \omega }{ \partial _{q} \eta ^{2} } \right\} \end{aligned}$$

or,

$$\begin{aligned} \kappa ~ \overline{\omega } (\xi , \kappa ) - \kappa ~ ARA_{q}~ \{\omega (0)\} = C^{2} \dfrac{d^{2}_{q}\omega }{d \eta ^{2}} \end{aligned}$$

or,

$$\begin{aligned} \dfrac{d^{2}_{q}\omega }{d \eta ^{2}} - \dfrac{\kappa }{C^{2}} \overline{\omega } = 0 \end{aligned}$$

            whose solution is

$$\begin{aligned} \overline{\omega } (\xi ,\kappa ) = A~ e_{q}^{\sqrt{\dfrac{\kappa }{C^{2} }}\eta } + B~ e_{q}^{-\sqrt{\dfrac{\kappa }{C^{2} }}\eta }&\end{aligned}$$
(11)

Since \( \omega \) is finite when \( \eta \rightarrow 0. \)

\( \therefore \overline{\omega }\) is finite when \( \eta \rightarrow \infty . \)

\( \therefore A = 0, \) otherwise \(\overline{\omega } \rightarrow \infty \) as \( \eta \rightarrow \infty . \)

Taking the q-ARA transform of the conditions

\( \omega (0, \xi ) = \lambda _{0}, \) we have

$$\begin{aligned} \overline{\omega } (0, \kappa )= & {} \int _{0}^{\infty } \lambda _{0}~ \dfrac{\kappa }{(1-q)} \xi ^{n-1}~ e_{q}^{-\kappa \xi }~ f(\xi )~ d_{q} \xi .\\= & {} \dfrac{ \lambda _{0} (n-1)!}{(1-q)~\kappa ^{n-1}}. \end{aligned}$$

\( \therefore \) From (11), we have \(\overline{\omega } (0, \kappa )\) = B = \(\dfrac{ \lambda _{0} (n-1)!}{(1-q)~\kappa ^{n-1}}.\)

Put n=2, then

$$\begin{aligned}&\overline{\omega } (\xi , \kappa ) = \dfrac{ \lambda _{0} }{(1-q)~\kappa } ~ e_{q}^{-\sqrt{\dfrac{\kappa }{C^{2} }}\eta }\\&\quad \therefore \omega (\eta , \xi ) = ARA^{-1}_{q} \left\{ \dfrac{ \lambda _{0} }{(1-q)~\kappa } ~ e_{q}^{-\sqrt{\dfrac{\kappa }{C^{2} }}\eta } \right\} \\&\quad = \lambda _{0}~ erfc_{q}~ \dfrac{n}{2C \sqrt{\xi } }. \end{aligned}$$

Application 4.7

Solve the boundary value problem

$$\begin{aligned} \dfrac{\partial _{q}^{2} \omega }{ \partial _{q} \xi ^{2}} = a^{2} \dfrac{\partial _{q}^{2} \omega }{ \partial _{q} \eta ^{2}}, (\eta>0,~ \xi >0) \end{aligned}$$
(12)

where \(\omega (\eta , 0) = 0, \omega _{\xi } (\eta , 0) = 0, ~ \eta > 0, ~ \omega (0, \xi ) = F(\xi ), \lim \limits _{\eta \rightarrow ~ \infty } \omega (\eta ,\xi )=0, \xi \ge 0.\)

Taking the q-ARA transform of both the sides of the equation (12), and

     the boundary conditions, we have

$$\begin{aligned} ARA_{q} \Big \{ \dfrac{\partial _{q}^{2} \omega }{ \partial _{q} \xi ^{2}} \Big \} = a^{2} ARA_{q} \Big \{ \dfrac{\partial _{q}^{2} \omega }{ \partial _{q} \eta ^{2}} \Big \} \end{aligned}$$
$$\begin{aligned} or, \dfrac{d_{q}^{2} \overline{\omega } }{d_{q} \eta ^{2} } - \dfrac{\kappa ^{2}}{a^{2}} \overline{\omega } = 0. \end{aligned}$$
(13)

Also and \( \omega (\eta , \kappa ) = 0 \)

as \(\eta \rightarrow \infty .\)

Now the solution of (13) is given by

$$\begin{aligned} \overline{\omega } (\eta , \kappa ) = A e_{q}^{\dfrac{\kappa \eta }{a}} + B e_{q}^{-\dfrac{\kappa \eta }{a}}. \end{aligned}$$

Since \( \omega (\eta , \kappa ) = 0 \) as \( \eta \rightarrow \infty . \) \(\therefore A= 0\).

and \( \overline{\omega } (0, \kappa ) = \overline{F} (\kappa ) = B. \)

Hence \( \overline{\omega } (\eta , \kappa ) = \overline{F} (\kappa )~ e_{q}^{-\dfrac{\kappa \eta }{a}}.\)

$$\begin{aligned} \therefore \omega (\eta , \xi ) = ARA_{q}^{-1} \Big \{ \overline{F} (\kappa )~ e_{q}^{-\dfrac{\kappa \eta }{a}} \Big \}. \end{aligned}$$

6 Discussion

As Saadeh et al. [25] have introduced a new integral transform, namely ARA transform as a powerful and versatile generalization that unifies some variants of the classical Laplace transform, namely, the Sumudu transform, the Elzaki transform, the Natural transform, the Yang transform, and the Shehu transform. Also, Saadeh et al. [25] have given applications of ARA transformation in solving ordinary and partial differential equations that arise in some branches of science like physics, engineering, and technology.

The quantum calculus, q-calculus, is a relatively new branch in which q-calculus can calculate the derivative of a real function without limits. So, sometimes quantum calculus is also called calculus without limits. q-calculus has seen some applications in physics Ciavarella [9]. Alanazi et al. [2] have applied quantum calculus in the falling body problem in mathematical and statistical physics. Aral et al. [3] have given some results on q-calculus in applying q-calculus in operator theory. In approximation theory, the applications of q-calculus have been a new area in the last three decades.

So, ARA transform in quantum calculus may be applicable in operator theory, approximation theory, mathematical and statistical physics, science, and technology.

7 Conclusions

In this paper, we have introduced the concept of ARA transform in q-calculus; namely, q-ARA transforms and establishes some properties. Furthermore, we explored several propositions concerned with the properties of q-ARA transform. We have also given some q-ARA transform applications for solving ordinary and partial differential equations with initial and boundary values problems that arise in some branches of science like physics, engineering, and technology.