Simulation of realistic granular soils in triaxial test using physics engine

Abstract

The discrete element method (DEM) is the most widely applied numerical tool to simulate triaxial test, a common geotechnical test to measure the shear strength of soil. However, the typical DEM model uses sphere clusters to approximate soil particles, which is not sufficiently accurate to simulate realistic soil particles. This paper shows the potential of using a physics engine technique as a promising alternative to typical DEM method. Originally developed for simulating realistic physical and mechanical processes in video games and computer-animated films, physics engines have developed quickly and are being applied in scientific computing. Physics engines use triangular face tesselations to represent realistic objectives, which provides higher accuracy to model realistic soil particle geometries. In this paper, physics engine is applied to simulate true triaxial tests of Monterey No. 0 sand. The numerical results agree well with experimental results. This study provides DEM modelers with the physics engine technique as another promising option to simulate realistic soil particles in geotechnical tests.

1 Introduction

1.1 Background

Triaxial test is a widely used type of geotechnical test applied to obtain the shear strength and stiffness of soil, which is very important in foundation design [1]. Compared to the direct shear test, another simple and common geotechnical test used to determine the shear strength of soil, the triaxial test has several advantages including the versatility of the failure plane, uniform distribution of stresses along the shear plane, the measurement of pore water pressures, and the controllability of the drainage in the soil specimen [2]. These advantages make the triaxial test a more versatile and reliable method for soil shear strength determination.

Compared to conventional triaxial test, which assumes the horizontal principal stresses σ₂ and σ₃ are equal to each other, the true triaxial test is capable of independent control of stresses in three perpendicular directions, making the test more similar to real conditions where σ₂ and σ₃ are different [3]. However, the accessibility of actual true triaxial test is limited by the high cost and complexity of true triaxial test apparatus, along with the cost of human resources and time.

These days, numerical methods, particularly the discrete element method (DEM), are applied by geotechnical engineers to simulate geotechnical tests including triaxial test. Compared to conducting an actual triaxial test, DEM simulation is a low-cost solution. Also, DEM simulation is able to obtain microscope particle behavior including particle velocity, particle rotation, and inter-particle contact force during simulation, which is intractable to measure in experiments [4].

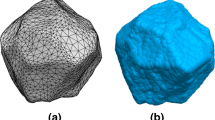
Typical DEM codes, such as Itasca PFC 2D/3D [5], LIGGGHTS [6], and YADE [7] usually use clumps of overlapping spheres (Fig. 1a) to model realistic soil particles because of the simplicity of contact detection and force calculations. Researchers, including Matsushima et al. [8], Price et al.[9], Ferellec and McDowell [10], Taghavi [5], and Zheng and Hryciw [11], have worked on the generation of sphere clumps. However, the sphere clump method cannot precisely approximate particle geometries unless applying a very large number of spheres, which becomes computationally highly-expensive. For example, the sphere cluster in Fig. 1a contains 1550 spheres, but visible artificial bumpy surfaces can still be observed.

Fig. 1

Realistic particle geometry representations. a Sphere clump with 1550 spheres. b Triangular face tessellation consisting of 5000 faces

The sphere clump method is not easily capable of approximating small and sharp corners on realistic soil particles [11]. However, these small and sharp corners are very important features on soil particle surface to create inter-particle locking and to reproduce the mechanical behavior of soils in simulations. A particle shape factor, roundness (R), is proposed by Wadell [12,13,14] to quantify the sharpness of corners. When R of soils changes by 0.1 (ranging from 0 to 1), the critical friction angle of soils will change 1.7° [15] and the peak friction angle will change 2.4° [16]. Such a large variance will significantly affect the accuracy of simulations.

Since the inability of sphere clump method to preserve the sharpness of corners limits its numerical accuracy when simulating realistic soil particles, research efforts have shifted to integrate triangular face tessellations (Fig. 1b) in DEM simulations, rather than using a sphere clump approximation, to improve the modeling accuracy of realistic soil particles. For example, Latham et al. [17, 18] scanned realistic particles with three-dimensional X-ray computed tomography (3D X-ray CT) and used triangular face tessellations to model these particle geometries in DEM simulations. Govender et al. [19,20,21,22] developed Blaze-DEM, a DEM code able to use triangular face tessellations to model realistic particles, to simulate the granular flow in a rotating drum. Recent commercial DEM codes, such as Itasca PFC 6.0 [23] and Rocky DEM [24], can also use triangular tessellations in the simulation of realistic particles.

We want to stress that the goal of this paper is not to replace any existing DEM codes such as PFC, LIGGGHTS, and YADE, Blaze-DEM, Rocky DEM, or any other DEM codes with physics engines. These existing codes represent state-of-the-art platforms for DEM researchers and applications. The goal of this paper is to provide geotechnical engineers with physics engine techniques as an alternative option that they might consider using when working on simulations of granular soils.

1.2 Introduction of physics engines

In the area of computer graphics, simulations of rigid bodies and their interactions are also important for creating immersive experiences in video games and computer-animated films. Therefore, an emerging technique, called physics engine, has been developed to perform such simulations. For example, in the popular video game Angry Birds, the collisions among birds, pigs, and blocks are simulated by a physics engine, called Box2D [25]. Recently, driven by the rapid development and high competitiveness of the computer gaming and movie industry, the accuracy, computational speed, and functionalities of physics engine techniques have significantly improved. Today, physics engines are increasingly used as scientific computational platform in various disciplines, including robotic control [26, 27], crowd simulation [28], biomedical engineering [29, 30], autonomous vehicle research [31], virtual and augmented reality [32], and psychological research [33].

The physics engine can use triangular face tessellations to simulate irregular particle shapes, hence it has been introduced in the area of geotechnical engineering as an alternative of typical DEM simulation platform. Izadi and Bezujian [34] simulated pluviation and vibration on three-dimensional (3D) randomly-shaped realistic particles with Bullet physics engine. Pytlos et al. [35] simulated biaxial compression tests of two-dimensional (2D) realistic particles with Box2D physics engine. Very recently, He and Zheng [36] simulated oedometer tests on 3D realistic particles with PhysX engine and He et al. [37] simulated direct shear tests with Project Chrono.

As reviewed by Ivaldi et al. [38], now there are many physics engines for researchers to use in scientific computation. We selected Project Chrono as the simulation platform in this paper for two reasons: Project Chrono can directly use triangular face tessellations to model realistic soil particles and Project Chrono includes a soft contact model which is suitable to simulate the mechanical behavior of granular soils.

Most physics engines use a hard contact model or impulse-based dynamics contact model [39]. However, DEM codes, such as Itasca PFC 2D/3D, LIGGGHTS, and YADE, use a soft contact model [40,41,42,43,44] to simulate inter-particle contacts. He et al. [45] compared the formulations of hard and soft contact models. Fleischmann et al. [49] has shown that the multi-time-step tangential contact displacement history, which is only integrated in soft contact model, is very important for reproducing accurate results when simulating the shearing behavior of soils. As the shearing behavior of soil is very significant in triaxial test, we used Project Chrono, one of the few physics engines integrating soft contact model, as the simulation platform.

In this study, we applied Project Chrono to simulate true triaxial tests with realistic soil particles. The soil particles were first scanned by a 3D laser scanner, then the geometries of these scanned realistic particles are imported into Project Chrono to form realistic soil specimen. The stress–strain behavior in the simulation was rigorously compared with actual experiment results, and the microscopic behavior, including particle motions (displacements, velocities, and rotations) and fabrics, were also obtained and analyzed.

2 Computational procedure of project chrono

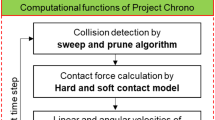
Project Chrono runs with a time-stepping procedure (Fig. 2), which is introduced and described in detail in this section.

Fig. 2

Computational procedure of Project Chrono

2.1 Contact detection

The contact detection method in physics engine includes a broad phase and a narrow phase. In the broad phase, Project Chrono searches for potentially contacting pairs of particles and rules out particle pairs certainly not contacting from all the particles in the simulations, to reduce unnecessary computational time costs in the following narrow phase. This method is called a sweep and prune algorithm [46].

Figure 3 illustrates the basic concept of the sweep and prune algorithm. In Fig. 3a, each particle has its own axis-aligned bounding box (AABB). The coordinates of corners for all the AABBs are sorted in ascending order in both X and Y directions in Fig. 3b. Then, Project Chrono sweeps through both lists to search the overlaps of corner coordinates. Potential contacts only exist if the AABBs overlap in both axes. For example, in the X axis, the X coordinates of boxes 2 and 3 overlap. In the Y axis, the Y coordinates of boxes 1 and 2, 1 and 3, and 2 and 3 overlap. Therefore, Boxes 2 and 3 overlap in both X and Y directions, so particles 2 and 3 are potentially contacting and pass the screening to the narrow phase. In 3D simulations, things are the same except the AABBs are sorted in X, Y, and Z axes.

Fig. 3

Illustration of the sweep and prune algorithm

In the narrow phase, the potential contacting particles will be evaluated by a Gilbert-Johnson-Keerthi (GJK) algorithm [47], which is able to efficiently compute the minimum distance between two potential contacting particles (such as d between particles 2 and 3 in Fig. 3a), to determine whether those two particles are in contact. After identifying the contacting particles, the contact force and then particle motions will be computed with the contact model.

2.2 Formation of contact model in project chrono

Particle motions include linear and angular movements (see Fig. 4). Based on Newton’s second law, linear and angular movements are described as:

$$ {\mathbf{F}} = m{\mathbf{a}} $$

(1)

$$ {\mathbf{M}} = I{{\varvec{\upbeta}}} $$

(2)

where F, m, and a are the force on the particle, the mass, and the linear acceleration of the particle, respectively; and M, I, and β are the moment on the particle, the moment of inertia, and the angular acceleration of the particle, respectively.

Fig. 4

Illustration of particle movements following Newton’s second law

The linear and angular velocities, along with the particle displacement and rotation, are calculated iteratively. In a semi-implicit Euler scheme, at time step t, the linear and angular velocities can be determined as:

$$ {\mathbf{v}}_{t + \Delta t} = {\mathbf{v}}_{t} + {\mathbf{a}}\Delta t = {\mathbf{v}}_{t} + \frac{{{\mathbf{F}}_{t} \Delta t}}{m} $$

(3)

$$ {{\varvec{\upomega}}}_{t + \Delta t} = {{\varvec{\upomega}}}_{t} + {{\varvec{\upbeta}}}\Delta t = {{\varvec{\upomega}}}_{t} + \frac{{{\mathbf{M}}_{t} \Delta t}}{I} $$

(4)

where Δt is the time step size used in the computation. Based on linear and angular velocities, the particle displacement and rotation at any time step t can be determined as:

$$ {\mathbf{x}}_{t + \Delta t} = {\mathbf{x}}_{t} + {\mathbf{v}}_{t + \Delta t} \Delta t $$

(5)

$$ {{\varvec{\uptheta}}}_{t + \Delta t} = {{\varvec{\uptheta}}}_{t} + {{\varvec{\upomega}}}_{t + \Delta t} \Delta t $$

(6)

where x_t and θ_t are the particle displacement and rotation at time step t, respectively.

Many soft contact models have been developed to determine interparticle contact forces [48]. The basic concept of these soft contact models is fundamentally the same. Overlaps between particles at contacts are allowed, and the magnitudes of contact forces are determined by the time-variant amounts of overlap.

The soft contact model used in Project Chrono is the Hertzian model [49], which is also widely applied in DEM codes. The Hertzian model is an analogy with a nonlinear spring-dashpot system, where the spring represents the elastic contact force and the dashpot governs the damping effect. For two contacting particles, the elastic force is positively correlated to the inter-particle overlap, while the damping force is determined by the damping ratio and the relative velocity. For example, two particles i and j are in contact in Fig. 5a and b, and the inter-particle normal and tangential contact forces f_n and f_s can be computed as:

$$ {\mathbf{f}}_{n} = \sqrt {R_{eff} \delta } (k_{n} {\mathbf{d}}_{n} - \gamma_{n} m_{eff} {\mathbf{v}}_{n} ) $$

(7)

$$ {\mathbf{f}}_{s} = \sqrt {R_{eff} \delta } ( - k_{s} {\mathbf{d}}_{s} - \gamma_{s} m_{eff} {\mathbf{v}}_{s} ) $$

(8)

where R_eff is the effective radius of curvature of two contacting particles; δ is the magnitude of overlap; k_n and k_s are the normal and tangential stiffness constants; d_n and d_s are the normal and tangential overlap vectors at the contact point; γ_n and γ_s are the normal and tangential damping coefficients; m_eff is the effective mass of two contacting particles; and v_n and v_s are the normal and tangential components of relative velocity at the contact point, respectively. With the masses of two contacting particles as m_i and m_j, the effective mass m_eff and effective radius of curvature R_eff can be computed as:

$$ m_{eff} = \frac{{m_{i} m_{j} }}{{m_{i} + m_{j} }} $$

(9)

$$ R_{eff} = \frac{{R_{i} R_{j} }}{{R_{i} + R_{j} }} $$

(10)

Fig. 5

Normal and tangential contact forces in soft contact model

The relative velocity v and its normal and tangential components v_n and v_s can be determined as:

$$ {\mathbf{v}} = ({\mathbf{v}}_{j} + {{\varvec{\upomega}}}_{j} \times {\mathbf{r}}_{j} ) - ({\mathbf{v}}_{i} + {{\varvec{\upomega}}}_{i} \times {\mathbf{r}}_{i} ) $$

(11)

$$ {\mathbf{v}}_{n} = ({\mathbf{v}} \cdot {\mathbf{n}}){\mathbf{n}} $$

(12)

$$ {\mathbf{v}}_{s} = {\mathbf{v}} - {\mathbf{v}}_{n} $$

(13)

where v_i and v_j are the linear velocities of particles i and j; ω_i and ω_j are the angular velocities of particles i and j; r_i and r_j are the vectors pointing from the centers of masses of particles i and j to the contact point; and n is the contact normal vector. Then, the normal and tangential overlapping vectors d_n and d_s can be determined as:

$$ {\mathbf{d}}_{n} = \delta {\mathbf{n}} $$

(14)

$$ {\mathbf{d}}_{s} = \int\limits_{{t_{0} }}^{t} {{\mathbf{v}}_{s} } dt - ({\mathbf{n}} \cdot \int\limits_{{t_{0} }}^{t} {{\mathbf{v}}_{s} } dt){\mathbf{n}} $$

(15)

where δ is the magnitude of overlap, t₀ is the time step at the beginning of contact, and t is the current time step.

The tangential contact force f_s can be determined using Coulomb’s law of friction (stick–slip condition) as shown in Fig. 5(b):

$$ \left| {{\mathbf{f}}_{s} } \right| = \left\{ {\begin{array}{*{20}l} {\left| {{\mathbf{f}}_{s} } \right|} \hfill & {{\text{if }}|{\mathbf{f}}_{s} | < \mu |{\mathbf{f}}_{n} |} \hfill \\ {\mu |{\mathbf{f}}_{n} |} \hfill & {{\text{if }}|{\mathbf{f}}_{s} | \ge \mu |{\mathbf{f}}_{n} |} \hfill \\ \end{array} } \right. $$

(16)

where μ is the friction coefficient. For low shear forces (|f_s|< μ|f_n|), there is no relative motion between two particles (stick). For high shear forces (|f_s|= μ|f_n|), there is relative motion between two particles (slip).

3 Soil specimen digitization

Monterey No. 0 sand, which is composed of subrounded to subangular grains comprising mainly quartz and feldspar [50], is used in this research. The characteristics of this type of sand are: mean diameter d_m = 0.45 mm, coefficient of uniformity C_u = 1.53, specific gravity SG = 2.65, target relative density D_r = 97% (maximum void ratio e_max = 0.860, minimum void ratio e_min = 0.565) [3, 50].

Based on the grain-size characteristics and angularity of the Monterey No. 0 sand, 500 sample particles scanned by a 3D laser scanner were selected from our particle library one by one, which are then stored as “STL” files (Fig. 6). Then these particle geometries are replicated to fill a 76 × 76 × 76 mm true triaxial test box, which has the same size as the soil specimen used in the true triaxial tests conducted by Lade and Duncan [3]. The size of particle geometries was magnified 10 times, otherwise, there would have been around 10,000,000 particles filling the triaxial test box, which greatly exceeds the computational capability. Therefore, the mean diameter of the scanned particles d_m’ = 4.5 mm, and around 10,000 particles were applied in the simulations (Fig. 7).

Fig. 6

Sample particles scanned by a 3D laser scanner

Fig. 7

Digitized soil specimen filled with scanned particles

4 Simulation setup

The simulation setup followed the experimental setup. The particles were rained into the test box to create the simulated specimen, which was then consolidated and vibrated to reach a dense state (void ratio e = 0.57), and then pre-stressed under the confining stress of 58.8 kPa. After that, in the shearing stage, the vertical strain ε₁ was constantly increased at a strain rate of 10% s⁻¹, until it reached 10%, while the horizontal strains ε₂ and ε₃ were controlled to apply specific horizontal stresses to the specimen. As Fig. 7 shows, the minimum horizontal stress is applied along x-axis, and its value σ₃ = 58.8 kPa. Then, the intermediate horizontal stress is applied along y-axis, and its value σ₂ is dependent on the intermediate principal stress ratio b [3], as:

$$ b = \frac{{\sigma_{2} - \sigma_{3} }}{{\sigma_{1} - \sigma_{3} }} $$

(17)

where σ₁ is the vertical stress which is dependent on the vertical strain ε₁.

The simulations were performed on a desktop computer with an Intel Xeon E5-1620 3.6 GHz 8-Core CPU, 16 GB memory, and an NVIDIA Quadro K620 GPU with 2 GB graphic memory. The simulation time for each specimen was about 4 h. The key modeling parameters are shown in Table 1. Specifically, the Young’s Modulus used here was around 1000 times smaller than the actual value, to maintain both the stability of simulation and the accuracy of results [49].

Table 1 Simulation parameters of soft and hard contact models

5 Results and discussions

5.1 Stress–strain behavior

From both numerical and experimental results (conducted by Lade and Duncan [3]), evolution of stress ratio and volumetric strain ε_v with increasing axial strain ε₁ and different b values is shown in Fig. 8. Specifically, the stress ratio η is defined as:

$$ \eta = \frac{{\sigma_{1} - \sigma_{3} }}{{\sigma_{1} + \sigma_{3} }} $$

(18)

Fig. 8

Evolution of numerical and experimental stress–strain behavior with different b values

Due to the limitation of experiment conditions, the experimental data after the failure of specimen could not be recorded. Thus, the simulation data go further than the experiment data do. According to Fig. 8, the stress ratios from experimental and numerical results have similar peak values, though the experimental stress ratios achieve their peak values earlier with the increasing of b value. As for the volumetric strain ε_v, the numerical and experimental results have quite good matches when b equals to 0 and 0.15, while the experimental ε_v raise earlier when b equals to 0.5, 0.75 and 1.

A summary of stress–strain behavior from simulation and experimental results is shown in Fig. 9. According to Fig. 9a, the peak stress ratio increases with b value first until b reaches 0.75, then decreases slightly. The relations between volumetric strain ε_v and axial strain ε₁ are shown in Fig. 9b, which shows the increase of the final volumetric strain with the increase of b value.

Fig. 9

Summary of stress–strain behavior from simulations and actual experiments: a stress ratio from simulations; b volumetric strain curves with different b values from simulations; c Peak friction angles d Peak dilation angles from both simulations and actual experiments

In triaxial tests, the friction angle ϕ is dependent on the stress ratio η, as:

$$ \phi = \arcsin (\eta ) $$

(19)

Figure 9c shows the relation between peak friction angle ϕ' and b value from both simulation and experiment results. In both results, the peak friction angle ϕ' increases with b located in the range between 0 and 0.75, then decreases with b reaches 1, which agrees with the observation in Fig. 9a. The agreement between numerical and experimental ϕ' is good, with the maximum divergence of 1.3°.

According to Hanson [51], the dilation angle ψ can be defined as:

$$ \psi = \arcsin \left( {\frac{{\left( {{{\Delta \varepsilon_{v} } \mathord{\left/ {\vphantom {{\Delta \varepsilon_{v} } {\Delta \varepsilon_{1} }}} \right. \kern-0pt} {\Delta \varepsilon_{1} }}} \right)}}{{\left( {{{\Delta \varepsilon_{v} } \mathord{\left/ {\vphantom {{\Delta \varepsilon_{v} } {\Delta \varepsilon_{1} }}} \right. \kern-0pt} {\Delta \varepsilon_{1} }} - 2} \right)}}} \right) $$

(20)

Figure 9d shows the relation between peak dilation angle ψ' and b value from both simulation and experiment results. In both results, the peak dilation angle ψ' increases with the increase of b value. Also, the agreement between numerical and experimental ψ' values is good, with the maximum divergence of 3°.

5.2 Particle motions

The displacement fields of all the particles with different b values are shown in Fig. 10. Each arrow represents the displacement vector of a particle. The color as well as the length of bar represent the magnitude of the displacement. According to Fig. 10, in all scenarios, particles close to top corners tend to have larger displacements than the particles close to the bottom-middle area, which is reasonable because the moving boundaries in the simulation are the top and side boundaries. Also, with the increase of b value, particle displacements get larger, and they tend to be mobilized along x-axis. This is reasonable because the minimum stress is along x-axis, and therefore the larger stresses occurring along other directions are pushing the particles to move along the direction with least resistance (x-axis).

Fig. 10

Particle displacement vectors with different b values

The particle rotations can be quantified in the form of quaternion. Assuming an object has a rotation θ about a rotation axis u = [u_x,u_y,u_z], where u_x,u_y,u_z are the components of u along x, y, and z axes as shown Fig. 11, a quaternion Q can be defined to represent the rotation of a particle:

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {q_{0} } \\ {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \left( {\frac{\theta }{2}} \right)} \\ {u_{x} \sin \left( {\frac{\theta }{2}} \right)} \\ {u_{y} \sin \left( {\frac{\theta }{2}} \right)} \\ {u_{z} \sin \left( {\frac{\theta }{2}} \right)} \\ \end{array} } \right] $$

(21)

Fig. 11

Illustration of particle rotation

Thus, with quaternion Q obtained by simulations, rotation θ can be calculated as:

$$ \theta = 2\arccos (q_{0} ) $$

(22)

The evolutions of average rotation (θ_mean) values during the shear stage with different b values are plotted in Fig. 12a, and the final θ_mean values with different b values are plotted in Fig. 12b. According to Fig. 12b, the final θ_mean value increases with the increase of b value as expected, since the larger b value leads to more violent movement in the specimen during the shear stage.

Fig. 12

a Evolutions of average particle rotations (θ_mean) during the shear stage with different b values. b Relation between b values and final θ_mean values

5.3 Fabrics

Soil specimen fabric can be quantified by scalar parameters (such as coordination number, contact index, the average branch vector length, etc.) and directional parameters (such as spatial distributions of particle long axes, contact normals, branch vectors, etc.) [52]. The coordination number and spatial distribution of contact normals are widely used for analyzing fabric evolution in DEM simulations, and therefore these parameters in both contact models are obtained and compared in this study.

5.3.1 Coordination numbers

The coordination number (CN) is quantified as the average number of contacts of a single particle in a granular system. Larger CN means stronger fabric formed in granular soils. If the total number of particles is N_p in the soil specimen and the total number of contacts is N_c, the CN is defined as:

$$ {\text{CN}} = \frac{{2N_{c} }}{{N_{p} }} $$

(23)

The CNs with different b values are shown in Fig. 13a. In all scenarios, CN values decrease with the shearing process. This is because the soil specimens dilate when they are sheared. Besides, higher b value leads to lower CN. This is because higher b value causes larger dilation, looser specimen, and therefore, smaller CN as shown in Fig. 13b.

Fig. 13

a The evolutions of coordination numbers (CNs) during the shear stage with different b values; b The relation between b values and final CNs

5.3.2 Contact normal distribution and anisotropy

Contact normals are vectors representing the normal directions of contact forces on contact points in a soil specimen. The spatial distribution of contact normals can be plotted as a 3D rose diagram as shown in Fig. 14c–h. Each bar represents the frequency of contact normals in this direction in the 3D space.

Fig. 14

Rose diagrams and density functions of contact normals before and after shear with different b values

Kanatani [53] showed that the rose diagram can be quantified by a density function f(n):

$$ f(n) = \frac{1}{2\pi }\left( {1 + D_{ij} n_{i} n_{j} + D_{ijkl} n_{i} n_{j} n_{k} n_{l} } \right)\left( {i,\;j\, = \,{1},{ 2},{ 3}} \right) $$

(24)

where n_i is the component of contact normal in axis i, and D_ij and D_ijkl are the second order deviatoric tensor, and the fourth order deviatoric tensors respectively:

$$ D_{ij} = \frac{2}{15}\left( {\phi_{ij} - \frac{1}{3}\delta_{ij} } \right) $$

(25)

$$ D_{ijkl} = \frac{2}{15}\left( {\phi_{ijkl} - \frac{6}{7}\delta_{ij} \phi_{kl} + \frac{3}{35}\delta_{ij} \delta_{kl} } \right) $$

(26)

where δ_ij is the Kronecker delta function:

$$ \delta_{ij} = \left\{ {\begin{array}{*{20}c} 1 & {i = j} \\ 0 & {i \ne j} \\ \end{array} } \right. $$

(27)

and φ_ij and φ_ijkl are second order and fourth order fabric tensors respectively:

$$ \varphi_{ij} = \frac{1}{{N_{c} }}\sum\limits_{m = 1}^{{N_{c} }} {n_{i}^{m} n_{j}^{m} } $$

(28)

$$ \varphi_{ijkl} = \frac{1}{{N_{c} }}\sum\limits_{m = 1}^{{N_{c} }} {n_{i}^{m} n_{j}^{m} } n_{k}^{m} n_{l}^{m} $$

(29)

where N_c is the total number of contact normals in the soil.

The contact normals for plotting the rose diagram are also used to determine density function based on Eqs. (24–29), which is also plotted in Fig. 14c–h. The density function is essentially the best fitting surface of the 3D rose diagrams. Both 3D rose diagram and density function illustrate the preferred direction of contact normals, but 3D rose diagram may be easier for visual observation of the preferred direction.

Figure 14a plots 3D rose diagrams and density functions of contact normals in the specimen before shear, while Fig. 14b–f plot the diagrams after shear with different b values. According to Fig. 14, the distribution of contact normal directions is highly isotropic in both x, y, and z axes before shear stage as shown in Fig. 14a. After shear stage (Fig. 14b), the distribution of contact normal directions is highly related to the b value: When b = 0, most of the contact normals are mobilized along the z-axis, while more contact normals get mobilized along the y-axis with the increase of b value, which is shown in the diagrams in Fig. 14b–f. This is reasonable because the intermediate horizontal stress σ_y increases with the increasing of b value, making the specimen more dense along the y-axis.

The second order fabric tensor φ_ij is a 3-by-3 matrix. Three principal values (eigenvalues) of the fabric tensor are φ₁, φ₂, and φ₃, which are commonly used for advanced geotechnical analysis, such as development anisotropic constitutive models and quantification of fabric anisotropy [54,55,56,57,58]. To measure the degree of fabric anisotropy, Barreto and O’Sullivan [59] proposed a generalized octahedral fabric factor based on φ₁, φ₂, and φ₃ values:

$$ \Psi = \frac{1}{\sqrt 2 }\left[ {\left( {\varphi_{1} - \varphi_{2} } \right)^{2} + \left( {\varphi_{1} - \varphi_{3} } \right)^{2} + \left( {\varphi_{2} - \varphi_{3} } \right)^{2} } \right]^{0.5} $$

(30)

The evolutions of φ₁, φ₂, and φ₃ with different b values are shown in Fig. 15a–e, and the evolution of Ψ with different b values during the shear stage are shown in Fig. 15f. According to Fig. 15a–e, in every scenario, φ₁, φ₂, and φ₃ are very close to each other before the shear stage starts. Then, the differences of these values increase in the strain hardening stage, and then decrease in the following strain softening stage. This agrees with the evolution of Ψ values shown in Fig. 15f: Ψ values are close to zero when axial strain ε_z = 0, then they increase until reaching their peaks before decreasing in the residual state.

Fig. 15

a–e Evolutions of fabric tensor eigenvalues with different b values; f Evolution of Ψ values with different b values

Specifically, in the final state (ε_z = 10%), the φ₁ value, reflecting fabric strength along x-axis (with constant minimum horizontal stress σ_x), keeps near 0.29 no matter how b value changes. In the meantime, the φ₂ value reflecting fabric strength along y-axis increases with the increasing of b value, but it never exceed φ₃ value reflecting fabric strength along z-axis, though it decreases with the increase of b value. Therefore, the final difference between fabric tensor eigenvalues keeps decreasing with the increase of b value, which agrees with Fig. 15f which shows that the final Ψ decreases with the increase of b value.

5.4 Force chains

Force chains are a key feature of DEM for visualizing the heterogeneity of granular systems under external loads, which allow DEM researchers to directly observe micro inter-particle force transmission and link micro and macro mechanical behavior of granular soils. This study developed functions that can be embedded into Project Chrono to plot force chains. Figure 16 shows the chain forces in both contact models with different shear strains. Each bar represents an inter-particle contact force, the color as well as the size of bar represent magnitude of the force, and the direction of the bar represents the direction of the contact force. According to Fig. 16, before the shear stage starts, the directions of contact force are highly randomly distributed, while after the shear stage, most contact forces are mobilized in the vertical direction, and the magnitudes of contact force increase a lot. This makes sense because the axial stress σ_z after shear stage is much larger than the one before shear stage. Besides, the magnitudes of contact force increase with the increase of b value, for the increase of b value also means the increase of the intermediate horizontal stress σ_y.

Fig. 16

Force chains of states before shear and after shear with different b values

6 Conclusion

This paper demonstrates the feasibility of using physics engine techniques for simulating true triaxial tests of realistic granular soils. A 3D laser scanner is used to scan realistic soil particles for simulation. The realistic particles are represented as triangular face tessellations in the physics engine, which precisely preserves particle geometries, especially the small and sharp corners on the particles, which is critical to reproducing the mechanical behavior of granular soils in simulations.

This study demonstrates that Project Chrono is able to yield stress–strain behaviors matching the experimental results when simulating true triaxial tests of irregular realistic particles, as well as output the important parameters for geotechnical analysis including particle displacements, particle rotations, coordination numbers, contact normals, contact forces, and force chains. Based on these parameters, advanced geotechnical analysis such as fabric evolution can be performed. The physics engine technique can be potentially used as a discrete element simulator for simulating realistic soil particles in geotechnical tests such as triaxial tests.