Simulating shearing behavior of realistic granular soils using physics engine

Abstract

The discrete element method (DEM) has become a preeminent numerical tool for investigating the mechanical behavior of granular soils. However, traditional DEM uses sphere clusters to approximate soil particles, which is not efficient in simulating realistic particles. This paper demonstrates the potential of using a physics engine technique to address limitations of the DEM method. Physics engines are originally developed for video games for simulating physical and mechanical processes that occur in the real world to create an immersive and realistic gaming experience. Physics engines use triangular face tesselations to represent objectives, which provides higher accuracy for modeling realistic particle geometries. This paper has three objectives. First, this paper introduces the physics engine technique to the geotechnical community. Second, this paper develops a series of pre-processing, servo-controlling, and post-processing functions embedded into physics engine to generate soil specimens with designed packing densities, perform direct shear tests, and output simulation results including stress–strain relations, fabrics, and force chains. Third, this paper develops a miniature direct shear test that can be scanned by X-ray computed tomography (X-ray CT) for evaluating the simulation accuracy of the physics engine. The numerical results agree well with experimental results. This study provides DEM modelers with physics engine as one more option for simulating realistic particles.

1 Introduction

1.1 Background

Granular materials are ubiquitous in nature and in industrial applications; they include sands, powders, chemicals, pharmaceuticals, and food products. Global annual production and processing of granular materials reach approximately ten billion metric tons, which consumes roughly 10% of all the energy produced on this planet [1]. Granular materials are one of the most processed materials in the global industry, second only to water [2]. In the U.S., the processing of granular materials costs approximately one trillion dollars annually [3]. Granular soils are critical construction materials for geotechnical infrastructures and are strongly related to geohazards, such as erosion, piping, and liquefaction.

The discrete element method (DEM) can explicitly simulate individual particles and obtain microscope particle behavior, including particle movements, inter-particle contact forces, and fabrics, which are difficult to measure in laboratory experiments [4]. Therefore, DEM has become a preeminent tool to study granular materials in various disciplines and has been used in geotechnical engineering to study the fundamental behavior of granular soils. However, the typical DEM uses spherical approximations rather than the actual particle shapes to simulate individual particles, which cannot provide adequately accurate insight into the mechanical behavior of granular soils and other granular materials consisting of non-spherical particles. Therefore, methods have been sought to simulate irregular particle shapes in DEM [5].

A significant process has been made to use idealized particle shapes, such as ellipsoids, spherical cylinders, pentagons, and rounded-cap elongated rectangles in DEM simulations [6,7,8,9,10,11,12,13]. However, these techniques cannot simulate realistic soil particles with irregular particle shapes. Clusters of overlapping spheres are currently the most popular method to model realistic soil particles in DEM [5, 14].

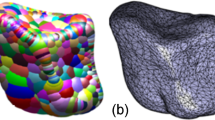
In computer graphics and computer-aided design, the 3D particle geometries are usually represented by triangular face tessellations, as shown in Fig. 1a. The sphere cluster method uses overlapping spheres to approximate triangle faces, as shown in Fig. 1b. This method assumes particles are rigid and cannot be crushed. Therefore, this method can simulate realistic particles while maintaining the ease of contact detection and force calculation. Many techniques have been developed to generate clusters such as Matsushima et al. [15], Price et al. [16], Ferellec and McDowell [14], Taghavi [17], and Zheng and Hryciw [5]. The sphere cluster method has been widely used in DEM codes such as Itasca PFC 2D/3D [17], LIGGGHTS [18], and YADE [19]. However, the sphere cluster method has limitations.

Fig. 1

Realistic particle geometry representations: a soil particle represented by a triangular face tessellation consisting of 2000 faces; b soil particle represented by a sphere cluster in discrete element method (DEM) consisting of 1054 spheres

To precisely represent particle geometries, especially the small and sharp corners on particles, the sphere cluster method must use a large number of spheres [5, 20]. However, the computational time will remarkably increase as increasing number of spheres. For example, the sphere cluster in Fig. 1b contains 1,054 spheres, but artificial bumpy surfaces can still be observed and some small corners are not well represented. To simulate 1000 sphere clusters and each particle consists of 1,054 spheres, a total of one million spheres must be used in the simulation, which exceeds the computational capabilities of standard desktops. High-performance computing resources have been used by some researchers to perform large-scale DEM simulations. However, these resources are generally not accessible to most researchers and practitioners [21].

Researchers have investigated the direct use of triangle face tessellations for DEM simulations (Fig. 1a) instead of using sphere cluster approximations. For example, Latham et al. [22, 23] used X-ray computed tomography (X-ray CT) to scan realistic particles and convert these particles to triangular tessellations for performing DEM simulations. Govender et al. [24,25,26,27,28] developed Blaze-DEM for using triangular tessellations for simulating realistic particles. The recent commercial DEM codes, Itasca PFC 6.0 [29], and Rocky DEM [30] can also use triangular tessellations in the simulation of realistic particles.

The goal of this paper is to introduce and evaluate a new platform, physics engine, to simulate realistic particles. This paper is not to use physics engines to replace any existing DEM codes such as PFC, LIGGGHTS, Yade, Blaze-DEM, Rocky DEM, or any other DEM codes. These existing codes are representing state-of-the-art platforms for DEM studies and applications. Our goal is to introduce physics engine to DEM modelers and provide DEM modelers with one more option that they may consider using when they are simulating realistic particles.

1.2 Introduction to physics engine techniques

In the area of computer science, simulations of rigid bodies and their interactions are critical in video games and computer-animated films. Thus, physics engines were developed for computer games to create a realistic and immersive gaming experience. For example, in the game Angry Birds, collisions among birds, pigs, and blocks are simulated by a physics engine, called Box2D [21]. In addition, physics engines have also been used in movie animations to create realistic virtual environments. For example, Matterhorn is one of Disney Animation’s proprietary physics engines, and it has been used in various movies by Disney (e.g., Frozen) [31].

The physics engines were initially developed for computer games and movie animations, so the computational speed and stability are primary focuses by compromising computational accuracy. However, driven by rapid development and high competitiveness of video gaming and movie industry, the accuracy of physics engines has been significantly improved in recent years. Therefore, physics engines have been increasingly used in scientifical computations in many disciplines, including robotic control [32, 33], granular materials [34,35,36], structural engineering [37], construction engineering [3, 38, 39], crowd simulation [40], biomedical engineering [41, 42], autonomous vehicle research [43], virtual and augmented reality [44], and psychological research [45].

The physics engine can use triangular face tessellations to simulate irregular particle shapes, and therefore it has been introduced by geotechnical researchers as a DEM simulation platform. Izadi and Bezujian [46] used a Bullet physics engine to simulate pluviation and vibration on three-dimensional (3D) randomly-shaped realistic particles. Pytlos et al. [47] used a Box2D physics engine to simulate biaxial compression tests of two-dimensional (2D) realistic particles. Very recently, He and Zheng [48] used a PhysX engine to simulate one-dimensional consolidation tests on 3D realistic particles.

There are many physics engines as reviewed by Ivaldi et al. [49]. This paper selects an open-source physics engine called Project Chrono as a simulation platform for two reasons: Project Chrono can directly use triangular face tessellations to represent irregular soil particles; Project Chrono integrates a soft contact model to simulate the mechanical behavior of granular soils.

Most physics engines use a hard contact model or impose-based dynamics contact model proposed by Mirtich and Canny [50]. However, the DEM codes use a soft contact model originally proposed by Cundall [51,52,53,54,55], such as Itasca PFC 2D/3D, LIGGGHTS, and YADE to simulate inter-particle contacts. The comparisons between the formations of hard and soft contact models can refer to He and Zheng [48].

However, Project Chrono cannot be directly used to simulate realistic granular soils because it cannot generate realistic particles; it does not contain servo-control algorithms to establish the boundary conditions for simulations of laboratory tests such as direct shear, and it does not output geotechnical parameters, such as stress, strain, and force chains. This study will customize and extend Project Chrono to include pre-processing, servo-control algorithms, and post-processing functions to address these limitations.

This paper develops a miniature direct shear test to evaluate the simulation accuracy of customized Project Chrono. The miniature direct shear test can generate a small soil specimen (30 mm × 30 mm × 16 mm) that can be scanned by X-ray Computed Tomography (X-ray CT). The X-ray CT scanned realistic particles are imported into Project Chrono to reconstruct realistic soil specimens. The Project Chrono is used to simulate the miniature direct shear tests. The simulation results are rigorously compared with experimental results to evaluate the accuracy of Project Chrono.

2 Process flow of Project Chrono

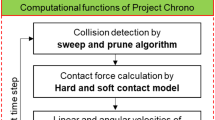
Project Chrono runs simulations with a time-stepping procedure as shown in Fig. 2. This section introduces the computational procedure in detail.

Fig. 2

Process flow of Project Chrono

2.1 Contact detection by sweep and prune algorithm

The contact detection in Project Chrono includes two phases: broad phase and narrow phase. In the broad phase, Project Chrono uses a sweep and prune algorithm to search pairs of particles that are potentially contacting, and to exclude pairs that are certainly not colliding, from all the particles in the simulations.

Three particles in Fig. 3a are used to illustrate the basic idea of sweep and prune algorithm. In Fig. 3a, the AABB (axis-aligned bounding box) is created for each particle. The corner coordinates for all the AABBs are sorted in ascending order in X and Y directions in Fig. 3b. Then, the Project Chrono sweeps through each list to search the overlaps of corner coordinates. For example, in the X axis, the X coordinates of boxes 2 and 3 overlap. In the Y axis, the Y coordinates of boxes 1 and 2, 1 and 3, and 2 and 3 overlap. Therefore, potential contacts can only exist if the bounding boxes overlap in both axes. Boxes 2 and 3 overlap in both X and Y directions. The particles 2 and 3 are potentially contacting.

Fig. 3

Illustration of the sweep and prune algorithm

In 3D simulations, the AABBs are sorted in X, Y, and Z axes. Then the potential contacting particles are identified by sweeping. The sweep and prune algorithm can quickly eliminate the vast majority of non-contacting particles and significantly increase simulation speed.

The potential contacting particles will be further evaluated in the narrow phase following a Gilbert-Johnson-Keerthi (GJK) algorithm [56]. This algorithm can efficiently compute the minimum distance between two potential contacting particles, such as the d between particles 2 and 3 in Fig. 3a, to determine whether these two particles are in contact. After identifying the contacting particles, the contact model will be used to compute contact force and particle movements.

2.2 Formation of contact model in Project Chrono

Particle motions consist of linear and angular movements as shown in Fig. 4. Based on Newton’s second law, linear and angular movements can be described as:

$${\mathbf{F}} = m{\mathbf{a}}$$

(1)

$${\mathbf{M}} = I{{\varvec{\upbeta}}}$$

(2)

where F, m, and a are the force applied on the particle, the mass, and the linear acceleration of the particle, respectively; and M, I, and β are the moment applied on the particle, the moment of inertia, and the angular acceleration of the particle, respectively.

Fig. 4

Illustration of particle movements following Newton’s second law

The linear and angular velocities, as well as the displacement and rotation of particle, are computed iteratively. For example, in a semi-implicit Euler scheme, at time t, the linear and angular velocities can be computed as:

$${\mathbf{v}}_{t + \Delta t} = {\mathbf{v}}_{t} + {\mathbf{a}}\Delta t = {\mathbf{v}}_{t} + \frac{{{\mathbf{F}}_{t} \Delta t}}{m}$$

(3)

$${{\varvec{\upomega}}}_{t + \Delta t} = {{\varvec{\upomega}}}_{t} + {{\varvec{\upbeta}}}\Delta t = {{\varvec{\upomega}}}_{t} + \frac{{{\mathbf{M}}_{t} \Delta t}}{I}$$

(4)

where Δt is the time step size used in the computation. Based on linear and angular velocities, the displacement and rotation of the particle at any time t can be computed as:

$${\mathbf{x}}_{t + \Delta t} = {\mathbf{x}}_{t} + {\mathbf{v}}_{t + \Delta t} \Delta t$$

(5)

$${{\varvec{\uptheta}}}_{t + \Delta t} = {{\varvec{\uptheta}}}_{t} + {{\varvec{\upomega}}}_{t + \Delta t} \Delta t$$

(6)

where x_t and θ_t are the displacement and rotation of the object at time t, respectively.

Many soft contact models have been developed to determine interparticle contact forces as reviewed by Horabik and Molenda [57]. The basic concept of these soft contact models is essentially the same. The soft contact model allows the contacting particles to overlap at contacts. The amount of overlapping determines the normal and frictional force following force–displacement laws. Details on how the overlap and gravity center are calculated are shown in “Appendix 1”. The key input contact parameters include normal stiffness, shear stiffness, and friction coefficient. The stiffnesses are usually set at very high values in order to yield small amounts of overlapping compared to particle size. Because of the high stiffnesses, the time step size in the computation has to be small to yield small elastic rebound at each step to ensure numerical stability.

The soft contact model in Project Chrono is the Hertzian model [58], which is also widely used in DEM codes. The Hertzian model may be an analogy with a nonlinear spring-dashpot system. The spring represents the elastic contact force, and the dashpot governs the damping effect. For two particles in contact, the elastic force is positively correlated to the inter-particle overlap, and the damping force is determined by the damping ratio and the relative velocity. For example, two particles i and j are in contact in Fig. 5a, b, the inter-particle normal and tangential components of contact forces f_n and f_s can be determined as:

$${\mathbf{f}}_{n} = \sqrt {R_{eff} \delta } (k_{n} {\mathbf{d}}_{n} - \gamma_{n} m_{eff} {\mathbf{v}}_{n} )$$

(7)

$${\mathbf{f}}_{s} = \sqrt {R_{eff} \delta } ( - k_{s} {\mathbf{d}}_{s} - \gamma_{s} m_{eff} {\mathbf{v}}_{s} )$$

(8)

where R_eff is the effective radius of curvature of two contacting particles; δ is the magnitude of overlap; k_n and k_s are the normal and tangential stiffness constants; d_n and d_s are the normal and tangential overlap vectors at the contact point; γ_n and γ_s are the normal and tangential damping coefficients; m_eff is the effective mass of two contacting particles; and v_n and v_s are the normal and tangential components of relative velocity at the contact point, respectively.

Fig. 5

Normal and tangential contact forces in soft contact model

Assuming the masses of two contacting particles are m_i and m_j, the effective mass m_eff and effective radius of curvature R_eff can be determined as:

$$m_{eff} = \frac{{m_{i} m_{j} }}{{m_{i} + m_{j} }}$$

(9)

$$R_{eff} = \frac{{R_{i} R_{j} }}{{R_{i} + R_{j} }}$$

(10)

The relative velocity v and its normal and tangential components v_n and v_s can be computed as:

$${\mathbf{v}} = ({\mathbf{v}}_{j} + {{\varvec{\upomega}}}_{j} \times {\mathbf{r}}_{j} ) - ({\mathbf{v}}_{i} + {{\varvec{\upomega}}}_{i} \times {\mathbf{r}}_{i} )$$

(11)

$${\mathbf{v}}_{n} = ({\mathbf{v}} \cdot {\mathbf{n}}){\mathbf{n}}$$

(12)

$${\mathbf{v}}_{s} = {\mathbf{v}} - {\mathbf{v}}_{n}$$

(13)

where v_i and v_j are the linear velocities of particles i and j; ω_i and ω_j are the angular velocities of particles i and j; r_i and r_j are the vectors pointing from the centers of masses of particles i and j to the contact point; and n is the contact normal vector. Then, the normal and tangential overlapping vectors d_n and d_s can be determined as:

$${\mathbf{d}}_{n} = \delta {\mathbf{n}}$$

(14)

$${\mathbf{d}}_{s} = \int\limits_{{t_{0} }}^{t} {{\mathbf{v}}_{s} } dt - ({\mathbf{n}} \cdot \int\limits_{{t_{0} }}^{t} {{\mathbf{v}}_{s} } dt){\mathbf{n}}$$

(15)

where δ is the degree of overlap, t₀ is the time at the beginning of contact, and t is the current time.

The tangential contact force f_s can be determined using Coulomb’s law of friction (stick–slip condition) as shown in Fig. 5b:

$$\left| {{\mathbf{f}}_{s} } \right| = \left\{ {\begin{array}{*{20}l} {\left| {{\mathbf{f}}_{s} } \right|} \hfill & {{\text{ if }}|{\mathbf{f}}_{s} | < \mu |{\mathbf{f}}_{n} |} \hfill \\ {\mu |{\mathbf{f}}_{n} |} \hfill & {{\text{if }}|{\mathbf{f}}_{s} | \ge \mu |{\mathbf{f}}_{n} |} \hfill \\ \end{array} } \right.$$

(16)

where μ is the friction coefficient. For low shear forces (|f_s|< μ|f_n|), there is no relative motion between two particles (stick). For high shear forces (|f_s|= μ|f_n|), there is relative motion between two particles (slip).

3 Miniature direct shear tests scanned by X-ray CT

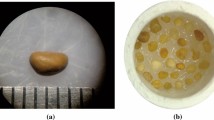
Despite shortcomings in the direct shear test such as a predefined failure plane, lack of measurement of pore water pressures, and non-uniformity of the stress and strain applied to the specimen due to effects of lateral boundary conditions, the direct shear test is routinely used to determine the stress–displacement and volume change behavior of sands during shear. The direct shear test provides a good means of determining the shear strength parameters when tested either dry or with water. The regular-sized direct shear box is too large for X-ray CT scanning because of the restrictions of the field of view and resolution of X-ray CT. Therefore, this study has constructed a miniature direct shear box as shown in Fig. 6a, b, d. This miniature direct shear box can create a 30 × 30 × 16 mm soil specimen. ASTM D3080 [65] specifies that the size of a test sample must be 6 to 10 times the largest particle size of the material being tested to reduce boundary effects. These size specifications allow the use of direct shear testing apparatus for small and large particles. Large size direct shear devices are routinely used to test particle sizes of up to 25 mm in size. The miniature direct shear box used in the research meets the ASTM standard requirements as the largest particle size tested was 0.841 mm, hence the small specimen size apparatus meets the criterion. Using the high-resolution X-ray CT at Iowa State University (ISU), the scanned image has a resolution of 10 μm/voxel. The image size of the specimen is 3000 × 3000 × 1600 voxels. The miniature direct shear box can be installed into an outer box as shown in Fig. 6c, e. Then the outer box can be installed into a direct shear device as shown in Fig. 6f. The routine direct shear testing procedure can be used to perform the miniature direct shear test.

Fig. 6

The X-ray CT scanned miniature direct shear test proposed in this study (unit is in mm): a the top cap and loading sphere; b miniature direct shear box; c outer box that can be installed into a direct shear device; d assembled miniature direct shear box; e assembled outer direct shear box; f outer direct shear box is installed into a direct shear device

Four types of sands—crushed limestone (very angular to sub-angular), Griffin sand (sub-angular to sub-rounded), Ottawa sand (rounded), and Glass beads (well-rounded)—are used in this study. These four sands span the range of typical particle shapes in natural sands. Particles in a range from 0.841 mm (#20 sieve) to 0.707 mm (#25 sieve) are used. After X-ray CT scan, the mean particle size are (0.774 mm)/(10 μm/voxel) = 77 voxels. Direct shear tests are performed on each sand under the normal stress of 100 kPa. Soil specimens are carefully prepared in dense conditions to protect against possible external disturbance during X-ray CT scanning. The target relative densities (D_r) are in a range of 95% to 100%. The index void ratios and relative densities for four sands are D_r = 96% (e_max = 1.08, e_min = 0.56) for crushed limestone, D_r = 97% (e_max = 0.86, e_min = 0.53) for Griffin sand, D_r = 96% (e_max = 0.75, e_min = 0.52) for Ottawa sand, and D_r = 96% (e_max = 0.75, e_min = 0.50) for glass beads.

The 3D volumetric image scanned by X-ray CT was processed using an improved watershed analysis developed by Sun et al. [59] to separate air and particles, segment contacting particles, and identify individual particles as shown in Fig. 7. Then the particles were converted into triangular face tessellations (each particle consisting of 2000 triangular faces). A series of pre-processing functions were developed in Project Chrono to read the triangular face tessellations and reconstruct direct shear specimens.

Fig. 7

The miniature direct shear specimen scanned by X-ray CT

The particle shape is quantified by roundness proposed by Wadell [60,61,62]:

$$R = \frac{{\text{Average radius of curvature of corners }}}{{\text{Radius of the largest inscribed circle}}} = \frac{1}{{r_{in} }}\left( {\frac{1}{N}\sum\limits_{i = 1}^{N} {r_{i} } } \right)$$

(17)

where r_i is the radius of the ith circle fitting to the ith corner to compute the radius of curvature, N is the total number of corners, and r_in is the radius of the maximum inscribed circle. Zheng and Hryciw [63, 64] developed a computational geometry algorithm, which can automatically compute R values of 3D particle geometries. The computational geometry code analyzed 3D particles in Fig. 7. The average R values for crushed limestone, Griffin sand, and Ottawa sand are shown in Fig. 8. For each sand, five typical particles are shown in Fig. 8. The R values for glass beads are 1.0, and therefore, glass beads are not plotted in Fig. 8.

Fig. 8

The typical particles of three natural sands and particle shape characterizations

4 Laboratory and simulation setups

In laboratory direct shear tests, the specimens were consolidated under the normal stress of 100 kPa. After the system reached its stable state, the shear stage started. During the shear stage, the specimens were sheared using a speed of 0.024 mm/min following ASTM D3080 [65] until the specimen deformation reached 3 mm.

A series of servo-control functions were developed to establish the boundary conditions for performing direct shear tests as shown in Fig. 9. The virtual direct shear tests in Project Chrono were also executed with the same normal stress and shear speed so that the experimental results can be compared to the simulation results. The simulations are performed on a desktop with an Intel Xeon E5-1620 3.6 GHz 8-Core CPU, 16 GB memory, and a NVIDIA Quadro K620 GPU with 2 GB graphic memory. The simulation time for each specimen was about 3 h.

Fig. 9

The direct shear simulation setups: a after consolidation; b after shear stage

The key modeling parameters are shown in Table 1. There is a large body of literature focusing on rigorous laboratory tests to determine inter-particle friction coefficients of various sands [66,67,68,69,70,71]. Sandeep and Senetakis [71] performed an excellent review of these studies and concluded that the inter-particle friction coefficients for crushed limestone, Quartz sands, and glass beads were 0.28 $\pm$ 0.08, 0.19 $\pm$ 0.08, and 0.12 $\pm$ 0.02, respectively. Therefore, inter-particle friction coefficients for Crushed limestone, Griffin sand (Quartz sand), Ottawa sand (Quartz sand), glass beads are set as 0.28, 0.19, 0.19, and 0.12, respectively. Details on determination of the contact stiffnesses and the damping coefficients are shown in “Appendix 2”.

Table 1 Simulation parameters of soft and hard contact models

5 Simulation results and analysis

5.1 Stress–strain behavior

The relationship between the ratio of shear force F to normal force N (F/N) versus shear strain ε_s (the ratio of horizontal displacement d_h to specimen length) is shown in Fig. 10a. The relationship between vertical displacement (d_v) and ε_s is shown in Fig. 10b.

Fig. 10

Stress–strain behavior from real and virtual direction shear tests (GB = glass beads, OT = Ottawa sands, GR = Griffin sands, CL = Crushed limestones)

The mobilized friction angle ϕ can be calculated as:

$$\phi = \arctan \left( \frac{F}{N} \right)$$

(18)

The dilation angle ψ can be calculated as:

$$\psi = \arctan \left( {\frac{{\Delta d_{v} }}{{\Delta d_{h} }}} \right)$$

(19)

The numerical and experimental peak friction angle (ϕ_p) and peak dilation angle (ψ_p) are compared Fig. 10c, d. The agreements are remarkable, with the maximum divergence of 1° for ϕ_p values and 3° for ψ_p values. In both simulation and laboratory results, ϕ_p and ψ_p decrease with increasing particle roundness R, or decreasing particle angularity, as shown in Fig. 10c, d. This observation agrees with the experimental observations of Santamarina and Cho [72], Cho et al. [73], Bareither et al. [74] and others. The agreement of the simulation and laboratory results for ϕ_p are excellent for each of the soil materials. There is some divergence in the simulation and laboratory results for ψ_p, which can be attributed to the divergence in the volume change results shown in Fig. 10b. Herein the simulations were conducted to 10 percent strain. To show that the critical state would be reached at higher strains a set of simulations were conducted on the crushed limestones whose shear/normal stress ratio curve reaches the peak and flattens most slowly, with the results shown in “Appendix 3”. The results show that the critical state is reached at strains higher than 10 percent.

The literature contains a number of papers wherein direct shear tests were simulated using FEM or DEM clump method. Generally, the FEM analyses are in terms of a continuum and the authors simulate the direct shear test while seeing the soil specimen as a whole continuous material. For example, Ziale Moayed et al. [75] applied finite element method to simulate direct shear test on a sandy clay. On the other hand, DEM clump method considers soil as a number of discrete particles, representing them as sphere clumps, and is more frequently applied in geotechnical simulations including direct shear test simulations. With the DEM clump method, Yan and Ji [76] simulated direct shear tests on irregular limestone rubbles and Wang et al. [77] and Indraratna et al. [78] simulated direct shear tests on railway ballast. In these simulations, the numerical stress–strain relations resembled the experiment results well. Herein, the use of realistic soil particles with irregular particle shapes in simulated direct shear testing using a physics engine has obtained similarly excellent agreement with experimental results.

5.2 Particle motion

Particle horizontal displacements as a function of particle vertical positions are shown in Fig. 11. The vertical position of the upper surface of lower half direct shear box is considered zero in the vertical axis. The horizontal displacements of particles in the upper and lower zones are tightly strained, while the displacements in the middle zone distribute among the entire horizontal axis. Based on visual examination of the results in Fig. 11, the middle zones can be considered as shear bands. The shear bands are located between -3.5 mm and 3.5 mm in the vertical axis for four soils. The particle shape does not affect the width of shear bands, and the possible reason is that the width of shear band depends highly on the gap width between the upper and lower parts of the direct shear box, which is the same in all simulations.

Fig. 11

Particle horizontal displacement versus vertical position

The particle rotations can be quantified in the form of quaternion. Assuming an object has a rotation θ about a rotation axis u = [u_x,u_y,u_z], where u_x,u_y,u_z are the components of u along x, y, and z axes as shown Fig. 12, a quaternion Q can be defined to represent the rotation of a particle:

$${\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {q_{0} } \\ {q_{1} } \\ {q_{2} } \\ {q_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \left( {\frac{\theta }{2}} \right)} \\ {u_{x} \sin \left( {\frac{\theta }{2}} \right)} \\ {u_{y} \sin \left( {\frac{\theta }{2}} \right)} \\ {u_{z} \sin \left( {\frac{\theta }{2}} \right)} \\ \end{array} } \right]$$

(20)

Fig. 12

Illustration of particle rotation

Thus, with quaternion Q obtained by simulations, rotation θ can be calculated as:

$$\theta = 2\arccos (q_{0} )$$

(21)

The average rotation (θ_mean) values of all the particles as well as of the particles in the shear bands are plotted in Fig. 13a. For all specimens, the θ_mean of particles in shear band is approximately twice larger than the θ_mean of all the particles. The θ_mean increases with the increasing R values as shown in Fig. 13b.

Fig. 13

Particle rotations for all the particles and particles in shear bands in different specimens (GB = Glass beads, OT = Ottawa sands, GR = Griffin sands, CL = Crushed limestones)

The interlocking of angular and elongated particles impedes rotation and sliding of particles and necessitates large volumetric increase (dilation) for shearing to occur. At high stress levels, particle crushing may also occur. Well-graded soils have smaller void ratios and more interparticle contacts. Smaller pore space and more contacts will also require greater dilatancy during shear.

5.3 Fabric analysis

Soil specimen fabric can be quantified by scalar parameters (such as coordination number, contact index, the average branch vector length, etc.) and directional parameters (such as spatial distributions of particle long axes, contact normals, branch vectors, etc.) [79]. The coordination number and spatial distribution of contact normals are widely used for analyzing fabric evolution in DEM simulations, and therefore these parameters in both contact models are obtained and compared in this study.

The coordination number (CN) is quantified as the average number of contacts of a single particle in a granular system. Larger CN means stronger fabric formed in granular soils. If the total number of particles is N_p in the soil specimen and the total number of contacts is N_c, the CN is defined as:

$${\text{CN}} = \frac{{2N_{c} }}{{N_{p} }}$$

(22)

The CN values of all the particles, as well as particles in shear bands are shown in Fig. 14a. The CN values decrease with the shear process because the soil specimens dilate when they are sheared. In addition, rounded soils lead to higher CN values because rounded cause smaller dilation, denser specimen, and therefore, larger CN as shown in Fig. 14b. The trends of CN evolution in shear band are the same as the trends of all particles, while the magnitude of CN in the shear band is larger than the CN of all the particles.

Fig. 14

The evolutions of coordination numbers (CNs) and the relationship between particle roundness and final CNs (GB = Glass beads, OT = Ottawa sands, GR = Griffin sands, CL = Crushed limestones)

Contact normals are vectors representing the normal directions of contact forces on contact points in a soil specimen. The spatial distribution of contact normals can be plotted as a 3D rose diagram as shown in Fig. 15b–i. Each bar represents the frequency of contact normals in this direction in the 3D space.

Fig. 15

Rose diagrams and density functions of contact normals for all the particles and particles in shear bands after shear stage (ε_s = 10%)

Kanatani [80] showed that the rose diagram can be quantified by a density function f(n):

$$f(n) = \frac{1}{2\pi }\left( {1 + D_{ij} n_{i} n_{j} + D_{ijkl} n_{i} n_{j} n_{k} n_{l} } \right)\quad \left( {i,j = \, 1, \, 2, \, 3} \right)$$

(23)

where n_i is the component of contact normal in axis i, and D_ij and D_ijkl are the second-order deviatoric tensor and the fourth-order deviatoric tensors, respectively:

$$D_{ij} = \frac{2}{15}\left( {\phi_{ij} - \frac{1}{3}\delta_{ij} } \right)$$

(24)

$$D_{ijkl} = \frac{2}{15}\left( {\phi_{ijkl} - \frac{6}{7}\delta_{ij} \phi_{kl} + \frac{3}{35}\delta_{ij} \delta_{kl} } \right)$$

(25)

where δ_ij is the Kronecker delta function:

$$\delta_{ij} = \left\{{\begin{array}{*{20}l} 1 \hfill &\quad {i = j} \hfill \\ 0 \hfill &\quad {i \ne j} \hfill \\ \end{array} } \right.$$

(26)

and φ_ij and φ_ijkl are second-order and fourth-order fabric tensors respectively:

$$\varphi_{ij} = \frac{1}{{N_{c} }}\sum\limits_{m = 1}^{{N_{c} }} {n_{i}^{m} n_{j}^{m} }$$

(27)

$$\varphi_{ijkl} = \frac{1}{{N_{c} }}\sum\limits_{m = 1}^{{N_{c} }} {n_{i}^{m} n_{j}^{m} } n_{k}^{m} n_{l}^{m}$$

(28)

where N_c is the total number of contact normals in the soil.

The contact normals for plotting the rose diagram are also used to determine density function based on Eqs. (23) to (28), which is also plotted in Fig. 15b–i. The density function is essentially the best fitting surface of the 3D rose diagrams. Both 3D rose diagram and density function illustrate the preferred direction of contact normals, but 3D rose diagram may be easier for visual observation of the preferred direction.

Figure 15b–h plot 3D rose diagrams and density functions for all the contact normals. After the shear stage as shown in Fig. 15a, the resistant force along the diagonal direction of the specimen mobilizes more contact normals in this direction. Therefore, the 3D rose diagrams are skewed diagonally, exhibiting an anisotropic fabric. Figure 15c–i plots 3D rose diagrams and density functions for contact normals in shear band. After shear, stronger preferred diagonal direction is observed for contact normals in shear band.

The second-order fabric tensor φ_ij is a 3-by-3 matrix. Three principal values (eigenvalues) of the fabric tensor are φ₁, φ₂, and φ₃, which are commonly used for advanced geotechnical analysis, such as development anisotropic constitutive models and quantification of fabric anisotropy [81,82,83,84,85]. To measure the degree of fabric anisotropy, Barreto and O’Sullivan [86] proposed a generalized octahedral fabric factor based on φ₁, φ₂, and φ₃ values:

$$\Psi = \frac{1}{\sqrt 2 }\left[ {\left( {\varphi_{1} - \varphi_{2} } \right)^{2} + \left( {\varphi_{1} - \varphi_{3} } \right)^{2} + \left( {\varphi_{2} - \varphi_{3} } \right)^{2} } \right]^{0.5}$$

(29)

The evolutions of Ψ during the shear stage of all particles and particles in shear bands of all specimens are shown in Fig. 16a. Particles display an isotropic fabric after consolidation as the Ψ is close to zero at ε_s = 0 as shown in Fig. 16a. Then, the degree of fabric anisotropy Ψ increases as the shear continues until it reaches the peak. Then, Ψ decreases in the residual state. The Ψ values in the shear band is larger than the Ψ values of all particles. Besides, the peak value of Ψ (Ψ_p) decreases with the increasing R as shown Fig. 16b.

Fig. 16

The evolution of generalized octahedral fabric factors (Ψ) and the relationship between particle roundness and peak Ψ values (GB = Glass beads, OT = Ottawa sands, GR = Griffin sands, CL = Crushed limestones)

5.4 Force chains

Force chains are a key feature of DEM for visualizing the heterogeneity of granular systems under external loads. Force chains allowed DEM researchers to directly observe micro inter-particle force transmission and link micro and macro mechanical behavior of granular soils. This study develops functions that can be embedded into Project Chrono to plot force chains as shown in Fig. 17 shows. Each bar represents an inter-particle contact force, the color as well as the size of bar represent magnitudes of the forces, and the direction of the bar represents the directions of forces. According to Fig. 17, for all specimens, after the shear stage (ε_s = 10%), most of inter-particle contact forces were mobilized in the diagonal direction, and the magnitude of contact forces increased with the increasing of the particle angularity. This is because the resistant force in the shear stage increases with the increasing of particle angularity.

Fig. 17

The force chains of different specimens after the shear stage

In summary, the comparisons between numerical and experimental results as shown in Fig. 10a, b demonstrate that Project Chrono can accurately reproduce macro stress–strain behavior of granular soils with different shapes. The Project Chrono can output micro particle scale properties that cannot be measured by laboratory tests explaining macro mechanical behavior. The angular particles including many small and sharp corners, leading strong interlocking and strong fabric anisotropy as shown in Fig. 16. Thus, the strong interlocking of angular particles impedes rotation and sliding of particles, resulting in small particle rotations as shown in Fig. 13, and necessitates large volumetric increase (dilation) as shown in Fig. 10d, large strength as shown in Fig. 10c, and large contact force as shown in Fig. 17. The large dilations of angular particles cause large void ratios, few interparticle contacts and small coordination numbers as shown in Fig. 14.

6 Conclusion

This paper demonstrates the feasibility of using physics engine techniques for simulating realistic particles of granular soils. X-ray CT is used to scan soil specimens to generate realistic particles for simulation. The realistic particles are represented as triangular face tessellations in the physics engine, which precisely preserve particle geometries. The small and sharp corners of particles can be preserved, which is critical to reproducing the mechanical behavior of granular soils in simulations. To address the deficiency of pre-processing, servo-controlling, and post-processing functions for DEM simulations, which is a major limitation of physics engine, a series of functions that can be embedded into Project Chrono are developed in Project Chrono, allowing it to perform direct shear simulations.

This study demonstrates that Project Chrono can yield stress–strain behaviors matching the experimental results when simulating direct shear tests of irregular realistic particles with different particle angularities, showing the increasing trends of shear/normal stress ratio and top plate dilation with the increasing of particle angularities; Besides, this study shows that Project Chrono can output the important parameters for geotechnical analysis including contact normals, contact forces, force chain, strain, and stress. Based on these parameters, advanced geotechnical analysis, such as fabric evolution, can be performed. These analysis have shown the increasing trends of resistant force and fabric anisotropy, as well as the decreasing trend of specimen density with the increasing of particle angularity.

In summary, the physics engine technique can be potentially used as a discrete element simulator for simulating realistic particles.

Appendices

Appendix 1

1.1 Calculation of particle gravity center

To calculate the particle gravity center, assume there are n triangular faces on a particle, and for the ith triangular face, there are three vertices V_i1, V_i2, V_i3, which located in (v_i1|_x, v_i1|_y, v_i1|_z), (v_i2|_x, v_i2|_y, v_i2|_z), (v_i3|_x, v_i3|_y,v_i3|_z), then, the location of the gravity center can be determined as (L|_x, L|_y, L|_z), where:

$$\begin{aligned} L|_{x} & = \frac{{\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{x} \cdot \sum\limits_{j = 1,k = 1}^{j = 3,k = 3} {\left[ {v_{ij} |_{x} v_{ik} |_{x} } \right]} }}{{4\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{x} \cdot \sum\limits_{j = 1}^{3} {\left[ {v_{ij} |_{x} } \right]} }}, \\ L|_{y} & = \frac{{\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{y} \cdot \sum\limits_{j = 1,k = 1}^{j = 3,k = 3} {\left[ {v_{ij} |_{y} v_{ik} |_{y} } \right]} }}{{4\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{x} \cdot \sum\limits_{j = 1}^{3} {\left[ {v_{ij} |_{x} } \right]} }}, \\ L|_{z} & = \frac{{\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{z} \cdot \sum\limits_{j = 1,k = 1}^{j = 3,k = 3} {\left[ {v_{ij} |_{z} v_{ik} |_{z} } \right]} }}{{4\sum\limits_{i = 1}^{n} {\left[ {({\mathbf{V}}_{2} - {\mathbf{V}}_{1} ) \times ({\mathbf{V}}_{3} - {\mathbf{V}}_{1} )} \right]} |_{x} \cdot \sum\limits_{j = 1}^{3} {\left[ {v_{ij} |_{x} } \right]} }} \\ \end{aligned}$$

(30)

1.2 Calculation of contact force eccentricities

With the locations of gravity center and contact point known, as well as the direction of contact force calculated, the eccentricity of contact force is easy to obtain: it is the distance between the contact point and the projection of gravity center on the plane which includes the contact point and perpendicular to the contact force direction.

Appendix 2

2.1 Determination of contact stiffnesses

The same parameters as the ones used in the paper authored by Fleischmann et al. [58] are used in this paper. Fleischmann et al. [87] state that the relation between contact stiffnesses k_n, k_t, and Poisson’s ratio ν is:

$$\frac{{k_{t} }}{{k_{n} }} \approx \frac{2(1 - \nu )}{{2 - \nu }}$$

(31)

Herein, k_t = 8 × 10¹¹ N/m, k_n = 10¹² N/m, ν = 0.3 (for all materials except crushed limestones) or 0.25 (for crushed limestones), approximately matched the relation above. Considering that the shearing behavior of a granular medium does not appear to be very sensitive to the exact values of k_n and k_t, this approximation is sufficient to get accurate simulation results.

2.2 Effects of damping coefficients

To investigate the effects of damping coefficients γ_n and γ_t on the results, three sets of damping coefficients (γ_n: 20 s⁻¹, γ_t: 10 s⁻¹; γ_n: 40 s⁻¹, γ_t: 20 s⁻¹, currently used for all other simulations; γ_n: 80 s⁻¹, γ_t: 40 s⁻¹) are used in the rerunning of the simulation for glass beads. The stress–strain behaviors are shown below:

As shown in Fig. 

Fig. 18

Stress–strain behaviors with different damping coefficient settings

18a, the peak shear/normal stress ratios are very close despite the change of damping coefficients, with a maximum divergence of 2%; As shown in Fig. 18b, the final top plate vertical displacement decreases with the increasing of damping coefficients (which is more apparent when normal and tangential damping coefficients reaches 80 s⁻¹ and 40 s⁻¹); Nevertheless, the maximum divergence does not exceed 5%. Therefore, it can be considered that the damping coefficients do not affect the simulation results markedly.

Appendix 3

3.1 Critical states in direct shear simulation

The final horizontal strain is set as 10% in this paper. As shown in Fig. 10, all specimens have reached the strain softening stage, and both the shear/normal stress ratio curves and the top plate dilation curves have been flattening at the end of the simulations. Although the curves have not totally flattened at 10% strain, they would be expected to flatten with higher horizontal strain, where they reach their critical states.

To show this, we reran the simulation with crushed limestones (whose shear/normal stress ratio curve reaches the peak and flattens most slowly), and kept the shear process going until horizontal strain reaches 20%. As shown in Fig. 

Fig. 19

a Shear/normal stress ratio curve; b top plate displacement curve with crushed limestones

19, the flattened shear/normal stress ratio curve and top plate dilation curve shows the critical state is reached:

Therefore, though not shown in Fig. 10, the critical states are bound to be reached in the simulations.