1 Introduction

Deformable particles are present in many complex multiphase flows such as aerosols, fibre flows, and biological flow. The physics of the particulate flows with suspended deformable particles is more complicated than the ones with rigid particles. Rigid particles exhibit no topology change in interaction with the surrounding flow while deformable particles undergo severe changes in their shape due to their elasticity which in turn leads to complex interaction with the carrier fluid. In the case of blood flow, the biological cells (e.g. RBC) can be described as deformable particles suspended in the blood plasma. During the blood transport process, the RBCs deform and migrate towards the centre of the blood vessel which leads to the formation of a cell-free layer (CFL) and changing the apparent viscosity of blood [1,2,3,4,5].

Mathematical modelling of the deformable particle in interaction with the surrounding fluid is a challenging task because of the level of complexity in their strongly coupled physics. Thus, modelling the dynamics of biological cells is still an active area in biomedical engineering research. Several continuum and discrete approaches have been developed for this purpose such as boundary element method (BEM), smoothed particle hydrodynamics (SPH), dissipative particle dynamics (DPD), and lattice Boltzmann method (LBM) [6,7,8,9,10,11,12,13,14,15,16,17,18]. Continuum-based approaches utilize fluid dynamics and elasticity theories to model deformable particles and the inner fluid as a homogeneous material. On the other hand, in discrete approaches the membrane structure is represented by a spring network structure and particles are used to model the surrounding and inner fluids.

Several mathematical models are available to study the behaviour of a single RBC as well as RBC aggregates in blood flow. A finite element model was developed by Dao et al. [7] to extract the elastic and viscoelastic properties of an RBC. The effects of various parameters on the deformation behaviour were studied to derive constitutive equations for RBC mechanics. Liu et al. [19] constructed an Eulerian–Lagrangian method where the Navier–Stokes equations were solved on an Eulerian mesh and the deformable particles were represented in a Lagrangian manner. They incorporated an immersed finite element method (IFEM) and protein molecular dynamics to study RBC dynamics and aggregation. Chee et al. [9] presented a continuum model where an RBC was represented as a hyperelastic membrane enclosing a deformable viscous capsule for the cytoplasm. Another continuum model was presented by Yoon and You [15] where a generalized Maxwell model was used to model the viscous dynamic behaviour of an RBC.

Cimrák et al. [20] also employed a LBM-based immersed boundary method to represent biological cells in plasma. Dupin et al. [21] utilized a LBM solver for fluid flow and a Lagrangian method for the RBC deformation. They incorporated the bending rigidity and the volume and surface-area conservation criterion of RBCs. Nakamura et al. [12] presented RBC as a shell membrane made up of spring networks based on the energy minimum concept and studied RBC deformation in a shear flow.

A coarse-grained multiscale model of RBC was developed by Pivkin and Karniadakis [10] based on DPD. Here, an RBC membrane constituted of spring network and the internal and external fluids were represented by colloidal particles. Fedosov et al. [11] further extended this model to consider the viscoelasticity of the membrane and the viscosity contrast between the internal and external fluids. Závodszky et al. [16] developed a coupled method which handles the fluid and solid structures independently. A LBM-algorithm was utilized for the plasma flow and immersed boundary layers were used to represent the biological cells. Furthermore, Kostalos et al. [22] introduced LBM-based immersed method with a nodal projective FEM (npFEM) to handle biological cells in blood plasma. It had the advantage of being more stable than spring network-based models. All these models can provide accurate simulation of RBCs; however, they prove to be computationally expensive when simulating complex flows. Model order reduction concept provides a methodology to reduce the complexity of the problem and impose a less computational cost. One of the existing reduced-order models for biological cells has been introduced by Pan et al. [23], where a red blood cell was represented by a torus arrangement of spheres connected by the worm-like chain (WLC) springs. This model can reduce the computational cost with a good degree of accuracy but lacked some of the critical behaviours of RBC such as viscoelasticity [24] and tank-treading behaviour.

Coupled simulation of fluid and particles has been gaining prominence due to their applicability for investigations on particle-laden flows such as fluidized beds and dispersion of pollutants. In coupled simulations, the fluid and particle phases are handled separately (i.e. continuous and dispersed phases, respectively) [25] and their interaction is determined through source terms in the governing equations. One such approach is resolved CFD–DEM, where the fluid flow is resolved on a finite volume grid and the particle presence is introduced utilizing discrete forcing [26]. The coupled nature of CFD–DEM makes it a feasible approach for developing reduced-order models for deformable particles. However, to the authors’ best knowledge, no reduced-order model in this context is developed so far.

Fig. 1
figure 1

a Schematic representation of the computational domain in CFD–DEM: \({\Omega }_\mathrm{{f}}\) is the fluid domain and \({\Omega }_\mathrm{{S}}\) and \({\Gamma }_\mathrm{{S}}\) are the particle domain and boundary, respectively. b The sub-domain \({\Gamma }_\mathrm{{sub}}\) with the corresponding grid resolution for resolved CFD–DEM

Full size image
Fig. 2
figure 2

a Schematic of the deformable particle model: The solid black lines represent the virtual elastic bonds, and the white dotted line is a constituent sphere. b Schematic of the bond with the forces and moments between two constituent spheres (right). The green band represents the virtual bond. The bond model is redrawn from [27]. (Color figure online)

Full size image

In the present work, a new CFD–DEM-based deformable particle model is presented, which follows the concept of model order reduction. In this model, a single RBC consists of constituent spheres with their centroids connected by the elastic mathematical bonds [27, 28]. The bond mechanics are controlled by a variety of parameters that are determined by calibration tests. First, a static calibration of the mechanical behaviour of different red blood cells was performed by validating the corresponding force–displacement curves against experimental data from the literature. Second, the viscoelastic behaviour of RBC was studied and the time-dependent creep behaviour was investigated as the dynamic calibration test. The model demonstrates a high degree of accuracy in reproducing the viscoelastic behaviour of an RBC. Finally, the suspension behaviour of a single RBC in blood flow is evaluated by coupling the proposed model with the fictitious domain method. Here, the drag force on the red blood cell was analyzed and revealed a consistent behaviour with the physics. Additionally, a global angular momentum is introduced in the fluid flow field to represent the membrane rotation which is an important component when considering the interaction between membrane and surrounding fluid. The proposed model can be employed in modelling blood flow in bio-microfluidic applications for future design prospects.

2 Mathematical model description

2.1 Resolved CFD–DEM

In the particulate flows, the physics of suspended particles and the carrier fluid is strongly coupled. The fluid flow can be described by the incompressible continuity and Navier–Stokes equations as:

$$\begin{aligned}&\nabla \cdot \mathbf{u } = 0 \end{aligned}$$
(1)
$$\begin{aligned}&\rho \frac{\partial {\mathbf{u }}}{\partial {t}} + \rho (\mathbf{u } \cdot \nabla ) \mathbf{u } = -\nabla p + \upmu \nabla ^2 \mathbf{u } + {\mathbf {F}} \end{aligned}$$
(2)

where \({\mathbf {F}}\) is the source term used to incorporate the continuous forcing between the fluid phase and the particles and is written as

$$\begin{aligned} {\mathbf {F}} = \frac{\lambda \rho (\mathbf {u}_\mathbf p - {\mathbf {u}})}{{\Delta } t} \end{aligned}$$
(3)

\(\lambda \) being the solid volume fraction in the finite volume computational cell. So, the forcing term is active only in the cells with \(\lambda = 1\).

And, particle physics is governed by Newton’s laws of motion. The conservation of linear and angular momentum reads:

$$\begin{aligned} m_p \frac{\mathrm{{d}}\mathbf {u}_\mathbf p }{\mathrm{{d}}t}= & {} m_p{{\mathbf {g}}} + f_{\mathrm{{p,f}}} + \sum _{N_p} f_{\mathrm{{p,p}}} + \sum _{N_w} f_{\mathrm{{p,w}}} \end{aligned}$$
(4)
$$\begin{aligned} I_p \frac{\mathrm{{d}} {{{\varvec{\omega }}}_\mathbf p }}{\mathrm{{d}} t}= & {} {{\mathbf {r}}} \times \left( f_{\mathrm{{p,f}}} + \sum _{N_p} f_{\mathrm{{p,p}}} + \sum _{N_w} f_{\mathrm{{p,w}}} \right) \end{aligned}$$
(5)

where \({\mathbf {g}}\) is the gravitational acceleration, \(f_{\mathrm{{p,f}}}\) is the fluid–particle interaction force, and \(f_{\mathrm{{p,p}}}\) and \(f_{\mathrm{{p,w}}}\) are the forces due to particle–particle and particle–wall interactions, respectively. \(I_\mathrm{{p}}\) is the second moment of inertia of the particle, \(\omega _\mathrm{{p}}\) is the angular velocity, and \({{\mathbf {r}}}\) is a position vector from the centroid to a point on the particle radius.

In the context of resolved CFD–DEM, these sets of equations are coupled. On the fluid side, the particle is seen as an immersed object (larger than the grid size) whose velocity is used to update the fluid velocity through forcing terms. This is shown in Fig. 1. Also in the particle conservation equations, the \(f_{\mathrm{{p,f}}}\), which comes from the stress between fluid and particle, is obtained by integrating the stress tensor \(\sigma \) over the \({\Gamma }_\mathrm{{s}}\). Using the divergence theory, the fluid–particle interaction force reads

$$\begin{aligned} f_{p,f} = \int _{{\Omega }_\mathrm{{S}}} \left[ \upmu \nabla ^2 {\mathbf {u}} - \nabla p \right] \mathrm{{d}}{\Omega }_\mathrm{{S}} \end{aligned}$$
(6)

For more details on the resolved CFD–DEM approach and the algorithm, the reader is referred to [26, 29,30,31].

2.2 Deformable particle model

The reduced-order modelling approach considers geometrical as well as mathematical simplification of the problem. In this study, we reduce the complex deformation of a soft particle to the mechanical behaviour of a finite number of rigid spheres interconnected by virtual mathematical bonds. The connected spheres can represent the granular behaviour of a larger deformable particle such as biological cells and flexible fibres [27]. As illustrated in Fig. 2, the deformable particle can be represented by a combination of overlapping constituent spheres forming the contour of the particle. These spheres do not interact with each other but with spheres from other particles. The centroids of the spheres are connected by means of flexible bonds (Fig. 2). As the spheres translate and rotate, the bonds also deform and transfer and damp inter-sphere forces to control the relative motion of the spheres. Forces and moments of the bonds between each pair of constituent spheres are calculated incrementally and read [28, 32]

$$\begin{aligned} \mathrm{{d}}F^b= & {} K^b \; v^r\;\mathrm{{d}}t \end{aligned}$$
(7)
$$\begin{aligned} \mathrm{{d}}M^b= & {} S^b \; \omega ^r \; \mathrm{{d}}t \end{aligned}$$
(8)
$$\begin{aligned} K^b= & {} \frac{E_\mathrm{{b}} A_\mathrm{{b}}}{l_\mathrm{{b}}} \; , \; S^b = \frac{G_\mathrm{{b}} A_\mathrm{{b}}}{l_\mathrm{{b}}} \end{aligned}$$
(9)

where \(\mathrm{{d}}F^b\) and \(\mathrm{{d}}M^b\) are the increments in the forces and moments of the bond. They are calculated both as normal and tangential components. The parameters used in Eqs. 7 and 8 are defined in Table 1.

Table 1 Elastic bond model parameters
Full size table

The damping of the bond forces should account for the dissipation of energy due to the elastic wave propagation within the bond and the particles [28]. The elastic bonds are modelled as cantilever beams, and thus, under no friction and or external damping, the beam is free to oscillate about its equilibrium position. When damping is provided, the oscillations will decrease and the beam will finally reach its equilibrium position. Force damping is essential to attain the equilibrium orientation of the deformable particle under load.

$$\begin{aligned} F^b_{d} = 2 \beta \sqrt{mK^b} \; v^r \end{aligned}$$
(10)

where \(\beta \) is the damping coefficient which determines the rate of energy dissipation.

By adding the effects of the bond forces to Newton’s second law of motion, Eq. 4 can be re-written for each constituent sphere as [28]

$$\begin{aligned} m \frac{\mathrm{{d}}\mathbf {u}_\mathbf p }{\mathrm{{d}}t} = F^c + F^b + m {{\mathbf {g}}} + F^c _d + F^b _d + f_{\mathrm{{p,f}}} + \sum _{N_w} f_{\mathrm{{p,w}}}\nonumber \\ \end{aligned}$$
(11)

\(F^c\) and \(F^c _d\) are the contact forces and the damping of the contact forces. Similarly, \(F^b\) and \(F^b _d\) are the bond forces and the damping of the bond forces. It has to be noted the moments of these forces can also be calculated for each sphere. However, the angular momentum for the herein proposed deformable particle model is accounted in a different way which is discussed later.

2.3 Global angular rotation of deformable particle

The motion of an RBC in simple shear flow is characterized by three main behaviours: tumbling, swinging and tank-treading [33,34,35,36]. The transition to the different trends is dependent on the shear rate, viscoelasticity, viscosity contrast and the near-wall effects. The transition from tumbling to a tank-treading motion is observed on increasing the Capillary number [34, 35, 37, 38]. The tank-treading behaviour is important in the migration of RBCs, platelet margination and cell-free layer formation [39]. During the tank-treading motion, it is observed that the RBC will maintain almost a constant inclination to the flow and the internal fluid follows a rotational motion comparable to the tank-treading [36, 37]. Taking this into account and tracking the motion of a point on the membrane during the tank-treading motion reveals that it follows a rotational motion about the centre of mass of the RBC.

As mentioned earlier Sect. 2.1, the fluid velocity is corrected by the particle velocity to introduce the particle presence in the flow field. This step is completed for each constituent sphere and eventually accounts for the axial translation of the deformable particle. However, this does not hold true for rotation. In other words, accounting for the angular velocity of the constituent spheres about their centroids do not conserve the angular momentum of the whole deformable particle. To compensate for the lack of a deformable particle rotation, the relative rotation of the constituent spheres about the centre of mass of the deformable particle is taken into account in this study.

Accordingly, the modification of the particle velocity in the finite volume computational cell is performed:

$$\begin{aligned} \mathbf {u}_\mathbf{p,i } = \mathbf {u}_\mathbf p + r_{fv} \times \omega _\mathrm{{p}} \end{aligned}$$
(12)

where \(\mathbf {u}_\mathbf{p,i }\) is the velocity of the constituent sphere as observed in the ith finite volume cell, \(\mathbf {u}_\mathbf p \) is the velocity of the constituent sphere from the DEM simulations, \(r_{fv}\) is the length vector between the centre of mass of the deformable particle and the cell-centre of the finite volume cell and \(\omega _\mathrm{{p}}\) is the rotation velocity of the constituent sphere about the centre of mass of the deformable particle given by

$$\begin{aligned} \omega _p = \frac{r \times \mathbf {u}_\mathbf{rel }}{|r|^2} \end{aligned}$$
(13)

where \(\mathbf {u}_\mathbf{rel }\) is the relative velocity between the centroid of the constituent sphere and the centre of mass of the deformable particle (\(\mathbf {u}_\mathbf{cm }\)) and r is the length vector between the centroid of the constituent sphere and the centre of mass of the deformable particle. Introducing this global angular rotational velocity provides the motion of the points on the surface of the constituent spheres relative to the centre of mass of the deformable particle.

3 Results and discussions

3.1 Static calibration of deformable particle model

The flexible bond model has been implemented in the open-source DEM software LIGGGHTS\(^{\circledR }\) [40] with application in flexible fibres [27, 28]. In our deformable particle model, we have adapted this bond model to connect the centroids of the constituent spheres. The determination of the bond parameters is a key step to accurate prediction of the deformability. Therefore, for each specific application, experimental data are required for calibration of the bond parameters. In the present study, we focus on the bio-microfluidic application. Thus, the model parameters are calibrated using RBC physical properties and force-displacement curves.

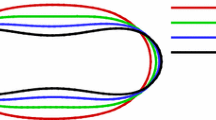
To this end, we considered a single RBC at an unstressed, undeformed equilibrium state and placed it in a domain isolated from the external flow. Then, a stretching force ranging from 0 to 200 pN is applied to the cell. The cell is allowed to deform until the equilibrium configuration is achieved for the given load. The calibration is performed for three resolution of constituent spheres N = 8, 10 and 16. The force-displacement curves for each N are plotted against the experimental data in Fig. 3a. The Young’s modulus and the shear modulus as given in the literature are in the range of 18.9–20.3 \(\upmu \)N/m and 2.5–6.9 \(\upmu \)N/m, respectively [11, 23, 41]. The values of \(K^b\) and \(S^b\) obtained here are 18.9 \(\upmu \)N/m and 6.3 \(\upmu \)N/m, respectively. The bond radius (\(r_\mathrm{{b}}\)) is taken as the radius of the constituent sphere. Accordingly, the values of the parameters in Table 1 can be calculated.

Fig. 3
figure 3

Force–displacement curves from single RBC: a the healthy RBC with different particle resolutions. b The RBCs at different stages of malaria infection. In both plots, the lines represent the simulation results and the dots represent the experimental data from [41]

Full size image

The results show that with increasing loads, the axial diameter increases and the radial diameter decreases. The values obtained from the simulation matches the experimental data well, and for all resolutions, the cell diameters lie within the error bar of the experiment. Small discrepancies can be observed due to the effect of the angle of observation. Thus, the force–displacement curve represents only the in-plane deformation of RBC. Additionally, by increasing the resolution of the model no significant change in the mechanical behaviour is observed, and an optimal resolution of 10 constituent spheres provides sufficient accuracy for the representation of the cell contour as well as the cell mechanics. Therefore, for the remainder of this study, we use \(N = 10\) to represent an RBC.

In order to test the performance of the model for different cell types, the RBC behaviour at different stages of malaria infection was also simulated and compared with the experiment. As the malaria infection period progresses, the shape and mechanical behaviour of RBC change as they become stiffer which relates to lower mechanical responses. Our model is capable of mimicking this mechanical behaviour of malaria-infected RBC under different conditions with great accuracy as shown in Fig. 3b.

Although the model can address the static and dynamic mechanical behaviour of RBC with good accuracy, certain characteristics have not been considered here. The surface area and volume of the RBC are shown to remain almost constant [42], and they form additional force constraints on the RBC [11, 16]. Additionally, the RBC is filled with cytoplasm which is incompressible in nature which is not considered in the current state of our model.

3.2 Dynamic calibration of the deformable particle

The red blood cells exhibit a time-dependent deformation at given loads according to the micropipette aspiration and optical tweezer tests [7, 43]. To provide accurate mechanical behaviour of the RBC by the proposed model, it is also important to incorporate the viscoelastic behaviour of the membrane. In the model presented in this study, RBC viscoelasticity is incorporated employing damping forces on the bonds. By varying the damping coefficient \(\beta \), the time-dependent deformation is controlled.

The viscoelastic behaviour of a red blood cell can be described using the normalized creep compliance, and it provides a measure of the time-dependent deformation of red blood cells.

$$\begin{aligned} \mathrm{{NCC}} = \frac{J_{\infty } - J_t}{J_{\infty } - J_0} \end{aligned}$$
(14)

where \(J_t\) is the strain per unit stress (i.e. \(J_t = {\epsilon _t}/{\sigma }\)) at a given moment in time (\(0 \;< \; t \; < \; \infty \)). The numerical setup for the dynamic test is similar to that for static calibration tests. A constant load of 7 pN was applied on the opposite sides of the RBC, and it was allowed to deform and attain its equilibrium state under different damping coefficients (\(\beta \)). The normalized creep compliance is plotted against time for the experiments and the simulations as in Fig. 4a. It highlights that the calibrated model with \(\beta \; = \; 1500\) shows a better agreement with experimental data in most of the times. This damping coefficient is then used for the rest of this study.

A similar test was performed with various forces, and the corresponding creeping behaviours are shown in Fig. 4b. With increasing the force, the rate of deformation is also affected showing a faster transition to the final equilibrium state. The presented model can reproduce the creep behaviour which was well documented in previous studies.

Fig. 4
figure 4

Normalized creep compliance of the red blood cell as a function of time: a simulation (solid lines) and experiment [43, 44] (dashed lines with markers) for the constant load of 7 pN and b simulation results for \(\beta \; = \; 1500\) for different loads

Full size image

3.3 Single RBC in a microchannel

After proper calibration of the model parameters, the deformable particle model can be coupled with fluid flow solver for more complex problems such as suspension of RBC in blood plasma. To this end, a modified version of the solver cfdemSolverIB (i.e. the resolved CFD–DEM technique [26]) is adapted from the open-source libraries of the CFDEMcoupling® software [40]. To study a single RBC behaviour in a microchannel, the drag force acting on RBC during the suspension is analyzed. Gironella Torrent and Ritort [45] have recently performed an experimental study to explore the viscoelastic properties of an RBC in fluid flow. They used a plasma buffer solution (i.e. Newtonian fluid) as the surrounding fluid. In one experiment, they utilized a microbead to entrap the RBC in the channel flow and measure the forces acting on it using optical tweezers. The drag force on the RBC was measured for different flow velocities ranging from 650 to \(1200 \; \upmu \)m/s.

Fig. 5
figure 5

Schematic of the simulations and experiment setup [45] top view (a) and side view (b). The blue sphere is the microbead, and the red particle is the RBC. (Color figure online)

Full size image

In the present study, we consider a similar configuration by using a rigid spherical particle attached to a single RBC in the flow stream as shown in Fig. 5. The computational domain (\(L_x = 50\, \upmu \mathrm{{m}}, L_y = 50 \,\upmu \mathrm{{m}}, Lz = 25\, \upmu \mathrm{{m}}\)) was discretized by a structured grid \({\Delta } x\). Periodic inlet and outlet conditions were applied along the x-direction, and periodic conditions were applied along the z-direction. The no-slip wall boundary was applied on walls along the y-direction. According to the grid dependency study (not presented here), the ratio \(D/{\Delta } x = 4\) was chosen for the simulation (where D is the size of each constituent sphere in the RBC model). This ratio provides a sufficiently accurate representation of each constituent sphere in the CFD domain (i.e. void fraction). The simulation for each case was performed for \(10^6\) simulation time steps corresponding to 1 s. To calculate the drag force in the simulation, (i) the effect of the rigid particle has been removed similarly to the experiment [45], and (ii) the force on the RBC is computed after it reached the equilibrium position and is time-averaged for all simulation time steps.

Fig. 6
figure 6

Drag coefficient obtained from simulation and experiment [45] along with the respective error bars

Full size image

The experimental and simulation results are compared in Figure 6 where the drag coefficient is plotted as \(C_\mathrm{{D}} (F_\mathrm{{D}}/u)\). The drag coefficient is shown to be within the range obtained from experiment [45] for the given velocity range. The discrepancy between the simulation and experiment arises from the reduced complexity of RBC shape in the presented model. In the presented model, the RBC thickness remains almost constant due to the fixed diameter of the constituent spheres. However, in reality, the thickness of the RBC also changes with the shear rate. While the model can capture the change in the axial and transverse diameters of RBC with good accuracy, its thickness does not vary. Nevertheless, the discrepancy between simulation and experiment varies from about \(4 \%\) at higher velocities to about \(9 \%\) at lower velocities. In fact, in many capillary-driven microfluidic applications, the flow velocity is in the range of 1000–10,000 \(\upmu \)m/s [46], where our model exhibits lower discrepancies with the experiment. Thus, this model can be employed to study the behaviour of RBCs (eventually whole blood) in microfluidic applications.

4 Conclusion

In this work, a reduced-order model for deformable particles is proposed with a particular focus on red blood cell dynamics in the bio-microfluidic systems. The model is first introduced in the framework of DEM in which a clump of rigid spheres interconnected utilizing mathematical bonds, form a bigger deformable particle. The deformability is preserved by such elastic bonds. After calibrating the bond parameters for a single RBC, the static and dynamic response of the RBC to different forces is analyzed and showed a good agreement with experimental data. The model is then coupled with the flow solver (i.e. the immersed boundary method of resolved CFD–DEM) to investigate the interaction of RBC with the surrounding fluid. The simulation results highlight the good accuracy of this reduced-order model to predict the drag force on the RBC in a plasma buffer solution. However, there are some modelling aspects to be improved in our future studies, such as accounting for the incompressibility of internal fluid in RBC which causes the volume conservation. Furthermore, the present model will be employed for the simulation of blood flow in realistic conditions where multiple RBCs are suspended and interact with other biological cells. Here, the prediction of blood flow characteristics in micro-capillaries such as cell-free layer formation and change in apparent viscosity will be investigated. Also, the proposed model can be used for the future development of bio-microfluidic devices.