Trajectory tracking of biomimetic autonomous underwater vehicle using different control strategies

Abstract

Autonomous underwater vehicle (AUV) is an uncrewed underwater robotic vehicle that operates independently of humans. The present work illustrates an effective design of the biomimetic autonomous underwater vehicle (BAUV) model and its trajectory control for the predefined path. The vehicle possesses a definitive biomimetic structure with specific lengths and widths. Three trajectory tracking control methods are used here: conventional proportional–integral–derivative (PID) control, $H_\infty$ control, and feedforward (along with feedback) control. The advantages and drawbacks of these would be governed by examining the characteristics of the methods. Finally, the future development of AUV trajectory tracking scenarios is discussed based on a comparison of control systems.

1 Introduction

An autonomous underwater vehicle (AUV) is a submerged robotic vehicle that operates without the need for human interaction. They are self-controlling and self-directing vehicles with no actual connection to their administrators. The development of AUVs began in the early 1970 s. Many kinds of research have been developed on different AUVs, focusing on further expansion with improved performances. The conventional AUVs use propellers, which are inefficient in several applications. This led to the development of biologically inspired propulsion mechanisms for underwater vehicles. A substantial amount of research has been done into this area, with most of them reproducing fish-like propulsion [1]. The type of AUV has been chosen based on the propulsive efficiency of the fish locomotion mechanisms. It is the ratio of thrust power to that of total mechanical power [2] output.

An intelligent control system is needed to develop the motion control algorithms of the AUVs. One of the problems in controlling the AUV is how these vehicles can follow a predetermined trajectory. Numerous control methods including proportional–integral (PI) control, proportional–derivative (PD) control, proportional–integral–derivative (PID) control [3], sliding mode control (SMC) [4], fuzzy logic control (FLC) [5], neural network-based control (NNC) [6], and predictive control have all been extensively investigated over the last several decades for the trajectory tracking control problem of AUVs. The PID and PD control methods are the most frequently used due to their simple structure and superior performance. However, selecting acceptable gain parameters is a challenging task. Sliding control methods produce acceptable results when the designer can determine uncertainty bounds on the AUV dynamics analytically. Elmokadem et al. suggest an SMC scheme regulation for a three-DOF underactuated autonomous vehicle [7]. The control architecture is validated by applying it to an AUV and simulating its output under various reference trajectory scenarios. The simulation results suggest that the proposed control scheme is effective in all three scenarios. The switching feature is critical to SMC anti-disturbance capability and induces the chattering phenomenon that causes to reduce the tracking efficiency [8] of the system.

Adaptive linear control is the most frequently used control approach for underwater vehicles. If the device characteristics are uncertain and time-varying, adaptive control automatically adjusts the controller parameters to maintain a reasonable level of performance[9]. Nonetheless, the adaptive control stability is not treated rigorously, and the system relatively slows the convergence [10]. Fuzzy logic is also a way to make the controller more intelligent and robust. Remarkably, this method, based on Zadeh’s fuzzy set theory, is extremely resistant to system non-linearity and uncertainties [5]. The fuzzy logic control approaches can be broadly categorized into the following types based on the differences in fuzzy control rules and their generating methods, including CFLC (conventional fuzzy control), hybrid fuzzy control, adaptive fuzzy control (AFLC), adaptive fuzzy control (AFLC), neuro-fuzzy control (NFLC), and fuzzy sliding mode control (FSMC) [11, 12]. The major drawback of this kind of system is that it entirely depends on human expertise and knowledge. Some other research works were also conducted for trajectory tracking of marine vehicles that uses control methods such as higher-order sliding mode [4], $H_\infty$ controller, learning control, Lyapunov-based techniques [13, 14] and Lyapunov’s direct method. Nonlinear Lyapunov-based techniques are used in [13, 14] to develop trajectory tracking controllers for under-actuated ships.

Though there is enough research in the underwater vehicle field, studies related to dynamics-based modeling of the flapping foil and the combined modeling of AUV-foil vehicles are a few and relatively unexplored. Furthermore, the research conducted on fish locomotion found that the thunniform mode of swimming is the most efficient, and there is no completely built biomimetic AUV based on fish locomotion. Various control methods have been extensively researched over the last several decades for the trajectory control problems of AUVs, but those bring several difficulties while employing different kinds of AUVs; hence, more exploration is also needed in this area.

Statement of Contributions: The main contribution of this paper is a practical design of biomimetic AUV (BAUV) and its trajectory tracking control for a predefined path. The proposed system possesses a basic Gertler geometric hull, a flapping foil tail (caudal fin), and a pair of dorsal fins. NACA63-015A foil is selected for the system design, which can mimic a tuna fish caudal fin with high propulsive efficiency. The same foil is chosen for dorsal fin design also. The main innovations of this study are as follows.

• 1. Since trajectory tracking is challenging, three control methods are used here to track the predetermined path. A conventional PID controller with manual tuning method has been introduced first in the presence and absence of sea current disturbance to get the required trajectory in this analysis. In order to enhance the performance of the system, an $H_\infty$ controller and a feedforward controller also have been implemented.

• 2. A comparative study on the performance of all the three control methods in terms of time-domain specifications such as rise time, overshoot, and settling time is included in this work. Likewise, steady-state error analysis and performance indices such as ISE, IAE, and ITAE are also comprised for the evaluation.

• 3. As another contribution of this communication, we demonstrate that, despite sparse benefits produced by the PID and $H_\infty$ controller, the feedforward methodology remains the most suitable technique for trajectory tracking control design. An observation study of existing controllers in this area with the proposed ones is also entailed to check the advantages, drawbacks, and future improvements.

The remainder of this paper is organized as follows: Sect. 2 summarizes the whole system model of the biomimetic autonomous underwater vehicle (BAUV). Section 3 presents the trajectory tracking control designs for BAUV, which includes different controllers for the tracking purpose, such as PID controller, $H_\infty$ controller, and the feedforward–feedback controller combination. Simulation results are addressed in Sect. 4. Finally, the conclusion is based on the results illustrated in Sect. 5.

2 System description

A virtual model of the biomimetic vehicle is used here for the trajectory tracking applications. The design of the vehicle is composed of a Gertler geometric-shaped hull with a flapping foil tail. The tail mimics the caudal fin of a fish which can produce a required thrust (say $\tau _\textrm{X}=100N$). The inputs given to the caudal fin are force and torque from the motor actuator. The fin motions produce a forward thrust and the angular moment, which are the inputs to the AUV hull sub-system. The caudal fin and hull sub-system is taken as a cascade connection, and the dorsal fin sub-system is connected parallel to this. The inputs to the dorsal fin are sway thrust and yaw moment, whereas the output from this system is sway and heave velocities. The whole system is subjected to the trajectory tracking application. Figure 1 discusses the structure, and Fig. 2 illustrates the MATLAB/Simulink model of the proposed biomimetic system.

Fig. 1

Biomimetic AUV model

Fig. 2

Simulink model of biomimetic AUV

2.1 Biomimetic AUV hull specification

Before deciding on a hull shape, it is necessary to describe the requirements first. The essential function of the hull is to provide the vehicle with a hydrodynamically efficient structure. Form drag and skin friction drag should be minimized in order to reduce power demands. The proposed system consists of a Gertler 4154-shaped hull [15, 16] which is axisymmetric with section radius [16]. Figure 3 shows the basic proposed geometry of the AUV hull, and it is possible to add modules at the midsection for batteries or other equipment [16, 17]. This geometry possesses an L/D ratio of 4, less drag, and an efficient hydrodynamic structure. All the hydrodynamic coefficients are determined using commercial CFD tools [18]. The total drag produced by the bare hull is 14.11N [18].

Fig. 3

Representation of gertler geometric hull (Mass: 320 Kg)

2.2 Caudal fin specifications

In the present study, a foil fitted at the backside of an AUV hull resembles the caudal fin of a fish, which can produce the required thrust. NACA63-015A foil is chosen [19] for the analysis. The caudal fin tail will undergo lateral and rotational motion, and motors are used to actuate the foil [20] system.

Fig. 4

NACA63-015A foil-caudal fin tail

2.2.1 Performance parameters

The study was undertaken here to design a foil that can produce a maximum thrust of $\tau _\textrm{X}=100N$. Flapping fin performance is evaluated by using its Strouhal number $(St=\frac{f A_{0}}{U_{0}})$ where $A_{0}$ is the double amplitude of fin oscillation, f is the oscillation frequency, [21] and $U_{0}$ is the velocity to the fin. The dimension parameters and frequency of the foil are illustrated in Table 1.

The thrust coefficient is obtained as;

$$\begin{aligned} C_\textrm{X}=\frac{\tau _\textrm{X}}{0.5 \rho U_{0}^{2} A} \end{aligned}$$

(1)

where A is the foil area and $\rho$ is the water density. Similarly, lift coefficient ($C_\textrm{L}$) and average power coefficient ($C_\textrm{P}$) are also obtained [21] from the analysis. The flapping foil efficiency is defined as the ratio of output power to input power.

$$\begin{aligned} \eta =\frac{\tau _\textrm{X}.U}{P}=\frac{C_x}{C_P} \end{aligned}$$

(2)

where P is the power required to oscillate the foil. All the performance parameters are described in Table 2.

Table 1 Dimension parameters of the flapping foil

Table 2 Performance parameters of the flapping foil

2.3 Dorsal fin specifications

A pair of dorsal fins are vertically arranged around the body, which undergoes sway–yaw motion [22], described as:

$$\begin{aligned} \begin{aligned} s(t)=s_{0} sin(\omega _\textrm{s}t)\\ y(t)=y_{0} sin(\omega _\textrm{s}t+a) \end{aligned} \end{aligned}$$

(3)

where $s_{0}$ and $y_{0}$ are the sway and yaw angle of the dorsal fin, a is the phase difference between the yawing and swaying motions, and $\omega _\textrm{s}$ is the flapping frequency. The angle a is taken as $\pi /2$ in all experiments, thus:

$$\begin{aligned} y(t)=y_{0} cos(\omega _\textrm{s}t) \end{aligned}$$

(4)

The dorsal fin produces a net force and moment denoted as $F_\textrm{f}$ and $N_\textrm{f}$, which are equal to the sway force ($\tau _\textrm{Y}$) and yaw moment ($\tau _\textrm{N}$).

2.3.1 Parameters of the dorsal fin

For the proposed dorsal fin, the thrust $\tau _\textrm{Y}=50 N$ and moment $\tau _\textrm{N}=1 Nm$. The dimensional and performance parameters of the dorsal fin are given in Tables 3 and 4.

Table 3 Dimension parameters of the dorsal fin

Table 4 Performance parameters of the dorsal fin

2.4 Mathematical modeling

Mathematical modeling of the proposed system includes the dynamics and state-space representation of the hull, caudal fin, and dorsal fin sub-systems. Figure 5 illustrates all the forces and hydrodynamic coefficients of the biomimetic AUV system.

Fig. 5

Mathematical model diagram of Biomimetic AUV

The detailed explanation of forces incorporated in this system is explained in the following subsections.

2.4.1 Caudal fin dynamics

The approach is inspired and borrowed by Lighthill [23]. Lighthill has modeled the thunniform tail, which produces lateral and rotational motions. The forces and moments produced by the foils are complicated, which is derived using unsteady aerodynamic theory [24, 25]. The proposed system is a motor-driven oscillating foil system. It experiences lateral displacement angular rotation. Theodorsen [25] derived the expression for the moment and lift, which act on the foil at the constant velocity free-stream where the foil is harmonically oscillating. Let $L_\textrm{a}$ and $M_\textrm{a}$ are the hydrodynamic lift and moment acting on the foil [20], respectively. According to the unsteady aerodynamic theory [24],

$$\begin{aligned} m(\ddot{Z_\textrm{a}} + \ddot{\alpha }b) = L_\textrm{a} + F_\textrm{a} \end{aligned}$$

(5)

where $F_\textrm{a}$ is the driving force, $Z_\textrm{a}$ is the vertical position and m is the mass.

$$\begin{aligned} J\ddot{\alpha } = M_\textrm{a} + \tau _\textrm{a} - F_\textrm{a}b \end{aligned}$$

(6)

where $\tau _\textrm{a}$ is the applied torque, J is the moment of inertia, $\alpha$ is the angular position (pitch angle), and b is the position of the axis of rotation along the chord. Harper et al. have done a complete derivation of lift and moment [20] including added mass, wake effect, quasi-steady lift and moment, and thrust and drag based on unsteady aerodynamic theory [25]. Therefore,

$$\begin{aligned} L_\textrm{a}= & {} 2 \pi \rho a U\left( -\dot{Z_\textrm{a}} + U \alpha + \left( \frac{a}{2} - b\right) \alpha \right) C(i \omega ) \nonumber \\{} & {} + \pi \rho a^{2}(-\ddot{Z_\textrm{a}} + U \dot{\alpha } - b \ddot{\alpha }) \end{aligned}$$

(7)

$$\begin{aligned} M_\textrm{a}= & {} -2 \pi \rho a U\left( \frac{a}{2}\right) ^{2} \dot{\alpha } + \pi \rho a^{2}U\left( -\dot{Z_\textrm{a}} + U \alpha \right. \nonumber \\{} & {} \left. + \left( \frac{a}{2} - b\right) \dot{\alpha }\right) C(i \omega ) - \frac{\pi }{8}\rho a^{4} \ddot{\alpha } \end{aligned}$$

(8)

where $\rho$ is density, a is half chord length of tail [26], U is free stream velocity and $C(i \omega )$ is Theodorsen function [20, 26]. A third-order transfer function obtained for the good approximation of Theodorsen function [25] in this study is

$$\begin{aligned} C(i \omega )= \frac{a_{3}(i \sigma )^{3}+a_{2}(i \sigma )^{2}+a_{1}(i \sigma )+a_{0}}{(i \sigma )^{3}+b_{2}(i \sigma )^{2}+b_{1}(i \sigma )+b_{0}} \end{aligned}$$

(9)

where $\sigma =\frac{\omega a}{U}$ which is a non-dimensional reduced frequency.

State-space representation of the caudal fin system Consider the dynamic equations of the fin (5) and (6). Substitute the lift and moment equations (7), (8) in (5) and (6).

$$\begin{aligned} m(\ddot{Z_\textrm{a}} + \ddot{\alpha }b)= & {} 2 \pi \rho a U(-\dot{Z} + U \alpha + (\frac{a}{2} - b)\alpha )C(i \omega ) \nonumber \\{} & {} + \pi \rho a^{2}(-\ddot{Z_\textrm{a}} + U \dot{\alpha } - b \ddot{\alpha }) + F_\textrm{a} \end{aligned}$$

(10)

$$\begin{aligned} J\ddot{\alpha }= & {} -2 \pi \rho a U(\frac{a}{2})^{2} \dot{\alpha } + \pi \rho a^{2}U(-\dot{Z_\textrm{a}} + U \alpha \nonumber \\{} & {} + (\frac{a}{2} - b) \dot{\alpha })C(i \omega ) - \frac{\pi }{8}\rho a^{4} \ddot{\alpha } + \tau _\textrm{a} - F_\textrm{a}b \nonumber \\ \end{aligned}$$

(11)

In this model the forces ($F_\textrm{a}=127N$, $\tau _\textrm{a}=10.16N$) are directly transmit from the actuators to the foil. Collecting coefficients of equations (10), (11) is written as,

$$\begin{aligned} E_{1} \begin{bmatrix} \ddot{Z_\textrm{a}} \\ \ddot{\alpha } \end{bmatrix} = E_{2}\begin{bmatrix} \dot{Z_\textrm{a}} \\ \dot{\alpha } \end{bmatrix} + E_{3} T_\textrm{f} + B_{0} \begin{bmatrix} F_\textrm{a} \\ \tau _\textrm{a} \end{bmatrix} \end{aligned}$$

(12)

The coefficient matrix of the equation 12 is obtained as,

$$\begin{aligned} E_{1}= & {} \begin{bmatrix} m + \pi \rho a ^2 &{} m b + \pi \rho a^2 b \\ 0 &{} J + \frac{\pi }{8} \rho a^4 \end{bmatrix} \end{aligned}$$

(13)

$$\begin{aligned} E_{2}= & {} \begin{bmatrix} 0 &{} \pi \rho a^2 U \\ 0 &{} -2 \pi \rho \frac{a^3}{4} U \end{bmatrix} \end{aligned}$$

(14)

$$\begin{aligned} E_{3}= & {} \begin{bmatrix} 2 \pi \rho a U \\ \pi \rho a^2 U \end{bmatrix} \end{aligned}$$

(15)

$$\begin{aligned} B_{0}= & {} \begin{bmatrix} 127 &{} 0 \\ -127b &{} 10.16 \end{bmatrix} \end{aligned}$$

(16)

where $F_\textrm{a}$ and $\tau _\textrm{a}$ are the control inputs. The common term in both the equations (10) and (11) is $[(\dot{Z_\textrm{a}} + U \dot{\alpha } + (\frac{a}{2}b)\dot{\alpha }) C(i \omega )]$, which taken for the analysis as,

$$\begin{aligned} T_\textrm{f}(s) = C_\textrm{f}(s) C(s) \end{aligned}$$

(17)

in which C(s) is the Laplace transform of Theodorsen function (9) by substituting $i \sigma$ as $\frac{as}{U}$. The Theodorsen function treated here as a linear filter in time domain.

$$\begin{aligned} C(s) = a_\textrm{c} + \frac{a_{2}s^{2} + a_{1}s + a_{0}}{s^{3} + b_{2}s^{2} + b_{1}s + b_{0}} \end{aligned}$$

(18)

where $a_\textrm{c} = a_{3}$. From the equation, system is realized to controllable canonical form.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} \dot{\phi _\textrm{t1}} \\ \dot{\phi _\textrm{t2}} \\ \dot{\phi _\textrm{t3}} \end{bmatrix} = \begin{bmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ -b_0 &{} -b_1 &{} -b_2 \end{bmatrix} \begin{bmatrix} \phi _\textrm{t1} \\ \phi _\textrm{t2} \\ \phi _\textrm{t3} \end{bmatrix}+ \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \psi _\textrm{t} \\&\gamma = \begin{bmatrix} a_{2} - a_{3}b_{2}&a_{1} - a_{3}b_{1}&a_{3} - a_{3}b_{0} \end{bmatrix} \begin{bmatrix} \phi _\textrm{t1} \\ \phi _\textrm{t2} \\ \phi _\textrm{t3} \end{bmatrix}+a_\textrm{3} \psi _\textrm{t} \end{aligned} \end{aligned}$$

(19)

The term in $C_\textrm{f}$ is;

$$\begin{aligned} C_\textrm{f}= & {} \dot{Z_\textrm{a}} + U \dot{\alpha } + (\frac{a}{2}b)\dot{\alpha } \end{aligned}$$

(20)

$$\begin{aligned} C_\textrm{f}= & {} C_\textrm{fk} \begin{bmatrix} Z_\textrm{a} \\ \alpha \end{bmatrix} + C_\textrm{fd} \begin{bmatrix} \dot{Z_\textrm{a}} \\ \dot{\alpha } \end{bmatrix} \end{aligned}$$

(21)

where $C_\textrm{fk} = \begin{bmatrix} 0&U \end{bmatrix}$ and $C_\textrm{fd} =\begin{bmatrix} \frac{a}{b}&-1 \end{bmatrix}$.

Table 5 Motions of AUV

Let $\phi _\textrm{t} = \begin{bmatrix} \phi _\textrm{t1}&\phi _\textrm{t2}&\phi _\textrm{t3} \end{bmatrix}^{T}$, $\dot{T_\textrm{f}} = \dot{\phi _\textrm{t}} = \begin{bmatrix} \dot{\phi _\textrm{t1}}&\dot{\phi _\textrm{t2}}&\dot{\phi _\textrm{t3}} \end{bmatrix}^{T}$, the equation (17) will be;

$$\begin{aligned} \begin{aligned} \dot{T_f} = \begin{bmatrix} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ -b_0 &{} -b_1 &{} -b_2 \end{bmatrix} \phi _\textrm{t} + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} C_f \\ =\Phi _\textrm{f1} \begin{bmatrix} Z_\textrm{a} \\ \alpha \end{bmatrix} + \Phi _\textrm{f2} \begin{bmatrix} \dot{Z}_\textrm{a} \\ \dot{\alpha }\end{bmatrix} + \Phi _\textrm{f3} \phi {t} \end{aligned} \end{aligned}$$

(22)

where $\Phi _\textrm{f1}=\begin{bmatrix} 0&0&1 \end{bmatrix} ^T C_\textrm{fk}$ and $\Phi _\textrm{f2} =\begin{bmatrix} 0&0&1 \end{bmatrix} ^T C_\textrm{fd}$. Substituting realization of $T_\textrm{f}$ in (12) and solving for $\begin{bmatrix} \ddot{Z}&\ddot{\alpha } \end{bmatrix}^T$,

$$\begin{aligned} \begin{bmatrix} \ddot{Z_\textrm{a}} \\ \ddot{\alpha } \end{bmatrix} = F_{1}\begin{bmatrix} \dot{Z_\textrm{a}} \\ \dot{\alpha } \end{bmatrix} + F_{2}\begin{bmatrix} Z \\ \alpha \end{bmatrix} + F_{3} \phi _\textrm{t} + B_{1} U_\textrm{c} \end{aligned}$$

(23)

where $F_{1}=E_{1}^{-1} (E_{2}+K_\textrm{f}\phi _\textrm{f2})$, $F_{2}=E_{1}^{-1}\phi _\textrm{f1}$, $F_{3}= E_{1}^{-1} E_{3}\phi _\textrm{f3}$, $B_{1}=E_{1}^{-1}B_{0}$ and $U_\textrm{c}=\begin{bmatrix} F_\textrm{a}&\tau _\textrm{a} \end{bmatrix}^{T}$. Thus, the state space representation of the caudal fin system is,

$$\begin{aligned} \begin{aligned} \dot{x} =\begin{bmatrix} 0_{2 x 2} &{} I_{2 x 2} &{} 0_{2 x 3} \\ F_{1} &{} F_{2} &{} F_{3} \\ \Phi _{f1} &{} \Phi _{f2} &{} \Phi _{f3} \end{bmatrix} x + \begin{bmatrix} 0_{2x2} \\ B_{1} \\ 0_{3x2} \end{bmatrix} U_\textrm{c} \\ \dot{x}= A x + B U_\textrm{c} \end{aligned} \end{aligned}$$

(24)

where the system coefficient matrices are A $\in$: $R^{7 \times 7}$ and B $\in$: $R^{7\times 2}$. The output equation:

$$\begin{aligned} \begin{aligned} Y =\begin{bmatrix} 100 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 \\ 0 &{} 2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix} x\\ y = Cx \end{aligned} \end{aligned}$$

(25)

where the values in the C matrix are the output thrust values ($\tau _\textrm{X}=100N$ and $\tau _{K}=2N$).

2.4.2 Vehicle dynamics

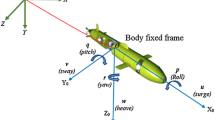
The dynamics of the body of a biomimetic vehicle is modeled using well-known theories of Fossen [27, 28]. A marine vehicle with 6 degrees of freedom (6-DOF) involves six independent linear and angular rigid-body motions. Linear motions of the system are surge, sway and heave, and angular motions are roll, pitch, and yaw. Table 5 lists all the motions and the notations used for forces and displacements of the rigid body motions.

The general motion of AUV can be given for a system by SNAME (1950) in which $\eta$ is the position and orientation vector concerning Earth fixed frame, v is the linear and angular velocity coordinates, and $g(\eta )$ is the gravitational and buoyancy matrix for the body-fixed frame.

$$\begin{aligned} \begin{aligned} \eta =\begin{bmatrix} \eta _{1}&\eta _{2} \end{bmatrix}=\begin{bmatrix} x&y&z&\phi&\psi&\theta \end{bmatrix}^T \\ V=\begin{bmatrix} \nu _{1}&\nu _{2} \end{bmatrix}=\begin{bmatrix} u&v&w&p&q&r \end{bmatrix}^T \\ \tau =\begin{bmatrix} \tau _{1}&\tau _{2} \end{bmatrix}=\begin{bmatrix} \tau _\textrm{X}&\tau _{Y}&\tau _{Z}&\tau _{K}&\tau _{M}&\tau _{N} \end{bmatrix}^T \end{aligned} \end{aligned}$$

(26)

Designing the AUV system is completely based on dynamic equations. The dynamic model of the vehicle on the horizontal plane is as given below:

$$\begin{aligned} M \dot{v} + C(v) v + D(v) v +g(\eta )= \tau \end{aligned}$$

(27)

where M is the inertia matrix, C(v) the Coriolis and centripetal matrix, D(v) the damping matrix and $\tau$ the input vector. The above equation is is derived from the Newton–Euler equation of a rigid body in fluid.

From the dynamic equation (27), we get the 1-DOF system equation of surge velocity as,

$$\begin{aligned} \left( m-X_{\dot{u}}\right) \dot{u}-X_\textrm{u}u=\tau _\textrm{X} \end{aligned}$$

(28)

where $X_\textrm{u}$ denotes the rate of change of surge force per unit velocity u and $X_{\dot{u}}$ denotes the added mass coefficient associated with acceleration $\dot{u}$. The $\tau _\textrm{X}$ is the thrust generated at the x-direction. The caudal fin model is connected in series with the aforementioned AUV hull dynamics model. This sub-system will produce a steady speed of $u_{0}=2.57 m/s$ for the proposed biomimetic AUV.

2.4.3 Dorsal fin dynamics

The hull with dorsal fin vehicle moving in x-y plane, and the coordinates of the center of gravity of the vehicle $[x_{g}, y_{g}, z_{g}]=[0.075, 0, 0]$. The sway and yaw equation of the neutrally buoyant vehicle [22] with a pair of dorsal fins is described below:

$$\begin{aligned}{} & {} \begin{aligned}&I_{z}\dot{r}+m[x_{g}(\dot{v}+ur)+y_{g}vr]\\&\quad =\frac{\rho }{2} l^{5}(N_{\dot{r}}\dot{r}+N_{r|r|}r|r|)+\frac{\rho }{2} l^{4}(N_{\dot{v}}\dot{v}+ N_{ur}ur)\\ {}&\qquad + \frac{\rho }{2} l^{3}(N_{uv}uv+N_{v|v|}v|v|)+N_{f} \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \begin{aligned}&m(\dot{v}+ur+x_{g}\dot{r}+y_{g}r^{2})\\&\quad =\frac{\rho }{2} l^{4}(Y_{\dot{r}}\dot{r}+Y_{r|r|}r|r|)+ \frac{\rho }{2} l^{3}(Y_{\dot{v}}\dot{v}+Y_{ur}ur)\\ {}&\qquad + \frac{\rho }{2} l^{2}(Y_{uv}uv+NY_{v|v|}v|v|)+F_{f} \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \dot{\psi }=r \end{aligned}$$

(31)

Here v is the sway velocity, $\psi$ is the yaw angle, and $F_{f}$ and $N_{f}$ are the net force and moment produced by the dorsal fin. A control mechanism keeps the forward velocity constant, and the heave is taken as zero. Nonlinear coefficients are eliminated from the analysis, and then the system will be

$$\begin{aligned}{} & {} \begin{bmatrix} (m-\frac{\rho }{2}l^{3} Y_{\dot{v}}) &{} (mx_{g}-\frac{\rho }{2}l^{4} Y_{\dot{r}}) \\ (mx_{g}-\frac{\rho }{2}l^{4} N_{\dot{v}}) &{} (I_{z}-\frac{\rho }{2}l^{5} N_{\dot{r}})\end{bmatrix} \begin{bmatrix} \dot{v} \\ \dot{r} \end{bmatrix} + \begin{bmatrix} mur \\ m x_{g}u \end{bmatrix} \begin{bmatrix} v \\ r \end{bmatrix} \nonumber \\{} & {} \qquad = \begin{bmatrix} N_{f} \\ F_{f} \end{bmatrix} \end{aligned}$$

(32)

The equation (32) is written as,

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} \dot{v} \\ \dot{r} \end{bmatrix} =- \begin{bmatrix} (m-\frac{\rho }{2}l^{3} Y_{\dot{v}}) &{} (mx_{g}-\frac{\rho }{2}l^{4} Y_{\dot{r}}) \\ (mx_{g}-\frac{\rho }{2}l^{4} N_{\dot{v}}) &{} (I_{z}-\frac{\rho }{2}l^{5} N_{\dot{r}})\end{bmatrix}^{-1} \begin{bmatrix} mur \\ m x_{g}u \end{bmatrix} \begin{bmatrix} v \\ r \end{bmatrix} \\ {}&\qquad \qquad + \begin{bmatrix} (m-\frac{\rho }{2}l^{3} Y_{\dot{v}}) &{} (mx_{g}-\frac{\rho }{2}l^{4} Y_{\dot{r}}) \\ (mx_{g}-\frac{\rho }{2}l^{4} N_{\dot{v}}) &{} (I_{z}-\frac{\rho }{2}l^{5} N_{\dot{r}})\end{bmatrix}^{-1} \begin{bmatrix} F_{f} \\ N_{f} \end{bmatrix} \end{aligned}\nonumber \\ \end{aligned}$$

(33)

This equation of the form of state space representation, $\dot{x}=Ax+Bu$, and the output equation will be,

$$\begin{aligned} y=\begin{bmatrix} 50&1 \end{bmatrix} \begin{bmatrix} v \\ r \end{bmatrix} \end{aligned}$$

(34)

where the values of C matrix is the value of $\tau _{Y}=50N$ and $\tau _{N}=1Nm$.

2.5 Ocean currents disturbances

For AUVs, ocean currents can be assumed to be the primary disturbance of the vehicle motion. Using Fossen’s methodology in marine disturbance modeling [27, 28], ocean currents can be represented in the equation of motion in terms of relative velocity ($v_r$) [28].

$$\begin{aligned} v_{r}=v-v_{c} \end{aligned}$$

(35)

Ocean current velocity is taken as a disturbance in the trajectory tracking control applications.

3 Trajectory tracking control design

AUV trajectory tracking or path following is a laborious field, and not many studies are conducted in this aspect [29]. An underwater vehicle must track the time parameterized trajectory, which is a geometric path with an associated temporal specification. In the proposed scenario, the plant/AUV system, ocean currents model, and hydrodynamics model blocks are only used to simulate trajectory tracking. Figure 6 describes the tracking system with the disturbance effect of AUV.

Fig. 6

Block diagram of trajectory tracking system with disturbance

3.1 PID controller-based trajectory tracking

PID controller is a linear and conventional controller used for trajectory tracking applications. The control deviation in the proposed system, a position error, is generated using the reference trajectory and actual trajectory [29]. The error e(t) is represented as

$$\begin{aligned} e(t)=T_\textrm{D}(t)-T_{o}(t) \end{aligned}$$

(36)

where $T_\textrm{D}(t)$ is the desired or reference trajectory and $T_{o}(t)$ is the actual trajectory. The control law of PID control is specified as follows:

$$\begin{aligned} u(t)=K_\textrm{P} e(t) + K_{i} \int _{0}^{t} e(t) dt + K_\textrm{D} \frac{d}{dt} e(t) \end{aligned}$$

(37)

where $K_\textrm{P}$, $K_\textrm{D}$, and $K_{i}$ are the gain parameters of the controller. PID controller with manual tuning method is used to obtain the system gain values. This is done by setting the reset time to its maximum value, and the rate to zero and increasing the gain until the loop oscillates at a constant amplitude [30]. The attained equation with gain values (37) with the absence and presence of current ocean disturbances using the manual tuning method is given as:

$$\begin{aligned}{} & {} \begin{aligned} y(t)&=1031.4 e(t) +766.14 \int e(t) dt \\&\quad + 11.75 \frac{d e(t)}{dt} \quad \text {without disturbance}\\ y(t)&=1830.54 e(t)+781.04 \int e(t) dt + 18.81 \frac{d e(t)}{dt} \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned}{} & {} \begin{aligned} y(t)&=2807.53 e(t) +264.84 \int e(t) dt\\&\quad + 27.92 \frac{d e(t)}{dt}\quad \text {with disturbance}\\ y(t)&=1937 e(t)+592.95 \int e(t) dt + 16.95 \frac{d e(t)}{dt} \end{aligned} \end{aligned}$$

(39)

A schematic diagram of PID tracking control for AUVs is illustrated in Fig. 7. The system generates the desired trajectory from the user inputs.

Fig. 7

Schematic diagram of PID controller-based trajectory system

3.2 Design of $H_\infty$ controller

The $H_\infty$ controller is a robust control technique that deals with improbability in its controller design approach. This controller design is based on the mixed-sensitivity method according to the control object model given by system representation equations. The main objective is to find the controller K that meets the requirements that minimize the disturbance output using minimum control energy.

$H_\infty$ Mixed sensitivity approach: The aim is to synthesize a controller which will ensure that the norm of the plant transfer function is bounded within limits. The formulation of a robust control problem [31] is depicted in Fig. 8. In the figure, G is the generalized plant, v is the measurement variables vector, u is the vector of all control variables, w is exogenous inputs, and z is the error variable.

Fig. 8

Robust control problem

The $H_\infty$ controller synthesis uses two transfer functions, sensitivity (S) and complimentary sensitivity ( T), in which the former explains stability and the latter says about performance. The S and T are given as,

$$\begin{aligned} \begin{aligned} S=\frac{1}{1+GK}\\ T=\frac{GK}{1+GK} \end{aligned} \end{aligned}$$

(40)

Now objective becomes minimizing the infinite norm; $W_s$ and $W_t$ are the weights given by the designer. Since the ultimate objective of the robust system is to avoid disturbance effect at the output, reduce S and its complementary function T [31]. It is achieved by making $\mid {S(j \omega )} \mid < \frac{1}{W_{s} (j \omega )}$ and $\mid T(j \omega ) \mid < \frac{1}{W_{t} (j \omega )}$. The weight functions are lead-lag compensators that can alter the system frequency response. Another method of limiting controller bandwidth and providing high-frequency gain is using high pass weight on an un-modeled dynamics uncertainty block. It may be added from the plant input to the plant output. The properties of this weighting function $W_ks$ are quite similar to the complementary sensitivity function. The mixed sensitivity problem is written as

$$\begin{aligned} P=\begin{bmatrix} W_{s} S \\ W_{ks} KS \\ W_{t} T \end{bmatrix} \end{aligned}$$

(41)

To find the controller K(s) and to make the closed loop system stable, the following expression is considered

$$\begin{aligned} min \Vert P\Vert = min \begin{bmatrix} W_{s} S \\ W_{ks} KS \\ W_{t} T \end{bmatrix} = \gamma \end{aligned}$$

(42)

where P is the transfer function from w to z;

$$\begin{aligned} \mid T_{wz} \mid = \gamma \end{aligned}$$

(43)

where $\mid T_{wz} \mid = P$ is the cost function. In order to make the $H_{\infty }$ norm of $\mid T_{zw} \mid$ less than unity [31], minimum gain theorem will be applied, i.e.,

$$\begin{aligned} min \Vert T_{zw}\Vert = min \begin{bmatrix} W_{s} S \\ W_{ks} KS \\ W_{t} T \end{bmatrix} <= 1 \end{aligned}$$

(44)

Solving the algebraic Riccati equations and reducing the cost function $\gamma$ can achieve the stabilizing controller K(s). The weights $W_s$, $W_{ks}$, and $W_t$ are the tuning parameters that typically require some iterations to obtain proper values, which yields a suitable controller.

In this study, the trajectory tracking plane dynamics of the vehicle are considered in the third order. Thus, the weighing functions $W_{S}$ and $W_{T}$ are designed as second-order low-pass and high-pass filters, respectively. The values are $W_{S}=\frac{58}{ s^{2}+8 s+ 13}$, $W_{T}=\frac{ s^{2}+15\,s+ 21}{268}$ in the absence of disturbance, and the control signal weighing function $W_{KS}$ is small in all the cases. Trajectory system with the presence of disturbance case, $W_{S}=\frac{207}{ s^{2}+11\,s+ 23}$ and $W_{T}=\frac{ s^{2}+24\,s+ 15}{391}$. Algorithms are coded in MATLAB, and the result are obtained. Figure 9 shows the schematic of H-infinity controller based trajectory tracking.

Fig. 9

Schematic diagram of $H_\infty$ controller based trajectory tracking system

3.3 Trajectory tracking using feedforward controller

A feedforward controller also can be used in the trajectory control system. Usually, a feedforward control mechanism is used to prevent problems before they occur. It acts when a disturbance happens without waiting for a deviation in the process variable. In order to do this, the controller produces its control action by measuring the disturbances. These controllers are always used along with feedback control because the feedback control system is required to track set point changes and suppress unmeasured disturbances in any natural process. There are different configurations for the feedforward control system. These configurations are used to find out suitable and most efficient trajectory for the AUV system [32]. Let the plant model be $G_p$, and disturbance model be $G_d$. Feedforward controller $C_{ff}=-(\frac{G_d}{Gp})$. Figure 10 shows the feedforward–feedback controller combination.

Fig. 10

Combined feedforward–feedback controller block diagram

4 Results and discussion

The simulations are implemented and validated using MathWorks MATLAB/Simulink. In order to verify the efficacy of the proposed trajectory tracking control system, simulations are carried out considering different predefined trajectories. The parameters of the model used in the simulation are listed in Table 6.

Table 6 Parameters of the model

Fig. 11

Trajectory tracking scenario of AUV using PID controller

Fig. 12

Trajectory tracking 3D curve scenario of AUV using PID controller

The parameters of this table are obtained from the CFD analysis [18] of the proposed underwater vehicle. All simulations take the initial value as zero, assuming that the vehicle is at rest.

In the first test scenario, a lemniscate (eight-shaped) trajectory in x-y has been generated with and without disturbances using PID controller manual tuning method illustrated in Fig. 11a and b. The blue curve is the desired trajectory, and the red curve is the actual trajectory of the proposed system. Reference trajectories are selected as of the form, $[A cos(\omega t); A sin(\frac{\omega t}{2} )]$ for a lemniscate path system scenario where A is the amplitude of the sine wave, which is taken as 5 units and the frequency, taken as 1 rad/sec.

Similarly, the three-dimensional reference trajectory is taken as the form $[A cos(\omega t); A sin(\omega t);t]$ with amplitude A is 1 unit and frequency taken as 1 rad/sec used for the analysis. Figure 12a and b describes x-y-z plane, three-dimensional trajectory with and without disturbances.

As the second test, an $H_\infty$ controller has been implemented for the same reference trajectories such as lemniscate and 3D curves. Closed-loop response simulation result of the $H_\infty$ controller for trajectory tracking, with and without disturbances, is illustrated in Fig. 13a and b.

Fig. 13

Trajectory tracking scenario of AUV using $H_\infty$ controller

Figure 14a and b describes x-y-z plane, three-dimensional trajectory with and without disturbances using $H_\infty$ controller.

Fig. 14

Trajectory tracking 3D curve scenario of AUV using $H_{\infty }$ controller

Feedforward controller is used for trajectory tracking systems to eliminate disturbance before it happens. It takes some anticipatory action to suppress the disturbance effect in the system. Figure 15a and b describes the trajectory scenario with and without disturbance of AUV using feedforward controller combined with a feedback controller.

Fig. 15

Trajectory tracking scenario of AUV using feedforward–feedback controller

Since the feedback controller is suitable for set-point tracking in general, the combined action of feedforward–feedback controller leads to enhanced performance. Figures 16 and 17 depict the combined action of feedforward–feedback controller. The two designs have identical performance for set-point tracking. However, the addition of feedforward control is beneficial for disturbance rejection, where Rsp1 and Rsp2 represent the set point, and d shows the disturbance in the figure below.

Fig. 16

Disturbance rejection scenario for AUV (sway motion)

Fig. 17

Disturbance rejection scenario for AUV (yaw motion)

Figure 18a and b illustrates x-y-z plane, three-dimensional trajectory with and without disturbances.

Fig. 18

Trajectory tracking 3D curve scenario of AUV using feedforward–feedback controller

A comparison study of proposed controllers: The time-domain specifications such as the rise time, settling time, and overshoot play a significant role in the analysis of control system performance. A comparison of performance measures of manual tuning PID controller with respect to $H_\infty$ controller and feedforward–feedback combination is provided in Table 7.

The values of settling time and overshoot are less in the feedforward controller compared to other controllers in both with and without disturbance cases. Similarly, the rise time is also low in the feedforward controller compared with the other controllers. Thus, it is clear from the results given in Table 7 that the performance of the vehicle is excellent while using feedforward controller compared to PID and $H_\infty$ controllers.

The parameter steady state error is the difference between the desired value and actual value when response has reached to steady state. This error representation using different controllers with and without sea current disturbance is given in Figs. 19, 20, 21. That is, the time history of steady-state errors of sway displacement (y) and yaw displacement $(\psi )$ can be seen in the following figures.

Table 7 Comparison of performance measure of controllers

Fig. 19

Trajectory tracking errors using PID controller

Fig. 20

Trajectory tracking errors using $H_\infty$ controller

Fig. 21

Trajectory tracking errors using feedforward controller

All the controllers in this study have acceptable transition characteristics and overshoot when the desired trajectory changes abruptly. Nevertheless, the proposed feedforward controller can obtain a better tracking accuracy after trajectory convergence.

Another comparison measure introduced in this work is performance indices such as ISE (integral square error), IAE (integral absolute error), and ITAE (integral time absolute error). Each of these indices calculates over some time interval, $0<t<T$. The time T is chosen to span much of the transient response, and here it is taken as $T=10s$. The obtained settling time of the proposed system is less than this T value. The performance index ITSE is not included in this analysis because it is less sensitive and computationally not comfortable. The illustration of performance indices with and without disturbance cases is given in Table 8.

Table 8 Performance indices comparison of controllers

The observations of indices from Table 8 show that the feedforward controller can produce exemplary results compared to all other controllers.

Comparison study of existing trajectory tracking AUV control systems: Several mathematical model control methodologies have been implemented in the trajectory tracking system of AUV, such as PID control, back-stepping control, sliding mode control, model predictive control, adaptive control, robust control, intelligent methods, etc. The efficiency of AUV trajectory tracking determines its operation accuracy. The main control performance indicators include accuracy, system response speed, stability, and robustness. Table 9 shows the performance comparison of different controllers in the field of AUV trajectory tracking.

Table 9 Comparison of trajectory tracking controllers

The analysis of the existing technology shows that the control strategies play a crucial role in trajectory tracking, which also affects the accuracy of underwater operations. In this analysis, the latest literature on the methodology of modeling methods and control strategies aimed at trajectory regulations has been systematically studied. It is concluded that most of the approximated models reported are an oversimplification of the AUV trajectory tracking systems, which are not useful for testing the behavior of the controllers under realistic conditions. Several control designs are producing modeling or tuning difficulties and precision errors. According to this study, a biomimetic underwater vehicle with a feedforward controller can improve outcomes compared with existing techniques. This theoretical contribution of control helps to boost operational performance and can also provide a steady speed of $u_{0}=2.57 m/s$ [35] with a propulsive efficiency of $78.74 \%$ [35]. However, the appropriate selection of biologically inspired models for underwater vehicles and the addition of more emerging technologies in this area for exceptional efficacy are still open problems that must be addressed in the short term.

5 Conclusion

This paper has considered the mathematical modeling and control of a Gertler geometric-shaped biomimetic AUV to produce a reference trajectory. Simulation results showed that the closed-loop system follows the different trajectories of distinct magnitudes, regardless of how PID controllers structured by the conventional technique give a slightly lousy performance. They also create poor robustness and high exceeding. A feedforward controller with feedback PID controller configuration and $H_\infty$ controller configuration is used for the system, producing more accurate results with minor errors even when current ocean disturbances are injected into the AUV system to overcome this problem. The feedforward controller configuration is giving a much better result.