1 Introduction

Nowadays AUVs are applied for surveying and monitoring some unreachable areas such as long pipe lines and surface of sea bottom in coastal areas. When an AUV is moving in shallow water, the disturbance of surface waves may cause severe roll motion on the vehicle. This harsh movement will damage the electrical equipments and other mechanisms like ballast pumps and driving motors. In addition, the effects of currents and other parameters, which are simplified on numerical calculations of the hydrodynamic coefficients of AUVs, are considerable near the free surface. Then, studying an effective control pattern for tackling with the problem of AUV motion control near the free surface is extremely necessary.

To stabilize the roll and limit the deviation of sway and yaw motions effectively, it is more convenient to use the stern plane and rudder as efficient actuators. To make effective roll stabilization and limit the deviation of sway and yaw, it is more convenient to employ a control law which produces a sufficient righting moment with stern planes and rudder motion. So, stern planes and rudder act as main actuators in this control law and in case of small AUVs there is no need for using fin stabilizer. On the other hand, in small AUVs the drag and wake generated by fin stabilizer can be diminished by applying this actuation method.

1.1 Literature review

Hydrodynamic analysis, maneuvering and navigation system design and motion control of AUVs have a vast literature. In this paper, topics of hydrodynamic coefficients, maneuvering simulation, and motion and trajectory control are investigated and reviewed in three distinct groups.

Until now, many projects have been carried out on hydrodynamic analysis and coefficient calculation of slender body AUVs. Fossen and Fjellstad [1] studied nonlinear modeling of marine vehicles in 6-DOF. Simulation and verification of a 6-DOF model for REMUS-AUV were carried out by Prestero [2]. The response sensitivity of an AUV in terms of variations of the hydrodynamic parameters is investigated by Perrault et al. [3]. Buckham et al. [4] described the development of a numerical model that accurately captured the dynamics of AUV. Working on modeling and performance evaluation of an AUV were carried out by Evans and Nahon [5]. Also, Issac et al. [6] planed some maneuvering experiments of MUN explorer AUV. Their purpose of these experiments was to collect a set of useful data for validating a hydrodynamic model of the vehicle. Unsteady rising maneuver of submarine in six degrees-of-freedom is studied by Watt [7]. Hydrodynamic analysis and maneuvering design of a test bed AUV named ISiMI is done by Jun et al. [8]. In addition, unsteady analysis of 6-DOF motion of a buoyantly rising submarine is studied by Bettle et al. [9]. Jinxin et al. [10] studied the hydrodynamic performance and motion simulation of an AUV considering its appendages. A simple online algorithm named incremental least square support vector machines (SVM) method is employed by Xu et al. [11] to identify the maneuvering parameters of AUV in diving plane. Studying maneuverability analysis of an AUV for deep-sea hydrothermal plume survey is carried out by Yi et al. [12]. Working on the fleet of the drag of prolate spheroids for determining the hydrodynamic effect of viscous interaction between hulls and to study the influence of the configurations shape of multiple hulls in the vee and echelon formulations is carried out by Rattanasiri et al. [13].

On the other hand, many researchers are focused on maneuvering simulation and motion investigation of these robots. Gertler and Hagen [14] presented standard equations of motion for submarine simulation. Nahon [15] modeled dynamic of streamline AUV. In his study the vehicle was decomposed into its elements including hull, control surfaces and propulsion system. Meanwhile, working on modeling and simulation of an AUV is done by Song et al. [16]. Ridley et al. [17] modeled AUV motions using nonlinear coefficients. Estimation of hydrodynamic coefficient and the control algorithm based on a nonlinear mathematical modeling for a test-bed AUV carried out by Kim and Choi [18]. Hegrenaes et al. [19] presented a simple and intuitive framework for obtaining steady-state maneuvering characteristics of a wide class of AUVs. Developing a test-bed AUV (named ISiMI) and applying some experiments on free running test and vision guided docking is carried out by Park et al. [20]. Also, Wang et al. [21] modeled a simulator for a mini AUV (named MAUV-II) in spatial motion. Studying a real time simulator for AUV development which simulated the motion and operation of main system of an AUV is addressed by Dantas and Barros [22]. Sanyal et al. [23] in their paper addressed the challenging control problem of tracking a desired continuous trajectory for maneuverable AUV in presence of gravity, buoyancy, and hydrodynamic forces and moments. Also, studying the captive model test of submerged body using computerized planar motion carriage (CPMC) is carried out by Kim et al. [24]. Philips et al. [25] investigated the maneuvering of an over-actuated AUV named Delphin2 which is a hover-capable AUV. Zhang et al. studied the motion equation in 6-DOF and analyzed the force and hydrodynamic coefficients of an AUV with fins in detail [26]. Meanwhile, Dantas et al. [27] released a real time simulator for AUV development which simulated the motion and operation of main system of an AUV. Also, Chen et al. [28] modeled AUV maneuvering and simulated the dynamic systems with Euler-Rodrigues quaternion method. Miller and Ellenrieder [29] modeled a simulator for an AUV-Towfish system. Studying a navigation system in order to estimate position, velocity and attitude of an AUV is addressed by Zanoni and Barros [30].

Furthermore, it should be indicated that working on exact tracking, path following and motion control of AUVs are always matters of concern for ocean engineers and marine control researchers. Healey and Lienard [31] designed a multivariable sliding mode autopilot based on state feedback to control maneuvering of an AUV including its steering and diving control. Meanwhile, Fjellstad and Fossen [32] designed a position and attitude tracking control law for AUV’s in 6-DOF. Studying a novel method for path following in AUVs is carried out by Encarnacao and Pascoal [33]. While, developing a multivariable optimal control for a semi-AUV is carried out by Jeon et al. [34]. Chen, Kouh, and Tsai [35] designed a simulator to model the guidance system based on line-of-sight (LOS) algorithm and horizontal plane PD controller. Subudhi et al. [36] presented a static output feedback control for path following of AUV in vertical plane. Position and orientation automatic control of an underwater vehicle without employing the previous knowledge of a dynamic model in control law is studied by Kuhn et al. [37] Ting et al. [38] worked on a wavelet-based grey particle filter for self-estimating trajectory of maneuvering AUV.

Among the researchers who worked on AUV motion control, considering wave disturbances, just some of them are focused on horizontal plane motions. Also, working on diving and course control of an AUV considering the presence of wave disturbances is carried out by Moreira and Soares [39]. They also developed a linear 6-DOF motion simulator. Liu et al. [40] worked on nonlinear observer–controller for station keeping of AUV in shallow water. They also worked on a non-linear output feedback tracking controller for AUVs operating in coastal areas [41].

Kamarlouei developed a control system for horizontal plane motions of the AUV in his master thesis [42] and this paper presents a part of this thesis. In this paper a 6-DOF maneuvering simulator is developed and the stability check through maneuvering simulation is carried out. Then a feedback linearization method is used for transforming the nonlinear system to a pseudo-linear one and then a H ∞ method is applied to resist against wave disturbance and uncertainties of dynamic system.

2 Maneuvering simulation and stability analysis

In this section, an AUV, entitled ISiMI, is considered as a sample vehicle for verification in nonlinear equation derivation and 6-DOF dynamic simulator design. Then the canonical form of feedback linearization function is achieved from AUV nonlinear equations. Nonlinear coefficients of this underwater vehicle are obtained through the dotcom method [42] and verified with experimental results from reference [20].

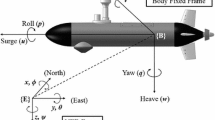
We can consider three displacements along x, y and z-axes which are respectively named as surge, sway and heave and also three rotations about x, y and z-axes which are respectively named as, roll, pitch and yaw for a 6-DOF underwater vehicle. Figure 1 shows the reference coordinate system and rigid body coordinate system. In this figure, three displacements and three rotational movements are shown for a slender-body AUV. It should be noted that the underwater vehicle’s body is considered as rigid body and in other words, flexibility and superficial strains of the body are disregarded since regarding these equations makes the problem more complicated and adds no more accuracy to it. On the other hand, these simplifications can be considered as a term of unknown variables or un-modeled hydrodynamics as an imperfection in control design. Geometrical and physical data of simulating model are presented in Table 1.

Fig. 1
figure 1

Reference coordinates and 6 DOF coordinates of AUV

Full size image
Table 1 Geometrical and physical data of simulating model
Full size table

After defining the mentioned variables for each of the different degrees of freedom of AUV, nonlinear equations can be taken into account. The first degree of freedom is force along x-axis as Eq. (1), likewise, force along y-axis is given in Eq. (2) and force along z-axis is also given in Eq. (3), as follows:

$$\begin{aligned} \left( {m - X_{{\dot{u}}} } \right)\dot{u} + mz_{g} \dot{q} - my_{g} \dot{r} = & X_{\text{HS}} + X_{u\left| u \right|} u\left| u \right| + \left( {X_{wq} - m} \right)wq + \left( {X_{qq} + mx_{g} } \right)q^{2} \\ & + \left( {X_{vr} + m} \right)vr + \left( {X_{rr} + mx_{g} } \right)r^{2} - mz_{g} pr + X_{\text{prop}} \\ \end{aligned}$$
(1)
$$\begin{aligned} \left( {m - Y_{{\dot{v}}} } \right)\dot{v} + mz_{g} \dot{p} - \left( {mx_{g} - Y_{{\dot{r}}} } \right)\dot{r} = & Y_{\text{HS}} + Y_{v\left| v \right|} v\left| v \right| + Y_{r\left| r \right|} r\left| r \right| + my_{g} r^{2} + \left( {Y_{ur} - m} \right)ur \\ & + \left( {Y_{wp} + m} \right)wp + \left( {Y_{pq} - mx_{g} } \right)pq + Y_{uv} uv + my_{g} p^{2} + mz_{g} qr + Y_{uu\delta r} u^{2} \delta_{r} \\ \end{aligned}$$
(2)
$$\begin{aligned} \left( {m - Z_{{\dot{w}}} } \right)\dot{w} + my_{g} \dot{p} - \left( {mx_{g} + Z_{{\dot{q}}} } \right)\dot{q} = & Z_{\text{HS}} + Z_{w\left| w \right|} w\left| w \right| + Z_{q\left| q \right|} q\left| q \right| + \left( {Z_{uq} + m} \right)uq \\ & + \left( {Z_{vp} - m} \right)vp + \left( {Z_{rp} - mx_{g} } \right)rp + Z_{uw} uw + mz_{g} \left( {p^{2} + q^{2} } \right) - my_{g} rq + Z_{uu\delta s} u^{2} \delta_{s} \\ \end{aligned}$$
(3)

After defining non-linear equations for three linear movements of underwater vehicle along the coordinate axes, non-linear equations of three rotating about coordinate axis should be stated. In this way, non-linear equations for rotating motion about x, y and z are respectively achieved in Eqs. (4), (5) and (6) [2].

$$\begin{aligned} - mz_{g} \dot{v} + my_{g} \dot{w} + \left( {I_{xx} - K_{{\dot{p}}} } \right)\dot{p} &= K_{\text{HS}} + K_{p\left| p \right|} p\left| p \right| - \left( {I_{zz} - I_{yy} } \right)qr + m\left( {uq - vp} \right) \\ & \\quad - mz_{g} \left( {wp - ur} \right) + K_{\text{prop}} \\ \end{aligned}$$
(4)
$$\begin{aligned} mz_{g} \dot{u} - \left( {mx_{g} + M_{{\dot{w}}} } \right)\dot{w} + \left( {I_{yy} - M_{{\dot{q}}} } \right)\dot{q} &= M_{HS} + M_{w\left| w \right|} w\left| w \right| + M_{q\left| q \right|} q\left| q \right| + \left( {M_{uq} - mx_{g} } \right)uq \\ & \quad + \left( {M_{vp} + mx_{g} } \right)vp + \left[ {M_{rp} - \left( {I_{xx} - I_{zz} } \right)} \right]rp \\ \end{aligned}$$
(5)
$$\begin{aligned} my_{g} \dot{u} - \left( {mx_{g} + N_{{\dot{v}}} } \right)\dot{v} + \left( {I_{zz} - N_{{\dot{r}}} } \right)\dot{r} &= N_{HS} + N_{v\left| v \right|} v\left| v \right| + N_{r\left| r \right|} r\left| r \right| + \left( {N_{ur} - mx_{g} } \right)ur \\ & \quad + \left( {N_{wp} + mx_{g} } \right)wp + \left[ {N_{pq} - \left( {I_{yy} - I_{xx} } \right)} \right]pq - my_{g} \left( {vr - wq} \right)\\&\quad + N_{uv} uv + N_{uu\delta r} u^{2} \delta_{r} \\ \end{aligned}$$
(6)

After achieving nonlinear equations, the matrix form of the equation can be presented in Eq. (7):

$$\left[ {\begin{array}{*{20}c} {m - X_{{\dot{u}}} } & 0 & 0 & 0 & {mz_{G} - X_{{\dot{q}}} } & { - my_{G} - X_{{\dot{r}}} } \\ 0 & {m - Y_{{\dot{v}}} } & 0 & { - mz_{G} - Y_{{\dot{p}}} } & 0 & {mx_{G} - Y_{{\dot{r}}} } \\ 0 & 0 & {m - Z_{{\dot{w}}} } & {my_{G} - Z_{{\dot{p}}} } & { - mx_{G} - Z_{{\dot{q}}} } & 0 \\ 0 & { - mz_{G} - Y_{{\dot{p}}} } & {my_{G} - Z_{{\dot{p}}} } & {I_{x} - K_{{\dot{p}}} } & { - I_{xy} - K_{{\dot{q}}} } & 0 \\ {mz_{G} - X_{{\dot{q}}} } & 0 & { - mx_{G} - Z_{{\dot{q}}} } & 0 & {I_{y} - M_{{\dot{q}}} } & 0 \\ { - my_{G} - X_{{\dot{r}}} } & {mx_{G} - Y_{{\dot{r}}} } & 0 & 0 & 0 & {I_{z} - N_{{\dot{r}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{w}} \\ {\dot{p}} \\ {\dot{q}} \\ {\dot{r}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum X } \\ {\sum Y } \\ {\sum Z } \\ {\sum K } \\ {\sum M } \\ {\sum N } \\ \end{array} } \right]$$
(7)

where, X, Y, Z and K, M, N are external forces and moments, respectively. Equation (7) is expressed as:

$$\left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{w}} \\ {\dot{p}} \\ {\dot{q}} \\ {\dot{r}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {m - X_{{\dot{u}}} } & 0 & 0 & 0 & {mz_{G} - X_{{\dot{q}}} } & { - my_{G} - X_{{\dot{r}}} } \\ 0 & {m - Y_{{\dot{v}}} } & 0 & { - mz_{G} - Y_{{\dot{p}}} } & 0 & {mx_{G} - Y_{{\dot{r}}} } \\ 0 & 0 & {m - Z_{{\dot{w}}} } & {my_{G} - Z_{{\dot{p}}} } & { - mx_{G} - Z_{{\dot{q}}} } & 0 \\ 0 & { - mz_{G} - Y_{{\dot{p}}} } & {my_{G} - Z_{{\dot{p}}} } & {I_{x} - K_{{\dot{p}}} } & { - I_{xy} - K_{{\dot{q}}} } & 0 \\ {mz_{G} - X_{{\dot{q}}} } & 0 & { - mx_{G} - Z_{{\dot{q}}} } & 0 & {I_{y} - M_{{\dot{q}}} } & 0 \\ { - my_{G} - X_{{\dot{r}}} } & {mx_{G} - Y_{{\dot{r}}} } & 0 & 0 & 0 & {I_{z} - N_{{\dot{r}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sum X } \\ {\sum Y } \\ {\sum Z } \\ {\sum K } \\ {\sum M } \\ {\sum N } \\ \end{array} } \right]$$
(8)

This matrix equation is solved by a time domain solver [42]. To achieve the speed matrix from acceleration in Eq. (8), 2nd order Runge–Kutta is employed in Eq. (9).

$$\left[ {\begin{array}{*{20}c} u \\ v \\ w \\ p \\ q \\ r \\ \end{array} } \right]_{{t_{0} + \delta t}} = \delta t \cdot \frac{1}{2} \cdot \left( {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{w}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{p}} \\ {\dot{q}} \\ {\dot{r}} \\ \end{array} } \\ \end{array} } \right]_{{(t_{0} + \delta t)}} + \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{w}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{p}} \\ {\dot{q}} \\ {\dot{r}} \\ \end{array} } \\ \end{array} } \right]_{{\left( {t_{0} } \right)}} } \right) + \left[ {\begin{array}{*{20}c} u \\ v \\ w \\ p \\ q \\ r \\ \end{array} } \right]_{{t_{0} }}$$
(9)

Then the position is achieved by Eq. (10) as follows:

$$\left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \phi \\ \theta \\ \psi \\ \end{array} } \right]_{{t_{0} + \delta r}} = \delta t \cdot \left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ {\dot{z}} \\ {\dot{\phi }} \\ {\dot{\theta }} \\ {\dot{\psi }} \\ \end{array} } \right]_{{t_{0} }} + \left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \phi \\ \theta \\ \psi \\ \end{array} } \right]_{{t_{0} }}$$
(10)

where, [x, y, z, ϕ, θ, ψ] are surge, sway, heave, roll, pitch and yaw motions of the AUV, respectively. Meanwhile, the block diagram of motion calculation is illustrated in Fig. 2. It is generally known that a precise control simulation is tied to an accurate maneuvering modeling.

Fig. 2
figure 2

Flowchart of motion simulation

Full size image

Firstly, for modification of the simulator results, a turning test is simulated and compared with ISiMI AUV model test. As it can be seen in Fig. 3, the steady turning radius for both experimental and simulation results are approximately equal to 6 m. While the difference between start points of turning is due to different control rules in experiment and simulation.

Fig. 3
figure 3

Verification of simulation with experimental turning test [20] of ISiMI AUV

Full size image

In addition, in this paper new algorithms [28] are applied for investigating the directional and straight-line stability of AUV. On the other hand, for testing the AUV’s straight-line stability in the horizontal plane, the pull-out maneuver is commanded for ISiMI AUV:

2.1 Pull-out test

  1. 1.

    Assuming that the AUV starts with initial conditions in \(\left[ {\begin{array}{*{20}c} \phi & \theta & \psi \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right]^{T}\) and with zero rudder angles.

  2. 2.

    Then rudder angle changes to \(\delta_{d} = 15^{^\circ }\) at timestamp t δ1 = 100.

  3. 3.

    Yaw rate r(t) changes unsteadily.

  4. 4.

    Yaw rate r(t) reaches the steady state whit in the tolerance error \(\dot{r}\left( t \right) \le 10^{ - 5}\).

  5. 5.

    Rudder goes back to its initial condition at timestamp t = t δ2 until the AUV reaches its final trimmed state the tolerance error \(\left( {t_{f} \cong 175 {\text{s}}} \right)\).

  6. 6.

    If \(\mathop {\lim }\nolimits_{{t \to t_{f} }} r\left( t \right) \le 10^{ - 5}\) and \(\mathop {\lim }\nolimits_{{t \to t_{f} }} \psi \left( t \right) = {\text{Const}}.,\) the AUV satisfies the straight stability condition.

All of the mentioned procedures are illustrated in the Fig. 4.

Fig. 4
figure 4

Rudder command in put-out test and variables including yaw angle ψ and rate r(t)

Full size image

2.2 Put-out test

  1. 7.

    The rudder angle changes inversely to \(\delta_{d} = - 15^{^\circ }\) at timestamp t δ3 = 200.

  2. 8.

    Yaw rate r(t) changes unsteadily

  3. 9.

    Yaw rate reaches the steady state. (such as step 4)

  4. 10.

    Rudder angle changes to its initial condition at timestamp t δ4 = 255 until the AUV reaches to its final trimmed state the tolerance error \(\dot{r}\left( t \right) \le 10^{ - 5}\) and \(\left( {t_{{f_{2} }} \cong 275 {\text{s}}} \right)\).

  5. 11.

    If \(\mathop {\lim }\nolimits_{{t \to t_{{f_{2} }} }} r\left( t \right) \le 10^{ - 5}\) and \(\mathop {\lim }\nolimits_{{t \to t_{{f_{2} }} }} \left| {\psi \left( t \right)} \right| \le \chi^{ \circ }\), where χ is the maximum tolerance angle, the AUV satisfies directional stability.

Also, Fig. 5 shows the spiral test of AUV as an extra maneuvering test. The trajectories of the robot in put-out test (Fig. 6) and spiral test (Fig. 7) give us an understanding on the course-change and course-keeping abilities of AUV. It should be indicated that the AUV’s steady velocity in turning and pull-out tests is u = 0.6 m/s. In addition, the tactical diameter of turning is the same amount of \(\left( {{\raise0.7ex\hbox{${D_{\text{turning}} }$} \!\mathord{\left/ {\vphantom {{D_{\text{turning}} } {L_{\text{AUV}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${L_{\text{AUV}} }$}} = {\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} {1.2}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1.2}$}} = 10} \right)\).

Fig. 5
figure 5

Rudder command in spiral test and variables including yaw angle ψ and rate r(t)

Full size image
Fig. 6
figure 6

Trajectory of robot in put-out test

Full size image
Fig. 7
figure 7

Trajectory of robot in spiral test

Full size image

3 Feedback linearization

In this paper, a feedback linearization control law is considered for controlling the vehicle in near-surface cruising. At first, for controlling the horizontal plane motion, Eq. (8) should be decoupled. Then the canonical form for feedback linearization is generated as follows:

$$\left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{v}} \\ {\dot{p}} \\ {\dot{r}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } & {b_{13} } \\ {b_{21} } & {b_{22} } & {b_{23} } \\ {b_{31} } & {b_{32} } & {b_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} v \\ p \\ r \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} + M_{\text{wave}} + M_{s} } \\ {F_{3} + M_{\delta } } \\ \end{array} } \right]$$
(11)

where \(\left[ {v,p,r} \right] = \left[ {\dot{D}_{s} ,\dot{\phi },\dot{\psi }} \right]\) and F i are known external forces illustrated in Eq. (14) while M wave, M s and M δ are wave moment as disturbance and righting moments due to stern plane and rudder deflections, respectively. Furthermore, a ij and b ij are calculated based on AUVs’ hydrodynamic coefficients as Eqs. (12) and (13), respectively:

$$a = \left[ {\begin{array}{*{20}c} {m - Y_{{\dot{v}}} } & { - \left( {mz_{G} + Y_{{\dot{p}}} } \right)} & {mx_{G} - Y_{{\dot{r}}} } \\ { - \left( {mz_{G} + K_{{\dot{v}}} } \right)} & {I_{x} - K_{{\dot{p}}} } & { - \left( {I_{xz} + K_{{\dot{r}}} } \right)} \\ {mx_{G} - N_{{\dot{v}}} } & { - \left( {I_{xz} + N_{{\dot{p}}} } \right)} & {I_{z} - N_{{\dot{r}}} } \\ \end{array} } \right]$$
(12)
$$b = \left[ {\begin{array}{*{20}c} {Y_{v} } & {Y_{p} - X_{{\dot{w}}} u} & {Y_{r} + \left( {X_{{\dot{u}}} - m} \right)u} \\ {K_{v} + X_{{\dot{w}}} u} & {K_{p} } & {K_{r} - X_{{\dot{u}}} u} \\ {N_{v} + \left( {m - X_{{\dot{u}}} } \right)u} & {N_{p} + X_{{\dot{u}}} u} & {N_{r} } \\ \end{array} } \right]$$
(13)
$$F = \left[ {\begin{array}{*{20}c} {\left( {mx_{G} - Z_{{\dot{p}}} } \right)p^{2} - Y_{{\dot{w}}} vp + \left( {X_{{\dot{p}}} - Z_{{\dot{r}}} } \right)pr + \left( {my_{G} + X_{{\dot{r}}} } \right)r^{2} + X_{{\dot{v}}} vr} \\ {\left( {Z_{{\dot{p}}} - mx_{G} } \right)pv - Y_{{\dot{w}}} v^{2} + \left( {Z_{{\dot{r}}} - Y_{{\dot{q}}} } \right)pr + \left( {M_{{\dot{r}}} - I_{yz} } \right)r^{2} - \left( {K_{{\dot{q}}} + I_{xy} } \right)pr + z_{G} W\phi } \\ {\left( {my_{G} + X_{{\dot{r}}} } \right)vr - X_{{\dot{v}}} v^{2} + \left( {Y_{{\dot{q}}} - X_{{\dot{p}}} } \right)pv + \left( {M_{{\dot{r}}} + I_{yz} } \right)pr + \left( {K_{{\dot{q}}} + I_{xy} } \right)p^{2} } \\ \end{array} } \right]$$
(14)

Also, the wave moment is calculated based on single-parameter Pierson–Moskowitz spectrum as Eq. (15) which is a well-known nonlinear wave spectrum in AUV dynamic control considering ocean disturbances. It is generally known that wave disturbance affects underwater vehicles’ motion up to 10.55 m depth. In this paper, the wave spectrum is divided into 30 wave bands, and then the wave moment is evaluated through summation of wave moments in each wave band (δω) as Eq. (16). The wave spectrum and flow chart for the calculation of the moment caused by the waves are illustrated in Figs. 8 and 9, respectively.

Fig. 8
figure 8

Pierson–Moskowitz spectrum with 30 bands and 20 directions

Full size image
Fig. 9
figure 9

Flow chart for the calculation of the moment caused by the waves

Full size image
$$S\left( \omega \right) = \frac{{8.1 \times 10^{ - 3} g^{2} }}{{\omega^{5} }}\exp \left[ {\frac{ - 3.11}{{H_{s}^{2} \omega^{4} }}} \right]$$
(15)
$$M_{\text{wave}} \left( t \right) = \mathop \sum \limits_{i = 1}^{N} M_{{{\text{wave}}_{i} }} \left( t \right) = - \mathop \sum \limits_{i = 1}^{N} C_{M} L\nabla \rho \left( {1 - 0.02u\,{ \cos }\,\gamma } \right) \text{sgn} \left( {\cos \gamma } \right)F_{i} \cos \left( {\omega_{{e_{i} }} t} \right)$$
(16)

where:

$$F_{i} = a_{i}^{2} \omega_{i}^{2} \exp \left[ {\frac{{ - \omega_{i}^{2} h\left( t \right)}}{g}} \right] \quad {\text{and}}\quad a_{i} = \left[ {2S_{{\left( {w_{{e_{i} }} } \right)}} \delta \omega } \right]^{\frac{1}{2}}$$
(17)

On the other hand, the righting moments, M s and M δ are calculated as follows:

$$M_{s} = L_{\text{fin}} l_{f} = \frac{\rho }{2}l^{3} u^{2} l_{f} \left( {K_{{\delta_{ss} }} \delta_{ss} - K_{{\delta_{sp} }} \delta_{sp} } \right)$$
(18)
$$M_{\delta } = \frac{\rho }{2}l^{3} u^{2} N_{\delta r} \delta_{r}$$
(19)

where, δ r is the rudder angle and δ ss and δ sp are the angle of deflection in starboard and port side of the AUV, respectively. Meanwhile, Fig. 10 shows how these moments work on AUV. Also, the fin parameters of Eqs. (18) and (19) are mentioned in Table 2. After defining the components, the Eq. (11) can be transformed into Eq. (20):

$$\left[ {\begin{array}{*{20}c} {\dot{v}} \\ {\dot{p}} \\ {\dot{r}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } \\ {c_{21} } & {c_{22} } & {c_{23} } \\ {c_{31} } & {c_{32} } & {c_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} v \\ p \\ r \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {d_{11} } & {d_{12} } & {d_{13} } \\ {d_{21} } & {d_{22} } & {d_{23} } \\ {d_{31} } & {d_{32} } & {d_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} + M_{wave} + M_{fin} } \\ {F_{3} + M_{\delta } } \\ \end{array} } \right]$$
(20)
$$\left\{ \begin{array} {ll}\dot{x} = A_{1} x + B_{1} u_{c} + \left( {B_{1} F + B_{1} u_{n} } \right) \hfill \\ y = C_{1} x \hfill \\ \end{array} \right.$$
(21)

where, \(\left[ {c_{ij} } \right] = \left[ {a_{ij} } \right]^{ - 1} \left[ {b_{ij} } \right], \, \left[ {d_{ij} } \right] = \left[ {a_{ij} } \right]^{ - 1}\) and the state variable \(x = \left[ {\begin{array}{*{20}c} v & p & r & {D_{s} } & \phi & \psi \\ \end{array} } \right]^{T}\), the output variable \(y = \left[ {\begin{array}{*{20}c} {D_{s} } & \phi & \psi \\ \end{array} } \right]^{T}\), the disturbance \(u_{n} = \left[ {\begin{array}{*{20}c} 0 & {M_{\text{wave}} } & 0 \\ \end{array} } \right]^{T}\) and the input of control system is \(u_{c} = \left[ {\begin{array}{*{20}c} 0 & {M_{s} } & {M_{\delta } } \\ \end{array} } \right]^{T}\). In addition, parameters in state space equation are considered as follows:

$$A_{1} = \left[ {\begin{array}{*{20}c} {\left[ {c_{ij} } \right]} & {0_{3 \times 3} } \\ {I_{3 \times 3} } & {0_{3 \times 3} } \\ \end{array} } \right],$$

\(B_{1} = \left[ {\begin{array}{*{20}c} {\left[ {d_{ij} } \right]} \\ {0_{3 \times 3} } \\ \end{array} } \right],\) \(C_{1} = \left[ {\begin{array}{*{20}c} {0_{3 \times 3} } & {I_{3 \times 3} } \\ \end{array} } \right],\) \(F = \left[ {\begin{array}{*{20}c} {F_{1} } & {F_{2} } & {F_{3} } \\ \end{array} } \right]^{T}\)

Fig. 10
figure 10

Righting moments due to control surface motions

Full size image
Table 2 Characteristics of control surface
Full size table

Then uncertainties in hydrodynamic coefficients are considered due to underwater currents and unknown parameters in calculation of these coefficients. So, Eq. (21) is separated as nominal and uncertain terms, viz.

$$\left\{ \begin{array}{ll} \dot{x} = \left( {A_{1}^{*} + \Delta A_{1} } \right)x + \left( {B_{1}^{*} + \Delta B_{1} } \right)u_{c} + \left[ {\left( {B_{1}^{*} + \Delta B_{1} } \right)F + \left( {B_{1}^{*} + \Delta B_{1} } \right)u_{n} } \right] \hfill \\ y = C_{1} x \hfill \\ \end{array} \right.$$
(22)

where \(A_{1}^{*}\) and \(B_{1}^{*}\) are nominal terms calculated through numerical or experimental methods while \(\Delta B_{1} = B_{1} - B_{1}^{*}\) and \(\Delta A_{1} = A_{1} - A_{1}^{*}\). Then with defining \(f\left( x \right) = A_{1}^{*} x + B_{1}^{*} F\) and \(g = B_{1}^{*}\) the other terms, \(\Delta f\left( x \right) = \Delta A_{1} x + \Delta B_{1} F + \left( {B_{1}^{*} + \Delta B_{1} } \right)u_{n}\) and Δg = ΔB 1, will generate uncertainties in state space equation. So the Eq. (22) can be transformed to Eq. (23).

$$\left\{ \begin{aligned} \dot{x} = f\left( x \right) + \Delta f\left( x \right) + \left( {g + \Delta g} \right)u_{c} \hfill \\ y = h\left( x \right) \hfill \\ \end{aligned} \right.$$
(23)

where, h(x) = C 1 x.

Although there is no sufficient manner to calculate Δf(x) and Δg, they can be considered as bounded values from the result of limited inputs in physical system. So, disturbance is supposed to fulfill the matching condition, \(\Delta f\left( x \right) = g \cdot m\left( x \right)\quad {\text{and}}\quad \Delta g = g \cdot n\left( x \right)\), where:

$$m\left( x \right) = \left[ {d_{ij}^{*} } \right]^{ - 1} \Delta f\left( x \right)\quad n\left( x \right) = \left[ {d_{ij}^{*} } \right]^{ - 1} \left[ {\Delta d_{ij} } \right]$$
(24)

So, with removing uncertainties, Eq. (23) turns to the following simple feedback linearization problem.

$$\left\{ \begin{aligned} \dot{x} = f\left( x \right) + gu_{c} \hfill \\ y = h\left( x \right) \hfill \\ \end{aligned} \right.$$
(25)

After checking the controllability and involutivity of Eq. (25) the relative degree of nominal system is calculated through continuous differentiation of system output y until system input u c appears. So, based on Eq. (27) the relative degree of each output is 2 and the whole relative degree of system is 6.

$$L_{{g_{i} }} h_{j} \left( x \right) = 0 \left( {i = 1, 2, 3;\quad j = 1, 2, 3} \right)$$
(26)
$$\textit{\"{y}} = \left[ {\begin{array}{*{20}c} {\textit{\"{D}}_{s} } \\ {\ddot{\phi }} \\ {\ddot{\psi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {L_{f}^{2} h_{1} \left( x \right)} \\ {L_{f}^{2} h_{2} \left( x \right)} \\ {L_{f}^{2} h_{3} \left( x \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {L_{{g_{1} }} L_{f} h_{1} \left( x \right)} & {L_{{g_{2} }} L_{f} h_{1} \left( x \right)} & {L_{{g_{3} }} L_{f} h_{1} \left( x \right)} \\ {L_{{g_{1} }} L_{f} h_{2} \left( x \right)} & {L_{{g_{2} }} L_{f} h_{2} \left( x \right)} & {L_{{g_{3} }} L_{f} h_{2} \left( x \right)} \\ {L_{{g_{1} }} L_{f} h_{3} \left( x \right)} & {L_{{g_{2} }} L_{f} h_{3} \left( x \right)} & {L_{{g_{3} }} L_{f} h_{3} \left( x \right)} \\ \end{array} } \right]u_{c} = B_{2} + A_{2} u_{c}$$
(27)

where, \(u_{c} = A_{2}^{ - 1} \left( { - B_{ 2} + u_{e} } \right)\) which \(u_{e} = - k_{r - 1} y^{r - 1} - \cdots - k_{1} \dot{y} - k_{0} y\) is the equivalent control input. It should be added that k i are selected so that \(K\left( s \right) = s^{r} + k_{r - 1} s^{r - 1} + \cdots + k_{1} s + k_{0}\) is Hurwitz. As a normal feedback linearization method, the genetic algorithm method is employed to achieve the best and optimized gains. So three constraints are considered including sway, roll and yaw amplitudes. On the other hand, to consider the effect of uncertainty and disturbance terms as Δf(x) and Δg, system in Eq. (23) should be transferred to following system:

$$\left\{ \begin{aligned} \dot{z} = A_{3} z + B_{3} \left[ {A_{2} m\left( x \right) - A_{2} n\left( x \right)A_{2}^{ - 1} B_{2} } \right] + B_{3} \left[ {I_{3 \times 3} + A_{2} n\left( x \right)A_{2}^{ - 1} } \right]u_{e} \hfill \\ y = C_{3} z \hfill \\ \end{aligned} \right.$$
(28)

where, \(z = \left[\begin{array}{llllll} h_{1} \left( x \right) & L_{f} h_{1} \left( x \right) & h_{2} \left( x \right) & L_{f} h_{2} \left( x \right) & h_{3} \left( x \right) & L_{f} h_{3} \left( x \right)\\ \end{array}\right] = \left[ \begin{array}{llllll} D_{s} & v & \phi & p & \psi & r \end{array}\right]\) and A 3, B 3 and C 3 are achieved through considering conditions in [43]. Now, robust control should be designed for transformed system in Eq. (28). Then controller designed for system Eq. (23) can be achieved by inverse coordinate transformation.

4 Robustification

Based on state feedback control designed in Eq. (28), S and KS are sensitivity function and sensitivity control function which guarantee the capacity of the system for facing with parameter uncertainties and limit the amplitude of control input in presence of known wave disturbance, respectively. Also, S and KS functions are indicated in Eqs. (29) and (30).

$$S = \left\{ {I_{3 \times 3} - K\left( {sI_{6 \times 6} - A_{3} } \right)^{ - 1} B_{3} \left[ {I_{3 \times 3} + A_{2} m\left( x \right)B_{2}^{ - 1} } \right]} \right\}^{ - 1}$$
(29)
$$KS = K^{\prime}\left\{ {I_{3 \times 3} - K\left( {sI_{6 \times 6} - A_{3} } \right)^{ - 1} B_{3} \left[ {I_{3 \times 3} + A_{2} m\left( x \right)B_{2}^{ - 1} } \right]} \right\}^{ - 1}$$
(30)

Sensitivity function can be introduced as a transfer function from reference input to tracking error while Control sensitivity function is considered as a transfer function from reference input to controller output. In Eq. (29), s is complex variable of Laplace Transform and K 3×6 is the gain matrix of state feedback as Eq. (31).

$$K = \left[ {\begin{array}{*{20}c} {K_{1} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {K_{2} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {K_{3} } & 0 \\ \end{array} } \right]\quad u_{e} = - Kz , K^{\prime} = \left[ {\begin{array}{*{20}c} {K_{1} } & 0 & 0 \\ 0 & {K_{2} } & 0 \\ 0 & 0 & {K_{3} } \\ \end{array} } \right]$$
(31)

According to robust theory of H ∞ method the most important consideration is to choose the reasonable weighted functions described by W 1(s) and W 2(s) considering following conditions:

$$\left\| \begin{array}{l} W_{1} \left( s \right) \cdot S \hfill \\ W_{2} \left( s \right) \cdot KS \hfill \\ \end{array} \right\|_{\infty } \le 1$$
(32)

and

$$L_{a} \left[ {S\left( {j\omega } \right)} \right] \le L_{a} \left[ {W_{1}^{ - 1} \left( {j\omega } \right)} \right]$$
(33)
$$L_{a} \left[ {KS\left( {j\omega } \right)} \right] \le L_{a} \left[ {W_{2}^{ - 1} \left( {j\omega } \right)} \right]$$
(34)

where, L a (.) denotes logarithm of amplitude of defined parameters.

It should be indicated that, W 1(s) is the weight of S and its amplitude arranges the system capacity on damping the parameters uncertainties and disturbances. Also W 2(s) is the weight of KS and limits the controller output in high frequency. Therefore, W 1(s) and W 2(s) can be considered as low-pass and high-pass filters, respectively. Furthermore, Fig. 11 shows the robustifying progress, where the error signal is \(\bar{e} = y_{\text{ref}} - y\)and the controller input signal is \(e = \bar{e} + n\). So, e is achieved by superposition of error signal and sensor noise. Additionally, Δ is the parametric uncertain term.

Fig. 11
figure 11

Robust process in presence of noise and uncertainties

Full size image

As mentioned before, K 1, K 2 and K 3 are determined based on pole placement of close loop system according to achieve desired performance for tracking of sway, roll and yaw motion. After that, S and KS are calculated through Eqs. (29) and (30). Then, inequalities of Eqs. (33) and (34) are checked and if those equations are not satisfied simultaneously, these gains should be reset. Finally the gains are applied in control law \(u_{c} = A_{2}^{ - 1} \left( { - B_{2} + u_{e} } \right)\). So u e and control law of original system is obtained through Eq. (35).

$$u_{c} = A_{2}^{ - 1} \left( { - B_{2} - Kz} \right)$$
(35)

5 Simulation results

To simulate the harshest condition for roll moment, the wave characteristics such as encounter angle γ and significant wave height are considered 90° and 1 m, respectively. Furthermore, other physical properties of simulation are mentioned in Table 1. It should be added that the mission depth and speed of AUV are considered as 10 m and 0.7 m/s, respectively. Moreover, the properties of control surfaces are indicated in Table 2. To model the uncertain terms of hydrodynamic coefficients in Eq. (11) the following sin functions are applied:

$$\begin{array}{*{20}l} {\Delta m = 0.04\left[ {1 + \sin \left( {0.1t} \right)} \right]m^{*} } \hfill & {\Delta I_{(.)} = 0.1\left[ {1 + \sin \left( {0.2t} \right)} \right]I_{(.)}^{*} } \hfill \\ {\Delta X_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]X_{(.)}^{*} } \hfill & {\Delta Y_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]Y_{(.)}^{*} } \hfill \\ {\Delta Z_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]Z_{(.)}^{*} } \hfill & {\Delta K_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]K_{(.)}^{*} } \hfill \\ {\Delta M_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]M_{(.)}^{*} } \hfill & {\Delta N_{(.)} = 0.08\left[ {1 + \sin \left( {0.2t} \right)} \right]N_{(.)}^{*} } \hfill \\ \end{array}$$

where, the sum of nominal values and uncertain terms for some hydrodynamic coefficients are illustrated in the Fig. 12. As it can be seen, uncertainty in mass moment I xx and added mass coefficients such as \(X_{{\dot{u}}}\), \(K_{{\dot{p}}}\), \(Y_{{\dot{v}}}\), \(M_{{\dot{w}}}\) and \(N_{{\dot{r}}}\) are shown in the Fig. 12.

Fig. 12
figure 12

The sum of uncertainties and nominal terms of some non-dimensional hydrodynamic coefficients

Full size image

The variation of sway, roll and yaw motions applying feedback linearization control law is shown in the Fig. 13a, c, e. However, Fig. 13b, d, f illustrates the effect of robust control on these motions, respectively. As can be seen in this figure, applying robust technique reduced the sway deviations to 25 % of feedback linearization method. Meanwhile, it reduced the roll deviations to one-third of feedback linearization method and yaw motion is reduced effectively to one-eighth of feedback linearization method. In addition, the deflections of rudder and stern plane angles are shown in Fig. 13g, h, respectively. In addition, the results in Table 3 show the performance of control system for sway, roll and yaw controlling with H ∞ approach.

Fig. 13
figure 13

Deflections of sway, roll and yaw with simple feedback linearization controller (a), (c) and (e) and with robust controller (b), (d) and (f) and deflection of rudder and stern plane fines (g) and (h)

Full size image
Table 3 Performance of robust control for sway, roll and yaw motion
Full size table

6 Conclusions

In this paper, a 6-DOF nonlinear dynamic simulator is developed for AUVs to control for horizontal plane motions. After defining a control mode on stern planes and rudder of the AUV, a simple state feedback control and a robust control is applied for horizontal plane motions. It should be indicated that, the gains in non-robust control system is tuned applying an evolutionary strategy. However, the constraints for optimization are considered as minimum deviations of sway, roll and yaw. The results show that the deviations of AUV motions in presence of uncertainties are reduced by robust control, effectively. While un-modeled hydrodynamics and wave disturbances as the main uncertainties in the problem are not resisted by feedback linearization method.